Dark Matter in Fractional Gravity III: Dwarf Galaxies Kinematics
Abstract
:1. Introduction
2. Methods
2.1. Dark Matter in Fractional Gravity
2.2. Dynamical Modeling
2.3. Data and Bayesian Analysis
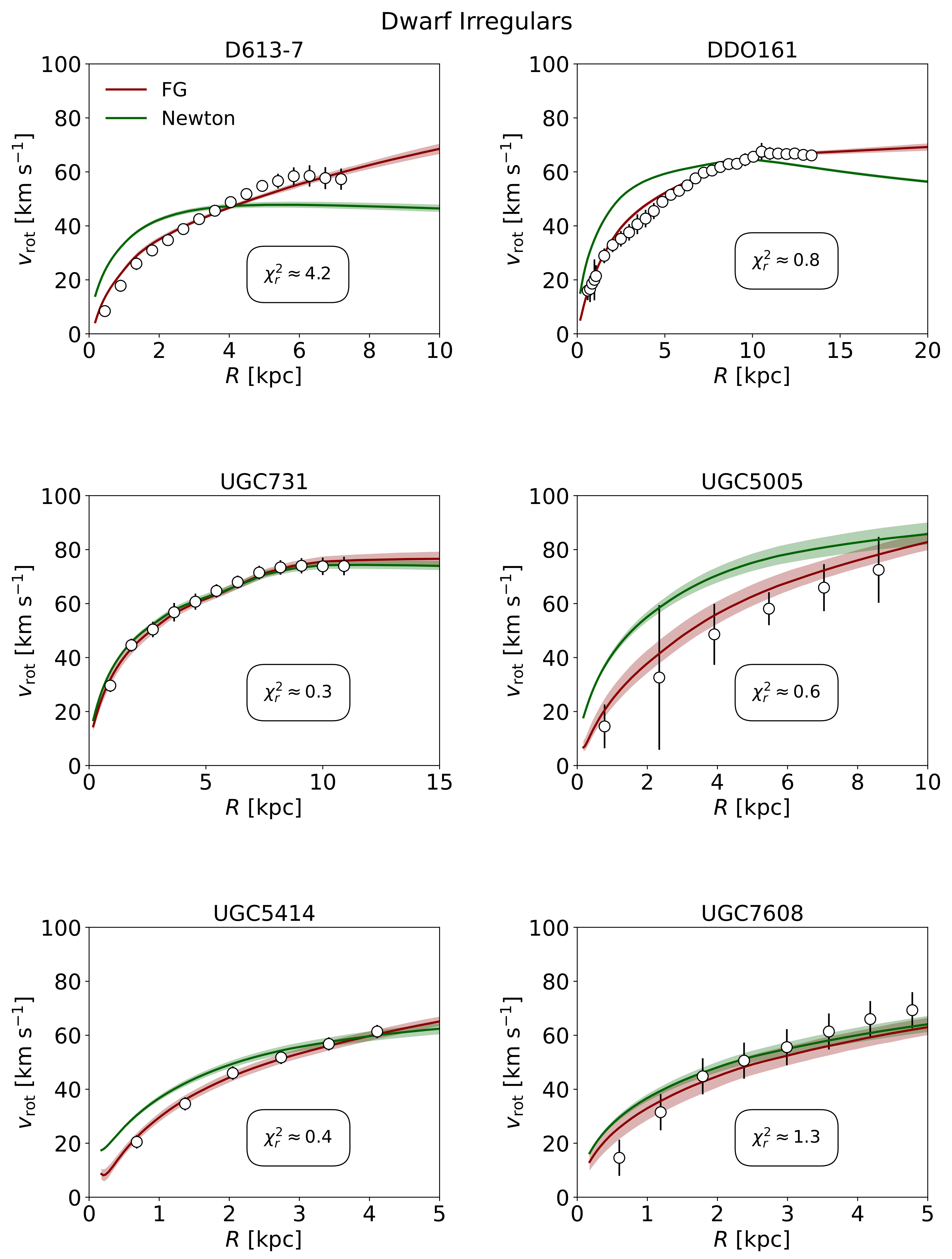
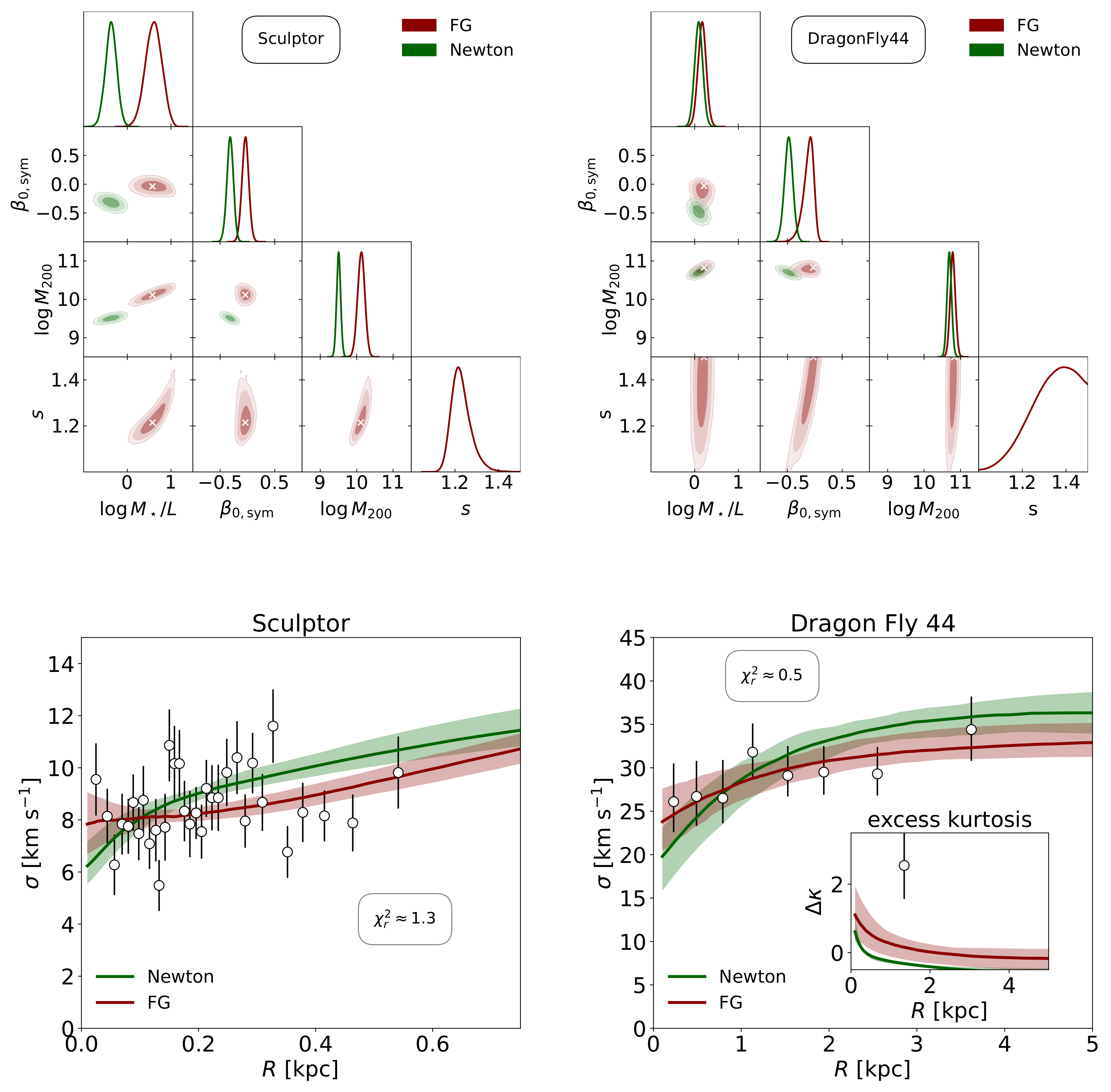
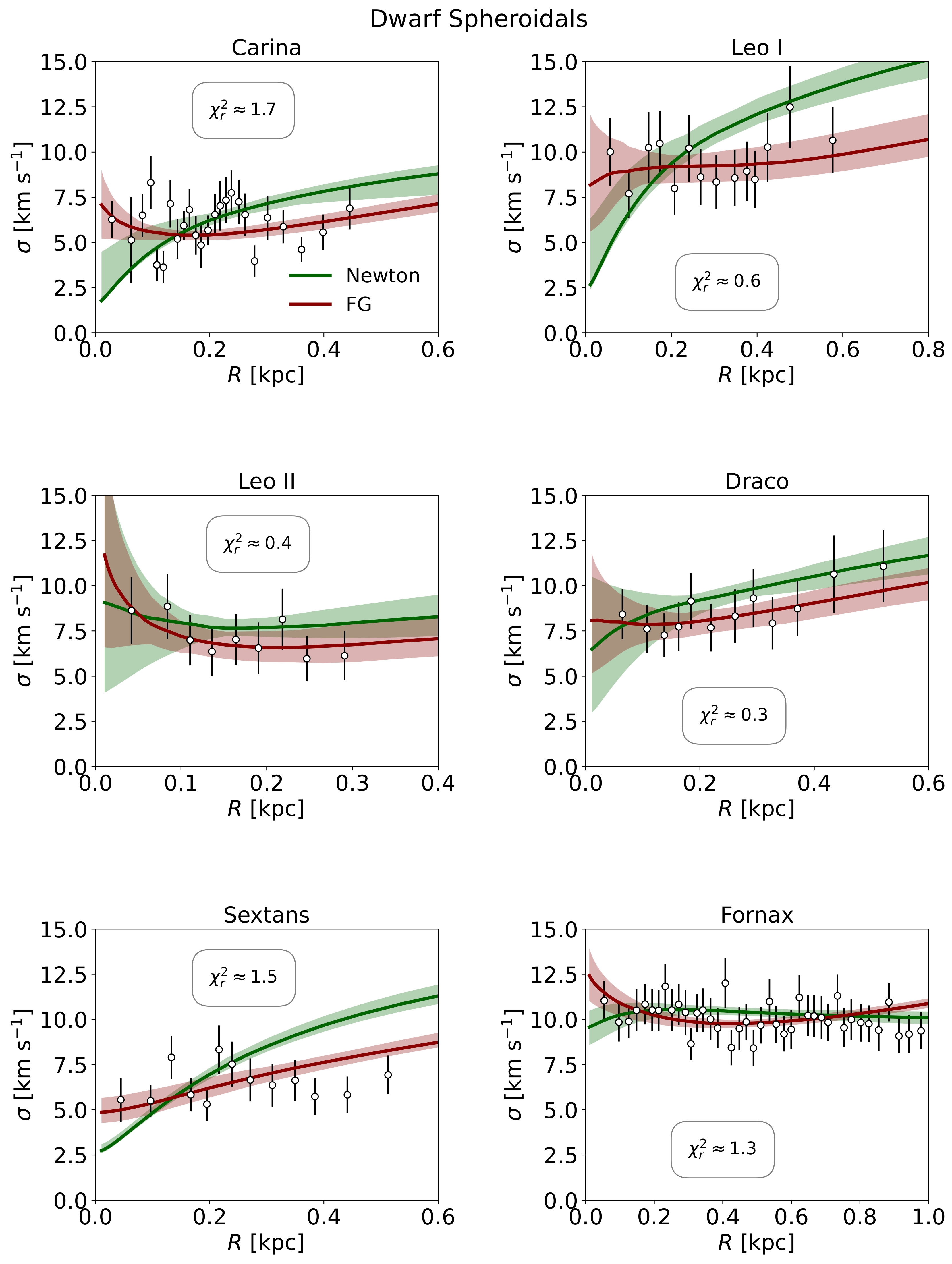
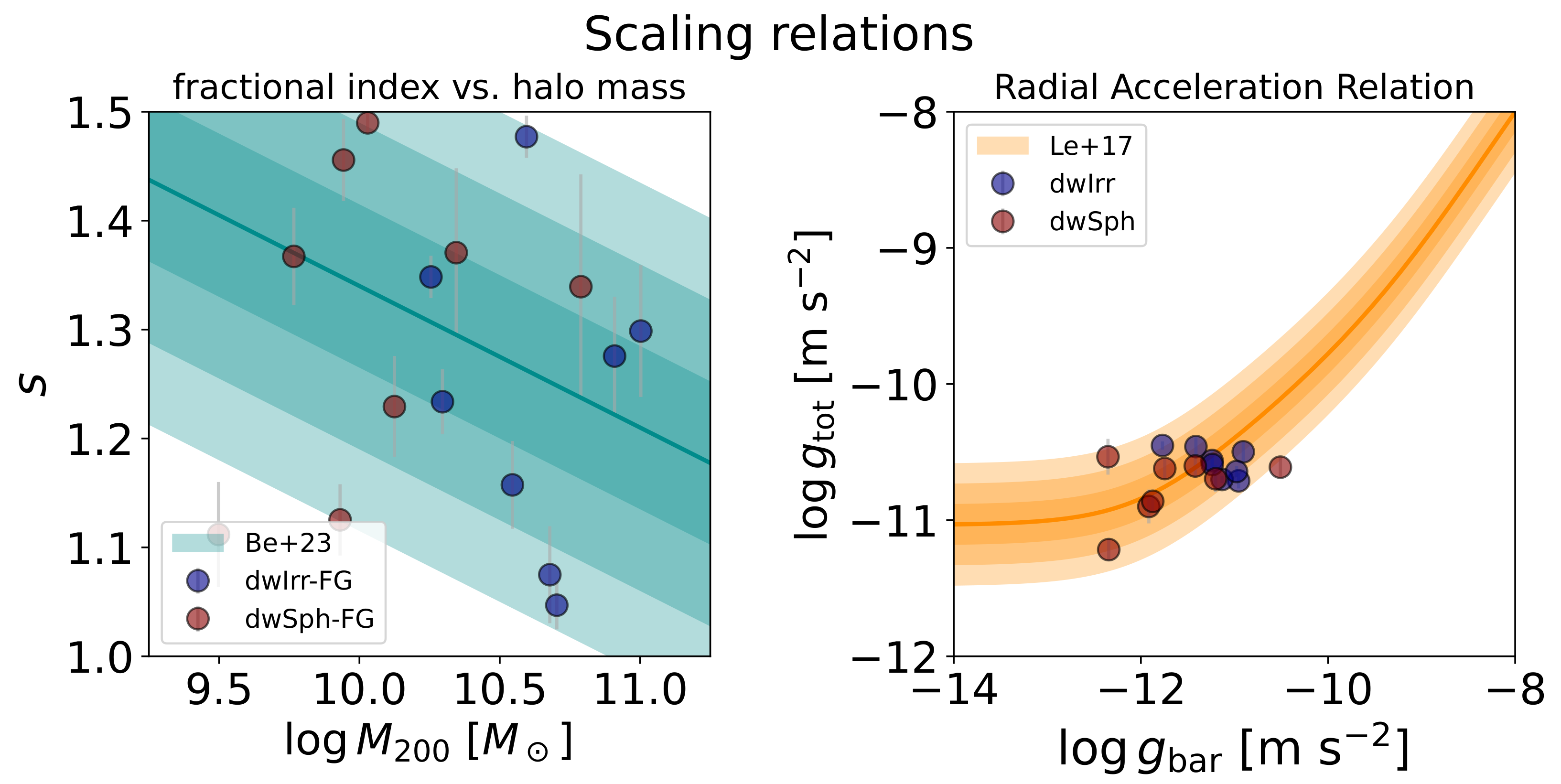
3. Results
4. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Projection Integrals
References
- Rubin, V.C.; Ford, W.K., Jr.; Thonnard, N. Rotational properties of 21 Sc galaxies with a large range of luminosities and radii, from NGC 4605 (R=4 kpc) to UGC 2885 (R=122 kpc). Astrophys. J. 1996, 281, 27. [Google Scholar] [CrossRef]
- Persic, M.; Salucci, P.; Stel, F. The universal rotation curve of spiral galaxies—I. The dark matter connection. Mon. Not. R. Astron. Soc. 1980, 238, 471. [Google Scholar]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493. [Google Scholar] [CrossRef]
- Dutton, A.A.; Maccio, A.V. Cold dark matter haloes in the Planck era: Evolution of structural parameters for Einasto and NFW profiles. Mon. Not. R. Astron. Soc. 2014, 441, 3359. [Google Scholar] [CrossRef]
- Wang, J.; Bose, S.; Frenk, C.S.; Gao, L.; Jenkins, A.; Springel, V.; White, S.D.M. Universal structure of dark matter haloes over a mass range of 20 orders of magnitude. Nature 2020, 585, 39. [Google Scholar] [CrossRef]
- Flores, R.A.; Primack, J.R. Observational and Theoretical Constraints on Singular Dark Matter Halos. Astrophys. J. 1994, 427, L1. [Google Scholar] [CrossRef]
- Gentile, G.; Salucci, P.; Klein, U.; Vergani, D.; Kalberla, P. The cored distribution of dark matter in spiral galaxies. Mon. Not. R. Astron. Soc. 2004, 351, 903. [Google Scholar] [CrossRef]
- De Blok, W.J.G.; Walter, F.; Brinks, E.; Trachternach, C.; Oh, S.-H.; Kennicutt, R.C., Jr. High-Resolution Rotation Curves and Galaxy Mass Models from THINGS. Astron. J. 2008, 136, 2648. [Google Scholar] [CrossRef]
- Oh, S.-H.; Hunter, D.A.; Brinks, E.; Elmegreen, B.G.; Schruba, A.; Walter, F.; Rupen, M.P.; Young, L.M.; Simpson, C.E.; Johnson, M.C.; et al. High-resolution Mass Models of Dwarf Galaxies from LITTLE THINGS. Astron. J. 2015, 149, 1800. [Google Scholar] [CrossRef]
- Bullock, J.S.; Boylan-Kolchin, M. Small-Scale Challenges to the ΛCDM Paradigm. Ann. Rev. Astron. Astrophys. 2017, 55, 343. [Google Scholar] [CrossRef]
- Klypin, A.; Kravtsov, A.V.; Valenzuela, O.; Prada, F. Where Are the Missing Galactic Satellites? Astrophys. J. 1999, 522, 82. [Google Scholar] [CrossRef]
- Moore, B.; Ghigna, S.; Governato, F.; Lake, G.; Quinn, T.; Stadel, J.; Tozzi, P. Dark Matter Substructure within Galactic Halos. Astrophys. J. 1999, 524, L19. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Bullock, J.S.; Kaplinghat, M. The Milky Way’s bright satellites as an apparent failure of ΛCDM. Mon. Not. R. Astron. Soc. 2012, 422, 1203. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Lelli, F.; Schombert, J.M. Radial Acceleration Relation in Rotationally Supported Galaxies. Phys. Rev. Lett. 2016, 117, 1101. [Google Scholar] [CrossRef] [PubMed]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M.; Pawlowski, M.S. One Law to Rule Them All: The Radial Acceleration Relation of Galaxies. Astrophys. J. 2017, 836, 152. [Google Scholar] [CrossRef]
- Donato, F.; Gentile, G.; Salucci, P.; Frigerio Martins, C.; Wilkinson, M.I.; Gilmore, G.; Grebel, E.K.; Koch, A.; Wyse, R. A constant dark matter halo surface density in galaxies. Mon. Not. R. Astron. Soc. 2009, 397, 1169. [Google Scholar] [CrossRef]
- Donato, F.; Gentile, G.; Salucci, P. Cores of dark matter haloes correlate with stellar scalelengths. Mon. Not. R. Astron. Soc. 2009, 353, L17. [Google Scholar] [CrossRef]
- Oman, K.A.; Navarro, J.F.; Fattahi, A.; Frenk, C.S.; Sawala, T.; White, S.D.M.; Bower, R.; Crain, R.A.; Furlong, M.; Schaller, M.; et al. The unexpected diversity of dwarf galaxy rotation curves. Mon. Not. R. Astron. Soc. 2009, 452, 3650. [Google Scholar] [CrossRef]
- Pontzen, A.; Governato, F. Cold dark matter heats up. Nature 2014, 506, 171. [Google Scholar] [CrossRef]
- Freundlich, J.; Dekel, A.; Jiang, F.; Ishai, G.; Cornuault, N.; Lapiner, S.; Dutton, A.A.; Maccio, A.V. A model for core formation in dark matter haloes and ultra-diffuse galaxies by outflow episodes. Mon. Not. R. Astron. Soc. 2020, 491, 4253. [Google Scholar] [CrossRef]
- El-Zant, A.; Shlosman, I.; Hoffman, Y. Dark Halos: The Flattening of the Density Cusp by Dynamical Friction. Astrophys. J. 2001, 560, 636. [Google Scholar] [CrossRef]
- Tonini, C.; Lapi, A.; Salucci, P. Angular Momentum Transfer in Dark Matter Halos: Erasing the Cusp. Astrophys. J. 2006, 649, 591. [Google Scholar] [CrossRef]
- Bode, P.; Ostriker, J.P.; Turok, N. Halo Formation in Warm Dark Matter Models. Astrophys. J. 2001, 556, 93. [Google Scholar] [CrossRef]
- Lovell, M.; Frenk, C.S.; Eke, V.R.; Jenkins, A.; Gao, L.; Theuns, T. The properties of warm dark matter haloes. Mon. Not. R. Astron. Soc. 2014, 439, 300. [Google Scholar] [CrossRef]
- Hu, W.; Barkana, R.; Gruzinov, A. Fuzzy Cold Dark Matter: The Wave Properties of Ultralight Particles. Phys. Rev. Lett. 2000, 85, 1158. [Google Scholar] [CrossRef]
- Hui, L.; Ostriker, J.P.; Tremaine, S.; Witten, E. Ultralight scalars as cosmological dark matter. Phys. Rev. D 2017, 95, 3541. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Zavala, J.; Cyr-Racine, F.-Y.; Pfrommer, C.; Bringmann, T.; Sigurdson, K. ETHOS-An effective theory of structure formation: Dark matter physics as a possible explanation of the small-scale CDM problems. Mon. Not. R. Astron. Soc. 2016, 460, 1399. [Google Scholar] [CrossRef]
- McDermott, S.D.; Witte, S.J. Cosmological evolution of light dark photon dark matter. Phys. Rev. D 2020, 101, 3030. [Google Scholar] [CrossRef]
- Bolton, J.S.; Caputo, A.; Liu, H.; Viel, M. Comparison of Low-Redshift Lyman-α Forest Observations to Hydrodynamical Simulations with Dark Photon Dark Matter. Phys. Rev. Lett. 2022, 129, 1102. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rev. 2004, 405, 279. [Google Scholar] [CrossRef]
- Adhikari, R.; Agostini, M.; Ky, N.A.; Araki, T.; Archidiacono, M.; Bahr, M.; Baur, J.; Behrens, J.; Bezrukov, F.; Bhupal Dev, P.S.; et al. A White Paper on keV sterile neutrino Dark Matter. Journ. Cosmol. Astropart. Phys. 2017, 1, 25. [Google Scholar] [CrossRef]
- Salucci, P.; Esposito, G.; Lambiase, G.; Battista, E.; Benetti, M.; Bini, D.; Boco, L.; Sharma, G.; Bozza, V.; Buoninfante, L.; et al. Einstein, Planck and Vera Rubin: Relevant encounters between the Cosmological and the Quantum Worlds. Front. Phys. 2021, 8, 603190. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified gravity and cosmology. Phys. Rep. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Lazkoz, R.; Salzano, V.; Moniz, P.V.; Capozziello, S.; Beltran, J.J.; De Laurentis, M.; Olmo, G.J. Modified Gravity and Cosmology: An Update by the CANTATA Network; Springer International Publishing: Cham, Switzerland, 2021; ISBN 978-3-030-83715-0. [Google Scholar]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 2017, 270, 365. [Google Scholar] [CrossRef]
- Famaey, B.; McGaugh, S.S. Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions. Liv. Rev. Relat. 2012, 15, 10. [Google Scholar] [CrossRef]
- Varieschi, G.U. Newtonian Fractional-Dimension Gravity and MOND. Found. Phys. 2020, 50, 1608. [Google Scholar] [CrossRef]
- Varieschi, G.U. Newtonian fractional-dimension gravity and rotationally supported galaxies. Mon. Not. R. Astron. Soc. 2021, 503, 1915. [Google Scholar] [CrossRef]
- Giusti, A. MOND-like fractional Laplacian theory. Phys. Rev. D 2020, 101, 124029. [Google Scholar] [CrossRef]
- Giusti, A.; Garrappa, R.; Vachon, G. On the Kuzmin model in fractional Newtonian gravity. EPJP 2020, 135, 798. [Google Scholar] [CrossRef]
- Calcagni, G.; Varieschi, G.U. Gravitational potential and galaxy rotation curves in multi-fractional spacetimes. J. High Energy Phys. 2022, 8, 24. [Google Scholar] [CrossRef]
- Verlinde, E.P. Emergent Gravity and the Dark Universe. Sci. Post. Phys. 2017, 2, 16. [Google Scholar] [CrossRef]
- Yoon, Y.; Park, J.-C.; Hwang, H.S. Understanding galaxy rotation curves with Verlinde’s emergent gravity. Class. Quant. Grav. 2023, 40, 02LT01. [Google Scholar] [CrossRef]
- Benetti, F.; Lapi, A.; Gandolfi, G.; Salucci, P.; Danese, L. Dark Matter in Fractional Gravity I: Astrophysical Tests on Galactic Scales. Astrophys. J. 2023, 949, 65. [Google Scholar] [CrossRef]
- Benetti, F.; Lapi, A.; Gandolfi, G.; Haridasu, B.S.; Danese, L. Dark Matter in Fractional Gravity II: Tests in Galaxy Clusters. Universe 2023, 9, 329. [Google Scholar] [CrossRef]
- Gandolfi, G.; Lapi, A.; Liberati, S. Self-gravitating Equilibria of Non-minimally Coupled Dark Matter Halos. Astrophys. J. 2021, 910, 76. [Google Scholar] [CrossRef]
- Gandolfi, G.; Lapi, A.; Liberati, S. Empirical Evidence of Nonminimally Coupled Dark Matter in the Dynamics of Local Spiral Galaxies? Astrophys. J. 2022, 929, 48. [Google Scholar] [CrossRef]
- Gandolfi, G.; Haridasu, B.S.; Liberati, S.; Lapi, A. Looking for Traces of Non-minimally Coupled Dark Matter in the X-COP Galaxy Clusters Sample. Astrophys. J. 2023, 952, 105. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. [Planck Collaboration]. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers: Background and Theory; Nonlinear Physical Science, Higher Education Press: Beijing, China; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-33910-3. [Google Scholar]
- Gomez-Aguilar, J.F.; Rosales-Garcıa, J.J.; Bernal-Alvarado, J.J.; Cordova-Fraga, T.; Guzman-Cabrera, R. Fractional mechanical oscillators. Riv. Mex. Phys. 2012, 58, 348. [Google Scholar]
- Ebaid, A.; El-Zahar, E.R.; Aljohani, A.F.; Salah, B.; Krid, M.; Tenreiro Machado, J. Analysis of the two-dimensional fractional projectile motion in view of the experimental data. Nonlin. Dynam. 2019, 97, 1711. [Google Scholar] [CrossRef]
- Pranjivan Mehta, P.; Pang, G.; Song, F.; Em Karniadakis, G. Discovering a Universal Variable-Order Fractional Model for Turbulent Couette Flow Using a Physics-informed Neural Network. Fract. Calc. Appl. Analys. 2019, 22, 6. [Google Scholar]
- Binney, J. Dynamics of elliptical galaxies and other spheroidal components. Ann. Rev. Astron. Astrophys. 1982, 20, 399. [Google Scholar] [CrossRef]
- Lokas, E.L.; Mamon, G.A. Properties of spherical galaxies and clusters with an NFW density profiles. Mon. Not. R. Astron. Soc. 2001, 321, 155. [Google Scholar] [CrossRef]
- Plummer, H.C. On the problem of distribution in globular star clusters. Mon. Not. R. Astron. Soc. 2001, 71, 460. [Google Scholar] [CrossRef]
- Van Dokkum, P.; Wasserman, A.; Danieli, S.; Abraham, R.; Brodie, J.; Conroy, C.; Forbes, D.A.; Martin, C.; Matuszewski, M.; Romanowsky, A.J.; et al. Spatially Resolved Stellar Kinematics of the Ultra-diffuse Galaxy Dragonfly 44. I. Observations, Kinematics, and Cold Dark Matter Halo Fits. Astrophys. J. 2019, 880, 91. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M. SPARC: Mass Models for 175 Disk Galaxies with Spitzer Photometry and Accurate Rotation Curves. Astron. J. 2016, 152, 157. [Google Scholar] [CrossRef]
- Li, P.; Lelli, F.; McGaugh, S.; Schombert, J. A Comprehensive Catalog of Dark Matter Halo Models for SPARC Galaxies. Astrophys. J. Suppl. Ser. 2020, 247, 31. [Google Scholar] [CrossRef]
- Walker, M.G.; Mateo, M.; Olszewski, E.W. Stellar Velocities in the Carina, Fornax, Sculptor, and Sextans dSph Galaxies: Data From the Magellan/MMFS Survey. Astron. J. 2009, 137, 3100. [Google Scholar] [CrossRef]
- Mateo, M.; Olszewski, E.W.; Walker, M.G. The Velocity Dispersion Profile of the Remote Dwarf Spheroidal Galaxy Leo I: A Tidal Hit and Run? Astrophys. J. 2009, 675, 201. [Google Scholar] [CrossRef]
- De Martino, I.; Diaferio, A.; Ostorero, L. Dynamics of dwarf galaxies in f(R) gravity. Mon. Not. R. Astron. Soc. 2023, 519, 4424. [Google Scholar] [CrossRef]
- Leisman, L.; Haynes, M.P.; Janowiecki, S.; Hallenbeck, G.; Jozsa, G.; Giovanelli, R.; Adams, E.A.K.; Bernal Neira, D.; Cannon, J.M.; Janesh, W.F.; et al. (Almost) Dark Galaxies in the ALFALFA Survey: Isolated H I-bearing Ultra-diffuse Galaxies. Astrophys. J. 2017, 842, 133. [Google Scholar] [CrossRef]
- Mancera Pina, P.E.; Fraternali, F.; Oman, K.A.; Adams, E.A.K.; Bacchini, C.; Marasco, A.; Oosterloo, T.; Pezzulli, G.; Posti, L.; Leisman, L.; et al. Robust H I kinematics of gas-rich ultra-diffuse galaxies: Hints of a weak-feedback formation scenario. Mon. Not. R. Astron. Soc. 2020, 495, 3636. [Google Scholar] [CrossRef]
- Mancera Piña, P.E.; Aguerri, J.A.L.; Peletier, R.F.; Venhola, A.; Trager, S.; Choque Challapa, N. The evolution of ultra-diffuse galaxies in nearby galaxy clusters from the Kapteyn IAC WEAVE INT Clusters Survey. Mon. Not. R. Astron. Soc. 2019, 485, 1036. [Google Scholar] [CrossRef]
- Sengupta, C.; Scott, T.C.; Chung, A.; Wong, O.I. Dark matter and H I in ultra-diffuse galaxy UGC 2162. Mon. Not. R. Astron. Soc. 2019, 488, 3222. [Google Scholar] [CrossRef]
- Van Dokkum, P.G.; Abraham, R.; Merritt, A.; Zhang, J.; Geha, M.; Conroy, C. Forty-seven Milky Way-sized, Extremely Diffuse Galaxies in the Coma Cluster. Astrophys. J. 2015, 798, L45. [Google Scholar] [CrossRef]
- Wasserman, A.; van Dokkum, P.; Romanowsky, A.J.; Brodie, J.; Danieli, S.; Forbes, D.A.; Abraham, R.; Martin, C.; Matuszewski, M.; Villaume, A.; et al. Spatially Resolved Stellar Kinematics of the Ultra-diffuse Galaxy Dragonfly 44. II. Constraints on Fuzzy Dark Matter. Astrophys. J. 2019, 885, 155. [Google Scholar] [CrossRef]
- Julio, M.P.; Brinchmann, J.; Zoutendijk, S.L.; Read, J.I.; Vaz, D.; Kamann, S.; Krajnovic, D.; Boogaard, L.A.; Steinmetz, M.; Bouche, N. The MUSE-Faint survey. V. Constraining Scalar Field Dark Matter with Antlia B. Astron. Astrophys. 2023, 678, A38. [Google Scholar] [CrossRef]
- Bell, E.F.; de Jong, R.S. Stellar Mass-to-Light Ratios and the Tully-Fisher Relation. Astrophys. J. 2001, 550, 212. [Google Scholar] [CrossRef]
- Portinari, L.; Sommer-Larsen, J.; Tantalo, R. On the mass-to-light ratio and the initial mass function in disc galaxies. Mon. Not. R. Astron. Soc. 2004, 346, 691. [Google Scholar] [CrossRef]
- Schombert, J. McGaugh, S. Lelli, F. The mass-to-light ratios and the star formation histories of disc galaxies. Mon. Not. R. Astron. Soc. 2019, 483, 1496. [Google Scholar]
- Moster, B.P.; Naab, T.; White, S.D.M. Galactic star formation and accretion histories from matching galaxies to dark matter haloes. Mon. Not. R. Astron. Soc. 2013, 428, 3121. [Google Scholar] [CrossRef]
- Lange, J.U.; van den Bosch, F.C.; Zentner, A.R.; Wang, K.; Villarreal, A.S. Updated results on the galaxy-halo connection from satellite kinematics in SDSS. Mon. Not. R. Astron. Soc. 2019, 487, 3112. [Google Scholar] [CrossRef]
- Lapi, A.; Salucci, P.; Danese, L. Precision Scaling Relations for Disk Galaxies in the Local Universe. Astrophys. J. 2018, 859, 2. [Google Scholar] [CrossRef]
- Mandelbaum, R.; Wang, W.; Zu, Y.; White, S.; Henriques, B.; More, S. Strong bimodality in the host halo mass of central galaxies from galaxy-galaxy lensing. Mon. Not. R. Astron. Soc. 2016, 457, 3002. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Swaters, R.A.; van Albada, T.S.; van der Hulst, J.M.; Sancisi, R. The Westerbork HI survey of spiral and irregular galaxies. I. HI imaging of late-type dwarf galaxies. Astron. Astrophys. 2002, 390, 829. [Google Scholar] [CrossRef]
- Saifollahi, T.; Trujillo, I.; Beasley, M.A.; Peletier, R.F.; Knapen, J.H. The number of globular clusters around the iconic UDG DF44 is as expected for dwarf galaxies. Mon. Not. R. Astron. Soc. 2019, 502, 5921. [Google Scholar] [CrossRef]
- Mamon, G.A.; Lokas, E.L. Dark matter in elliptical galaxies—II. Estimating the mass within the virial radius. Mon. Not. R. Astron. Soc. 2016, 363, 705. [Google Scholar] [CrossRef]


| Galaxy | [kpc] | ||
|---|---|---|---|
| D631-7 | |||
| DDO64 | |||
| DDO161 | |||
| UGC731 | |||
| UGC5005 | |||
| UGC5414 | |||
| UGC7608 | |||
| NGC3741 | |||
| Carina | |||
| Leo I | |||
| Leo II | |||
| Sculptor | |||
| Draco | |||
| Sextans | |||
| Fornax | |||
| DragonFly 44 |
| Galaxy | [] | s | BIC | ||
|---|---|---|---|---|---|
| D631-7 | 63 | ||||
| 1 | 279 | ||||
| DDO64 | 14 | ||||
| 1 | 25 | ||||
| DDO161 | 31 | ||||
| 1 | 450 | ||||
| UGC731 | 12 | ||||
| 1 | 14 | ||||
| UGC5005 | 15 | ||||
| 1 | 35 | ||||
| UGC5414 | 8 | ||||
| 1 | 34 | ||||
| UGC7608 | 14 | ||||
| 1 | 14 | ||||
| NGC3741 | 20 | ||||
| 1 | 97 |
| Galaxy | s | BIC | ||||
|---|---|---|---|---|---|---|
| Carina | 48 | |||||
| 1 | 87 | |||||
| Leo I | 17 | |||||
| 1 | 39 | |||||
| Leo II | 11 | |||||
| 1 | 9 | |||||
| Sculptor | 54 | |||||
| 1 | 65 | |||||
| Draco | 14 | |||||
| 1 | 15 | |||||
| Sextans | 24 | |||||
| 1 | 38 | |||||
| Fornax | 69 | |||||
| 1 | 62 | |||||
| DragonFly 44 | 12 | |||||
| 1 | 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benetti, F.; Lapi, A.; Gandolfi, G.; Butt, M.A.; Boumechta, Y.; Haridasu, B.S.; Baccigalupi, C. Dark Matter in Fractional Gravity III: Dwarf Galaxies Kinematics. Universe 2023, 9, 478. https://doi.org/10.3390/universe9110478
Benetti F, Lapi A, Gandolfi G, Butt MA, Boumechta Y, Haridasu BS, Baccigalupi C. Dark Matter in Fractional Gravity III: Dwarf Galaxies Kinematics. Universe. 2023; 9(11):478. https://doi.org/10.3390/universe9110478
Chicago/Turabian StyleBenetti, Francesco, Andrea Lapi, Giovanni Gandolfi, Minahil Adil Butt, Yacer Boumechta, Balakrishna S. Haridasu, and Carlo Baccigalupi. 2023. "Dark Matter in Fractional Gravity III: Dwarf Galaxies Kinematics" Universe 9, no. 11: 478. https://doi.org/10.3390/universe9110478
APA StyleBenetti, F., Lapi, A., Gandolfi, G., Butt, M. A., Boumechta, Y., Haridasu, B. S., & Baccigalupi, C. (2023). Dark Matter in Fractional Gravity III: Dwarf Galaxies Kinematics. Universe, 9(11), 478. https://doi.org/10.3390/universe9110478







