Mu2e Run I Sensitivity Projections for the Neutrinoless μ− → e− Conversion Search in Aluminum
Abstract
1. Introduction
2. Mu2e Experiment
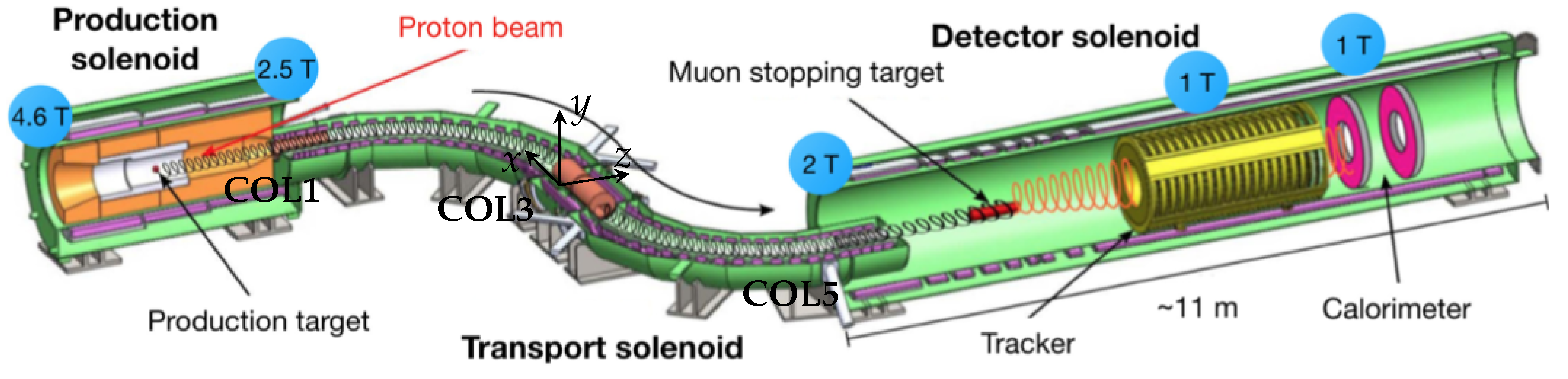
2.1. Muon Beamline
2.2. Signal and Main Backgrounds
- Cosmic particles interacting and decaying in the detector volume are a source of electrons whose momentum spectrum covers the region around 100 . Most cosmic particles entering the detector are muons; suppression of the cosmic background requires identifying muons and vetoing them.
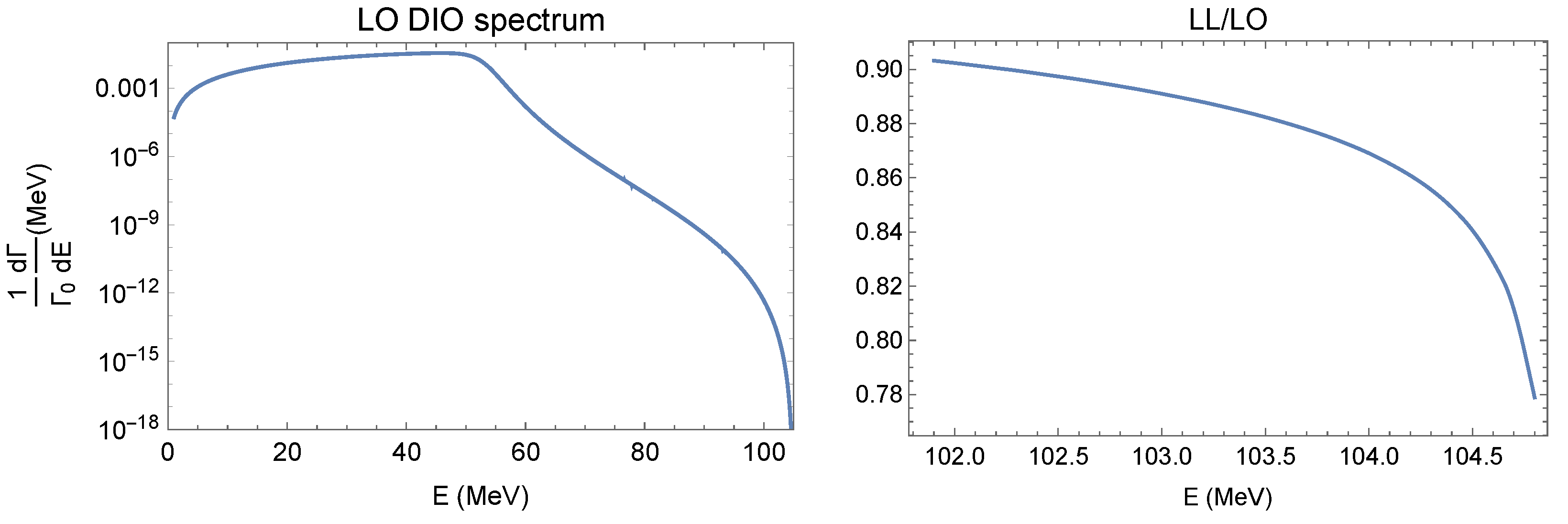
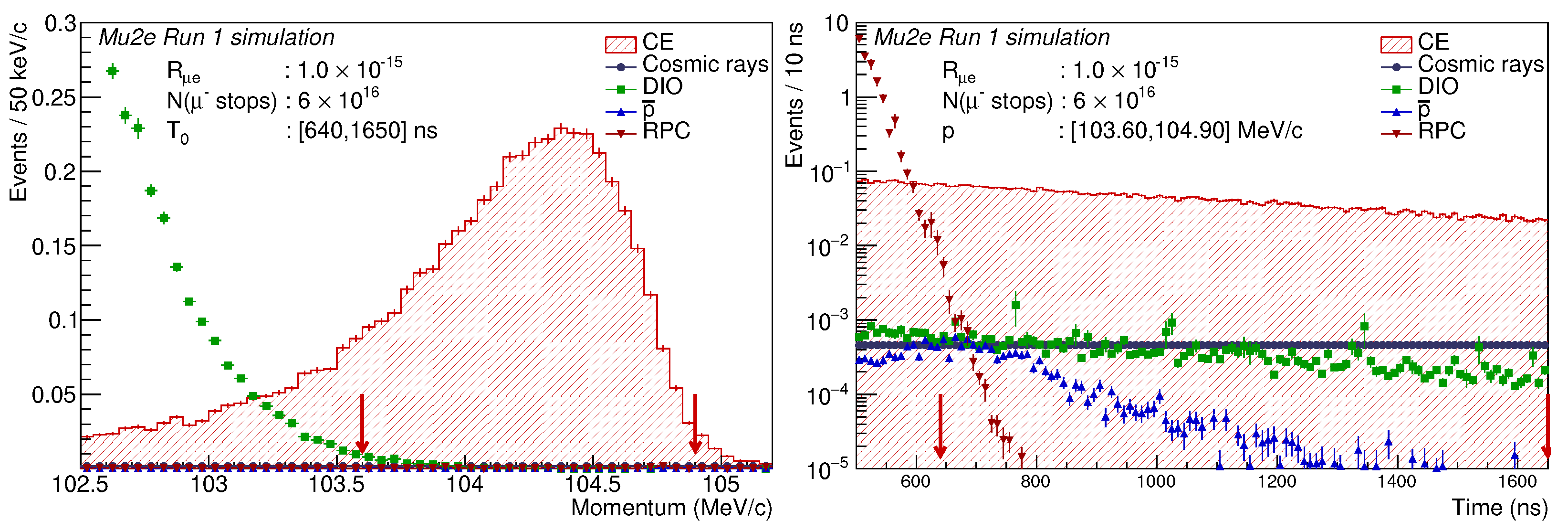
- Decays in orbit (DIO) of muons stopped in the stopping target and captured by the Al atoms produce electrons with a momentum spectrum extending up to and rapidly falling towards the spectrum endpoint. Observing a peak from conversion in the presence of the DIO background requires searching for the signal in a 1–2 wide momentum window and a detector with an excellent momentum resolution , full width at half maximum (FWHM), ≲ 1 .
- Antiprotons produced by the proton beam and annihilating either in the stopping target or the TS also generate electrons. The antiproton background is suppressed by several absorption elements installed in the TS. Presence of the absorbers reduces the number of stopped muons by ∼5%.
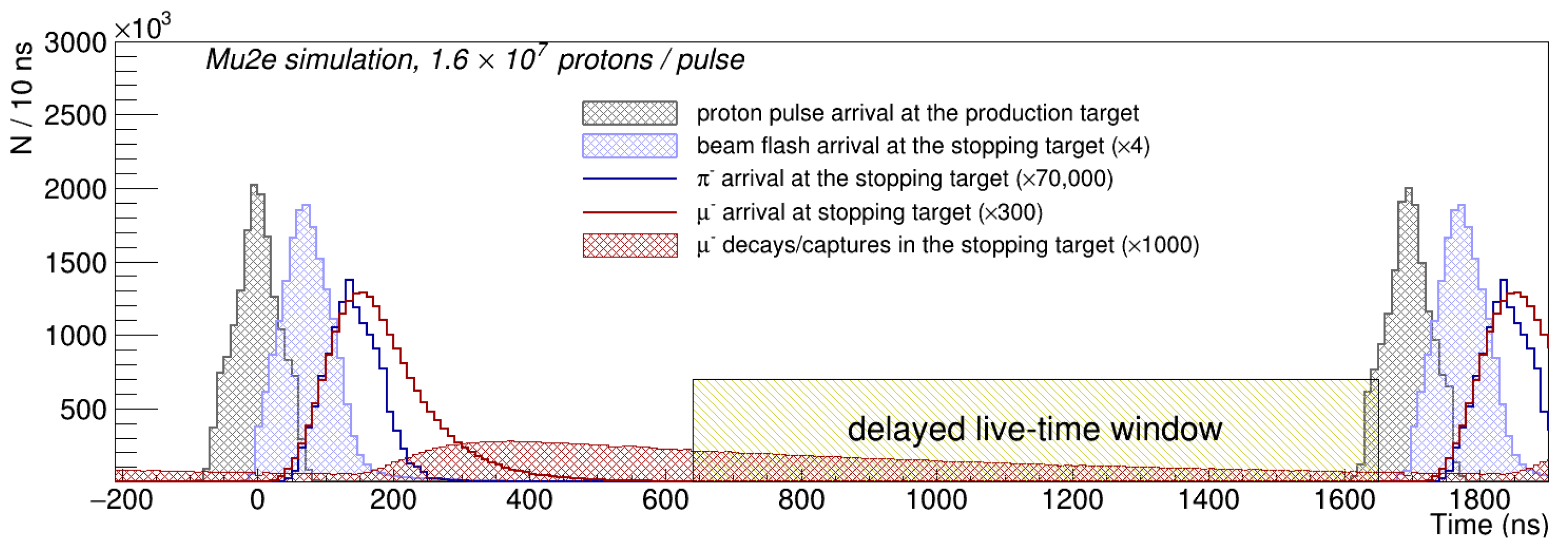
- Radiative capture of pions (RPC) contaminating the muon beam and stopping in the Al target generates a significant background which rapidly falls in time. Suppressing the RPC background requires the live-time window to be delayed with respect to the proton pulse arrival at the production target by several hundred nanoseconds, as schematically shown in Figure 2. The delayed live-time window technique is not efficient against secondary particles produced by protons arriving at the production target between the proton pulses. Suppressing the contribution of those protons requires the proton beam extinction , where is the relative fraction of the beam protons between the pulses.
- Electrons with momenta entering the DS and scattering in the Al stopping target. Similar to RPC, suppressing this background requires the delayed live-time window and an excellent proton beam extinction.
- Decays in flight of negative muons and pions entering the DS and producing electrons with .
- Radiative muon capture (RMC), a process analogous to RPC, but with a lower maximal energy. In aluminum this energy is ∼102 MeV.
2.3. Detector
2.4. Mu2e Run I Data-Taking Plan
3. Simulation Framework
Pileup Simulation
4. Event Reconstruction
4.1. Calorimeter Reconstruction
4.2. Track Reconstruction
4.3. CRV Reconstruction
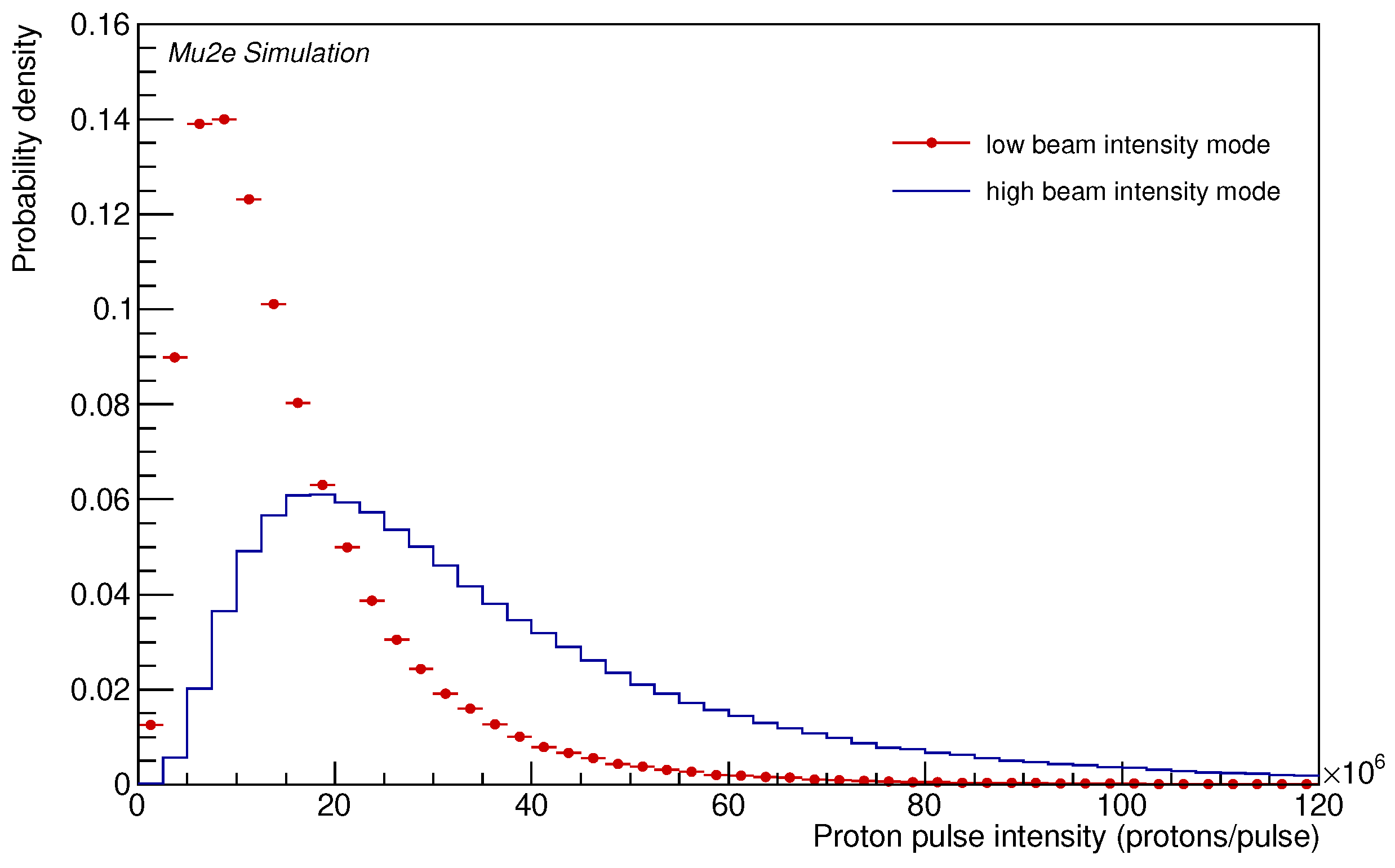
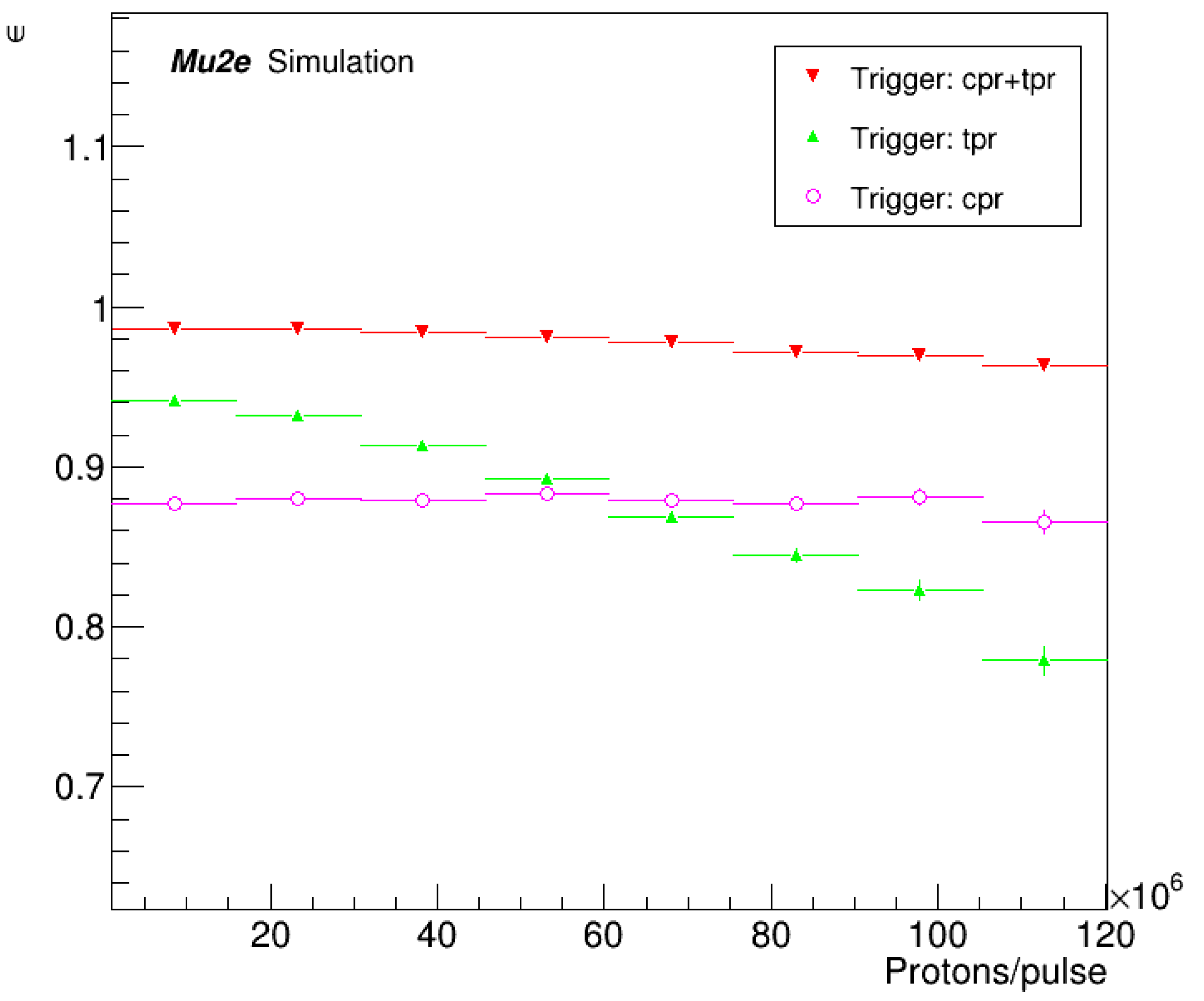
5. Trigger Simulation
6. Event Selection
- N(hits) ≥ 20: the track has a sufficient number of hits in the tracker.
- < 100 mm: the reconstructed track impact parameter, , is consistent with the particle coming from the stopping target.
- R(max) < 680 mm: the maximal distance from the reconstructed trajectory to the DS axis is less than the radius of the tracker, so the reconstructed trajectory is fully contained within the tracker fiducial volume.
- : the angle between the track momentum vector and the DS axis, at the tracker entrance, is consistent with a track of a particle produced at the stopping target. As the DS magnetic field is graded and is higher at the DS entrance, typical values of for particles entering the DS from the TS are greater than 1.0.
- ns: the uncertainty on the reconstructed track time, , returned by the fit is consistent with a downstream electron hypothesis. This requirement implies that the Kalman fit with the calorimeter cluster included has successfully converged (see Section 4).
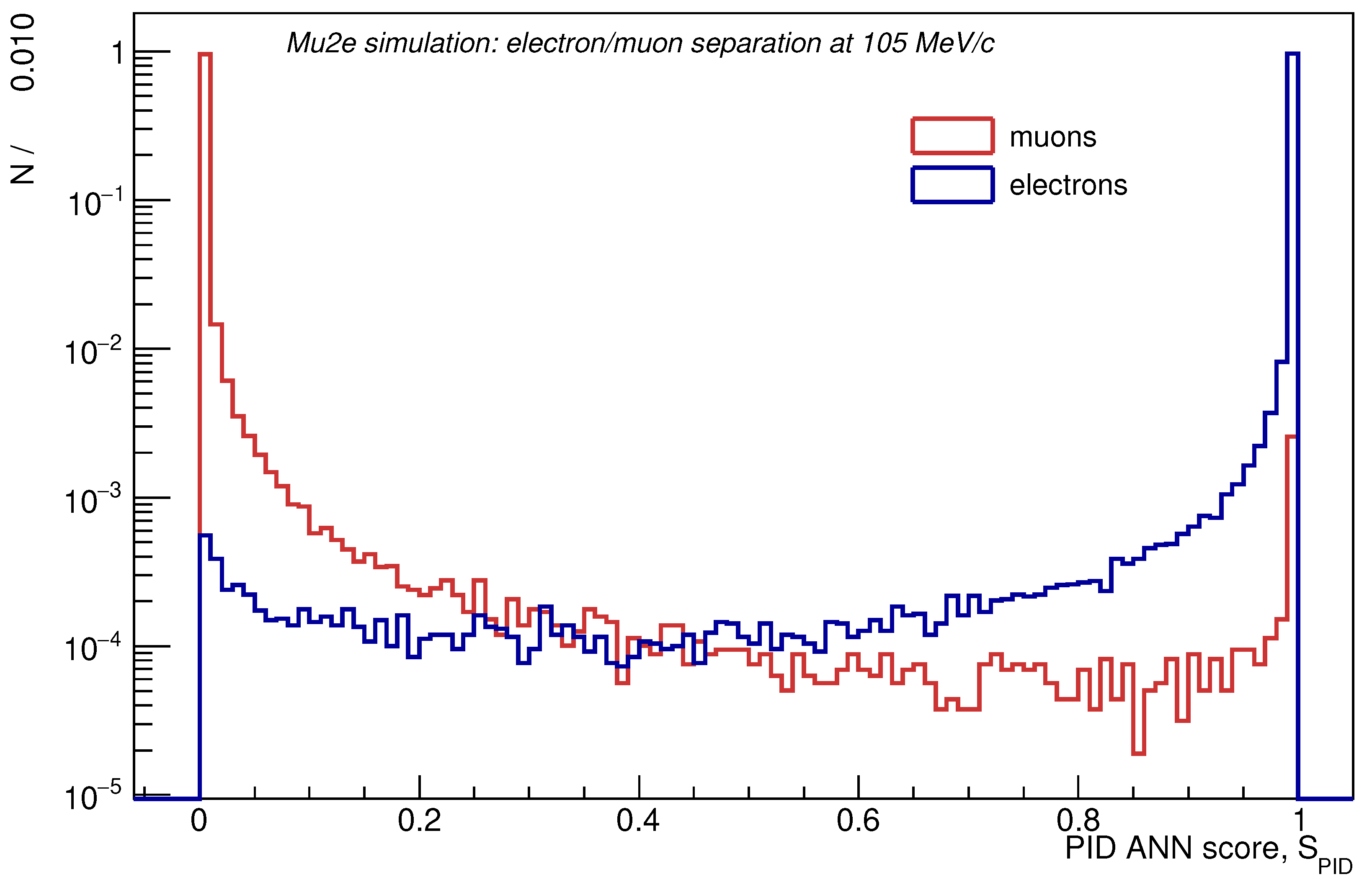
Particle Identification
7. Backgrounds
7.1. Cosmic Rays
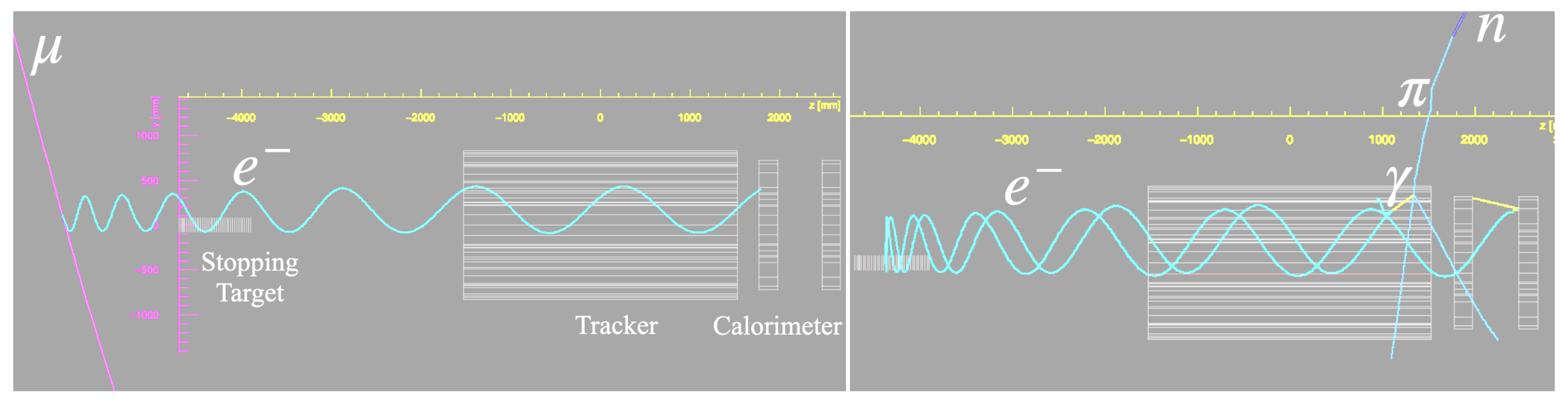
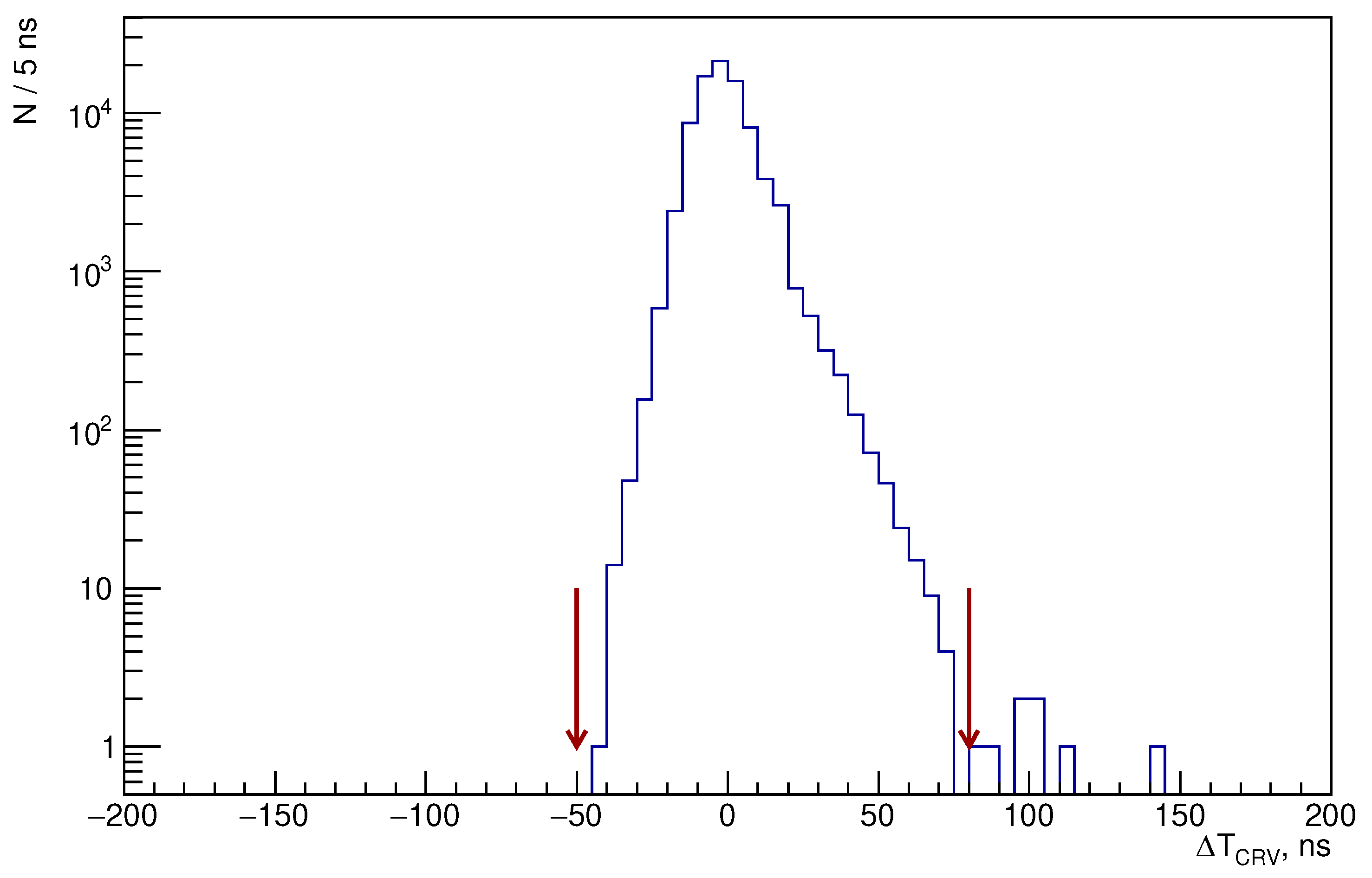
- A typical cosmic background event consists of a reconstructed downstream propagating electron and a CRV stub, see Figure 8 (left). The distribution of the timing residuals between the reconstructed electron and the CRV stub is shown in Figure 9. Cosmic event candidates are identified by the timing window ns.
- A cosmic ray particle can also interact in the calorimeter or decay in the tracker volume producing a particle moving upstream, see Figure 8 (right). Both upstream and downstream moving electrons are reconstructed and the upstream component of the track can be used to reject this type of cosmic background events.
7.2. Muon Decays in Orbit
7.2.1. Calibration of the Tracker Resolution and Momentum Scale
7.2.2. Systematic Uncertainties
- Uncertainty on the absolute momentum scale/ Currently, this is the dominant systematic uncertainty on the DIO background. We expect the momentum scale of the Mu2e tracker to be calibrated to an accuracy of better than 100 at . However, it is not possible to predict the exact value of the resulting systematic uncertainty, so a conservative estimate of 100 is used. Shifting the optimized momentum window by changes the DIO background estimate asymmetrically by [+59%, −37%]. For the high beam intensity running mode, the relative uncertainty is slightly lower. This is expected: at higher occupancy, the momentum resolution degrades, and although the absolute value of the background increases, the slope of the measured DIO spectrum becomes less steep, reducing the relative uncertainty.
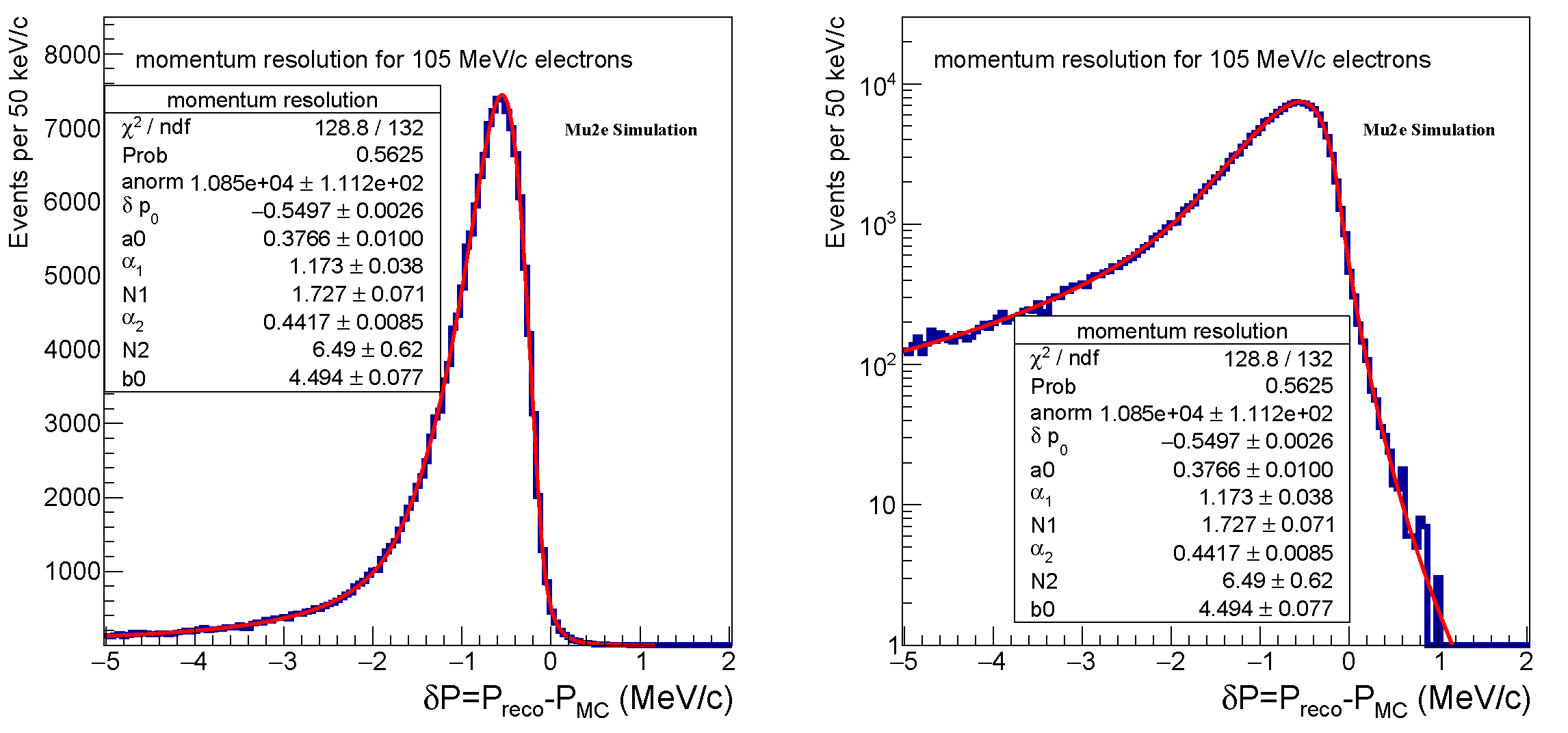
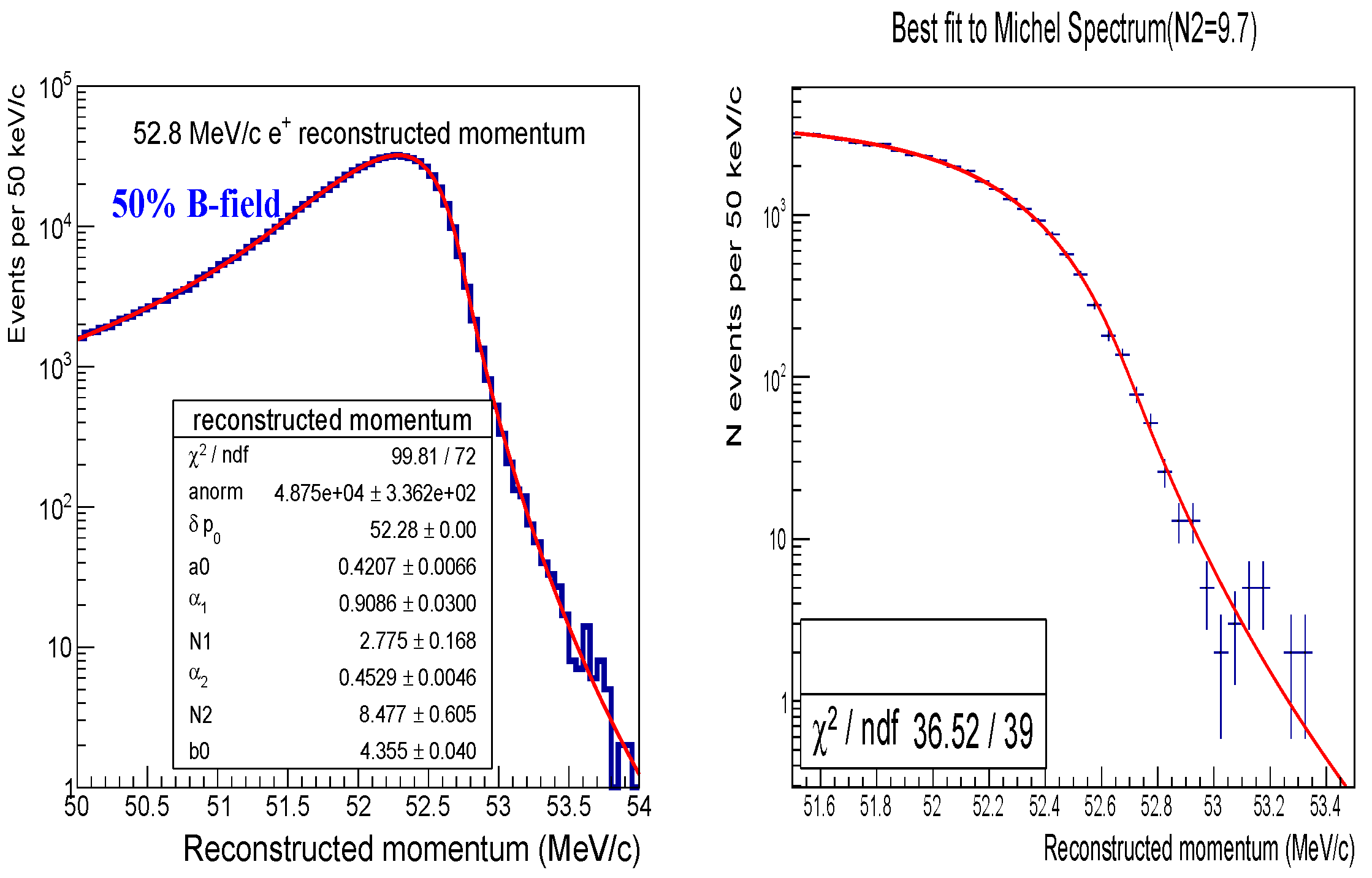
- Uncertainty on the momentum resolution tail. The momentum resolution function shown in Figure 11 has a non-Gaussian tail on the high-momentum side. As the DIO spectrum is rapidly falling towards the endpoint, the uncertainty on the tail may lead to a non-negligible uncertainty on the expected background. The resolution tail at 100 can not be studied directly using the data—there is no physics process which could be used for that. We therefore plan to perform a detailed study of the detector momentum response using the sharp high energy (∼52 MeV) edge of the positron spectrum measured from the decays of stopped positive muons. The magnetic field in the tracker will be reduced by ∼50% to match the curvature of the reconstructed positron tracks with the curvature of the conversion electron tracks in the nominal magnetic field. Below, we outline the proposed method and demonstrate that its intrinsic uncertainty is small.From Equation (2), the uncertainty on the tail is dominated by the uncertainty on the parameter N. A direct fit of the resolution function for simulated 52.8 positrons, shown in Figure 12 (left), returns . To determine the value of from the analysis of the Michel spectrum, we assume that all parameters in Equation (2), except , are fixed from the studies of cosmic and events, and for the present study their values are taken from the fit of the 52.8 positron dataset. A convolution of the theoretical Michel spectrum with the resolution function corresponding to different values of produces multiple templates. Each template is used to fit the spectrum of Michel positrons simulated and reconstructed in B = 0.5 T, with the only floating parameter in the fit being the overall normalization. The analysis of the distribution dependence on yields the best value of . The best fit is shown in Figure 12 (right). The two results are statistically consistent, and their relative difference of 14% can be used to estimate the systematic uncertainty of the method. Assuming the relative uncertainty scales with the track curvature, the resolution function for 100 electrons reconstructed at B = 1 T should have the same relative uncertainty on . Under this assumption, convolving the momentum resolution function at 105 from Figure 11 with the DIO spectrum results in the relative uncertainty on the DIO background of . This uncertainty, contributed to by the experimental procedure, is already small compared to the uncertainty due to the momentum scale and can be further reduced in the future.
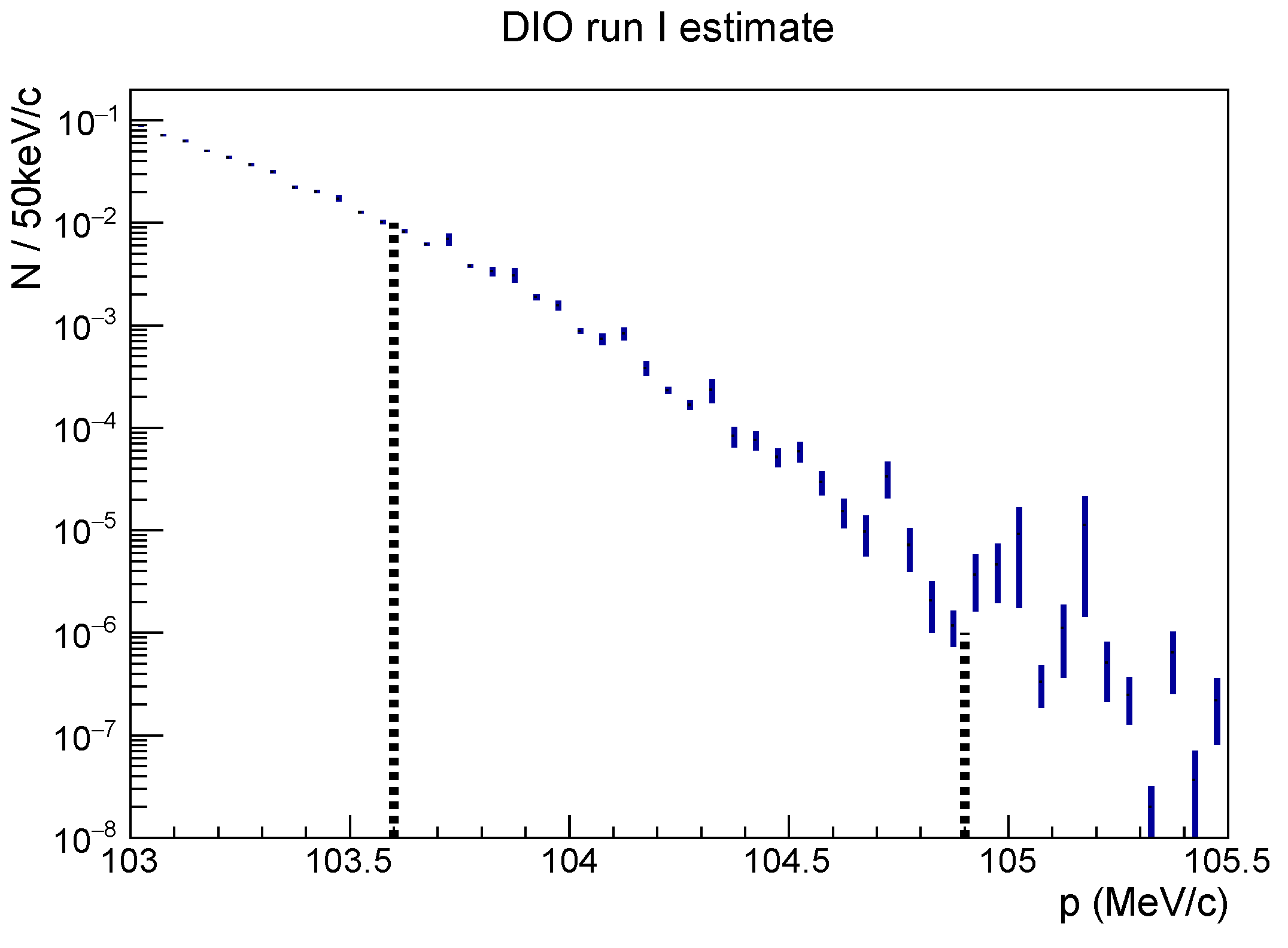
7.2.3. Expected Yield of the DIO Electrons
7.3. Radiative Pion Capture
7.3.1. RPC Sources
- In-time RPC: radiative capture of pions produced by protons arriving in the beam pulse. The rate of in-time RPC rapidly decreases with time roughly following the negative pion lifetime, and the corresponding background can be minimized by sufficiently delaying the live-time search window with respect to the beam pulse.
- Out-of-time RPC: radiative capture of pions produced by out-of-time protons. A delayed live-time window cannot eliminate such pions, only extinction of out-of-time protons can do this.
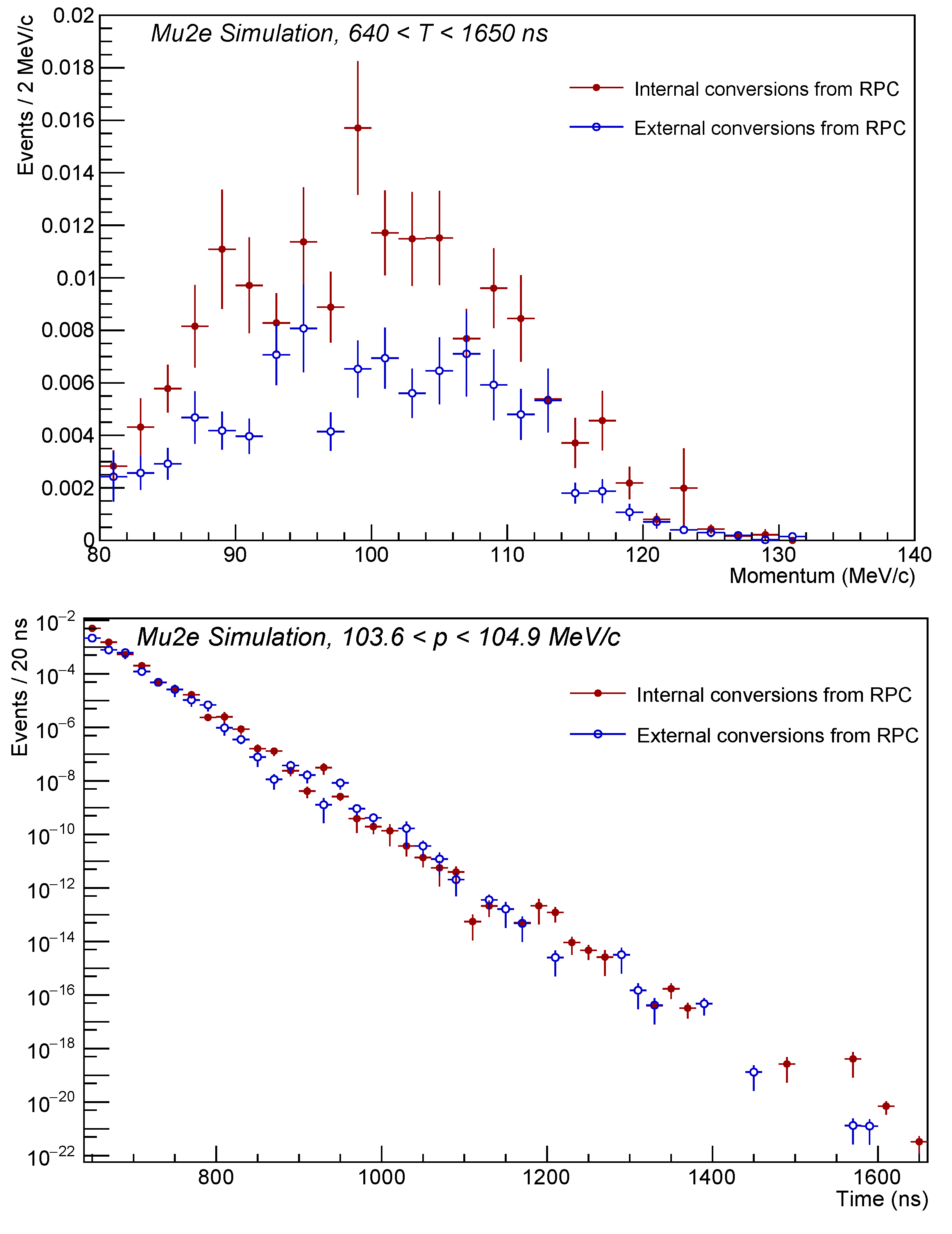
7.3.2. Momentum and Time Distributions
7.3.3. Systematic Uncertainties
- RPC Photon SpectrumA RPC branching rate of , taken from Ref. [46], is used in this study. A relative uncertainty of 9.3% on this measured rate is assigned as the corresponding systematic uncertainty on for Al.
- Internal Conversion FractionThe internal conversion fraction measured in Ref. [45], , is used. Its value is assumed to be independent of the photon energy. The measurement presented in Ref. [45] was performed using hydrogen, where MeV. As the energy region of interest for the conversion search is around 105 MeV, and the theory predicts a decrease of as the photon energy goes down, this assumption is conservative.
- Proton Pulse ShapeThe variation in the pion-capture background due to uncertainty in the simulated shape of the incoming proton beam time structure was found to be negligible.
- Pion Production Cross SectionThe Run I data taking plan assumes collection of stopped negative muons (see Table 1). As muons are primarily produced in pion decays, one might think that the ratio of the number of stopped negative pions to the number of stopped negative muons, , is constant, and that, for a fixed number of stopped muons, the RPC background would not depend on the pion production cross section. However, the pions which stop in the stopping target have momenta significantly lower than the pions producing stopped muons, so the ratio depends on the energy spectrum of the produced pions. As there is no experimental data on production of charged pions with momenta below 100 , model-dependent predictions have to be used. For a fixed number of stopped negative muons, different hadro-production models implemented in Geant4 predict variations of the RPC background. The relative change in the RPC background yield depends on the model used, and results in an asymmetric systematic, shown in Table 3.
7.3.4. Summary of Systematic Uncertainties on the RPC Yield
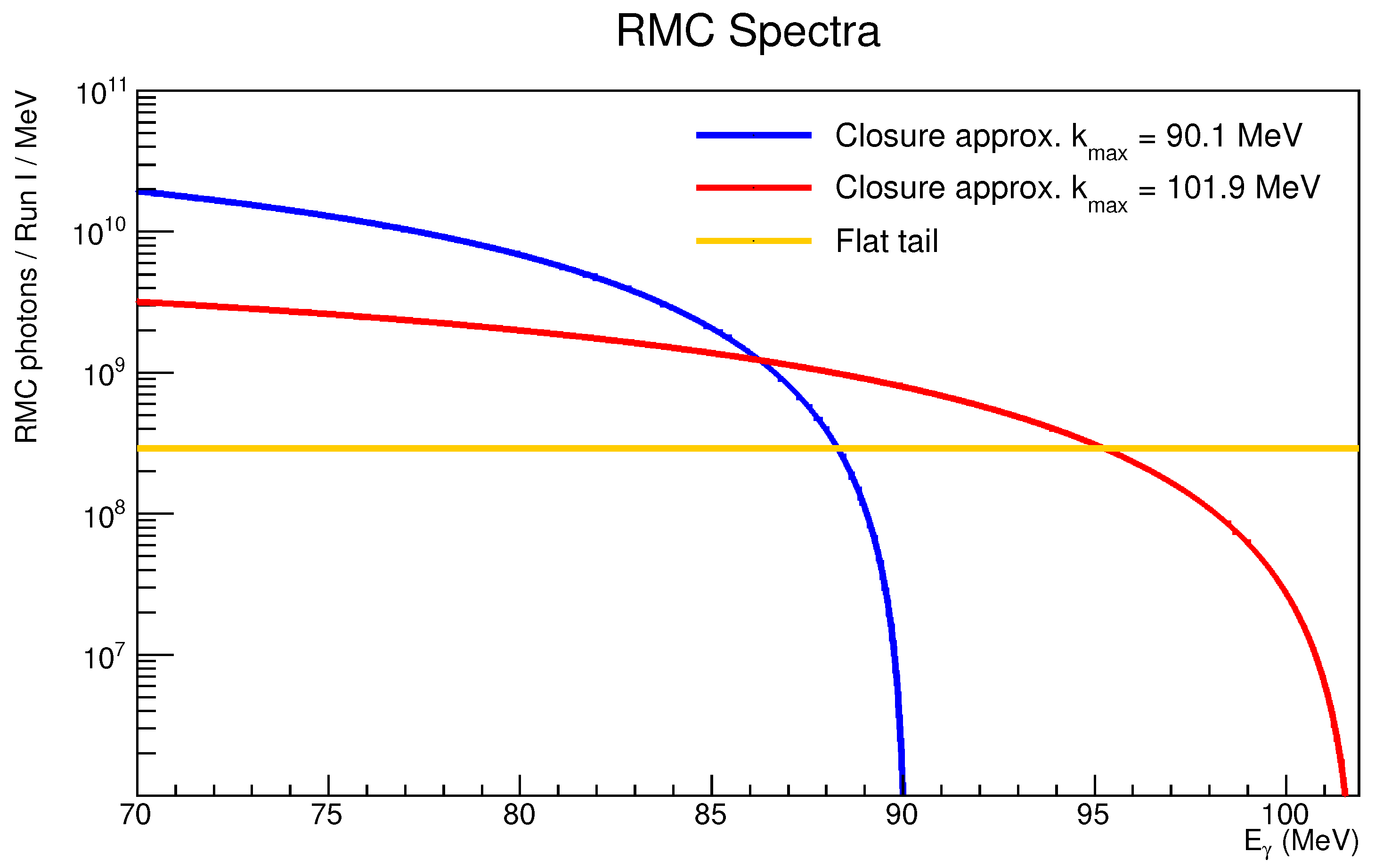
7.4. Radiative Muon Capture
7.5. Antiprotons
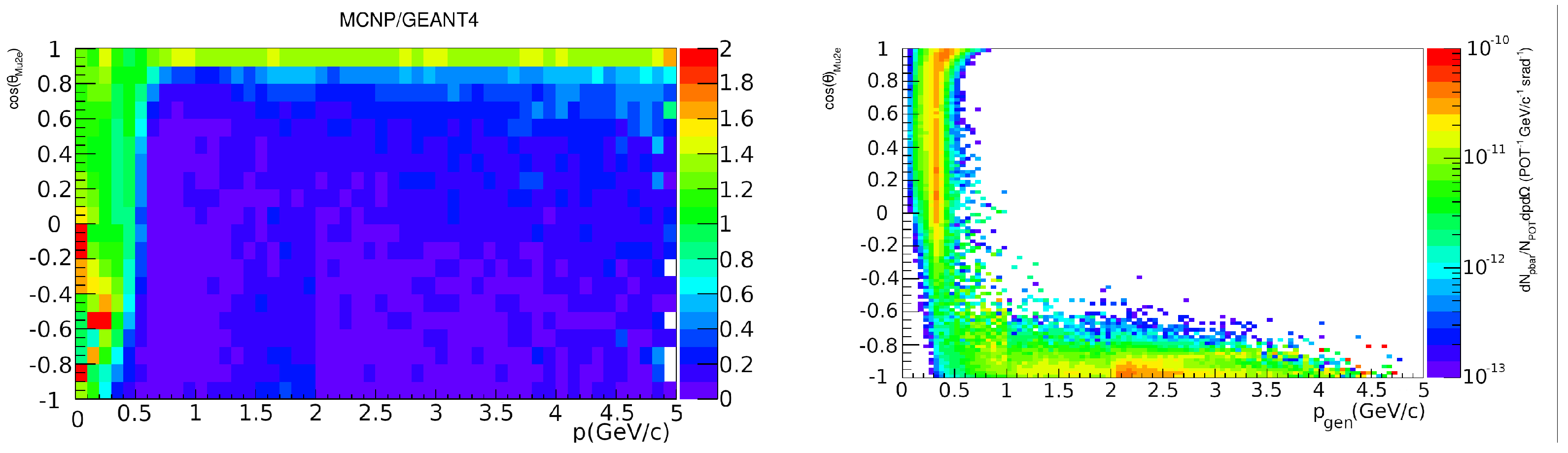
7.5.1. Antiproton Production Cross Section
7.5.2. Antiproton Simulation
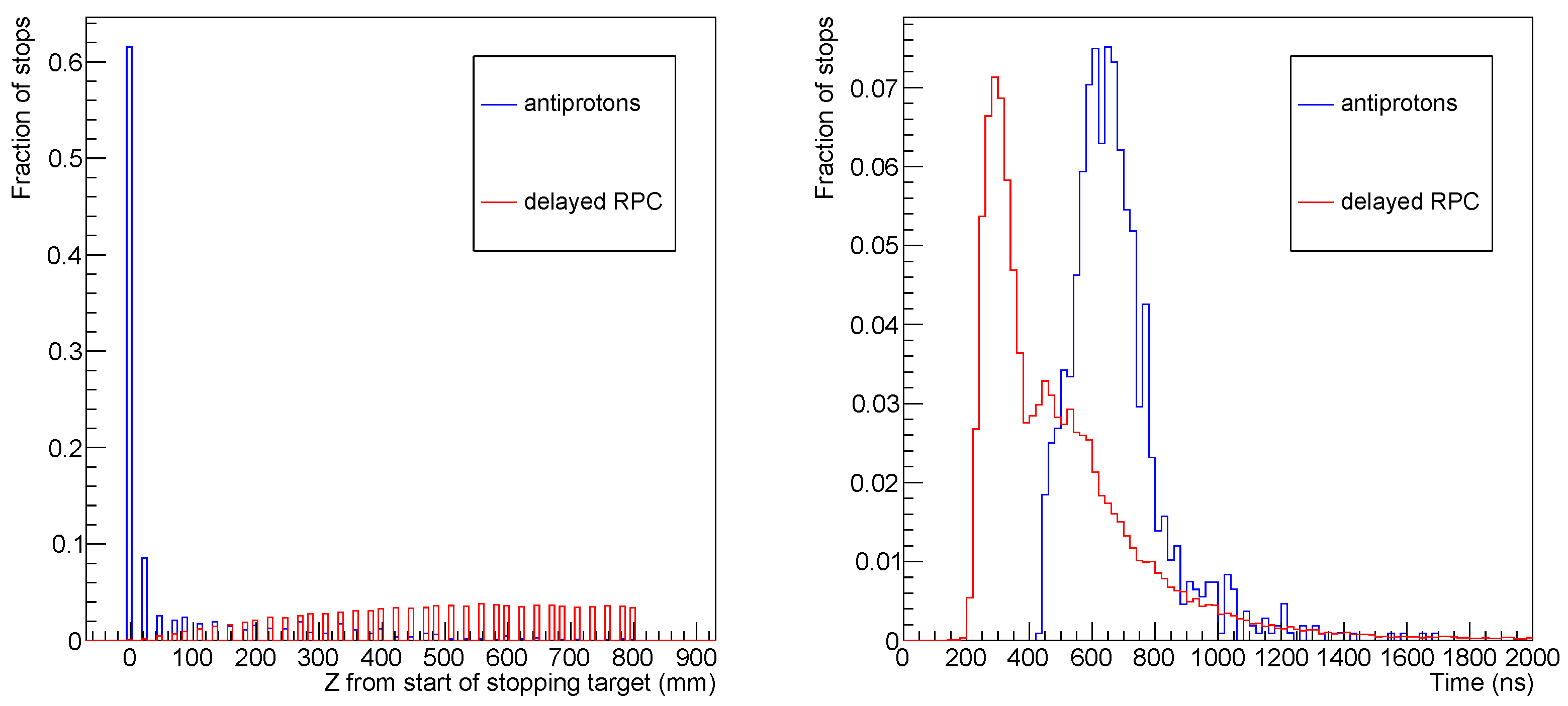
7.5.3. Delayed RPC Simulations
7.6. Other Background Sources
- Beam electrons with momentum around 105 that arrive at the stopping target and scatter there could get reconstructed in the detector and fake the signal. The main source of such electrons are muons decaying in the downstream half of the TS and in the DS, in front of the stopping target. The small, , probability of a large angle scattering in the stopping target combined with the beam extinction of reduces the expected contribution from beam electrons to a level below events;
- Negative muons and pions that enter the DS and decay in flight there, producing electrons with momenta above 100 . The electrons could get reconstructed without scattering in the stopping target and mimic the conversion signal. The estimated contribution from decays in flight is below events.
- The expected background from the DIO of muons stopped in the TS is negligibly small.
8. Sensitivity Optimization
8.1. Optimization Strategy
8.2. Optimization of the Momentum and Time Signal Windows
8.3. Including Systematic Uncertainties
8.4. Sensitivity Estimate
9. Summary
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Membership of the Mu2e Collaboration
Affiliations
- Argonne National Laboratory, Lemont, IL 60439, USA
- Department of Physics, Boston University, Boston, MA 02215, USA
- Brookhaven National Laboratory, Upton, NY 11973-5000, USA
- Department of Physics, University of California, Berkeley, CA 94720-7300, USA
- Department of Physics and Astronomy, University of California, Davis, CA 95616, USA
- Department of Physics and Astronomy, University of California, Irvine, CA 92697-4575, USA
- Division of Physics, Mathematics and Astronomy, Caltech, Pasadena, CA 91125, USA
- Physics Department, The City College of New York, NY 10031, USA
- Joint Institute for Nuclear Research, 141980 Dubna, Russia
- Department of Physics, Duke University, Durham, NC 27708, USA
- Fermi National Accelerator Laboratory, Batavia, IL 60510-5011, USA
- Laboratori Nazionali di Frascati, 00044 Frascati (Roma), Italy
- Istituto Nazionale di Fisica Nucleare, Sezione di Genova, 16146 Genova, Italy
- Helmholtz-Zentrum Dresden-Rossendorf, 01328 Dresden, Germany
- Department of Physics, University of Houston, Houston, TX 77204-5005, USA
- Department of Physics, Kansas State University, Manhattan, KS 66506-2601, USA
- Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
- Istituto Nazionale di Fisica Nucleare, Sezione di Lecce and Universita del Salento, 73100 Lecce, Italy
- Department of Physics, Lewis University, Romeoville, IL 60446, USA
- Department of Physics, University of Liverpool, Liverpool L69 3BX, UK
- Department of Physics and Astronomy, University College London, London WC1E 6BT, UK
- Department of Physics and Astronomy, University of Louisville, Louisville, KY 40292, USA
- Department of Physics and Astronomy, University of Manchester, Manchester M13 9PL, UK
- Laboratori Nazionali di Frascati and Universita Marconi, 00193 Roma, Italy
- Department of Physics, University of Michigan, Ann Arbor, MI 48109-1040, USA
- School of Physics and Astronomy, University of Minnesota, Minneapolis, MN 55455, USA
- Institute for Nuclear Research, 117312 Moscow, Russia
- Muons Inc., Batavia, IL 60510-1274, USA
- Department of Physics, Northern Illinois University, DeKalb, IL 60115, USA
- Department of Physics and Astronomy, Northwestern University, Evanston, IL 60208-3112, USA
- Novosibirsk State University and Budker Institute of Nuclear Physics, 630090 Novosibirsk, Russia
- Istituto Nazionale di Fisica Nucleare, Sezione di Pisa, 56127 Pisa, Italy
- Department of Physics and Astronomy, Purdue University, West Lafayette, IN 47907-2036, USA
- Department of Physics, University of South Alabama, North Mobile, AL 36688, USA
- School of Physics, Sun Yat-Sen University, Guangzhou City 510275, China
- Istituto Nazionale Fisica Nucleare, Sezione di Trieste, 34127 Trieste, Italy
- Department of Physics, University of Virginia, Charlottesville, VA 22904-4714, USA
- Department of Physics, Yale University, New Haven, CT 06520-8120, USA
- *
- Correspondence: murat@fnal.gov
- Deceased.
References
- Zyla, P.A. et al. [Particle Data Group] Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Esteban, I.; Gonzalez-Garcia, M.C.; Maltoni, M.; Schwetz, T.; Zhou, A. The fate of hints: Updated global analysis of three-flavor neutrino oscillations. J. High Energy Phys. 2020, 2020, 178. [Google Scholar] [CrossRef]
- Hambye, T. CLFV and the origin of neutrino masses. Nucl. Phys. Proc. Suppl. 2014, 248–250, 13–19. [Google Scholar] [CrossRef]
- Eliezer, S.; Ross, D.A. A “Cabbibo” theory for leptons and the neutrino masses. Phys. Rev. D 1974, 10, 3088–3092. [Google Scholar] [CrossRef]
- Marciano, W.J.; Mori, T.; Roney, J.M. Charged Lepton Flavor Violation Experiments. Annu. Rev. Nucl. Part. Sci. 2008, 58, 315–341. [Google Scholar] [CrossRef]
- de Gouvêa, A.; Vogel, P. Lepton flavor and number conservation, and physics beyond the standard model. Prog. Part. Nucl. Phys. 2013, 71, 75–92. [Google Scholar] [CrossRef]
- Kinsho, M.; Ikegami, M.; Kawamura, N.; Kobayashi, H.; Matsumoto, H.; Mibe, T.; Miyake, Y.; Mihara, S.; Nishiguchi, H.; Ohomori, C.; et al. Proposal of an Experimental Search for μ→e Conversion in Nuclear Field at Sensitivity of 10−14 with Pulsed Proton Beam from RCS. 2010. Available online: http://deeme.phys.sci.osaka-u.ac.jp/documents/deeme-proposal-r28.pdf (accessed on 24 October 2022).
- Blondel, A.; Bravar, A.; Pohl, M.; Bachmann, S.; Berger, N.; Kiehn, M.; Straumann, U. Research Proposal for an Experiment to Search for the Decay μ→eee. arXiv 2013, arXiv:1301.6113. [Google Scholar]
- Bartoszek, L. et al. [Mu2e Collaboration] Mu2e Technical Design Report. arXiv 2015, arXiv:1501.05241. [Google Scholar]
- Baldini, A.M.; Baracchini, E.; Bemporad, C.; Berg, F.; Biasotti, M.; Boca, G.; Zhang, Y. The design of the MEG II experiment. Eur. Phys. J. C 2018, 78, 380. [Google Scholar] [CrossRef]
- Abramishvili, R. et al. [COMET Collaboration] COMET Phase-I technical design report. Prog. Theor. Exp. Phys. 2020, 2020, 033C01. [Google Scholar] [CrossRef]
- Kuno, Y.; Okada, Y. Muon decay and physics beyond the standard model. Rev. Mod. Phys. 2001, 73, 151–202. [Google Scholar] [CrossRef]
- Bertl, W.; Engfer, R.; Hermes, E.A.; Kurz, G.; Kozlowski, T.; Kuth, J.; Otter, G.; Rosenbaum, F.; Ryskulov, N.M.; van der Schaaf, A.; et al. A search for μ-e conversion in muonic gold. Eur. Phys. J. Part. Fields 2006, 47, 337–346. [Google Scholar] [CrossRef]
- Dzhilkibaev, R.; Lobashev, V. On the Search for μ→e Conversion on Nuclei. (In Russian). Sov. J. Nucl. Phys. 1989, 49, 384–385. [Google Scholar]
- Nagaslaev, V.; Brown, K.A.; Tomizawa, M. Third integer resonance extraction with presence of higher multipoles. Phys. Rev. Accel. Beams 2019, 22, 043501. [Google Scholar] [CrossRef]
- Nagaslaev, V.; Amundson, J.; Johnstone, J.; Michelotti, L.; Park, C.S.; Werkema, S.; Syphers, M. Third interger resonance slow extraction scheme for a μ→e experiment at Fermilab. arXiv 2012, arXiv:1207.6621. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Catanesi, M.G. et al. [HARP Collaboration] Large-angle production of charged pions with 3–12.9 GeV/c incident protons on nuclear targets. Phys. Rev. C 2008, 77, 055207. [Google Scholar] [CrossRef]
- Armutlijski, D.; Baatar, T.; Batsajkhan, T.; Kanarek, T.; Kladnitskaya, E.N.; Sultanov, M.U.; Tuvdendorzh, D. Hadron spectra in hadron—Nucleus collisions. 1991; Preprint. [Google Scholar]
- Czarnecki, A.; Garcia i Tormo, X.; Marciano, W.J. Muon decay in orbit: Spectrum of high-energy electrons. Phys. Rev. D 2011, 84, 013006. [Google Scholar] [CrossRef]
- Szafron, R. Radiative Corrections in Bound States. Acta Phys. Polon. B 2017, 48, 2183. [Google Scholar] [CrossRef]
- Suzuki, T.; Measday, D.F.; Roalsvig, J.P. Total nuclear capture rates for negative muons. Phys. Rev. C 1987, 35, 2212–2224. [Google Scholar] [CrossRef]
- Atanova, O.; Cordelli, M.; Corradi, G.; Colao, F.; Davydov, Y.; Donghia, R.; Falco, S.D.; Giovannella, S.; Happacher, F.; Martini, M.; et al. Measurement of the energy and time resolution of a undoped CsI MPPC array for the Mu2e experiment. J. Instrum. 2017, 12, P05007. [Google Scholar] [CrossRef]
- Artikov, A.; Baranov, V.; Blazey, G.C.; Chen, N.; Chokheli, D.; Davydov, Y.; Dukes, E.C.; Dychkant, A.; Ehrlich, R.; Francis, K.; et al. Photoelectron yields of scintillation counters with embedded wavelength-shifting fibers read out with silicon photomultipliers. Nucl. Instrum. Methods Phys. Res. Sect. A: Accel. Spectrometers Detect. Assoc. Equip. 2018, 890, 84–95. [Google Scholar] [CrossRef]
- Agostinelli, S. et al. [Geant4 Collaboration] Geant4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.E.; Araujo, H.A.; Dubois, P.A.; Asai, M.A.; Barr, G.A.; Capra, R.A.; Chauvie, S.A.; Chytracek, R.A.; et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 2006, 53, 270–278. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barr, G.J.; et al. Recent developments in Geant4. Nucl. Instrum. Methods Phys. Res. Sect. A 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Szafron, R.; Czarnecki, A. Bound muon decay spectrum in the leading logarithmic accuracy. Phys. Rev. D 2016, 94, 051301. [Google Scholar] [CrossRef]
- Gaponenko, A.; Grossheim, A.; Hillairet, A.; Marshall, G.M.; Mischke, R.E.; Olin, A. Charged-particle spectra from μ- capture on Al. Phys. Rev. C 2020, 101, 035502. [Google Scholar] [CrossRef]
- Edmonds A., et al. [AlCap Collaboration] Measurement of proton, deuteron, triton, and α particle emission after nuclear muon capture on Al, Si, and Ti with the AlCap experiment. Phys. Rev. C 2022, 105, 035501. [Google Scholar] [CrossRef]
- Kozłowski, T.; Zgliński, A. The nuclear excitations and particle emission following muon capture. Nucl. Phys. A 1978, 305, 368–380. [Google Scholar] [CrossRef]
- Macdonald, B.; Diaz, J.A.; Kaplan, S.N.; Pyle, R.V. Neutrons from Negative-Muon Capture. Phys. Rev. 1965, 139, B1253–B1263. [Google Scholar] [CrossRef]
- Pezzullo, G.; Brown, D.; Murat, P. CTD2020: The Track finder algorithm for the Trigger System of the Mu2e experiment at Fermilab. In Proceedings of the Connecting The Dots/Intelligent Tracker Workshop, Princeton, NJ, USA, 20–30 April 2020. [Google Scholar] [CrossRef]
- Pezzullo, G.; Murat, P. The calorimeter-seeded track reconstruction for the Mu2e experiment at Fermilab. In Proceedings of the 2015 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), San Diego, CA, USA, 31 October–7 November 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Edmonds, A.; Brown, D.; Vinas, L.; Pagan, S. Using machine learning to select high-quality measurements. J. Instrum. 2021, 16, T08010. [Google Scholar] [CrossRef]
- Hagmann, C.; Lange, D.; Wright, D.M. Cosmic-ray shower generator (CRY) for Monte Carlo transport codes. In Proceedings of the 2007 IEEE Nuclear Science Symposium Conference Record, Honolulu, HI, USA, 26 October–3 November 2007; Volume 2, pp. 1143–1146. [Google Scholar]
- Gordon, M.; Goldhagen, P.; Rodbell, K.; Zabel, T.; Tang, H.; Clem, J.; Bailey, P. Measurement of the flux and energy spectrum of cosmic-ray induced neutrons on the ground. IEEE Trans. Nucl. Sci. 2004, 51, 3427–3434. [Google Scholar] [CrossRef]
- Miyake, S.; Kataoka, R.; Sato, T. Cosmic ray modulation and radiation dose of aircrews during the solar cycle 24/25. Space Weather 2017, 15, 589–605. [Google Scholar] [CrossRef]
- Heck, D.; Knapp, J.; Capdevielle, J.N.; Schatz, G.; Thouw, T. CORSIKA: A Monte Carlo Code to Simulate Extensive Air Showers; Technical Report; Forschungszentrum Karlsruhe: Karlsruhe, Germany, 1998. [Google Scholar]
- Szafron, R.; Czarnecki, A. High-energy electrons from the muon decay in orbit: Radiative Corrections. Phys. Lett. B 2016, 753, 61–64. [Google Scholar] [CrossRef]
- Moyal, J. Theory of ionization fluctuations. Philos. Mag. J. Sci. 1955, 46, 263–280. [Google Scholar] [CrossRef]
- Landau, L.D. On the energy loss of fast particles by ionization. J. Phys. 1944, 8, 201–205. [Google Scholar]
- Kroll, N.M.; Wada, W. Internal Pair Production Associated with the Emission of High-Energy Gamma Rays. Phys. Rev. 1955, 98, 1355–1359. [Google Scholar] [CrossRef]
- Joseph, D.W. Electron pair creation in π+p capture reactions from rest. Il Nuovo C. 1960, 16, 997–1013. [Google Scholar] [CrossRef]
- Samios, N.P. Dynamics of Internally Converted Electron-Positron Pairs. Phys. Rev. 1961, 121, 275–281. [Google Scholar] [CrossRef]
- Bistirlich, J.A.; Crowe, K.M.; Parsons, A.S.L.; Skarek, P.; Truöl, P. Photon Spectra from Radiative Absorption of Pions in Nuclei. Phys. Rev. C 1972, 5, 1867–1883. [Google Scholar] [CrossRef]
- Plestid, R.; Hill, R.J. The high energy spectrum of internal positrons from radiative muon capture on nuclei. arXiv 2020, arXiv:2010.09509. [Google Scholar] [CrossRef]
- Christillin, P.; Rosa-Clot, M.; Servadio, S. Radiative muon capture in medium-heavy nuclei. Nucl. Phys. A 1980, 345, 331–366. [Google Scholar] [CrossRef]
- Bergbusch, P.C.; Armstrong, D.S.; Blecher, M.; Chen, C.Q.; Doyle, B.C.; Gorringe, T.P.; Gumplinger, P.; Hasinoff, M.D.; Jonkmans, G.; Macdonald, J.A.; et al. Radiative muon capture on O, Al, Si, Ti, Zr, and Ag. Phys. Rev. C 1999, 59, 2853–2864. [Google Scholar] [CrossRef]
- Ahmad, S.; Azuelos, G.; Blecher, M.; Bryman, D.A.; Burnham, R.A.; Clifford, E.T.H.; Depommier, P.; Dixit, M.S.; Gotow, K.; Hargrove, C.K.; et al. Search for muon-electron and muon-positron conversion. Phys. Rev. D 1988, 38, 2102–2120. [Google Scholar] [CrossRef]
- Amann, J.F.; Macek, R.J.; Sanford, T.W. Measurement of Production Cross Sections for Negative Pions, Kaons, and Protons at 10,18 and 24 GeV; Technical Report LA-9486-MS; Los Alamos National Laboratory: Los Alamos, NM, USA, 1982. [Google Scholar] [CrossRef]
- Sibirtsev, A.A.; Safronov, G.A.; Smirnov, G.N.; Tregbukhovskii, Y.V. Production of antiprotons in the proton-nucleus interaction at 10.1 GeV/c. Yad. Fiz. 1991, 53, 191–199. [Google Scholar]
- Kiselev, Y.T.; Sheinkman, V.A.; Akindinov, A.V.; Chumakov, M.M.; Martemyanov, A.N.; Smirnitsky, V.A.; Terekhov, Y.V.; Paryev, E.Y. Probing of compact baryonic configurations in nuclei in A(p,)X reactions and antiproton formation length in nuclear matter. Phys. Rev. C 2012, 85, 054904. [Google Scholar] [CrossRef]
- Barabash, L.Z.; Egorov, O.K.; Kuzichev, V.F.; Lapitsky, Y.Y.; Lepikhin, Y.B.; Prudnik, A.N.; Smirnitsky, V.A.; Sheinkman, V.A. Measurement of the Cross-Section d2σ/dpdΩ in the Reaction pA →X at 10-GeV/c Proton Momenta in Be, Al, Cu and Au Nuclei; Technical Report ITEP-48-1980; Moscow Institute for Theoretical and Experimental Physics: Moscow, Russia, 1980. [Google Scholar] [CrossRef]
- Boyarinov, S.V.; Evseev, I.I.; Kiselev, Y.T.; Leksin, G.A.; Martemyanov, A.N.; Mikhailov, K.R.; Pozdnyakov, S.A.; Terekhov, Y.V.; Ushakov, V.I.; Sheinkman, V.A. Yields of p, p¯, π±, and K± Emitted at an Angle of 97 degree in the Laboratory System from Nuclei Irradiated by 10.14 GeV Protons. Phys. At. Nucl. 1994, 57, 1379–1388. [Google Scholar]
- De Felice, G. An Updated Estimate of the Mu2e Experiment Sensitivity. Ph.D. Thesis, University of Pisa, Pisa, Italy, 2020. [Google Scholar] [CrossRef]
- Danielewicz, P. Multiparticle interactions in backward proton production, subthreshold anti-proton production, and inclusive electron scattering from nuclei. Phys. Rev. C 1990, 42, 1564. [Google Scholar] [CrossRef]
- Letaw, J.R.; Silberberg, R.; Tsao, C.H. Proton-nucleus total inelastic cross sections: An empirical formula for energies bigger than 10 mega ev. Astrophys. J. 1983, 51, 271–275. [Google Scholar] [CrossRef]
- Goorley, T.; James, M.; Booth, T.; Brown, F.; Bull, J.; Cox, L.J.; Zukaitis, T. Initial MCNP6 Release Overview. Nucl. Technol. 2012, 180, 298–315. [Google Scholar] [CrossRef]
- Battistoni, G.; Cerutti, F.; Ferrari, A.; Ranft, J.; Roesler, S.; Sala, P.R. Hadron production simulation by FLUKA. J. Phys. Conf. Ser. 2013, 408, 012051. [Google Scholar] [CrossRef]
- Mashnik, S.; Gudima, K.; Prael, R.; Sierk, A.; Baznat, M.; Mokhov, N. CEM03.03 and LAQGSM03.03 Event Generators for the MCNP6, MCNPX, and MARS15 Transport Codes. Nucl. Instrum. Methods Phys. Res. Sect. Beam Interact. Mater. Atoms 2009, 267, 3426–3433. [Google Scholar]
- Bhattiprolu, P.N.; Martin, S.P.; Wells, J.D. Criteria for projected discovery and exclusion sensitivities of counting experiments. Eur. Phys. J. 2021, 81, 123. [Google Scholar] [CrossRef]
- Feldman, G.J.; Cousins, R.D. Unified approach to the classical statistical analysis of small signals. Phys. Rev. D 1998, 57, 3873–3889. [Google Scholar] [CrossRef]
- Conrad, J.; Botner, O.; Hallgren, A.; Pérez de los Heros, C. Including systematic uncertainties in confidence interval construction for Poisson statistics. Phys. Rev. D 2003, 67, 012002. [Google Scholar] [CrossRef]


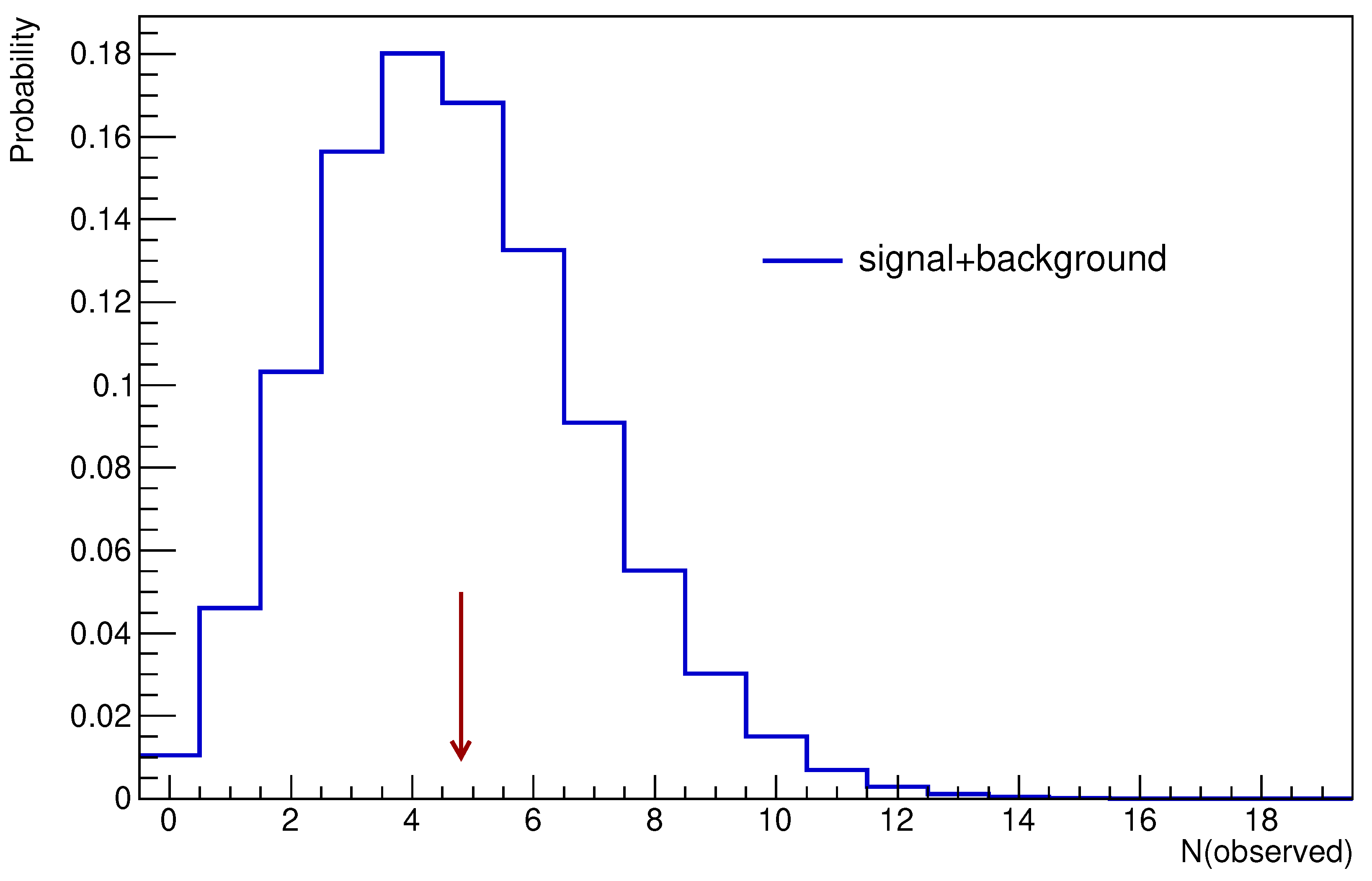
| Running Mode | Mean Proton Pulse Intensity | Running Time (s) | N (POT) | N (Stopped Muons) |
|---|---|---|---|---|
| Low intensity | ||||
| High intensity | ||||
| Total |
| Source | Low Intensity Running Mode | High Intensity Running Mode | Run I Error |
|---|---|---|---|
| Momentum Scale | +62%,−38% | +50%,−34% | +59%,−37% |
| Theory | ± 2.5% | ±2.5% | ±2.5% |
| Total | +62%,−38% | +50%,−34% | +59%,−37% |
| Systematic Contribution | Internal Conversions | External Conversions |
|---|---|---|
| RPC fraction [46] | 9.3% | |
| Internal conversion coefficient [45] | 4.5% | |
| Pion production model | ||
| Total systematic uncertainty |
| RMC Tail Parameterization | Production Mechanism | Run I Background |
|---|---|---|
| Closure approx., = 101.9 MeV | On-shell | |
| Closure approx., = 101.9 MeV | Off-shell | |
| Flat | On-shell | |
| Flat | Off-shell |
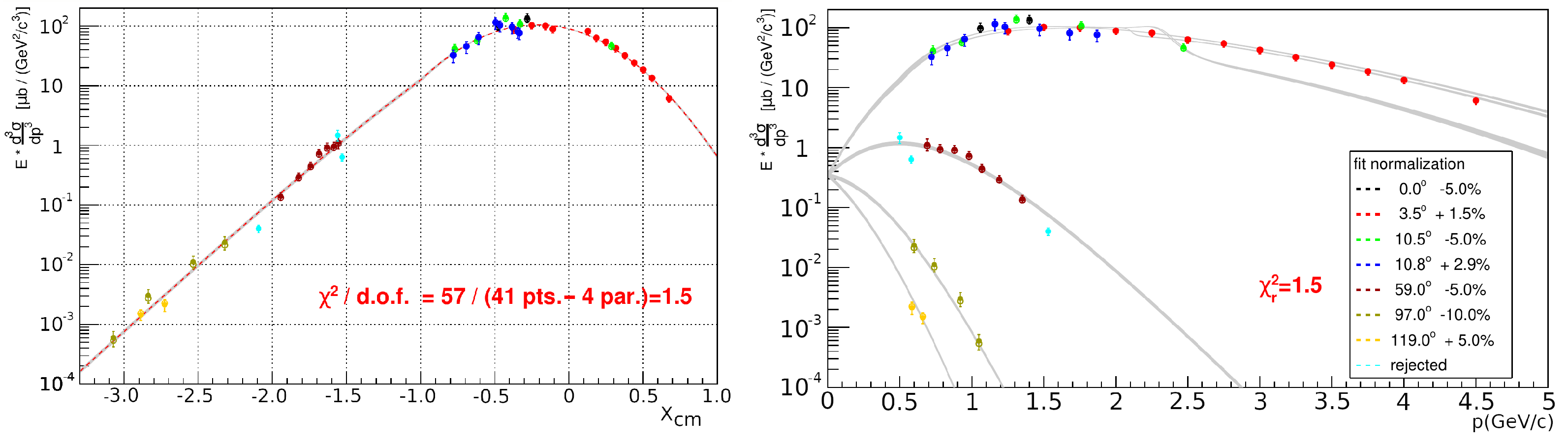
| () | (, o) | () | Nuclear Target, Reference | |
|---|---|---|---|---|
| 2 | 10 | 0 | Tungsten, Anmann et al. [51] | |
| 13 | 10 | 3.5 | Tantalum, Sibirtsev et al. [52] | |
| 5 | 10 | 10.5 | Tantalum, Kiselev et al. [53] | |
| 8 | 10 | 10.8 | Gold, Barabash et al. [54] | |
| 8 | 10 | 59 | Tantalum, Kiselev et al. [53] | |
| 4 | 10 | 97 | Tantalum, Boyarinov et al. [55] | |
| 2 | 10 | 119 | Tantalum, Boyarinov et al. [55] |
| Parameter | Total Relative Uncertainty | Dominant Contribution |
|---|---|---|
| Signal acceptance | 4% | Momentum scale |
| Antiproton background | 100% | production cross section |
| Cosmic background | 20% | Cosmic flux normalization |
| DIO background | 59% | Momentum scale |
| RPC background | 29% | Pion production cross section |
| Muon flux | 10% | Flux measurement |
| Configuration | Discovery | (90% CL Limit) | N(Discovery Events) |
|---|---|---|---|
| No systematics | 5 | ||
| With systematics | 5 |
| Channel | Mu2e Run I |
|---|---|
| SES | |
| Cosmic rays | |
| DIO | |
| Antiprotons | |
| RPC in-time | |
| RPC out-of-time () | |
| RMC | |
| Decays in flight | |
| Beam electrons | |
| Total |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu2e Collaboration. Mu2e Run I Sensitivity Projections for the Neutrinoless μ− → e− Conversion Search in Aluminum. Universe 2023, 9, 54. https://doi.org/10.3390/universe9010054
Mu2e Collaboration. Mu2e Run I Sensitivity Projections for the Neutrinoless μ− → e− Conversion Search in Aluminum. Universe. 2023; 9(1):54. https://doi.org/10.3390/universe9010054
Chicago/Turabian StyleMu2e Collaboration. 2023. "Mu2e Run I Sensitivity Projections for the Neutrinoless μ− → e− Conversion Search in Aluminum" Universe 9, no. 1: 54. https://doi.org/10.3390/universe9010054
APA StyleMu2e Collaboration. (2023). Mu2e Run I Sensitivity Projections for the Neutrinoless μ− → e− Conversion Search in Aluminum. Universe, 9(1), 54. https://doi.org/10.3390/universe9010054







