Might the 2PN Perihelion Precession of Mercury Become Measurable in the Next Future?
Abstract
1. Introduction
2. The 2PN Precession of the Pericenter
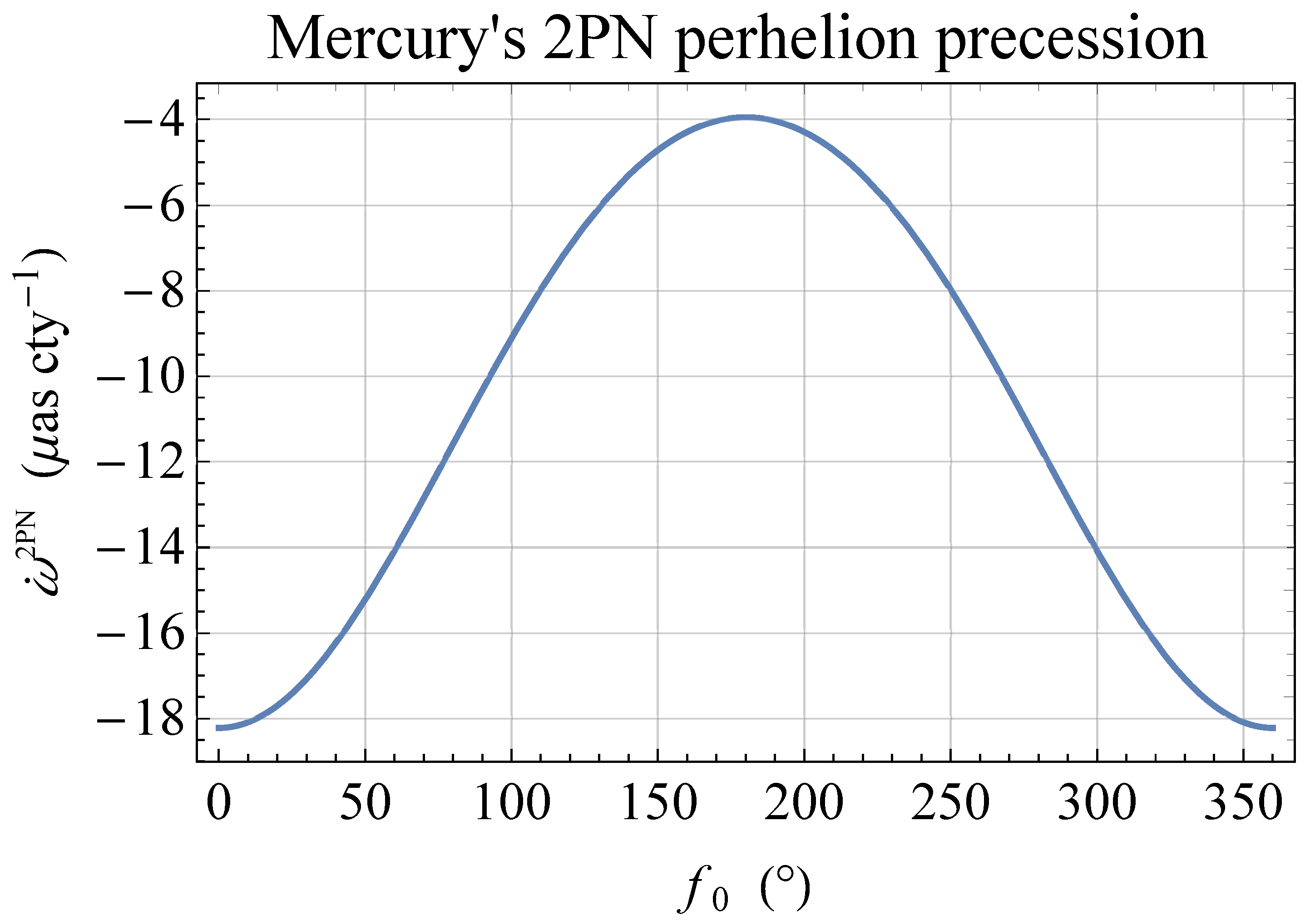
3. The 2PN Perihelion Precession of Mercury
4. Summary and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | |
| 2 | Here and in the following, the angular brackets denoting the orbital average are omitted. |
| 3 | It is calculated perturbatively in the usual way by evaluating the right hand side of the Gauss equation for [23], calculated with , onto a fixed Keplerian ellipse, and integrating it over a Keplerian orbital period. |
| 4 | It is obtained by keeping a and e fixed during the integration of the right hand side of the Gauss equation for , calculated with , over a Keplerian orbital period. |
| 5 | For a recent comparative study of Mercury’s perihelion advance induced by some classical dynamical effects, see [37]. |
| 6 | EPM stands for Ephemeris of Planets and the Moon. |
| 7 | See https://iaaras.ru/en/dept/ephemeris/epm/2017/ (accessed on 30 December 2022) for details. |
| 8 | Until now, the simpler model of the NASA Jet Propulsion Laboratory (JPL) was pre-applied to the normal points published by it; see https://ssd.jpl.nasa.gov/dat/planets/messenger.txt (accessed on 30 December 2022). |
| 9 | D. Pavlov, private communication to the present author, November 2022. |
| 10 | |
| 11 | The one due to the Sun’s Love number is much smaller, being, thus, of no concern. |
References
- Damour, T. The problem of motion in Newtonian and Einsteinian gravity. In Three Hundred Years of Gravitation; Hawking, S., Israel, W., Eds.; Cambridge University Press: Cambridge, UK, 1987; pp. 128–198. [Google Scholar]
- Asada, H.; Futamase, T. Chapter 2. Post–Newtonian Approximation: Its Foundation and Applications. Prog. Theor. Phys. Suppl. 1997, 128, 123–181. [Google Scholar] [CrossRef][Green Version]
- Blanchet, L. On the Accuracy of the Post–Newtonian Approximation. In Proceedings of the 2001: A Relativistic Spacetime Odyssey; Ciufolini, I., Dominici, D., Lusanna, L., Eds.; World Scientific: Singapore, 2003; pp. 411–430. [Google Scholar] [CrossRef]
- Blanchet, L. Gravitational Radiation from Post–Newtonian Sources and Inspiralling Compact Binaries. Living Rev. Relativ. 2006, 9, 4. [Google Scholar] [CrossRef] [PubMed]
- Futamase, T.; Itoh, Y. The Post–Newtonian Approximation for Relativistic Compact Binaries. Living Rev. Relativ. 2007, 10, 2. [Google Scholar] [CrossRef] [PubMed]
- Will, C.M. Theory and Experiment in Gravitational Physics, 2nd ed.; Cabridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Will, C.M. On the unreasonable effectiveness of the post-Newtonian approximation in gravitational physics. Proc. Natl. Acad. Sci. USA 2011, 108, 5938–5945. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, I.I.; Ash, M.E.; Smith, W.B. Icarus: Further Confirmation of the Relativistic Perihelion Precession. Phys. Rev. Lett. 1968, 20, 1517–1518. [Google Scholar] [CrossRef]
- Shapiro, I.I.; Pettengill, G.H.; Ash, M.E.; Ingalls, R.P.; Campbell, D.B.; Dyce, R.B. Mercury’s Perihelion Advance: Determination by Radar. Phys. Rev. Lett. 1972, 28, 1594–1597. [Google Scholar] [CrossRef]
- Shapiro, I.I.; Smith, W.B.; Ash, M.E.; Herrick, S. General Relativity and the Orbit of Icarus. Astron. J. 1971, 76, 588. [Google Scholar] [CrossRef]
- Shapiro, I.I. Solar system tests of general relativity: Recent results and present plans. In Proceedings of the General Relativity and Gravitation, 1989; Ashby, N., Bartlett, D.F., Wyss, W., Eds.; Cambridge University Press: Cambridge, UK, 1990; pp. 313–330. [Google Scholar]
- Lucchesi, D.M.; Peron, R. Accurate Measurement in the Field of the Earth of the General-Relativistic Precession of the LAGEOS II Pericenter and New Constraints on Non–Newtonian Gravity. Phys. Rev. Lett. 2010, 105, 231103. [Google Scholar] [CrossRef]
- Lucchesi, D.M.; Peron, R. LAGEOS II pericenter general relativistic precession (1993-2005): Error budget and constraints in gravitational physics. Phys. Rev. D 2014, 89, 082002. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; McLaughlin, M.A.; Lyne, A.G.; Ferdman, R.D.; Burgay, M.; Lorimer, D.R.; Possenti, A.; D’Amico, N.; et al. Tests of General Relativity from Timing the Double Pulsar. Science 2006, 314, 97–102. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; Wex, N.; Deller, A.T.; Coles, W.A.; Ali, M.; Burgay, M.; Camilo, F.; Cognard, I.; et al. Strong-Field Gravity Tests with the Double Pulsar. Phys. Rev. X 2021, 11, 041050. [Google Scholar] [CrossRef]
- Gravity Collaboration; Abuter, R.; Amorim, A.; Bauböck, M.; Berger, J.P.; Bonnet, H.; Brandner, W.; Cardoso, V.; Clénet, Y.; de Zeeuw, P.T.; et al. Detection of the Schwarzschild precession in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2020, 636, L5. [Google Scholar] [CrossRef]
- Schäfer, G.; Wex, N. Second post-Newtonian motion of compact binaries. Phys. Lett. A 1993, 174, 196–205. [Google Scholar] [CrossRef]
- Wex, N. The second post-Newtonian motion of compact binary-star systems with spin. Class. Quantum Gravity 1995, 12, 983–1005. [Google Scholar] [CrossRef]
- Tucker, A.; Will, C.M. Pericenter advance in general relativity: Comparison of approaches at high post-Newtonian orders. Class. Quantum Gravity 2019, 36, 115001. [Google Scholar] [CrossRef]
- Damour, T.; Schäfer, G. Higher-order relativistic periastron advances and binary pulsars. Nuovo Cimento B 1988, 101, 127–176. [Google Scholar] [CrossRef]
- Damour, T.; Deruelle, N. General relativistic celestial mechanics of binary systems. I. The post-Newtonian motion. Ann. De L’Institut Henri Poincaré Sect. A 1985, 43, 107–132. [Google Scholar]
- Iorio, L. On the 2PN Periastron Precession of the Double Pulsar PSR J0737-3039A/B. Universe 2021, 7, 443. [Google Scholar] [CrossRef]
- Kopeikin, S.M.; Efroimsky, M.; Kaplan, G. Relativistic Celestial Mechanics of the Solar System; Wiley-VCH: Weinheim, Germany, 2011. [Google Scholar] [CrossRef]
- Klioner, S.A.; Kopeikin, S.M. The Post-Keplerian Orbital Representations of the Relativistic Two-Body Problem. Astrophys. J. 1994, 427, 951. [Google Scholar] [CrossRef]
- Hu, H.; Kramer, M.; Wex, N.; Champion, D.J.; Kehl, M.S. Constraining the dense matter equation-of-state with radio pulsars. Mon. Not. R. Astron. Soc. 2020, 497, 3118–3130. [Google Scholar] [CrossRef]
- Burgay, M.; D’Amico, N.; Possenti, A.; Manchester, R.N.; Lyne, A.G.; Joshi, B.C.; McLaughlin, M.A.; Kramer, M.; Sarkissian, J.M.; Camilo, F.; et al. An increased estimate of the merger rate of double neutron stars from observations of a highly relativistic system. Nature 2003, 426, 531–533. [Google Scholar] [CrossRef] [PubMed]
- Lyne, A.G.; Burgay, M.; Kramer, M.; Possenti, A.; Manchester, R.N.; Camilo, F.; McLaughlin, M.A.; Lorimer, D.R.; D’Amico, N.; Joshi, B.C.; et al. A Double-Pulsar System: A Rare Laboratory for Relativistic Gravity and Plasma Physics. Science 2004, 303, 1153–1157. [Google Scholar] [CrossRef]
- Deng, X.M. The second post-Newtonian light propagation and its astrometric measurement in the solar system. Int. J. Mod. Phys. D 2015, 24, 1550056. [Google Scholar] [CrossRef]
- Xie, Y.; Huang, T.Y. Second post-Newtonian approximation of Einstein-aether theory. Phys. Rev. D 2008, 77, 124049. [Google Scholar] [CrossRef]
- Xie, Y.; Ni, W.T.; Dong, P.; Huang, T.Y. Second post-Newtonian approximation of scalar-tensor theory of gravity. Adv. Space Res. 2009, 43, 171–180. [Google Scholar] [CrossRef]
- Deng, X.M.; Xie, Y. Two-post-Newtonian light propagation in the scalar-tensor theory: An N-point mass case. Phys. Rev. D 2012, 86, 044007. [Google Scholar] [CrossRef]
- Deng, X.M. Two-post-Newtonian approximation of the scalar-tensor theory with an intermediate-range force for general matter. Sci. China Phys. Mech. Astron. 2015, 58, 1–8. [Google Scholar] [CrossRef]
- Deng, X.M. The second post-Newtonian light propagation and its astrometric measurement in the Solar System: Light time and frequency shift. Int. J. Mod. Phys. D 2016, 25, 1650082. [Google Scholar] [CrossRef]
- Iorio, L. Post–Newtonian direct and mixed orbital effects due to the oblateness of the central body. Int. J. Mod. Phys. D 2015, 24, 1550067. [Google Scholar] [CrossRef]
- Mioc, V.; Radu, E. Perturbations in the anomalistic period of artificial satellites caused by the direct solar radiation pressure. Astron. Nachrichten 1979, 300, 313–315. [Google Scholar] [CrossRef]
- Kopeikin, S.M.; Potapov, V.A. Relativistic shift of the periastron of a double pulsar in the post-post-Newtonian approximation of General Relativity. Astron. Rep. 1994, 38, 104–114. [Google Scholar]
- Pogossian, S.P. Comparative study of Mercury’s perihelion advance. Celest. Mech. Dyn. Astron. 2022, 134, 33. [Google Scholar] [CrossRef]
- Iorio, L. Calculation of the Uncertainties in the Planetary Precessions with the Recent EPM2017 Ephemerides and their Use in Fundamental Physics and Beyond. Astron. J. 2019, 157, 220. [Google Scholar] [CrossRef]
- Pitjeva, E.V.; Pitjev, N.P. Masses of the Main Asteroid Belt and the Kuiper Belt from the Motions of Planets and Spacecraft. Astron. Lett. 2018, 44, 554–566. [Google Scholar] [CrossRef]
- Aksim, D.; Pavlov, D. Improving the solar wind density model used in processing of spacecraft ranging observations. Mon. Not. R. Astron. Soc. 2022, 514, 3191–3201. [Google Scholar] [CrossRef]
- Benkhoff, J.; Murakami, G.; Baumjohann, W.; Besse, S.; Bunce, E.; Casale, M.; Cremosese, G.; Glassmeier, K.H.; Hayakawa, H.; Heyner, D.; et al. BepiColombo - Mission Overview and Science Goals. Space Sci. Rev. 2021, 217, 90. [Google Scholar] [CrossRef]
- Iess, L.; Asmar, S.W.; Cappuccio, P.; Cascioli, G.; De Marchi, F.; di Stefano, I.; Genova, A.; Ashby, N.; Barriot, J.P.; Bender, P.; et al. Gravity, Geodesy and Fundamental Physics with BepiColombo’s MORE Investigation. Space Sci. Rev. 2021, 217, 21. [Google Scholar] [CrossRef]
- van der Zwaard, R.; Dirkx, D. The Influence of Dynamic Solar Oblateness on Tracking Data Analysis from Past and Future Mercury Missions. Remote Sens. 2022, 14, 4139. [Google Scholar] [CrossRef]
- Love, A.E.H. Some Problems of Geodynamics; Cambridge University Press: Cambridge, UK, 1911. [Google Scholar]
- Kopal, Z. Close Binary Systems; Chapman & Hall: London, UK, 1959. [Google Scholar]
- Poisson, E.; Will, C.M. Gravity; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Konopliv, A.S.; Park, R.S.; Ermakov, A.I. The Mercury gravity field, orientation, love number, and ephemeris from the MESSENGER radiometric tracking data. Icarus 2020, 335, 113386. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iorio, L. Might the 2PN Perihelion Precession of Mercury Become Measurable in the Next Future? Universe 2023, 9, 37. https://doi.org/10.3390/universe9010037
Iorio L. Might the 2PN Perihelion Precession of Mercury Become Measurable in the Next Future? Universe. 2023; 9(1):37. https://doi.org/10.3390/universe9010037
Chicago/Turabian StyleIorio, Lorenzo. 2023. "Might the 2PN Perihelion Precession of Mercury Become Measurable in the Next Future?" Universe 9, no. 1: 37. https://doi.org/10.3390/universe9010037
APA StyleIorio, L. (2023). Might the 2PN Perihelion Precession of Mercury Become Measurable in the Next Future? Universe, 9(1), 37. https://doi.org/10.3390/universe9010037





