Abstract
In this paper, we present an analysis of how alpha–proton drift speeds (the difference between the magnitudes of alpha and bulk proton speeds) are constrained in the inner heliosphere using observations from the WIND and twin HELIOS spacecraft. The solar wind is separated based on its bulk proton speed into the fast wind (>600 km/s) and slow wind (<400 km/s). The slow wind is again separated based on its normalized cross-helicity; slow wind intervals with average absolute normalized cross-helicity greater than 0.6 are considered Alfvénic, and those less than 0.6 are considered non-Alfvénic. Analysis of different types of wind intervals between 0.3 to 1 au have shown that the alpha-proton drift speeds are very much constrained by the angle between the B and V vectors for fast and slow Alfvénic wind intervals. Depending on the polarity of the magnetic field, there is a clear correlation or anti-correlation between the drift speeds and the angle between the B and V vectors. Interestingly, we did not observe any such relation in the non-Alfvénic slow wind intervals. Large-amplitude Alfvénic fluctuations present in the fast and slow Alfvénic winds control the drift between the alpha and proton core in the Alfvénic solar wind. The drift speeds can be modeled using the equation , where is the Alfvén speed and is the Alfvén ratio. Because the observations of drift speed constrained by the angle between the B and V vector for the fast and slow Alfvénic wind intervals are observed throughout the inner heliosphere, it is possible to consider this observed behavior to be a universal phenomenon of Alfvénic wind above the Alfvénic surface.
1. Introduction
The solar wind is the magnetized plasma expanding away from the Sun into space. It provides a large natural laboratory to study the space plasma through in situ measurements. Proton and Alpha particles constitute the major positive ion components of the solar wind; while the proton population constitutes around 95–99%, the alpha population varies between 1–5%, with the relative proportions varying depending on the solar wind speed [1,2,3,4,5]. Even though alphas make up a smaller proportion, they represent around 15–20% of the total solar wind mass density.
After the identification of protons and alphas in the in situ data, it took considerable time to realize that there is a clear speed difference between protons and alphas. One of the reasons for this was due to measurement errors; another important factor was the lack of fast wind data for analysis. The velocity differences are not significant in the slow wind, of which the majority of analyzed data once consisted of. As more and more fast wind streams became available for analysis, differences in the speed of protons and alphas became evident [6,7,8].
A major study on alpha–proton velocity differences and their evolution in the inner heliosphere was presented by Marsch et al. [9] using Helios data between 0.3 and 1 au. The authors showed that alpha particles could drift up to Alfvén speeds, and suggested that wave–particle interactions are the primary cause of preferential alpha particle acceleration. Recently, Durovcová et al. [10] carried out a comprehensive study on alpha proton velocity differences using the entire Helios dataset between 0.3 to 1 au by separating the ion distributions into proton core, proton beam, and alphas. Their study validated previous observations of differential streaming in the inner heliosphere.
Studies by Berger et al. [11] using the data from the ACE mission have shown for the first time that there is a good correlation/anti-correlation between the magnitude of the difference in the speeds of proton and alphas () and the angle between the magnetic field and velocity vector (). The correlation or anti-correlation is dependent on the polarity of the magnetic field. Several authors have looked into this, using only fast wind intervals due to instrumental limitations; despite such limitations, these studies suggest that the observed relation between the magnitude of the difference in the speeds of protons and alphas and the angle between the magnetic field and velocity vector may be a general behavior that can be observed in all types of solar wind.
In this article, we use different intervals of solar wind streams from different spacecraft at different distances (0.3 to 1 au) to show the necessary conditions required to observe the correlation/anti-correlation between the differential speed and the . We discuss whether this correlation has a radial dependence, and present reasons for the observed behavior. The rest of this article is structured as follows: in Section 2, we explain the datasets used for our analysis and the methodology followed in our analysis; in Section 3, we present the results; and in Section 4, we discuss the obtained results in detail.
2. Data and Methodology
This study was performed using data from three spacecraft: WIND and HELIOS 1 and 2.
The WIND spacecraft is positioned in a halo orbit around the L1 Lagrange point. It observes the Sun from the ecliptic plane at a constant distance of 1 au. Alpha and proton moments required for our analysis were generated from the three-dimensional velocity distribution function measurements of Solar Wind Experiment (SWE) [12]. The resolution of these data is 92 s. In addition, we used the magnetic field measured by the Magnetic Field Investigation (MFI) experiment Lepping et al. [13], specifically, the averaged 92 s resolution data, to match the proton and the alpha measurements. Our study sample consisted of data from the years 2005 to 2020.
HELIOS 1 and 2 were twin spacecraft orbiting close to the ecliptic plane with elliptical orbits around the Sun. Their perihelia were at around 0.3 au and their aphelia was 1 au. Alpha and proton moments required for analysis were generated from the velocity distribution function measurements by the onboard electrostatic analyzers [14], and the magnetic fields were measured by the fluxgate magnetometers [15,16]. The moments used for our analysis are taken from the works of Stansby et al. [17,18]; the method of fitting the ion distributions and generating the moments can be found in the mentioned references. The magnetic field data are averaged values over the time of distribution measurement.
The first step in our analysis is to separate the data on the basis of their speed. If the speed is greater than 600 km/s, it is considered as fast wind, and if the speed is less than 400 km/s it is considered as slow wind. Winds with intervals between 400 km/s and 600 km/s are considered mixed wind. The slow wind is again divided on the basis of the Alfvénicity into the slow Alfvénic wind and non-Alfvénic wind; the selected intervals are called Alfvénic if the normalized absolute cross-helicity values are greater or equal to 0.6.
Normalized absolute cross-helicity is estimated as below:
Here, stands for the Alfvén normalized magnetic field fluctuation, defined as
where stands for the velocity fluctuation, , and .
The polarity of the interval is estimated by taking the median of the radial magnetic field of the considered interval.
3. Results
In Figure 1, we show a number of the plasma properties of one of the intervals we analyzed. In panel (a), we show how the magnetic field magnitude () and component vary, while in panel (b) we show the speed of the protons (), which shows that the interval considered is a fast solar wind. In panel (c), we show the bulk speed of the alphas (); it can be observed that for a number of the cases the speed of the alpha particles is lower than the proton speed. In panel (d), we show the , which is the difference in speed between the alphas and protons, and in panel (e) we show the values of . Figure 1 provides a glimpse of the correlation between the and .
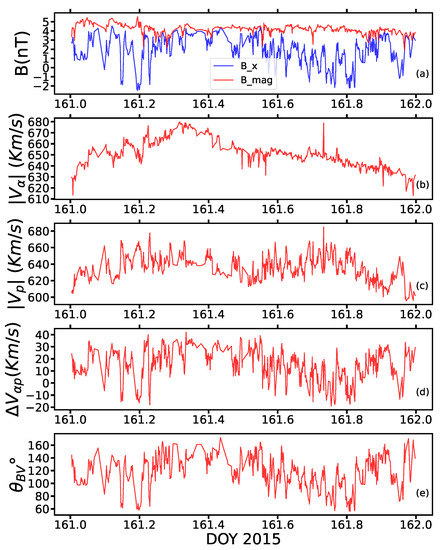
Figure 1.
Illustration of typical parameters of a fast wind interval at 1 au using WIND data from 10 June 2015. Panel (a) shows the magnitude of the magnetic field and the component; Panel (b) shows the alpha bulk speed; Panel (c) shows the proton bulk speed; Panel (d) shows the difference between the alpha and proton bulk speed; and Panel (e) shows the angle between the B and V vectors.
In Figure 2, we plot a 2D histogram plot of the vs. and vs using the same data of the fast solar wind stream shown in Figure 1. Figure 2a shows that there is no correlation between the and . Figure 2b shows that there is a nice anti-correlation between and . Similar behavior has been observed in different works, e.g., Matteini et al. [19,20], where the authors show that in the fast wind streams there is a clear correlation and anti-correlation between and depending on the polarity. It has been suggested that the reason for the nice correlation/anti-correlation due to the Alfvénicity of the wind is that Alfvénic fluctuations control the speed of the protons.
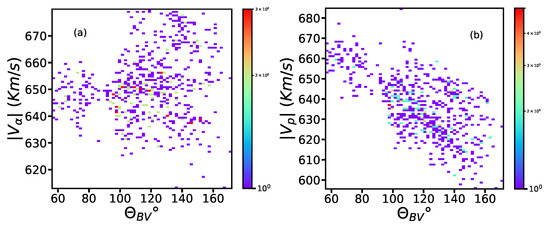
Figure 2.
2D histogram plot of (a) alpha bulk speed () and (b) proton bulk speed () vs. for the fast wind interval shown in Figure 1. The time of the interval is 10 June 2015. The color bar represents the number of counts.
In Figure 3a,b, we show a similar plot to Figure 2a,b for a different fast wind stream. Here, it can be observed that this fast wind stream is made up of two streams with different base speeds; and as functions of show the two populations clearly. There is no correlation between and , as observed before, whereas vs. shows a nice correlation for both the populations. Interestingly, a correlation is observed here, not an anti-correlation as before; this difference is due to the variation in the magnetic field polarity of the intervals.
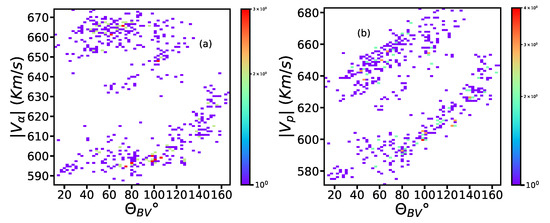
Figure 3.
2D histogram plot of (a) alpha bulk speed () and (b) proton bulk speed () vs. of the fast wind interval observed by WIND at 1 au on 15 March 2007. The color bar represents the number of counts.
In Figure 4, we show the drift speed of the protons and alphas () as a function of for the cases shown in Figure 2 and Figure 3, which have opposite magnetic field polarities. It can be observed that there is a clear correlation and anti-correlation between and depending on the polarity of the magnetic field. Interestingly, the two different populations which are clearly evident in Figure 3 are not visible in Figure 4b. The drift speeds of a fast stream with two different base speeds are dependent only on .
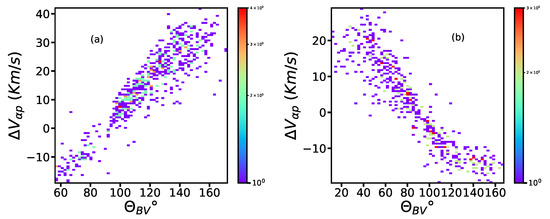
Figure 4.
2D histogram plot of alpha proton drift speed as a function of of the fast wind intervals observed by WIND at 1 au on 10 June 2015 (a) and 15 March 2007 (b). The color bar represents the number of counts.
In Figure 5, we show the drift speed of the protons and alphas () as a function of for slow Alfvénic (Figure 5a) and slow non-Alfvénic (Figure 5b) wind intervals at 1 au. It can be observed that there is a nice anti-correlation between and for the slow Alfvénic wind case, as in the fast wind case. This is the first time that such a phenomenon has been reported for the case of the slow wind. In the case of the slow non-Alfvénic wind, there is no correlation between and .
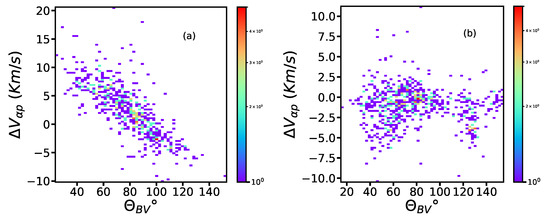
Figure 5.
2D histogram plot of alpha proton drift speed as a function of of the slow wind intervals observed by WIND at 1 au for the slow Alfvénic wind interval of 19 December 2000 (a) and slow non-Alfvénic wind interval on 5 February 2015 (b). The color bar represents the number of counts.
In Figure 6, we show similar plots as before for data closer to the sun (∼0.3 au). In Figure 6a,b, similar behavior of anti-correlation/correlation between and can be seen for the fast wind and slow Alfvénic wind. On the other hand, Figure 6c shows that there is no correlation between and for the case of the non-Alfvénic slow solar wind, even closer to the sun.
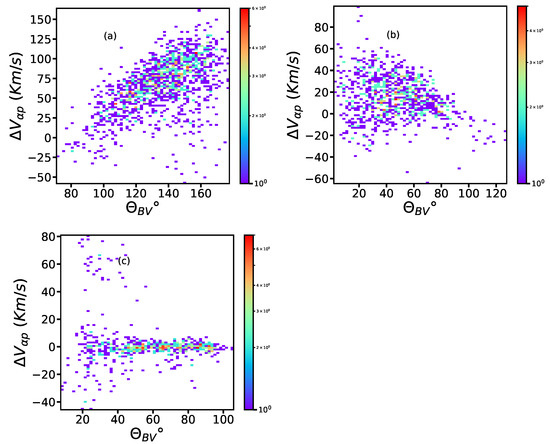
Figure 6.
2D histogram plot of alpha proton drift speed as a function of for the intervals around 0.3 au using the HELIOS 1 and 2 data. (a): fast wind interval from HELIOS 2 on 17 April 1976; (b): slow Alfvénic wind interval from HELIOS 1 on 23 March 1975; (c): slow non-Alfvénic wind interval from HELIOS 1 on 19 March 1975. The color bar represents the number of counts.
Our analysis of different samples at 1 au and around 0.3 au point to the fact that correlations/anti-correlations are only observed for the cases of Alfvénic wind streams, irrespective of distance and speed; therefore, the observed phenomena could be considered a general behavior of the Alfvénic wind.
Model Fitting
In this section, we look at possible models which could explain the relationship between the alpha proton drift speed () and . Previous studies by Matteini et al. [19,20] have shown that when large-amplitude Alfvénic fluctuations are present, the proton bulk speed can be reasonably estimated by the relation
where is the proton base speed, is the Alfvén velocity and is the Alfvén ratio.
The alpha bulk speed can be estimated by the relation
With the above Equations (3) and (4), we have a relation to explain how the drift speed might vary if the large-amplitude Alfvénic fluctuations control the proton and alpha particle motions:
Using Equation (5), we can fit the analyzed samples; an example of such fitting is shown in Figure 7. It can be observed that the mentioned equation accurately models the drift speed as a function of at 1 au and 0.3 au. This fitting is observed in all seventeen of the analyzed Alfvénic samples. This indicates that Alfvénic fluctuations control the drift speed between the alphas and protons in Alfvénic streams.
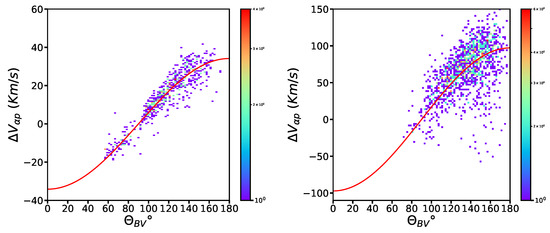
Figure 7.
2D histogram plot of alpha proton drift speed as a function of ; the red curve is fitted using the equation , where for the fast wind interval of 10 June 2015 (left) from WIND at 1 au and the fast wind interval of 17 April 1976 (right) from HELIOS 2 ∼0.3 au. The color bar represents the number of counts.
4. Discussion and Conclusions
In this study, we used the alpha proton drift speed () as an indicator in order to analyze how the alpha proton dynamics are regulated in different types of solar wind streams in the inner heliosphere. Our analysis was performed using the data from the WIND and HELIOS 1 and 2 missions.
In order to understand how the alpha proton drift speeds () are constrained in the inner heliopshere, we analyzed the relationship between and the angle between the magnetic (B) and velocity (V) field vectors (). We separated the solar wind into three types (fast, slow Alfvénic, and slow non-Alfvénic) at different distances from the sun. For this study, we used the alpha and proton moments along with the magnetic fields from the WIND mission at 1 au. To verify whether the observed relations are a general behavior or are confined to 1 au, we looked into similar data at different distances from the sun using the HELIOS 1 and 2 data.
Our studies at 1 au show that there is good correlation/anti-correlation between and in the fast wind and slow Alfvénic wind intervals. There is no correlation for the case of slow non-Alfvénic wind. Similarly, analysis of the intervals in the inner-heliosphere between 0.3 to 1 au shows the same behavior. We observed good correlation/anti-correlation between and in the fast and slow Alfvénic wind intervals, and no correlation in the case of the slow non-Alfvénic wind. The reason for these observations is that alphas are expected to not respond to the magnetic field oscillations; instead, they “surf” the large amplitude fluctuations in the solar wind [9,20,21]. On the other hand, protons are affected by large-amplitude magnetic field fluctuations; depending on their polarity, they show a nice correlation/anti-correlation between and , as shown in the studies of Matteini et al. [19,20].
We observed this correlation between and only in highly Alfvénic wind intervals, irrespective of the distance and speed of the streams. Correlation or anti-correlation is dependent on the polarity of the interval. The correlation behaviour is observed at different radial distances from the sun, indicating generalized behaviour in the Alfvénic wind.
The nascent solar wind studies by UVCS instrument on board SOHO have shown that minor ions become greatly accelerated compared to protons, and are constrained by the Alfvén speed [22,23,24]. Similarly, in our analysis we observe that the drift speed is always constrained by the local Alfvén speed. However, as the Alfvén speed decreases with distance from the sun and the proton speed is nearly constant, alphas are decelerated in interplanetary space.
To the best of our knowledge, this is the first time such a clear correlation between the alpha proton drift speed and the angle between the magnetic field vector and velocity vector has been shown in slow wind intervals. These slow wind intervals are special in that they are Alfvénic. All the observed properties are dependent on the Alfvénicity of the solar wind, which suggests that large-amplitude Alfvénic fluctuations are responsible for constraining alpha–proton drift speeds in the inner heliosphere. Importantly, from our studies it can be understood that even when in situ instruments are not able to measure the distribution of alphas, the bulk speed of the alpha particles can be estimated to a good approximation using the proton speed and the angle between the magnetic (B) and velocity (V) field vectors () when the wind is Alfvénic.
Author Contributions
Conceptualization, V.K.J.; Methodology, V.K.J. and R.B.; Validation, R.D.M.; Formal analysis, V.K.J.; Investigation, V.K.J., R.B., R.D.M., R.D., D.P., D.T. and N.E.R.; Writing—original draft, V.K.J.; Writing—review & editing, V.K.J., R.B. and R.D.M.; Supervision, R.B. and N.E.R.; Funding acquisition, R.B. and N.E.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used in this study are available at https://cdaweb.gsfc.nasa.gov/ and https://helios-data.ssl.berkeley.edu/, accessed on 7 December 2022.
Acknowledgments
V.K.J. acknowledges support from the Parker Solar Probe mission as part of NASA’s Living with a Star (LWS) program under contract NNN06AA01C, as well as the support of the Italian Space Agency (ASI) under contract 2018-30-HH.0.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Robbins, D.E.; Hundhausen, A.J.; Bame, S.J. Helium in the solar wind. J. Geophys. Res. 1970, 75, 1178. [Google Scholar] [CrossRef]
- Bame, S.J.; Asbridge, J.R.; Feldman, W.C.; Felthauser, H.E.; Gosling, J.T. A search for a general gradient in the solar wind speed at low solar latitudes. J. Geophys. Res. 1977, 82, 173. [Google Scholar] [CrossRef]
- Kasper, J.C.; Stevens, M.L.; Lazarus, A.J.; Steinberg, J.T.; Ogilvie, K.W. Solar Wind Helium Abundance as a Function of Speed and Heliographic Latitude: Variation through a Solar Cycle. Astrophys. J. 2007, 660, 901–910. [Google Scholar] [CrossRef]
- Ebert, R.W.; McComas, D.J.; Elliott, H.A.; Forsyth, R.J.; Gosling, J.T. Bulk properties of the slow and fast solar wind and interplanetary coronal mass ejections measured by Ulysses: Three polar orbits of observations. J. Geophys. Res. Space Phys. 2009, 114, A01109. [Google Scholar] [CrossRef]
- Kasper, J.C.; Abiad, R.; Austin, G.; Balat-Pichelin, M.; Bale, S.D.; Belcher, J.W.; Berg, P.; Bergner, H.; Berthomier, M.; Bookbinder, J.; et al. Solar Wind Electrons Alphas and Protons (SWEAP) Investigation: Design of the Solar Wind and Coronal Plasma Instrument Suite for Solar Probe Plus. Space Sci. Rev. 2016, 204, 131–186. [Google Scholar] [CrossRef]
- Ogilvie, K.W. Differences between the bulk speeds of hydrogen and helium in the solar wind. J. Geophys. Res. 1975, 80, 1335. [Google Scholar] [CrossRef]
- Asbridge, J.R.; Bame, S.J.; Feldman, W.C.; Montgomery, M.D. Helium and hydrogen velocity differences in the solar wind. J. Geophys. Res. 1976, 81, 2719. [Google Scholar] [CrossRef]
- Grünwaldt, H.; Rosenbauer, H. Study of Helium and Hydrogen Velocity Differences as derived from Heos-2 S-210 Solar Wind Measurements. In Pleins Feux sur la Physique Solaire; Dumont, S., Roesch, J., Eds.; Centre National de la Recherche Scientifique: Paris, France, 1978; p. 377. [Google Scholar]
- Marsch, E.; Rosenbauer, H.; Schwenn, R.; Muehlhaeuser, K.H.; Neubauer, F.M. Solar wind helium ions: Obsevations of the Helios solar probes between 0.3 and 1 AU. J. Geophys. Res. 1982, 87, 35–51. [Google Scholar] [CrossRef]
- Durovcová, T.; Šafránková, J.; Němeček, Z. Evolution of Relative Drifts in the Expanding Solar Wind: Helios Observations. Sol. Phys. 2019, 294, 97. [Google Scholar] [CrossRef]
- Berger, L.; Wimmer-Schweingruber, R.F.; Gloeckler, G. Systematic Measurements of Ion-Proton Differential Streaming in the Solar Wind. Phys. Rev. Lett. 2011, 106, 151103. [Google Scholar] [CrossRef]
- Ogilvie, K.W.; Chornay, D.J.; Fritzenreiter, R.J.; Hunsaker, F.; Keller, J.; Lobell, J.; Miller, G.; Scudder, J.D.; Sittler, E.C.; Torbert, R.B.; et al. SWE, A Comprehensive Plasma Instrument for the Wind Spacecraft. Space Sci. Rev. 1995, 71, 55–77. [Google Scholar] [CrossRef]
- Lepping, R.P.; Acũna, M.H.; Burlaga, L.F.; Farrell, W.M.; Slavin, J.A.; Schatten, K.H.; Mariani, F.; Ness, N.F.; Neubauer, F.M.; Whang, Y.C.; et al. The Wind Magnetic Field Investigation. Space Sci. Rev. 1995, 71, 207–229. [Google Scholar] [CrossRef]
- Schwenn, R.; Rosenbauer, H.; Miggenrieder, H. Das Plasmaexperiment auf Helios (E1). Raumfahrtforschung 1975, 19, 226–232. [Google Scholar]
- Musmann, G.; Neubauer, F.M.; Maier, A.; Lammers, E. The Foerstersonden magnetic field experiment /E 2/. Raumfahrtforschung 1975, 19, 232–237. [Google Scholar]
- Scearce, C.; Cantarano, S.; Ness, N.; Mariani, F.; Terenzi, R.; Burlaga, L. The Rome-GSFC magnetic field experiment for Helios A and B (E3). Raumfahrtforschung 1975, 19, 237–240. [Google Scholar]
- Stansby, D.; Salem, C.; Matteini, L.; Horbury, T. A New Inner Heliosphere Proton Parameter Dataset from the Helios Mission. Sol. Phys. 2018, 293, 155. [Google Scholar] [CrossRef]
- Stansby, D.; Perrone, D.; Matteini, L.; Horbury, T.S.; Salem, C.S. Alpha particle thermodynamics in the inner heliosphere fast solar wind. Astron. Astrophys. 2019, 623, L2. [Google Scholar] [CrossRef]
- Matteini, L.; Horbury, T.S.; Neugebauer, M.; Goldstein, B.E. Dependence of solar wind speed on the local magnetic field orientation: Role of Alfvénic fluctuations. Geophys. Res. Lett. 2014, 41, 259–265. [Google Scholar] [CrossRef]
- Matteini, L.; Horbury, T.S.; Pantellini, F.; Velli, M.; Schwartz, S.J. Ion Kinetic Energy Conservation and Magnetic Field Strength Constancy in Multi-fluid Solar Wind Alfvénic Turbulence. Astrophys. J. 2015, 802, 11. [Google Scholar] [CrossRef]
- Goldstein, B.E.; Neugebauer, M.; Smith, E.J. Alfvén waves, alpha particles, and pickup ions in the solar wind. Geophys. Res. Lett. 1995, 22, 3389–3392. [Google Scholar] [CrossRef]
- Kohl, J.L.; Noci, G.; Antonucci, E.; Tondello, G.; Huber, M.C.E.; Cranmer, S.R.; Strachan, L.; Panasyuk, A.V.; Gardner, L.D.; Romoli, M.; et al. UVCS/SOHO Empirical Determinations of Anisotropic Velocity Distributions in the Solar Corona. Astrophys. J. 1998, 501, L127–L131. [Google Scholar] [CrossRef]
- Li, X.; Habbal, S.R.; Kohl, J.L.; Noci, G. The Effect of Temperature Anisotropy on Observations of Doppler Dimming and Pumping in the Inner Corona. Astrophys. J. 1998, 501, L133–L137. [Google Scholar] [CrossRef]
- Cranmer, S.R.; Kohl, J.L.; Noci, G.; Antonucci, E.; Tondello, G.; Huber, M.C.E.; Strachan, L.; Panasyuk, A.V.; Gardner, L.D.; Romoli, M.; et al. An Empirical Model of a Polar Coronal Hole at Solar Minimum. Astrophys. J. 1999, 511, 481–501. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).