Dark Matter Searches with Top Quarks
Abstract
1. Introduction
2. Models with BSM Signatures Involving Top Quarks
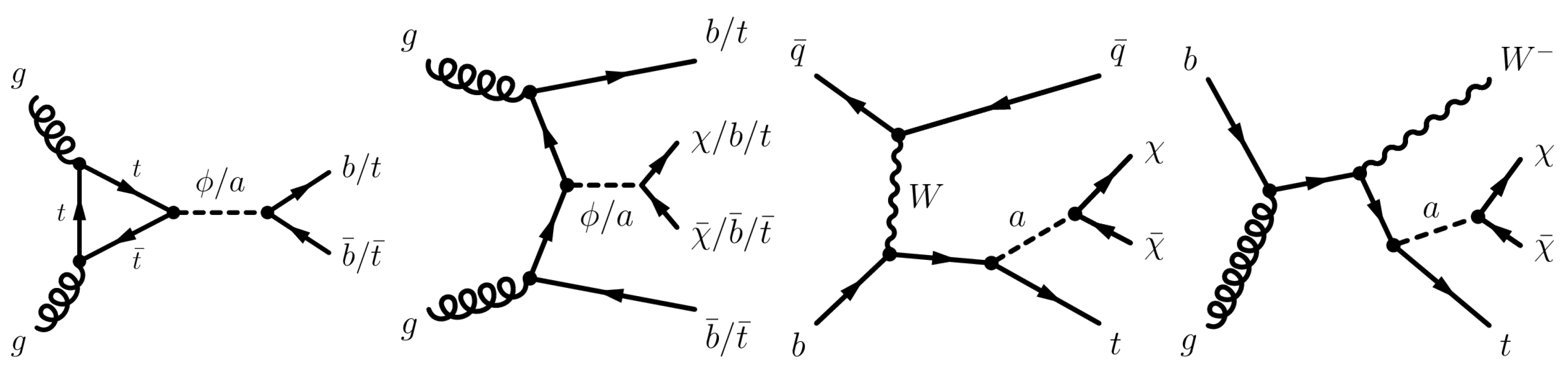
2.1. Vector and Axial-Vector Mediators
2.1.1. Flavor-Conserving Interaction
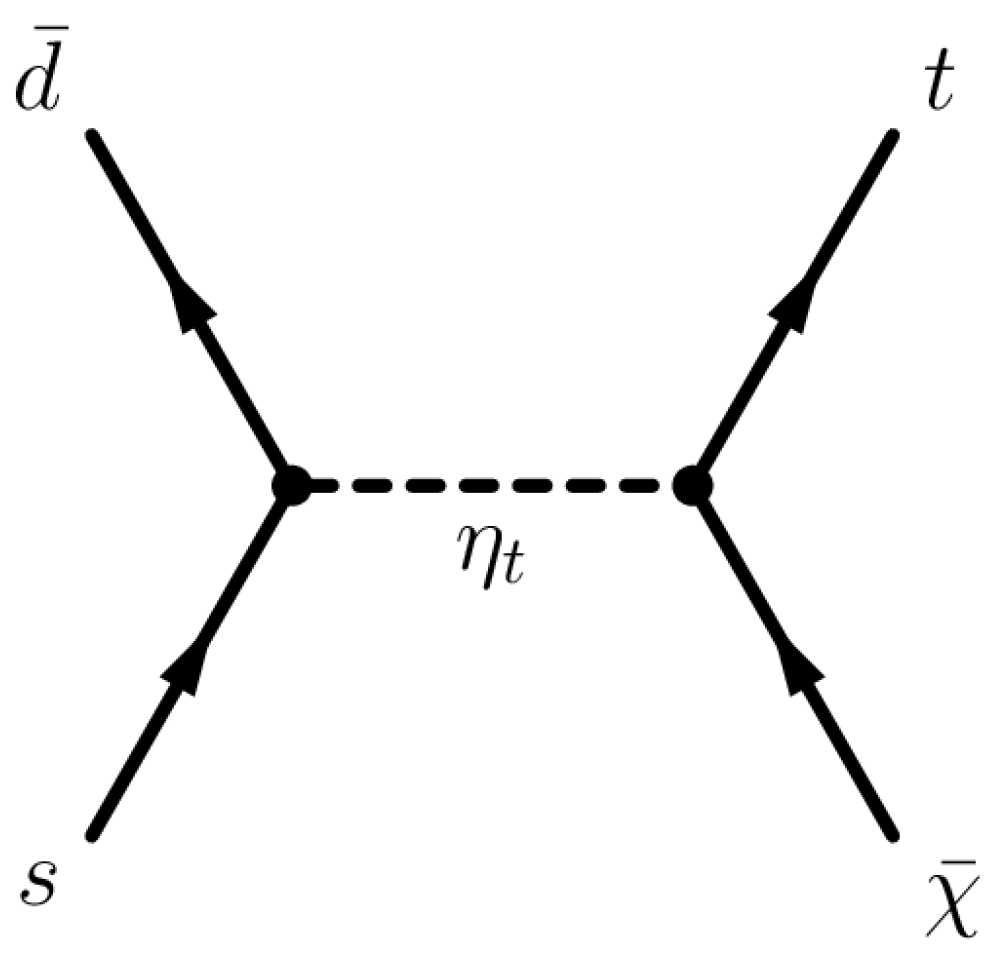
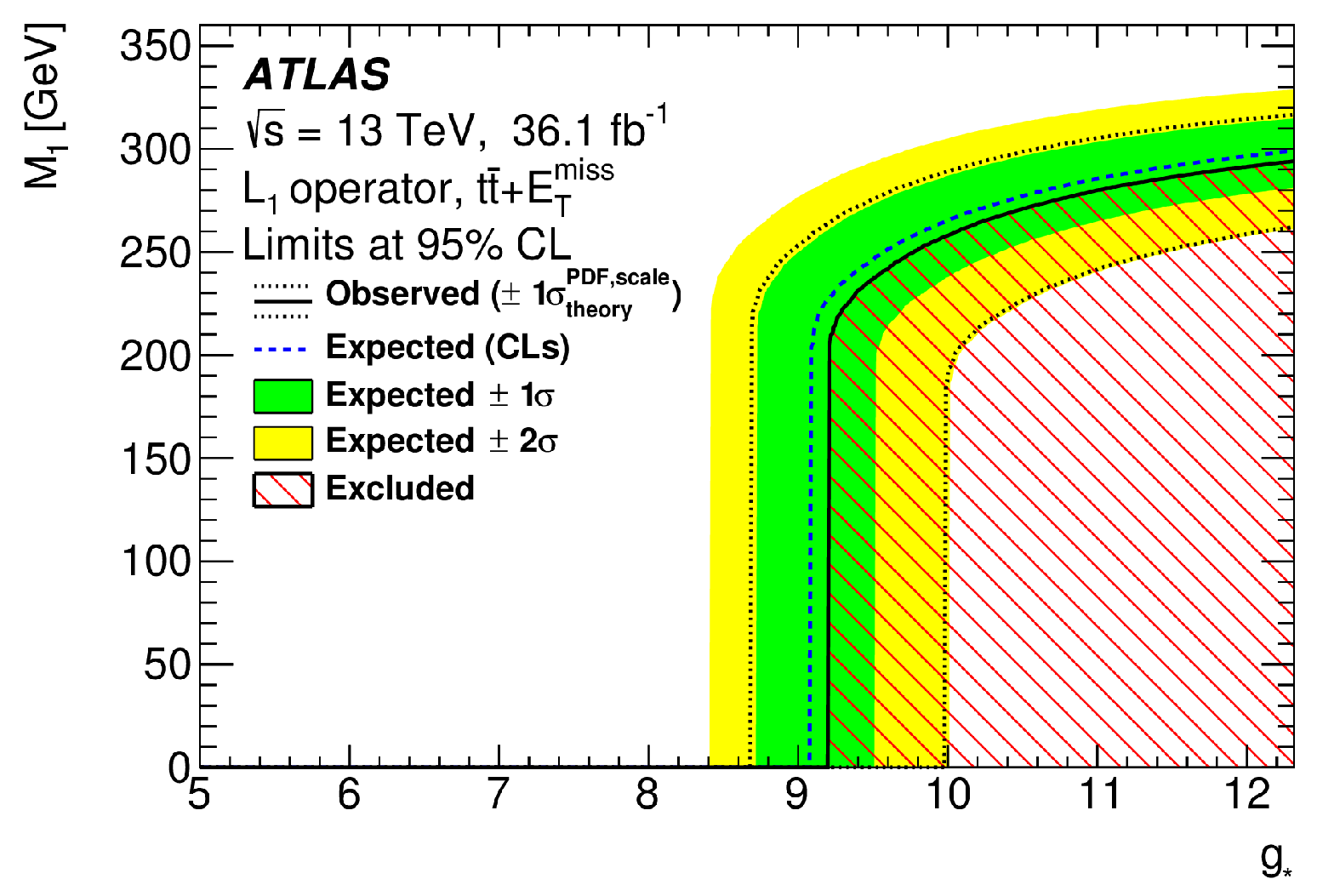
2.1.2. Flavor-Changing Interaction
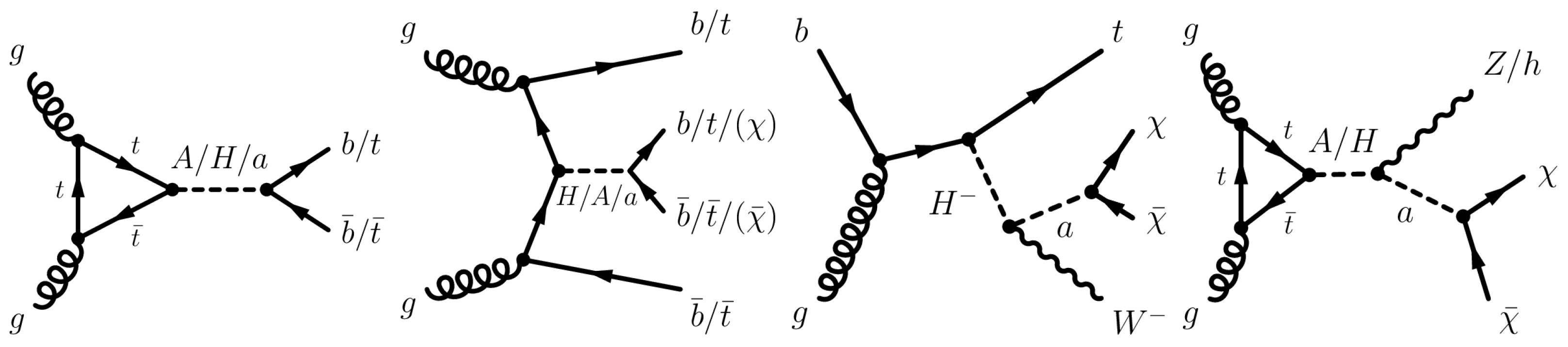
2.2. Scalar and Pseudoscalar Mediators
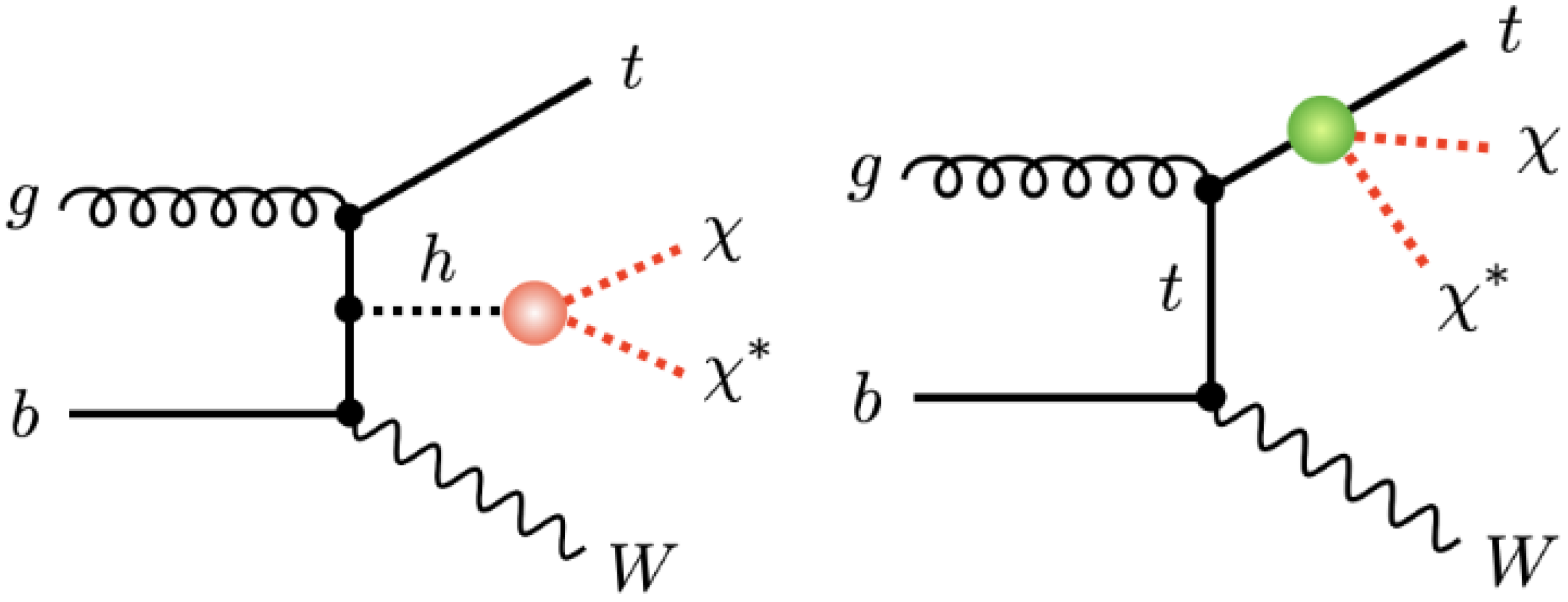
2.2.1. Color-Neutral Interaction
- Visible decay of a mediator produced via gluon-fusion to heavy-flavor quarks, resulting in a resonant or signal.
- Associated production of a mediator that decays either visibly or invisibly with heavy-flavor quarks, leading to a + / signature in the case of invisible mediator decay or characteristic fully visible , , signatures.
- Associated production of an invisibly decaying mediator with a top quark and a light () quark, leading to a + signature.
- Associated production of an invisibly decaying mediator with a top quark and a W boson, resulting in a + signature.
2.2.2. Color-Charged Interaction
2.3. Extended Higgs Sectors
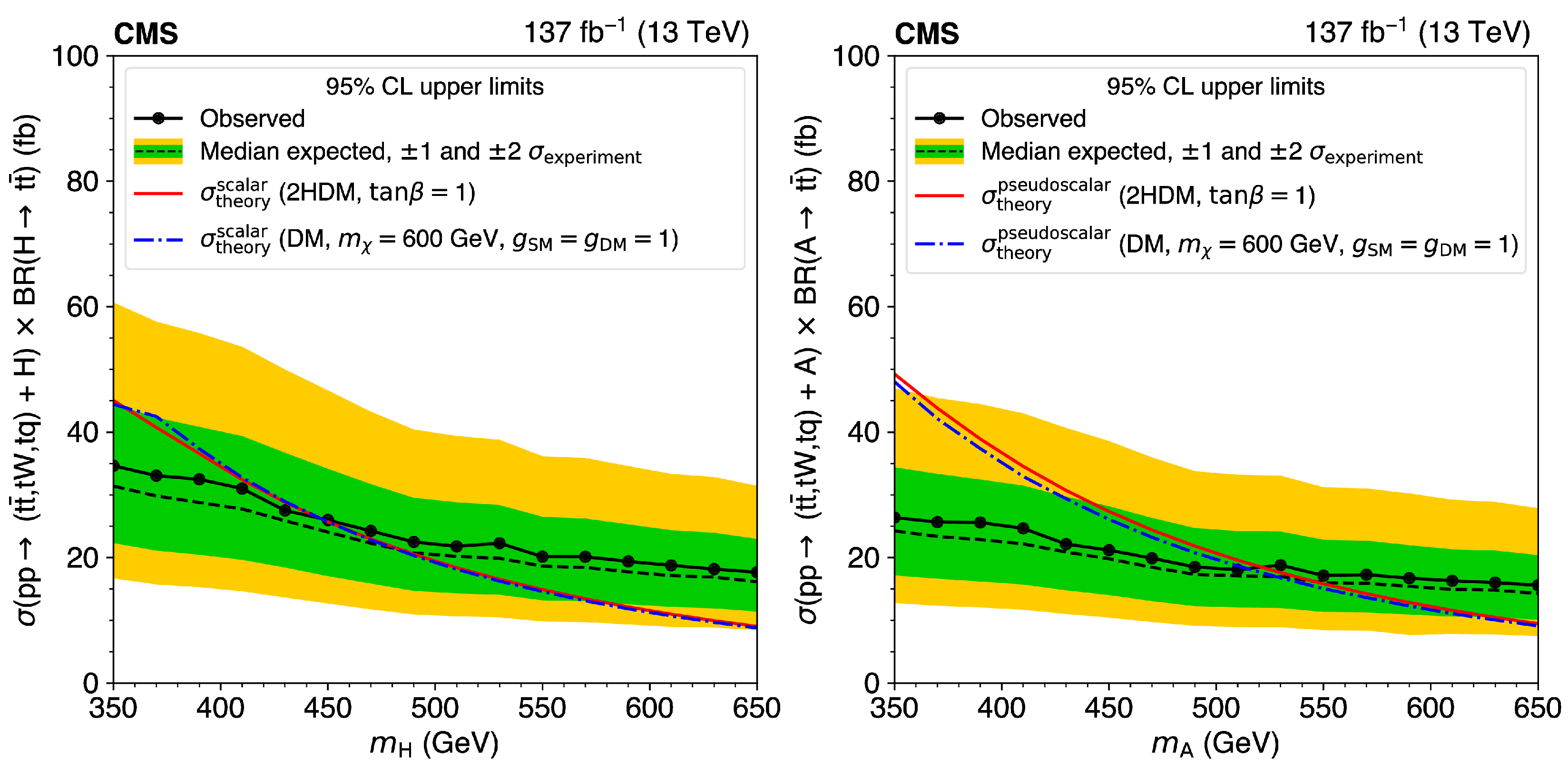
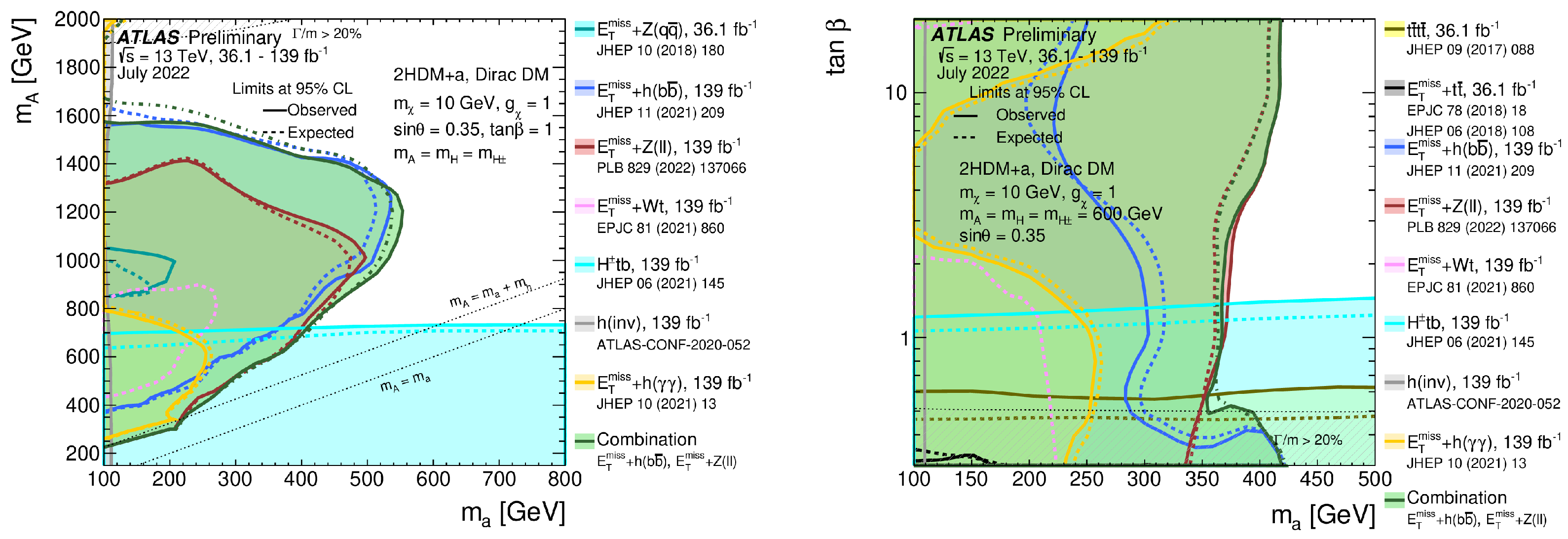
2HDM with a Pseudoscalar Mediator
2.4. EFT Model of Scalar Dark Energy
3. Experimental Signatures
3.1. Final States with Invisible Decays
3.1.1. + t
3.1.2. + and +
3.1.3. +
3.1.4. + , + and +
3.2. Final States without Invisible Decays
3.2.1. Same-Sign
3.2.2.
3.2.3.
3.2.4.
4. Results
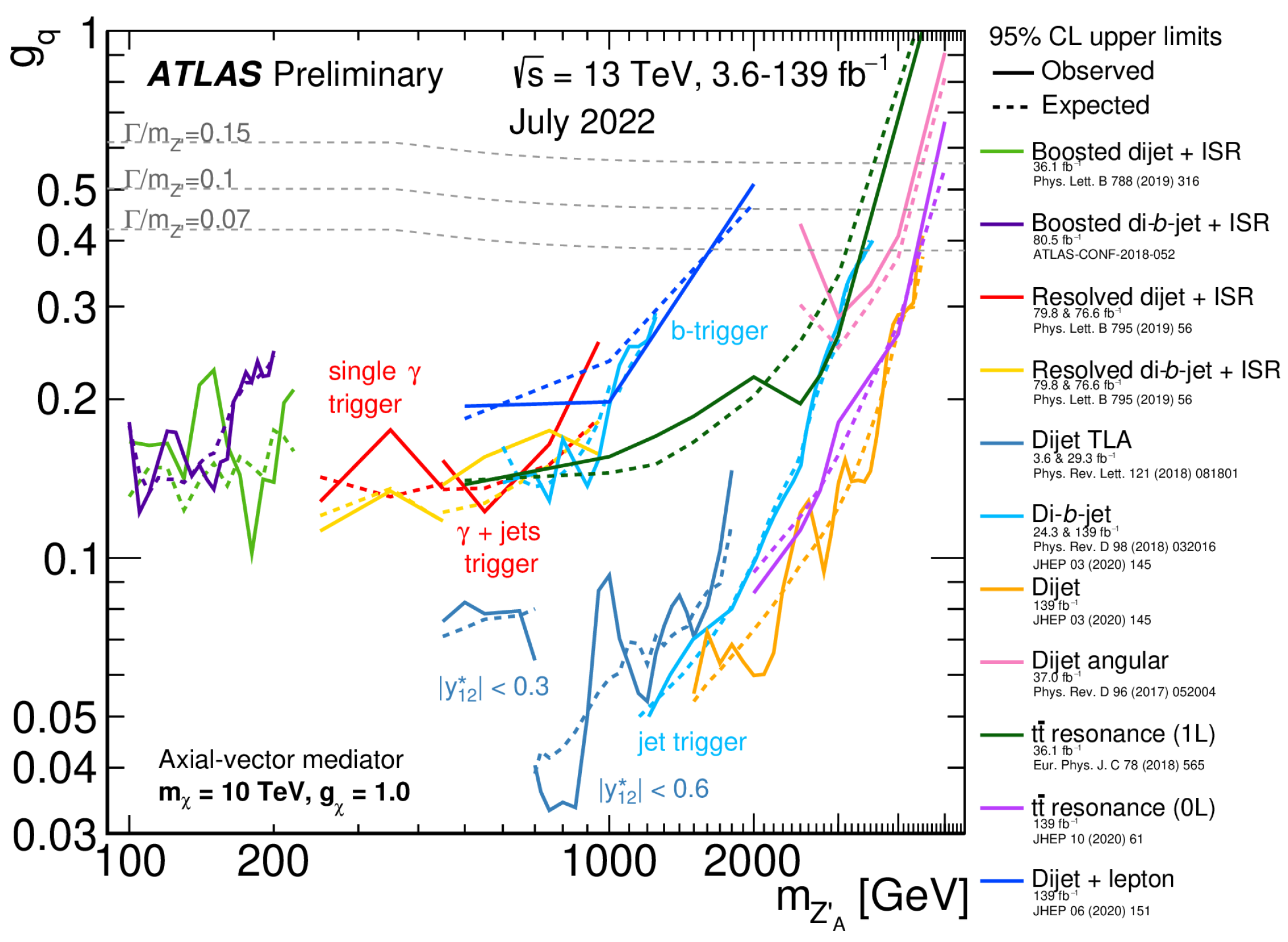
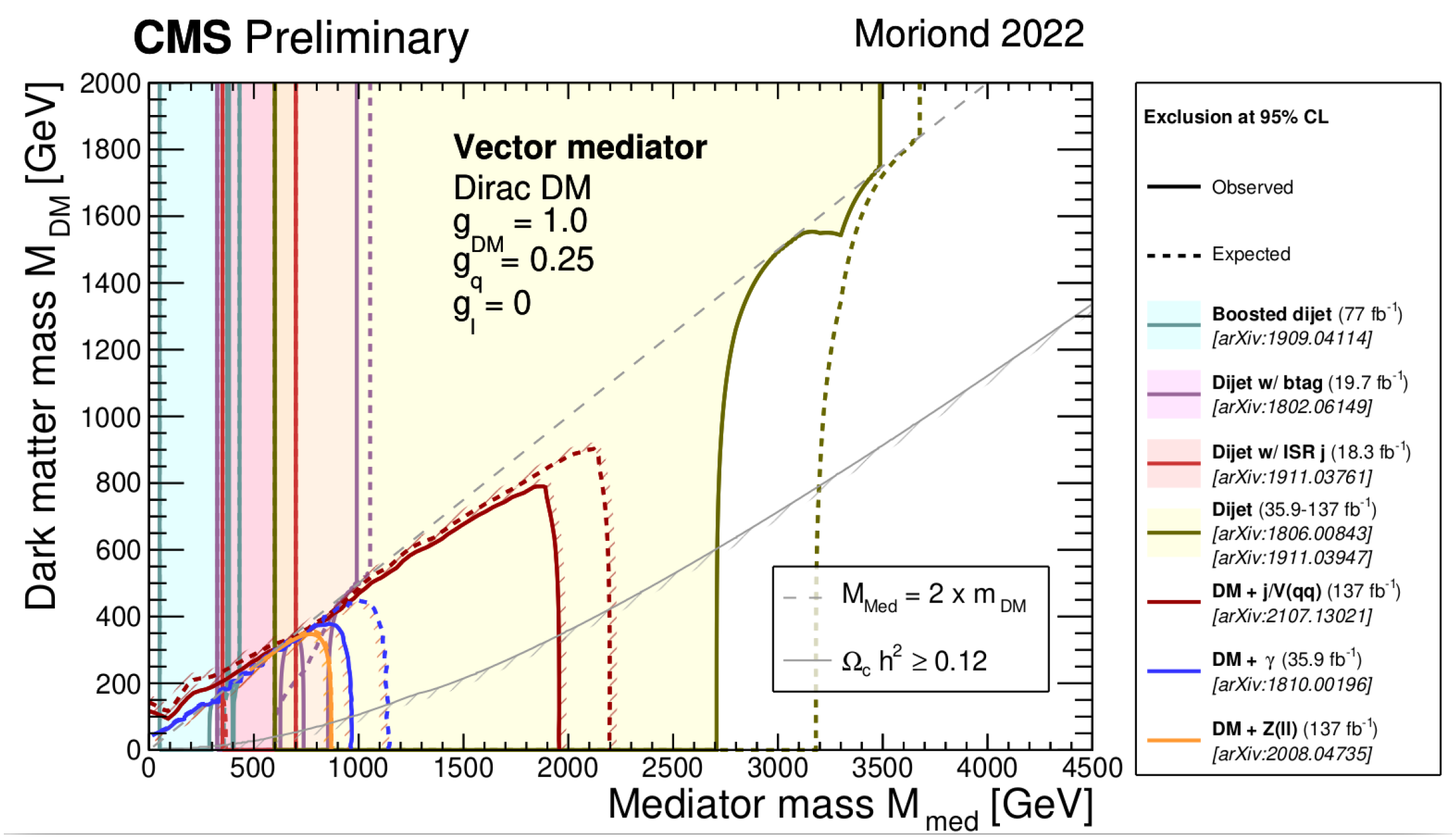
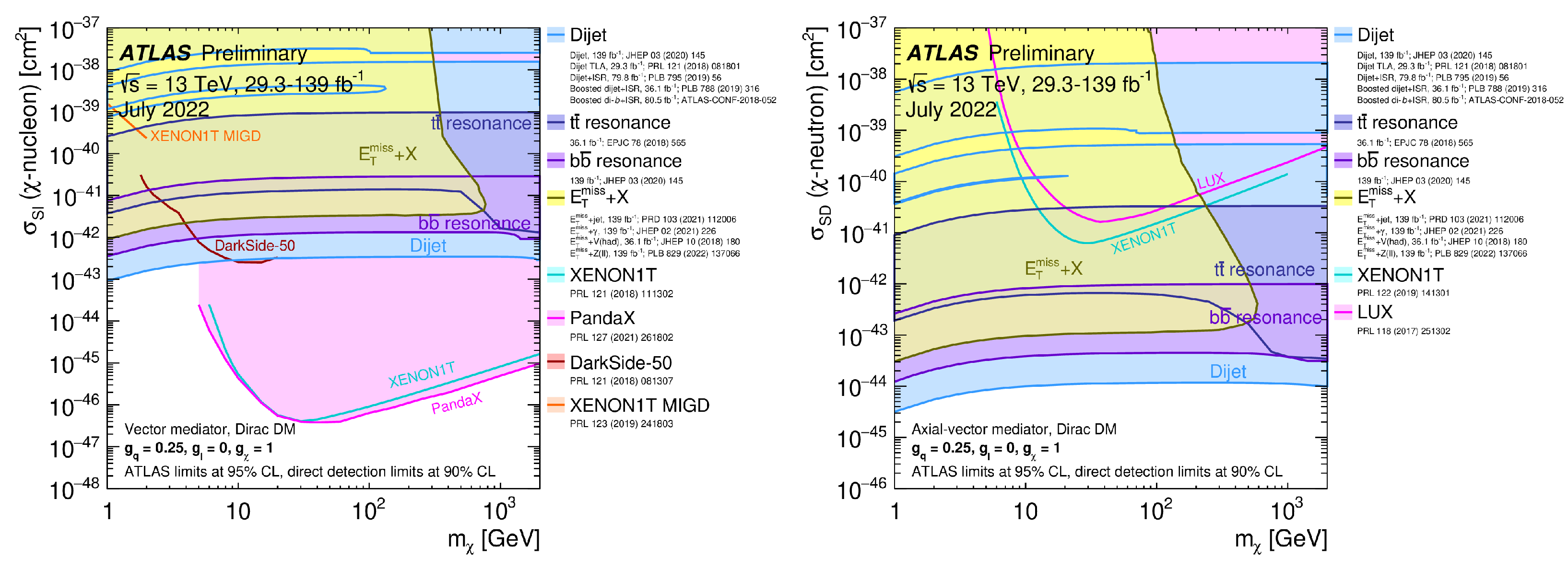
4.1. Vector and Axial-Vector Mediators
4.1.1. Flavor-Conserving Interaction
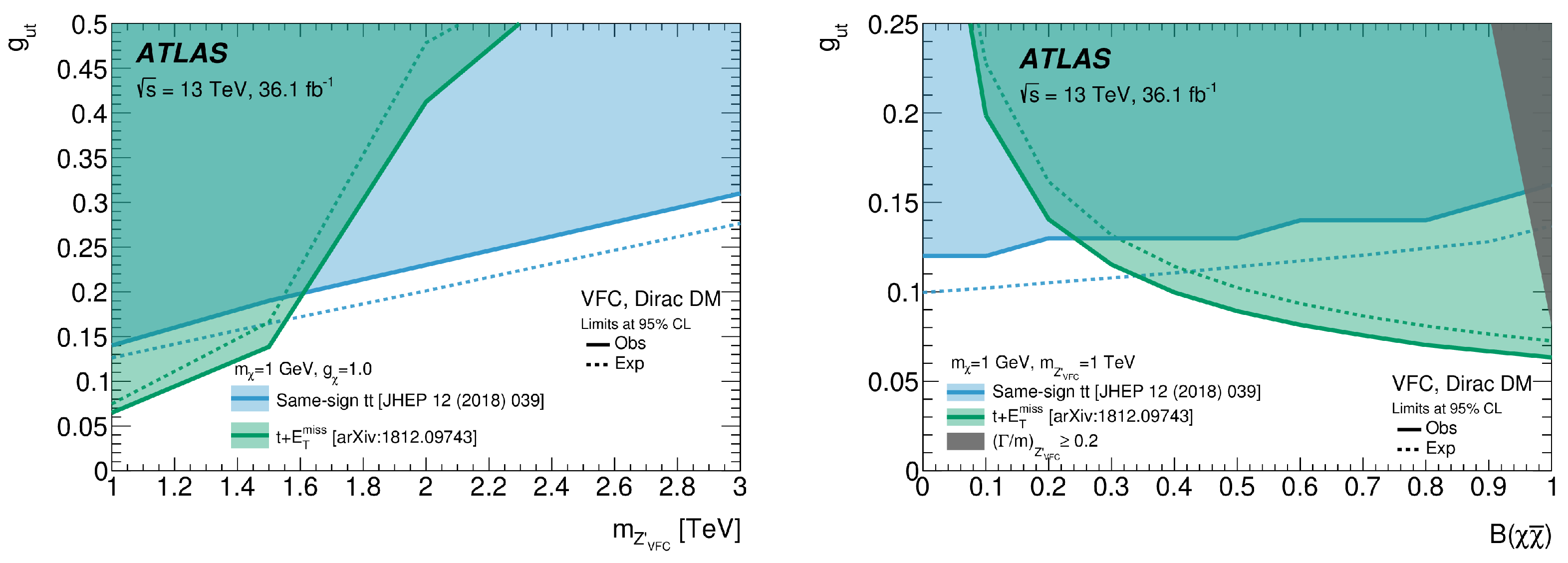
4.1.2. Flavor-Changing Interaction
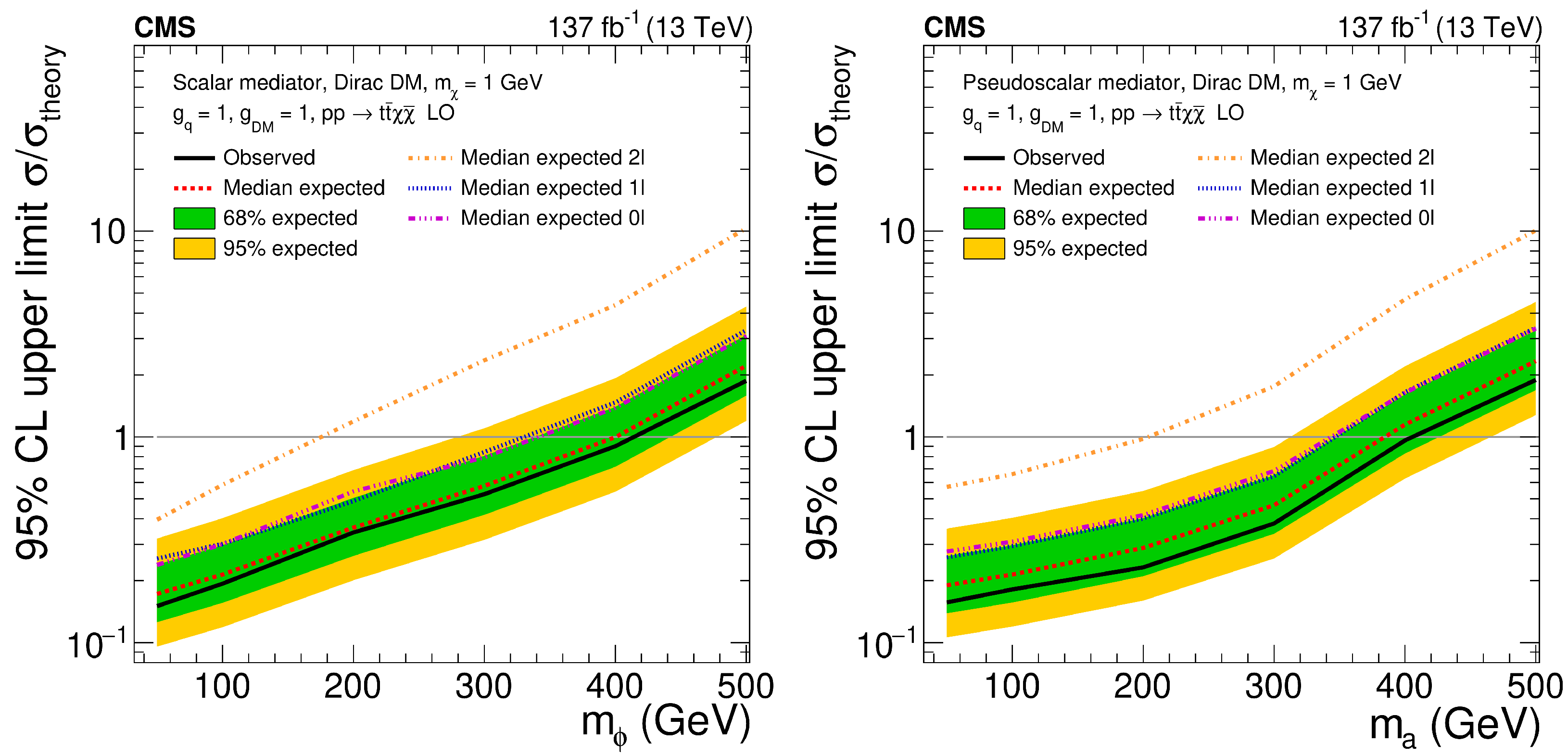
4.2. Scalar and Pseudoscalar Mediators
4.2.1. Color-Neutral Interaction
4.2.2. Color-Charged Interaction
4.3. Extended Higgs Sectors
4.3.1. 2HDM with a Pseudoscalar Mediator
4.4. Scalar DE EFT Model
5. Discussion
6. Outlook
6.1. LHC Run 3
6.1.1. ALPs
6.1.2. Composite Pseudo-Nambu–Goldstone Bosons
6.1.3. Dark Mesons
6.2. HL-LHC and HE-LHC
6.3. FCC-hh
6.4. Future Colliders
6.5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DM | Dark matter |
| DE | Dark energy |
| EFT | Effective field theory |
References
- Trimble, V. Existence and Nature of Dark Matter in the Universe. Annu. Rev. Astron. Astrophys. 1987, 25, 425. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rep. 2005, 405, 279. [Google Scholar] [CrossRef]
- Feng, J.L. Dark Matter Candidates from Particle Physics and Methods of Detection. Annu. Rev. Astron. Astrophys. 2010, 48, 495. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.M.; Nolta, R.; Halpern, M.; Hill, R.S.; Odegard, N. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. Suppl. 2013, 208, 19. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2018 results. I. Overview and the cosmological legacy of Planck. Astron. Astrophys. 2020, 641, A1. [Google Scholar] [CrossRef]
- Steigman, G.; Turner, M.S. Cosmological constraints on the properties of weakly interacting massive particles. Nucl. Phys. B 1985, 253, 375. [Google Scholar] [CrossRef]
- Evans, L.; Bryant, P. LHC Machine. JINST 2008, 3, S08001. [Google Scholar] [CrossRef]
- Billard, J.; Boulay, M.; Cebrián, S.; Covi, L.; Fiorillo, G.; Green, A.; Kopp, J.; Majorovits, B.; Palladino, K.; Petricca, F. Direct detection of dark matter—APPEC committee report. Rept. Prog. Phys. 2022, 85, 056201. [Google Scholar] [CrossRef]
- Heros, P.d.l. Status, Challenges and Directions in Indirect Dark Matter Searches. Symmetry 2020, 12, 1648. [Google Scholar] [CrossRef]
- ATLAS Collaboration. The ATLAS Experiment at the CERN Large Hadron Collider. JINST 2008, 3, S08003. [Google Scholar]
- CMS Collaboration. The CMS experiment at the CERN LHC. JINST 2008, 3, S08004. [Google Scholar]
- Buchmueller, O.; Doglioni, C.; Wang, L.T. Search for dark matter at colliders. Nat. Phys. 2017, 13, 217–223. [Google Scholar] [CrossRef]
- Boveia, A.; Doglioni, C. Dark Matter Searches at Colliders. Ann. Rev. Nucl. Part. Sci. 2018, 68, 429. [Google Scholar] [CrossRef]
- CDF Collaboration. Observation of top quark production in ppbar collisions with the Collider-Detector at Fermilab. Phys. Rev. Lett. 1995, 74, 2626. [Google Scholar] [CrossRef] [PubMed]
- D0 Collaboration. Observation of the Top Quark. Phys. Rev. Lett. 1995, 74, 2632. [Google Scholar] [CrossRef] [PubMed]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- ATLAS/CMS Dark Matter Forum. Dark Matter benchmark models for early LHC Run-2 Searches: Report of the ATLAS/CMS Dark Matter Forum. Phys. Dark Univ. 2020, 27, 100371. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Constraints on mediator-based dark matter and scalar dark energy models using = 13 TeV pp collision data collected by the ATLAS detector. JHEP 2019, 5, 142. [Google Scholar]
- Kamenik, J.F.; Zupan, J. Discovering Dark Matter Through Flavor Violation at the LHC. Phys. Rev. D 2011, 84, 111502. [Google Scholar] [CrossRef]
- Boucheneb, I.; Cacciapaglia, G.; Deandrea, A.; Fuks, B. Revisiting monotop production at the LHC. JHEP 2015, 1, 17. [Google Scholar] [CrossRef]
- ATLAS Collaboration, Search for new phenomena in events with same-charge leptons and b-jets in pp collisions at = 13 TeV with the ATLAS detector. JHEP 2018, 12, 39.
- D’Ambrosio, G.; Giudice, G.F.; Isidori, G.; Strumia, A. Minimal flavor violation: An Effective field theory approach. Nucl. Phys. B 2002, 645, 155. [Google Scholar] [CrossRef]
- Buckley, M.R.; Feld, D.; Goncalves, D. Scalar Simplified Models for Dark Matter. Phys. Rev. D 2015, 91, 015017. [Google Scholar] [CrossRef]
- Fayet, P. Supersymmetry and weak, electromagnetic and strong interactions. Phys. Lett. B 1976, 64, 159. [Google Scholar] [CrossRef]
- Fayet, P. Spontaneously broken supersymmetric theories of weak, electromagnetic and strong interactions. Phys. Lett. B 1977, 69, 489. [Google Scholar] [CrossRef]
- Djouadi, A. The Higgs sector of supersymmetric theories and the implications for high-energy colliders. Eur. Phys. J. C 2009, 59, 389. [Google Scholar] [CrossRef]
- Particle Data Group. The Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Carena, M.; Ellis, J.; Lee, J.S.; Pilaftsis, A.; Wagner, C.E. CP Violation in Heavy MSSM Higgs Scenarios. JHEP 2016, 2, 123. [Google Scholar] [CrossRef]
- Fuchs, E.; Weiglein, G. Impact of CP-violating interference effects on MSSM Higgs searches. Eur. Phys. J. C 2018, 78, 87. [Google Scholar] [CrossRef]
- Berlin, A.; Lin, T.; Wang, L.T. Mono-Higgs Detection of Dark Matter at the LHC. JHEP 2014, 6, 078. [Google Scholar] [CrossRef]
- Bauer, M.; Haisch, U.; Kahlhoefer, F. Simplified dark matter models with two Higgs doublets: I. Pseudoscalar mediators. JHEP 2017, 5, 138. [Google Scholar] [CrossRef]
- Goncalves, D.; Machado, P.A.N.; No, J.M. Simplified Models for Dark Matter Face their Consistent Completions. Phys. Rev. D 2017, 95, 055027. [Google Scholar] [CrossRef]
- Bell, N.F.; Busoni, G.; Sanderson, I.W. Self-consistent Dark Matter Simplified Models with an s-channel scalar mediator. JCAP 2017, 3, 15. [Google Scholar] [CrossRef][Green Version]
- Abe, T.; Fujiwara, M.; Hisano, J. Loop corrections to dark matter direct detection in a pseudoscalar mediator dark matter model. JHEP 2019, 2, 28. [Google Scholar] [CrossRef]
- Gunion, J.F.; Haber, H.E. The CP conserving two Higgs doublet model: The Approach to the decoupling limit. Phys. Rev. D 2003, 67, 075019. [Google Scholar] [CrossRef]
- Branco, G.C.; Ferreira, P.M.; Lavoura, L.; Rebelo, M.N.; Sher, M.; Silva, J.P. Theory and phenomenology of two-Higgs-doublet models. Phys. Rept. 2012, 516, 1. [Google Scholar] [CrossRef]
- LHC Dark Matter Working Group. LHC Dark Matter Working Group: Next-generation spin-0 dark matter models. Phys. Dark Univ. 2020, 27, 100351. [Google Scholar] [CrossRef]
- ATLAS Collaboration. ATLAS-CONF-2021-036. Available online: https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/CONFNOTES/ATLAS-CONF-2021-036 (accessed on 10 October 2022).
- Brax, P.; Burrage, C.; Englert, C.; Spannowsky, M. LHC Signatures Of Scalar Dark Energy. Phys. Rev. D 2016, 94, 084054. [Google Scholar] [CrossRef]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363. [Google Scholar] [CrossRef]
- Joyce, A.; Jain, B.; Khoury, J.; Trodden, M. Beyond the Cosmological Standard Model. Phys. Rept. 2015, 568, 1. [Google Scholar] [CrossRef]
- ATLAS Collaboration. ATLAS-CONF-2022-036. Available online: https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/CONFNOTES/ATLAS-CONF-2022-036/ (accessed on 10 October 2022).
- CMS Collaboration. Search for dark matter in events with energetic, hadronically decaying top quarks and missing transverse momentum at = 13 TeV. JHEP 2018, 6, 027. [Google Scholar]
- Cacciari, M.; Salam, G.P.; Soyez, G. The anti-kt jet clustering algorithm. JHEP 2008, 4, 63. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Performance of top-quark and W-boson tagging with ATLAS in Run 2 of the LHC. Eur. Phys. J. C 2019, 79, 375. [Google Scholar] [CrossRef]
- ATLAS Collaboration. ATL-PHYS-PUB-2020-017. Available online: https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/PUBNOTES/ATL-PHYS-PUB-2020-017/ (accessed on 10 October 2022).
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. KDD 2016, 16, 785. [Google Scholar]
- Thaler, J.; Tilburg, K.V. Identifying Boosted Objects with N-subjettiness. JHEP 2011, 3, 15. [Google Scholar] [CrossRef]
- Larkoski, A.J.; Salam, G.P.; Thaler, J. Energy Correlation Functions for Jet Substructure. JHEP 2013, 6, 108. [Google Scholar] [CrossRef]
- Moult, I.; Necib, L.; Thaler, J. New Angles on Energy Correlation Functions. JHEP 2016, 12, 153. [Google Scholar] [CrossRef]
- Hoecker, A.; Speckmayer, P.; Stelzer, J.; Therhaag, J.; Toerne, E.; Voss, H.; Backes, M.; Carli, T.; Cohen, O.; Christov, A.; et al. TMVA—Toolkit for Multivariate Data Analysis. arXiv 2007, arXiv:0703039. [Google Scholar]
- ATLAS Collaboration. Search for large missing transverse momentum in association with one top-quark in proton-proton collisions at = 13 TeV with the ATLAS detector. JHEP 2019, 5, 41. [Google Scholar]
- CMS Collaboration. Search for dark matter produced in association with a single top quark or a top quark pair in proton-proton collisions at = 13 TeV. JHEP 2019, 3, 141. [Google Scholar]
- ATLAS Collaboration. Search for dark matter produced in association with a single top quark in = 13 TeV pp collisions with the ATLAS detector. Eur. Phys. J. C 2021, 81, 860. [Google Scholar]
- ATLAS Collaboration. ATLAS-CONF-2022-012. Available online: https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/CONFNOTES/ATLAS-CONF-2022-012/ (accessed on 10 October 2022).
- CMS Collaboration. Combined searches for the production of supersymmetric top quark partners in proton-proton collisions at = 13 TeV. Eur. Phys. J. C 2021, 81, 970. [Google Scholar] [CrossRef]
- CMS Collaboration. Search for top squark production in fully-hadronic final states in proton-proton collisions at s = 13 TeV. Phys. Rev. D 2021, 104, 052001. [Google Scholar] [CrossRef]
- CMS Collaboration. Search for direct top squark pair production in events with one lepton, jets, and missing transverse momentum at 13 TeV with the CMS experiment. JHEP 2020, 5, 32. [Google Scholar]
- CMS Collaboration. Search for top squark pair production using dilepton final states in pp collision data collected at = 13 TeV. Eur. Phys. J. C 2021, 81, 3. [Google Scholar] [CrossRef]
- CMS Collaboration. Identification of heavy, energetic, hadronically decaying particles using machine-learning techniques. JINST 2020, 15, P06005. [Google Scholar] [CrossRef]
- CMS Collaboration. Performance of missing transverse momentum reconstruction in proton-proton collisions at = 13 TeV using the CMS detector. JINST 2019, 14, P07004. [Google Scholar] [CrossRef]
- CMS Collaboration. Search for top squarks and dark matter particles in opposite-charge dilepton final states at = 13 TeV. Phys. Rev. D 2018, 97, 032009. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Search for a scalar partner of the top quark in the all-hadronic plus missing transverse momentum final state at = 13 TeV with the ATLAS detector. Eur. Phys. J. C 2020, 80, 737. [Google Scholar]
- ATLAS Collaboration. Search for new phenomena with top quark pairs in final states with one lepton, jets, and missing transverse momentum in pp collisions at = 13 TeV with the ATLAS detector. JHEP 2021, 4, 174. [Google Scholar]
- ATLAS Collaboration. Search for new phenomena in events with two opposite-charge leptons, jets and missing transverse momentum in pp collisions at = 13 TeV with the ATLAS detector. JHEP 2021, 4, 165. [Google Scholar]
- ATLAS Collaboration. Constraints on spin-0 dark matter mediators and invisible Higgs decays using ATLAS 13 TeV pp collision data with two top quarks and missing transverse momentum in the final state. arXiv 2022, arXiv:2211.05426. [Google Scholar]
- ATLAS Collaboration. Search for resonances in fully hadronic final states in pp collisions at = 13 TeV with the ATLAS detector. JHEP 2020, 10, 061. [Google Scholar]
- ATLAS Collaboration. Search for heavy particles decaying into top-quark pairs using lepton-plus-jets events in proton–proton collisions at = 13 TeV with the ATLAS detector. Eur. Phys. J. C 2018, 78, 565. [Google Scholar] [CrossRef] [PubMed]
- CMS Collaboration. Search for resonant production in proton-proton collisions at = 13 TeV. JHEP 2019, 4, 31. [Google Scholar]
- ATLAS Collaboration. Search for Heavy Higgs Bosons A/H Decaying to a Top Quark Pair in pp Collisions at = 8 TeV with the ATLAS Detector. Phys. Rev. Lett. 2017, 119, 191803. [Google Scholar] [CrossRef]
- CMS Collaboration. Search for heavy Higgs bosons decaying to a top quark pair in proton-proton collisions at = 13 TeV. JHEP 2020, 4, 171. [Google Scholar]
- ATLAS Collaboration. Evidence for production in the multilepton final state in proton–proton collisions at = 13 TeV with the ATLAS detector. Eur. Phys. J. C 2020, 80, 1085. [Google Scholar]
- ATLAS Collaboration. Search for H/A→ production in the multilepton final state in proton-proton collisions at =13 TeV with the ATLAS detector. arXiv 2022, arXiv:2211.01136. [Google Scholar]
- Baldi, P.; Cranmer, K.; Faucett, T.; Sadowski, P.; Whiteson, D. Parameterized neural networks for high-energy physics. Eur. Phys. J. C 2016, 76, 235. [Google Scholar] [CrossRef]
- ATLAS Collaboration. ATL-PHYS-PUB-2022-036. Available online: https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/PUBNOTES/ATL-PHYS-PUB-2022-036/ (accessed on 10 October 2022).
- ATLAS Collaboration. Search for new phenomena in a lepton plus high jet multiplicity final state with the ATLAS experiment using = 13 TeV proton-proton collision data. JHEP 2017, 9, 088. [Google Scholar]
- CMS Collaboration. Search for production of four top quarks in final states with same-sign or multiple leptons in proton-proton collisions at = 13 TeV. Eur. Phys. J. C 2020, 80, 75. [Google Scholar] [CrossRef]
- ATLAS Collaboration. ATLAS-CONF-2021-048. Available online: https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/CONFNOTES/ATLAS-CONF-2021-048/ (accessed on 10 October 2022).
- ATLAS Collaboration. Search for charged Higgs bosons decaying into a top quark and a bottom quark at = 13 TeV with the ATLAS detector. JHEP 2021, 6, 145. [Google Scholar]
- ATLAS Collaboration. ATLAS-CONF-2022-008. Available online: https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/CONFNOTES/ATLAS-CONF-2022-008/ (accessed on 10 October 2022).
- CMS Collaboration. Search for charged Higgs bosons decaying into a top and a bottom quark in the all-jet final state of pp collisions at s = 13 TeV. JHEP 2020, 7, 126. [Google Scholar]
- CMS Collaboration. Search for a charged Higgs boson decaying into top and bottom quarks in events with electrons or muons in proton-proton collisions at s = 13 TeV. JHEP 2020, 1, 096. [Google Scholar]
- CMS Collaboration. CMS Exotica Summary Plots for 13 TeV Data. Available online: https://twiki.cern.ch/twiki/bin/view/CMSPublic/SummaryPlotsEXO13TeV#DM_summary_plots (accessed on 10 October 2022).
- CMS Collaboration. Search for new particles in events with energetic jets and large missing transverse momentum in proton-proton collisions at = 13 TeV. JHEP 2021, 11, 153. [Google Scholar]
- CMS Collaboration. Search for low mass vector resonances decaying into quark-antiquark pairs in proton-proton collisions at = 13 TeV. Phys. Rev. D 2019, 100, 11. [Google Scholar]
- CMS Collaboration. Search for high mass dijet resonances with a new background prediction method in proton-proton collisions at = 13 TeV. JHEP 2020, 5, 033. [Google Scholar]
- Boveia, A.; Buchmueller, O.; Busoni, G.; D’Eramo, F.; De Roeck, A.; De Simone, A.; Doglioni, C.; Dolan, M.J.; Genest, M.-H.; Hahn, K.; et al. Recommendations on presenting LHC searches for missing transverse energy signals using simplified ss-channel models of dark matter. Phys. Dark Univ. 2020, 27, 100365. [Google Scholar] [CrossRef]
- Haisch, U.; Polesello, G. Searching for production of dark matter in association with top quarks at the LHC. J. High Energy Phys. 2019, 2019, 29. [Google Scholar] [CrossRef]
- Pani, P.; Polesello, G. Dark matter production in association with a single top-quark at the LHC in a two-Higgs-doublet model with a pseudoscalar mediator. Phys. Dark Univ. 2018, 21, 8. [Google Scholar] [CrossRef]
- Pinna, D.; Zucchetta, A.; Buckley, M.R.; Canelli, F. Single top quarks and dark matter. Phys. Rev. D 2017, 96, 035031. [Google Scholar] [CrossRef]
- Gavela, M.B.; Parga, N. Ward identities and the physical interpretations of anomalies in stochastic quantization. Phys. Lett. B 1986, 169, 73. [Google Scholar] [CrossRef]
- Choi, K.; Kang, K.; Kim, J.E. Effects of η’ in low-energy axion physics. Phys. Lett. B 1986, 181, 145–149. [Google Scholar] [CrossRef]
- Gavela, M.B.; No, J.M.; Sanz, V.; de Trocóniz, J.F. Nonresonant Searches for Axionlike Particles at the LHC. Phys. Rev. Lett. 2020, 124, 051802. [Google Scholar] [CrossRef]
- CMS Collaboration. Search for heavy resonances decaying to ZZ or ZW and axion-like particles mediating nonresonant ZZ or ZH production at = 13 TeV. JHEP 2022, 4, 87. [Google Scholar]
- Carra, S.; Goumarre, V.; Gupta, R.; Heim, S.; Heinemann, B.; Küchler, J.; Meloni, F.; Quilez, P.; Yap, Y.C. Constraining off-shell production of axionlike particles with Zγ and WW differential cross-section measurements. Phys. Rev. D 2021, 104, 092005. [Google Scholar] [CrossRef]
- Bonilla, J. Available online: https://ep-news.web.cern.ch/content/non-resonant-searches-open-new-avenues-hunt-axion-particles (accessed on 10 October 2022).
- Carmona, A.; Elahi, F.; Scherb, C.; Schwaller, P. The ALPs from the top: Searching for long lived axion-like particles from exotic top decays. J. High Energy Phys. 2022, 2022, 122. [Google Scholar] [CrossRef]
- Brivio, I.; Gavela, M.B.; Merlo, L.; Mimasu, K.; No, J.M.; Del Rey, R.; Sanz, V. ALPs Effective Field Theory and Collider Signatures. Eur. Phys. J. C 2017, 77, 572. [Google Scholar] [CrossRef]
- Renner, S.; Schwaller, P. A flavoured dark sector. J. High Energy Phys. 2018, 2018, 052. [Google Scholar] [CrossRef]
- Froggatt, C.; Nielsen, H.B. Hierarchy of Quark Masses, Cabibbo Angles and CP Violation. Nucl. Phys. B 1979, 147, 277. [Google Scholar] [CrossRef]
- Haisch, U.; Polesello, G.; Schulte, S. Searching for pseudo Nambu-Goldstone boson dark matter production in association with top quarks. JHEP 2021, 9, 206. [Google Scholar] [CrossRef]
- Kribs, G.D.; Martin, A.; Ostdiek, B.; Tong, T. Dark Mesons at the LHC. JHEP 2019, 7, 133. [Google Scholar] [CrossRef]
- Dainese, A.; Mangano, M.; Meyer, A.B.; Nisati, A.; Salam, G.; Vesterinen, M.A. Report on the Physics at the HL-LHC, and Perspectives for the HE-LHC. CERN-2019-007. Available online: https://cds.cern.ch/record/2703572 (accessed on 10 October 2022).
- Benedikt, M.; Capeans, G.M.; Cerutti, F.; Goddard, B.; Gutleber, J.; Jimenez, J.M.; Mangano, M.; Mertens, V.; Osborne, J.A.; Otto, T. FCC-hh: The Hadron Collider: Future Circular Collider Conceptual Design Report Volume 3. Future Circular Collider. CERN-ACC-2018-0058. Available online: https://cds.cern.ch/record/2651300 (accessed on 10 October 2022).
- Dutta, B.; Kamon, T.; Ko, P.; Li, J. Prospects for discovery and spin discrimination of dark matter in Higgs portal DM models and their extensions at 100 TeV pp collider. Eur. Phys. J. C 2018, 78, 595. [Google Scholar] [CrossRef]
- Harris, P. Prospects for Discovery and Spin Discrimination of Dark Matter in Higgs Portal DM Models and Their Extensions at 100 TeV pp Collider. Talk at FCC Week 2017. Available online: https://indico.cern.ch/event/556692/contributions/2592531/attachments/1469109/2272523/PCH_FCC_DM_v2.pdf (accessed on 10 October 2022).
- Behnke, T.; James, E.B.; Brian, F.; Juan, F.; Mike, H.; James, M.E.P.; Michael, P.; Marcel, S.; Nicholas, W.; Hitoshi, Y. The International Linear Collider Technical Design Report—Volume 1: Executive Summary. arXiv 2013, arXiv:1306.6327. [Google Scholar]
- Aicheler, M.; Burrows, P.; Draper, M.; Garvey, T.; Lebrun, P.; Peach, K.; Phinney, N.; Schmickler, H.; Schulte, D.; Toge, N. A Multi-TeV Linear Collider Based on CLIC Technology: CLIC Conceptual Design Report. CERN Yellow Reports: Monographs 2012. Available online: https://cds.cern.ch/record/1500095 (accessed on 10 October 2022).
- Linssen, L.; Miyamoto, A.; Stanitzki, M.; Weerts, H. Physics and Detectors at CLIC: CLIC Conceptual Design Report. arXiv 2012, arXiv:1202.5940. [Google Scholar]
- The FCC Collaboration. FCC Physics Opportunities. Eur. Phys. J. C 2019, 79, 474. [Google Scholar] [CrossRef]
- The FCC Collaboration. FCC—The lepton collider. Eur. Phys. J. S. T. 2019, 228, 261. [Google Scholar]
- CEPC Study Group. CEPC Conceptual Design Report: Volume 1—Accelerator. arXiv 2018, arXiv:1809.00285. [Google Scholar]
- CEPC Study Group. CEPC Conceptual Design Report: Volume 2—Physics & Detector. arXiv 2018, arXiv:1811.10545. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behr, J.K.; Grohsjean, A. Dark Matter Searches with Top Quarks. Universe 2023, 9, 16. https://doi.org/10.3390/universe9010016
Behr JK, Grohsjean A. Dark Matter Searches with Top Quarks. Universe. 2023; 9(1):16. https://doi.org/10.3390/universe9010016
Chicago/Turabian StyleBehr, J. Katharina, and Alexander Grohsjean. 2023. "Dark Matter Searches with Top Quarks" Universe 9, no. 1: 16. https://doi.org/10.3390/universe9010016
APA StyleBehr, J. K., & Grohsjean, A. (2023). Dark Matter Searches with Top Quarks. Universe, 9(1), 16. https://doi.org/10.3390/universe9010016







