Big Bang Nucleosynthesis Constraints on f (T, TG) Gravity
Abstract
:1. Introduction
2. Gravity
3. Big Bang Nucleosynthesis Constraints
4. BBN Constraints on Gravity
4.1. Model I:
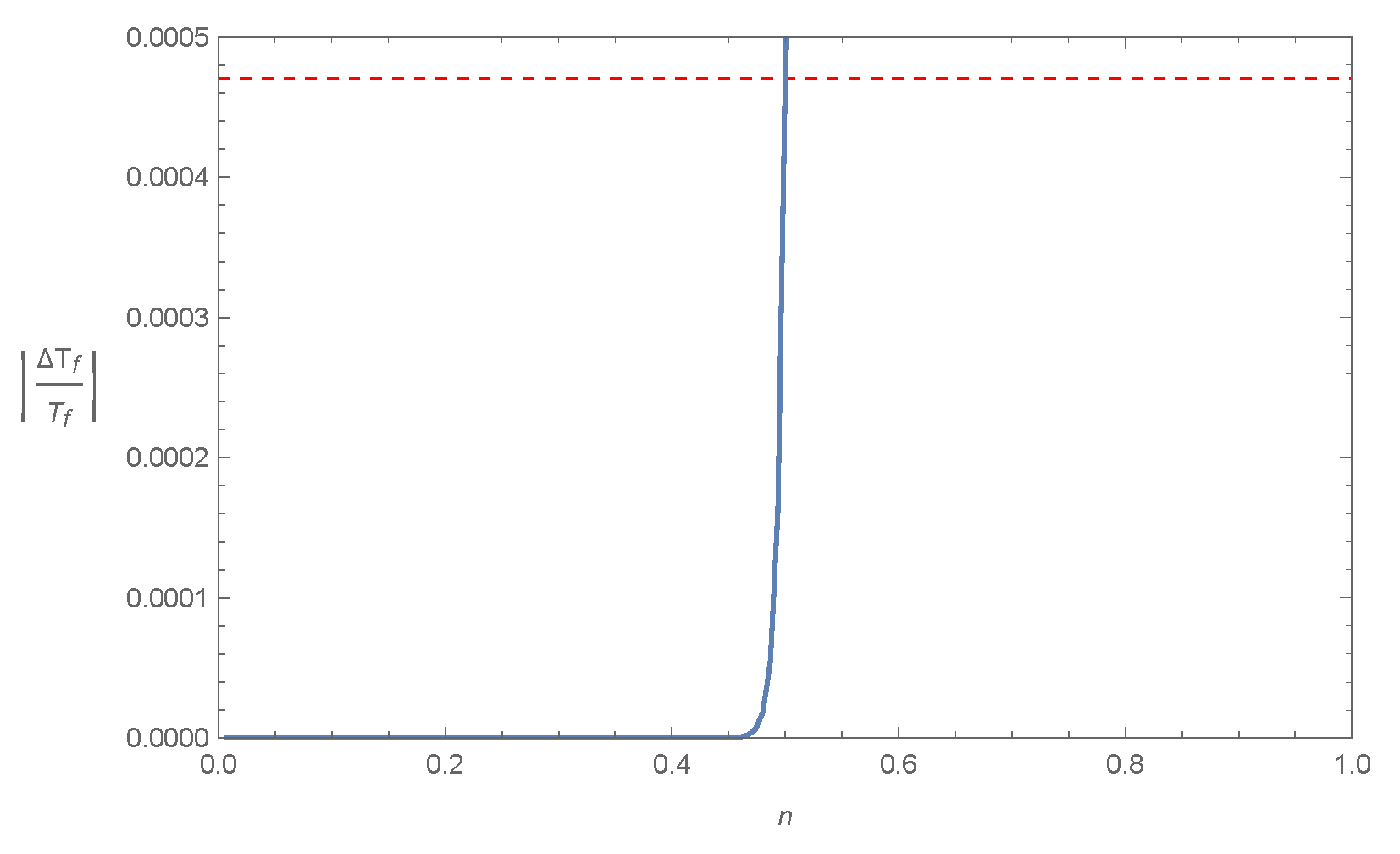
4.2. Model II:
4.3. Model III:
4.4. Model IV:
4.5. Model V:
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stelle, K.S. Renormalization of Higher Derivative Quantum Gravity. Phys. Rev. D 1977, 16, 953. [Google Scholar] [CrossRef]
- Addazi, A.; Alvarez-Muniz, J.; Batista, R.A.; Amelino-Camelia, G.; Antonelli, V.; Arzano, M.; Asorey, M.; Atteia, J.L.; Bahamonde, S.; Bajardi, F.; et al. Quantum gravity phenomenology at the dawn of the multi-messenger era—A review. arXiv 2021. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified Gravity and Cosmology. Phys. Rep. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Lazkoz, R.; Salzano, V.; Moniz, P.V.; Capozziello, S.; Jiménez, J.B.; Laurentis, M.D.; Olmo, G.J.; Akrami, Y.; Bahamonde, S.; et al. Modified gravity and cosmology: An update by the CANTATA network. arXiv 2021. [Google Scholar] [CrossRef]
- Ishak, M. Testing General Relativity in Cosmology. Living Rev. Relativ. 2019, 22, 1–204. [Google Scholar] [CrossRef]
- Abdalla, E.; Abellán, G.F.; Aboubrahim, A.; Agnello, A.; Akarsu, Ö.; Akrami, Y.; Alestas, G.; Aloni, D.; Amendola, L.; Anchordoqui, L.A.; et al. Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies. J. High Energy Astrophys. 2022, 34, 49–211. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models without Singularity. Phys. Lett. 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Capozziello, S. Curvature Quintessence. Int. J. Mod. Phys. 2002, 11, 483–491. [Google Scholar] [CrossRef] [Green Version]
- Felice, A.D.; Tsujikawa, S. f (R) theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef] [PubMed]
- Antoniadis, I.; Rizos, J.; Tamvakis, K. Singularity—Free cosmological solutions of the superstring effective action. Nucl. Phys. B 1994, 415, 497–514. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified Gauss-Bonnet theory as gravitational alternative for dark energy. Phys. Lett. B 2005, 631, 1–6. [Google Scholar] [CrossRef]
- Felice, A.D.; Tsujikawa, S. Construction of cosmologically viable f(G) dark energy models. Phys. Lett. B 2009, 675, 1–8. [Google Scholar] [CrossRef]
- Yousaf, Z.; Bhatti, M.Z.; Khan, S.; Sahoo, P.K. f(G,TαβTαβ) theory and complex cosmological structures. Phys. Dark Univ. 2022, 36, 101015. [Google Scholar] [CrossRef]
- Erices, C.; Papantonopoulos, E.; Saridakis, E.N. Cosmology in cubic and f (P) gravity. Phys. Rev. D 2019, 99, 1235277. [Google Scholar] [CrossRef]
- Marciu, M. Note on the dynamical features for the extended f (P) cubic gravity. Phys. Rev. D 2020, 101, 10. [Google Scholar] [CrossRef]
- Jiménez, J.B.; Jiménez-Cano, A. On the strong coupling of Einsteinian Cubic Gravity and its generalisations. J. Cosmol. Astropart. Phys. 2021, 1, 69. [Google Scholar] [CrossRef]
- Lovelock, D. The Einstein tensor and its generalizations. J. Math. Phys. 1971, 12, 498–501. [Google Scholar] [CrossRef]
- Deruelle, N.; Farina-Busto, L. The Lovelock Gravitational Field Equations in Cosmology. Phys. Rev. D 1990, 41, 3696. [Google Scholar] [CrossRef] [Green Version]
- Mannheim, P.D.; Kazanas, D. Exact Vacuum Solution to Conformal Weyl Gravity and Galactic Rotation Curves. Astrophys. J. 1989, 342, 635–638. [Google Scholar] [CrossRef]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Deffayet, C.; Esposito-Farese, G.; Vikman, A. Covariant Galileon. Phys. Rev. D 2009, 79, 84003. [Google Scholar] [CrossRef]
- Bengochea, G.R.; Ferraro, R. Dark torsion as the cosmic speed-up. Phys. Rev. D 2009, 79, 124019. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; Laurentis, M.D.; Saridakis, E.N. f (T) teleparallel gravity and cosmology. Rep. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef]
- Kofinas, G.; Saridakis, E.N. Teleparallel equivalent of Gauss-Bonnet gravity and its modifications. Phys. Rev. D 2014, 90, 84044. [Google Scholar] [CrossRef]
- Kofinas, G.; Leon, G.; Saridakis, E.N. Dynamical behavior in f (T, TG) cosmology. Class. Quantum Gravity 2014, 31, 175011. [Google Scholar] [CrossRef]
- Kofinas, G.; Saridakis, E.N. Cosmological applications of F(T, TG) gravity. Phys. Rev. D 2014, 90, 84045. [Google Scholar] [CrossRef]
- Bahamonde, D.; Böhmer, C.G.; Wright, M. Modified teleparallel theories of gravity. Phys. Rev. D 2015, 92, 104042. [Google Scholar] [CrossRef]
- Bahamonde, S.; Capozziello, S. Noether Symmetry Approach in f (T, B) teleparallel cosmology. Eur. Phys. J. C 2017, 77, 107. [Google Scholar] [CrossRef] [Green Version]
- Geng, C.Q.; Lee, C.C.; Saridakis, E.N.; Wu, Y.P. “Teleparallel” dark energy. Phys. Lett. B 2011, 704, 384–387. [Google Scholar] [CrossRef]
- Wu, P.; Yu, H.W. Observational constraints on f (T) theory. Phys. Lett. B 2010, 693, 415–420. [Google Scholar] [CrossRef]
- Myrzakulov, R. Accelerating universe from F(T) gravity. Eur. Phys. J. C 2011, 71, 1752. [Google Scholar] [CrossRef]
- Zheng, R.; Huang, Q.G. Growth factor in f (T) gravity. J. Cosmol. Astropart. Phys. 2011, 3, 2. [Google Scholar] [CrossRef]
- Tamanini, N.; Boehmer, C.G. Good and bad tetrads in f (T) gravity. Phys. Rev. D 2012, 86, 44009. [Google Scholar] [CrossRef]
- Bamba, K.; Myrzakulov, R.; Nojiri, S.; Odintsov, S.D. Reconstruction of f (T) gravity: Rip cosmology, finite-time future singularities and thermodynamics. Phys. Rev. D 2012, 85, 104036. [Google Scholar] [CrossRef]
- Dong, H.; Wang, Y.B.; Meng, X.H. Extended Birkhoff’s Theorem in the f (T) Gravity. Eur. Phys. J. C 2012, 72, 2002. [Google Scholar] [CrossRef]
- Karami, K.; Abdolmaleki, A. Generalized second law of thermodynamics in f (T)-gravity. J. Cosmol. Astropart. Phys. 2012, 4, 7. [Google Scholar] [CrossRef]
- Liu, D.; Reboucas, M.J. Energy conditions bounds on f (T) gravity. Phys. Rev. D 2012, 86, 83515. [Google Scholar] [CrossRef]
- Otalora, G. Scaling attractors in interacting teleparallel dark energy. J. Cosmol. Astropart. Phys. 2013, 7, 44. [Google Scholar] [CrossRef]
- Ong, Y.C.; Izumi, K.; Nester, J.M.; Chen, P. Problems with Propagation and Time Evolution in f (T) Gravity. Phys. Rev. D 2013, 88, 24019. [Google Scholar] [CrossRef]
- Chen, P.; Izumi, K.; Nester, J.M.; Ong, Y.C. Remnant Symmetry, Propagation and Evolution in f(T) Gravity. Phys. Rev. D 2015, 91, 64003. [Google Scholar] [CrossRef]
- Farrugia, G.; Said, J.L. Stability of the flat FLRW metric in f (T) gravity. Phys. Rev. D 2016, 94, 124054. [Google Scholar] [CrossRef]
- Bejarano, C.; Ferraro, R.; Guzmán, M.J. McVittie solution in f (T) gravity. Eur. Phys. J. C 2017, 77, 825. [Google Scholar] [CrossRef]
- Hohmann, M.; Jarv, L.; Ualikhanova, U. Dynamical systems approach and generic properties of f (T) cosmology. Phys. Rev. D 2017, 96, 43508. [Google Scholar] [CrossRef]
- Bahamonde, S.; Böhmer, C.G.; Krššák, M. New classes of modified teleparallel gravity models. Phys. Lett. B 2017, 775, 37–43. [Google Scholar] [CrossRef]
- Abedi, H.; Capozziello, S.; D’Agostino, R.; Luongo, O. Effective gravitational coupling in modified teleparallel theories. Phys. Rev. D 2018, 97, 84008. [Google Scholar] [CrossRef]
- Golovnev, A.; Koivisto, T. Cosmological perturbations in modified teleparallel gravity models. J. Cosmol. Astropart. Phys. 2018, 11, 12. [Google Scholar] [CrossRef]
- Krssak, M.; van den Hoogen, R.J.; Pereira, J.G.; Böhmer, C.J.; Coley, A.A. Teleparallel theories of gravity: Illuminating a fully invariant approach. Class. Quantum Gravity 2019, 36, 183001. [Google Scholar] [CrossRef]
- Deng, X.M. Probing f (T) gravity with gravitational time advancement. Class. Quantum Gravity 2018, 35, 175013. [Google Scholar] [CrossRef]
- Caruana, M.; Farrugia, G.; Said, J.L. Cosmological bouncing solutions in f (T, B) gravity. Eur. Phys. J. C 2020, 80, 640. [Google Scholar] [CrossRef]
- Ren, X.; Wong, T.H.T.; Cai, Y.F.; Saridakis, E.N. Data-driven Reconstruction of the Late-time Cosmic Acceleration with f (T) Gravity. Phys. Dark Univ. 2021, 32, 100812. [Google Scholar] [CrossRef]
- Briffa, R.; Escamilla-Rivera, C.; Levi, J.S.; Mifsud, J.; Pullicino, N.L. Impact of H0 priors on f (T) late time cosmology. Eur. Phys. J. Plus 2022, 137, 532. [Google Scholar] [CrossRef]
- Benisty, D.; Guendelman, E.I.; van de Venn, A.; Vasak, D.; Struckmeier, J.; Stoecker, H. The dark side of the torsion: Dark energy from propagating torsion. Eur. Phys. J. C 2022, 82, 264. [Google Scholar] [CrossRef]
- Dialektopoulos, K.F.; Said, J.L.; Oikonomopoulou, Z. Classification of teleparallel Horndeski cosmology via Noether symmetries. Eur. Phys. J. C 2022, 82, 259. [Google Scholar] [CrossRef]
- Papagiannopoulos, G.; Basilakos, S.; Saridakis, E.N. Dynamical system analysis of Myrzakulov gravity. arXiv 2022. [Google Scholar] [CrossRef]
- Papanikolaou, T.; Tzerefos, C.; Basilakos, S.; Saridakis, E.N. No constraints for f (T) gravity from gravitational waves induced from primordial black hole fluctuations. arXiv 2022. [Google Scholar] [CrossRef]
- Wang, T. Static Solutions with Spherical Symmetry in f (T) Theories. Phys. Rev. D 2011, 84, 24042. [Google Scholar] [CrossRef]
- Boehmer, C.G.; Mussa, A.; Tamanini, N. Existence of relativistic stars in f (T) gravity. Class. Quantum Gravity 2011, 28, 245020. [Google Scholar] [CrossRef]
- Ferraro, R.; Fiorini, F. Spherically symmetric static spacetimes in vacuum f (T) gravity. Phys. Rev. D 2011, 84, 83518. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.H.; Wang, Y.B. Birkhoff’s theorem in the f (T) gravity. Eur. Phys. J. C 2011, 71, 1755. [Google Scholar] [CrossRef]
- Rodrigues, M.E.; Houndjo, M.J.S.; Saez-Gomez, D.; Rahaman, F. Anisotropic Universe Models in f (T) Gravity. Phys. Rev. D 2012, 86, 104059. [Google Scholar] [CrossRef]
- Rodrigues, M.E.; Houndjo, M.J.S.; Tossa, J.; Momeni, D.; Myrzakulov, R. Charged Black Holes in Generalized Teleparallel Gravity. J. Cosmol. Astropart. Phys. 2013, 11, 24. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Spherically symmetric charged-dS solution in f (T) gravity theories. Phys. Rev. D 2013, 88, 104034. [Google Scholar] [CrossRef]
- Bejarano, C.; Ferraro, R.; Guzmán, M.J. Kerr geometry in f (T) gravity. Eur. Phys. J. C 2015, 75, 77. [Google Scholar] [CrossRef]
- Das, A.; Rahaman, F.; Guha, B.K.; Ray, S. Relativistic compact stars in f (T) gravity admitting conformal motion. Astrophys. Space Sci. 2015, 358, 36. [Google Scholar] [CrossRef]
- Mai, Z.F.; Lu, H. Black Holes, Dark Wormholes and Solitons in f (T) Gravities. Phys. Rev. D 2017, 95, 124024. [Google Scholar] [CrossRef]
- Mustafa, G.; Abbas, G.; Xia, T. Wormhole solutions in F(T, TG) gravity under Gaussian and Lorentzian non-commutative distributions with conformal motions. Chin. J. Phys. 2019, 60, 362–378. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Capozziello, S. Stable and self-consistent compact star models in teleparallel gravity. Eur. Phys. J. C 2020, 80, 969. [Google Scholar] [CrossRef]
- Pfeifer, C.; Schuster, S. Static spherically symmetric black holes in weak f(T)-gravity. Universe 2021, 7, 153. [Google Scholar] [CrossRef]
- Ren, X.; Zhao, Y.; Saridakis, E.N.; Cai, Y.F. Deflection angle and lensing signature of covariant f (T) gravity. J. Cosmol. Astropart. Phys. 2021, 10, 62. [Google Scholar] [CrossRef]
- Bahamonde, S.; Golovnev, A.; Guzmán, M.J.; Said, J.L.; Pfeifer, C. Black holes in f(T,B) gravity: Exact and perturbed solutions. J. Cosmol. Astropart. Phys. 2022, 1, 37. [Google Scholar] [CrossRef]
- Bahamonde, S.; Ducobu, L.; Pfeifer, C. Scalarized black holes in teleparallel gravity. J. Cosmol. Astropart. Phys. 2022, 4, 18. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, J.; Ren, X.; Saridakis, E.N.; Cai, Y.F. N-body simulations, halo mass functions, and halo density profile in f (T) gravity. arXiv 2022. [Google Scholar] [CrossRef]
- Zhao, Y.; Ren, X.; Ilyas, A.; Saridakis, E.N.; Cai, Y.F. Quasinormal modes of black holes in f (T) gravity. arXiv 2022. [Google Scholar] [CrossRef]
- Bernstein, J.; Brown, L.S.; Feinberg, G. Cosmological helium production simplified. Rev. Mod. Phys. 1989, 61, 25. [Google Scholar] [CrossRef]
- Kolb, E.W.; Turner, M.S. The Early Universe. Front. Phys. 1990, 69, 1–547. [Google Scholar]
- Olive, K.A.; Steigman, G.; Walker, T.P. Primordial nucleosynthesis: Theory and observations. Phys. Rep. 2000, 333, 389–407. [Google Scholar] [CrossRef]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A.; Yeh, T.H. Big Bang Nucleosynthesis: 2015. Rev. Mod. Phys. 2016, 88, 15004. [Google Scholar] [CrossRef]
- Asimakis, P.; Basilakos, S.; Mavromatos, N.E.; Saridakis, E.N. Big bang nucleosynthesis constraints on higher-order modified gravities. Phys. Rev. D 2022, 105, 8. [Google Scholar] [CrossRef]
- Torres, D.F.; Vucetich, H.; Plastino, A. Early universe test of nonextensive statistics. Phys. Rev. Lett. 1997, 79, 1588–1590. [Google Scholar] [CrossRef]
- Lambiase, G. Lorentz invariance breakdown and constraints from big-bang nucleosynthesis. Phys. Rev. D 2005, 72, 87702. [Google Scholar] [CrossRef]
- Lambiase, G. Dark matter relic abundance and big bang nucleosynthesis in Horava’s gravity. Phys. Rev. D 2011, 83, 107501. [Google Scholar] [CrossRef]
- Anagnostopoulos, F.K.; Gakis, V.; Saridakis, E.N.; Basilakos, S. New models and Big Bang Nucleosynthesis constraints in f (Q) gravity. arXiv 2022. [Google Scholar] [CrossRef]
- Coc, A.; Vangioni-Flam, E.; Descouvemont, P.; Adahchour, A.; Angulo, C. Updated Big Bang nucleosynthesis confronted to WMAP observations and to the abundance of light elements. Astrophys. J. 2004, 600, 544–552. [Google Scholar] [CrossRef]
- Olive, K.A.; Skillman, E.; Steigman, G. The Primordial abundance of He-4: An Update. Astrophys. J. 1997, 483, 788. [Google Scholar] [CrossRef]
- Izotov, Y.I.; Thuan, T.X. The Primordial abundance of 4-He revisited. Astrophys. J. 1998, 500, 188. [Google Scholar] [CrossRef]
- Fields, B.D.; Olive, K.A. On the evolution of helium in blue compact galaxies. Astrophys. J. 1998, 506, 177. [Google Scholar] [CrossRef]
- Izotov, Y.I.; Chaffee, F.H.; Foltz, C.B.; Green, R.F.; Guseva, N.G.; Thuan, T.X. Helium abundance in the most metal-deficient blue compact galaxies: I zw 18 and sbs 0335-052. Astrophys. J. 1999, 527, 757–777. [Google Scholar] [CrossRef]
- Kirkman, D.; Tytler, D.; Suzuki, N.; O’Meara, J.M.; Lubin, D. The Cosmological baryon density from the deuterium to hydrogen ratio towards QSO absorption systems: D/H towards Q1243+3047. Astrophys. J. Suppl. 2003, 149, 1. [Google Scholar] [CrossRef]
- Izotov, Y.I.; Thuan, T.X. Systematic effects and a new determination of the primordial abundance of He-4 and dY/dZ from observations of blue compact galaxies. Astrophys. J. 2004, 602, 200–230. [Google Scholar] [CrossRef] [Green Version]
- Aghanim, N. et al. [Planck Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Visser, M. Jerk and the cosmological equation of state. Class. Quantum Gravity 2004, 21, 2603–2616. [Google Scholar] [CrossRef]
- Al Mamon, A.; Bamba, K. Observational constraints on the jerk parameter with the data of the Hubble parameter. Eur. Phys. J. C 2018, 78, 862. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asimakis, P.; Saridakis, E.N.; Basilakos, S.; Yesmakhanova, K. Big Bang Nucleosynthesis Constraints on f (T, TG) Gravity. Universe 2022, 8, 486. https://doi.org/10.3390/universe8090486
Asimakis P, Saridakis EN, Basilakos S, Yesmakhanova K. Big Bang Nucleosynthesis Constraints on f (T, TG) Gravity. Universe. 2022; 8(9):486. https://doi.org/10.3390/universe8090486
Chicago/Turabian StyleAsimakis, Petros, Emmanuel N. Saridakis, Spyros Basilakos, and Kuralay Yesmakhanova. 2022. "Big Bang Nucleosynthesis Constraints on f (T, TG) Gravity" Universe 8, no. 9: 486. https://doi.org/10.3390/universe8090486
APA StyleAsimakis, P., Saridakis, E. N., Basilakos, S., & Yesmakhanova, K. (2022). Big Bang Nucleosynthesis Constraints on f (T, TG) Gravity. Universe, 8(9), 486. https://doi.org/10.3390/universe8090486






