Big Bang Nucleosynthesis Constraints on f (T, T_G) Gravity

Abstract

We confront $f(T,T_G)$ gravity, with big bang nucleosynthesis (BBN) requirements. The former is obtained using both the torsion scalar, as well as the teleparallel equivalent of the Gauss–Bonnet term, in the Lagrangian, resulting to modified Friedmann equations in which the extra torsional terms constitute an effective dark energy sector. We calculate the deviations of the freeze-out temperature $T_f$, caused by the extra torsion terms in comparison to $\Lambda$CDM paradigm. Then, we impose five specific $f(T,T_G)$ models and extract the constraints on the model parameters in order for the ratio $|\Delta T_f/T_f|$ to satisfy the observational BBN bound. As we find, in most of the models the involved parameters are bounded in a narrow window around their general relativity values as expected, asin the power-law model, where the exponent n needs to be $n\lesssim 0.5$. Nevertheless, the logarithmic model can easily satisfy the BBN constraints for large regions of the model parameters. This feature should be taken into account in future model building.

1. Introduction

There are two motivations that lead to the construction of modifications of gravity. The first is purely theoretical, namely, to construct gravitational theories that do not suffer from the renormalizability problems of general relativity and thus are closer to a quantum description [1,2]. The second is cosmological, namely, to construct gravitational theories that at a cosmological framework can describe the early and late accelarating eras [3,4,5,6,7], as well as to alleviate various observational tensions [8].

There is a rich literature on modified and extended theories of gravity. One may start from the Einstein–Hilbert Lagrangian and add extra terms, resulting in $f\left(R\right)$ gravity [9,10,11], in $f\left(G\right)$ gravity [12,13,14], in $f(G,\mathcal{T})$ theories [15], in $f\left(P\right)$ gravity [16,17,18] in Lovelock gravity [19,20], in Weyl gravity [21], in Horndeski/Galileon scalar-tensor theories [22,23], etc. Nevertheless, one can follow a different approach and add new terms to the equivalent torsional formulation of gravity, resulting in $f\left(T\right)$ gravity [24,25], in $f(T,T_G)$ gravity [26,27,28], in $f(T,B)$ gravity [29,30], in scalar-torsion theories [31], etc. Torsional gravity has been proven to exhibit interesting phenomenology, both at the cosmological framework [32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57] and at the level of local, spherically symmetric solutions [58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75].

One crucial test that every modification of gravity should pass that is usually underestimated in the literature is the confrontation with Big Bang Nucleosynthesis (BBN) data [76,77,78,79,80]. Specifically, the amount of modification needed in order to fulfill the late-time cosmological requirements must not at the same time spoil the successes of early-time cosmology, and among them the BBN phase. Hence, whatever are the advantages of a specific modified theory of gravity, if it cannot satisfy the BBN constraints it must be excluded [81,82,83,84].

In the present manuscript, we are interested in investigating the BBN epoch in a universe governed by $f(T,T_G)$ gravity. In particular, we desire to study various specific models that are known to lead to viable phenomenology and extract constraints on the involved model parameters. The plan of the article is as follows: In Section 2, we briefly present $f(T,T_G)$ gravity, extracting the field equations and applying them to a cosmological framework. In Section 3, we summarize the BBN formalism and provide the difference in the freeze-out temperature caused by the extra torsion terms. Then, in Section 4, we investigate five specific $f(T,T_G)$ models, confronting them with the observational BBN bounds. Finally, Section 5 is devoted to the Conclusions.

2. $\mathit{f}(\mathit{T},{\mathit{T}}_{\mathit{G}})$ Gravity

In this section, we briefly review $f(T,T_G)$ gravity [26,27,28]. As usual in torsional formulation of gravity, we use the tetrad field as the dynamical variable, which forms an orthonormal basis at the tangent space. In a coordinate basis, one can relate it with the metric through $g_{\mu \nu }\left(x\right)={\eta }_{AB}{e}_{\mu }^A\left(x\right)e_{\nu }^B\left(x\right)$, where ${\eta }_{AB}=\mathrm{diag}(-1,1,1,1)$, and with Greek and Latin letters, denoting coordinate and tangent indices, respectively. Applying the Weitzenböck connection $W_{\nu \mu }^{\lambda }\equiv e_A^{\lambda }{\partial }_{\mu }{e}_{\nu }^A$ [25], the corresponding torsion tensor is

$$T_{\mu \nu }^{\lambda }\equiv W_{\nu \mu }^{\lambda }-W_{\mu \nu }^{\lambda }=e_A^{\lambda }({\partial }_{\mu }{e}_{\nu }^A-{\partial }_{\nu }{e}_{\mu }^A),$$

(1)

and then the torsion scalar is obtained through the contractions

$$T\equiv \frac{1}{4}{T}^{\rho \mu \nu }{T}_{\rho \mu \nu }+\frac{1}{2}{T}^{\rho \mu \nu }{T}_{\nu \mu \rho }-T_{\rho \mu }^{\rho }{T}_{\nu }^{\nu \mu },$$

(2)

and incorporates all information of the gravitational field. Used as a Lagrangian, the torsion scalar gives rise to exactly the same equations with general relativity, which is why the theory was named the teleparallel equivalent of general relativity (TEGR).

Similarly to curvature gravity, where one can construct higher-order invariants such as the Gauss–Bonnet one, in torsional gravity one may construct higher-order torsional invariants, too. In particular, since the curvature (Ricci) scalar and the torsion scalar differ by a total derivative, in [26] the authors followed the same recipe and extracted a higher-order torsional invariant that differs from the Gauss–Bonnet one by a boundary term, namely

$$\begin{array}{ccc}& & T_G=\left(K_{\phi \pi }^{\kappa }{K}_{\rho }^{\phi \lambda }{K}_{\chi \sigma }^{\mu }{K}_{\tau }^{\chi \nu }-2K_{\pi }^{\kappa \lambda }{K}_{\phi \rho }^{\mu }{K}_{\chi \sigma }^{\phi }{K}_{\tau }^{\chi \nu }\right.\hfill \\ & & \left.+2K_{\pi }^{\kappa \lambda }{K}_{\phi \rho }^{\mu }{K}_{\chi }^{\phi \nu }{K}_{\sigma \tau }^{\chi }+2K_{\pi }^{\kappa \lambda }{K}_{\phi \rho }^{\mu }{K}_{\sigma ,\tau }^{\phi \nu }\right){\delta }_{\kappa \lambda \mu \nu }^{\pi \rho \sigma \tau },\hfill \end{array}$$

(3)

where $K_{\rho }^{\mu \nu }\equiv -\frac{1}{2}\left(T_{\rho }^{\mu \nu }-T_{\rho }^{\nu \mu }-T_{\rho }^{\mu \nu }\right)$ is the contortion tensor, and the generalized ${\delta }_{\kappa \lambda \mu \nu }^{\pi \rho \sigma \tau }$ denotes the determinant of the Kronecker deltas. Note that similarly to the Gauss–Bonnet term, the teleparallel equivalent of the Gauss–Bonnet term $T_G$ is also a topological invariant in four dimensions.

Using the above torsional invariants, one can construct the new class of $f(T,T_G)$ gravitational modifications, characterized by the action [26]

$$\begin{array}{c}\hfill S=\frac{M_P^2}{2}\int d^{4}xef(T,T_G),\end{array}$$

(4)

with $M_P^2$ the reduced Planck mass. The general field equations of the above action can be found in [26], where one can clearly see that the theory is different from $f\left(R\right)$, $f(R,G)$, and $f\left(T\right)$ gravitational modifications, and thus it corresponds to a novel class of modified gravity.

In this work, we are interested in the cosmological applications of $f(T,T_G)$ gravity. Hence, we consider a spatially flat Friedmann–Robertson–Walker (FRW) metric of the form

$$d{s}^2=-d{t}^2+a^2\left(t\right){\delta }_{ij}d{x}^{i}d{x}^j,$$

(5)

with $a\left(t\right)$ the scale factor, which corresponds to the diagonal tetrad

$$e_{\mu }^A=\mathrm{diag}(1,a\left(t\right),a\left(t\right),a\left(t\right)).$$

(6)

In this case, the torsion scalar (2) and the teleparallel equivalent of the Gauss–Bonnet term (3) become

$$\begin{array}{ccc}\hfill & & T=6H^2\hfill \end{array}$$

(7)

$$\begin{array}{ccc}& & T_G=24H^2\left(\dot{H}+H^2\right),\hfill \end{array}$$

(8)

with $H=\frac{\dot{a}}{a}$ the Hubble parameter and where dots denote derivatives with respect to t.

The general field equations for the FRW geometry are [27]

$$\begin{array}{ccc}& & f-12H^2{f}_T-T_G{f}_{T_G}+24H^3\dot{f_{T_G}}=2M_P^{-2}({\rho }_r+{\rho }_m)\hfill \end{array}$$

(9)

$$\begin{array}{ccc}& & f-4\left(3H^2+\dot{H}\right)f_T-4H\dot{f_T}-T_G{f}_{T_G}\hfill \\ & & +\frac{2}{3H}{T}_G\dot{f_{T_G}}+8H^2\ddot{f_{T_G}}=-2M_P^{-2}(p_r+p_m),\hfill \end{array}$$

(10)

with $\dot{f_T}=f_{TT}\dot{T}+f_{T{T}_G}{\dot{T}}_G$, $\dot{f_{T_G}}=f_{T{T}_G}\dot{T}+f_{T_G{T}_G}{\dot{T}}_G$, and $\ddot{f_{T_G}}=f_{TT{T}_G}{\dot{T}}^2+2f_{T{T}_G{T}_G}\dot{T}{\dot{T}}_G+f_{T_G{T}_G{T}_G}{\dot{T}}_G^2+f_{T{T}_G}\ddot{T}+f_{T_G{T}_G}{\ddot{T}}_G$, and where $f_{TT}$, $f_{T{T}_G}$,... denote multiple partial differentiations with respect to T and $T_G$. Note that in the above equations, we have also introduced the radiation and matter sectors, corresponding to perfect fluids with energy densities ${\rho }_r$, ${\rho }_m$ and pressures $p_r$, $p_m$, respectively. Lastly, we mention that the above equations for $f(T,T_G)=-T+\Lambda$ recover the TEGR and general relativity equations, where $\Lambda$ is the cosmological constant.

As we can see, we can re-write the Friedmann Equations (9) and (10) in the usual form

$$\begin{array}{ccc}\hfill & & 3M_P^2{H}^2=\left({\rho }_r+{\rho }_m+{\rho }_{DE}\right)\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill & & -2M_P^2\dot{H}=\left({\rho }_r+p_r+{\rho }_m+p_m+{\rho }_{DE}+p_{DE}\right),\hfill \end{array}$$

(12)

where we have defined the effective dark energy density and pressure as

$${\rho }_{DE}\equiv \frac{M_P^2}{2}\left(6H^2-f+12H^2{f}_T+T_G{f}_{T_G}-24H^3\dot{f_{T_G}}\right),$$

(13)

$$\begin{array}{ccc}\hfill & & p_{DE}\equiv \frac{M_P^2}{2}\left[-2(2\dot{H}+3H^2)+f-4\left(\dot{H}+3H^2\right)f_T\right.\hfill \\ & & \left.-4H\dot{f_T}-T_G{f}_{T_G}+\frac{2}{3H}{T}_G\dot{f_{T_G}}+8H^2\ddot{f_{T_G}}\right],\hfill \end{array}$$

(14)

of gravitational origin.

3. Big Bang Nucleosynthesis Constraints

Big bang nucleosynthesis (BBN) was a process that took place during radiation era. Let us first present the framework, which provides the BBN constraints through standard cosmology [76,77,78,79,80]. The first Friedmann equation from Einstein–Hilbert action can be written as

$$3H^2=M_P^{-2}\rho ,$$

(15)

where $\rho ={\rho }_r+{\rho }_m$. In the radiation era, the radiation sector dominates; hence, we can write

$$\begin{array}{c}\hfill H^2\approx \frac{M_P^{-2}}{3}{\rho }_r\equiv H_{GR}^2.\end{array}$$

(16)

In addition, it is known that the energy density of relativistic particles is

$$\begin{array}{c}\hfill {\displaystyle {\rho }_r=\frac{{\pi }^2}{30}{g}_{*}{T}^4},\end{array}$$

(17)

where $g_{*}$ ∼ 10 is the effective number of degrees of freedom and T is the temperature. Thus, if we combine (16) with (17) we obtain

$$\begin{array}{c}\hfill H\left(T\right)\approx {\left(\frac{4{\pi }^3{g}_{*}}{45}\right)}^{1/2}\frac{T^2}{M_{Pl}},\end{array}$$

(18)

where $M_{Pl}={\left(8\pi \right)}^{\frac{1}{2}}{M}_P=1.22\times {10}^{19}$ GeV is the Planck mass.

During the radiation era, the scale factor evolves as $a\left(t\right)\sim t^{1/2}$. Therefore, using the relation of the Hubble parameter with the scale factor, we find that in the radiation era the Hubble parameter evolves as $H\left(t\right)=\frac{1}{2t}$. Combining the last one with (18), we find the relation between temperature and time. Thus, we have ${\displaystyle \frac{1}{t}\simeq {\left(\frac{32{\pi }^3{g}_{*}}{90}\right)}^{1/2}\frac{T^2}{M_{Pl}}}$ (or $T\left(t\right)\simeq {(t/\sec )}^{-1/2}$ MeV).

During the BBN, we have interactions between particles. For example, we have interactions between neutrons, protons, electrons, and neutrinos, namely, $n+{\nu }_e\to p+e^{-}$, $n+e^{+}\to p+{\overline{\nu }}_e$, and $n\to p+e^{-}+{\overline{\nu }}_e$. We name the conversion rate from a particle A to particle B as ${\lambda }_{BA}$. Hence, the conversion rate from neutrons to protons is ${\lambda }_{pn}$, and it is equal to the sum of the three interaction conversion rates written above. Therefore, the calculation of the neutron abundance arises from the protons-neutron conversion rate [78,79]

$${\lambda }_{pn}\left(T\right)={\lambda }_{(n+{\nu }_e\to p+e^{-})}+{\lambda }_{(n+e^{+}\to p+{\overline{\nu }}_e)}+{\lambda }_{(n\to p+e^{-}+{\overline{\nu }}_e)}$$

(19)

and its inverse ${\lambda }_{np}\left(T\right)$, and therefore for the total rate we have ${\lambda }_{tot}\left(T\right)={\lambda }_{np}\left(T\right)+{\lambda }_{pn}\left(T\right)$. Now, we assume that the various particle (neutrino, electron, and photon) temperatures are the same and low enough in order to use the Boltzmann distribution instead of the Fermi-Dirac one, and we neglect the electron mass compared to the electron and neutrino energies. The final expression for the conversion rate is [81,82,83,84]

$${\lambda }_{tot}\left(T\right)=4A{T}^3(4!T^2+2\times 3!QT+2!Q^2),$$

(20)

where $Q=m_n-m_p=1.29\times {10}^{-3}$ GeV is the mass difference between neutron and proton and $A=1.02\times {10}^{-11}$ GeV⁻⁴.

We proceed in calculating the corresponding freeze-out temperature. This will arise comparing the universe expansion rate $\frac{1}{H}$ with ${\lambda }_{tot}\left(T\right)$. In particular, if $\frac{1}{H}\ll {\lambda }_{tot}\left(T\right)$, namely, if the expansion time is much smaller than the interaction time, we can consider thermal equilibrium [76,77]. On the contrary, if $\frac{1}{H}\gg {\lambda }_{tot}\left(T\right)$ then particles do not have enough time to interact so they decouple. The freeze-out temperature $T_f$, in which the decoupling takes place, corresponds to $H\left(T_f\right)={\lambda }_{tot}\left(T_f\right)\simeq c_q{T}_f^5$, with $c_q\equiv 4A4!\simeq 9.8\times {10}^{-10}{\mathrm{GeV}}^{-4}$ [81,82,83,84]. Now, if we use (18) and $H\left(T_f\right)={\lambda }_{tot}\left(T_f\right)\simeq c_q{T}_f^5$, we acquire

$$T_f={\left(\frac{4{\pi }^3{g}_{*}}{45M_{Pl}^2{c}_q^2}\right)}^{1/6}\sim 0.0006\mathrm{GeV}.$$

(21)

Using modified theories, we obtain extra terms in energy density due to the modification of gravity. The first Friedmann Equation (11) during radiation era becomes

$$3M_P^2{H}^2={\rho }_r+{\rho }_{DE},$$

(22)

where ${\rho }_{DE}$ must be very small compared to ${\rho }_r$ in order to be in accordance with observations. Hence, we can write (22) using (16) as

$$H=H_{GR}\sqrt{1+\frac{{\rho }_{DE}}{{\rho }_r}}=H_{GR}+\delta H,$$

(23)

where $H_{GR}$ is the Hubble parameter of standard cosmology. Thus, we have $\Delta H=\left(\sqrt{1+\frac{{\rho }_{DE}}{{\rho }_r}}-1\right)H_{GR}$, which quantifies the deviation from standard cosmology, i.e., form $H_{GR}$. This will lead to a deviation in the freeze-out temperature $\Delta T_f$. Since $H_{GR}={\lambda }_{tot}\approx c_q{T}_f^5$ and $\sqrt{1+\frac{{\rho }_{DE}}{{\rho }_r}}\approx 1+\frac{1}{2}\frac{{\rho }_{DE}}{{\rho }_r}$, we easily find

$$\left(\sqrt{1+\frac{{\rho }_{DE}}{{\rho }_r}}-1\right)H_{GR}=5c_q{T}_f^4\Delta T_f,$$

(24)

and finally

$$\frac{\Delta T_f}{T_f}\simeq \frac{{\rho }_{DE}}{{\rho }_r}\frac{H_{GR}}{10c_q{T}_f^5},$$

(25)

where we used that ${\rho }_{DE}<<{\rho }_r$ during BBN era. This theoretically calculated $\frac{\Delta T_f}{T_f}$ should be compared with the observational bound

$$\left|\frac{\Delta T_f}{T_f}\right|<4.7\times {10}^{-4},$$

(26)

which is obtained from the observational estimations of the baryon mass fraction converted to ${}^{4}He$ [85,86,87,88,89,90,91].

4. BBN Constraints on $\mathit{f}(\mathit{T},{\mathit{T}}_{\mathit{G}})$ Gravity

In this section, we will apply the BBN analysis in the case of $f(T,T_G)$ gravity. Let us mention here that in general, in modified gravity, inflation is not straightaway driven by an inflaton field, but the inflaton is hidden inside the gravitational modification, i.e., it is one of the extra scalar degrees of freedom of the modified graviton. Hence, in such frameworks reheating is usually performed gravitationally, and the reheating and BBN temperatures may differ from standard ones. Nevertheless, in the present work we make the assumption that we do not deviate significantly from the successful concordance scenario, in order to examine whether $f(T,T_G)$ gravity can at first pass BBN constraints or not. Clearly a more general analysis should be performed in a separate project, to cover more radical cases too. In the following, we will examine five specific models that are considered to be viable in the literature.

4.1. Model I: $f=-T+{\beta }_1\sqrt{T^2+{\beta }_2{T}_G}$

Firstly, we investigate the model $f=-T+{\beta }_1\sqrt{T^2+{\beta }_2{T}_G}$ [28]. Since in our analysis we focus on the radiation era where the Hubble parameter $H\left(t\right)=\frac{1}{2t}$, we can express the derivatives of the Hubble parameter as powers of the Hubble parameter itself, e.g., $\dot{H}=-2H^2$ and $\ddot{H}=8H^3$. Additionally, in order to eliminate one model parameter we will apply the Friedmann equation at present time, requiring

$${\Omega }_{DE0}\equiv {\rho }_{DE0}/\left(3M_P^2{H}_0^2\right),$$

(27)

where ${\Omega }_{DE}$ is the dark energy density parameter and with the subscript “0” denoting the value of a quantity at present time. Doing so, and inserting $f=-T+{\beta }_1\sqrt{T^2+{\beta }_2{T}_G}$ into (13) and then into (25), we finally find

$$\begin{array}{l}\frac{\Delta T_f}{T_f}={\left(10c_q{T}_f^3\right)}^{-1}\zeta H_0{\Omega }_{DE0}{\left(3-2{\beta }_2\right)}^{-3/2}\\ ·\left(9-15{\beta }_2+6{\beta }_2^2\right){\left[\left(3+2{\beta }_2\right)H_0^2+2{\beta }_2{\dot{H}}_0\right]}^{3/2}\\ ·{\left[\left(9+3{\beta }_2-2{\beta }_2^2\right)H_0^4+9{\beta }_2{H}_0^2{\dot{H}}_0+{\beta }_2^2{H}_0{\ddot{H}}_0\right]}^{-1},\end{array}$$

(28)

where

$$\begin{array}{c}\hfill \zeta \equiv {\left(\frac{4{\pi }^3{g}_{*}}{45}\right)}^{\frac{1}{2}}{M}_{Pl.}^{-1}.\end{array}$$

(29)

In this expression, we insert [92]

$$\begin{array}{c}\hfill {\Omega }_{DE0}\approx 0.7,H_0=1.4\times {10}^{-42}\mathrm{GeV},\end{array}$$

(30)

and the derivatives of the Hubble function at present are calculated through ${\dot{H}}_0=-H_0^2\left(1+q_0\right)$ and ${\ddot{H}}_0=H_0^3\left(j_0+3q_0+2\right)$ with $q_0=-0.503$ the current decceleration parameter of the Universe [92], and $j_0=1.011$ the current jerk parameter [93,94]. Hence, ${\dot{H}}_0\approx -9.7\times {10}^{-85}$ GeV² and ${\ddot{H}}_0\approx 4.1\times {10}^{-126}$ GeV³.

Using the BBN constraint (26), we conclude that ${\beta }_2\in \left(-2.98,-2.93\right)$ ∪ $\left(0.99,1.01\right)$, where we have used (27) to find

$$\begin{array}{l}{\beta }_1=\sqrt{3}{H}_0{\Omega }_{DE0}{\left[\left(3+2{\beta }_2\right)H_0^2+2{\beta }_2{\dot{H}}_0\right]}^{3/2}\\ ·{\left[\left(9+3{\beta }_2-2{\beta }_2^2\right)H_0^4+9{\beta }_2{H}_0^2{\dot{H}}_0+{\beta }_2^2{H}_0{\ddot{H}}_0\right]}^{-1}.\end{array}$$

(31)

Using the above range of ${\beta }_2$, we find that ${\beta }_1\in \left(2.09\times {10}^{-26},0.001\right)$ ∪ $\left(1.380,1.384\right)$.

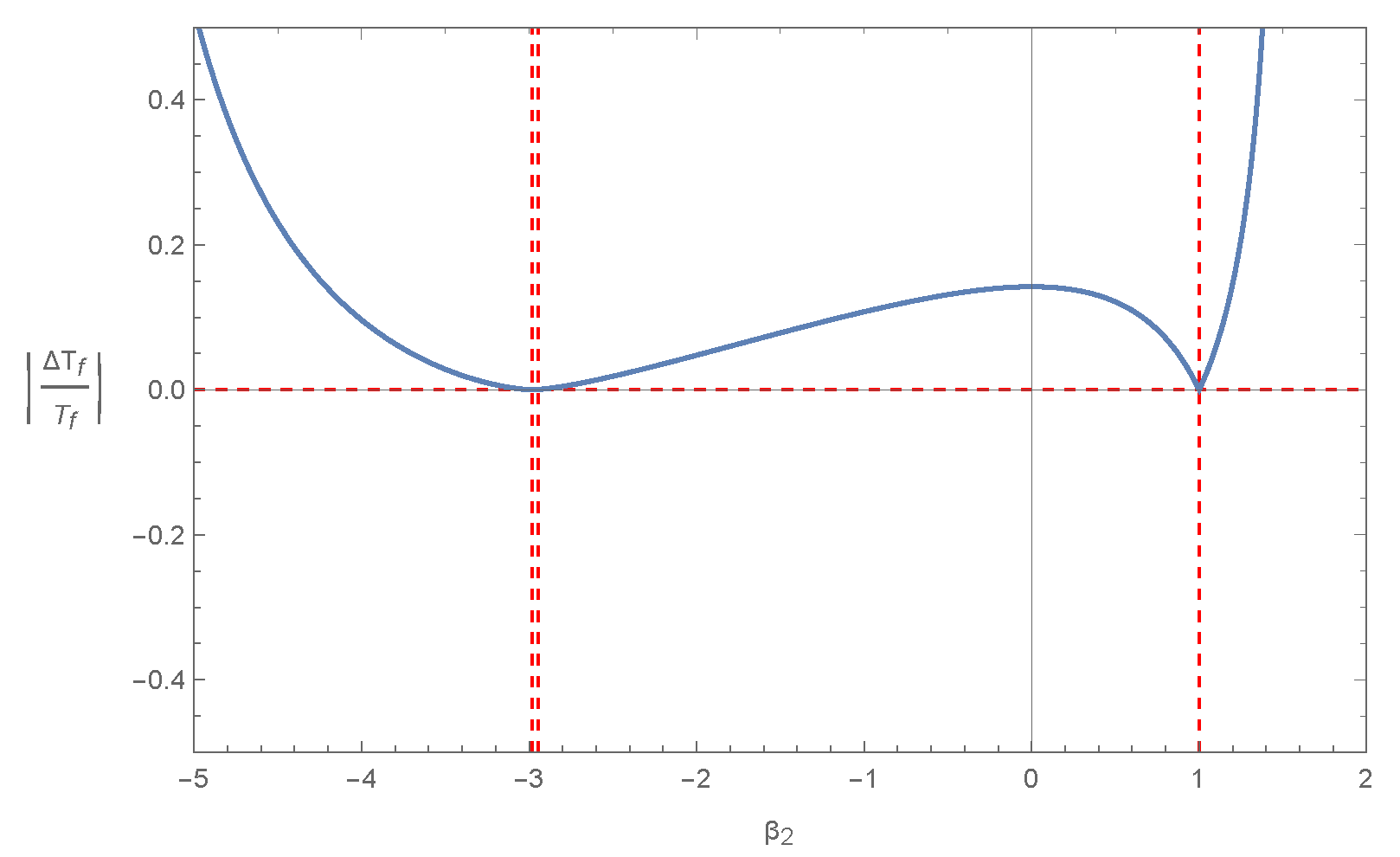
In Figure 1, we depict $|\Delta T_f/T_f|$ appearing in (28) versus the model parameter ${\beta }_2$. As we can see, the allowed range is within the vertical dashed lines.

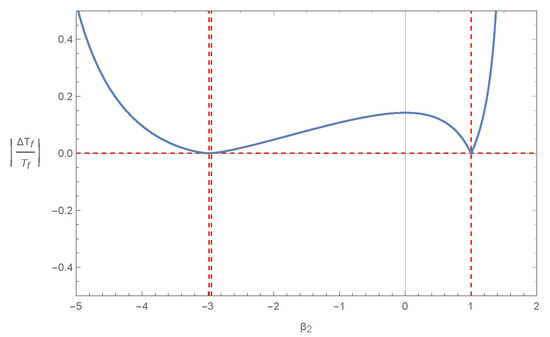
Figure 1. $|\Delta T_f/T_f|$ vs. the model parameter ${\beta }_2$ (blue solid curve), for Model I: $f=-T+{\beta }_1\sqrt{T^2+{\beta }_2{T}_G}$. The allowed range of ${\beta }_2$, where (26) is satisfied (horizontal red dashed line), is within the vertical dashed lines.

4.2. Model II: $f=-T+a_1{T}^2+a_{2}T\sqrt{|T_G|}$

Let us now study the case $f=-T+a_1{T}^2+a_{2}T\sqrt{|T_G|}$, where $a_1$, $a_2$ are the free parameters of the theory [28]. In this case, we find

$$\begin{array}{c}\hfill \frac{\Delta T_f}{T_f}=\frac{3}{10}{c}_q^{-1}{\zeta }^3{T}_f\left\{\frac{{\Omega }_{DE0}}{3H_0^2}-\sqrt{6}{a}_2\left[\frac{\sqrt{H_0^2+\dot{H_0}}}{6H_0}\left(6-\frac{2{\dot{H}}_0^2-H_0{\ddot{H}}_0}{H_0^2+{\dot{H}}_0}\right)-1\right]\right\}.\end{array}$$

(32)

Using the constraint (26), and according to (32), $\Delta T_f/T_f$ is linear in $a_2$; we deduce that (32) is valid for a small region around $2.7\times {10}^{83}{\mathrm{GeV}}^{-2}$, where we have used the constraint from current cosmological era (27)

$$\begin{array}{c}\hfill a_1=\frac{{\Omega }_{DE0}}{18H_0^2}-\sqrt{6}{a}_2\frac{\sqrt{H_0^2+\dot{H_0}}}{36H_0}\left[6-\frac{2{\dot{H}}_0^2-H_0{\ddot{H}}_0}{{\left(H_0^2+{\dot{H}}_0\right)}^2}\right].\end{array}$$

(33)

Using the above value of $a_2$, we find that $a_1=-1.1\times {10}^{83}{\mathrm{GeV}}^{-2}$.

4.3. Model III: $f=-T+{\beta }_1\sqrt{T^2+{\beta }_2{T}_G}+a_1{T}^2+a_{2}T\sqrt{|T_G|}$

Now, we analyze the model $f=-T+{\beta }_1\sqrt{T^2+{\beta }_2{T}_G}+a_1{T}^2+a_{2}T\sqrt{|T_G|}$, where we have four free parameters, namely, ${\beta }_1$, ${\beta }_2$, $a_1$, $a_2$ [28]. In order to simplify the analysis, we will impose the constraint $-2.99<{\beta }_2<\frac{3}{2}$, obtained above.

In this case, we find

$$\begin{array}{c}\frac{\Delta T_f}{T_f}=-{\left(60c_q{T}_f^3\right)}^{-1}\left\{3\sqrt{12}{\beta }_1{\left(3-2{\beta }_2\right)}^{-1/2}\left(1+{\beta }_2-2{\beta }_1\right)\right.\hfill \\ -18\{\frac{{\Omega }_{DE0}}{3H_0^2}+\frac{\sqrt{12}{\beta }_1}{18H_0^3}{\left[\left(3+2{\beta }_2\right)H_0^2+2{\beta }_2{\dot{H}}_0\right]}^{-1/2}\\ ·\left[\left(3-6{\beta }_1+2{\beta }_2\right)H_0^2+2{\beta }_2{\dot{H}}_0\right]\\ -\frac{a_2}{\sqrt{6}{H}_0}\sqrt{H_0^2+{\dot{H}}_0}\left[6-\frac{2{\dot{H}}_0^2-H_0{\ddot{H}}_0}{{(H_0^2+{\dot{H}}_0)}^2}\right]+\sqrt{6}{a}_2\\ -\frac{\sqrt{12}{\beta }_1{\beta }_2}{18H_0^3}{\left[\left(3+2{\beta }_2\right)H_0^2+2{\beta }_2{\dot{H}}_0\right]}^{-3/2}\\ ·\left[\left(3+2{\beta }_2\right)H_0^4+\left(9+8{\beta }_2\right)H_0^2{\dot{H}}_0\right.\\ \hfill \left.\left.+{\beta }_2\left(4{\dot{H}}_0^2+H_0{\ddot{H}}_0\right)\right]\}{\zeta }^2{T}_f^4\right\}\zeta .\end{array}$$

Observing that expression (34) is linear in $a_2$, and using the constraint (26) and two values for ${\beta }_1$ from the aforementioned range we extracted in model I, i.e., ${\beta }_1=1.4$ and ${\beta }_2=1$, we find that (32) is valid for a small region around the point $-3.5\times {10}^{83}{\mathrm{GeV}}^{-2}$. Using another set of values (${\beta }_1=0.001$, ${\beta }_2\approx -2.96$), we find that (32) is valid for a small region around the point $-5.3\times {10}^{83}{\mathrm{GeV}}^{-2}$, where we have used

$$\begin{array}{c}{a}_1=\frac{{\Omega }_{DE0}}{18H_0^2}+\frac{\sqrt{12}{\beta }_1}{108H_0^3}{\left[\left(3+2{\beta }_2\right)H_0^2+2{\beta }_2{\dot{H}}_0\right]}^{-1/2}\hfill \\ \left[\left(3-6{\beta }_1+2{\beta }_2\right)H_0^2+2{\beta }_2{\dot{H}}_0\right]\\ -\frac{\sqrt{6}}{36}\frac{a_2}{H_0}\sqrt{H_0^2+{\dot{H}}_0}\left(6-\frac{2{\dot{H}}_0^2-H_0{\ddot{H}}_0}{{\left(H_0^2+{\dot{H}}_0\right)}^2}\right)\\ -\frac{\sqrt{12}{\beta }_1{\beta }_2}{108H_0^3}{\left[\left(3+2{\beta }_2\right)H_0^2+2{\beta }_2{\dot{H}}_0\right]}^{-3/2}\\ \times \left[\left(3+2{\beta }_2\right)H_0^4+\left(9+8{\beta }_2\right)H_0^2{\dot{H}}_0+{\beta }_2\left(4{\dot{H}}_0^2+H_0{\ddot{H}}_0\right)\right],\end{array}$$

(34)

from (27). Imposing the above range of $a_2$, we find that $a_1=1.4\times {10}^{83}{\mathrm{GeV}}^{-2}$ for the first case and $a_1=2.2\times {10}^{83}{\mathrm{GeV}}^{-2}$ for the second.

4.4. Model IV: $f=-T+{\beta }_1{\left(T^2+{\beta }_2{T}_G\right)}^n$

As a next model, we consider the power-law model $f=-T+{\beta }_1{\left(T^2+{\beta }_2{T}_G\right)}^n$, where the free parameters are ${\beta }_1$, ${\beta }_2$, n. In this model, we use values of ${\beta }_1$, ${\beta }_2$ in order to constrain the power n. In this case, repeating the above steps, we find

$$\begin{array}{ccc}\hfill & & \frac{\Delta T_f}{T_f}={\left(10c_q\right)}^{-1}{\Omega }_{DE0}{H}_0^{2\left(1-n\right)}{\zeta }^{4n-1}{T}_f^{8n-7}{\left(3-2{\beta }_2\right)}^{n-2}\hfill \\ & & ·{\left[\left(3+2{\beta }_2\right)H_0^2+2{\beta }_2{\dot{H}}_0\right]}^{2-n}\left[\left(9-12{\beta }_2+4{\beta }_2^2\right)\right.\hfill \\ & & \left.-2n\left(18-39{\beta }_2+18{\beta }_2^2\right)+16n^2{\beta }_2\left(2{\beta }_2-3\right)\right]\hfill \\ & & ·\left\{\left(9+12{\beta }_2+4{\beta }_2^2\right)H_0^4+4{\beta }_2\left(3+2{\beta }_2\right)H_0^2{\dot{H}}_0+4{\beta }_2^2{\dot{H}}_0^2\right.\hfill \\ & & -2n\left[\left(18+15{\beta }_2+2{\beta }_2^2\right)H_0^4+{\beta }_2\left(27+12{\beta }_2\right)H_0^2{\dot{H}}_0\right.\hfill \\ & & \left.+6{\beta }_2^2{\dot{H}}_0^2+2{\beta }_2^2{H}_0{\ddot{H}}_0\right]+2n^2{\beta }_2\left[4\left(3+2{\beta }_2\right)H_0^2{\dot{H}}_0\right.\hfill \\ & & {\left.\left.+4{\beta }_2{\dot{H}}_0^2+2{\beta }_2{H}_0{\ddot{H}}_0\right]\right\}}^{-1}.\hfill \end{array}$$

(35)

We use the constraint (26) and four values for ${\beta }_2$ from the range we extracted in model I above. For ${\beta }_2\approx -2.9$, we find that the constraint (26) is valid for $n\lesssim 0.5$. Similarly, using the value ${\beta }_2=-2$, we find $n\lesssim 0.47$, while for ${\beta }_2=-1$ we find $n\lesssim 0.46$. Finally, for ${\beta }_2=1$, we find $n\lesssim 0.47$. We mention that we have used the relation

$$\begin{array}{l}{\beta }_1=-6{\left(12\right)}^{-n}{H}_0^{2(1-n)}{\Omega }_{DE0}{\left[\left(3+2{\beta }_2\right)H_0^2+2{\beta }_2{\dot{H}}_0\right]}^{2-n}\\ ·\left\{\left(9+12{\beta }_2+4{\beta }_2^2\right)H_0^4+4{\beta }_2\left(3+2{\beta }_2\right)H_0^{2}t{H}_0+4{\beta }_2^2{\dot{H}}_0^2\right.\\ -2n\left[\left(18+15{\beta }_2+2{\beta }_2^2\right)H_0^4+{\beta }_2\left(27+12{\beta }_2\right)H_0^2{\dot{H}}_0\right.\\ \left.+6{\beta }_2^2{\dot{H}}_0^2+2{\beta }_2^2{H}_0{\ddot{H}}_0\right]+2n^2{\beta }_2\left[4\left(3+2{\beta }_2\right)H_0^2{\dot{H}}_0\right.\\ {\left.\left.+4{\beta }_2{\dot{H}}_0^2+2{\beta }_2{H}_0{\ddot{H}}_0\right]\right\}}^{-1},\end{array}$$

(36)

which arises from (27).

Now, taking ${\beta }_2\approx -2.9$, $n\lesssim 0.5$ we find ${\beta }_1\in \left[-6.1\times {10}^{-82},0.0007\right]{\mathrm{GeV}}^{2\left(1-2n\right)}$. Similarly, for ${\beta }_2=-2$, $n\lesssim 0.47$ we find ${\beta }_1\in \left[-3.5\times {10}^{-74},5.9\times {10}^{-6}\right]{\mathrm{GeV}}^{2\left(1-2n\right)}$, while using ${\beta }_2=-1$, $n\lesssim 0.46$ we find ${\beta }_1\in \left[-4.4\times {10}^{-58},1.2\times {10}^{-6}\right]{\mathrm{GeV}}^{2\left(1-2n\right)}$. Finally, for ${\beta }_2=1$, $n\lesssim 0.47$ we find ${\beta }_1\in \left[-6.4\times {10}^{-8},9.0\times {10}^{-6}\right]{\mathrm{GeV}}^{2\left(1-2n\right)}$.

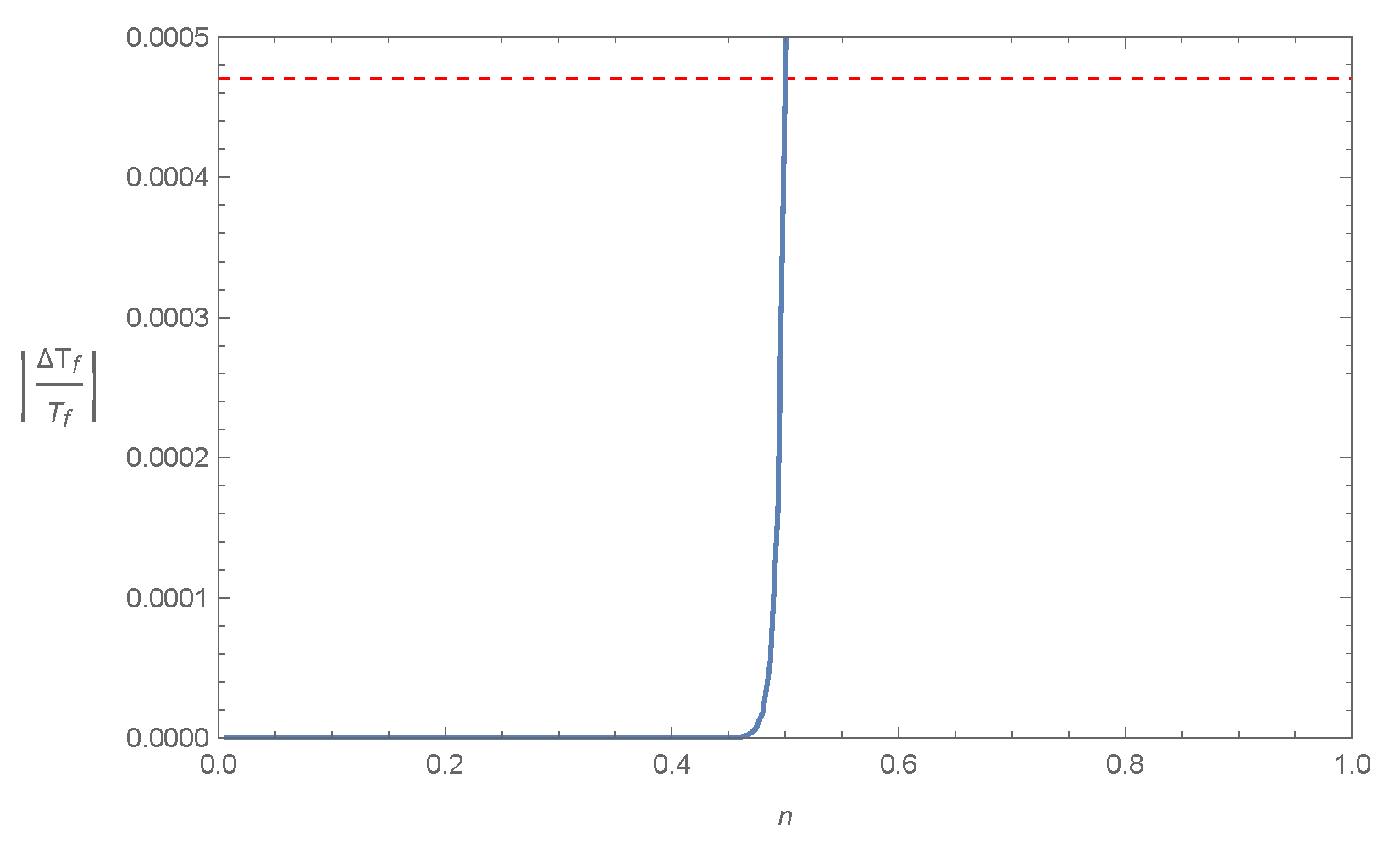
In order to provide the above results in a more transparent way, in Figure 2, we present $|\Delta T_f/T_f|$ from (35) in terms of the model parameter n. As we observe, n needs to be $n\lesssim 0.5$ to pass the BBN constraint (26).

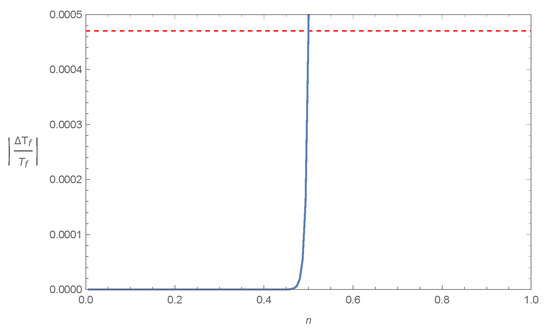
Figure 2. $|\Delta T_f/T_f|$ vs. the model parameter n (blue solid curve), for Model IV: $f=-T+{\beta }_1{\left(T^2+{\beta }_2{T}_G\right)}^n$ with ${\beta }_2\approx -2.90$, and the upper bound for $|\Delta T_f/T_f|$ from (26) (red dashed line). As we observe, constraints from BBN require $n\lesssim 0.5$.

4.5. Model V: $f=-T+\alpha \ln {\beta }_1{\left(T^2+{\beta }_2{T}_G\right)}^n$

In the last model we examine is the logarithmic one, characterized by $f=-T+\alpha \ln {\beta }_1{\left(T^2+{\beta }_2{T}_G\right)}^n$, where ${\beta }_1$, ${\beta }_2$, n are the free parameters. Repeating the above analysis, we find

$$\begin{array}{l}\frac{\Delta T_f}{T_f}={\left(10c_q\zeta T_f^7\right)}^{-1}{H}_0^2{\Omega }_{DE0}\{\ln {\beta }_1+n\left[\ln 12\right.\\ +4\ln \left(\zeta T_f^2\right)+\ln \left(3-2{\beta }_2\right)\\ \left.-2{\left(3-2{\beta }_2\right)}^{-2}\left(18-39{\beta }_2+18{\beta }_2^2\right)\right]\}\\ ·\{\ln {\beta }_1+n\left\{\ln 12+2\ln \left(H_0\right)+\ln [(3+2{\beta }_2)H_0^2+2{\beta }_2{\dot{H}}_0]\right.\\ -2{\left[\left(3+2{\beta }_2\right)H_0^2+2{\beta }_2{\dot{H}}_0\right]}^{-2}\left[\left(18+15{\beta }_2+2{\beta }_2^2\right)H_0^4\right.\\ \left.\left.+{\beta }_2\left(27+12{\beta }_2\right)H_0^2{\dot{H}}_0+6{\beta }_2^2{\dot{H}}_0^2+2{\beta }_2^2{H}_0{\ddot{H}}_0\right]\right\}{\}}^{-1},\end{array}$$

(37)

where using relation (27) we find

$$\begin{array}{l}\alpha =-6H_0^2{\Omega }_{DE0}\{\ln {\beta }_1+n\{\ln 12+2\ln \left(H_0\right)\\ +\ln \left[\left(3+2{\beta }_2\right)H_0^2+2{\beta }_2{\dot{H}}_0\right]\\ -2{\left[(3+2{\beta }_2)H_0^2+2{\beta }_2{\dot{H}}_0\right]}^{-2}[(18+15{\beta }_2+2{\beta }_2^2)H_0^4\\ +{\beta }_2\left(27+12{\beta }_2\right)H_0^2{\dot{H}}_0+6{\beta }_2^2{\dot{H}}_0^2+2{\beta }_2^2{H}_0{\ddot{H}}_0\left]\right\}{\}}^{-1}.\end{array}$$

(38)

We consider the values ${\beta }_1=0.001{\mathrm{GeV}}^{-4n}$, ${\beta }_2\approx -2.9$, and we find that n is allowed to take every value apart from $-0.0003$ and a very small region around it since (37) diverges. Moreover, $\alpha$ is allowed to take every value apart from 0, which is the value it obtains using the above narrow window for n. Using the same considerations as the above models, we find that for ${\beta }_1=0.001{\mathrm{GeV}}^{-4n}$, ${\beta }_2=-2$ the value of n is allowed to take every value apart from $-0.012$ and a every value but 0. Similarly, for ${\beta }_1=0.001{\mathrm{GeV}}^{-4n}$, ${\beta }_2=-1$ we find that $n\ne -0.018$ and $a\ne 0$, while for ${\beta }_1=0.001{\mathrm{GeV}}^{-4n}$, ${\beta }_2=1$ we find $n\ne -0.018$ and $a\ne 0$.

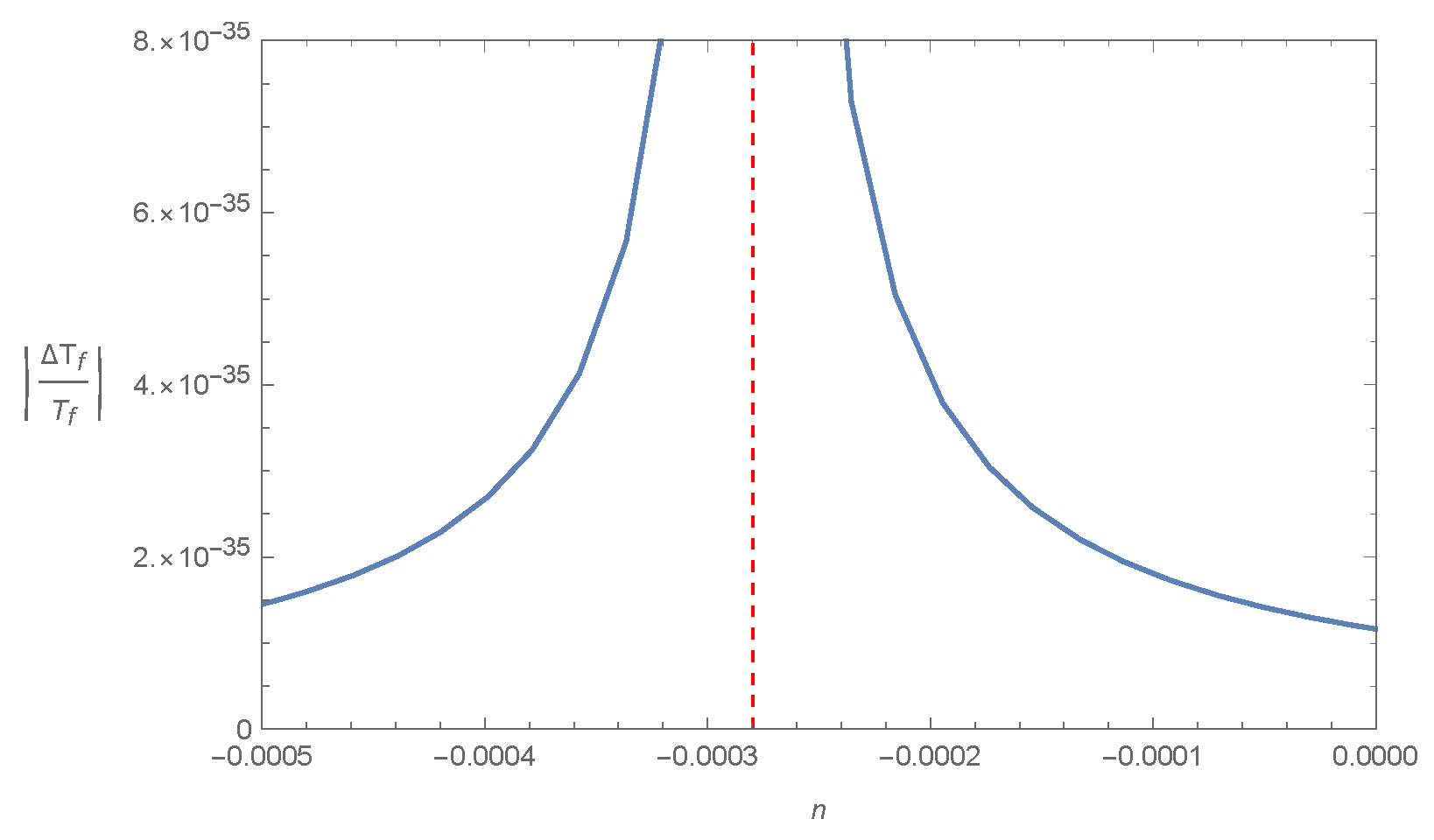
As an example, in Figure 3 we present $|\Delta T_f/T_f|$ from (37) as a function of the model parameter n. The model parameter n is allowed to take all possible values except those values around a very small region centered at $-0.0003$, in which (37) diverges. Hence, we conclude that the logarithmic $f(T,T_G)$ model can easily satisfy the BBN bounds.

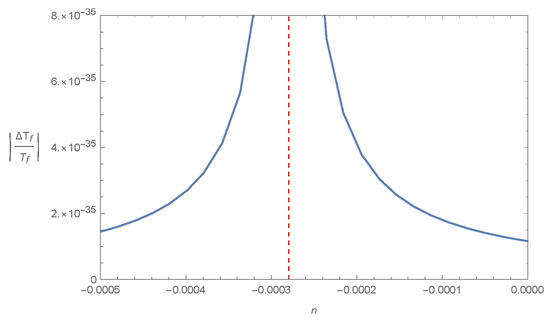
Figure 3. $|\Delta T_f/T_f|$ vs. the model parameter n (blue solid curve), for Model V: $f=-T+\alpha \ln {\beta }_1{\left(T^2+{\beta }_2{T}_G\right)}^n$, choosing ${\beta }_1=0.001{\mathrm{GeV}}^{-4n}$, ${\beta }_2\approx -2.7$. The vertical dashed line at $n-0.0003$ denotes the point where (37) diverges.

5. Conclusions

Modified gravity aims to provide explanations for various epochs of the universe evolution, and at the same time to improve the renormalizability issues of general relativity. Nevertheless, despite the specific advantages at a given era of cosmological evolution, one should be very careful not to spoil the other, well understood and significantly constrained, phases, such as the big bang nucleosynthesis (BBN) one.

In particular, there are many modified gravity models, which are constructed phenomenologically in order to be able to describe the late-time universe evolution at both the background and perturbation level. Typically, these models are confronted with observational data such as Supernovae Type Ia (SNIa), Baryonic Acoustic Oscillations (BAO), cosmic microwave background (CMB), cosmic chronometers (CC), gamma-ray bursts (GRB), growth data, etc. The problem is that although modified gravity scenarios, through the extra terms they induce, are very efficient in describing the late-time universe, quite often they induce significant terms at early times too, thus spoiling the early-time evolution, such as the BBN phase, in which the concordance cosmological paradigm is very successful. Hence, independently of the late-universe successes that a modified gravity model may have, one should always examine whether the model can pass the BBN constraints too.

In the present work, we confronted one interesting class of gravitational modification, namely, $f(T,T_G)$ gravity, with BBN requirements. The former is obtained using both the torsion scalar, as well as the teleparallel equivalent of the Gauss–Bonnet term, in the Lagrangian. Hence, one obtains modified Friedmann equations in which the extra torsional terms constitute an effective dark energy sector.

We started by calculating the deviations of the freeze-out temperature $T_f$, caused by the extra torsion terms, in comparison to $\Lambda$CDM paradigm. We imposed five specific $f(T,T_G)$ models that have been proposed in the literature in phenomenological grounds, i.e., in order to be able to describe the late-time evolution and lead to acceleration without an explicit cosmological constant. Hence, we extracted the constraints on the model parameters in order for the ratio $|\Delta T_f/T_f|$ to satisfy the BBN bound $\left|\frac{\Delta T_f}{T_f}\right|<4.7\times {10}^{-4}$. As we found, in most of the models the involved parameters are bounded in a narrow window around their general relativity values, as expected. However, the logarithmic model can easily satisfy the BBN constraints for large regions of the model parameters, which acts as an advantage for this scenario.

We stress here that we did not fix the cosmological parameters to their general relativity values; on the contrary, we left them completely free and we examined which parameter regions are allowed if we want the models to pass the BBN constraints. The fact that in most models the parameter regions are constrained to a narrow window around their general relativity values was in some sense expected, but in general is not guaranteed or known a priori since many modified gravity models are completely excluded under the BBN analysis since for all parameter regions their early-universe effect is huge.

In conclusion, $f(T,T_G)$ gravity, apart from having interesting cosmological implications both in the inflationary and late-time phase, possesses particular sub-classes that can safely pass BBN bounds; nevertheless, the torsional modification is constrained in narrow windows around the general relativity values. This feature should be taken into account in future model building.