1. Introduction
As little as we know stellar dynamo physics in sufficient detail, one thing appears to be clear: the connection between stellar activity and angular momentum. Since Skumanich (1972) [
1], it is common consensus, at least for cool main sequence stars, that both rotation rate and magnetic activity decline with the inverse square root of the stellar age (now known as the Skumanich law). Reiners & Mohanty (2012) [
2] demonstrated that the magnetic braking time-scale itself depends on mass and radius. For main sequence stars, given their mass-radius relation, they result in an increasing magnetic braking time-scale with decreasing stellar mass, very similar to how the evolution timescale relates to the mass. That behaviour is reflected in the picture of strong and weak Ca II emission of the Mt. Wilson sample of the cool main sequence stars, compared in the HRD (Schröder et al., 2013 [
3]), where the decrease of stellar activity appears to be related to the fraction of main sequence life time already spent by the star, rather than on stellar age in absolute terms.
The picture of stellar activity across the Herzsprung–Russel-Diagram (HRD), however, becomes a lot more complicated with evolved stars. In the first place, we need to understand how giant activity is possible at all. The vast expansion of the convective shell and faster magnetic braking time scales are obvious factors in producing the low rotation rates observed of giant photospheres. In addition, the lack of coronal detections among cool giants initially led to the idea that such evolved stars would have become inactive (Linsky & Haisch (1979) [
4]). However, that is not necessarily so, as was demonstrated by Ayres et al. in several publications (see Ayres et al., 2003 and references therein [
5]). In fact, the existence of active cool giants was considered over a decade earlier, e.g., by Fekel & Balachandran (1993); see Schröder et al. (2018) [
6,
7] for a recent discussion of this problem from a chromospheric point of view. In conclusion, it now seems that coronal emission is not a good indicator of magnetic activity across the HRD, for various reasons given by the last two authors cited and further explained below.
After Hubrig et al. (1994) [
8] introduced the idea, that cool giants could have photospheric magnetic fields—however, suffering from their then very limited Zeeman-detection accuracy—Konstantinova-Antonova et al. (2013) and Auriere et al. (2015) [
9,
10] demonstrated convincingly that such a magnetic longitudional field is rather common, even with giants as far evolved as onto the AGB. That observational evidence rather points to magnetic activity living on into late stages of stellar evolution, despite coronal detections becoming rather rare with such evolved cool giants.
Approaching this question from a very different angle, Beck et al. (2012) [
11] found evidence from asteroseismology with Kepler-data that the contracting radiative cores of Hertzsprung Gap crossers are rotating much faster than the convective envelopes of these stars. This gap in the HRD between the main sequence and the giant branch opens up for stars more massive than about two solar masses due to experiencing a fast phase of stellar evolution here, in which the core stops burning, and is therefore bound to contract and spin up, while the envelope above the hydrogen-burning shell expands, resulting in a cooler effective temperature. The above find now raises the question, which we are going to discuss in this review, whether there is a connection between core spin-up phases, perhaps transferring angular momentum to the convective envelope, and the distribution of magnetic activity among cool giant stars across the HRD.
Supposing that a substantial fraction of stellar angular momentum is maintained by the core, both observational and theoretical means to study its co-evolution with the star are unfortunately very limited. On the one hand, the frequency of the (gravity dependent) modes, which are used by asteroseismology to detect faster rotating cores in the Hertzsprung gap and base of the RGB, become inconveniently long, when moving up in the HR diagramme on the RGB or AGB. Such evolved stars have much lower surface gravity, i.e., the relevant mode-periods are increasing from hours to many days or even weeks.
On the other hand, stellar structure models still suffer from many shortcomings. These begin with the approximate descriptions of convection and convective overshooting (see Shaviv and Salpeter (1973) [
12]), quantified only by semi-empirical approaches as by Schröder et al., 1997 [
13], or Miller Bertolami et al., 2016 [
14]). Of direct relevance to the questions discussed here are the interrelated problems of how to describe the interaction of magnetic flux tubes with the convective envelope and the latters’ effective viscosity (Aerts et al., 2019 [
15]), which seem far from being modeled well yet.
Hence, we need to use every bit of empirical evidence at hand. A very important information comes from fast rotating White Dwarfs—which, at the same time, do not show any indication of having obtained their angular momentum from a merger event in a close binary or any close companion, see, e.g., Hermes et al. (2018), Redding et al. (2020), or Kilic et al. (2021) [
16,
17,
18] for recent finds. These observations are testimony that at least some stellar cores have maintained a noticeable fraction of their angular momentum to the very end-stage of their evolution, sufficient to spin-up during core-contraction. Either, angular momentum transfer from the core to the convective envelope is fine-tuned, or the interaction, which transfers core angular momentum upwards, may take place only during certain episodes.
The find, that some angular momentum survives in the stellar core over the course of stellar evolution, gives way to some simple arguments: Whenever the core is contracting, at least if that happens on a short enough time scale to be faster than magnetic braking and dissipation of angular momentum from the core to its envelope, the core can spin up—as is observed, indeed, for recent Hertzsprung Gap crossers (Beck et al., 2012 [
11] and a growing number of more recent studies). A second phase of noticeable core contraction, albeit less fast, sets in after central Helium burning, i.e., leaving the blue loop, when the stellar energy production is changing over to the two shells burning while ascending the AGB. In absolute terms, time scales here are relatively short for massive AGB stars.
Since it was well established some time ago that some of the most active cool subgiants are recent Hertzsprung Gap crossers (see e.g., Schröder et al., 1998 [
19]), the question arises here, of whether should we then see an increase of magnetic activity among the ascending AGB stars as well? Indeed, as we will discuss below, there is evidence for this from both chromospheric emission measures (Schröder et al., 2018 [
7]) and magnetic field detection in the photosphere (Konstantinova-Antova et al., 2010, 2013, 2014, Georgiev et al., 2020 [
9,
20,
21,
22]).
At the same time, K giant activity during the core Helium burning phase is decreasing with the time spent in that phase (Schröder et al., 2020 [
23]). These observations, albeit still from only a few case studies, hint on a picture, where stellar activity depends on an interplay of core rotation dissipated into the convective envelope in phases of core contraction, either starting strongly (on the base of the RGB) or rejuvenating (ascend to AGB) dynamo action, while by contrast magnetic braking slowly decreased the magnetic activity in phases of a rather stable core (core Hydrogen and core Helium burning).
In addition, Charbonnel et al. (2017) [
24] demonstrated that the properties of the convective envelope and its evolution play a role as well, because the convective turnover time has an impact on the activity degree by shaping the Rossby number. In stellar dynamo models, operating in a rotating and convective envelope, the Rossby number
reduces to the ratio of the rotation period of the star over the convective turn-over time of the envelope, in which the magnetic field is generated—a most decisive parameter in such dynamo models. For a discussion of solar mean-field dynamo models, see Brandenburg et al., 1990 [
25], and for a computational simulation point of view on this wide field and its many facets, see Brun and Browning (2015) [
26] and the references given therein. In order to have a stable dynamo, empirical evidence suggests that the Rossby number should be smaller than unity, and the smaller it is, the stronger seems to be the activity level (see Mittag et al., 2018 [
27] and references given therein).
If we see the core spin and its angular momentum reservoir as the motor of activity, then the convective envelope and the Rossby number it provides needs to be recognized for its role as the driver. Both these very different approaches are internal to the stellar structure, which is what they have in common.
However, in that respect, we shall also mention a very different possibility: External angular momentum given to the convective envelope by the capture of planets, as the giant evolution dooms any orbiting object to even beyond the orbit of Earth (Schröder and Smith (2008) [
28], and references given therein) to be engulfed and eventually merges with the convective envelope (to our knowledge, starting with Siess and Livio (1999) [
29]). While any planet may seem negligible in mass, compared to the convective envelope (even a “hot Jupiter”), its angular momentum is not, since in close orbits, planets can have a shorter period than the giant rotation. Obviously, the vast envelope expansion, before a star reaches the tip of the RGB, allows for the capture of several planets and their angular momentum (see, e.g., Gaulme et al., 2020 [
30]), but it has to be observed whether that explains the whole picture of giant activity.
We shall try to seek arguments in favour or against each one of these lines of explanation when discussing below the available observational evidence and the application of dynamo theory to the specific problems posed by the structure of cool giants.
2. The Conundrum of the Dynamo Operation in Cool Giants
The aforementioned, combined evidence of chromospheric emission and photospheric magnetic field detections leaves no doubt that giant magnetic activity is a common phenomenon in intermediate–mass stars, despite detections of coronal flux becoming rare. In several well-studied cases, even solar-type magnetic cycles have been established from the monitoring of the Ca II H&K emissions (see, e.g., Schröder et al., 2020 [
23] and references therein for the case of two Hyades K giants).
As similar as giant magnetic activity therefore appears to be to solar activity in the time domain, as surprising that this is, because: Given the so vastly different stellar structures—namely, (1) the sheer geometric extent of the giant convective envelopes, (2) dissimilar structures of differential rotation and (3) the different characteristics of the core, one might also expect very different types of dynamo at work in the sun and a cool giant.
Two problems arise from these huge differences, which need to be understood: First of all, where in a giant convective envelope is the magnetic field formed, and how does it surface? For the sun, most dynamo models suggest magnetic field production by the omega effect to happen near the bottom of the convection zone. By contrast, giant convection zones are so extended, that flux tube loops
cannot be understood how to reach the photosphere undisturbed—their journey through a dynamic environment is simply too long to not disintegrate or assimilate (see Holzwarth & Schüssler 2001 [
31] for an attempt to model this problem).
Hence, in giants, at least part of the toroidal magnetic field may be produced further up in the convective envelope, i.e., by a “stratified dynamo” (as described and illustrated for the sun by Brandenburg et al., 1992 [
32]) or even by a near-surface dynamo—concepts which would solve this problem. But then we need to ask, whether it is by coincidence, that the time behaviour (i.e., cycle periods and their dependence on Rossby number) of giant and solar-type dynamos are similar. If they were different, where in the HRD does one get replaced by the other? Or are our classical ideas of the solar dynamo wrong—i.e., has the sun indeed a stratified dynamo? The Zeeman Doppler Imaging (ZDI) map of the fast rotating giant V390 Aur may support the stratified dynamo concept, see Konstantinova-Antova et al. (2012) [
33], who found a significant toroidal field component close to the surface.
The second problem brings us to the subject of this paper, the question of where does the required angular momentum come from, and how exactly does it drive the dynamo?
In the sun, we find differential rotation in latitude throughout the convective envelope, which winds up, stretches and reinforces any poloidal field, and so the part of the magnetic field production (the omega process) is explained very easily for the Sun. While there is observational evidence for differential latitudional rotation for a number of giants, too (see the abundant work of Strassmeier et al., as well as, e.g., Konstantinova-Antova et al., 2012 and Tsvetkova et al., 2017 [
33,
34]), the observed differences between the much faster rotating core and giant photosphere in asteroseismology is striking, without any parallel to the sun, and may provide the actual motor for the dynamo action in these very active, recent gap-crosser giants on the base of the RGB.
Hence, there must be a sheer layer with an enormous rotation gradient in the lower regions of the convective envelope of such a giant, through which angular momentum could be dissipated into the latter. So to speak, does the dog wag the tail? Meaning, that this angular momentum handed up from the contracting, spinning-up core feed the giant dynamo directly (by means of its sheer layer) or indirectly (by means of a more complicated, meridional rotation pattern further above, causing the observed differential rotation in latitude)?
In their combination, these two problems are even more difficult to resolve, because current theoretical approaches prefer a small viscosity and so predict a very steep rotational gradient, expecting a geometrically very thin sheer layer at the very bottom of the giant convective envelope—from where the magnetic field tubes are not understood how to rise all the way to the surface. Furthermore, if one assumes a large effective viscosity, perhaps by means of a “magnetic stiffening” of the convective envelope, then the dissipation of angular momentum could become too large, as the core would not keep part of it to the very end, as observations of White Dwarfs seem to suggest—unless any such angular momentum transfer phases from the core to the envelope is very short, such as a dredge-up episode.
Interestingly, Aerts et al. (2019) [
15] point out that empirical evidence from main sequence stars suggest larger core angular momentum losses to the convective envelope than predicted by theoretical models.
In addition, in the Cool Stars 21 conference [
35] announced the asteroseismological detection of a strong (30 to 100 kG) field in the cores of three red giants in the vicinity of the hydrogen burning shell. Certainly, our grasp of this key problem is very incomplete, nor do we even know all the players on the field. The effective viscosity may be a complicated function of height within the sheer layer, and it could vary over time, influenced by magnetic fields. Keep in mind that the above mentioned contradictions only arise from the oversimplified idea of a single, constant viscosity value.
On the contrary, when arguing that the core angular momentum should not have any effect on the convective envelope, because the viscosity would indeed be too small and/or the sheer layer much too thin (i.e., sheer not most of the envelope), then it seems reasonable that instead the convective envelope receives its angular momentum from the outside, by means of engulfed planets—so to speak: Does instead the tail wag the dog?
Now, if that was true, every giant would obtain a boost of its magnetic activity at the moments of its own capture events, which happen along with the evolutionary envelope expansion. Consequently, across the HRD we should find an erratic display of very active giants all over the giant branches.
However, in fact, we have not observed any very active giants with masses lower than 1.5 . If planet engulfment was the main reason for giant activity, then the lower mass giants should rather be even more driven by this process than the more massive ones, because any planet has a larger impact on them, and so low mass giants should be detected as active.
On the other hand, there is a good evolutionary explanation for this observational evidence: These are the stars, which had had convective envelopes already on the main sequence, were magnetically active and, consequently, have suffered since the beginning from magnetic braking. In addition, their evolution from the main sequence to the Red Giant Branch is slow, and so is their core contraction, when compared to intermediate-mass stars. Hence, the scenario drawn below for core contraction inciting magnetic activity does not apply to these giants, which in this context would precisely be expected to be much less active.
In the case of the angular momentum being transferred from the core to the convective envelope of intermediate-mass giants, those with the largest activity should be concentrated—systematically—around and just after core contraction phases. Moreover, so they do, as shown below. However, since any core contraction is going hand in hand with envelope expansion (the so-called “mirror principle” in stellar evolution), the difference in the HRD between these two scenarios may be rather subtle. We are taking a closer look at the available empirical evidence in the next section. Moreover, of course, it is also possible that both mechanisms may work side by side, since the working of one does not rule out the feasibility of the other.
3. An Unbiased Picture of Magnetic Activity across the HRD
3.1. Historic Misunderstanding of X-ray Detections
As mentioned above, the first attempts to understand the picture of magnetic activity across the HR diagramme in terms of coronal X-ray detection were misled by the bias of this activity indicator against extended chromospheres, especially among luminous (low gravity) red giants—worse, when early X-ray observations were not reaching deep, as was the case with the data used by Linsky and Haisch (1979) [
4] and contemporary research. That led to the initial misunderstanding that evolved stars may mostly spin down and become, sooner or later, magnetically dead.
However, already at the same time, O.C. Wilson started to question this strictly age-related picture, based on the evidence of chromospheric emissions from giants he was accumulating. He took a particular interest in the four Hyades K giants, which were included in the Mount Wilson Ca II monitoring project. Peculiarly, these data demonstrate that two of these giants are active, while two are not. That made Wilson raise the important question of how that can be possible, given that these giants are of the same cluster and so have exactly the same age (according to D. Reimers, priv. comm., as early as 1972, see Baliunas et al. (1983) [
36] for a discussion of this question). Obviously, beyond the main sequence, the existence and strength of giant activity is not only a question of age, but a more complicated picture emerges.
Indeed, the first findings of “hybrid giants”, with far UV signatures of both, cool winds and transition layer emission (using IUE observations of Mg II, C IV and Si IV emission lines) by Reimers et al. (1996) [
37] and others, successful ROSAT detections among the nearest giants (Hünsch et al., 1996 [
38]) and even of a few exceptional M giants (Hünsch et al., 1998 [
39]), as well as by very deep X-ray pointings (Ayres et al., 2003 [
5]), leading to the idea of coronal loops, may just be buried under a huge and extended chromospheric column density.
In addition to this geometrical implication of a large, extended chromosphere, it also requires more energy input to reach the Athay point, at which the Hydrogen ionization balance tips, and chromospheric plasma jumps to coronal temperature—for a full description of this abrupt transition, see Athay (1981) [
40]). In giants, larger column densities are met with smaller basal (non-magnetic) chromospheric energy flux input. These trends become ever stronger when moving up the giant branches (see Schröder (2018) [
7]). In consequence, it is simply not right to conclude that evolved stars would be magnetically dead. Rather, coronal detections are not the best means to account for magnetic activity, but give an incomplete, or at least biased picture, when it comes to cool luminous giants.
3.2. The Evidence from Chromospheric Emission Measures
Hence, we need to restrict this review of suitable evidence to the lesser biased indicators of (i) chromospheric emission, which reflects one to one the chromospheric energy input—but of both mechanical and magnetic heating, so the former must be considered when quantifying the latter—and of (ii) magnetic field detection in the photospheres (see below). Unfortunately, the average longitudional magnetic field, which can be expected from such detections, is expected to be low, because contributions by any strong local toroidal fields mostly cancel out.
For an analysis of chromospheric Ca II H&K emission measures of many giants across the HR diagramme, in the context of stellar evolution, the Mount Wilson project (Duncan et al., 1991 [
41]), with numerous calibrated S-index data, can be used as a uniform characterisitic of chromospheric emission.
S is a measure proportional to the chromospheric line core emission in Ca II H&K, measured by their added counts in about 1 Å wide bands
and
, taken relative to two 20 Å wide count measures of pseudo-continua reference bands
and
, which are symmetrically placed around the Ca II doublet:
These choices of definition make any S-index observation independent of the transparency of the night. See Schröder et al. (2020) [
23] and references therein for further detail. More importantly, a calibration process for the prefactor
, using 40 stars of little variability, was given by Baliunas et al. (1995). The frequent observation of these calibration stars allows one to eliminate all instrumental effects and compare directly to original Mount Wilson data from the 1970s onwards.
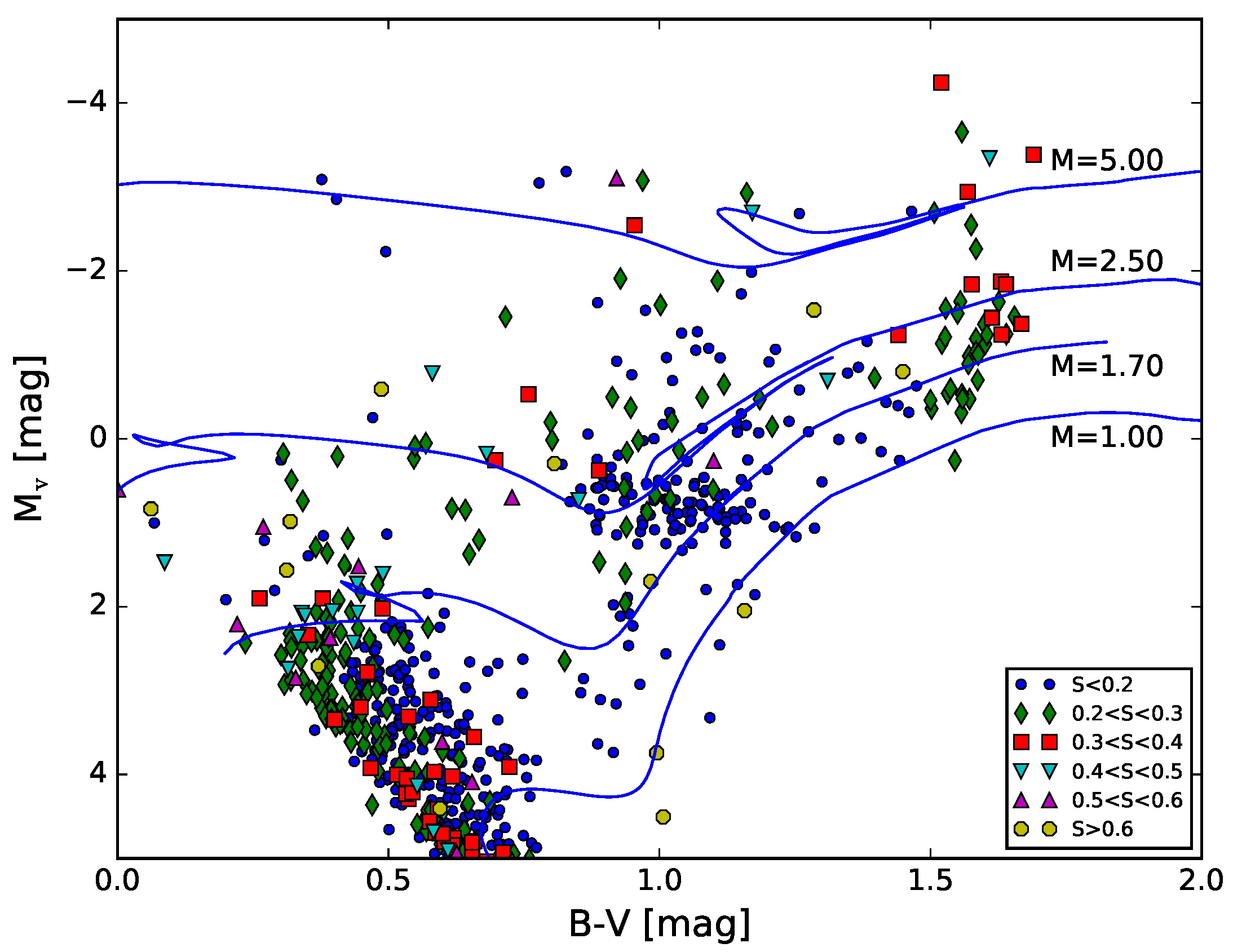
Such S-index observations aross the HRD (see
Figure 1) and considering the related surface fluxes (accounting for contrast gains against the photospheric spectrum in cooler giants, as well as for non-magnetic basal flux), lead Schröder et al., (2018) [
7] to conclude that more massive, mid-AGB K giants indeed become more magnetically active again. The cores of these stars are contracting faster again, albeit the gain of chromospheric heating is by no means as significant as in the cases of the recent Hertzsprung gap crosser on the base of the RGB (where the first magnetic strip is observed, see below). These chromospherically more active AGB K giants are apparently of the same type as those forming the below-mentioned second magnetic strip.
We may caution that active M giants, found even further up on the AGB, may form a different case, at least a more complex one, as pulsations and oscillations may be interacting with their magnetic processes, and convection cell sizes reach a considerable fraction of the stellar radius, e.g., the AGB star
Grux (see Palladini et al., 2018). It seems that the observed activity indicators variability of M giants cannot be explained with the characteristics of magnetic activity alone (see Georgiev et al., 2020; Konstantinova-Antova et al., 2022, in prep. [
22]).
3.3. The Evidence from Magnetic Field Detection
The new generation of spectropolarimeters of the 21st century, such as ESPaDOnS and Narval (Doati et al., 2006; Auriere 2003), have enabled us to obtain more precise Zeeman measurements and detections of a weaker magnetic fields than before. These instrumental advances, combined with the Least Square Deconvolution (LSD, Donati et al., 1998) technique, allowed magnetic field strengths down to 1 G or even less can be measured for cool giant stars, which provide us with the benefit of tens of thousand photospheric lines in their spectra.
At first, a magnetic field of about 15 G was Zeeman-detected in the fast-rotating G9 giant V390 Aur with Narval (Konstantinova-Antova et al., 2008 [
42]). Later on, a pilot study on a sample of 49 G and K single giants was performed with Narval and ESPaDOnS (see Konstantinova-Antova et al. 2013; Auriere et al., 2015 [
10,
42]). That sample includes both fast and slow rotators. It was selected by using different indicators for magnetic activity (namely, rotation velocity, chromospheric emission and X-ray detection). More than half of these giants were then indeed Zeeman-detected, and their longitudinal magnetic field strengths cover a large range, from less than 1 G to about 100 G.
By a comparison with evolution models, it was found by Auriere et al. (2015) [
10] that a majority of these Zeeman-detected giants are situated in the locus of the HR diagram, where the first dredge–up takes place (on the base of the RGB, i.e., right after crossing the Hertzsprung gap) and the central He-burning. However, the fast rotators, in particular, are concentrated on the base of the RGB. These very active stars form the so-called ”first magnetic strip“, and some of them coincide with early, strong X-ray detections (see Hünsch et al., 1996 [
38]).
The analysis of the respective rotation periods and Rossby numbers by Auriere et al., (2015) [
10], and their clear relation with the activity degree similar to solar-type stars, suggests that an alpha-omega dynamo is a likely candidate for generating the observed magnetic activity in those (activity-selected) giants.
A second study was devoted to an unbiased sample of northern, solar vicinity G, K and M single giants down to 4 magnitude in the V-filter, hence including apparently inactive giants, to—again using observations at Pic du Midi Observatory, France (Konstantinova-Antova et al., 2014; Konstantinova-Antova et al., 2022, in prep. [
21]). From this unbiased sample, it was found that still about 50 percent of giants possess magnetic fields of the order of 1 G and more. The so detected giants form, by their HRD distribution,
two magnetic strips (
Figure 2). This first one is in the same place as above, i.e., on the base of the RGB just after the Hertzsprung gap was crossed, which again sees some very active giants here.
In addition to these gap crossers (in fact, recently crossed the Hertzsprung Gap, HG), the unbiased giant sample reveals a second concentration, or well-enough defined strip, which is situated in the region of the higher mid-AGB (see
Figure 2). A significantly enhanced fraction, more than 60 percent, of all stars in the unbiased sample in this area of the HRD are magnetically active. Charbonnel et al. (2017) [
24] used evolution models, which consider the stellar rotation
and convective turnover time (
, see below), and so were able to explain both magnetic strips by their coincidence with evolutionary phases in which the convective envelope provides favourable conditions for the operation of an alpha–omega dynamo—a small Rossby number (
inside each strip, where a dynamo is deemed impossible for
), which is produced mainly by increasing convective turn-over times (as
) in these strips.
However, some of the giants in these magnetic strips are much faster rotators than others, and their much stronger magnetic field and activity cannot be explained in such simple evolutionary terms. An additional gain of angular momentum (transferred from the interior, or of an external origin) is required to explain their faster rotation and higher activity. Alternatively, some stars may carry forward a larger magnetic field than others from their time on the main sequence (consider, e.g., Ap stars).
In some cases, a binary nature may explain any larger activity and some variability, in terms of external angular momentum transferred to the convective envelope and other consequences.
There are also some giants on the low activity side of the detected distribution, which do not fit the above picture. These are slow rotators with a very weak magnetic field (see Figure 5 in Auriere et al., 2015 [
10]). It is unclear which dynamo type operates there. Maybe it does not depend on rotation but could be a so-called turbulent dynamo (which operates locally on convection alone, without a need for rotation, see Soker&Zoabi (2002) [
43]), for example.
Another type of exception is formed by three, fast rotating, very active giants
outside the magnetic strips. Namely, OP And and V1192 Ori are two cases of fast rotators and very active giants, which seem to out-lie from the first magnetic strip. They are of moderate mass and must have passed their first dredge-up phase. In addition, OP is known as a Lithium-rich giant. These stars may be special cases, in which fast rotation and magnetic activity can be explained by recent planet or substellar companion engulfment, according to the models by Privitera et al. (2016) [
44].
A very interesting fast rotator, which much out-lies from the second magnetic strip, is the 1.5
M giant RZ Ari. It is an early AGB star with unusually high magnetic activity (Konstantinova-Antova et al. 2022, in prep.). In addition, it, too, has a high Lithium abundance, which is contradicting the expectation from stellar evolution theory. It is very likely, therefore, that RZ Ari has engulfed a planet, too. In the latter case, magnetic activity cannot be explained by an alpha-omega dynamo, because the Rossby number is large here. However, other types of dynamo could work to explain the activity of this M giant, such as (i) an
-
type dynamo, which may work with larger Rossby numbers in AGB stars, or (ii) a “turbulent” dynamo as of Soker and Zoabi 2002 [
43], similar to the “local” dynamo, as proposed for the supergiant Betelgeuse (Auriére et al., 2010 [
45]), given large convective cells should occur in RZ Ari.
Those giants in both magnetic strips, where larger magnetic field measures coincide with enhanced chromospheric emission and heating, not only provide dynamo-friendly envelope conditions, but as pointed out above, in both phases also see a relatively fast core contraction. Plausibly, it is fast enough to out-compete magnetic braking, and the result is angular momentum transfer from the core into the convective envelope.
However, in the same phases we see the convective envelope expand, and so the same statement could be made for the capture of planets and their angular momentum—provided, that then apparently most giants would have plenty of planets at their disposal in suitably wide orbits. It is difficult, therefore, to conceive how planet capture should produce the observed picture of two concentrations (magnetic strips) in the giant branches. It seems, however, a much better explanation for those exceptional, very active cases outside the magnetic strips, than for the general picture itself.
3.4. The Emerging Picture of Giant Activity in the HRD
For the general picture of magnetic activity in the giant branches, the match between the two strips of larger magnetic activity in the HR diagramme and phases of faster core contraction is evident on both accounts: (i) the base RGB G-type stars having crossed the Hertzsprung Gap, and (ii) more massive, mid-AGB K- and M-type stars.
The former stars were not cool enough on the main sequence to have had convective envelopes; hence, they did not suffer any magnetic braking there in the first magnetic strip yet, but rather started their activity very strongly by virtue of their unconsumed angular momentum—meeting a first-time convective envelope with quickly growing convective turn-over times and dropping Rossby numbers, which are, indeed, very “dynamo-friendly” conditions.
The latter (mid-AGB) giants, by contrast, had observed magnetic braking during their central Helium burning, but now may be transferring angular momentum again from the contracting, spinning-up core to their convective envelopes, thereby rejuvenating their magnetic activity, helped by favourably small Rossby numbers of the convective envelopes, which see increasing convective turn-over times here in the second magnetic strip—a dynamo-friendly convective envelope again.
In between these two magnetic strips lies the evolutionary phase of central helium burning, providing stability to the core. Here, the findings of Schröder et al. (2020) [
23] of the four Hyades K giants—two inactive ones identifying with late, and two active ones with early central Helium burning—suggest that in the absence of any core contraction, magnetic braking prevails and decreases stellar activity during a stable phase, much like the solar-type, central Hydrogen-burning stars on the main sequence.
In summarizing the interpretation of the available observational evidence, the picture of magnetic activity across the HR diagramme can easily be explained by an interplay of (1) stable evolutionary phases such as core helium-burning, in which magnetic braking slows down an initially strong activity, and (2) phases initiated or accompanied by faster core contraction (foot-RGB, AGB), where angular momentum from the spinning-up core can dissipate into the convective envelope, which at the same time is very dynamo-friendly in terms of increasing convective turnover times and thereby decreasing the Rossby number. Here, the timescale of core contraction and spin-up must be comparable or shorter than the one of magnetic braking.
Together, these effects originate in stellar evolution, and are explaining the observed magnetic strips in the HRD rather well, but important details remain unsolved, as shown below. This interpretation does of course not exclude the possibility of additional, sudden angular momentum gains from the capture of planets, as in the same phases the convective envelope expands and may engulf any planets in its way, which could explain very active cases that out-lie the magnetic strips, or some active cases hidden among the other active giants in those strips.
4. Can We Trace, Where in a Giant the Dynamo Operates?
Models based on mean-field dynamo theory require a Rossby number (the ratio between rotation period and convective turn-over time of the given stellar structure) smaller than one. The smaller is, the stronger is the magnetic field and the chromospheric heating. At least in a very approximate way, therefore, this relation opens a connection between the observable rotation period of a giant and its hidden interior properties: We may estimate the Rossby number by the activity level and so obtain an approximate convective turn-over time effective in the dynamo.
For main sequence stars, this approach seems feasible, as Mittag et al. (2018) [
27] demonstratethat—with decreasing activity—the observed rotation periods converge towards an upper limit, which for solar type stars is about 35.5 days. Assuming that here we see stars, which have reached a Rossby number of one, then this value would also be the (empirical) convective turnover time of the envelope. This indeed agrees well with the value of 37.5 days, which was derived for a solar model of Kim and Demarque (1996) [
46], using a more detailed convection description to find a global ”nonlocal“ turn-over time.
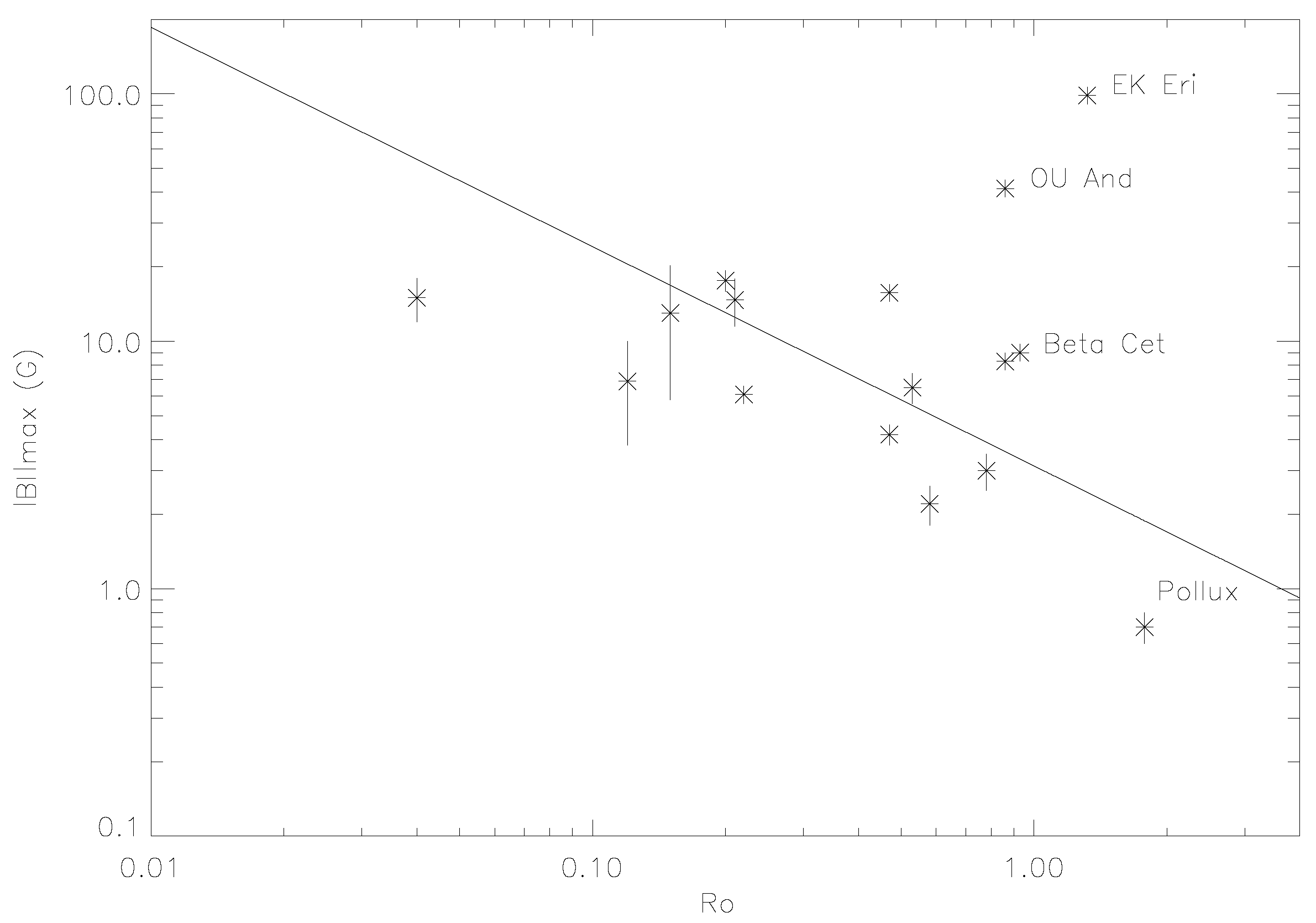
In principle, applying this same approach to giants may give us clues to where in the giant envelope this dynamo operates. In fact, activity levels have been established for many more giants. As pointed out before, more than 10 (e.g., 18) giant rotation periods are already known (Auriere et al., 2015) [
10].
In the cases of the two more active Hyades K giants, these are about 140 days (see Schröder et al., 2020 [
23]). The periods found for the 18 giants by Auriere et al. (2015) [
10] cover the large range of 10 days (very fast rotators) to 200–300 days (see
Figure 3). Over their entire distribution, these periods are about an order of magnitude larger than we observe for solar-type main sequence stars. This should not come by surprise: It is a natural consequence of the longer convective turn-over times in the presence of the large geometrical scales of giants, implying longer convection lengths and pressure scale heights (see below); however, a more detailed description also depends on the evolutionary phase. Long turn-over times allow for a suitably small Rossby number (<1) despite such longer rotation periods.
In addition, the observed relations between the magnetic field strength (and chromospheric activity level) with the rotation periods of these giant stars and their Rossby numbers (
Figure 3 and
Figure 4) provide indirect evidence for the operation of a dynamo in convective envelopes of giants, which could be of the alpha-omega type, as the one supposed to work in the sun. However, such a dynamo must not necessarily operate at the bottom of the convective envelope but could be stratified into larger heights, if velocity gradients exist there.
However, there are several fundamental difficulties, when it comes to the convective turn-over times of contemporary evolution models of giants, to which we would have to compare. To begin with, their convection description is oversimplified. The idea of representative, rising bubbles, leading to a scaled description with an empirically quantified convection length, may be good enough for a global model of a giant, but could fail utterly, when its internal dynamics are applied to detail. These shortcomings seem to be even more fundamental in view of the effects (e.g., meridional currents) of the large radial velocity gradient around the fast rotating core within the convective envelope.
Then, there is the big question of the nature of the convective turn-over time
. Would it be of a global nature (which seems to work well for the sun accordng to Kim and Demarque, 1996 [
46]), or should we be looking at local turn-over times, but then, in which layers of the convective envelope? The exact depth makes a huge difference here: Close to the bottom of the convective envelope of giants, the convection velocity
and pressure scale-height
change dramatically.
Usually, as applied by Kim and Demarque (1996) [
46] and others, the bottom of the convection zone is represented by taking the local convective turn-over time (see below) at exactly half a pressure height above the radiative core. We should also note that for giants, a global convective turnover time makes no sense, according to Charbonnel et al. (2017) [
24]. Given the large geometrical dimensions, rather, the maximum convective turnover time in the whole envelope should be of interest.
In the case of the sun, despite its convective envelope being rather humble compared to a giant, the difference between the above concepts (global or local) makes already more than a factor of 2 (see discussion in Schröder et al., 2020 [
23]).
A practical advantage of the local convective turn-over time
is the availability of a recipe, given by simple convection theory (see, e.g., Cox and Giuli 1968 [
47] for a more general description), i.e.,
—presuming that within the aforementioned limitations of currrent stellar models, the adiabatic bubble’s temperature gain
and the global gas properties
(gas temperature),
(gas pressure), and
(gas density) would be sufficiently reliable, and considering that
(for
) as a generalization of the convection length over pressure scale height. The local convective turn-over time is then obtained by the simple relation
Even if we trusted the convection description to at least provide us with the right order of magnitude, then the crucial problem remains of
where we should take this quantity. Should we really treat giant convective envelopes such as the one of the sun and only look at its bottom? If so, is half a pressure scale height a good choice for giants, too? In addition, the here-derived properties depend directly on the model assumptions for angular momentum transfer, e.g., the effective viscosity of the shear layer on the bottom of the convective envelope, and indirectly on any angular momentum loss by magnetic breaking on the top of the convective envelope, when an attempt is made to follow the rotation through stellar evolution, as undertaken by Charbonnel et al. (2017) [
24].
Reminding the reader of the discussion above, that for giants the bottom of their enormous convection zones seems to be an unlikely place from where the magnetic field can be brought all the way up to the photosphere, then using this, a local convective turn-over time, for that bottom region may even mean to bark up the wrong tree altogether. What is needed here are much more detailed models of the convection with magnetic fields and radial velocity gradient, to see if turn-over times could be computed using more realistic physical conditions, for a variety of depth in the convective envelope, and how these compare to the respective rotation time.
In general,
is larger (hence,
smaller) further up in the convective envelope, which would favour the idea of a distributed dynamo, operating not only at the bottom, and so better enabling the rise of magnetic field all the way to the photosphere, where we observe it. In addition, if the dynamo operates in higher layers with longer convective turn-over times, then that means a general decrease in the Rossby numbers, which would allow for some lesser magnetic activity in a much larger fraction of the giants outside the two strips, where the maximum activity is predicted by Charbonnel et al. (2017) [
24]. Outside the strips, with a Rossby number closer to one, a dynamo may still operate but produce a magnetic field too weak to be detected directly, but strong enough still to produce some chromosphric emission.
Moreover, in fact, using the measures of chromospheric emission, we do find that only a very small minority of giants are heated by only the basal (non-magnetic) flux. The latter is supposed to be related to mechanical flux heating by, in the simplest case, acoustic waves. Those cases seem to be stars near the end of their central Helium burning. Among all other giants, some degree of magnetic chromospheric heating is the normal. Consequently, a wider range of giants could have dynamo-friendly convective envelopes than suggested by the work of Charbonnel et al. (2017) [
24]. Alternatively, since Charbonnel et al. considered only the case for ALPHA-OMEGA friendly convective envelopes, a different, less efficient type of dynamo may be operating outside the magneic strips, which would not require
to be smaller than 1. Whatever the absolute scale of
among red giants, Charbonnel et al. (2017) [
24] correctly point to where in the HRD we find indeed the best conditions for an
–
dynamo, which therefore appears to be the most effective type of dynamo, which operates in giants.
Hence, while we seem to be far away from a good understanding on the side of theoretical modelling, observers should feel even more encouraged to determine more rotation periods (
) of giants, as initiated by the work of Auriere et al. (2015) [
10], see
Figure 3, and also consider Gaulme et al. (2020) [
30]. These we need to estimate the Rossby numbers (see
Figure 4) and convective turn-over times across the giant branches.
What we know so far, that giants rotate an order of magnitude slower than main sequence stars, could lead the way to some understanding: Using the Hyades K giant’s rotation periods to compare to those of solar-type stars with the same elevated activity level (same
), then apparently there is a trend of
which may provide some hint to the depths, where actually the giant dynamo operates, and how they may change with the size of the convective envelope of such intermediate-mass giants.
However, remarkably, and as mentioned above already, no low-mass single giants are known to be very active. In their solar vicinity sample Konstantinova-Antova et al. (2014) [
21] also find only intermediate-mass giants to exhibit magnetic activity, but no low-mass ones. Further studies will have to confirm this, but in such case, these low-mass stars may just have suffered too long from magnetic braking during their magnetically active time on the main sequence.
5. Discussion and Conclusions
As shown in this short review, the empirical picture of magnetic activity in intermediate mass giants across the HRD—focusing on chromospheric emission and the photospheric magnetic field, thus avoiding the biased picture of coronal detections—is very consistent with enhanced activity in two evolutionary phases with core contraction, where it spins up: (i) Just after the star has crossed the Hertzsprung gap—these stars have not had convective envelopes, activity or magnetic braking before, and their unconsumed angular momentum of a contracting, spinning-up core (Beck et al., 2012 [
11]) meets a new convective envelope, which provides a small Rossby number because of the long convective turnover time at this certain evolutionary phase (Charbonnel et al., 2017 [
24]). Such perfect conditions for a dynamo explain the concentration of very active giants in this first magnetic strip, with large chromospheric and X-ray emissions. (ii) After central Helium burning is over, the intermediate–mass giants ascend on the AGB. Again their cores contract, presumably spin up, providing internal angular momentum to the convective envelope above, which sees at the same time turn-over times increasing, and so Rossby numbers decreasing again, rejuvenating the dynamo action—the second magnetic strip, where we also observe increasing chromospheric emission again. Compared to the first strip, here all is in moderation: activity, core contraction, and envelope expansion.
Planet capture with external angular momentum supply to the exanding convective envelope may well add exceptional cases of activity to this picture, i.e., very active giants, which out-lie from those two magnetic strips in the HRD. However, over all, from the purely observational point of view and the panorama it gives, it seems quite plausible that angular momentum transfer from spinning-up cores stirs up giant activity after the Hertzsprung Gap is crossed and later rejuvenates it on the ascension of the AGB.
That leaves, however, a long list of problems to be solved by theoretical modelling. These include how the sheer layer, its effective viscosity and magnetic angular momentum transfer should be described, and finally where and how the dynamo operates in a giant convective envelope. The best information, that observers can contribute to test solutions and to probe the giant dynamo physics, is rotation rates of a number of well-studied giants of different gravities. Monitoring their chromospheric emission with dedicated robotic telescopes, such as TIGRE, reveals two quantities most relevant to characterize any mean field dynamo: the Rossby number (by estimate from the activity level) and the rotation rate imprinted on the variations of the giant activity.
On the other hand, we know the not magnetic-activity-related heating rates quite well—empirically at least. These seem to be mostly independent of gravity and a strong decreasing function of effective temperature, as shown in Perez et al. (2014) [
48] and the references discussed therein. Hence, the universality of magnetic chromospheric heating among cool giants is evident from the excess of the basal flux in most cool giants. This evidence suggests the working of at least a very weak dynamo outside the magnetic strips, just enough to still produce some Ca II line emission in faculae, as on the Sun during spotless, minimal activity, when magnetic fields are more than an order of magnitude lower than what a sunspot group requires. Furthermore, additional processes may work in AGB stars, e.g., pulsations or convective oscillatory modes.
For simple geometrical reasons, we must doubt that the standard solar mean field dynamo model should also work for a giant, where the convective envelope is so large that it becomes impossible to have a magnetic field rising all the way up from the very bottom to the top. A stratified or surface dynamo seems to be the better choice for a giant. Nevertheless, since the observed characteristics of giant and solar-type activity—namely the observed relations between activity level, cycle period and Rossby number (where known)—are similar, the giant dynamo that operates in the magnetic strips seems to be of the alpha-omega-type, too.