Abstract
Nucleosynthesis at latge magnetic induction levels relevant to core-collapse supernovae and neutron star mergers is considered. For respective magnetic fields of a strength up to ten teratesla, atomic nuclei exhibit a linear magnetic response due to the Zeeman effect. Such nuclear reactivity can be described in terms of magnetic susceptibility. Susceptibility maxima correspond to half-filled shells. The neutron component rises linearly with increasing shell angular momentum, while the contribution of protons grows quadratically due to considerable income from orbital magnetization. For a case j = l + 1/2, the proton contribution makes tens of nuclear magnetons and significantly exceeds the neutron values which give several units. In a case j = l − 1/2, the proton component is almost zero up to the g shell. A noticeable increase in the generation of corresponding explosive nucleosynthetic products with antimagic numbers is predicted for nuclei at charge freezing conditions. In the iron group region, new seeds are also created for the r-process. In particular, the magnetic enhancement of the volume of 44Ti isotopes is consistent with results from observations and indicates the substantial increase in the abundance of the main titanium isotope (48Ti) in the Galaxy’s chemical composition. Magnetic effects are proven to result in a shift of the r-process path towards smaller mass numbers, as well as an increase in the volume of low-mass nuclides in peaks of the r-process nuclei.
1. Introduction
Promising site candidates for the synthesis of heavy nuclei are represented by core-collapse supernovae (CCSNe) explosions and neutron star mergers (NSMs) [1,2,3]. Very strong magnetization with intensities up to tens of teratesla (TT) can develop in these processes due to strong convection and/or magnetorotational instabilities (MRI). Such effects result in dynamo processes generating shock waves, as was predicted by numerical models of CCSN explosions and confirmed by observations of soft-gamma repeaters (SGR) and anomalous X-ray pulsars (AXP) (c.f., e.g., [4,5,6,7] and the references therein). Besides, such high magnetic induction arises inside magnetar crust [8] and at collisions of heavy ions [9]. The magnetic effects can affect the nuclear structure, as is well-known from studies of hyperfine interaction [10], and the fields generated by the electronic environment on the surfaces of nuclei can rise up to several megatesla (MT), much lower than the TT range. The nuclides formed at CCSNe and NSMs contain information about the structure of matter and the mechanisms that underlie explosion processes.
Strong magnetic fields can modify the composition of nuclei, requiring us to consider the potential effect of magnetism on the structure, transformation and transmutation of nuclides. Using the corresponding data in analyzing nucleosynthesis and chains of nuclear transformations can provide more detailed information. In the case of CCSNe and neutron stars, we can obtain information on, for example, the magnetodynamics of CCSN stellar explosions and the formation of neutron star crusts, along with the processes that form chemical elements. The chemical composition of galaxies and CCSN remnants contain, in turn, information about explosion processes.
In this work, we analyze the effects of corresponding relatively weak magnetic fields on the structure of nuclei and explore the potential of using radioactive nuclides to probe internal fields in explosion processes. The effect of the Zeeman splitting of nucleon energy levels on the structure, properties and composition of nuclei is briefly considered and applied to r-process scenarios.
2. Termination of Reactions with Charged Nuclei
The formation of heavy nuclei is related to fast cooling and preferable creation of the most tightly bound nuclei, with the largest binding energies in the mass range of the iron group A~56 in an Earth-based environment. The temperature determines the width of the composition distribution. Thus, in the first stage of this scenario, high temperatures lead to nuclear (photo)disintegration into neutrons, protons and α particles due to the energy distribution of the blackbody photon gas. During the subsequent cooling and expansion of matter, the creation of heavier nuclei sets in, still governed by the trend of keeping matter at nuclear statistical equilibrium (NSE). Magnetic effects in the structure of a nucleus influence the efficiency of nuclide generation in the corresponding process of explosive nucleosynthesis. NSE approach has been used for over 50 years to describe the abundance of iron-group nuclei and similar nuclides, as well as to provide reasonable approximation for r-process nuclei. Under NSE conditions, the yield Yi of a nucleus i = AZ composed of N neutrons and Z protons is determined by partition functions ∑ = ∑iexp{−ei/kT}, where ei is the energy of nuclear particles in the ith state and k is the Boltzmann constant. The particular YA abundance is given by the well-known Saha equation YA = , where Yn and Yp denote the abundances of neutrons and protons, respectively.
At a presence of magnetic field H, we introduce relative yield
where the ratio Si(H) = Σi(H)/Σi(0) gives respective magnetic effect in the partition function. At moderate field strengths H ≤ 103 TT, the Pauli-type spin magnetic response dominates, and for nucleons we get Sα = cosh(gαωL/2kT), where the Larmor frequency ωL = μN H with nuclear magneton μN and gα represent the spin g-factors well-known for protons and neutrons (gp ≈ 5.586 and gn ≈ −3.826), and cosh(x) is the hyperbolic cosine.
At conditions of small-value T dln(S(H))/dT << 1, the relation (1) is reduced to the familiar form
where a change in free energy ∆Q = kT2 dln(S(H))/dT. For atomic nuclei in the limit of zero temperature, this value corresponds to a magnetic change of binding energy. For free nucleons, the energy component due to an interaction with a magnetic field can be written as the following relation, ∆Qα = (gα ωL/2) tanh(gα ωL/2kT), where tanh(x) is the hyperbolic tangent.
y = exp{ (∆QA − Z ∆Qp − N ∆Qn)/kT},
2.1. Nuclear Magnetic Susceptibility
Magnetic induction leads to a shift mNH of nucleon energy levels with magnetic moments mN due to an interaction with a field H and gives rise to the well-known Zeeman–Paschen–Back effect. The spin–orbit coupling value δso ≈ 5/A1/3 MeV, see [10], for atomic nuclei with mass numbers A ensures well-conserved quantum numbers of total spin j and spin projection mj up to magnetic induction H ≤ δso/μN. Consequently, for heavy nuclei of mass numbers A ≥ 50 at field strengths H ≤ 101.5 TT, the Zeeman reactivity originates the predominant nuclear magnetic response. At the same time, conditions of level crossing bring considerable change in nuclear structure. The nuclear level spacing ε~1 MeV gives a respective field strength scale of Hcross~ε/μN~101.5 TT. Therefore, for a nucleosynthesis scenario with moderate magnetic induction H < 101.5 TT, perturbative treatment of the Zeeman response is well-justified. Then, atomic nuclei are described by the total Hamiltonian H that can be written within the non-relativistic approximation and a linear limit in a weak magnetic field H as
where H0 represents the Hamiltonian for isolated nuclei, the magnetic moment projection on a field (i.e., z) direction Mz = ΣI (gαo mi + gα σi), where om and σ denote angular momentum and spin projection operators on the z-axis for the ith nucleon, the sum indicates nucleons in the nucleus, and gαo indicates the orbital g-factor: = 1 and = 0, with the spin g-factors being defined above in Equation (1).
H = H0 − MzωL,
The self-consistent mean field (SMF) approach, e.g., density functional theory, see [10], constitutes a useful framework for the reliable description and analysis of properties of atomic nuclei. Employing the angular momentum framework for spherical nuclei, single-particle states |i⟩ are specified by [10] the radial quantum number n, the angular momentum l, the total spin j and the spin projection mj on the magnetic field direction Z; energies εnljmj and eigenfunctions |nljmj⟩. In the linear regime, only the open shells contribute to magnetic change of energy given by (cf., e.g., [4,5])
where α = p, n, ⟨lm,1/2σ∣jmj⟩ is the Clebsch–Gordan coefficient, = / represents the shell-filling parameter with the occupation number of lj-shell and total number of states = 2j + 1 and gives the maximum value of magnetic susceptibility for a shell with angular momentum l and total spin j, which corresponds to a half-filled shell = 1/2. The parameters κα describe, therefore, the combined susceptibility of independent nucleons spatially confined due to the mean field. Thus, the values κα are considerably different from the nuclear g-factor corresponding to the nuclear magnetic moment in the ground state interacting with the field. Within the shell model, the nuclear magnetic moment is determined by unpaired valent nucleons [10,11], and the g-factor is associated with a nucleon occupying the state with maximum spin projection mj. Expression (4) yields a more reliable nuclear energy in magnetic fields H > 0.1 TT than the g-factor of the nucleus in the ground state [5].
As is seen in Figure 1, the maximum magnetic susceptibility contribution of neutrons rises linearly with increasing shell angular momentum, and the portion of protons grows quadratically due to the considerable contribution of orbital magnetization. For the case j = l + 1/2, the proton part of the susceptibility makes tens of nuclear magnetons and significantly exceeds the neutron component by several units. In the case j = l − 1/2, the proton contribution is almost zero up to the g shell. It is worthy to notice that the considered spherical mean field approximation gives the upper limit for magnetic susceptibility values for major shells corresponding to a pronounced shell closure region. Residual interaction, shape effects, etc., lead to a quenching of susceptibility values similar to the effects for a g-factor of atomic nuclei, see [10,11]. However, magnetic field and finite size effect, in conjunction with considerable temperature, significantly reduce pairing correlations; see [5] and references therein.
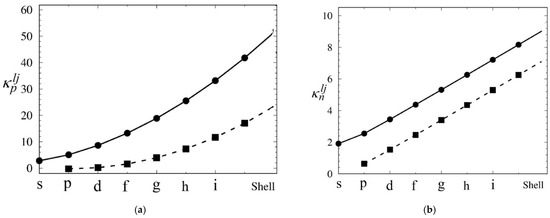
Figure 1.
Maximum magnetic susceptibility related to a half-filled shell = ½ for protons—(a) and neutrons—(b). Solid lines and circles indicate the case j = l + ½; dashed lines and squares represent subshells with j = l − ½.
In the case of magic numbers, the condition κ = 0, see Equation (4) and Figure 2a, implies that magnetic effects in nucleosynthesis are associated with the change of the partition function and the free energy of free nucleons interacting with the field. The magnetization of non-degenerated nucleon gas originates the magnetic pressure. Consequently, the free (or binding) energy of a magic nucleus effectively decreases, see Equation (2), which results in a suppression of the yield of relevant chemical elements. We notice, however, that such a reduction factor is less pronounced at realistic geometry of a magnetic induction [7]. Large magnetic moment and large susceptibility κ values give rise to an increasing binding energy of ultramagnetized antimagic nuclei in the field. The growing volume of nucleosynthesis products associated with such a property of open-shell nuclei is sensitive to the spatial structure of magnetic field [7].
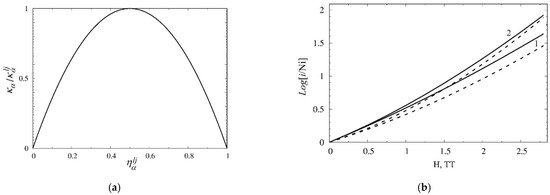
Figure 2.
(a) Dependence of magnetic susceptibility on shell filling parameter ηαlj. (b) Yield ratios [i/Ni] for 56Ni plotted as functions of a magnetic field for i = 48Cr—solid lines and 44Ti—dashed lines. Curves 1 and 2 represent results of Saha equation and free energy approximation, respectively.
2.2. Abundances of Tightly Bound Nuclei
As is mentioned above, the presence of magnetic induction can affect the yield of iron-group nuclei. Let us consider the normalized yield coefficient of antimagic even–even symmetric nuclei of the 1 shells and the double magic nucleus Ni, i.e.,. As seen in Figure 2b, the volume of synthesis of Ti and Cr increases sharply with growing magnetic induction. We notice that deformations of 44Ti and 48Cr, see [12,13], are consistent with the valent nucleons’ magnetic alignment. Exponential approximation based on a free energy Equation (2) overestimates such an increasing effect, especially at high magnetic induction. It is worth recalling, in this connection, the mysteriously large abundance of titanium obtained in direct observations of SN-type II remnants, see refs. [4,5]. Observational data suggest a Ti nucleus yield for type II SNe far exceeding model predictions and similar results for type I Sne. As one can see from Equations (1), (2) and (4) and Figure 2b, the magnetic increase in the synthesis of nuclides by an order of magnitude corresponds to a field strength of several TT. Such magnetic induction is consistent with simulation predictions and an explosion energy of CCSNe [4,7].
It is worth noting that these conditions assume even stronger enrichment in 48Cr isotopes since maximum magnetic susceptibility κ corresponds to a half-filled shell. With the filling of shell 1f7/2 (iron-group nuclei), this condition is met when Z = N = 24 (see above). The considerable magnitude of κCr = 17.51 results in a notable magnetic increase in generating nuclide 48Cr. The sequence of radioactive decay 48Cr → 48V → 48Ti generates an excess of the predominant titanium isotope. Therefore, magnetic effects create additional seed nuclei for operation of the r-process. Such effects smear out the shell closure effect and overbound property of magic nuclei, with a particularly growing yield of antimagic components with lower mass numbers.
3. R-Process in Magnetic Field
The r-process nuclides can form as a result of the merging of neutron stars [2,3]. One such event produces 100 times more nuclides than CCSN explosion processes. At the first stage of the r-process generation of nuclei, matter is subjected to explosion, burning at high temperatures reaching those typical of NSE [1], with the nuclide composition given by relation (1). When reactions involving charged particles are terminated and complete chemical equilibrium occurs, which will lead to a high ratio of neutrons to nuclei, the actual r-process, based solely on the large frequency for the capture of neutrons, can begin at temperatures T ≤ 3 × 109 K, and all nuclear reactions must be carried out, generally, in all details.
However, the waiting point approximation [1,2] provides significant simplification. Since reactions with charged particles are excluded at a temperature of about 3 × 109 K, only beta decays provide the connection between isotopic chains. Large neutron densities result in the time period for neutron capture processes being much shorter as compared to the beta decay and capable of originating nuclei with neutron separation energies up to δn ≤ 2 MeV. This is the energy obtained by capturing a neutron on the A−1 nucleus and/or the photon energy required to release a neutron from the A nucleus by photo-break up reaction. At the neutron drip line, δn approaches 0, i.e., for very large neutron densities of an r-process, it proceeds close to the neutron drip line. At temperatures of about 109 K (γ, n), photo-breakup processes can still be very active at such small values δn since only temperatures related to about 30 kT ≥ δn are required to dominate these reverse reactions. Since both reaction directions proceed more frequently than the time range of the process (and beta decays), NSE can be established between neutron capture and photo-breakup. In this case, the complete chemical equilibrium or NSE discussed in Section 2 is split into a set of (quasi) equilibrium groups representing each isotopic chain of heavy nuclei. Under the condition of equilibrium (n, γ) ↔ (γ, n), no detailed knowledge of neutron capture cross sections is required. By making use of the detailed balance principle, we account that only photons with energies exceeding the neutron separation energy δn contribute to the neutron breakup reaction. Then, the abundance distribution in each isotope chain corresponds to the ratio of two neighboring isotopes and is given by the Saha equation, see Equations (1) and (2).
with neutron density nn, and nucleon mass M, and the neutron separation (or binding) energy δn(A + 1) for the nucleus (Z, A + 1). The abundance portions depend only on nn, T and δn. Neutron separation energy δn thereby introduces a dependence on nuclear masses, namely a nuclear mass model for these very neutron-rich unstable nuclei and conditions of r-process: Nn~1020 cm−3, T~109 K at timescale ≤ 1 s. As is illustrated schematically in Figure 3b, the r-process path proceeds through a chain of nuclei with small neutron separation energy δn located away from the stability line. The dynamic rate along the r-process nuclei is determined by β-decays. Since β-decay periods are longer for nuclei closer to the stability region, the nuclear material is concentrated near the upper corner of the kinks in the path at the neutron shell closures N = 50, 82 and 126. The mass numbers A along the path at the neutron shell closure (Nshell) are smaller than mass numbers on the stability line with the same neutron shell closure Nshell. This feature persists after β-decay chains bring nuclei to the stability line at the end of the process and gives rise to a peak of r-process nuclei.
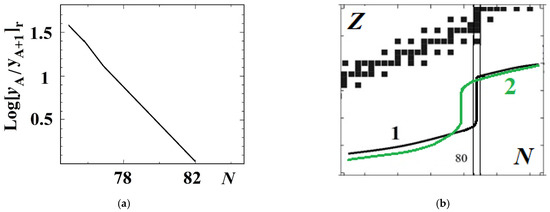
Figure 3.
(a) Magnetic enhancement in a yield of nuclei with open shells at field strength H = 2 TT and temperature T = 109 K. (b) Magnetic effect in the r-process path is shown schematically by line 2 with respect to standard scenario line 1.
The magnetic field leads to an increasing neutron gamma capture reaction cross section [14] and increasing rates of A (n, γ) (A + 1) transformations. Such an enhancement leads to more effective r-process scenario at high magnetic induction. For the ratio of relative abundances of nuclei (Z, A + 1) and (Z, A) in the magnetic field, we write
indicating, thereby, magnetic enhancement in volumes of nuclei with smaller mass numbers. Figure 3a shows the increasing yield of nuclei with smaller numbers of neutrons with respect to magic number N = 82. From Equations (6) and (7), we write magnetic field-dependent neutron separation energy as
One sees that magnetic field gives rise to an increasing neutron separation energy, especially for states with the spin projection mj directed along the field vector. Such a case is related to the nuclei close to the neutron magic numbers, e.g., N = 82, see Figure 3b. Therefore, the r-process path with magnetized nuclei corresponds to larger neutron separation energies, i.e., is associated with smaller mass numbers closer to the stability line. Consequently, in the considered case, magnetic effects result in a shift of the r-process peak towards nuclides with smaller masses.
4. Discussion
We analyzed nucleosynthesis processes in magnetic fields up to ten teratesla arising at core-collapse supernovae and neutron star mergers. At such field strengths, nuclear magnetic response is determined by the Zeeman effect, and the linear magnetic susceptibility is represented as a combined reactivity of valent nucleons with maxima at half-filled shells. The proton contribution makes tens of nuclear magnetons for the case j = l + ½ and is almost zero up to the g shell at j = l − ½. The neutron portion gives several nuclear magnetons and grows linearly with increasing shell angular momentum, while the contribution of protons rises quadratically due to significant income from orbital magnetization. Consequently, the portion of antimagic nuclei is predicted to gain considerably for charge freezing point. At nuclear statistical equilibrium an approximation based on free energy overestimates results of the Saha equation for such magnetic enhancement. The volume of antimagic 44Ti and 48Ti isotopes in an Earth-based environment increases due to high magnetic induction in conjunction with direct observations of 44Ti isotope. We posit that magnetic effects originate a change of the r-process path with increasing portions of nuclei with masses lower than the magic one, as well as an increase in the volume of low-mass nuclides in the r-process peak.
5. Conclusions
At high magnetic induction levels reaching up to ten teratesla, atomic nuclei display linear magnetic response with a magnetic susceptibility of tens of nuclear magnetons. Such properties originate a volume enhancement of smaller-mass nuclides in nucleosynthesis at core-collapse supernovae and neutron star mergers.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Thielemann, F.-K.; Arcones, A.; Käppeli, R.; Liebendörfer, M.; Rauscher, T.; Winteler, C.; Fröhlich, C.; Dillmann, I.; Fischer, T.; Martinez-Pinedo, G.; et al. What are the astrophysical sites for the r-process and the production of heavy elements? Progress Part. Nucl. Phys. 2011, 66, 346. [Google Scholar] [CrossRef]
- Thielemann, F.K.; Eichler, M.; Panov, I.V.; Wehmeyer, B. Neutron Star Mergers and Nucleosynthesis of Heavy Elements. Annu. Rev. Nucl. Part. Sci. 2017, 67, 253–274. [Google Scholar] [CrossRef]
- Pian, E.; D’Avanzo, P.; Vergani, D. Spectroscopic identification of r-process nucleosynthesis in a double neutron-star merger. Nature 2017, 551, 67–70. [Google Scholar] [CrossRef] [PubMed]
- Kondratyev, V.N. Explosive nucleosynthesis at strong magnetic field. Eur. Phys. J. A 2014, 50, 7–13. [Google Scholar] [CrossRef]
- Kondratyev, V.N. Zeeman splitting in structure and composition of ultramagnetized spherical nuclei. Phys. Lett. B 2018, 782, 167–169. [Google Scholar] [CrossRef]
- Price, D.J.; Rosswog, S. Producing Ultrastrong Magnetic Fields in Neutron Star Mergers. Science 2006, 312, 719. [Google Scholar] [CrossRef] [PubMed]
- Kondratyev, V.N.; Korovina, Y.V. Synthesis of chemical elements in dynamo active supernovae. JETP Lett. 2015, 102, 131–134. [Google Scholar] [CrossRef]
- Kondratyev, V.N. Magnetoemission of Magnetars. Phys. Part. Nucl. 2019, 50, 613–615. [Google Scholar] [CrossRef]
- Voronyuk, V.; Toneev, V.D.; Cassing, W.; Bratkovskaya, E.L.; Konchakovski, V.P.; Voloshin, S.A. Electromagnetic field evolution in relativistic heavy-ion collisions. Phys. Rev. C 2011, 83, 054911. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P. The Nuclear Man-Body Problem; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Arima, A. A short history of nuclear magnetic moments and GT transitions. Sci. China Phys. Mech. Astron. 2011, 54, 188. [Google Scholar] [CrossRef]
- Ogasawara, H.; Yoshida, K.; Yamagami, M.; Mizutori, S.; Matsuyanagi, K. Triaxiality Dependence of Octupole Excitations on Superdeformed States in 44Ti. Progr. Theor. Phys. 2008, 120, 1169. [Google Scholar] [CrossRef]
- Ha, E.; Cheoun, M.-K.; Sagawa, H.; So, W.Y. Neutron-proton pairing correlations and deformation for N=Z nuclei in the pf shell within the deformed BCS and Hartree-Fock-Bogoliubov approach. Phys. Rev. C 2018, 97, 064322. [Google Scholar] [CrossRef]
- Kondratyev, V.N. Neutron capture reactions in strong magnetic fields of magnetars. Phys. Rev. C 2004, 69, 038801. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).