Ulysses Flyby in the Heliosphere: Comparison of the Solar Wind Model with Observational Data
Abstract
1. Introduction
2. Ulysses Data and Modeling
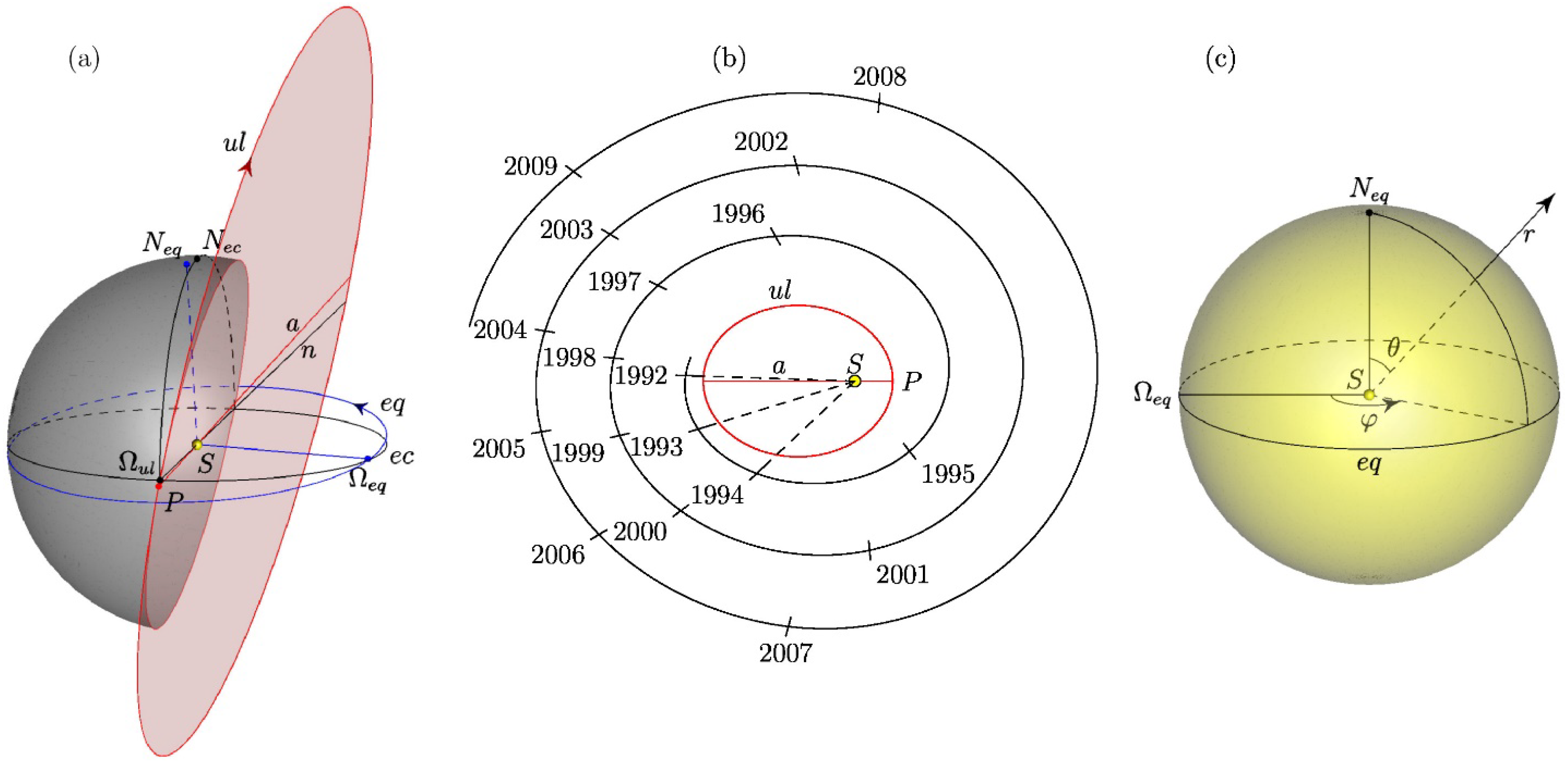
2.1. Flight of the Ulysses Spacecraft
2.2. The Model: Basic Assumptions and Equations
- (A1) The axes of the magnetic dipole and the symmetric quadrupole of the Sun coincide with the axis of its rotation;
- (A2) SW flow at distances is quasi-stationary and axisymmetric (where is the solar radius);
- (A3) Magnetic field is frozen into the plasma, the magnetic diffusion and viscosity are not taken into account;
- (A4) SW plasma satisfies the equation of state of a monatomic ideal gas;
- (A5) Thermodynamic processes that take place in SW plasma are adiabatic.
3. Results
3.1. The Initial Data on the Boundary Sphere
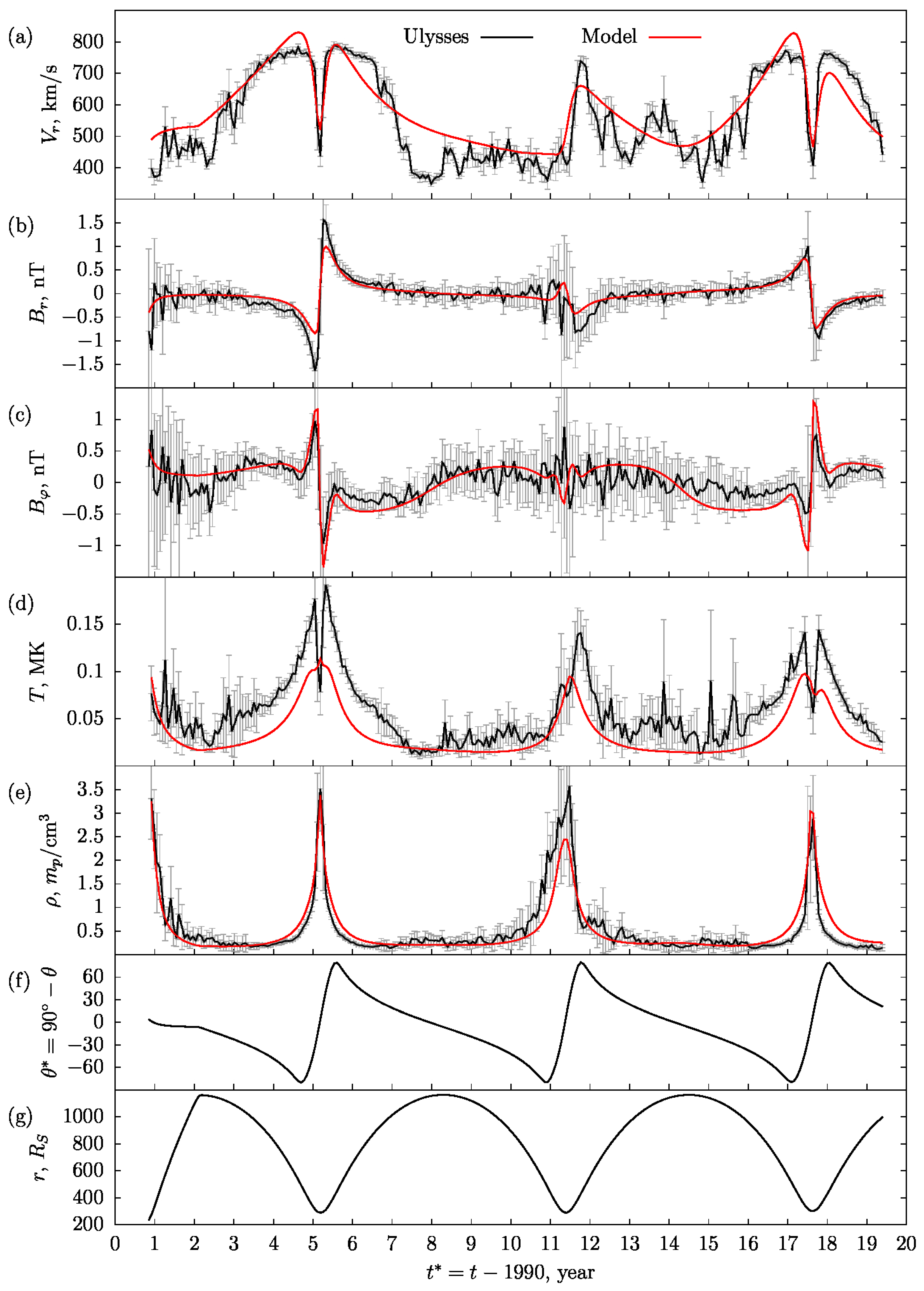
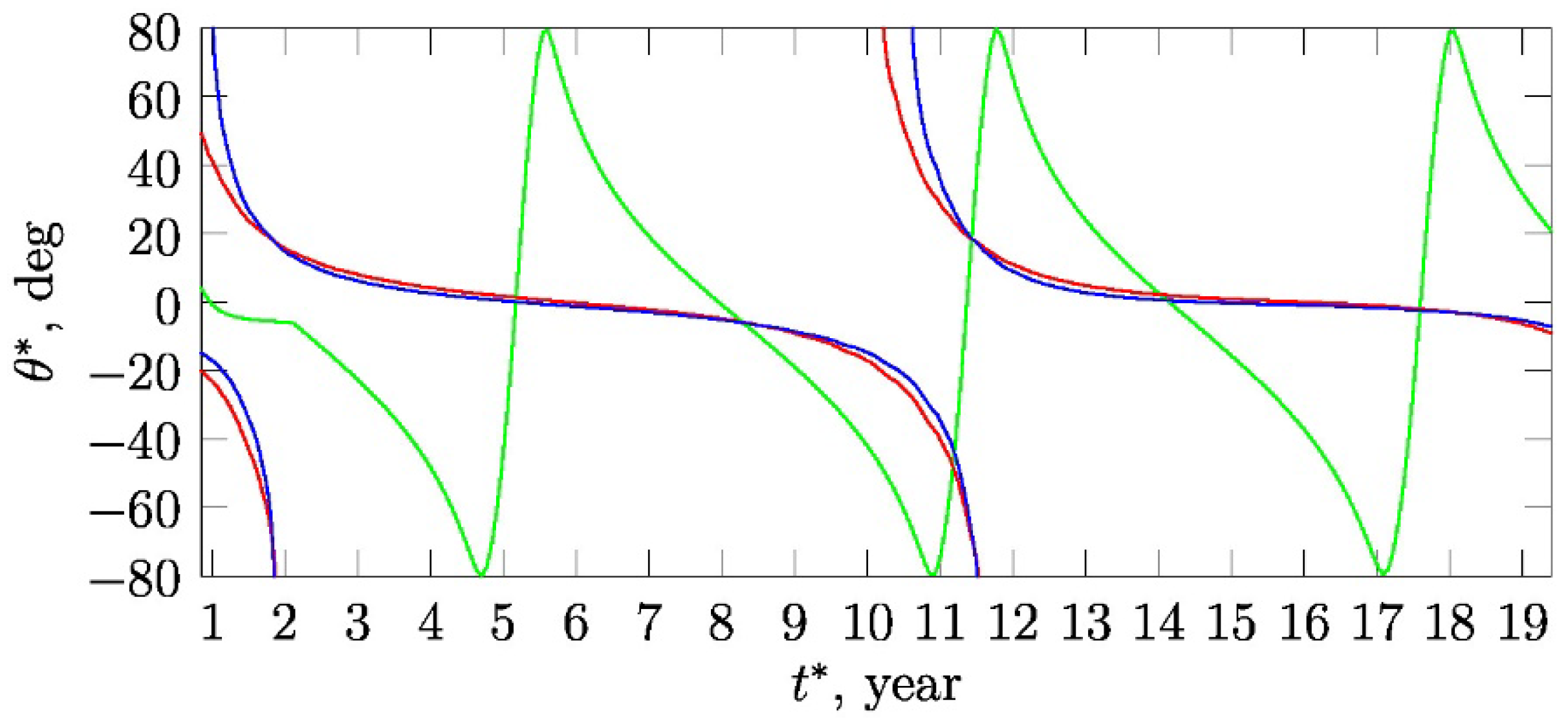
3.2. Comparison of Numerical Results with the Observational Data
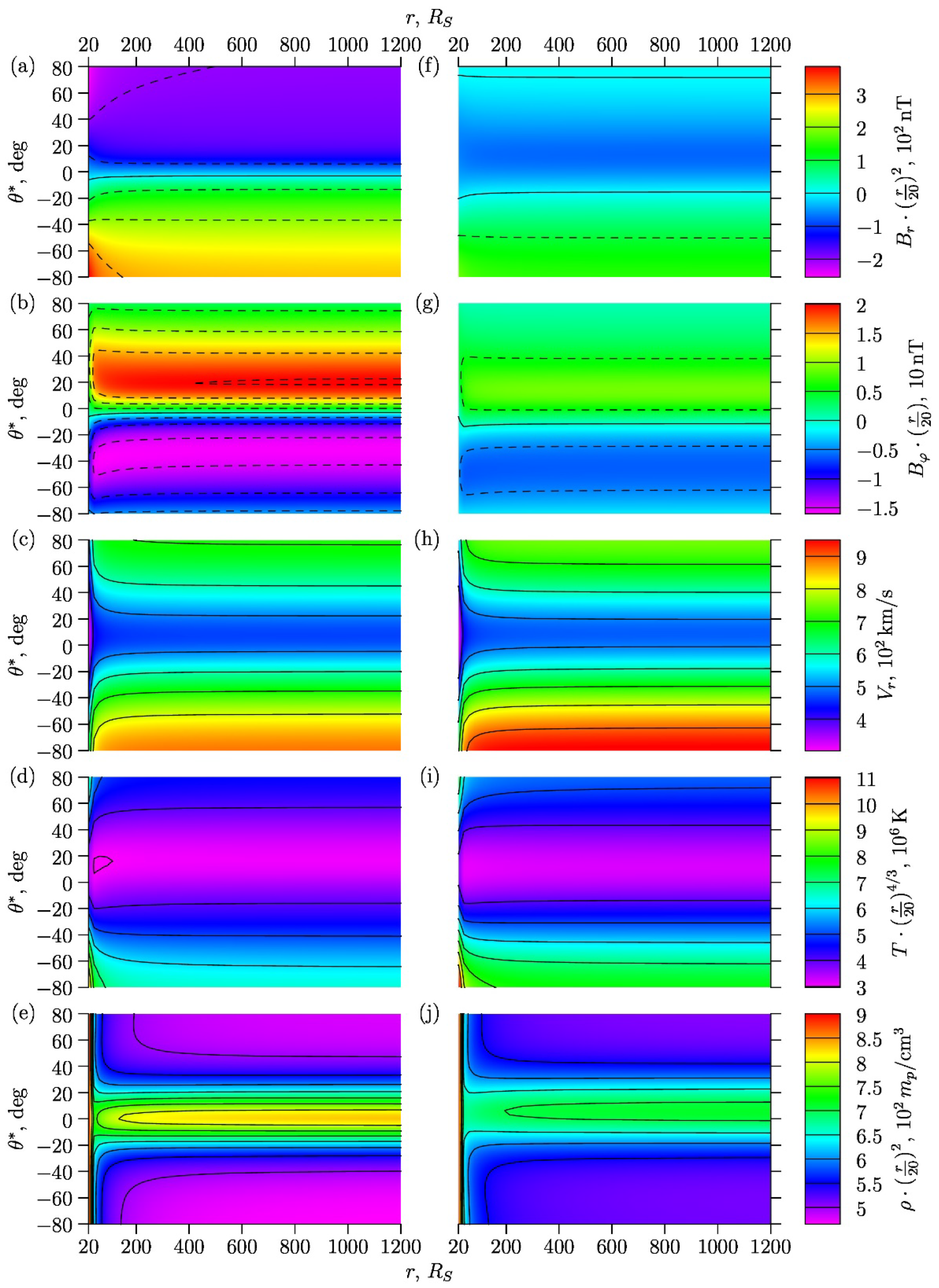
3.3. Description of the Solar Wind Structures in the Framework of an Axisymmetric Model
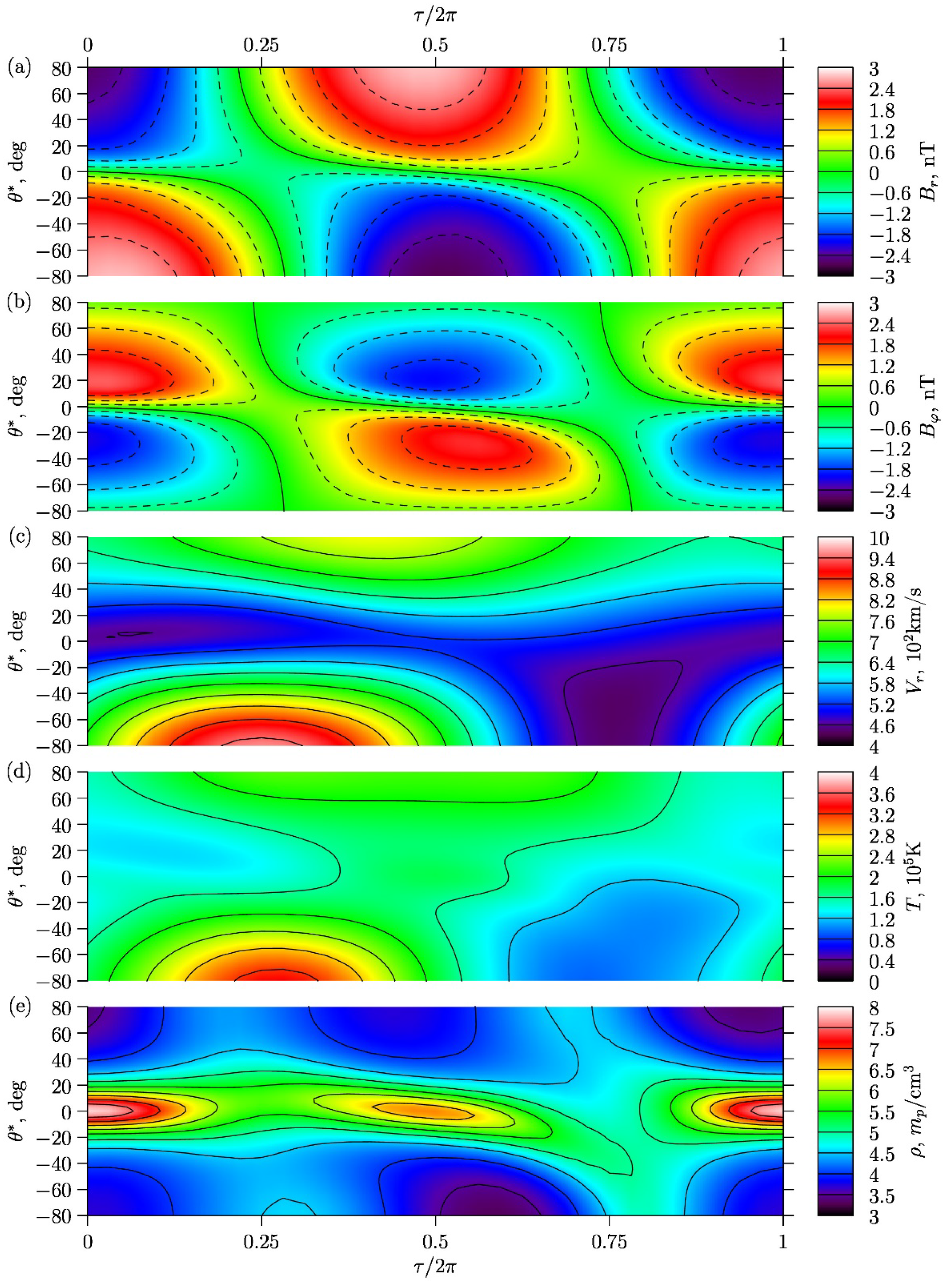
3.4. Geometry of Neutral Surfaces in the Solar Wind
4. Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Parker, E.N. Dynamics of the interplanetary gas and magnetic fields. Astrophys. J. 1958, 128, 664. [Google Scholar] [CrossRef]
- Bondi, H. On spherically symmetric accretion. MNRAS 1952, 112, 195. [Google Scholar] [CrossRef]
- Neugebauer, M.; Snyder, C.W. Mariner 2 Observations of the Solar Wind, 2, Relation of Plasma Properties to the Magnetic Field. J. Geophys. Res. 1967, 72, 1823. [Google Scholar] [CrossRef]
- Veselovsky, I.S. Magnetic Domains in the Heliosphere During Solar Maximum Years. Space Sci. Rev. 2001, 97, 109–112. [Google Scholar] [CrossRef]
- Abbo, L.; Ofman, L.; Antiochos, S.K.; Hansteen, V.H.; Harra, L.; Ko, Y.-K.; Lapenta, G.; Li, B.; Riley, P.; Strachan, L.; et al. Slow Solar Wind: Observations and Modeling. Space Sci. Rev. 2016, 201, 55–108. [Google Scholar] [CrossRef]
- Bruno, R.; Carbone, V. The Solar Wind as a Turbulence Laboratory. Living Rev. Sol. Phys. 2013, 10, 2. [Google Scholar] [CrossRef]
- Matthaeus, W.H.; Velli, M. Who Needs Turbulence? Space Sci. Rev. 2011, 160, 145–168. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Y.F.; Zheng, H.N. Magnetic reconnection in multiple heliospheric current sheets. Sol. Phys. 1997, 173, 409–426. [Google Scholar] [CrossRef]
- Balogh, A.; Erdõs, G. The Heliospheric Magnetic Field. Space Sci. Rev. 2013, 176, 177–215. [Google Scholar] [CrossRef]
- Hoeksema, J.T. The Large-Scale Structure of the Heliospheric Current Sheet during the ULYSSES Epoch. Space Sci. Rev. 1995, 72, 137. [Google Scholar] [CrossRef]
- Khabarova, O.; Zank, G.P.; Li, G.; Le Roux, J.A.; Webb, G.M.; Dosch, A.; Malandraki, O.E. Small-scale Magnetic Islands in the Solar Wind and Their Role in Particle Acceleration. I. Dynamics of Magnetic Islands Near the Heliospheric Current Sheet. Astrophys. J. 2015, 808, 181. [Google Scholar] [CrossRef]
- Khabarova, O.V.; Zank, G.P.; Li, G.; Malandraki, O.E.; Le Roux, J.A.; Webb, G.M. Small-scale Magnetic Islands in the Solar Wind and Their Role in Particle Acceleration. II. Particle Energization inside Magnetically Confined Cavities. Astrophys. J. 2016, 827, 122. [Google Scholar] [CrossRef]
- Malandraki, O.E.; Khabarova, O.V.; Bruno, R.; Zank, G.P.; Li, G.; Jackson, B.; Bisi, M.M.; Greco, A.; Pezzi, O.; Matthaeus, W.; et al. Current Sheets, Magnetic Islands, and Associated Particle Acceleration in the Solar Wind as Observed by Ulysses near the Ecliptic Plane. Astrophys. J. 2019, 881, 116. [Google Scholar] [CrossRef]
- Gary, S.P. Microinstabilities upstream of the earth’s bow shock: A brief review. J. Geophys. Res. 1981, 86, 4331–4336. [Google Scholar] [CrossRef]
- Kasper, J.C.; Lazarus, A.J.; Gary, S.P. Wind/SWE observations of firehose constraint on solar wind proton temperature anisotropy. Geophys. Res. Lett. 2002, 29, 20-1–20-4. [Google Scholar] [CrossRef]
- Klein, K.G.; Alterman, B.L.; Stevens, M.L.; Vech, D.; Kasper, J.C. Majority of Solar Wind Intervals Support Ion-Driven Instabilities. Phys. Rev. Lett. 2018, 120, 205102. [Google Scholar] [CrossRef]
- Maruca, B.A.; Chasapis, A.; Gary, S.P.; Bandyopadhyay, R.; Chhiber, R.; Parashar, T.N.; Matthaeus, W.H.; Shay, M.A.; Burch, J.L.; Moore, T.E.; et al. MMS Observations of Beta-dependent Constraints on Ion Temperature Anisotropy in Earth’s Magnetosheath. Astrophys. J. 2018, 866, 25. [Google Scholar] [CrossRef]
- Alfven, H. Electric currents in cosmic plasmas. Rev. Geophys. S Phys. 1977, 15, 27. [Google Scholar] [CrossRef]
- Israelevich, P.L.; Gombosi, T.I.; Ershkovich, A.I.; Hansen, K.C.; Groth, C.P.T.; DeZeeuw, D.L.; Powell, K.G. MHD simulation of the three-dimensional structure of the heliospheric current sheet. Astron. Astrophys. 2001, 376, 288–291. [Google Scholar] [CrossRef]
- Richardson, J.D.; Burlaga, L.F. The Solar Wind in the Outer Heliosphere and Heliosheath. Space Sci. Rev. 2013, 176, 217–235. [Google Scholar] [CrossRef]
- Pogorelov, N.V.; Fichtner, H.; Czechowski, A.; Lazarian, A.; Lembege, B.; le Roux, J.A.; Potgieter, M.S.; Scherer, K.; Stone, E.C.; Strauss, R.D.; et al. Heliosheath Processes and the Structure of the Heliopause: Modeling Energetic Particles, Cosmic Rays, and Magnetic Fields. Space Sci. Rev. 2017, 212, 193–248. [Google Scholar] [CrossRef]
- Lacombe, C.; Salem, C.; Mangeney, A.; Steinberg, J.-L.; Maksimovic, M.; Bosqued, J.M. Latitudinal distribution of the solar wind properties in the low- and high-pressure regimes: Wind observations. Ann. Geophys. 2000, 18, 852–865. [Google Scholar] [CrossRef]
- Eselevich, E.G.; Fainshtein, V.G.; Rudenko, G.V. Study of the structure of streamer belts and chains in the solar corona. Sol. Phys. 1999, 188, 277. [Google Scholar] [CrossRef]
- Crooker, N.U.; Kahler, S.W.; Larson, D.E.; Lin, R.P. Large-scale magnetic field inversions at sector boundaries. J. Geophys. Res. 2004, 109, A03108. [Google Scholar] [CrossRef]
- Winterhalter, D.; Smith, E.J.; Burton, M.E.; Murphy, N.; McComas, D. The heliospheric plasma sheet. J. Geophys. Res. 1994, 99, 6667–6680. [Google Scholar] [CrossRef]
- Büchner, J.; Zelenyi, L.M. Regular and chaotic charged particle motion in magnetotaillike field reversals: 1. Basic theory of trapped motion. J. Geophys. Res. 1989, 94, 11821. [Google Scholar] [CrossRef]
- Malova, H.V.; Popov, V.Y.; Grigorenko, E.E.; Petrukovich, A.A.; Delcourt, D.; Sharma, A.S.; Khabarova, O.V.; Zelenyi, L.M. Evidence for quasi-adiabatic motion of charged particles in strong current sheets in the solar wind. Astrophys. J. 2017, 834, 34. [Google Scholar] [CrossRef]
- Malova, K.V.; Popov, V.Y.; Khabarova, O.V.; Grigorenko, E.E.; Petrukovich, A.A.; Zelenyi, L.M. Structure of Current Sheets with Quasi-Adiabatic Dynamics of Particles in the Solar Wind. Cos. Res. 2018, 56, 445. [Google Scholar] [CrossRef]
- Mursula, K.; Hiltula, T. Systematically asymmetric heliospheric magnetic field: Evidence for a quadrupole mode and non-axisymmetry with polarity flip-flops. Sol. Phys. 2004, 224, 133–143. [Google Scholar] [CrossRef]
- Wilcox, J.M.; Hoeksema, J.T.; Scherrer, P.H. Origin of the warped heliospheric current sheet. Science 1980, 209, 603. [Google Scholar] [CrossRef][Green Version]
- Echer, E.; Bolzan, M.J.A.; Franco, A.M.S. Statistical analysis of solar wind parameter variation with heliospheric distance: Ulysses observations in the ecliptic plane. Adv. Space Res. 2020, 65, 2846. [Google Scholar] [CrossRef]
- Reisenfeld, D.B.; Wiens, R.C.; Barraclough, B.L.; Steinberg, J.T.; Neugebauer, M.; Raines, J.; Zurbuchen, T.H. Solar Wind Conditions and Composition during the Genesis Mission as Measured by In Situ Spacecraft. Space Sci. Rev. 2013, 175, 125. [Google Scholar] [CrossRef]
- Tokumaru, M.; Fujiki, K.; Iju, T. North-south asymmetry in global distribution of the solar wind speed during 1985–2013. J. Geophys. Res. 2015, 120, 3283. [Google Scholar] [CrossRef]
- Vsekhsvyatskiy, S.K. The Solar Wind and Solar Corpuscular Streams. Geomagn. Aeron. 1964, 4, 255. [Google Scholar]
- Parker, E.N. Dynamical Theory of the Solar Wind. Space Sci. Rev. 1965, 4, 666. [Google Scholar] [CrossRef]
- Gringauz, K.I.; Bezrokikh, V.V.; Ozerov, V.D.; Rybchinskii, R.E. A Study of the Interplanetary Ionized Gas, High-Energy Electrons and Corpuscular Radiation from the Sun by Means of the Three-Electrode Trap for Charged Particles on the Second Soviet Cosmic Rocket. Sov. Phys. Dokl. 1960, 5, 361. [Google Scholar]
- Gringauz, K.I.; Zastenker, G.N.; Khokhlov, M.Z. Velocity and temperature of the solar wind from data of the interplanetary station Venus 3. Kosm. Issled. 1970, 8, 948–951. [Google Scholar]
- Schatten, K.H.; Wilcox, J.M.; Ness, N.F. A model of interplanetary and coronal magnetic fields. Sol. Phys. 1969, 6, 442–455. [Google Scholar] [CrossRef]
- Schatten, K.H. Current Sheet Magnetic Model for the Solar Corona. Cosm. Electrodyn. 1971, 2, 232–245. [Google Scholar]
- Arge, C.N.; Pizzo, V.J. Improvement in the prediction of solar wind conditions using near-real time solar magnetic field updates. J. Geophys. Res. 2000, 105, 10465–10480. [Google Scholar] [CrossRef]
- Levine, R.H.; Schulz, M.; Frazier, E.N. Simulation of the magnetic structure of the inner heliosphere by means of a non-spherical source surface. Sol. Phys. 1982, 77, 363–392. [Google Scholar] [CrossRef][Green Version]
- Schultz, M.; Frazier, E.N.; Boucher, D.J. Coronal magnetic-field model with non-spherical source surface. Sol. Phys. 1978, 60, 83. [Google Scholar] [CrossRef]
- Wang, Y.M.; Young, P.R.; Muglach, K. Evidence for two separate heliospheric current sheets of cylindrical shape during Mid-2012. Astrophys. J. 2014, 780, 103. [Google Scholar] [CrossRef]
- Schultz, M. Conical Current Sheets in a Source-Surface Model of the Heliosphere. AGU Fall Meeting Abstracts, SAO/NASA Astrophysics Data System. 2007, SH53A-1069. Available online: https://ui.adsabs.harvard.edu/abs/2007AGUFMSH53A1069S (accessed on 10 April 2022).
- Maiewski, E.V.; Malova, H.V.; Kislov, R.A.; Popov, V.Y.; Petrukovich, A.A.; Khabarova, O.V.; Zelenyi, L.M. Formation of Multiple Current Sheets in the Heliospheric Plasma Sheet. Cosm. Res. 2020, 58, 411–425. [Google Scholar] [CrossRef]
- Gombosi, T.I.; van der Holst, B.; Manchester, W.B.; Sokolov, I.V. Extended MHD modeling of the steady solar corona and the solar wind. Living Rev. Sol. Phys. 2018, 15, 4. [Google Scholar] [CrossRef]
- Riley, P.; Linker, J.A.; Mikić, Z. Modeling the heliospheric current sheet: Solar cycle variations. J. Geophys. Res. 2002, 107, SSH 8-1–SSH 8-6. [Google Scholar] [CrossRef]
- Usmanov, A.V.; Matthaeus, W.H.; Goldstein, M.L.; Chhiber, R. The Steady Global Corona and Solar Wind: A Three-dimensional MHD Simulation with Turbulence Transport and Heating. Astrophys. J. 2018, 865, 25. [Google Scholar] [CrossRef]
- van der Holst, B.; Huang, J.; Sachdeva, N.; Kasper, J.C.; Manchester, W.B.; Borovikov, D.; Chandran, B.D.G.; Case, A.W.; Korreck, K.E.; Larson, D.; et al. Improving the Alfvén Wave Solar Atmosphere Model Based on Parker Solar Probe Data. Astrophys. J. 2022, 925, 146. [Google Scholar] [CrossRef]
- Neugebauer, M.; Forthyth, R.J.; Galvin, A.B.; Harvey, K.L.; Hoeksema, J.T.; Lazarus, A.J.; Lepping, R.P.; Linker, J.A.; Mikic, Z.; Steinberg, J.T.; et al. Spatial structure of the solar wind and comparisons with solar data and models. J. Geophys. Res. 1998, 103, 14587. [Google Scholar] [CrossRef]
- Georgieva, K. Space weather and space climate—What the look from the earth tells us about the sun. In The Environments of the Sun and the Stars; Rozelot, J.-P., Neiner, C., Eds.; Springer: Berlin, Germany, 2013; pp. 53–107. [Google Scholar]
- Usmanov, A.V. A Global Numerical Three-Dimensional Magnetohydrodynamic Model of the Solar Wind. Sol. Phys. 1993, 146, 377–396. [Google Scholar] [CrossRef]
- Kim, T.K.; Pogorelov, N.V.; Zank, G.P.; Elliott, H.A.; McComas, D.J. Modeling the Solar Wind at the Ulysses, Voyager and New Horizons Spacecraft. Astrophys. J. 2016, 832, 72. [Google Scholar] [CrossRef]
- Maiewski, E.V.; Kislov, R.A.; Malova, H.V.; Popov, V.Y.; Petrukovich, A.A. Model of Solar Wind in the Heliosphere at Low and High Latitudes. Plasma Phys. Rep. 2018, 44, 80–91. [Google Scholar] [CrossRef]
- Maiewski, E.V.; Kislov, R.A.; Khabarova, O.V.; Malova, H.V.; Popov, V.Y.; Petrukovich, A.A.; Zelenyi, L.M. Magnetohydrodynamic modeling of the solar wind key parameters and current sheets in the heliosphere: Radial and solar cycle evolution. Astrophys. J. 2020, 892, 12. [Google Scholar] [CrossRef]
- Pneuman, G.W.; Kopp, R.A. Gas-Magnetic Field Interactions in the Solar Corona. Sol. Phys. 1971, 18, 258–270. [Google Scholar] [CrossRef]
- Marsden, R.G. (Ed.) The High Latitude Heliosphere; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995; ISBN 0-7923-3229-6. [Google Scholar]
- Dmitriev, A.V.; Suvorova, A.V.; Veselovsky, I.S.; Zeldovich, M.A. Coronal Imprints in the Heliospheric Plasma and Magnetic Fields at the Earth’s Orbit during the Last Three Solar Minima. Adv. Space Res. 2000, 25, 1965–1968. [Google Scholar] [CrossRef]
- Usmanov, A.V. Interplanetary magnetic field structure and solar wind parameters as inferred from solar magnetic field observations and by using a numerical 2-D MHD model. Sol. Phys. 1993, 143, 345–363. [Google Scholar] [CrossRef]
- Kislov, R.A.; Khabarova, O.V.; Malova, H.V. Quasi-stationary Current Sheets of the Solar Origin in the Heliosphere. Astrophys. J. 2019, 875, 28. [Google Scholar] [CrossRef]
- Priest, E. Magnetohydrodynamics of the Sun, 2nd ed.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Ulysses Final Archive. The Directory VHM_FGM Contains the Ulysses Prime Resolution Data of the Magnetic Field, Directory SWOOPS Presents Plasma Speed, Density and Temperature Data. Available online: http://ufa.esac.esa.int/ufa/#data (accessed on 13 April 2022).
- Lee, M.A.; Mewaldt, R.A.; Giacalone, J. Shock Acceleration of Ions in the Heliosphere. Space Sci. Rev. 2012, 173, 247–281. [Google Scholar] [CrossRef]
- Cranmer, S.R.; Gibson, S.E.; Riley, P. Origins of the Ambient Solar Wind: Implications for Space Weather. Space Sci. Rev. 2017, 212, 1345. [Google Scholar] [CrossRef]
- Poppe, A.R.; Lee, C.O. The Effects of Solar Wind Structure on Nanodust Dynamics in the Inner Heliosphere. J. Geophys. Res. 2020, 125, e28463. [Google Scholar] [CrossRef]
- Yermolaev, Y.I.; Stupin, V.V. Helium abundance and dynamics in different types of solar wind streams: The Prognoz 7 observations. J. Geophys. Res. 1997, 102, 2125–2136. [Google Scholar] [CrossRef]
- Gazis, P.R.; Barnes, A.; Mihalov, J.D. Pioneer and Voyager Observations of Large-Scale Spatial and Temporal Variations in the Solar Wind. Space Sci. Rev. 1995, 72, 117–120. [Google Scholar] [CrossRef]
- Smith, E.J. The heliospheric current sheet. J. Geophys. Res. 2001, 106, 15819–15832. [Google Scholar] [CrossRef]
- Burlaga, L.F.; Ness, N.F.; Wang, Y.-M.; Sheeley, N.R. Heliospheric magnetic field strength and polarity from 1 to 81 AU during the ascending phase of solar cycle 23. J. Geophys. Res. 2002, 107, 1410. [Google Scholar] [CrossRef]
- Tsareva, O.O. Generalization of Stormer theory for an axisymmetric superposition of dipole and quadrupole fields. J. Geophys. Res. Space Phys. 2019, 124, 2844–2853. [Google Scholar] [CrossRef]
- Sokoloff, D.D.; Malova, H.V.; Yushkov, E. Symmetries of Magnetic Fields Driven by Spherical Dynamos of Exoplanets and Their Host Stars. Symmetry 2020, 12, 2085. [Google Scholar] [CrossRef]
- Richardson, I.G.; Cane, H.V. Regions of abnormally low proton temperature in the solar wind (1965–1991) and their association with ejecta. J. Geophys. Res. 1995, 100, 23397–23412. [Google Scholar] [CrossRef]
- Richardson, J.D.; Paularena, K.I.; Lazarus, A.J.; Belcher, J.W. Radial evolution of the solar wind from IMP 8 to Voyager 2. Geophys. Res. Lett. 1995, 22, 325–328. [Google Scholar] [CrossRef]
- Zhao, G.-Q.; Feng, H.-Q.; Wu, D.-J.; Liu, Q.; Zhao, Y.; Tian, Z.-J. On Mechanisms of Proton Perpendicular Heating in the Solar Wind: Test Results Based on Wind Observations. Res. Astr. Astrophys. 2022, 22, 015009. [Google Scholar] [CrossRef]
- Gloeckler, G. Observation of Injection and Pre-Acceleration Processes in the Slow Solar Wind. Space Sci. Rev. 1999, 89, 91–104. [Google Scholar] [CrossRef]
- Mewaldt, R.A.; Cohen, C.M.S.; Mason, G.M. The Source Material for Large Solar Energetic Particle Events. Geophys. Union Geophys. Monogr. Ser. 2006, 165, 115–126. [Google Scholar] [CrossRef]
- Keesee, A.M.; Elfritz, J.G.; Fok, M.-C.; McComas, D.J.; Scime, E.E. Superposed epoch analyses of ion temperatures during CME- and CIR/HSS-driven storms. J. Atmos. Sol. Terr. Phys. 2014, 115, 67–78. [Google Scholar] [CrossRef]
- Squire, J.; Meyrand, R.; Kunz, M.W.; Arzamasskiy, L.; Schekochihin, A.A.; Quataert, E. High-frequency heating of the solar wind triggered by low-frequency turbulence. Nat. Astr. 2022. [Google Scholar] [CrossRef]
- Adhikari, L.; Zank, G.P.; Zhao, L.-L. A Solar Coronal Hole and Fast Solar Wind Turbulence Model and First-orbit Parker Solar Probe (PSP) Observations. Astrophys. J. 2020, 901, 102. [Google Scholar] [CrossRef]
- Zank, G.P.; Zhao, L.-L.; Adhikari, L.; Telloni, D.; Kasper, J.C.; Bale, S.D. Turbulence transport in the solar corona: Theory, modeling, and Parker Solar Probe. Phys. Plasmas 2021, 28, 080501. [Google Scholar] [CrossRef]
- Kiyani, K.H.; Chapman, S.C.; Sahraoui, F.; Hnat, B.; Fauvarque, O.; Khotyaintsev, Y.V. Enhanced Magnetic Compressibility and Isotropic Scale Invariance at Sub-ion Larmor Scales in Solar Wind Turbulence. Astrophys. J. 2013, 763, 10. [Google Scholar] [CrossRef]
- Hadid, L.Z.; Sahraoui, F.; Galtier, S. Energy Cascade Rate in Compressible Fast and Slow Solar Wind Turbulence. Astrophys. J. 2017, 838, 9. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.; Chasapis, A.; Chhiber, R.; Parashar, T.N.; Maruca, B.A.; Matthaeus, W.H.; Schwartz, S.J.; Eriksson, S.; Le Contel, O.; Breuillard, H.; et al. Solar Wind Turbulence Studies Using MMS Fast Plasma Investigation Data. Astrophys. J. 2018, 866, 81. [Google Scholar] [CrossRef]
- Qudsi, R.A.; Bandyopadhyay, R.; Maruca, B.A.; Parashar, T.N.; Matthaeus, W.H.; Chasapis, A.; Gary, S.P.; Giles, B.L.; Gershman, D.J.; Pollock, C.J.; et al. Intermittency and Ion Temperature-Anisotropy Instabilities: Simulation and Magnetosheath Observation. Astrophys. J. 2020, 895, 83. [Google Scholar] [CrossRef]
- Réville, V.; Brun, A.S.; Matt, S.P.; Strugarek, A.; Pinto, R.F. The effect of magnetic topology on thermally driven wind: Toward a general formulation of the braking law. Astrophys. J. 2015, 798, 116. [Google Scholar] [CrossRef]
- Burlaga, L.F.; Ness, N.F.; Richardson, J.D. Heliosheath magnetic field and plasma observed by Voyager 2 during 2011. J. Geophys. Res. 2014, 119, 6062–6073. [Google Scholar] [CrossRef]
- Huang, S.Y.; Zhang, J.; Yuan, Z.G.; Jiang, K.; Wei, Y.Y.; Xu, S.B.; Xiong, Q.Y.; Zhang, Z.H.; Lin, R.T.; Yu, L. Intermittent Dissipation at Kinetic Scales in the Turbulent Reconnection Outflow. Geophys. Res. Lett. 2022, 49, e2021GL096403. [Google Scholar] [CrossRef]
- Reames, D.V. Abundances, Ionization States, Temperatures, and FIP in Solar Energetic Particles. Space Sci. Rev. 2018, 214, 61. [Google Scholar] [CrossRef]
- Marirrodriga, C.G.; Pacros, A.; Strandmoe, S.; Arcioni, M.; Arts, A.; Ashcroft, C.; Ayache, L.; Bonnefous, Y.; Brahimi, N.; Cipriani, F.; et al. The Solar Orbiter: Mission and spacecraft design. Astr. Astrophys. 2021, 646, A121. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maiewski, E.V.; Malova, H.V.; Popov, V.Y.; Zelenyi, L.M. Ulysses Flyby in the Heliosphere: Comparison of the Solar Wind Model with Observational Data. Universe 2022, 8, 324. https://doi.org/10.3390/universe8060324
Maiewski EV, Malova HV, Popov VY, Zelenyi LM. Ulysses Flyby in the Heliosphere: Comparison of the Solar Wind Model with Observational Data. Universe. 2022; 8(6):324. https://doi.org/10.3390/universe8060324
Chicago/Turabian StyleMaiewski, Evgeniy V., Helmi V. Malova, Victor Yu. Popov, and Lev M. Zelenyi. 2022. "Ulysses Flyby in the Heliosphere: Comparison of the Solar Wind Model with Observational Data" Universe 8, no. 6: 324. https://doi.org/10.3390/universe8060324
APA StyleMaiewski, E. V., Malova, H. V., Popov, V. Y., & Zelenyi, L. M. (2022). Ulysses Flyby in the Heliosphere: Comparison of the Solar Wind Model with Observational Data. Universe, 8(6), 324. https://doi.org/10.3390/universe8060324





