Gasflows in Barred Galaxies with Big Orbital Loops—A Comparative Study of Two Hydrocodes
Abstract
1. Introduction
2. The Model
3. Orbital Analysis
3.1. Stellar Response Models
3.2. Orbits
3.2.1. Peridic Orbits (POs)
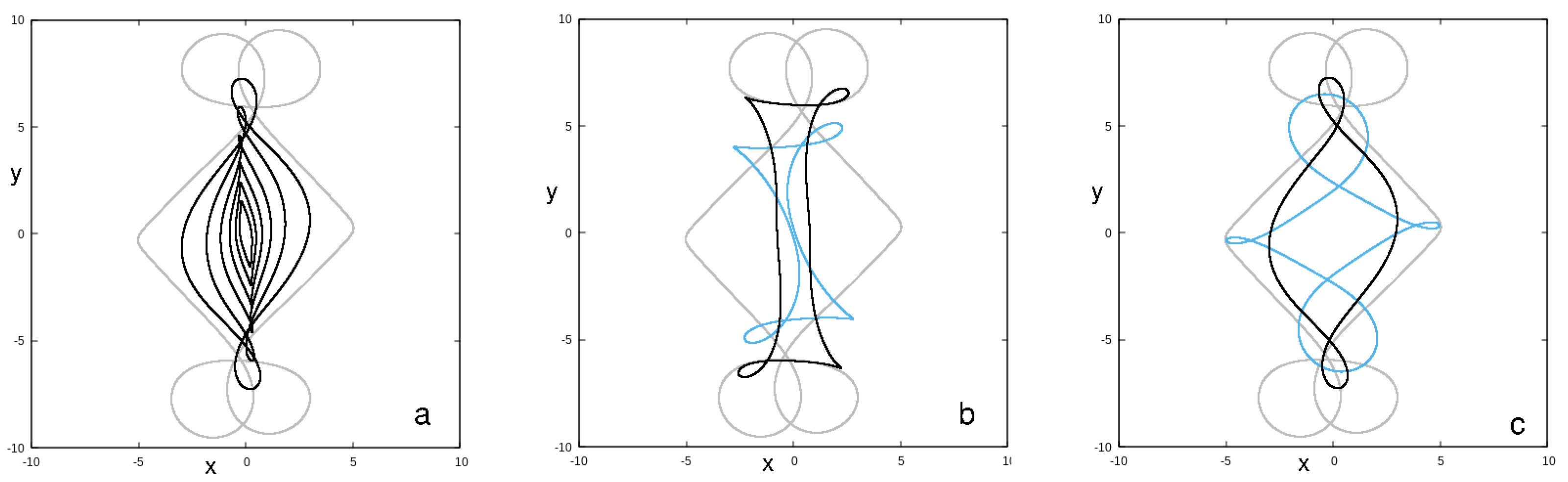
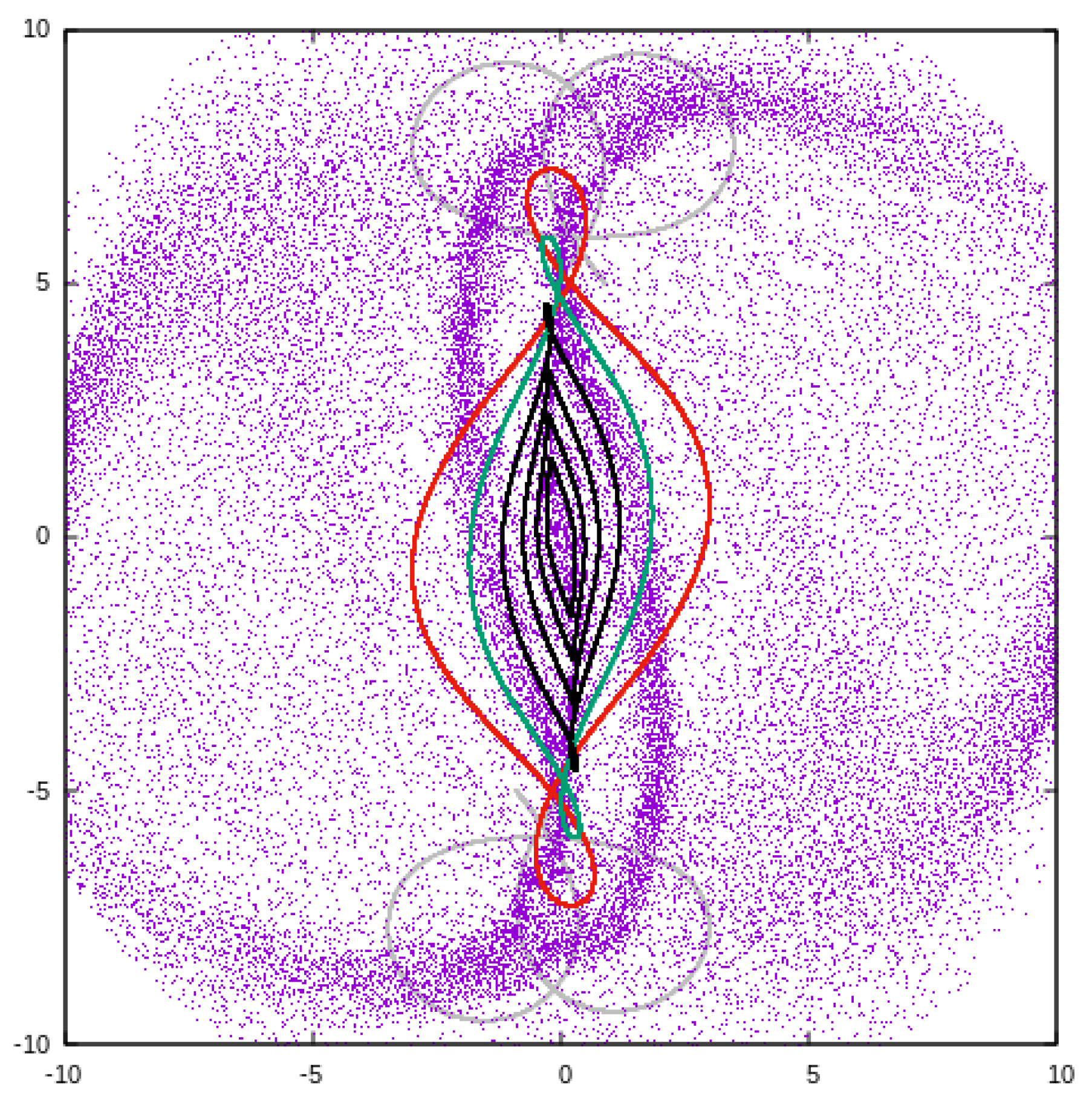
- The family x1. The main building block for the bar of the model is, as expected, the x1 family. However, we have to underline that, due to the presence of the sine terms in Equation (1), its orbits cross the axis with . We find that essentially all x1 orbits are cuspy and they develop loops, which are conspicuous for . Representatives of the x1 family are depicted with the black color in Figure 4a. All of them are stable, with the orbit with the largest loop and the longest projection on the y-axis being at 121,468.
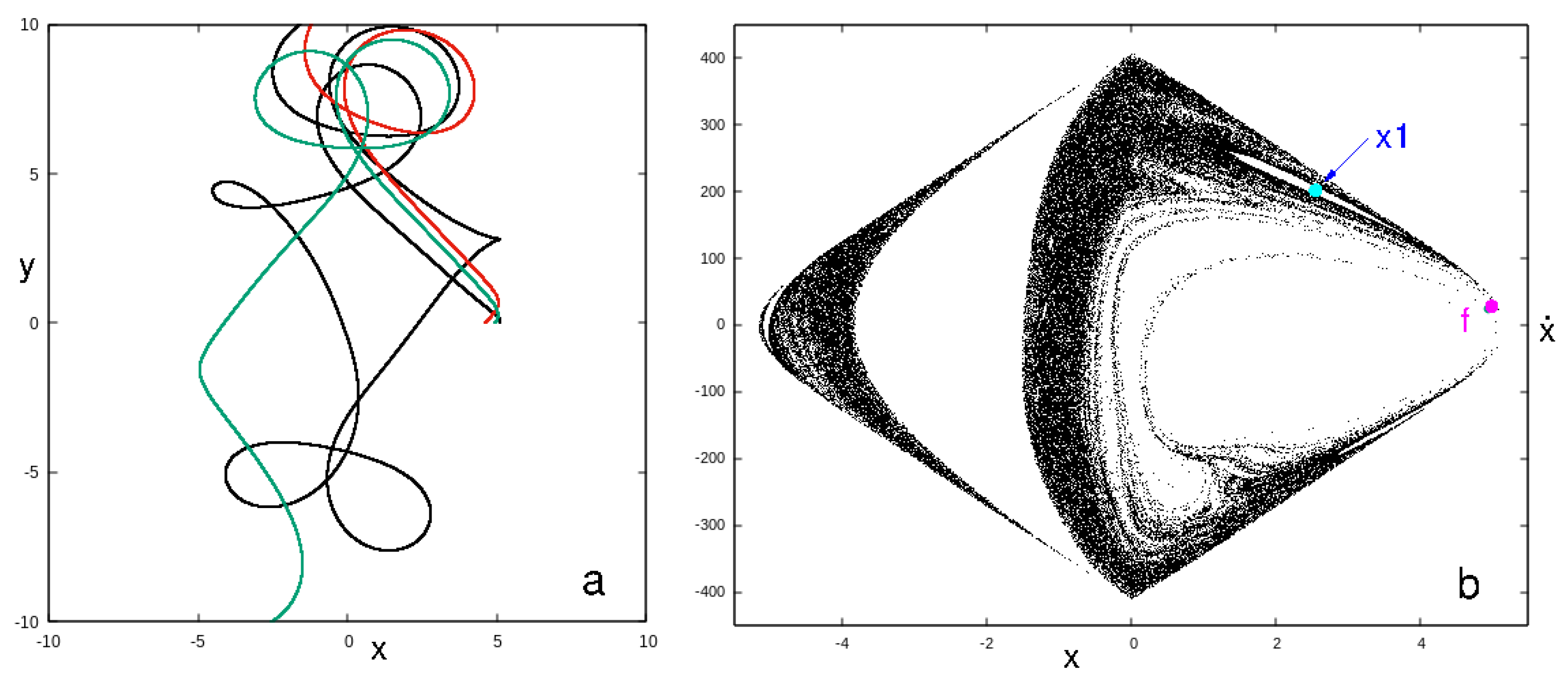
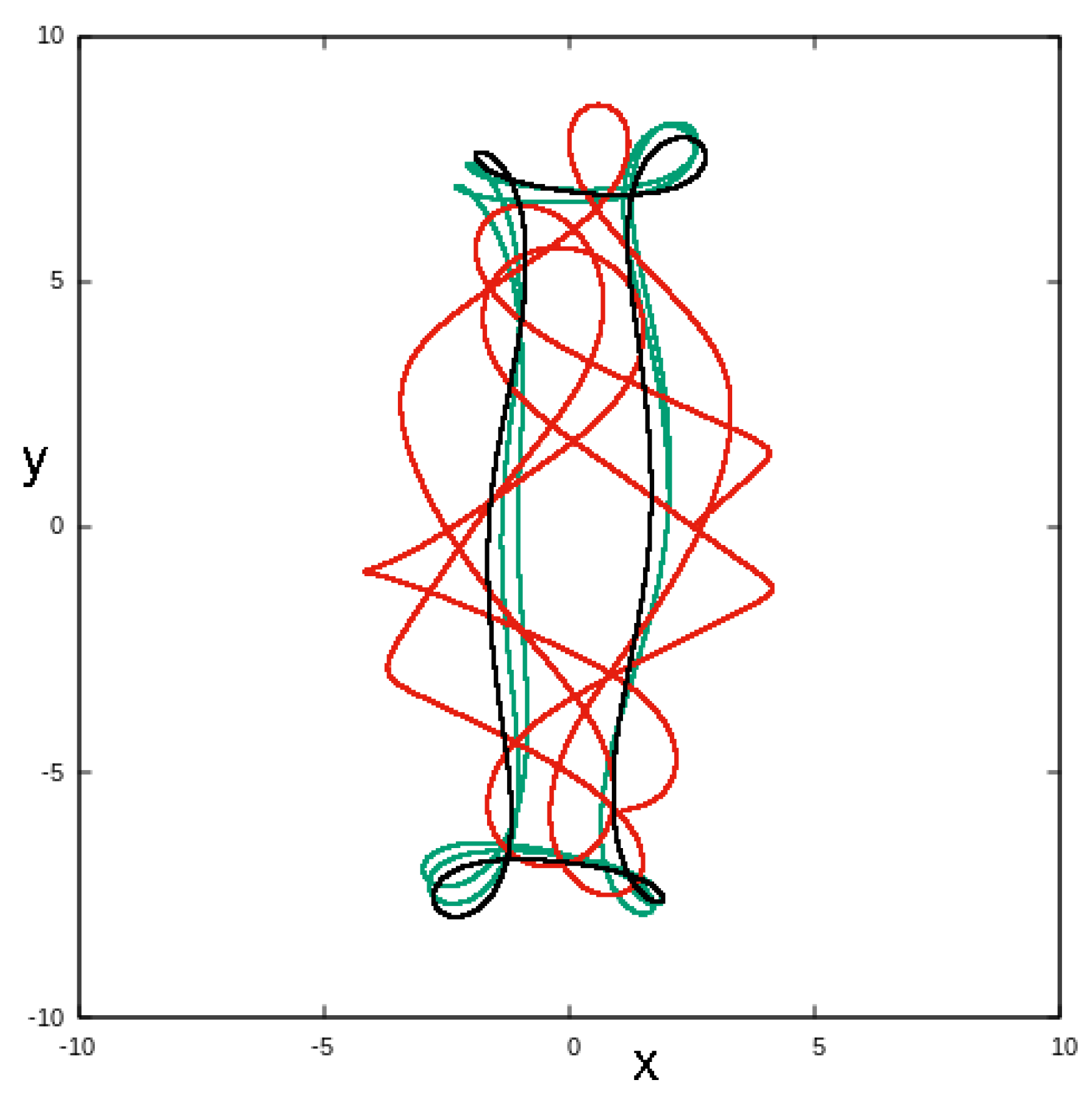
- The family that we indicate as “f” in Figure 3 has a stable and an unstable part. As we observe in Figure 3, it changes its stability practically at . Orbits of this family are given in Figure 4b. The cyan- and black-colored orbits are stable at 124,157 and −120,000, respectively. The grey orbit, which has developed loops reaching the L and L regions, is at 111,723 and is unstable. As energy increases, the initial condition of the orbits of family f increases, leading to hexagonal, rhomboidal shapes. We have, in this case, along the charactristic of f in Figure 3, a transition from a 4:1 to 6:1 resonance morphology. Changes in the morphology of POs along a characteristic are observed as the curve passes through the region of a resonance (see, e.g., Figure 3.7 in [14]). For , the POs of family f are unstable. Thus, there are no stable, rectangular-like orbits, which could help the bar reach corotation. The x1 orbits at these energies already have big loops at the increasing part of the characteristic, for 121,468. They also have shorter projections on the y-axis than the outermost x1 orbit, drawn in black in Figure 4a. The situation with the orbital loops at and beyond the 4:1 resonance region is summarized in Figure 4c, where we give x1 at 121,468 (black), x1 at 112,503 (cyan) and f at 111,723 (gray).
3.2.2. Non-Periodic Orbits
4. Gas Response
4.1. SPH
4.2. RAMSES
5. Discussion
5.1. Code Dependence of the Responses
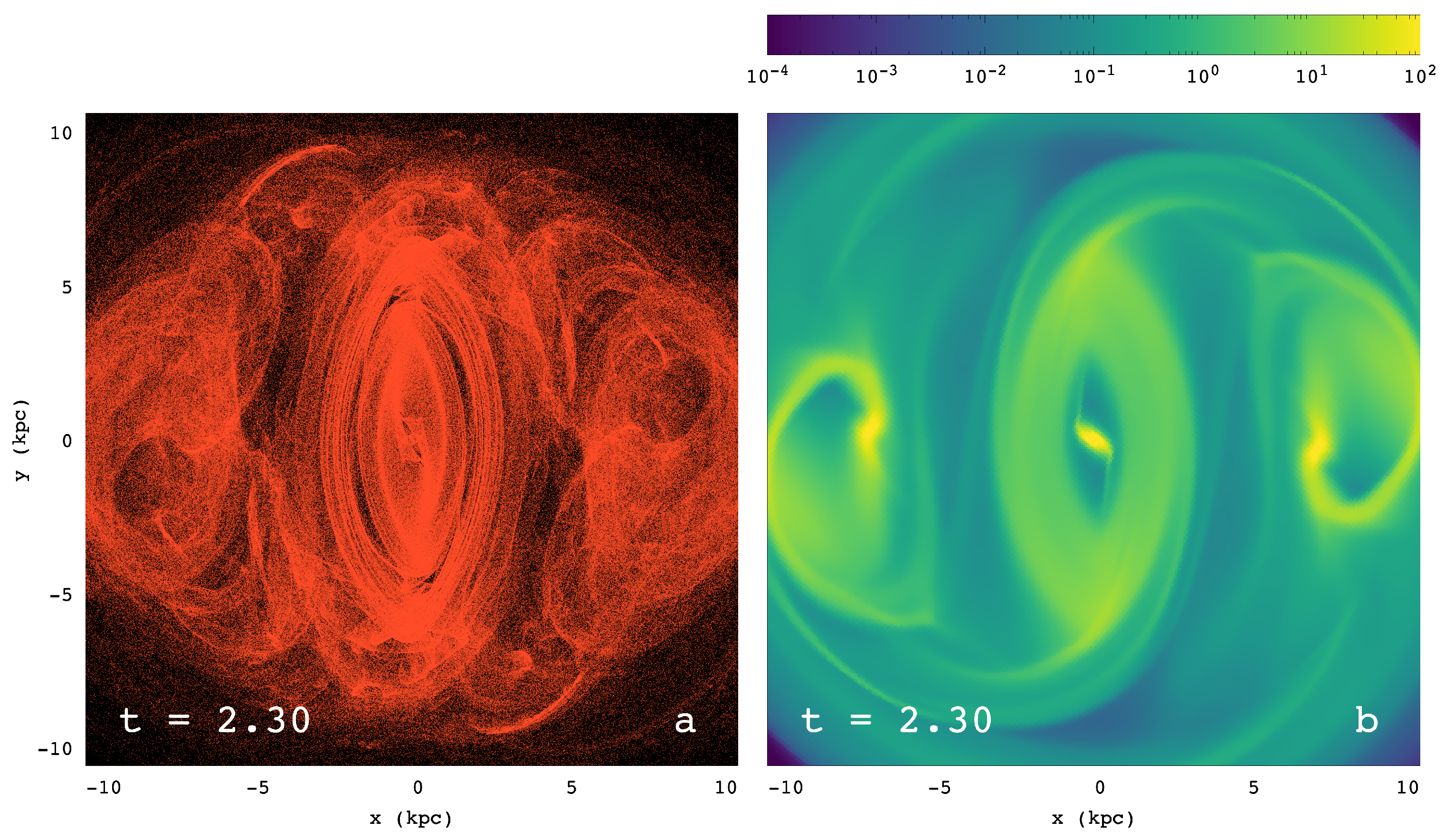
5.2. Stellar vs. Gas Response
6. Conclusions
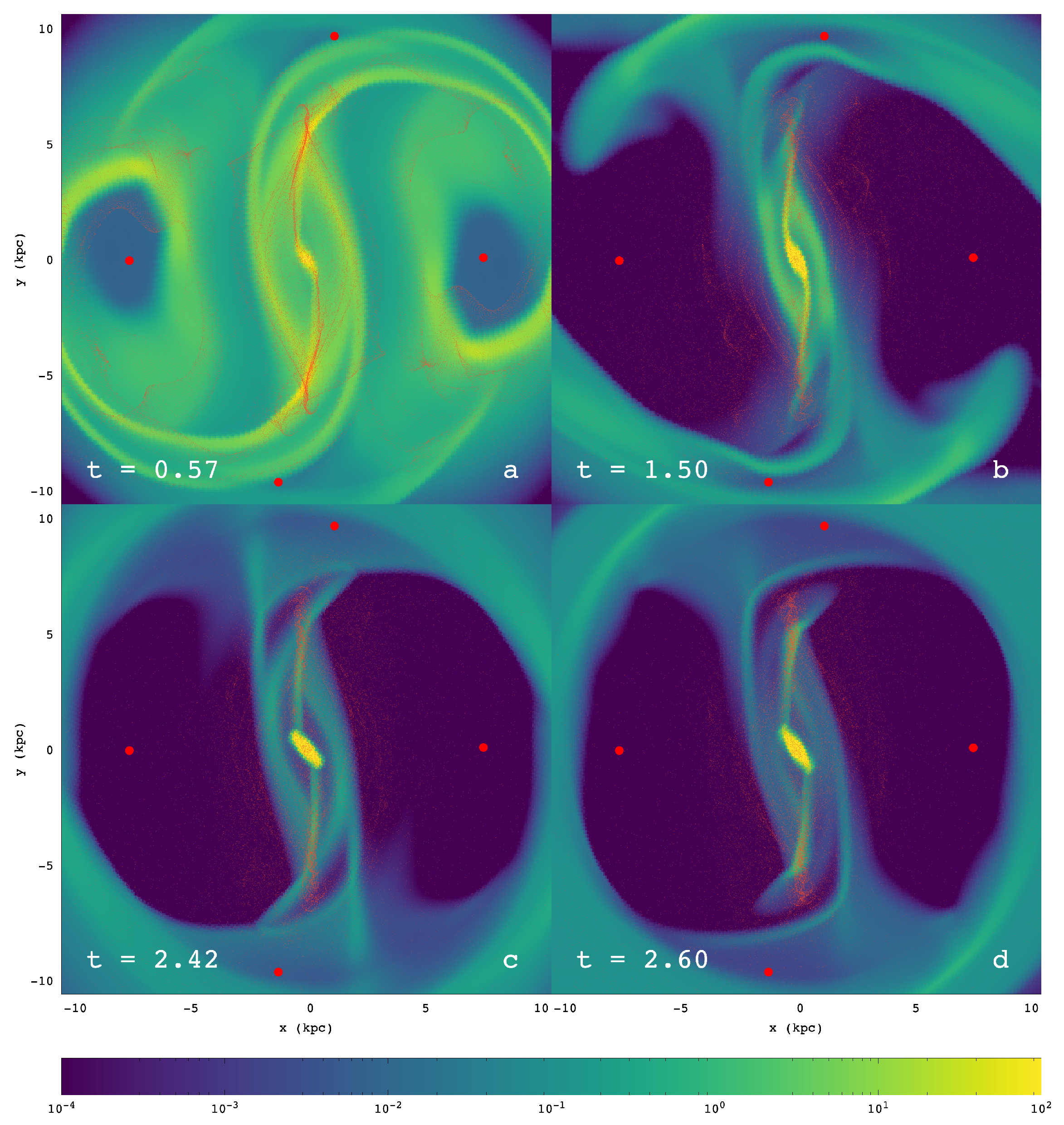
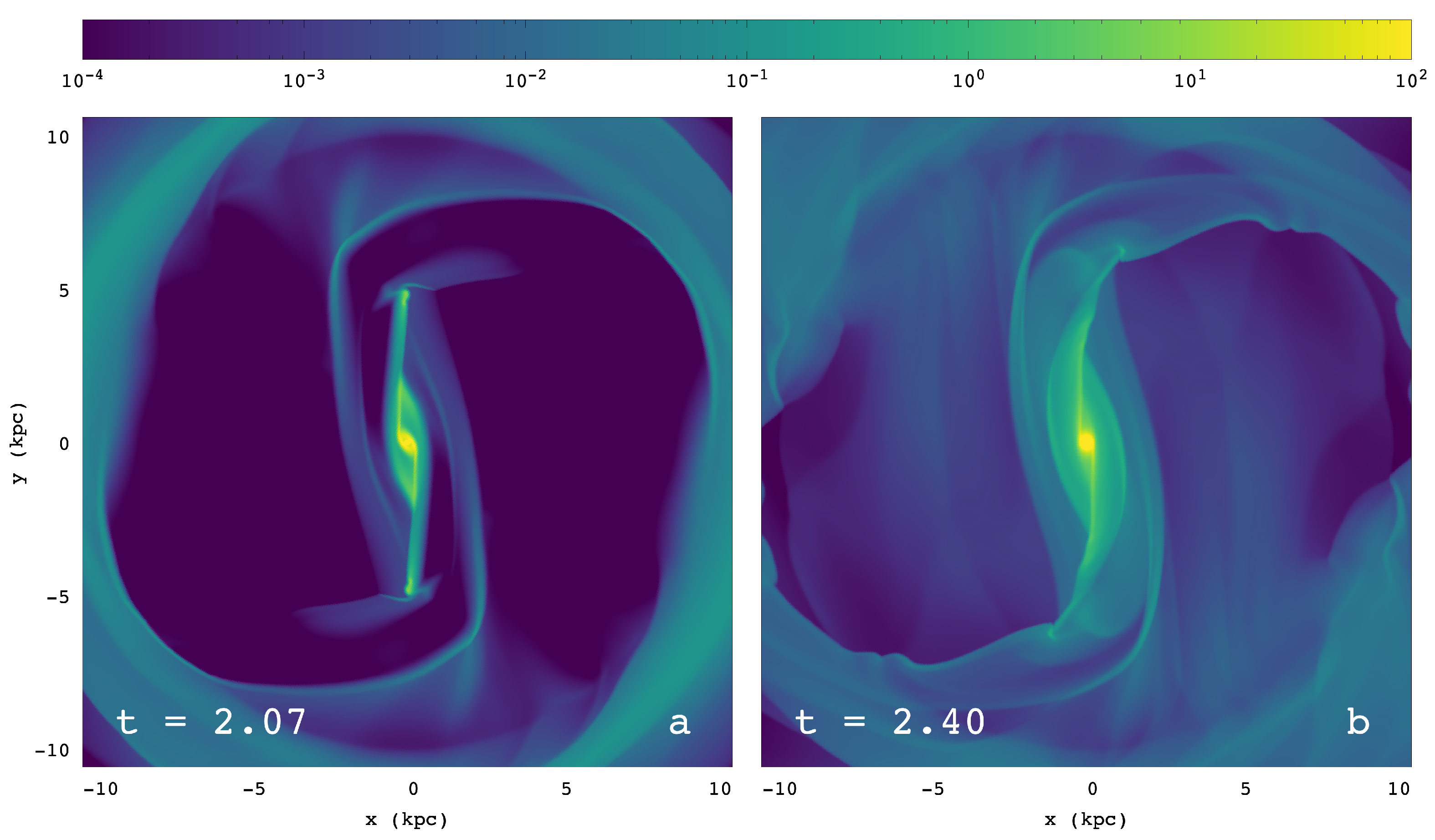
- The basic conclusion of the present study is that the dust-lane shocks in the gas responses of barred galaxies models avoid the regions in which the stable POs of the x1 family have developed sufficiently big loops. They deviate from these regions and, as they bypass them, they form extensions at an angle with the straight-line shocks. Ahead of them, in the direction of rotation, we find low-density regions, which in many cases have a “triangular”-like shape, as, e.g., model 12 in [1]. This morphology is encountered in both codes we used (SPH and RAMSES).
- Responses during the growing-bar phase are smoother, in the sense that we observe fewer regions with strong density gradients. As the amplitude of the perturbation during this phase is always smaller than the final, maximum one, the models do not develop x1 POs with big loops (Figure 2a). Thus, the straight-line, dust -lane shocks extend to larger distances.
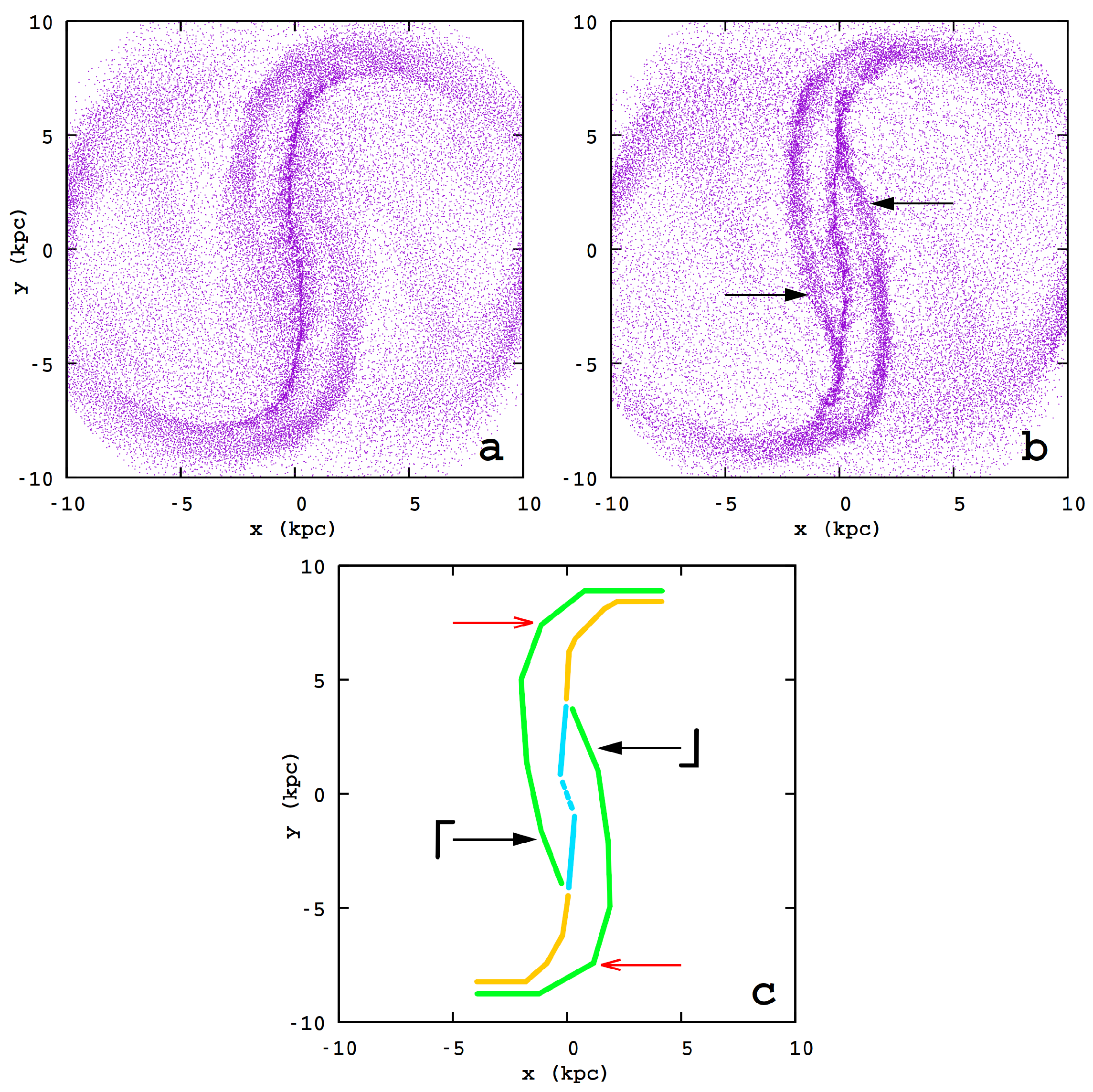
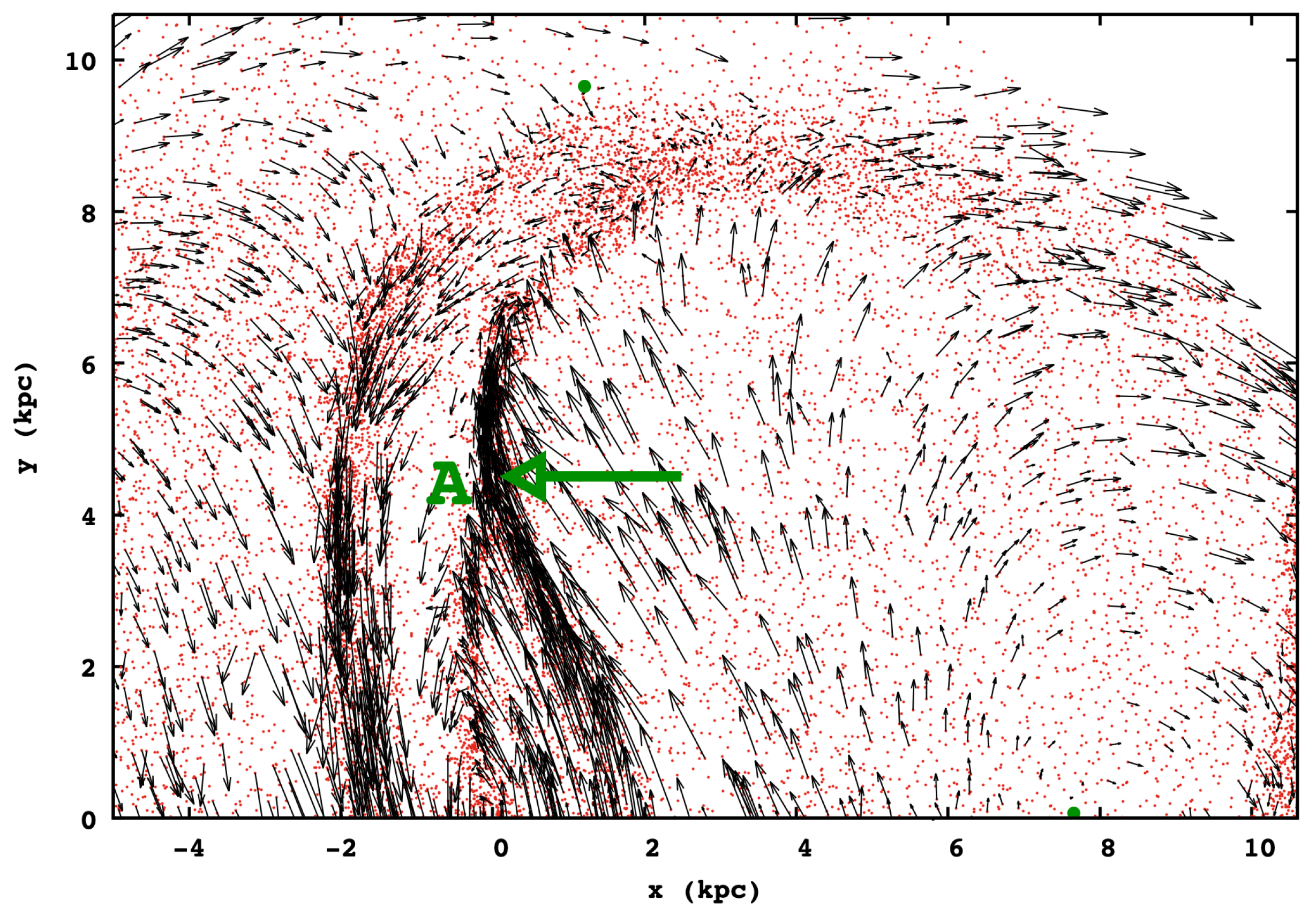
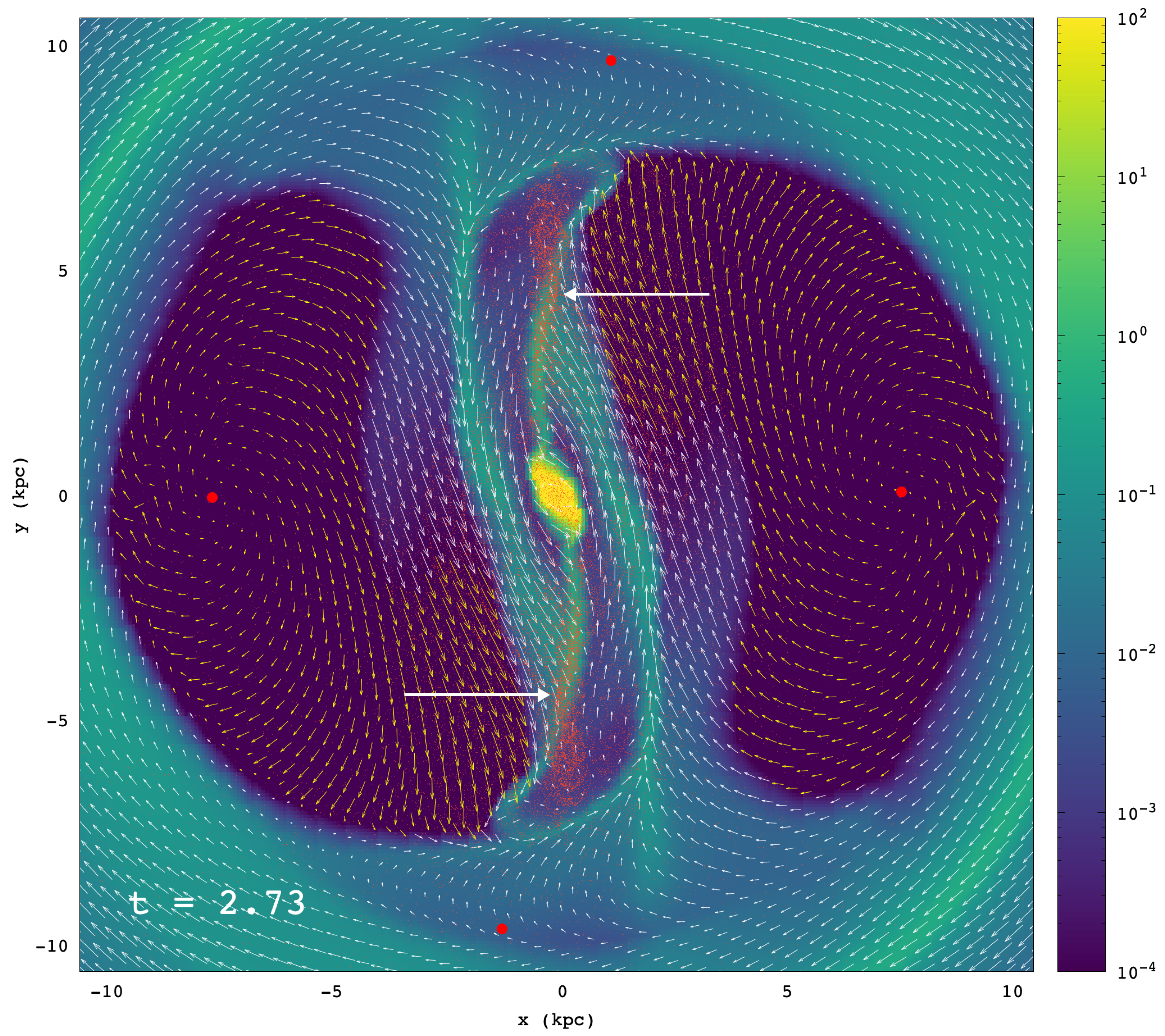
- A characteristic feature of the models are the “tails”, which are dense regions that appear bifurcating from the straight dust-lane shocks at specific points along them. The bifurcating points are identified with the points at which the x1 POs start having considerable loops (indicated with arrows in Figure 8). Gas is streaming along these lanes towards the points where the three density enhancement join.
- The SPH models can be followed for a long time only with replenishment of particles that are manually removed mainly from the overdense regions, but it gives, after a certain time, an invariant response. RAMSES, on the other hand, has a short, relatively turbulent phase for and then reaches a repeating cycle, where the morphology of the straight-line dust-lane shocks and their extensions characterize the snapshots. Nevertheless, there is a dominating “mean” morphology, given in Figure 15.
- Both codes give information valuable for understanding the dynamics of the model and should be used when comparison with the morphology of specific galaxies is attempted. With the Lagrangian SPH method, we can obtain detailed velocity fields in the the dense regions of the model, while with the grid code RAMSES, we can obtain an overall picture of the kinematics of the models. Both modeling techniques are useful for understanding gas dynamics in barred-spiral galaxies.
- Finally, as regards the stellar response, in this model, like in the case of the models for NGC 4314 we studied in [6] and for NGC 1300 in [9], we find a second bar, which is a “chaotic” envelope around the x1 bar. It is “chaotic”, in the sense that it is supported by chaotic orbits. The consistency of its appearance in the models indicates that this is rather a common feature in barred galaxies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PO(s) | Periodic orbit(s) |
| SPH | Smoothed particle hydrodynamics |
| 1 | Available in https://bitbucket.org/rteyssie/ramses/src/master/, accessed on 16 May 2022. |
References
- Athanassoula, E. The existence and shapes of dust lanes in galactic bars. Mon. Not. R. Astron. Soc. 1992, 259, 345–364. [Google Scholar] [CrossRef]
- Athanassoula, E. Morphology of bar orbits. Mon. Not. R. Astron. Soc. 1992, 259, 328–344. [Google Scholar] [CrossRef]
- Quillen, A.C.; Frogel, J.A.; Gonzalez, R. The Gravitational Potential of the Bar in NGC 4314. Astrophys. J. 1994, 437, 162–172. [Google Scholar] [CrossRef]
- Boonyasait, V. Structures and Dynamics of NGC 3359: Observational and Theoretical Studies of a Barred Spiral Galaxy. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 2003. [Google Scholar]
- Kalapotharakos, C.; Patsis, P.A.; Grosbøl, P. NGC 1300 dynamics–I. The gravitational potential as a tool for detailed stellar dynamics. Mon. Not. R. Astron. Soc. 2010, 403, 83–95. [Google Scholar] [CrossRef]
- Patsis, P.A.; Athanassoula, E.; Quillen, A. Orbits in the Bar of NGC 4314. Astrophys. J. 1997, 483, 731–744. [Google Scholar] [CrossRef]
- Patsis, P.A.; Kaufmann, D.E.; Gottesman, S.T.; Boonyasait, V. Stellar and gas dynamics of late-type barred-spiral galaxies: NGC 3359, a test case. Mon. Not. R. Astron. Soc. 2009, 394, 142–156. [Google Scholar] [CrossRef]
- Tsigaridi, L.; Patsis, P.A. The backbones of stellar structures in barred-spiral models–The concerted action of various dynamical mechanisms on galactic discs. Mon. Not. R. Astron. Soc. 2013, 434, 2922–2939. [Google Scholar] [CrossRef]
- Patsis, P.A.; Kalapotharakos, C.; Grosbøl, P. NGC1300 dynamics—III. Orbital analysis. Orbital analysis. Mon. Not. R. Astron. Soc. 2010, 408, 22–39. [Google Scholar] [CrossRef]
- Quillen, A.C.; Frogel, J.A.; Kenney, J.D.P.; Pogge, R.W.; Depoy, D.L. An Estimate of the Gas Inflow Rate along the Bar in NGC 7479. Astrophys. J. 1995, 441, 549–560. [Google Scholar] [CrossRef][Green Version]
- Laine, S. Observations and Modeling of the Gas Dynamics of the Barred Spiral Galaxy NGC 7479. Ph.D. Thesis, University of Florida, Gainesville, FL, USA, 1996. [Google Scholar]
- Laine, S.; Shlosman, I.; Heller, C.H. Pattern speed of the stellar bar in NGC 7479. Mon. Not. R. Astron. Soc. 1998, 297, 1052–1059. [Google Scholar] [CrossRef][Green Version]
- Contopoulos, G.; Harsoula, M. Stickiness in Chaos. Int. J. Bif. Chaos 2008, 18, 2929–2949. [Google Scholar] [CrossRef]
- Contopoulos, G. Order and Chaos in Dynamical Astronomy; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Hénon, M. Exploration numérique du problème restreint. II. Masses égales, stabilité des orbites. Ann. d’Astrophys. 1965, 28, 992–1007. [Google Scholar]
- Patsis, P.A. On the relation between orbital structure and observed bar morphology. Mon. Not. R. Astron. Soc. 2005, 358, 305–315. [Google Scholar] [CrossRef][Green Version]
- Chatzopoulos, S.; Patsis, P.A.; Boily, C.M. A taxonomic algorithm for bar-building orbits. Mon. Not. R. Astron. Soc. 2011, 416, 479–492. [Google Scholar] [CrossRef][Green Version]
- Poincaré, H. Les Méthodes Nouvelles de la Mécanique Céleste; Gauthier Villars: Paris, France, 1892. [Google Scholar]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astrophys. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Teyssier, R. Cosmological hydrodynamics with adaptive mesh refinement. A new high resolution code called RAMSES. Astron. Astrophys. 2002, 385, 337–364. [Google Scholar] [CrossRef]
- Patsis, P.A.; Athanassoula, E. SPH simulations of gas flow in barred galaxies. Effect of hydrodynamical and numerical parameters. Mon. Not. R. Astron. Soc. 2000, 358, 45–56. [Google Scholar]
- Bate, M.R.; Bonnell, I.A.; Price, N.M. Modelling accretion in protobinary systems. Mon. Not. R. Astron. Soc. 1995, 277, 362–376. [Google Scholar] [CrossRef]
- Kitsionas, S.; Whitworth, A.P. Smoothed Particle Hydrodynamics with particle splitting, applied to self-gravitating collapse. Mon. Not. R. Astron. Soc. 2002, 330, 129–136. [Google Scholar] [CrossRef]
- Few, C.G.; Dobbs, C.; Pettitt, A.; Konstandin, L. Testing hydrodynamics schemes in galaxy disc simulations. Mon. Not. R. Astron. Soc. 2016, 460, 4382–4396. [Google Scholar] [CrossRef][Green Version]
- Fragkoudi, F.; Athanassoula, E.; Bosma, A. Constraining the dark matter content of NGC 1291 using hydrodynamic gas response simulations. Mon. Not. R. Astron. Soc. 2016, 466, 474–488. [Google Scholar] [CrossRef]
- Pastras, S. Comparing Hydrodynamics Codes for Modeling the Gas Flow in Barred Spiral Galaxies. Master’s Thesis, University of Athens, Athens, Greece, 2022. [Google Scholar]
- Contopoulos, G. The 4: 1 resonance in barred galaxies. Astron. Astrophys. 1988, 201, 44–50. [Google Scholar]
- Patsis, P.A.; Tsigaridi, L. The flow in the spiral arms of slowly rotating bar-spiral models. Astrophys. Space Sci. 2017, 362, 129–135. [Google Scholar] [CrossRef]
- Treuthardt, P.; Seigar, M.S.; Sierra, S.; Al-Baidhany, I.; Salo, H.; Kennefick, D.; Kennefick, J.; Lacy, C.H.S. On the link between central black holes, bar dynamics and dark matter haloes in spiral galaxies. Mon. Not. R. Astron. Soc. 2012, 423, 3118–3133. [Google Scholar] [CrossRef]
- Sormani, M.C.; Binney, J.; Magorrian, J. Gas flow in barred potentials. Mon. Not. R. Astron. Soc. 2015, 449, 2421–2435. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pastras, S.; Patsis, P.A.; Athanassoula, E. Gasflows in Barred Galaxies with Big Orbital Loops—A Comparative Study of Two Hydrocodes. Universe 2022, 8, 290. https://doi.org/10.3390/universe8050290
Pastras S, Patsis PA, Athanassoula E. Gasflows in Barred Galaxies with Big Orbital Loops—A Comparative Study of Two Hydrocodes. Universe. 2022; 8(5):290. https://doi.org/10.3390/universe8050290
Chicago/Turabian StylePastras, Stavros, Panos A. Patsis, and E. Athanassoula. 2022. "Gasflows in Barred Galaxies with Big Orbital Loops—A Comparative Study of Two Hydrocodes" Universe 8, no. 5: 290. https://doi.org/10.3390/universe8050290
APA StylePastras, S., Patsis, P. A., & Athanassoula, E. (2022). Gasflows in Barred Galaxies with Big Orbital Loops—A Comparative Study of Two Hydrocodes. Universe, 8(5), 290. https://doi.org/10.3390/universe8050290




