Abstract
The simultaneous detection of gravitational waves and light from the binary neutron star merger GW170817 led to independent measurements of distance and redshift, providing a direct estimate of the Hubble constant that does not rely on a cosmic distance ladder, nor assumes a specific cosmological model. By using gravitational waves as “standard sirens”, this approach holds promise to arbitrate the existing tension between the value inferred from the cosmic microwave background and those obtained from local measurements. However, the known degeneracy in the gravitational-wave analysis between distance and inclination of the source led to a value from GW170817 that was not precise enough to resolve the existing tension. In this review, we summarize recent works exploiting the viewing-angle dependence of the electromagnetic signal, namely the associated short gamma-ray burst and kilonova, to constrain the system inclination and improve on . We outline the key ingredients of the different methods, summarize the results obtained in the aftermath of GW170817 and discuss the possible systematics introduced by each of these methods.
1. Introduction
The Hubble constant () measures the present expansion rate of our Universe and sets its absolute distance scale. In the local Universe, can be approximated by a simple linear equation
where is the luminosity distance and is the Hubble flow velocity, equal to the speed of light c times the redshift z. The exact value of has been the subject of a myriad of studies and of contentious debate, from the first measurement by Edwin Hubble in 1929 [1] to the present day nearly a century later. Most notably, an increasing tension has emerged between values measured from probes of the early Universe, e.g., the cosmic microwave background (CMB [2]), and those inferred from probes of the late Universe, e.g., Type Ia supernovae (SNe Ia [3]). Whether this tension is caused by hidden systematics or indicative of new physics is hotly debated (see, e.g., [4] for a recent review).
Gravitational waves (GWs) from compact object mergers have been proposed as “standard sirens” [5,6] to measure , where the source distance is inferred directly from the GW signal while its redshift z is obtained either from an electromagnetic (EM) counterpart and its parent galaxy or statistically from galaxy clustering. This independent approach to measure holds promise to arbitrate the existing tension and has been vitalized following the observation of the binary neutron star (BNS) merger GW170817 on 17 August 2017 [7], made by the Advanced Laser Interferometer Gravitational-wave Observatory (LIGO [8]) and Virgo [9] detectors. The simultaneous detection of GW and EM radiation from this single source led to independent measurements of the distance and redshift of the source, thus providing a direct estimate of [10]. Nevertheless, a degeneracy in the GW signal between the distance and inclination of the merging system translates into large (∼15%) uncertainties on , with the inferred value currently unable to resolve the tension between early- and late-Universe measurements of the Hubble constant.
In this respect, an independent estimate of the system inclination can reduce the existing degeneracy and provide better constraints on . Fortunately, not only the GW signal but also the EM emission from the neutron star (NS) merger is viewing-angle-dependent. This anisotropic emission includes a non-thermal short gamma-ray burst (GRB) “afterglow” powered by the interaction between a relativistic jet and the circum-burst environment, and a thermal “macronova/kilonova” (KN) powered by the radioactive decay of —process nuclei synthesized during and after the merger. A constraint on the viewing angle from these EM probes can pin down the inclination of NS mergers, helping to relieve the degeneracy between distance and inclination and thus improving on . Improved constraints on have been presented for GW170817 using constraints on the inclination from model fitting of the associated gamma-ray burst GRB 170817A [11,12,13] and KN AT 2017gfo [14,15,16,17].
This review article aims to summarize the recent efforts to constrain from NS mergers using GWs alone as standard sirens or through a combination of GWs and EM light. The article is organized as follows. Section 2 summarizes the current status of the tension, whereas Section 3 outlines the key ingredients of the standard siren approach to measure with GWs. The rest of the article provides an overview of the various works in the literature using additional information from GRBs (Section 4) and KNe (Section 5) in combination with GW data to improve on . Finally, Section 6 provides a summary and some discussion about the systematics introduced by the different approaches.
2. The Hubble Constant Tension
In recent years, a remarkable increase in accuracy obtained by a broad range of independent cosmological observations has provided compelling support for our current standard cold dark matter (CDM) model. This concordance cosmology successfully explains the measurements of fluctuations in the temperature and polarization of the CMB radiation [2], as well as observations of large-scale structure and matter fluctuations in the universe, e.g., baryon acoustic oscillations (BAO [18]).
With an improved accuracy of recent observations, some discrepancies have been noted. The prima facie most significant tension, now at the 5 level of significance, is between the CMB-inferred value of the Hubble constant, km s Mpc, and the direct measurement of its local value [3]. The local measurements are based on a calibration of the absolute luminosity of SNe Ia using independent distances to host galaxies of nearby SNe Ia, known as the “cosmic distance ladder”. This claimed tension, if confirmed, could provide evidence for new fundamental physics beyond the standard model of cosmology (e.g., see [19,20] for a summary of the potential non-standard cosmologies as a solution). It could, however, be a sign of unknown sources of systematic error. At the early Universe end of the distance scale, independent evaluations of with the Atacama Cosmology Telescope (ACT) combined with the Wilkinson Microwave Anisotropy Probe (WMAP) missions [21] yield a low value of . Moreover, replacing the CMB entirely with big bang nucleosynthesis for early universe constraints on shows a consistency between the two methods, e.g., [22,23]. Currently, the local methods have slight differences in their values. The tip of the red giant branch (TRGB [24]) and Cepheid [3] distance scales yield values of 69.8 ± 1.7 and 73.04 ± 1.04 km s Mpc, respectively. Understanding these differences is important for discerning whether the tension is a sign of novel physics or a yet-to-be-revealed systematic error. To date, only the TRGB and Cepheid measurements have measured at a ∼2–3% or better precision. Therefore, while the distance ladder estimates are precise, given the ∼2 level internal discordance between the different methods, new and independent measurements of at the ∼1–2% level are imperative.
Promising methods for the precise determination of , independent of the distance ladder, include Type II-P SNe (SNIIP [25]), megamaser distances [26] and time-delay cosmography using lensed transients. While strongly lensed quasars have previously been shown to be precise estimators of [27], sources of systematics, e.g., the mass-sheet transformation, need to be accounted for and, hence, the final estimate does not, as yet, have competitive uncertainties [28]. These can be overcome with the use of lensed SNe Ia, as standardizable candles, with future surveys such as Rubin Observatory’s Legacy Survey of Space and Time (VRO/LSST [29]). SNIIP’s and megamaser galaxies are currently hampered by large peculiar velocity uncertainties since the brightness of these sources has only allowed for measurements in the nearby Hubble flow, which is expected to change with future observatories. These would be highly complementary to the EM-GW constraints on from standard sirens, which we will discuss in Section 3.
3. Gravitational Waves as Standard Sirens
The use of GW observations to probe the expansion history of the Universe and determine was originally proposed by Schutz in 1986 [5] and further developed by Holz and Hughes [6], who first introduced the term “standard sirens”1 as opposed to “standard candles” to stress the aural rather than visual nature of the GW signals. This method relies on the fact that the strain amplitude h of the GW is inversely proportional to the luminosity distance according to Einstein’s quadrupole formula [30].
where G is the gravitational constant and I is the source’s mass quadrupole moment. Both h and the rate of change in the frequency of the signal depend on the binary masses and through the same combination, i.e., the so-called “chirp” mass . The luminosity distance can therefore be extracted from the GW signal by measuring the two observables h and . At the same time, the redshift of the source can be inferred directly if an EM counterpart and its host galaxy are identified (“bright sirens”) or otherwise statistically based on galaxy clustering (“dark sirens”). From the independent measurements of and z, is obtained directly from Equation (1) and without relying on a cosmic distance ladder or assuming a specific cosmological model (see Section 2).
Focusing on the mergers of binary black holes (BBHs), Holz and Hughes [6] found that the luminosity distance could be measured with an accuracy of 1–10% for a single event. However, the relatively large uncertainties can be greatly reduced if an EM counterpart to the GW event is identified. First, an EM counterpart identification reduces the pointing errors and breaks the correlations in the GW signal between the position and distance, therefore improving the accuracy on to . Second, an EM counterpart leads to the identification of the host galaxy, from which, a redshift can be extracted and used to directly measure . Therefore, while the statistical “dark siren” method may lead to a 1%—level accuracy on in the long run, e.g., [31,32,33,34,35,36,37,38,39,40], the “bright siren” method remains a better prospect since the knowledge of the source redshift greatly improves the determination on single events [36,41,42,43,44,45,46] (see also [47] for biases in from the dark sirens). Nevertheless, a number of ∼50–200 GW events [36,44] with an identified EM counterpart might be needed to reach a —level accuracy on and arbitrate the current tension (although the exact number is subject to uncertainties, such as the BNS and BH-NS merger rates).
The power of the standard siren approach was showcased in the aftermath of GW 170817 [10]. The detection of the short gamma-ray burst GRB170817A within a region compatible with the LIGO and Virgo sky localization for the GW source [48,49,50] prompted an intensive follow-up campaign [7] that led to the discovery of an optical transient originating from the radioactive decay of —process nuclei synthesized in the merger of two NSs (a KN, see Section 5.1). This transient was located on the outskirts of the NGC 4993 galaxy [51,52,53,54,55,56] with a chance association deemed to be at the level of [10]. Thanks to the EM counterpart identification, the luminosity distance of GW170817 could be constrained from the GW signal alone to Mpc. At the same time, a redshift was inferred for NGC 4993; after correcting for peculiar velocities, the measurement led to a Hubble flow velocity km s. By combining the distribution for from the GW signal and that for from the EM data, a posterior distribution on was inferred and a maximum a posteriori (MAP) value with a credible interval was constrained to be km s Mpc. For completeness, we note that a symmetric interval (median plus the range) of km s Mpc is also quoted for this measurement in the literature. As shown in Figure 1, this value is consistent with both CMB [2] and local distance-ladder [3] measurements and demonstrates the potential of the standard siren method. Owing to the -level uncertainties, however, the inferred value cannot arbitrate the existing tension, and multi-messenger detections of future compact binary mergers are needed to achieve this in a statistical sense [44].
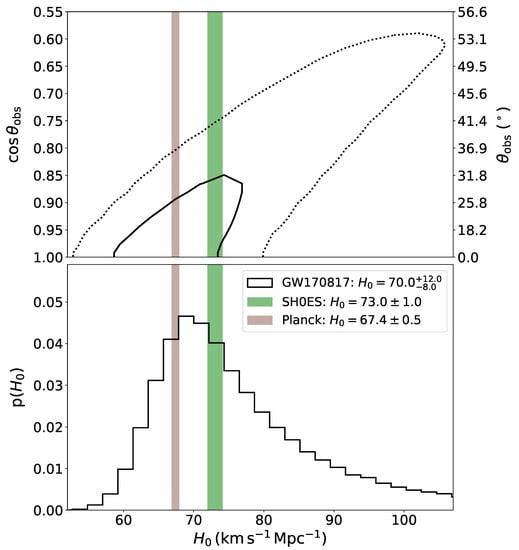
Figure 1.
Constraint on from the BNS merger GW170817 [10]. Figure adapted from [10] and using publicly available data from Gravitational Wave Open Science Center (https://www.gw-openscience.org, aeecssed on 3 May 2022). Copyright 2017 LVK. (Top) 2D posterior density of and the viewing angle , where () and () contours are shown with solid and dotted black lines, respectively. The viewing angle is calculated relative to a face-on observer, i.e., , where i is the system inclination obtained from the GW data. (Bottom) Marginalized 1D posterior density for . In both panels, values inferred from Planck [2] and SHOES [3] are shown with their intervals in brown and green, respectively. The inferred values are reported in the legend.
The uncertainties on derived by Abbott et al. [10] are driven by those on the luminosity distance 2, which are largely due to a well-known degeneracy between distance and orbital inclination i of the binary. This degeneracy can be easily seen from the following equation for h valid in the limit of small angles:
That is, a similar GW amplitude h is produced by a binary far away and viewed close to face-on/face-off and a binary nearer by but viewed at larger inclinations. In principle, constraints on the inclination i can be extracted directly from the GW data by measuring the two polarization amplitudes
where the constant of proportionality is the same for both and and depends on the chirp mass , luminosity distance and frequency f [61]. In practice, this is challenging for two main reasons. First, only upper limits on the viewing angle = min[i,]3 can be achieved at small inclinations since . Second, the LIGO detectors are almost aligned and thus sensitive to only one polarization; hence, a third detector (e.g., Virgo) is needed to measure both polarization amplitudes with good accuracy. Indeed, GW170817 was observed at relatively small angles and seen only by the two LIGO detectors. As shown in Figure 1, this led to poor constraints on the inclination angle of (). Recent simulations [62] show that, in the absence of an EM counterpart, the International Gravitational-Wave Observatory Network (IGWN) at design sensitivity would be able to constrain the inclination of the system only if , i.e., for systems that are close to edge-on and thus more difficult to detect in GWs.
While it might be challenging to pin down the inclination angle from the GW data alone, constraints can be placed by exploiting the viewing-angle dependence of the EM signals. In particular, both GRB and KNe are not isotropic signals and constraining the orientation from these EM probes can alleviate the distance–inclination degeneracy in the GW analysis, thus offering a promising pathway to improve on on a single-event base. In the following, we will review studies using GRB (Section 4) and KN (Section 5) observables to constrain the system inclination and improve on . The systematic effects introduced by these approaches will be mentioned in each section and, together with those from the GW standard siren approach, further expanded on in Section 6. The main results in terms of inferred viewing angles and values are summarized in Figure 2 and Table 1.
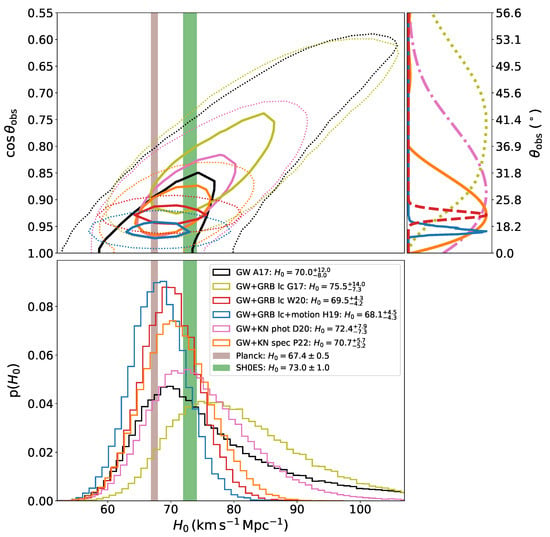
Figure 2.
Improved constraints on from the BNS merger GW170817 through combination of GW and EM data. (Top-right) Posterior distributions on the observer viewing-angle from model fitting of the associated short GRB and KN. Constraints from GRB 170817A are shown for model fits with (cyan [12]) or without (light green [11]; red [13]) information from the jet superluminal motion [95,96]. Constraints from the KN AT 2017gfo are shown for model fits of broad-band photometry (pink [14]) and spectroscopy (orange [17]). The color scheme is the same in the remaining two panels. (Top-left) Same as in Figure 1 but adding improvements to the 2D posterior density contours when the viewing-angle constraints from GRB and KN fitting are used as priors for the inclination in the GW analysis. (Bottom) Marginalized 1D posterior density distributions for when using the original standard siren approach (black, same as in Figure 1) and when adding constraints on the viewing-angle from EM probes. The inferred values are reported in the legend.

Table 1.
values obtained for GW170817 with the standard siren approach (’GW’), together with improvements using inclination constraints from model fitting of the different EM probes: the associated GRB afterglow light curve with (’GW + GRB lc + motion’) or without (’GW + GRB lc’) constraints on from the jet superluminal motion; and the KN broad-band photometry (’GW + KN photometry’) and spectroscopy (’GW + KN spectroscopy’). The column shows the percentage improvement in the () interval. values derived from CMB and are shown for comparison.
4. Inclination Constraints from the Gamma-Ray Burst
4.1. Afterglow
The association between short GRBs and NS mergers, originally put forward in the late 1980’s [63,64,65,66], led to the conjecture that a relativistic jet could be launched from the compact object formed after the merger of BNS and BH-NS binaries. In this scenario, the interaction between the relativistic jet and the surrounding circum-merger environment is believed to produce a long-lasting non-thermal emission, the so-called “afterglow”, powered by synchrotron radiation from electrons accelerated within the shocked medium and shining from X-ray to radio wavelengths. This paradigm was spectacularly confirmed by the detection of the short GRB 170817A [48,49,50] and its afterglow [67,68,69,70,71] in association with the GW-detected BNS merger GW170817. For more details about the theory and observations of short GRBs and their afterglow, we refer the reader to the multiple reviews in the literature, e.g., [72,73,74,75,76,77]. Here, we focus on the viewing-angle dependence of the afterglow signal.
Radiation from a relativistic jet moving at a velocity is beamed into a narrow cone with a half-opening angle , where is the Lorentz factor. In particular, radiation propagating from the edge of the jet is beamed into a cone around the jet half-opening angle . An “on-axis” observer within this narrow cone () would detect the beamed radiation, whereas an “off-axis” observer outside the cone () would be blind to it. As the jet decelerates with time due to the interaction with the circum-merger environment, the cone widens and the afterglow emission becomes detectable at larger and larger inclinations. As a consequence, the afterglow light curve for an off-axis observer is predicted to rise continuously until the jet decelerates enough to include the observer. The gradual rise in the light curve reaches a peak at a Lorentz factor ) and then start declining. Provided that the jet dominates the afterglow emission and that its opening angle is much smaller than the observer angle, , analytic relations [78,79] calibrated using hydrodynamical simulations [80] show that the time and flux of the light curve peak can be expressed as and , where is the power-law index of the electrons distribution4. That is, the viewing-angle dependence is such that an off-axis afterglow peaks later and at a lower luminosity the farther away the observer is from the jet axis.
The non-thermal emission in GW170817 was consistent with an afterglow observed at a moderate angle away from the jet axis. X-ray and radio light curves displayed a gradual rise starting from the first detection at 9 [71] and 16 [69] days, respectively, until they reached a peak at around ∼150 days. The peak was later followed by a steep decline in both X-ray and radio bands. A similar behaviour was seen in the optical, although the first detection had to wait ∼110 days [81] for the afterglow light to start dominating over the fading KN emission. Constraints on the viewing angle of GW170817 were inferred by different studies via the model fitting of the afterglow emission both pre- and post-peak, e.g., [11,13,82,83,84,85,86,87]. The values derived span a relatively wide range of angles, , with typical errors that are small enough to make some of these estimates incompatible with each other. This discrepancy is due in part to the different models used but also to the existing degeneracy between and (see below). Tighter constraints were extracted from fitting the light curves using additional information from the very long baseline interferometer (VLBI); see Section 4.2.
Notwithstanding the uncertainties in the light curve modelling, two studies in the literature [11,13] used the inferred constraints on the viewing angle to reduce the distance–inclination degeneracy in the standard siren approach and therefore improve on . Guidorzi et al. [11] modelled the first ∼40 days of X-ray and radio data of GW170817 for two different choices of the jet opening angle, and , and for varying viewing angles, jet parameters and densities of the circum-burst material. A uniform top-hat jet model was assumed [88,89]. The inferred viewing-angle distribution spanned a relatively wide range of , with a slight preference for a jet opening angle of . When adding this inclination constraint as a prior to the Hubble constant determination, MAP values of and km s Mpc were found for and , respectively. The mild () improvement on derived with the wider opening angle is shown with light-green curves in Figure 2. A similar analysis was later carried out by Wang and Giannios [13], who modelled the radio data of GW170817 up to days with a realistic jet structure derived from general-relativistic magnetohydrodynamical simulations. The modelling of this extended dataset covering the light curve peak led to a significant improvement on the inclination constraint compared to Guidorzi et al. [11], with an inferred value of . We note that this precise value for may be partly due to the specific model adopted displaying a rather strong viewing-angle dependence. The Hubble constant was constrained to km s Mpc, with the uncertainties reduced by more than a factor of two compared to those from the GW-only analysis. The constraints from Wang and Giannios [13] are shown in red in Figure 2.
The uncertainties in the modelling of the GRB afterglow light curves can potentially bias the inclination estimates and introduce systematics in the measurement. In particular, different studies [87,90,91,92,93,94] have highlighted a clear degeneracy between the observer viewing angle and the jet structure adopted. For instance, Ryan et al. [87] and Takahashi and Yota [90] showed that, for both a Gaussian and a power-law jet, the ratio is much better constrained than any of the two angles individually. This was further generalized by Nakar and Piran [92], who demonstrated that this is a fundamental degeneracy general to all of the jet structures. Furthermore, they provided a simple analytical formula to extract the ratio from the shape of the light curve peak (see their Equation (3)). The value required to fit the peak of GW170817 was found to be in good agreement with the ratio derived from the aforementioned studies fitting for the two angles individually. Moreover, Lamb et al. [93] showed that the inclusion/omission of a lateral spreading of the blastwave can shift by up to a factor of 2. All of these studies caution against using viewing-angle constraints from the light curve fitting alone, unless systematic uncertainties are properly modelled and taken into account. Alternatively, more accurate constraints on the viewing angle can be achieved if additional information is used to break the degeneracy between and the jet structure. One promising avenue for the latter is offered by the jet proper motion from VLBI radio images, as will be discussed in the next section.
4.2. Superluminal Motion
A relativistic jet moving at a velocity close to the speed of light, , and seen from a small angle can appear to move on the plane of the sky with a superluminal velocity, [97,98]. This apparent superluminal motion is caused by the jet “chasing” the emitted radiation along the line-of-sight to the observer with a relativistic velocity . As a consequence, the difference in path travelled by two signals emitted with a time interval is reduced from to . Equivalently, the two signals are detected by the off-axis observer with a reduced time separation of . The apparent velocity in the plane of the sky is therefore equal to the side-way distance travelled by the jet, , divided by , i.e.,
For sufficiently small angles and large velocities, can become larger than the speed of light; hence, the motion appears superluminal. The apparent velocity reaches a maximum when , that is, for and at an angle . Therefore, a measurement of around the time of peak offers a way to constrain and the angle , which, at this time, is equal to (see Section 4.1).
A superluminal motion of the jet was observed in the aftermath of GW170817 using radio observations with the VLBI. Mooley et al. [95] found a shift of mas in the centroid of the radio image from 75 to 230 days. These measurements were confirmed by Ghirlanda et al. [96] with additional VLBI observations at 203 days, finding a displacement of mas compared to the position at 75 days. The apparent velocity was estimated to be c, which then constrained and rad [95]. When combined with the radio light curves of GW170817, this constraint greatly reduces the degeneracy between and discussed in Section 4.1 [92] and leads to more precise measurements of both angles when the afterglow light curves are fitted. Specifically, Mooley et al. [95] found that only afterglow models with a jet opening angle and viewed from orientations are consistent with both the superluminal motion and radio light curves. The simulation providing the best fit to the data corresponds to and . Ghirlanda et al. [96] found similar values for these two angles, namely and .
The radio measurements presented in the study by Mooley et al. [95] were used by Hotokezaka et al. [12] to constrain the value derived from GW170817 [10]. While the luminosity distance was fixed to Mpc in the previous work, this was taken as a free parameter in both the superluminal motion analysis () and the light curve fitting. The viewing angle was constrained to or depending on whether a power-law or a Gaussian jet model was used. The tight constraints on the viewing angle led to large improvements on the Hubble constant measurement, with the median and 68% credible intervals improved from the GW-only analysis as km s Mpc to () km s Mpc assuming a power-law (Gaussian) jet model. The constraints derived with the power-law jet model are shown with cyan curves in Figure 2. This is a significant () improvement and corresponds to a precision on , which is, however, insufficient to arbitrate the Hubble constant tension. Hotokezaka et al. [12] suggest that ∼ 15 more GW170817-like events with VLBI and light curve data will be enough to reach a precision and potentially resolve the tension, in contrast to the events required without radio data. However, Mastrogiovanni et al. [99] carried out a detailed forecast study and argued that afterglow data (photometry + imaging) will be rare in future GW runs and may therefore not significantly contribute to narrowing down in the long run (see also [13]).
5. Inclination Constraints from the Kilonova
5.1. Matter Outflows as Kilonova Engines
The neutron-rich outflow that is ejected during and after NS mergers is the environment from which the KN emission originates. The radioactive decay of newly synthesized heavy elements from “rapid neutron capture” or the “r-process” powers a thermal emission known as KN that is commonly described as a rather isotropic component potentially visible from all orientations [100,101]. The exact properties of the ejecta, e.g., their mass, velocity, geometry and composition, depend on binary properties such as the total mass, mass ratio, spin and internal structure of the NSs. Knowledge about the ejecta properties are key to properly modelling KN observables and, to date, these are best revealed by numerical-relativity simulations [102,103,104,105,106,107,108].
Although potentially visible from all orientations, the KN emission is expected to be viewing-angle-dependent due to the anisotropic ejection of matter in NS mergers. In general, one can distinguish different types of ejecta. The first class are dynamical ejecta arising from the tidal stripping of the NS(s) (tidal ejecta) and from the NS contact interface, as well as core bounces (shock-driven ejecta). Tidal ejecta are distributed around the orbital plane and retain the high neutronization of the parent NS(s), i.e., they are generally characterized by a low-electron fraction , where and are the proton and neutron densities, respectively. In contrast, shock-driven ejecta are dominantly located in the polar regions and have an increased [103,105]. The other main ejecta class are post-merger ejecta (also referred to as disk-wind or secular ejecta), e.g., [109,110,111]. In general, post-merger ejecta are produced through remnant accretion disk winds driven by neutrino emission, magnetic fields, viscous evolution and/or nuclear recombination energy, e.g., [112,113,114]. Long-term hydrodynamics simulations reveal that about ∼10–40% of the debris disk mass can get ejected, e.g., [110,115]. The properties of the post-merger ejecta depend noticeably on the central engine: while a central magnetar will lead to ejecta with a high , e.g., [116,117], the will be small if the central object is a BH formed quickly after the merger. However, in both cases, the outflow is roughly spherically symmetric. In contrast, viscous effects after the merger could lead to an angular momentum transport and mass ejection centered around the orbital plane. If this happens, spiral wind outflows form and shocks in the contact region of the spiral arms can lead to an increased electron fraction of [118].
The range of values predicted in NS mergers leads to distinct nucleosynthesis yields across the different ejecta components. Regions of the ejecta characterized by an electron fraction value , e.g., tidal ejecta, experience a more complete —process nucleosynthesis that can reproduce the third peak observed in the solar abundances around atomic mass number [119,120]. These heavy elements include the so-called “lanthanides” () and “actinides” (); hence, these ejecta components are typically referred to as “lanthanide-rich” in the literature. Regions of the ejecta with higher values for the electron fraction, , such as shock-driven and post-merger ejecta, have a small-enough ratio of free neutrons to seed nuclei that prevents the r-process nucelosynthesis to proceed beyond . These relatively high values can therefore reproduce the first and second solar peak but not heavier elements, such as the lanthanides; hence, the corresponding ejecta component are typically referred to as “lanthanide-free”.
The different compositions found in the ejecta of NS mergers have profound implications in terms of the opacity of matter to radiation. While opacities of —process elements are in general orders of magnitude higher than those of iron typically found in SNe [121,122], a clear difference is seen between “lanthanide-rich” and “lanthanide-free” compositions. In the former, the multitude of line transitions from heavy elements at near-ultraviolet (UV)/optical wavelengths reprocess radiation to the infrared (IR), thus producing a so-called “red” KN [123]. In the latter, instead, the lower opacities lead to more flux escaping at shorter wavelengths, thus giving rise to a so-called “blue” KN [124]. As we will describe in the next sections, the coexistence of multiple components within NS merger outflows with different compositions/opacities and different geometries lead to a clear viewing-angle imprint on KN observables such as light curves, spectra and polarization.
5.2. Constraints from Kilonova Spectro-Photometry
The KN emission in NS mergers is generally thought of as a relatively isotropic component compared to the beamed GRB and its associated afterglow. As discussed in Section 5.1, however, the neutron-rich outflows ejected in these mergers comprise different components with a variety of compositions and geometry. The KN emission is therefore intrinsically anisotropic and characterized by a clear viewing-angle dependence. The viewing angle of the KN signal has been characterized in several studies using either analytic function parametrizing the viewing-angle dependence [125,126] or with detailed multi-dimensional radiative transfer simulations incorporating reprocessing effects [127,128,129,130,131,132]. The broad distinction between lanthanide-free outflows close to the jet axis and lanthanide-rich outflows around the orbital plane makes KNe increasingly fainter when moving from the jet axis (face-on view) to the orbital plane (edge-on view), an effect that can be amplified by the presence of a jet [94,133]. The viewing-angle dependence of the signal varies with wavelength and time, and is controlled by the detailed properties of the ejecta, but can be as strong as ∼5 mag in optical bands ∼1 day after the merger, e.g., [17,130,131,132]. A strong viewing-angle dependence of the signal is predicted also in terms of colors, with KNe observed at an inclination closer to the jet axis being, in general, bluer than those observed closer to the orbital plane, e.g., [131].
The viewing-angle dependence of the KN signal has been used to place constraints on the inclination of GW170817 and therefore improve on the measurement from the GW standard-siren approach [10]. This was first carried out by Dhawan et al. [14], where a two-component KN grid from Bulla et al. [129] was fitted to the available near-UV/optical/IR light curves of AT 2017gfo to extract a 1D probability distribution for the viewing angle . The result of this analysis is summarized with pink curves in Figure 2. The distribution for the viewing angle was found to peak at around () and was used as a prior for the inclination in the GW analysis. The combination of GW data and the constraint on led to km s Mpc, which is a improvement in terms of uncertainties compared to those in the study by Abbot et al. [10]. Early-time photometry was found to be crucial to pinpoint the viewing angle and reduce the uncertainties on , with the improvement reducing drastically when removing photometric data earlier than ∼2 days.
A different approach to improve on was used by Coughlin et al. [15] and applied to a sample of five KNe: the KN associated with GW170817, as in Dhawan et al. [14], together with four KNe, suggested [134] to be observed in connection with the short gamma-ray bursts GRB 150101B27 [135], GRB 05070928 [136], GRB 160821B29 [137] and GRB 060614 [138]. This effort applied KN “standardization” [139], where correlations between the light curve flux and color evolution, which do not depend on the overall luminosity of the transient, are compared to models. These correlations are used to directly obtain the distance modulus of each event, resulting in measurements of km and if models from the studies by Bulla et al. [129] or Kasen et al. [140] are chosen, respectively.
While these first studies [14,15] derived constraints on using broad-band photometric data of GW170817, a recent work highlighted the key role of spectroscopy to reduce the uncertainties on even further [17]. This study was carried out in the context of MAAT (Mirror-slicer Array for Astronomical Transients), an integral field unit (IFU) to be mounted on the OSIRIS spectrograph of the 10.4 m Gran Telescopio CANARIAS (GTC) and planned to become operational from 2023 [141]. Using the Very Large Telescope (VLT) X-shooter spectra of AT 2017gfo [142,143], as seen by MAAT, Pérez-García et al. [17] found that fitting a BNS KN grid [16] to the entire Å spectral range brings a clear improvement to the viewing-angle constraint of GW170817 compared to the one from broad-band photometry (see orange line in Figure 2, right panel). The inferred MAP value of is a % improvement from Abbott et al. [10], which is significantly higher than the 34% from near-UV/optical/near-IR photometry [14] and the 5% when restricting to broad-band photometry in the same Å range observed by MAAT [17]. This study highlights how critical early-time spectroscopy of KN candidates is to improve at a significant level from single sources.
Similarly to the case of GRB modelling (see Section 4.1), the modelling of KNe can potentially introduce systematic uncertainties on the inclination angle and bias the value inferred [144]. Our understanding on the physical processes controlling the KN emission is still incomplete and various source of uncertainties are expected to impact the predicted KN emission, including but not limited to the role of the ejecta geometry [145] and —process heating rates [146], thermalization efficiencies [147] and opacities [148,149]. For instance, Heinzel et al. [145] found that the assumption about the ejecta geometry [128,129,140] has a strong impact on the inclination angle, advocating for the inclusion of large systematic uncertainties (∼1 mag) when inferring the viewing angle from fits to the KN light curves. Although values are currently limited by statistical uncertainties, the combination of GW and KNe is expected to deliver accurate (and not just precise) measurements only when model systematics can be understood and controlled. Until then, these analyses should include large systematic uncertainties on the KN light curves and/or be carried out using multiple KN models, e.g., [15,16].
5.3. Constraints from Kilonova Polarimetry
As is the case for SNe [150], the KN emission can be linearly polarized by Thomson scattering on free electrons that can be copious at early times when the ejected material is very hot and highly ionized. The polarization level is effectively determined by the properties and geometry of the ejected material. The ejecta properties—such as density, temperature and composition—determine the opacities of the ejecta and therefore how important electron scattering is compared to other processes such as bound–bound, bound–free and free–free interactions that are expected to depolarize the radiation [151,152,153]. The ejecta geometry, instead, controls how polarizing contributions from different regions of the ejecta combine to determine the final polarization level5: a complete cancellation of all of the contributions and therefore null polarization is predicted for spherically symmetric ejecta, whereas an incomplete cancellation and thus a net polarization is found for asymmetric ejecta. Asymmetric ejecta look different, as seen in projections from different observer orientations, and the polarization signal can therefore be viewing-angle-dependent. This suggests KN polarimetry as a potential probe for the inclination of the merging system.
At the relevant wavelengths (near-UV, optical, IR) and times (≳1 d) for KN emission, the dominant sources of opacity in NS mergers are bound–bound transitions from —process elements and Thomson scattering [121,122,154]. The interplay between these two processes—the former depolarising and the latter polarising the radiation—is therefore key to determining the final polarization state of photons escaping the system. In particular, the ratio between Thomson scattering and bound–bound line opacity, , is a sensitive function of wavelength and time [154]. The electron scattering opacity is wavelength-independent and equal to , where cm is the Thomson cross section and and the electron and mass density, respectively. In contrast, the bound–bound line opacity from r-process elements shows a strong dependence on the wavelength and rapidly decreases from near-UV/optical to IR wavelengths [148]. As a result, the ratio and therefore polarization state of escaping photons tend to increase, moving to longer wavelengths. Moreover, the time-dependence of the ratio is extremely rapid. As a result of the rapid expansion and cooling of the ejecta, atoms start recombining and the number of free electrons drops. This leads to a rapid increase in the bound–bound opacity and modest decrease in electron scattering opacity, i.e., rapidly decreases with time.
The exact values of and and therefore their relative contribution is determined by the local properties of the material ejected in NS mergers. In this respect, a key property controlling the r-process nucleosynthesis and thus the corresponding matter opacity is the electron fraction . As described in Section 5.1, at least two ejecta components with different compositions are predicted in BNS mergers: a “lanthanide-rich” ejecta component distributed around the orbital plane and characterized by high opacities from heavy r-process elements such as lanthanides and actinides; and a “lanthanide-free” ejecta component at higher latitudes and characterized by lower opacities from lighter r-process elements. As shown in the study by Bulla et al. [154], in the lanthanide-rich component from ∼1.5 d onward and at wavelengths up to ∼1.5 m. In contrast, in the lanthanide-free component at optical and IR wavelengths for the first ∼2–3 days after the merger. As a result, radiation escaping from equatorial regions of the ejecta is typically unpolarized (except at mid-IR wavelengths and very early times), whereas radiation escaping from higher latitudes is polarized at optical and IR wavelengths. This effect is illustrated schematically in the left panel of Figure 3.
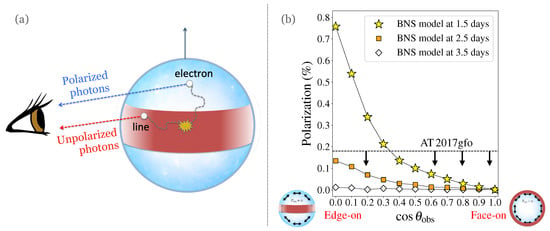
Figure 3.
Polarized light from KNe. (a) Sketch illustrating the origin of polarization in KNe. Photons escaping from lanthanide-rich dynamical ejecta around the equatorial plane (in red) are preferentially depolarized by bound–bound line interactions; photons escaping from a lanthanide-free wind (in blue) can be linearly polarized by Thomson scattering. Figure adapted with permission from [155]. Copyright 2018 Bulla. (b) Polarization predictions from [154] for a two-component BNS model. Polarization levels are shown at 7000 Å as a function of viewing angle for three different epochs: 1.5 (yellow stars), 2.5 (orange squares) and 3.5 (white diamonds) days from the merger. The —band polarization upper limit derived for AT 2017gfo at 1.5 days is shown with a horizontal dashed line and is consistent with an observer viewing the system from an angle within from the jet axis ().
In BNS mergers, the combination of unpolarized light from equatorial regions and polarized light from polar regions leads to an imperfect cancellation of the different polarizing contributions and thus to a net polarization signal for most viewing angles. As illustrated in Figure 3, this effect is stronger when the system is viewed edge-on (i.e., 90° away from the jet axis; see “Edge-on” inset in the right panel) and decreases when moving towards the jet axis, at which point, the ejecta become symmetric in projection and all of the polarising contributions cancel each other (see ’Face-on’ inset in the right panel). Bulla et al. [154] predict a maximum polarization level of ∼0.8% in the optical (7000 Å) 1.5 days after the BNS merger, rapidly dropping to zero within ∼1–2 days (right panel of Figure 3). These predictions can be compared to polarimetric observations taken for AT 2017gfo with the VLT FORS2 instrument [156]. The —band polarization of AT 2017gfo at 1.5 days was consistent with being caused (at least in part) by interstellar dust in our own galaxy, and an upper limit of was placed by Bulla et al. [154] after the careful removal of the interstellar contribution. Comparing these upper limits with the polarization predictions at 1.5 days (Figure 3), the viewing angle of the system is constrained to be relative to the jet axis ().
The relatively small polarization levels expected in KNe accompanying BNS mergers and their rapid decrease with time make polarization detection quite challenging. The upper limit on polarization derived for AT 2017gfo translates into a poor constraint on the viewing angle; hence, no attempt to improve the measurements was carried out by [154]. A polarization detection in future KNe may lead to a stronger constraint on the inclination angle and, therefore, on . KNe accompanying BH-NS mergers might be better targets in this respect since the ejecta distribution is more strongly asymmetric compared to the BNS case. Indeed, Bulla et al. [157] found that polarization levels of up to 6% may be achieved in these system for favorable viewing angles and when observing at near-IR wavelengths (≳m). The required polarimetric accuracy at these long wavelengths (J, H and K bands) can be achieved for KNe at the distance of 150–200 Mpc with the instruments currently available.
Although KN polarimetry has the potential to constrain the source inclination in the future, a better exploration of the model systematics is required. In particular, the non-trivial dependence of the polarization signals on, e.g., the ejecta geometry and densities (i.e., masses), can bias the inferred inclination angle if the full parameter space is not sampled properly. While Bulla et al. [154,157] focused on polarization predictions for individual models, follow-up studies should explore the range of polarization signals expected for a large grid of models varying parameters such as the geometry and masses, in a similar fashion to what was carried out in terms of light curves by, e.g., Dietrich et al. [16] and Anand et al. [158].
6. Summary and Outlook
The use of GWs as standard sirens [5,6] holds promise to arbitrate the existing tension between early- [2] and late- [3] Universe probes of the Hubble constant . Without additional information, however, this is unlikely to happen in the near future, since ∼50–200 GW events [36,44] with an EM counterpart are needed to reach a precision of ∼1% on . This goal might be achieved earlier and with fewer events if a constraint on the system inclination can be obtained from the GRB and/or the KN accompanying NS mergers detected with GWs. Indeed, a few proof-of-concept studies have shown that a constraint on the viewing angle of GW170817 from the GRB afterglow [11,13], the GRB superluminal motion [12] and the KN [14,15] can greatly reduce the degeneracy between the distance and inclination in the GW data and therefore the uncertainties on . Improved constraints leading to ∼6%-level uncertainties on for GW170817 can be reached when information from the different EM probes are combined together in a truly multi-messenger analysis, as shown in the study by Dietrich et al. [16].
Nevertheless, a few questions remain. While the required precision on might be achieved in the future as more NS mergers are detected in both gravitational and electromagnetic waves, the accuracy of the inferred value will depend crucially on whether the systematics from the standard siren approach are under control, as well as those from the GRB/KN modelling. First, the standard siren approach can be affected by systematic uncertainties both from the GW and the EM analysis. On the GW side, calibration errors potentially affecting the inferred and hence are subdominant compared to statistical uncertainties on single events, e.g., [159,160,161], and even when combining multiple (≳100) sources in the most realistic case studied by Huang et al. [162]. On the EM side, possible sources of systematic uncertainties come from estimates of peculiar velocities in nearby events [57,58,59] and viewing-angle selection effects biasing the discovery of EM counterparts towards systems viewed close to face-on [163]. Secondly, additional source of systematics are introduced by the uncertainties on models used to fit GRB [87,90,91,92,93,94] and KN [144,145,146,147] observables to constrain the inclination. In a recent study, Chen et al. [163] showed that the viewing-angle effects are likely to dominate the systematics budget and be a major challenge to resolve the tension with GWs and light from NS mergers. Specifically, a ∼2% bias on can be introduced by viewing-angle selection effects and a ∼3% bias if the inclination constraints from EM probes are not controlled under ∼.
Looking ahead, the detection of more NS mergers in both GW and light will be essential for enabling a thorough understanding of the source of systematic uncertainties and, thus, for the standard siren approach to show its full potential. In the next decade, the number of GW detectors and their sensitivities is expected to increase [164], and this will be accompanied by the advent of new optical sky surveys, such as the VRO/LSST [165]. This combined network will facilitate multi-messenger detections of NS mergers beyond GW170817 and potentially lead to both precise and accurate values of the Hubble constant.
Author Contributions
Conceptualization, M.B., M.W.C., S.D., T.D.; methodology, M.B., M.W.C., S.D., T.D.; software, M.B., M.W.C., S.D., T.D.; validation, M.B., M.W.C., S.D., T.D.; formal analysis, M.B., M.W.C., S.D., T.D.; investigation, M.B., M.W.C., S.D., T.D.; resources, M.B., M.W.C., S.D., T.D.; data curation, M.B., M.W.C., S.D., T.D.; writing—original draft preparation, M.B., M.W.C., S.D., T.D.; writing—review and editing, M.B., M.W.C., S.D., T.D.; visualization, M.B., S.D.; supervision, M.B., M.W.C., S.D., T.D.; project administration, M.B., M.W.C., S.D., T.D.; funding acquisition, M.B., M.W.C., S.D., T.D. All authors have read and agreed to the published version of the manuscript.
Funding
M.B. acknowledges support from the Swedish Research Council (Reg. no. 2020-03330). M.W.C. acknowledges support from the National Science Foundation with grant numbers PHY-2010970 and OAC-2117997. S.D. acknowledges support from the Marie Curie Individual Fellowship under grant ID 890695 and a junior research fellowship at Lucy Cavendish College. T.D. acknowledges financial support through the Max Planck Society.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
This research has made use of data, software and/or web tools obtained from the Gravitational Wave Open Science Center (https://www.gw-openscience.org, aeecssed on 3 May 2022), a service of LIGO Laboratory, the LIGO Scientific Collaboration and the Virgo Collaboration. This material is based upon work supported by NSF’s LIGO Laboratory which is a major facility fully funded by the National Science Foundation. Virgo is funded by the French Centre National de Recherche Scientifique (CNRS), the Italian Istituto Nazionale della Fisica Nucleare (INFN) and the Dutch Nikhef, with contributions by Polish and Hungarian institutes.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACT | Atacama Cosmology Telescope |
| BAO | Baryon Acoustic Oscillations |
| BBH | Binary Black Hole |
| BH | Black Hole |
| BNS | Binary Neutron Star |
| CMB | Cosmic Microwave Background |
| GRB | Gamma-ray burst |
| GTC | Gran Telescopio CANARIAS |
| GW | Gravitational Wave |
| IFU | Integral Field Unit |
| IGWN | International Gravitational-Wave Observatory Network |
| IR | Infrared |
| KN | Kilonova |
| CDM | Cold Dark Matter |
| LIGO | Laser Interferometer Gravitational-wave Observatory |
| LSST | Legacy Survey of Space and Time |
| MAAT | Mirror-slicer Array for Astronomical Transients |
| MAP | Maximum a posteriori |
| NS | Neutron Star |
| SNe | Supernovae |
| TRGB | Tip of the red giant branch |
| UV | Ultraviolet |
| VLBI | Very Long Baseline Interferometer |
| VLT | Very Large Telescope |
| VRO | Vera Rubin Observatory |
| WMAP | Wilkinson Microwave Anisotropy Probe |
Notes
| 1 | As admitted by the authors, the term was coined by Sterl Phinney and Sean Carroll |
| 2 | We note that another relatively large contributor to the error budget is given by uncertainties on peculiar velocities [57,58,59], which, however, are expected to be negligible at the large distances at which NS mergers will be detected in the future [8,60]. |
| 3 | Note that the viewing angle is measured from the jet axis whereas the inclination i is measured from the axis orthogonal to the binary’s orbital plane. Therefore, this relation between and i assumes that the jet axis is orthogonal to the orbital plane. |
| 4 | These relations are valid for frequencies (where is the self-absorption frequency, is the synchrotron break frequency and is the cooling break frequency), a condition that is satisfied from X-ray to radio wavelengths as long as the density of the circum-merger environment is not much higher than the one inferred for GW170817. |
| 5 | The polarization signal of extragalactic events as supernovae and KNe is the result of integrating over all the contributions coming from different regions of the ejecta. |
References
- Hubble, E. A relation between distance and radial velocity among extra-galactic nebulae. Proc. Nat. Acad. Sci. USA 1929, 15, 168–173. [Google Scholar] [CrossRef] [PubMed]
- Planck Collaboration. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Breuval, L.; Brink, T.G.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team. arXiv 2021, arXiv:2112.04510. [Google Scholar]
- Verde, L.; Treu, T.; Riess, A.G. Tensions between the Early and the Late Universe. Nat. Astron. 2019, 3, 891. [Google Scholar] [CrossRef]
- Schutz, B.F. Determining the Hubble Constant from Gravitational Wave Observations. Nature 1986, 323, 310–311. [Google Scholar] [CrossRef]
- Holz, D.E.; Hughes, S.A. Using gravitational-wave standard sirens. Astrophys. J. 2005, 629, 15–22. [Google Scholar] [CrossRef]
- Abbott, B.P.; Bloemen, S.; Canizares, P.; Falcke, H.; Fender, R.P.; Ghosh, S.; Groot, P.; Hinderer, T.; Hörandel, J.R.; Jonker, P.G. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Advanced LIGO. Class. Quant. Grav. 2015, 32, 074001. [Google Scholar] [CrossRef]
- Acernese, F.; Agathos, M.; Agatsuma, K.; Aisa, D.; Allemandou, N.; Allocca, A.; Amarni, J.; Astone, P.; Balestri, G.; Ballardin, G.; et al. Advanced Virgo: A second-generation interferometric gravitational wave detector. Class. Quant. Grav. 2015, 32, 024001. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85–88. [Google Scholar] [CrossRef]
- Guidorzi, C.; Margutti, R.; Brout, D.; Scolnic, D.; Fong, W.; Alexander, K.D.; Cowperthwaite, P.S.; Annis, J.; Berger, E.; Blanchard, P.K.; et al. Improved Constraints on H0 from a Combined Analysis of Gravitational-wave and Electromagnetic Emission from GW170817. Astrophys. J. Lett. 2017, 851, L36. [Google Scholar] [CrossRef]
- Hotokezaka, K.; Nakar, E.; Gottlieb, O.; Nissanke, S.; Masuda, K.; Hallinan, G.; Mooley, K.P.; Deller, A.T. A Hubble constant measurement from superluminal motion of the jet in GW170817. Nat. Astron. 2019, 3, 940–944. [Google Scholar] [CrossRef]
- Wang, H.; Giannios, D. Multimessenger parameter estimation of GW170817: From jet structure to the Hubble constant. Astrophys. J. 2021, 908, 200. [Google Scholar] [CrossRef]
- Dhawan, S.; Bulla, M.; Goobar, A.; Carracedo, A.S.; Setzer, C.N. Constraining the observer angle of the kilonova AT2017gfo associated with GW170817: Implications for the Hubble constant. Astrophys. J. 2019, 888, 67. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Antier, S.; Dietrich, T.; Foley, R.J.; Heinzel, J.; Bulla, M.; Christensen, N.; Coulter, D.A.; Issa, L.; Khetan, N. Measuring the Hubble Constant with a sample of kilonovae. Nat. Commun. 2020, 11, 4129. [Google Scholar] [CrossRef] [PubMed]
- Dietrich, T.; Coughlin, M.W.; Pang, P.T.H.; Bulla, M.; Heinzel, J.; Issa, L.; Tews, I.; Antier, S. Multimessenger constraints on the neutron-star equation of state and the Hubble constant. Science 2020, 370, 1450–1453. [Google Scholar] [CrossRef]
- Pérez-García, M.A.; Izzo, L.; Barba, D.; Bulla, M.; Sagués-Carracedo, A.; Pérez, E.; Albertus, C.; Dhawan, S.; Prada, F.; Agnello, A.; et al. Hubble constant and nuclear equation of state from kilonova spectro-photometric light curves. arXiv 2022, arXiv:2204.00022. [Google Scholar]
- Macaulay, E.; Nichol, R.C.; Bacon, D.; Brout, D.; Davis, T.M.; Zhang, B.; Bassett, B.A.; Scolnic, D.; Möller, A.; D’Andrea, C.B.; et al. First cosmological results using Type Ia supernovae from the Dark Energy Survey: Measurement of the Hubble constant. Mon. Not. R. Astron. Soc. 2019, 486, 2184–2196. [Google Scholar] [CrossRef]
- Knox, L.; Millea, M. Hubble constant hunter’s guide. Phys. Rev. D 2020, 101, 043533. [Google Scholar] [CrossRef]
- Shah, P.; Lemos, P.; Lahav, O. A buyer’s guide to the Hubble constant. Astron. Astrophys. Rev. 2021, 29, 9. [Google Scholar] [CrossRef]
- Aiola, S.; Calabrese, E.; Maurin, L.; Naess, S.; Schmitt, B.L.; Abitbol, M.H.; Addison, G.E.; Ade, P.A.R.; Alonso, D.; Amiri, M.; et al. The Atacama Cosmology Telescope: DR4 maps and cosmological parameters. J. Cosmol. Astropart. Phys. 2020, 2020, 047. [Google Scholar] [CrossRef]
- Addison, G.E.; Watts, D.J.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Weiland, J.L. Elucidating ΛCDM: Impact of Baryon Acoustic Oscillation Measurements on the Hubble Constant Discrepancy. Astrophys. J. 2018, 853, 119. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Abdalla, F.B.; Annis, J.; Bechtol, K.; Blazek, J.; Benson, B.A.; Bernstein, R.A.; Bernstein, G.M.; Bertin, E.; Brooks, D.; et al. Dark Energy Survey Year 1 Results: A Precise H0 Estimate from DES Y1, BAO, and D/H Data. Mon. Not. R. Astron. Soc. 2018, 480, 3879–3888. [Google Scholar] [CrossRef]
- Freedman, W.L. Measurements of the Hubble Constant: Tensions in Perspective. Astrophys. J. 2021, 919, 16. [Google Scholar] [CrossRef]
- Vogl, C. Cosmological distances of Type II supernovae from radiative transfer modeling. Ph.D. Thesis, Munich University of Technology, Munich, Germany, 2020. [Google Scholar]
- Pesce, D.W.; Braatz, J.A.; Reid, M.J.; Riess, A.G.; Scolnic, D.; Condon, J.J.; Gao, F.; Henkel, C.; Impellizzeri, C.M.V.; Kuo, C.Y.; et al. The Megamaser Cosmology Project. XIII. Combined Hubble Constant Constraints. Astrophys. J. Lett. 2020, 891, L1. [Google Scholar] [CrossRef]
- Wong, K.C.; Suyu, S.H.; Chen, G.C.F.; Rusu, C.E.; Millon, M.; Sluse, D.; Bonvin, V.; Fassnacht, C.D.; Taubenberger, S.; Auger, M.W.; et al. H0LiCOW—XIII. A 2.4 per cent measurement of H0 from lensed quasars: 5.3σ tension between early- and late-Universe probes. Mon. Not. R. Astron. 2020, 498, 1420–1439. [Google Scholar] [CrossRef]
- Birrer, S.; Shajib, A.J.; Galan, A.; Millon, M.; Treu, T.; Agnello, A.; Auger, M.; Chen, G.C.F.; Christensen, L.; Collett, T.; et al. TDCOSMO. IV. Hierarchical time-delay cosmography—joint inference of the Hubble constant and galaxy density profiles. Astron. Astrophys. 2020, 643, A165. [Google Scholar] [CrossRef]
- Birrer, S.; Dhawan, S.; Shajib, A.J. The Hubble Constant from Strongly Lensed Supernovae with Standardizable Magnifications. Astrophys. J. 2022, 924, 2. [Google Scholar] [CrossRef]
- Einstein, A. Über Gravitationswellen. Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys.) 1918, 1918, 154–167. [Google Scholar]
- MacLeod, C.L.; Hogan, C.J. Precision of Hubble constant derived using black hole binary absolute distances and statistical redshift information. Phys. Rev. D 2008, 77, 043512. [Google Scholar] [CrossRef]
- Del Pozzo, W. Inference of the cosmological parameters from gravitational waves: Application to second generation interferometers. Phys. Rev. D 2012, 86, 043011. [Google Scholar] [CrossRef]
- Messenger, C.; Read, J. Measuring a cosmological distance-redshift relationship using only gravitational wave observations of binary neutron star coalescences. Phys. Rev. Lett. 2012, 108, 091101. [Google Scholar] [CrossRef] [PubMed]
- Petiteau, A.; Babak, S.; Sesana, A. Constraining the dark energy equation of state using LISA observations of spinning Massive Black Hole binaries. Astrophys. J. 2011, 732, 82. [Google Scholar] [CrossRef]
- Oguri, M. Measuring the distance-redshift relation with the cross-correlation of gravitational wave standard sirens and galaxies. Phys. Rev. D 2016, 93, 083511. [Google Scholar] [CrossRef]
- Chen, H.Y.; Fishbach, M.; Holz, D.E. A two per cent Hubble constant measurement from standard sirens within five years. Nature 2018, 562, 545–547. [Google Scholar] [CrossRef]
- Fishbach, M.; Gray, R.; Hernandez, I.M.; Qi, H.; Sur, A.; Acernese, F.; Aiello, L.; Allocca, A.; Aloy, M.A.; Amato, A.; et al. A Standard Siren Measurement of the Hubble Constant from GW170817 without the Electromagnetic Counterpart. Astrophys. J. Lett. 2019, 871, L13. [Google Scholar] [CrossRef]
- Gray, R.; Hernandez, I.M.; Qi, H.; Sur, A.; Brady, P.R.; Chen, H.Y.; Farr, W.M.; Fishbach, M.; Gair, J.R.; Ghosh, A.; et al. Cosmological inference using gravitational wave standard sirens: A mock data analysis. Phys. Rev. D 2020, 101, 122001. [Google Scholar] [CrossRef]
- Chatterjee, D.; Holder, G.; Holz, D.E.; Perkins, S.; Yagi, K.; Yunes, N. Cosmology with Love: Measuring the Hubble constant using neutron star universal relations. Phys. Rev. D 2021, 104, 083528. [Google Scholar] [CrossRef]
- Ghosh, T.; Biswas, B.; Bose, S. Simultaneous Inference of Neutron Star Equation of State and Hubble Constant with a Population of Merging Neutron Stars. arXiv 2022, arXiv:2203.11756. [Google Scholar]
- Dalal, N.; Holz, D.E.; Hughes, S.A.; Jain, B. Short grb and binary black hole standard sirens as a probe of dark energy. Phys. Rev. D 2006, 74, 063006. [Google Scholar] [CrossRef]
- Nissanke, S.; Holz, D.E.; Hughes, S.A.; Dalal, N.; Sievers, J.L. Exploring short gamma-ray bursts as gravitational-wave standard sirens. Astrophys. J. 2010, 725, 496–514. [Google Scholar] [CrossRef]
- Nissanke, S.; Holz, D.E.; Dalal, N.; Hughes, S.A.; Sievers, J.L.; Hirata, C.M. Determining the Hubble constant from gravitational wave observations of merging compact binaries. arXiv 2013, arXiv:1307.2638. [Google Scholar]
- Feeney, S.M.; Peiris, H.V.; Williamson, A.R.; Nissanke, S.M.; Mortlock, D.J.; Alsing, J.; Scolnic, D. Prospects for resolving the Hubble constant tension with standard sirens. Phys. Rev. Lett. 2019, 122, 061105. [Google Scholar] [CrossRef] [PubMed]
- Mortlock, D.J.; Feeney, S.M.; Peiris, H.V.; Williamson, A.R.; Nissanke, S.M. Unbiased Hubble constant estimation from binary neutron star mergers. Phys. Rev. D 2019, 100, 103523. [Google Scholar] [CrossRef]
- Feeney, S.M.; Peiris, H.V.; Nissanke, S.M.; Mortlock, D.J. Prospects for Measuring the Hubble Constant with Neutron-Star–Black-Hole Mergers. Phys. Rev. Lett. 2021, 126, 171102. [Google Scholar] [CrossRef]
- Trott, E.; Huterer, D. Challenges for the statistical gravitational-wave method to measure the Hubble constant. arXiv 2021, arXiv:2112.00241. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Goldstein, A.; Veres, P.; Burns, E.; Briggs, M.S.; Hamburg, R.; Kocevski, D.; Wilson-Hodge, C.A.; Preece, R.D.; Poolakkil, S.; Roberts, O.J.; et al. An Ordinary Short Gamma-Ray Burst with Extraordinary Implications: Fermi-GBM Detection of GRB 170817A. Astrophys. J. Lett. 2017, 848, L14. [Google Scholar] [CrossRef]
- Savchenko, V.; Ferrigno, C.; Kuulkers, E.; Bazzano, A.; Bozzo, E.; Brandt, S.; Chenevez, J.; Courvoisier, T.J. -L.; Diehl, R.; Domingo, A.; et al. INTEGRAL Detection of the First Prompt Gamma-Ray Signal Coincident with the Gravitational-wave Event GW170817. Astrophys. J. Lett. 2017, 848, L15. [Google Scholar] [CrossRef]
- Coulter, D.A.; Foley, R.J.; Kilpatrick, C.D.; Drout, M.R.; Piro, A.L.; Shappee, B.J.; Siebert, M.R.; Simon, J.D.; Ulloa, N.; Kasen, D.; et al. Swope Supernova Survey 2017a (SSS17a), the Optical Counterpart to a Gravitational Wave Source. Science 2017, 358, 1556. [Google Scholar] [CrossRef]
- Soares-Santos, M.; Holz, D.E.; Annis, J.; Chornock, R.; Herner, K.; Berger, E.; Brout, D.; Chen, H.-Y.; Kessler, R.; Sako, M.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/Virgo GW170817. I. Discovery of the Optical Counterpart Using the Dark Energy Camera. Astrophys. J. Lett. 2017, 848, L16. [Google Scholar] [CrossRef]
- Valenti, S.; Sand, D.J.; Yang, S.; Cappellaro, E.; Tartaglia, L.; Corsi, A.; Jha, S.W.; Reichart, D.E.; Haislip, J.; Kouprianov, V. The discovery of the electromagnetic counterpart of GW170817: Kilonova AT 2017gfo/DLT17ck. Astrophys. J. Lett. 2017, 848, L24. [Google Scholar] [CrossRef]
- Arcavi, I.; Hosseinzadeh, G.; Howell, D.A.; McCully, C.; Poznanski, D.; Kasen, D.; Barnes, J.; Zaltzman, M.; Vasylyev, S.; Maoz, D.; et al. Optical emission from a kilonova following a gravitational-wave-detected neutron-star merger. Nature 2017, 551, 64. [Google Scholar] [CrossRef]
- Tanvir, N.R.; Levan, A.J.; González-Fernández, C.; Korobkin, O.; Mandel, I.; Rosswog, S.; Hjorth, J.; D’Avanzo, P.; Fruchter, A.S.; Fryer, C.L.; et al. The Emergence of a Lanthanide-Rich Kilonova Following the Merger of Two Neutron Stars. Astrophys. J. Lett. 2017, 848, L27. [Google Scholar] [CrossRef]
- Lipunov, V.M.; Gorbovskoy, E.; Kornilov, V.G.; Tyurina, N.; Balanutsa, P.; Kuznetsov, A.; Vlasenko, D.; Kuvshinov, D.; Gorbunov, I.; Buckley, D.A.H.; et al. MASTER Optical Detection of the First LIGO/Virgo Neutron Star Binary Merger GW170817. Astrophys. J. Lett. 2017, 850, L1. [Google Scholar] [CrossRef]
- Howlett, C.; Davis, T.M. Standard siren speeds: Improving velocities in gravitational-wave measurements of H0. Mon. Not. Roy. Astron. Soc. 2020, 492, 3803–3815. [Google Scholar] [CrossRef]
- Nicolaou, C.; Lahav, O.; Lemos, P.; Hartley, W.; Braden, J. The Impact of Peculiar Velocities on the Estimation of the Hubble Constant from Gravitational Wave Standard Sirens. Mon. Not. Roy. Astron. Soc. 2020, 495, 90–97. [Google Scholar] [CrossRef]
- Mukherjee, S.; Lavaux, G.; Bouchet, F.R.; Jasche, J.; Wandelt, B.D.; Nissanke, S.M.; Leclercq, F.; Hotokezaka, K. Velocity correction for Hubble constant measurements from standard sirens. Astron. Astrophys. 2021, 646, A65. [Google Scholar] [CrossRef]
- Petrov, P.; Singer, L.P.; Coughlin, M.W.; Kumar, V.; Almualla, M.; Anand, S.; Bulla, M.; Dietrich, T.; Foucart, F.; Guessoum, N. Data-driven Expectations for Electromagnetic Counterpart Searches Based on LIGO/Virgo Public Alerts. Astrophys. J. 2022, 924, 54. [Google Scholar] [CrossRef]
- Sathyaprakash, B.S.; Schutz, B.F. Physics, Astrophysics and Cosmology with Gravitational Waves. Living Rev. Rel. 2009, 12, 2. [Google Scholar] [CrossRef]
- Chen, H.Y.; Vitale, S.; Narayan, R. Viewing angle of binary neutron star mergers. Phys. Rev. X 2019, 9, 031028. [Google Scholar] [CrossRef]
- Blinnikov, S.I.; Novikov, I.D.; Perevodchikova, T.V.; Polnarev, A.G. Exploding Neutron Stars in Close Binaries. Sov. Astron. Lett. 1984, 10, 177–179. [Google Scholar]
- Goodman, J. Are gamma-ray bursts optically thick? Astrophys. J. Lett. 1986, 308, L47–L50. [Google Scholar] [CrossRef]
- Paczynski, B. Gamma-ray bursters at cosmological distances. Astrophys. J. Lett. 1986, 308, L43–L46. [Google Scholar] [CrossRef]
- Eichler, D.; Livio, M.; Piran, T.; Schramm, D.N. Nucleosynthesis, Neutrino Bursts and Gamma-Rays from Coalescing Neutron Stars. Nature 1989, 340, 126–128. [Google Scholar] [CrossRef]
- Alexander, K.D.; Berger, E.; Fong, W.; Williams, P.K.G.; Guidorzi, C.; Margutti, R.; Metzger, B.D.; Annis, J.; Blanchard, P.K.; Brout, D.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/VIRGO GW170817. VI. Radio Constraints on a Relativistic Jet and Predictions for Late-Time Emission from the Kilonova Ejecta. Astrophys. J. Lett. 2017, 848, L21. [Google Scholar] [CrossRef]
- Haggard, D.; Nynka, M.; Ruan, J.J.; Kalogera, V.; Bradley Cenko, S.; Evans, P.; Kennea, J.A. A Deep Chandra X-ray Study of Neutron Star Coalescence GW170817. Astrophys. J. Lett. 2017, 848, L25. [Google Scholar] [CrossRef]
- Hallinan, G.; Corsi, A.; Mooley, K.P.; Hotokezaka, K.; Nakar, E.; Kasliwal, M.M.; Kaplan, D.L.; Frail, D.A.; Myers, S.T.; Murphy, T.; et al. A Radio Counterpart to a Neutron Star Merger. Science 2017, 358, 1579. [Google Scholar] [CrossRef]
- Margutti, R.; Berger, E.; Fong, W.; Guidorzi, C.; Alexander, K.D.; Metzger, B.D.; Blanchard, P.K.; Cowperthwaite, P.S.; Chornock, R.; Eftekhari, T.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/VIRGO GW170817. V. Rising X-ray Emission from an Off-Axis Jet. Astrophys. J. Lett. 2017, 848, L20. [Google Scholar] [CrossRef]
- Troja, E.; Piro, L.; van Eerten, H.; Wollaeger, R.T.; Im, M.; Fox, O.D.; Butler, N.R.; Cenko, S.B.; Sakamoto, T.; Fryer, C.L.; et al. The X-ray counterpart to the gravitational wave event GW 170817. Nature 2017, 551, 71–74. [Google Scholar] [CrossRef]
- Piran, T. The physics of gamma-ray bursts. Rev. Mod. Phys. 2004, 76, 1143–1210. [Google Scholar] [CrossRef]
- Meszaros, P. Gamma-Ray Bursts. Rept. Prog. Phys. 2006, 69, 2259–2322. [Google Scholar] [CrossRef]
- Nakar, E. Short-Hard Gamma-Ray Bursts. Phys. Rept. 2007, 442, 166–236. [Google Scholar] [CrossRef]
- Gehrels, N.; Ramirez-Ruiz, E.; Fox, D.B. Gamma-Ray Bursts in the Swift Era. Ann. Rev. Astron. Astrophys. 2009, 47, 567–617. [Google Scholar] [CrossRef]
- Berger, E. Short-Duration Gamma-Ray Bursts. Ann. Rev. Astron. Astrophys. 2014, 52, 43–105. [Google Scholar] [CrossRef]
- Kumar, P.; Zhang, B. The physics of gamma-ray bursts \& relativistic jets. Phys. Rept. 2014, 561, 1–109. [Google Scholar] [CrossRef]
- Granot, J.; Panaitescu, A.; Kumar, P.; Woosley, S.E. Off-axis afterglow emission from jetted gamma-ray bursts. Astrophys. J. Lett. 2002, 570, L61–L64. [Google Scholar] [CrossRef]
- Nakar, E.; Piran, T. GRBs light curves—Another clue on the inner engine. Astrophys. J. Lett. 2002, 572, L139–L142. [Google Scholar] [CrossRef]
- Gottlieb, O.; Nakar, E.; Piran, T. Detectability of neutron star merger afterglows. Mon. Not. Roy. Astron. Soc. 2019, 488, 2405–2411. [Google Scholar] [CrossRef]
- Lyman, J.D.; Lamb, G.P.; Levan, A.J.; Mandel, I.; Tanvir, N.R.; Kobayashi, S.; Gompertz, B.; Hjorth, J.; Fruchter, A.S.; Kangas, T.; et al. The optical afterglow of the short gamma-ray burst associated with GW170817. Nat. Astron. 2018, 2, 751–754. [Google Scholar] [CrossRef]
- Lazzati, D.; Perna, R.; Morsony, B.J.; López-Cámara, D.; Cantiello, M.; Ciolfi, R.; Giacomazzo, B.; Workman, J.C. Late time afterglow observations reveal a collimated relativistic jet in the ejecta of the binary neutron star merger GW170817. Phys. Rev. Lett. 2018, 120, 241103. [Google Scholar] [CrossRef] [PubMed]
- Hajela, A.; Margutti, R.; Alexander, K.D.; Kathirgamaraju, A.; Baldeschi, A.; Guidorzi, C.; Giannios, D.; Fong, W.; Wu, Y.; MacFadyen, A.; et al. Two Years of Nonthermal Emission from the Binary Neutron Star Merger GW170817: Rapid Fading of the Jet Afterglow and First Constraints on the Kilonova Fastest Ejecta. Astrophys. J. Lett. 2019, 886, L17. [Google Scholar] [CrossRef]
- Lamb, G.P.; Lyman, J.D.; Levan, A.J.; Tanvir, N.R.; Kangas, T.; Fruchter, A.S.; Gompertz, B.; Hjorth, J.; Mandel, I.; Oates, S.R.; et al. The optical afterglow of GW170817 at one year post-merger. Astrophys. J. Lett. 2019, 870, L15. [Google Scholar] [CrossRef]
- Troja, E.; van Eerten, H.; Ryan, G.; Ricci, R.; Burgess, J.M.; Wieringa, M.H.; Piro, L.; Cenko, S.B.; Sakamoto, T. A year in the life of GW 170817: The rise and fall of a structured jet from a binary neutron star merger. Mon. Not. Roy. Astron. Soc. 2019, 489, 1919–1926. [Google Scholar] [CrossRef]
- Wu, Y.; MacFadyen, A. GW170817 Afterglow Reveals that Short Gamma-Ray Bursts are Neutron Star Mergers. Astrophys. J. Lett. 2019, 880, L23. [Google Scholar] [CrossRef]
- Ryan, G.; van Eerten, H.; Piro, L.; Troja, E. Gamma-Ray Burst Afterglows in the Multimessenger Era: Numerical Models and Closure Relations. Astrophys. J. 2020, 896, 166. [Google Scholar] [CrossRef]
- van Eerten, H.; Zhang, W.; MacFadyen, A. Off-Axis Gamma-Ray Burst Afterglow Modeling Based On A Two-Dimensional Axisymmetric Hydrodynamics Simulation. Astrophys. J. 2010, 722, 235–247. [Google Scholar] [CrossRef]
- van Eerten, H.J.; MacFadyen, A.I. Observational implications of gamma-ray burst afterglow jet simulations and numerical light curve calculations. Astrophys. J. 2012, 751, 155. [Google Scholar] [CrossRef]
- Takahashi, K.; Ioka, K. Inverse reconstruction of jet structure from off-axis gamma-ray burst afterglows. Mon. Not. Roy. Astron. Soc. 2020, 497, 1217–1235. [Google Scholar] [CrossRef]
- Beniamini, P.; Granot, J.; Gill, R. Afterglow light curves from misaligned structured jets. Mon. Not. Roy. Astron. Soc. 2020, 493, 3521–3534. [Google Scholar] [CrossRef]
- Nakar, E.; Piran, T. Afterglow constraints on the viewing angle of binary neutron star mergers and determination of the Hubble constant. Astrophys. J. 2021, 909, 114. [Google Scholar] [CrossRef]
- Lamb, G.P.; Fernández, J.J.; Hayes, F.; Kong, A.K.H.; Lin, E.T.; Tanvir, N.R.; Hendry, M.; Heng, I.S.; Saha, S.; Veitch, J. Inclination Estimates from Off-Axis GRB Afterglow Modelling. Universe 2021, 7, 329. [Google Scholar] [CrossRef]
- Nativi, L.; Lamb, G.P.; Rosswog, S.; Lundman, C.; Kowal, G. Are interactions with neutron star merger winds shaping the jets? Mon. Not. Roy. Astron. Soc. 2021, 509, 903–913. [Google Scholar] [CrossRef]
- Mooley, K.P.; Deller, A.T.; Gottlieb, O.; Nakar, E.; Hallinan, G.; Bourke, S.; Frail, D.A.; Horesh, A.; Corsi, A.; Hotokezaka, K. Superluminal motion of a relativistic jet in the neutron-star merger GW170817. Nature 2018, 561, 355–359. [Google Scholar] [CrossRef] [PubMed]
- Ghirlanda, G.; Salafia, O.S.; Paragi, Z.; Giroletti, M.; Yang, J.; Marcote, B.; Blanchard, J.; Agudo, I.; An, T.; Bernardini, M.G.; et al. Compact radio emission indicates a structured jet was produced by a binary neutron star merger. Science 2019, 363, 968. [Google Scholar] [CrossRef] [PubMed]
- Rees, M.J. Appearance of Relativistically Expanding Radio Sources. Nature 1966, 211, 468–470. [Google Scholar] [CrossRef]
- Sari, R. Linear polarization and proper motion in the afterglow of beamed grbs. Astrophys. J. Lett. 1999, 524, L43–L46. [Google Scholar] [CrossRef]
- Mastrogiovanni, S.; Duque, R.; Chassande-Mottin, E.; Daigne, F.; Mochkovitch, R. The potential role of binary neutron star merger afterglows in multimessenger cosmology. Astron. Astrophys. 2021, 652, A1. [Google Scholar] [CrossRef]
- Metzger, B.D. Kilonovae. Living Rev. Rel. 2020, 23, 1. [Google Scholar] [CrossRef]
- Nakar, E. The electromagnetic counterparts of compact binary mergers. Phys. Rept. 2020, 886, 1–84. [Google Scholar] [CrossRef]
- Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Okawa, H.; Sekiguchi, Y.I.; Shibata, M.; Taniguchi, K. Mass ejection from the merger of binary neutron stars. Phys. Rev. D 2013, 87, 024001. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Kiuchi, K.; Kyutoku, K.; Shibata, M. Dynamical mass ejection from binary neutron star mergers: Radiation-hydrodynamics study in general relativity. Phys. Rev. D 2015, 91, 064059. [Google Scholar] [CrossRef]
- Dietrich, T.; Ujevic, M. Modeling dynamical ejecta from binary neutron star mergers and implications for electromagnetic counterparts. Class. Quant. Grav. 2017, 34, 105014. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Hotokezaka, K.; Fromm, S.A.; Bernuzzi, S.; Roberts, L.F. Binary Neutron Star Mergers: Mass Ejection, Electromagnetic Counterparts and Nucleosynthesis. Astrophys. J. 2018, 869, 130. [Google Scholar] [CrossRef]
- Krüger, C.J.; Foucart, F. Estimates for Disk and Ejecta Masses Produced in Compact Binary Mergers. Phys. Rev. D 2020, 101, 103002. [Google Scholar] [CrossRef]
- Most, E.R.; Papenfort, L.J.; Tootle, S.; Rezzolla, L. Fast ejecta as a potential way to distinguish black holes from neutron stars in high-mass gravitational-wave events. Astrophys. J. 2021, 912, 80. [Google Scholar] [CrossRef]
- Nedora, V.; Radice, D.; Bernuzzi, S.; Perego, A.; Daszuta, B.; Endrizzi, A.; Prakash, A.; Schianchi, F. Dynamical ejecta synchrotron emission as a possible contributor to the changing behaviour of GRB170817A afterglow. Mon. Not. Roy. Astron. Soc. 2021, 506, 5908–5915. [Google Scholar] [CrossRef]
- Fernández, R.; Kasen, D.; Metzger, B.D.; Quataert, E. Outflows from accretion discs formed in neutron star mergers: Effect of black hole spin. Mon. Not. Roy. Astron. Soc. 2015, 446, 750–758. [Google Scholar] [CrossRef]
- Siegel, D.M.; Metzger, B.D. Three-Dimensional General-Relativistic Magnetohydrodynamic Simulations of Remnant Accretion Disks from Neutron Star Mergers: Outflows and r-Process Nucleosynthesis. Phys. Rev. Lett. 2017, 119, 231102. [Google Scholar] [CrossRef]
- Fernández, R.; Tchekhovskoy, A.; Quataert, E.; Foucart, F.; Kasen, D. Long-term GRMHD simulations of neutron star merger accretion discs: Implications for electromagnetic counterparts. Mon. Not. Roy. Astron. Soc. 2019, 482, 3373–3393. [Google Scholar] [CrossRef]
- Just, O.; Bauswein, A.; Pulpillo, R.A.; Goriely, S.; Janka, H.T. Comprehensive nucleosynthesis analysis for ejecta of compact binary mergers. Mon. Not. Roy. Astron. Soc. 2015, 448, 541–567. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Hotokezaka, K.; Bernuzzi, S.; Fromm, S.A.; Roberts, L.F. Viscous-Dynamical Ejecta from Binary Neutron Star Merger. Astrophys. J. Lett. 2018, 869, L35. [Google Scholar] [CrossRef]
- Shibata, M.; Hotokezaka, K. Merger and Mass Ejection of Neutron-Star Binaries. Ann. Rev. Nucl. Part. Sci. 2019, 69, 41–64. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Bernuzzi, S.; Zhang, B. Long-lived Remnants from Binary Neutron Star Mergers. Mon. Not. Roy. Astron. Soc. 2018, 481, 3670–3682. [Google Scholar] [CrossRef]
- Siegel, D.M.; Ciolfi, R. Electromagnetic emission from long-lived binary neutron star merger remnants I: Formulation of the problem. Astrophys. J. 2016, 819, 14. [Google Scholar] [CrossRef]
- Siegel, D.M.; Ciolfi, R. Electromagnetic emission from long-lived binary neutron star merger remnants II: Lightcurves and spectra. Astrophys. J. 2016, 819, 15. [Google Scholar] [CrossRef]
- Nedora, V.; Bernuzzi, S.; Radice, D.; Perego, A.; Endrizzi, A.; Ortiz, N. Spiral-wave wind for the blue kilonova. Astrophys. J. Lett. 2019, 886, L30. [Google Scholar] [CrossRef]
- Rosswog, S.; Liebendoerfer, M.; Thielemann, F.K.; Davies, M.B.; Benz, W.; Piran, T. Mass ejection in neutron star mergers. Astron. Astrophys. 1999, 341, 499–526. [Google Scholar]
- Freiburghaus, C.; Rosswog, S.; Thielemann, F.K. R-Process in Neutron Star Mergers. Astrophys. J. Lett. 1999, 525, L121–L124. [Google Scholar] [CrossRef]
- Kasen, D.; Badnell, N.R.; Barnes, J. Opacities and Spectra of the r-process Ejecta from Neutron Star Mergers. Astrophys. J. 2013, 774, 25. [Google Scholar] [CrossRef]
- Tanaka, M.; Hotokezaka, K. Radiative Transfer Simulations of Neutron Star Merger Ejecta. Astrophys. J. 2013, 775, 113. [Google Scholar] [CrossRef]
- Barnes, J.; Kasen, D. Effect of a High Opacity on the Light Curves of Radioactively Powered Transients from Compact Object Mergers. Astrophys. J. 2013, 775, 18. [Google Scholar] [CrossRef]
- Metzger, B.D.; Fernández, R. Red or blue? A potential kilonova imprint of the delay until black hole formation following a neutron star merger. Mon. Not. Roy. Astron. Soc. 2014, 441, 3444–3453. [Google Scholar] [CrossRef]
- Villar, V.A.; Guillochon, J.; Berger, E.; Metzger, B.D.; Cowperthwaite, P.S.; Nicholl, M.; Alexander, K.D.; Blanchard, P.K.; Chornock, R.; Eftekhari, T.; et al. The Combined Ultraviolet, Optical, and Near-Infrared Light Curves of the Kilonova Associated with the Binary Neutron Star Merger GW170817: Unified Data Set, Analytic Models, and Physical Implications. Astrophys. J. Lett. 2017, 851, L21. [Google Scholar] [CrossRef]
- Nicholl, M.; Margalit, B.; Schmidt, P.; Smith, G.P.; Ridley, E.J.; Nuttall, J. Tight multimessenger constraints on the neutron star equation of state from GW170817 and a forward model for kilonova light-curve synthesis. Mon. Not. Roy. Astron. Soc. 2021, 505, 3016–3032. [Google Scholar] [CrossRef]
- Kasen, D.; Fernandez, R.; Metzger, B. Kilonova light curves from the disc wind outflows of compact object mergers. Mon. Not. Roy. Astron. Soc. 2015, 450, 1777–1786. [Google Scholar] [CrossRef]
- Wollaeger, R.T.; Korobkin, O.; Fontes, C.J.; Rosswog, S.K.; Even, W.P.; Fryer, C.L.; Sollerman, J.; Hungerford, A.L.; van Rossum, D.R.; Wollaber, A.B. Impact of ejecta morphology and composition on the electromagnetic signatures of neutron star mergers. Mon. Not. Roy. Astron. Soc. 2018, 478, 3298–3334. [Google Scholar] [CrossRef]
- Bulla, M. POSSIS: Predicting spectra, light curves and polarization for multi-dimensional models of supernovae and kilonovae. Mon. Not. Roy. Astron. Soc. 2019, 489, 5037–5045. [Google Scholar] [CrossRef]
- Darbha, S.; Kasen, D. Inclination Dependence of Kilonova Light Curves from Globally Aspherical Geometries. Astrophys. J. 2020, 897, 150. [Google Scholar] [CrossRef]
- Kawaguchi, K.; Shibata, M.; Tanaka, M. Diversity of Kilonova Light Curves. Astrophys. J. 2020, 889, 171. [Google Scholar] [CrossRef]
- Korobkin, O.; Wollaeger, R.T.; Fryer, C.L.; Hungerford, A.L.; Rosswog, S.; Fontes, C.J.; Mumpower, M.R.; Chase, E.A.; Even, W.P.; Miller, J.; et al. Axisymmetric Radiative Transfer Models of Kilonovae. Astrophys. J. 2021, 910, 116. [Google Scholar] [CrossRef]
- Klion, H.; Duffell, P.C.; Kasen, D.; Quataert, E. The effect of jet–ejecta interaction on the viewing angle dependence of kilonova light curves. Mon. Not. Roy. Astron. Soc. 2021, 502, 865–875. [Google Scholar] [CrossRef]
- Ascenzi, S.; Coughlin, M.W.; Dietrich, T.; Foley, R.J.; Ramirez-Ruiz, E.; Piranomonte, S.; Mockler, B.; Murguia-Berthier, A.; Fryer, C.L.; Lloyd-Ronning, N.M.; et al. A luminosity distribution for kilonovae based on short gamma-ray burst afterglows. Mon. Not. Roy. Astron. Soc. 2019, 486, 672–690. [Google Scholar] [CrossRef]
- Fong, W.; Margutti, R.; Chornock, R.; Berger, E.; Shappee, B.J.; Levan, A.J.; Tanvir, N.R.; Smith, N.; Milne, P.A.; Laskar, T.; et al. The Afterglow and Early-Type Host Galaxy of the Short GRB 150101B at z= 0.1343. Astrophys. J. 2016, 833, 151. [Google Scholar] [CrossRef]
- Fox, D.B.; Frail, D.A.; Price, P.A.; Kulkarni, S.R.; Berger, E.; Piran, T.; Soderberg, A.M.; Cenko, S.B.; Cameron, P.B.; Gal-Yam, A.; et al. The afterglow of grb050709 and the nature of the short-hard gamma-ray bursts. Nature 2005, 437, 845–850. [Google Scholar] [CrossRef]
- Kasliwal, M.M.; Korobkin, O.; Lau, R.M.; Wollaeger, R.; Fryer, C.L. Infrared emission from kilonovae: The case of the nearby short hard burst GRB 160821B. Astrophys. J. Lett. 2017, 843, L34. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, B.B.; Liang, E.W.; Gehrels, N.; Burrows, D.N.; Meszaros, P. Making a Short Gamma-Ray Burst from a Long one: Implications for the Nature of GRB 060614. Astrophys. J. Lett. 2007, 655, L25–L28. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Dietrich, T.; Heinzel, J.; Khetan, N.; Antier, S.; Bulla, M.; Christensen, N.; Coulter, D.A.; Foley, R.J. Standardizing kilonovae and their use as standard candles to measure the Hubble constant. Phys. Rev. Res. 2020, 2, 022006. [Google Scholar] [CrossRef]
- Kasen, D.; Metzger, B.; Barnes, J.; Quataert, E.; Ramirez-Ruiz, E. Origin of the heavy elements in binary neutron-star mergers from a gravitational-wave event. Nature 2017, 551, 80–84. [Google Scholar] [CrossRef]
- Prada, F.; Content, R.; Goobar, A.; Izzo, L.; Pérez, E.; Agnello, A.; del Burgo, C.; Dhillon, V.; Diego, J.M.; Galbany, L.; et al. White Paper on MAAT@GTC. arXiv 2020, arXiv:2007.01603. [Google Scholar]
- Smartt, S.J.; Chen, T.-W.; Jerkstrand, A.; Coughlin, M.; Kankare, E.; Sim, S.A.; Fraser, M.; Inserra, C.; Maguire, K.; Chambers, K.C.; et al. A kilonova as the electromagnetic counterpart to a gravitational-wave source. Nature 2017, 551, 75–79. [Google Scholar] [CrossRef] [PubMed]
- Pian, E.; D’Avanzo, P.; Benetti, S.; Branchesi, M.; Brocato, E.; Campana, S.; Cappellaro, E.; Covino, S.; D’Elia, V.; Fynbo, J.P.U.; et al. Spectroscopic identification of r-process nucleosynthesis in a double neutron star merger. Nature 2017, 551, 67–70. [Google Scholar] [CrossRef] [PubMed]
- Doctor, Z. Thunder and Lightning: Using Neutron-Star Mergers as Simultaneous Standard Candles and Sirens to Measure Cosmological Parameters. Astrophys. J. Lett. 2020, 892, L16. [Google Scholar] [CrossRef]
- Heinzel, J.; Coughlin, M.W.; Dietrich, T.; Bulla, M.; Antier, S.; Christensen, N.; Coulter, D.A.; Foley, R.J.; Issa, L.; Khetan, N. Comparing inclination dependent analyses of kilonova transients. Mon. Not. Roy. Astron. Soc. 2021, 502, 3057–3065. [Google Scholar] [CrossRef]
- Rosswog, S.; Feindt, U.; Korobkin, O.; Wu, M.R.; Sollerman, J.; Goobar, A.; Martinez-Pinedo, G. Detectability of compact binary merger macronovae. Class. Quant. Grav. 2017, 34, 104001. [Google Scholar] [CrossRef]
- Barnes, J.; Zhu, Y.L.; Lund, K.A.; Sprouse, T.M.; Vassh, N.; McLaughlin, G.C.; Mumpower, M.R.; Surman, R. Kilonovae Across the Nuclear Physics Landscape: The Impact of Nuclear Physics Uncertainties on r-process-powered Emission. Astrophys. J. 2021, 918, 44. [Google Scholar] [CrossRef]
- Tanaka, M.; Kato, D.; Gaigalas, G.; Kawaguchi, K. Systematic Opacity Calculations for Kilonovae. Mon. Not. Roy. Astron. Soc. 2020, 496, 1369–1392. [Google Scholar] [CrossRef]
- Banerjee, S.; Tanaka, M.; Kato, D.; Gaigalas, G.; Kawaguchi, K.; Domoto, N. Opacity of the highly ionized lanthanides and the effect on the early kilonova. arXiv 2022, arXiv:2204.06861. [Google Scholar]
- Wang, L.; Wheeler, J.C. Spectropolarimetry of Supernovae. Ann. Rev. Astron. Astrophys. 2008, 46, 433–474. [Google Scholar] [CrossRef]
- Jeffery, D.J. Analysis of SN 1987A Polarimetry. Astrophys. J. 1991, 375, 264. [Google Scholar] [CrossRef]
- Hoflich, P.; Wheeler, J.C.; Hines, D.C.; Trammell, S.R. Analysis of the polarization and flux spectra of SN1993J. Astrophys. J. 1996, 459, 307. [Google Scholar] [CrossRef][Green Version]
- Kasen, D.; Nugent, P.; Wang, L.; Howell, D.A.; Wheeler, J.C.; Hoeflich, P.; Baade, D.; Baron, E.; Hauschildt, P.H. Analysis of the flux and polarization spectra of the Type Ia supernova SN 2001el: Exploring the geometry of the high-velocity ejecta. Astrophys. J. 2003, 593, 788–808. [Google Scholar] [CrossRef]
- Bulla, M.; Covino, S.; Kyutoku, K.; Tanaka, M.; Maund, J.R.; Patat, F.; Toma, K.; Wiersema, K.; Bruten, J.; Jin, Z.P.; et al. The origin of polarization in kilonovae and the case of the gravitational-wave counterpart AT 2017gfo. Nat. Astron. 2019, 3, 99–106. [Google Scholar] [CrossRef]
- Bulla, M.; Covino, S.; Patat, F.; Kyutoku, K.; Maund, J.R.; Tanaka, M.; Toma, K.; Wiersema, K.; D’Avanzo, P.; Higgins, A.B.; et al. Shedding Light on the Geometry of Kilonovae. Messenger 2018, 174, 34–36. [Google Scholar] [CrossRef]
- Covino, S.; Wiersema, K.; Fan, Y.Z.; Toma, K.; Higgins, A.B.; Melandri, A.; D’Avanzo, P.; Mundell, C.G.; Palazzi, E.; Tanvir, N.R.; et al. The unpolarized macronova associated with the gravitational wave event GW170817. Nat. Astron. 2017, 1, 791–794, Erratum: Nat. Astron. 2017, 1, 805. [Google Scholar] [CrossRef]
- Bulla, M.; Kyutoku, K.; Tanaka, M.; Covino, S.; Bruten, J.R.; Matsumoto, T.; Maund, J.R.; Testa, V.; Wiersema, K. Polarized kilonovae from black hole–neutron star mergers. Mon. Not. Roy. Astron. Soc. 2021, 501, 1891–1899. [Google Scholar] [CrossRef]
- An, S.; Coughlin, M.W.; Kasliwal, M.M.; Bulla, M.; Ahumada, T.; Sagués, C.A.; Almualla, M.; Andreoni, I.; Stein, R.; Foucart, F.; et al. Optical follow-up of the neutron star–black hole mergers S200105ae and S200115j. Nat. Astron. 2021, 5, 46–53. [Google Scholar] [CrossRef]
- Vitale, S.; Del Pozzo, W.; Li, T.G.F.; Van Den Broeck, C.; Mandel, I.; Aylott, B.; Veitch, J. Effect of calibration errors on Bayesian parameter estimation for gravitational wave signals from inspiral binary systems in the Advanced Detectors era. Phys. Rev. D 2012, 85, 064034. [Google Scholar] [CrossRef]
- Payne, E.; Talbot, C.; Lasky, P.D.; Thrane, E.; Kissel, J.S. Gravitational-wave astronomy with a physical calibration model. Phys. Rev. D 2020, 102, 122004. [Google Scholar] [CrossRef]
- Vitale, S.; Haster, C.J.; Sun, L.; Farr, B.; Goetz, E.; Kissel, J.; Cahillane, C. Physical approach to the marginalization of LIGO calibration uncertainties. Phys. Rev. D 2021, 103, 063016. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, H.Y.; Haster, C.J.; Sun, L.; Vitale, S.; Kissel, J. Impact of calibration uncertainties on Hubble constant measurements from gravitational-wave sources. arXiv 2022, arXiv:2204.03614. [Google Scholar]
- Chen, H.Y. Systematic Uncertainty of Standard Sirens from the Viewing Angle of Binary Neutron Star Inspirals. Phys. Rev. Lett. 2020, 125, 201301. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Prospects for observing and localizing gravitational-wave transients with Advanced LIGO, Advanced Virgo and KAGRA. Living Rev. Rel. 2018, 21, 3. [Google Scholar] [CrossRef] [PubMed]
- Ivezić, Ž; Kahn, S.M.; Tyson, J.A.; Abel, B.; Acosta, E.; Allsman, R.; Alonso, D.; AlSayyad, Y.; Anderson, S.F.; Andrew, J.; et al. LSST: From Science Drivers to Reference Design and Anticipated Data Products. Astrophys. J. 2019, 873, 111. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).