Extended Gravity Constraints at Different Scales †
Simple Summary
Abstract
1. Introduction
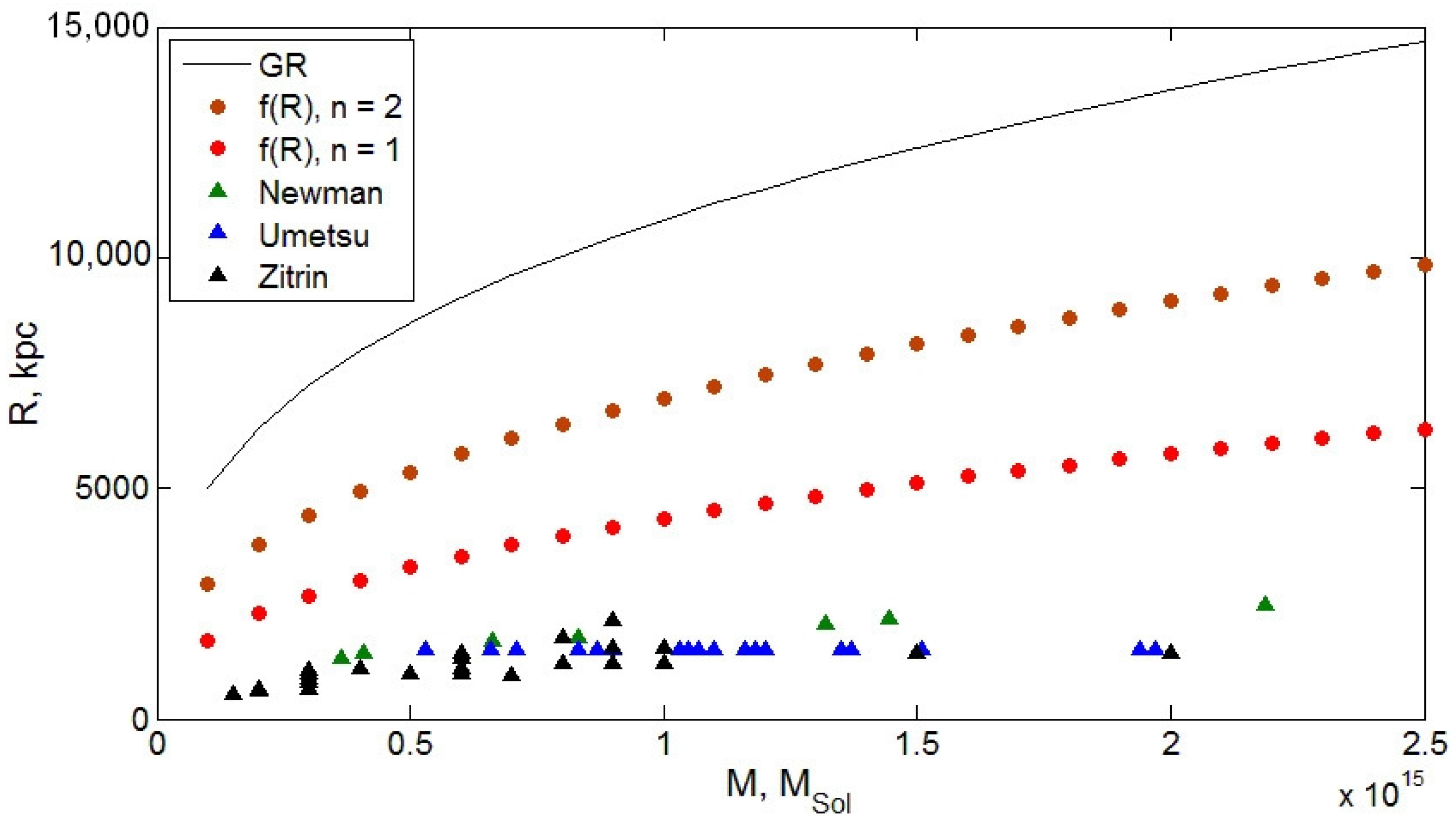
2. Galaxy Clusters Scales: Dark Energy Explanations
3. Black Hole Shadows: Deviations from GR
4. Gravitational Wave Astronomy: Deviations from GR
5. Binary Pulsars: Deviations from GR
6. Solar System: Newtonian Limit and Deviations from it
7. Large Hadron Collider: Constraints at TeV Scale
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rept. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Rel. 2010, 13, 3. [Google Scholar] [CrossRef] [PubMed]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Kobayashi, T. Horndeski theory and beyond: A review. Rept. Prog. Phys. 2019, 82, 086901. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Callister, T.A. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Ezquiaga, J.M.; Zumalacárregui, M. Dark Energy After GW170817: Dead Ends and the Road Ahead. Phys. Rev. Lett. 2017, 119, 251304. [Google Scholar] [CrossRef]
- Baker, T.; Bellini, E.; Ferreira, P.G.; Lagos, M.; Noller, J.; Sawicki, I. Strong constraints on cosmological gravity from GW170817 and GRB 170817A. Phys. Rev. Lett. 2017, 119, 251301. [Google Scholar] [CrossRef]
- Ageeva, Y.; Petrov, P.; Rubakov, V. Nonsingular cosmological models with strong gravity in the past. Phys. Rev. D 2021, 104, 063530. [Google Scholar] [CrossRef]
- Berti, E.; Barausse, E.; Cardoso, V.; Gualtieri, L.; Pani, P.; Sperhake, U.; Zilhao, M. Testing General Relativity with Present and Future Astrophysical Observations. Class. Quant. Grav. 2015, 32, 243001. [Google Scholar] [CrossRef]
- Borka, D.; Jovanović, V.B.; Capozziello, S.; Zakharov, A.F.; Jovanović, P. Estimating the Parameters of Extended Gravity Theories with the Schwarzschild Precession of S2 Star. Universe 2021, 7, 407. [Google Scholar] [CrossRef]
- Chernin, A.D.; Emelyanov, N.V.; Karachentsev, I.D. Dark energy domination in the local flow of giant galaxies. Mon. Not. R. Astron. Soc. 2015, 449, 2069–2078. [Google Scholar] [CrossRef]
- Alexeyev, S.O.; Latosh, B.N.; Echeistov, V.A. Searching for Constraints on Starobinsky’s Model with a Disappearing Cosmological Constant on Galaxy Cluster Scales. J. Exp. Theor. Phys. 2017, 125, 1083–1089. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- Kocherlakota, P.; Rezzolla, L.; Falcke, H.; Fromm, C.M.; Kramer, M.; Mizuno, Y.; Mejias, A.M. Constraints on black-hole charges with the 2017 EHT observations of M87*. Phys. Rev. D 2021, 103, 104047. [Google Scholar] [CrossRef]
- Will, C.M. Testing gravity using space gravitational-wave detectors. Class. Quant. Grav. 2003, 20, S219–S225. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Bouffanais, Y. All-sky search for short gravitational-wave bursts in the third Advanced LIGO and Advanced Virgo run. Phys. Rev. D 2021, 104, 122004. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Boudart, V. Observation of Gravitational Waves from Two Neutron Star–Black Hole Coalescences. Astrophys. J. Lett. 2021, 915, L5. [Google Scholar] [CrossRef]
- Weisberg, J.M.; Taylor, J.H. Observations of Post-Newtonian Timing Effects in the Binary Pulsar PSR 1913+16. Phys. Rev. Lett. 1984, 52, 1348–1350. [Google Scholar] [CrossRef]
- Hulse, R.A.; Taylor, J.H. Discovery of a pulsar in a binary system. Astrophys. J. Lett. 1975, 195, L51–L53. [Google Scholar] [CrossRef]
- Damour, T.; Taylor, J.H. Strong field tests of relativistic gravity and binary pulsars. Phys. Rev. D 1992, 45, 1840–1868. [Google Scholar] [CrossRef]
- Dyadina, P.I.; Avdeev, N.A.; Alexeyev, S.O. Horndeski gravity without screening in binary pulsars. Mon. Not. R. Astron. Soc. 2019, 483, 947–963. [Google Scholar] [CrossRef]
- Will, C.M. Theory and Experiment in Gravitational Physics; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Dyadina, P.I.; Labazova, S.P.; Alexeyev, S.O. Post-Newtonian Limit of Hybrid Metric-Palatini f(R)-Gravity. J. Exp. Theor. Phys. 2019, 129, 838–848. [Google Scholar] [CrossRef]
- Landsberg, G. Black Holes at the Large Hadron Collider. Fundam. Theor. Phys. 2015, 178, 267–292. [Google Scholar] [CrossRef]
- Barrau, A.; Grain, J.; Alexeyev, S.O. Gauss-Bonnet black holes at the LHC: Beyond the dimensionality of space. Phys. Lett. B 2004, 584, 114. [Google Scholar] [CrossRef]
- Alexeyev, S.O.; Calmet, X.; Latosh, B.N. Gravity induced non-local effects in the standard model. Phys. Lett. B 2018, 776, 111–114. [Google Scholar] [CrossRef]
- Rubakov, V.A.; Tinyakov, P.G. Infrared-modified gravities and massive gravitons. Phys. Usp. 2008, 51, 759–792. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Troisi, A. Reconciling dark energy models with f(R) theories. Phys. Rev. D 2005, 71, 043503. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Disappearing cosmological constant in f(R) gravity. JETP Lett. 2007, 86, 157–163. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Faraoni, V. Turnaround radius in modified gravity. Phys. Dark Univ. 2016, 11, 11–15. [Google Scholar] [CrossRef]
- Newman, A.B.; Treu, T.; Ellis, R.S.; Sand, D.J.; Nipoti, C.; Richard, J.; Jullo, E. The Density Profiles of Massive, Relaxed Galaxy Clusters: I. The Total Density Over 3 Decades in Radius. Astrophys. J. 2013, 765, 24. [Google Scholar] [CrossRef]
- Umetsu, K.; Medezinski, E.; Nonino, M.; Merten, J.; Postman, M.; Meneghetti, M.; Zitrin, A. CLASH: Weak-Lensing Shear-and-Magnification Analysis of 20 Galaxy Clusters. Astrophys. J. 2014, 795, 163. [Google Scholar] [CrossRef]
- Zitrin, A.; Fabris, A.; Merten, J.; Melchior, P.; Meneghetti, M.; Koekemoer, A.; Moustakas, J. Hubble Space Telescope Combined Strong and Weak Lensing Analysis of the CLASH Sample: Mass and Magnification Models and Systematic Uncertainties. Astrophys. J. 2015, 801, 44. [Google Scholar] [CrossRef]
- Arnold, C.; Puchwein, E.; Springel, V. Scaling relations and mass bias in hydrodynamical f(R) gravity simulations of galaxy clusters. Mon. Not. R. Astron. Soc. 2014, 440, 833–842. [Google Scholar] [CrossRef]
- Bernal, T.; López-Corona, O.; Mendoza, S. Dynamics of clusters of galaxies with extended F(χ) gravity. Rev. Mex. Astron. Astrofis. 2019, 55, 237–254. [Google Scholar] [CrossRef]
- Brax, P.; Rizzo, L.A.; Valageas, P. K-mouflage effects on clusters of galaxies. Phys. Rev. D 2015, 92, 043519. [Google Scholar] [CrossRef]
- De Martino, I. f(R) -gravity model of the Sunyaev-Zeldovich profile of the Coma cluster compatible with Planck data. Phys. Rev. D 2016, 93, 124043. [Google Scholar] [CrossRef]
- Ferraro, S.; Schmidt, F.; Hu, W. Cluster Abundance in f(R) Gravity Models. Phys. Rev. D 2011, 83, 063503. [Google Scholar] [CrossRef]
- Li, B.; He, J.h.; Gao, L. Cluster gas fraction as a test of gravity. Mon. Not. R. Astron. Soc. 2016, 456, 146–155. [Google Scholar] [CrossRef]
- Schmidt, F.; Vikhlinin, A.; Hu, W. Cluster Constraints on f(R) Gravity. Phys. Rev. D 2009, 80, 083505. [Google Scholar] [CrossRef]
- Terukina, A.; Lombriser, L.; Yamamoto, K.; Bacon, D.; Koyama, K.; Nichol, R.C. Testing chameleon gravity with the Coma cluster. J. Cosmol. Astropart. Phys. 2014, 4, 13. [Google Scholar] [CrossRef]
- Terukina, A.; Yamamoto, K.; Okabe, N.; Matsushita, K.; Sasaki, T. Testing a generalized cubic Galileon gravity model with the Coma Cluster. J. Cosmol. Astropart. Phys. 2015, 10, 64. [Google Scholar] [CrossRef]
- Wilcox, H.; Bacon, D.; Nichol, R.C.; Rooney, P.J.; Terukina, A.; Romer, A.K.; Viana, P.T. The XMM Cluster Survey: Testing chameleon gravity using the profiles of clusters. Mon. Not. R. Astron. Soc. 2015, 452, 1171–1183. [Google Scholar] [CrossRef]
- Alexeev, S.O.; Pomazanov, M.V. Black hole solutions with dilatonic hair in higher curvature gravity. Phys. Rev. D 1997, 55, 2110–2118. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories Of Gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- Alexeyev, S.; Kovalkov, K. Extended gravity at galaxy cluster’s scales. Int. J. Mod. Phys. A 2020, 35, 2040057. [Google Scholar] [CrossRef]
- Zakharov, A.F. Constraints on a charge in the Reissner-Nordstrom metric for the black hole at the Galactic Center. Phys. Rev. 2014, D90, 062007. [Google Scholar] [CrossRef]
- Zakharov, A.F. Constraints on tidal charge of the supermassive black hole at the Galactic Center with trajectories of bright stars. Eur. Phys. J. C 2018, 78, 689. [Google Scholar] [CrossRef]
- Becerra-Vergara, E.A.; Arguelles, C.R.; Krut, A.; Rueda, J.A.; Ruffini, R. Geodesic motion of S2 and G2 as a test of the fermionic dark matter nature of our Galactic core. Astron. Astrophys. 2020, 641, A34. [Google Scholar] [CrossRef]
- Becerra-Vergara, E.A.; Argüelles, C.R.; Krut, A.; Rueda, J.A.; Ruffini, R. Hinting a dark matter nature of Sgr A* via the S-stars. Mon. Not. R. Astron. Soc. 2021, 505, L64–L68. [Google Scholar] [CrossRef]
- Benisty, D.; Davis, A.C. Dark energy interactions near the Galactic Center. Phys. Rev. D 2022, 105, 024052. [Google Scholar] [CrossRef]
- Borka, D.; Jovanović, P.; Jovanović, V.B.; Zakharov, A.F. Constraining the range of Yukawa gravity interaction from S2 star orbits. J. Cosmol. Astropart. Phys. 2013, 11, 050. [Google Scholar] [CrossRef]
- Capozziello, S.; Borka, D.; Jovanović, P.; Jovanović, V.B. Constraining Extended Gravity Models by S2 star orbits around the Galactic Centre. Phys. Rev. D 2014, 90, 044052. [Google Scholar] [CrossRef]
- Capozziello, S.; Lambiase, G.; Sakellariadou, M.; Stabile, A. Constraining models of extended gravity using Gravity Probe B and LARES experiments. Phys. Rev. D 2015, 91, 044012. [Google Scholar] [CrossRef]
- Cheng, X.T.; Xie, Y. Probing a black-bounce, traversable wormhole with weak deflection gravitational lensing. Phys. Rev. D 2021, 103, 064040. [Google Scholar] [CrossRef]
- de Martino, I.; della Monica, R.; de Laurentis, M. f(R) gravity after the detection of the orbital precession of the S2 star around the Galactic Center massive black hole. Phys. Rev. D 2021, 104, L101502. [Google Scholar] [CrossRef]
- Della Monica, R.; de Martino, I.; de Laurentis, M. Orbital precession of the S2 star in Scalar–Tensor–Vector Gravity. Mon. Not. R. Astron. Soc. 2022, 510, 4757–4766. [Google Scholar] [CrossRef]
- Della Monica, R.; de Martino, I. Unveiling the nature of SgrA* with the geodesic motion of S-stars. J. Cosmol. Astropart. Phys. 2022, 3, 7. [Google Scholar] [CrossRef]
- Guerrero, M.; Olmo, G.J.; Rubiera-Garcia, D.; Gómez, D.S.C. Shadows and optical appearance of black bounces illuminated by a thin accretion disk. J. Cosmol. Astropart. Phys. 2021, 8, 36. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, X.; Zhao, W. Constraining f(R) gravity in solar system, cosmology and binary pulsar systems. Phys. Lett. B 2018, 777, 286–293. [Google Scholar] [CrossRef]
- Psaltis, D.; Johannsen, T. Sgr A*: The Optimal Testbed of Strong-Field Gravity. J. Phys. Conf. Ser. 2011, 283, 012030. [Google Scholar] [CrossRef]
- Will, C.M. Testing the general relativistic no-hair theorems using the Galactic center black hole SgrA*. Astrophys. J. Lett. 2008, 674, L25–L28. [Google Scholar] [CrossRef]
- Newman, E.T.; Janis, A.I. Note on the Kerr Spinning-Particle Metric. J. Math. Phys. 1965, 6, 915–917. [Google Scholar] [CrossRef]
- Alexeyev, S.O.; Petrov, A.N.; Latosh, B.N. Maeda-Dadhich Solutions as Real Black Holes. Phys. Rev. 2015, D92, 104046. [Google Scholar] [CrossRef]
- Prokopov, V.; Alexeyev, S.; Zenin, O. Black Hole Shadows: How to Fix the Extended Gravity Theory. arXiv 2021, arXiv:2107.01115. [Google Scholar]
- Tsukamoto, N. Black hole shadow in an asymptotically flat, stationary, and axisymmetric spacetime: The Kerr-Newman and rotating regular black holes. Phys. Rev. D 2018, 97, 064021. [Google Scholar] [CrossRef]
- Alexeyev, S.O.; Prokopov, V.A. Shadows from spinning black holes in extended gravity. J. Exp. Theor. Phys. 2020, 130, 666–670. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Cavalieri, R. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Cahillane, C. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Bloemen, S.; Canizares, P.; Falcke, H.; Fender, R.P.; Ghosh, S.; Williamson, A.R. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Latosh, B. Fab Four Effective Field Theory Treatment. Eur. Phys. J. C 2018, 78, 991. [Google Scholar] [CrossRef]
- Damour, T.; Esposito-Farese, G. Tensor - scalar gravity and binary pulsar experiments. Phys. Rev. D 1996, 54, 1474–1491. [Google Scholar] [CrossRef] [PubMed]
- Creminelli, P.; Vernizzi, F. Dark Energy after GW170817 and GRB170817A. Phys. Rev. Lett. 2017, 119, 251302. [Google Scholar] [CrossRef] [PubMed]
- Kopeikin, S.M. Supplementary Parameters in the Parameterized Post-Keplerian Formalism. Astrophys. J. Lett. 1994, 434, L67. [Google Scholar] [CrossRef]
- Taylor, J.H. Binary pulsars and relativistic gravity. Rev. Mod. Phys. 1994, 66, 711–719. [Google Scholar] [CrossRef]
- Dyadina, P.I.; Labazova, S.P. On Shapiro time delay in massive scalar-tensor theories. J. Cosmol. Astropart. Phys. 2022, 1, 29. [Google Scholar] [CrossRef]
- Damour, T.; Esposito-Farese, G. Testing gravity to second postNewtonian order: A Field theory approach. Phys. Rev. D 1996, 53, 5541–5578. [Google Scholar] [CrossRef]
- Avdeev, N.; Dyadina, P.; Labazova, S. Test of hybrid metric-Palatini f(R)-gravity in binary pulsars. J. Exp. Theor. Phys. 2020, 131, 537–547. [Google Scholar] [CrossRef]
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Rel. 2014, 17, 4. [Google Scholar] [CrossRef]
- Bergmann, P.G. Comments on the scalar tensor theory. Int. J. Theor. Phys. 1968, 1, 25–36. [Google Scholar] [CrossRef]
- Chiba, T. 1/R gravity and scalar - tensor gravity. Phys. Lett. B 2003, 575, 1–3. [Google Scholar] [CrossRef]
- Olmo, G.J. The Gravity Lagrangian according to solar system experiments. Phys. Rev. Lett. 2005, 95, 261102. [Google Scholar] [CrossRef] [PubMed]
- Olmo, G.J. Limit to general relativity in f(R) theories of gravity. Phys. Rev. D 2007, 75, 023511. [Google Scholar] [CrossRef]
- Koivisto, T.; Kurki-Suonio, H. Cosmological perturbations in the palatini formulation of modified gravity. Class. Quant. Grav. 2006, 23, 2355–2369. [Google Scholar] [CrossRef]
- Koivisto, T. The matter power spectrum in f(r) gravity. Phys. Rev. D 2006, 73, 083517. [Google Scholar] [CrossRef]
- Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Metric-Palatini gravity unifying local constraints and late-time cosmic acceleration. Phys. Rev. D 2012, 85, 084016. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Hybrid metric-Palatini gravity. Universe 2015, 1, 199–238. [Google Scholar] [CrossRef]
- Nutku, Y. The Post-Newtonian Equations of Hydrodynamics in the Brans-Dicke Theory. Astrophys. J. 1969, 155, 999. [Google Scholar] [CrossRef]
- Calmet, X.; Croon, D.; Fritz, C. Non-locality in Quantum Field Theory due to General Relativity. Eur. Phys. J. C 2015, 75, 605. [Google Scholar] [CrossRef]
- Schwinger, J.S. Brownian motion of a quantum oscillator. J. Math. Phys. 1961, 2, 407–432. [Google Scholar] [CrossRef]
- Keldysh, L.V. Diagram technique for nonequilibrium processes. Zh. Eksp. Teor. Fiz. 1964, 47, 1515–1527. [Google Scholar]
- ATLAS Collaboration; Aad, G.; Abbott, B.; Abdallah, J.; Khalek, A.S.; Abdinov, O.; Aben, R.; Abi, B.; Barlow, N.; Abolins,, M.; et al. Search for contact interactions and large extra dimensions in the dilepton channel using proton-proton collisions at s = 8 TeV with the ATLAS detector. Eur. Phys. J. C 2014, 74, 3134. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alexeyev, S.; Prokopov, V. Extended Gravity Constraints at Different Scales. Universe 2022, 8, 283. https://doi.org/10.3390/universe8050283
Alexeyev S, Prokopov V. Extended Gravity Constraints at Different Scales. Universe. 2022; 8(5):283. https://doi.org/10.3390/universe8050283
Chicago/Turabian StyleAlexeyev, Stanislav, and Vyacheslav Prokopov. 2022. "Extended Gravity Constraints at Different Scales" Universe 8, no. 5: 283. https://doi.org/10.3390/universe8050283
APA StyleAlexeyev, S., & Prokopov, V. (2022). Extended Gravity Constraints at Different Scales. Universe, 8(5), 283. https://doi.org/10.3390/universe8050283




