Einstein Field Equation, Recursion Operators, Noether and Master Symmetries in Conformable Poisson Manifolds
Abstract
1. Introduction
2. Conformable Differential and Formulation of Takeuchi Lemma
- (i)
- for all ;
- (ii)
- for all ;
- (iii)
- for all constant functions ;
- (iv)
- ;
- (iv)
- , where f is also a differentiable coordinates function on .
3. Recursion Operator in Conformable Minkowski Phase Space
3.1. Symplectic Structure, Poisson Bracket and Lie Algebra
- Antisymmetry
- Jacobi identity
- Derivation
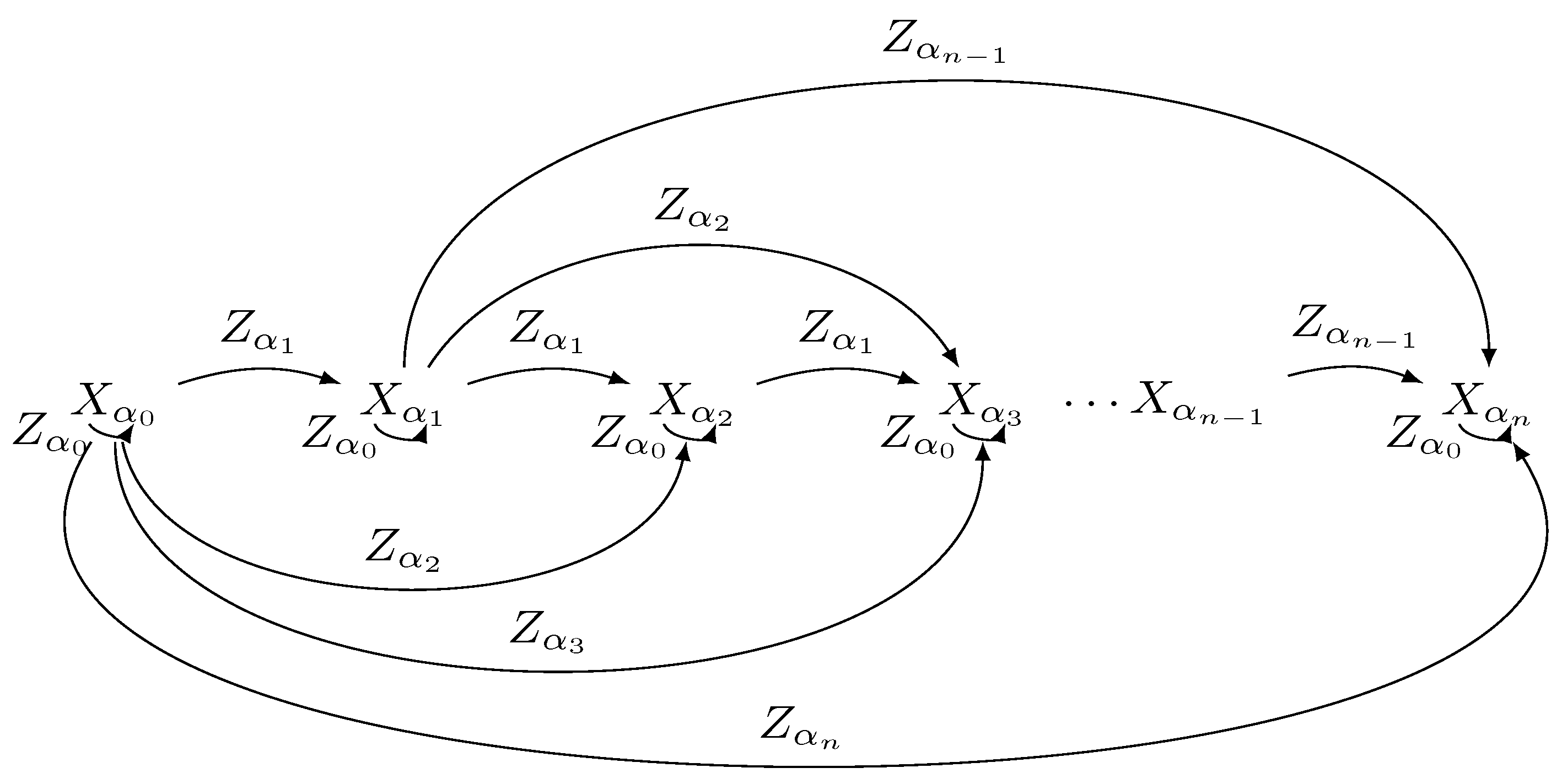
3.2. Noether Symmetry and Recursion Operator
4. Conformable Einstein Field Equation
4.1. Recursion Operator in Conformable Schwarzschild Metric
4.2. Recursion Operator in Conformable FLRW Metric
5. Family of Conserved Quantities
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Valéro, D.; Machado, J.; Kiryakova, V. Some pioneers of the applications of fractional calculus. Fract. Calc. Appl. Anal. 2014, 17, 552–578. [Google Scholar] [CrossRef]
- Agrawal, O. Formulation of Euler-Lagrange equations for fractional variational problems. J. Math. Anal. Appl. 2002, 272, 368–379. [Google Scholar] [CrossRef]
- Almeida, R.; Torres, D. Calculus of variations with fractional derivatives and fractional integrals. Appl. Math. Lett. 2009, 22, 1816–1820. [Google Scholar] [CrossRef]
- Baleanu, D. Fractional variational principles in action. Phys. Scr. 2009, T136, 014006. [Google Scholar] [CrossRef]
- Chung, W.S. Fractional Newton mechanics with conformable fractional derivative. J. Comput. Appl. Math. 2015, 290, 150–158. [Google Scholar] [CrossRef]
- Efe, M. Battery power loss compensated fractional order sliding mode control of a quadrotor UAV. Asian J. Control 2012, 14, 413–425. [Google Scholar] [CrossRef]
- Herrmann, R. Gauge invariance in fractional field theories. Phys. Lett. A 2008, 372, 5515. [Google Scholar] [CrossRef][Green Version]
- Iomin, A. Fractional-time quantum dynamics. Phys. Rev. E 2009, 80, 022103. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A 2004, 37, R161. [Google Scholar] [CrossRef]
- Jahanshahi, S.; Babolian, E.; Torres, D.F.M.; Vahidi, A. Solving Abel integral equations of first kind via fractional calculus. J. King Saud Univ. Sci. 2015, 27, 161–167. [Google Scholar] [CrossRef]
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Tarasov, V.E. Lattice fractional calculus. Appl. Math. Comput. 2015, 257, 12–33. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Chung, W.S.; Hassanabadi, H. Dynamics of a Particle in a Viscoelastic Medium with Conformable Derivative. Int. J. Theor. Phys. 2017, 56, 851. [Google Scholar] [CrossRef]
- Chung, W.S.; Hassanabadi, H. Deformed classical mechanics with α-deformed translation symmetry and anomalous diffusion. Mod. Phys. Lett. 2019, B33, 1950368. [Google Scholar] [CrossRef]
- Kiskinov, H.; Petkova, M.; Zahariev, A. About the Cauchy Problem for Nonlinear System with Conformable Derivatives and Variable Delays. AIP Conf. Proc. 2019, 2172, 050006. [Google Scholar]
- Khalil, R.; Al Horani, M.; Yousef, A.; Hammad, M.A. Geometric meaning of conformable derivative via fractional cords. J. Math. Comput. Sci. 2019, 19, 241–245. [Google Scholar] [CrossRef]
- Chung, W.S.; Hounkonnou, M.N. Deformed special relativity based on α-deformed binary operations. arXiv 2020, arXiv:2005.11155. [Google Scholar]
- Liouville, R. Sur le mouvement d’un corps solide pesant suspendu par l’un de ses points. Acta Math. 1897, 20, 239–284. [Google Scholar] [CrossRef]
- Poincaré, H. Sur les quadratures mécaniques. Acta Math. 1899, 13, 1. [Google Scholar] [CrossRef]
- De Filippo, S.; Marmo, G.; Salerno, M.; Vilasi, G. A New Characterization of Completely Integrable Systems. Nuovo Cimento B 1984, 83, 97–112. [Google Scholar] [CrossRef]
- Gelfand, I.M.; Dorfman, I.Y. The Schouten Bracket and Hamiltonian Operators. Funct. Anal. Appl. 1980, 14, 71–74. [Google Scholar] [CrossRef]
- Magri, F. A simple model of the integrable Hamiltonian equation. J. Math. Phys. 1978, 19, 1156–1162. [Google Scholar] [CrossRef]
- Vilasi, G. On the Hamiltonian Structures of the Korteweg-de Vries and Sine- Gordon Theories. Phys. Lett. B 1980, 94, 195–198. [Google Scholar] [CrossRef]
- Lax, P.D. Integrals of nonlinear equations of evolution and solitary ways. Commun. Pure Appl. Math. 1968, 21, 467–490. [Google Scholar] [CrossRef]
- Hounkonnou, M.N.; Landalidji, M.J.; Mitrović, M. Noncommutative Kepler Dynamics: Symmetry groups and bi-Hamiltonian structures. Theor. Math. Phys. 2021, 207, 751–769. [Google Scholar] [CrossRef]
- Hounkonnou, M.N.; Landalidji, M.J. Hamiltonian dynamics for the Kepler problem in a deformed phase space. In Trends in Mathematics, Proceedings of the XXXVII Workshop on Geometric Methods in Physics, Bialowieża, Poland, 1–7 July 2018; Springer Nature Switzerland AG: Cham, Switzerland, 2019; pp. 34–48. [Google Scholar]
- Takeuchi, T. A Construction of a Recursion Operator for Some Solutions of Einstein Field Equations. Proc. Fifteenth Int. Conf. Geom. Integr. Quantization 2014, 15, 249–258. [Google Scholar]
- Hounkonnou, M.N.; Landalidji, M.J.; Baloïtcha, E. Recursion Operator in a Noncommutative Minkowski Phase Space. In Trends in Mathematics, Proceedings of the XXXVI Workshop on Geometric Methods in Physics, Bialowieża, Poland, 2–8 July 2017; Springer Nature Switzerland AG: Cham, Switzerland, 2019; pp. 83–93. [Google Scholar]
- Rudolph, G.; Schmidt, M. Differential Geometry and Mathematical Physics, Part I. Manifolds, Lie Group and Hamiltonian Systems; Springer: New York, NY, USA, 2013. [Google Scholar]
- Smirnov, R.G. Magri-Morosi-Gel’fand-Dorfman’s bi-Hamiltonian constructions in the action-angle variables. J. Math. Phys. 1997, 38, 6444. [Google Scholar] [CrossRef]
- Smirnov, R.G. The action-angle coordinates revisited: Bi-Hamiltonian systems. Rep. Math. Phys. 1999, 44, 199–204. [Google Scholar] [CrossRef]
- Dubrovin, B. Bihamiltonian Structures of PDEs and Frobenius Manifolds, Lectures at the ICTP Summer School “Poisson Geometry”, Trieste, 2005. Available online: https://indico.ictp.it/event/a04198/session/47/contribution/26/material/0/0.pdf (accessed on 21 April 2017).
- Román-Roy, N. A summary on symmetries and conserved quantities of autonomous Hamiltonian systems. J. Geom. Mech. 2020, 12, 3. [Google Scholar] [CrossRef]
- Bretón, N. An introduction to general relativity, black holesand gravitational waves, VIII Workshop of the Gravitation and Mathematical Physics Division of the Mexican Physical Society. AIP Conf. Proc. 2011, 1396, 5–25. [Google Scholar]
- Rañada, M.F. A system of n=3 coupled oscillators with magnetic terms: Symmetries and integrals of motion. SIGMA 2005, 1, 004. [Google Scholar] [CrossRef]
- Caseiro, R. Master integrals, superintegrability and quadratic algebras. Bull. Sci. Math. 2002, 126, 617–630. [Google Scholar] [CrossRef]
- Damianou, P.A. Symmetries of Toda equations. J. Phys. A 1993, 26, 3791–3796. [Google Scholar] [CrossRef]
- Fernandes, R.L. On the master symmetries and bi-Hamiltonian structure of the Toda lattice. J. Phys. A Math. Gen. 1993, 26, 3797–3803. [Google Scholar] [CrossRef]
- Rañada, M.F. Superintegrability of the Calogero-Moser system: Constants of motion, master symmetries, and time-dependent symmetries. J. Math. Phys. 1999, 40, 236–247. [Google Scholar] [CrossRef]
- Hounkonnou, M.N.; Landalidji, M.J.; Mitrović, M. Hamiltonian Dynamics of a spaceship in Alcubierre and Gödel metrics: Recursion operators and underlying master symmetries. Theor. Math. Phys. 2022; in press. [Google Scholar]
- Oevel, W. A Geometrical Approach to Integrable Systems Admitting Time Dependent Invatiants. In Proceedings of the Conference on Nonlinear Evolution Equations, Solitons and the Inverse Scattering Transform, Oberwolfach, Germany, 27 July–2 August 1986; Ablowitz, M., Fuchssteiner, B., Kruskal, M., Eds.; World Scientific: Singapore, 1987. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hounkonnou, M.N.; Landalidji, M.J.; Mitrović, M. Einstein Field Equation, Recursion Operators, Noether and Master Symmetries in Conformable Poisson Manifolds. Universe 2022, 8, 247. https://doi.org/10.3390/universe8040247
Hounkonnou MN, Landalidji MJ, Mitrović M. Einstein Field Equation, Recursion Operators, Noether and Master Symmetries in Conformable Poisson Manifolds. Universe. 2022; 8(4):247. https://doi.org/10.3390/universe8040247
Chicago/Turabian StyleHounkonnou, Mahouton Norbert, Mahougnon Justin Landalidji, and Melanija Mitrović. 2022. "Einstein Field Equation, Recursion Operators, Noether and Master Symmetries in Conformable Poisson Manifolds" Universe 8, no. 4: 247. https://doi.org/10.3390/universe8040247
APA StyleHounkonnou, M. N., Landalidji, M. J., & Mitrović, M. (2022). Einstein Field Equation, Recursion Operators, Noether and Master Symmetries in Conformable Poisson Manifolds. Universe, 8(4), 247. https://doi.org/10.3390/universe8040247






