Numerical Equilibrium Configurations and Quadrupole Moments of Post-Merger Differentially Rotating Relativistic Stars
Abstract
1. Introduction
2. Theoretical Framework
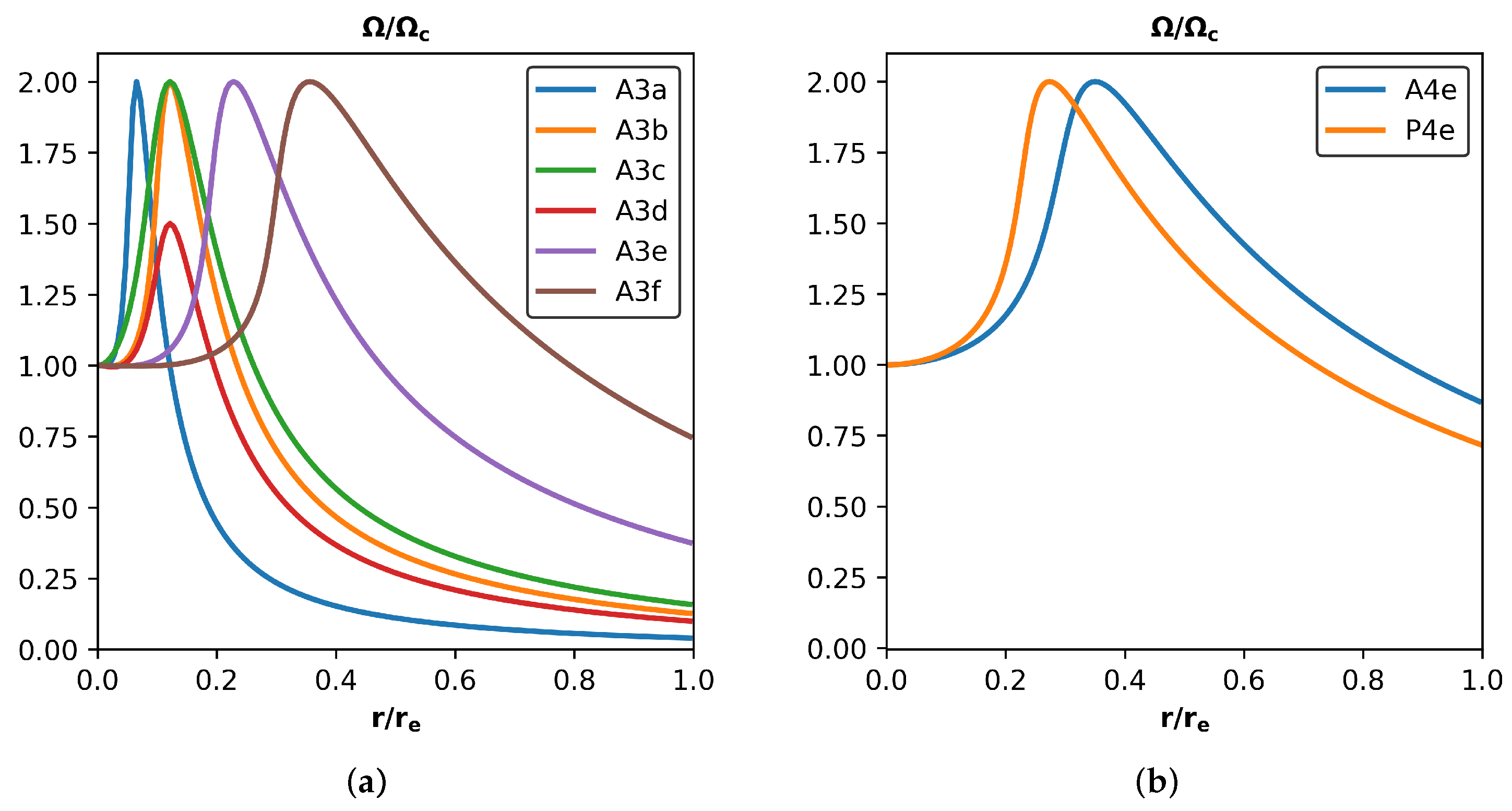
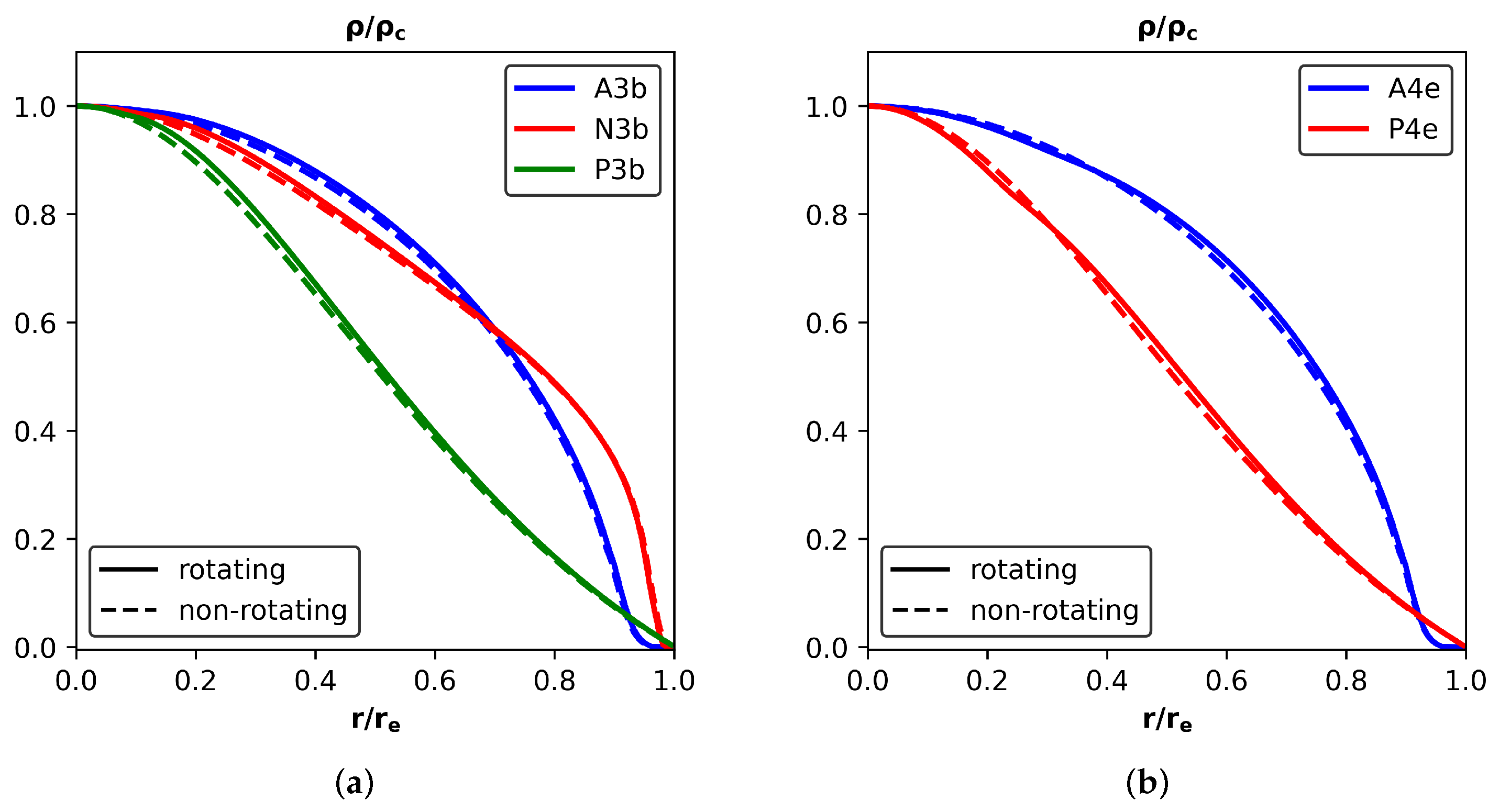
3. Equilibrium Configurations and Quadrupole Moments
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Implementation of the Uryū Laws in the XNS Code
Appendix A.1. The Uryu3 Law
- initialization of the values of the parameters , , and p;
- evaluation of and ;
- evaluation of the integral (A14).
Appendix A.2. The Uryu4 Law
- initialization of the values of the parameters , and ;
- evaluation of and ;
- evaluation of the integral (A19).
References
- Abbott, B.P. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Bailes, M. Gravitational-wave physics and astronomy in the 2020s and 2030s. Nat. Rev. Phys. 2021, 3, 344–366. [Google Scholar] [CrossRef]
- Hotokezaka, K.; Kyutoku, K.; Okawa, H.; Shibata, M.; Kiuchi, K. Binary neutron star mergers: Dependence on the nuclear equation of state. Phys. Rev. D 2011, 83, 124008. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Kiuchi, K.; Kyutoku, K.; Shibata, M. Gravitational Waves and Neutrino Emission from the Merger of Binary Neutron Stars. Phys. Rev. Lett. 2011, 107, 051102. [Google Scholar] [CrossRef] [PubMed]
- Kastaun, W.; Galeazzi, F. Properties of hypermassive neutron stars formed in mergers of spinning binaries. Phys. Rev. D 2015, 91, 064027. [Google Scholar] [CrossRef]
- De Pietri, R.; Feo, A.; Maione, F.; Löffler, F. Modeling equal and unequal mass binary neutron star mergers using public codes. Phys. Rev. D 2016, 93, 064047. [Google Scholar] [CrossRef]
- Ciolfi, R.; Kastaun, W.; Giacomazzo, B.; Endrizzi, A.; Siegel, D.M.; Perna, R. General relativistic magnetohydrodynamic simulations of binary neutron star mergers forming a long-lived neutron star. Phys. Rev. D 2017, 95, 063016. [Google Scholar] [CrossRef]
- Kiuchi, K.; Kyutoku, K.; Sekiguchi, Y.; Shibata, M. Global simulations of strongly magnetized remnant massive neutron stars formed in binary neutron star mergers. Phys. Rev. D 2018, 97, 124039. [Google Scholar] [CrossRef]
- Ciolfi, R.; Kastaun, W.; Kalinani, J.V.; Giacomazzo, B. First 100 ms of a long-lived magnetized neutron star formed in a binary neutron star merger. Phys. Rev. D 2019, 100, 023005. [Google Scholar] [CrossRef]
- De Pietri, R.; Feo, A.; Font, J.A.; Löffler, F.; Pasquali, M.; Stergioulas, N. Numerical-relativity simulations of long-lived remnants of binary neutron star mergers. Phys. Rev. D 2020, 101, 064052. [Google Scholar] [CrossRef]
- Mösta, P.; Radice, D.; Haas, R.; Schnetter, E.; Sebastiano Bernuzzi, S. A magnetar engine for short GRBs and kilonovae. Astrophys. J. Lett. 2020, 901, L37. [Google Scholar] [CrossRef]
- Kastaun, W.; Ohme, F. Numerical inside view of hypermassive remnant models for GW170817. Phys. Rev. D 2021, 104, 023001. [Google Scholar] [CrossRef]
- Nedora, V.; Bernuzzi, S.; Radice, D.; Daszuta, B.; Endrizzi, A.; Perego, A.; Prakash, A.; Safarzadeh, M.; Schianchi, F.; Logoteta, D. Numerical Relativity Simulations of the Neutron Star Merger GW170817: Long-term Remnant Evolutions, Winds, Remnant Disks, and Nucleosynthesis. Astron. J. 2021, 906, 98. [Google Scholar] [CrossRef]
- Uryū, K.; Tsokaros, A.; Baiotti, L.; Galeazzi, F.; Taniguchi, K.; Yoshida, S. Modeling differential rotations of compact stars in equilibriums. Phys. Rev. D 2017, 96, 103011. [Google Scholar] [CrossRef]
- Galeazzi, F.; Yoshida, S.; Eriguchi, Y. Differentially-rotating neutron star models with a parametrized rotation profile. Phys. Rev. D 2012, 541, A156. [Google Scholar] [CrossRef]
- Camelio, G.; Dietrich, T.; Rosswog, S.; Haskell, B. Axisymmetric models for neutron star merger remnants with realistic thermal and rotational profiles. Phys. Rev. D 2021, 103, 063014. [Google Scholar] [CrossRef]
- Bonazzola, S.; Gourgoulhon, E.; Salgado, M.; Marck, J.A. Axisymmetric rotating relativistic bodies: A new numerical approach for ’exact’ solutions. Astron. Astrophys. 1993, 278, 421–443. [Google Scholar]
- Pili, A.G.; Bucciantini, N.; Del Zanna, L. General relativistic models for rotating magnetized neutron stars in conformally flat space-time. Mon. Not. R. Astron. Soc. 2017, 470, 2469–2493. [Google Scholar] [CrossRef]
- Camelio, G.; Dietrich, T.; Marques, M.; Rosswog, S. Rotating neutron stars with nonbarotropic thermal profile. Phys. Rev. D 2019, 100, 123001. [Google Scholar] [CrossRef]
- Zhou, E.; Tsokaros, A.; Uryū, K.; Xu, R.; Shibata, M. Differentially rotating strange star in general relativity. Phys. Rev. D 2019, 100, 043015. [Google Scholar] [CrossRef]
- Passamonti, A.; Andersson, N. Merger-inspired rotation laws and the low-T/W instability in neutron stars. Mon. Not. R. Astron. Soc. 2020, 498, 5904–5915. [Google Scholar] [CrossRef]
- Xie, X.; Hawke, I.; Passamonti, A.; Andersson, N. Instabilities in neutron-star postmerger remnants. Phys. Rev. D 2020, 102, 044040. [Google Scholar] [CrossRef]
- Iosif, P.; Stergioulas, N. Equilibrium sequences of differentially rotating stars with post-merger-like rotational profiles. Mon. Not. R. Astron. Soc. 2021, 503, 850–866. [Google Scholar] [CrossRef]
- Iosif, P.; Stergioulas, N. Models of binary neutron star remnants with tabulated equations of state. Mon. Not. R. Astron. Soc. 2022, 510, 2948–2967. [Google Scholar] [CrossRef]
- Bucciantini, N.; Del Zanna, L. GRMHD in axisymmetric dynamical spacetimes-the X-ECHO code. Astron. Astrophys. 2011, 528, A101. [Google Scholar] [CrossRef]
- Pili, A.G.; Bucciantini, N.; Del Zanna, L. Axisymmetric equilibrium models for magnetized neutron stars in General Relativity under the Conformally Flat Condition. Mon. Not. R. Astron. Soc. 2014, 439, 3541–3563. [Google Scholar] [CrossRef]
- Cordero-Carrión, I.; Cerdá-Durán, P.; Dimmelmeier, H.; Jaramillo, J.L.; Novak, J.; Gourgoulhon, E. Improved constrained scheme for the Einstein equations: An approach to the uniqueness issue. Phys. Rev. D 2009, 79, 024017. [Google Scholar] [CrossRef]
- Bucciantini, N.; Pili, A.G.; Del Zanna, L. The role of currents distribution in general relativistic equilibria of magnetized neutron stars. Mon. Not. R. Astron. Soc. 2015, 447, 3278–3290. [Google Scholar] [CrossRef]
- Soldateschi, J.; Bucciantini, N.; Del Zanna, L. Axisymmetric equilibrium models for magnetised neutron stars in scalar-tensor theories. Astron. Astrophys. 2020, 640, A44. [Google Scholar] [CrossRef]
- Soldateschi, J.; Bucciantini, N.; Del Zanna, L. Magnetic deformation of neutron stars in scalar-tensor theories. Astron. Astrophys. 2021, 645, A39. [Google Scholar] [CrossRef]
- Soldateschi, J.; Bucciantini, N.; Del Zanna, L. Quasi-universality of the magnetic deformation of neutron stars in general relativity and beyond. Astron. Astrophys. 2021, 654, A162. [Google Scholar] [CrossRef]
- Del Zanna, L.; Zanotti, O.; Bucciantini, N.; Londrillo, P. ECHO: An Eulerian Conservative High Order scheme for general relativistic magnetohydrodynamics and magnetodynamics. Astron. Astrophys. 2007, 473, 11–30. [Google Scholar] [CrossRef]
- Franceschetti, K.; Del Zanna, L. General Relativistic Mean-Field Dynamo Model for Proto-Neutron Stars. Universe 2020, 6, 83. [Google Scholar] [CrossRef]
- Komatsu, H.; Eriguchi, Y.; Hachisu, I. Rapidly rotating general relativistic stars. I-Numerical method and its application to uniformly rotating polytropes. Mon. Not. R. Astron. Soc. 1989, 237, 355–379. [Google Scholar] [CrossRef]
- Stergioulas, N. Rotating Stars in Relativity. Living Rev. Relativ. 2003, 6, 3. [Google Scholar] [CrossRef] [PubMed]
- Stergioulas, N.; Apostolatos, T.A.; Font, J.A. Non-linear pulsations in differentially rotating neutron stars: Mass-shedding-induced damping and splitting of the fundamental mode. Mon. Not. R. Astron. Soc. 2004, 352, 1089–1101. [Google Scholar] [CrossRef]
- Espino, P.L.; Paschalidis, V. Revisiting the maximum mass of differentially rotating neutron stars in general relativity with realistic equations of state. Phys. Rev. D 2019, 99, 083017. [Google Scholar] [CrossRef]
- Bauswein, A.; Stergioulas, N. Semi-analytic derivation of the threshold mass for prompt collapse in binary neutron-star mergers. Mon. Not. R. Astron. Soc. 2017, 471, 4956–4965. [Google Scholar] [CrossRef]
- Bozzola, G.; Stergioulas, N.; Bauswein, A. Universal relations for differentially rotating relativistic stars at the threshold to collapse. Mon. Not. R. Astron. Soc. 2018, 474, 3557–3564. [Google Scholar] [CrossRef]
- Carter, B. The commutation property of a stationary, axisymmetric system. Commun. Math. Phys. 1970, 17, 233–238. [Google Scholar] [CrossRef]
- Carter, B. Black Hole Equilibrium States. In Black holes (Les astres occlus); DeWitt, C., DeWitt, B.S., Eds.; Gordon and Breach: New York, NY, USA, 1973; pp. 57–214. [Google Scholar]
- Gourgoulhon, E.; Markakis, C.; Uryū, K.; Eriguchi, Y. Magnetohydrodynamics in stationary and axisymmetric spacetimes: A fully covariant approach. Phys. Rev. D 2011, 83, 104007. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation. Astrophys. J. 1972, 178, 347–369. [Google Scholar] [CrossRef]
- Iosif, P.; Stergioulas, N. On the accuracy of the IWM–CFC approximation in differentially rotating relativistic stars. Gen. Relativ. Gravit. 2014, 86, 1800. [Google Scholar] [CrossRef][Green Version]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804. [Google Scholar] [CrossRef]
- Fortin, M.; Providencia, C.; Raduta, A.R.; Gulminelli, F.; Zdunik, J.L.; Haensel, P.; Bejger, M. Neutron star radii and crusts: Uncertainties and unified equations of state. Phys. Rev. C 2016, 94, 035804. [Google Scholar] [CrossRef]
- Urbanec, M.; Miller, J.C.; Stuchlík, Z. Quadrupole moments of rotating neutron stars and strange stars. Mon. Not. R. Astron. Soc. 2013, 433, 1903–1909. [Google Scholar] [CrossRef]
- Breu, C.; Rezzolla, L. Maximum mass, moment of inertia and compactness of relativistic star. Mon. Not. R. Astron. Soc. 2016, 459, 646–656. [Google Scholar] [CrossRef]
- Cerdá-Durán, P.; Quilis, V.; Font, J.A. AMR simulations of the low bar-mode instability of neutron stars. Comput. Phys. Commun. 2007, 177, 288–297. [Google Scholar] [CrossRef][Green Version]
- Thorne, K.S. Multipole expansions of gravitational radiation. Rev. Mod. Phys. 1980, 52, 299. [Google Scholar] [CrossRef]
- Frieben, J.; Rezzolla, L. Equilibrium models of relativistic stars with a toroidal magnetic field. Mon. Not. R. Astron. Soc. 2012, 427, 3406–3426. [Google Scholar] [CrossRef]
- Stergioulas, N.; Friedman, J.L. Comparing Models of Rapidly Rotating Relativistic Stars Constructed by Two Numerical Methods. Astrophys. J. 1995, 444, 306. [Google Scholar] [CrossRef]
- Pili, A.; Bucciantini, N.; Del Zanna, L. General relativistic neutron stars with twisted magnetosphere. Mon. Not. R. Astron. Soc. 2015, 447, 2821–2835. [Google Scholar] [CrossRef]
- Soldateschi, J.; Bucciantini, N. Detectability of Continuous Gravitational Waves from Magnetically Deformed Neutron Stars. Galaxies 2021, 9, 101. [Google Scholar] [CrossRef]
- Cutler, C. Gravitational Waves from Neutron Stars with Large Toroidal B-fields. Phys. Rev. D 2002, 66, 084025. [Google Scholar] [CrossRef]
- Del Zanna, L.; Tomei, N.; Franceschetti, K.; Bugli, M.; Bucciantini, N. General Relativistic Magnetohydrodynamics Mean-Field Dynamos. Fluids 2022, 7, 87. [Google Scholar] [CrossRef]

| Model | (×10−3) | J (×10−1) | (×10−3) | I (×10) | |||||
|---|---|---|---|---|---|---|---|---|---|
| A3a | 0.4 | 6.42 | 7.59 | 0.88 | 0.528 | 1.214 | 1.122 | 0.86 | 6.008 |
| A3b | 0.8 | 6.42 | 7.62 | 2.79 | 1.645 | 1.240 | 1.145 | 6.02 | 5.897 |
| A3c | 0.8 | 6.42 | 7.63 | 3.49 | 2.022 | 1.250 | 1.154 | 8.30 | 5.800 |
| A3d | 0.8 | 6.42 | 7.60 | 2.20 | 1.270 | 1.225 | 1.133 | 3.71 | 5.784 |
| A3e | 1.5 | 6.58 | 7.87 | 8.28 | 4.926 | 1.322 | 1.219 | 32.4 | 5.950 |
| A3f | 2.5 | 7.02 | 8.48 | 16.5 | 10.53 | 1.467 | 1.351 | 84.3 | 6.376 |
| A4a | 0.4 | 6.42 | 7.60 | 2.02 | 0.958 | 1.218 | 1.127 | 2.00 | 4.750 |
| A4b | 0.8 | 6.46 | 7.67 | 4.83 | 2.348 | 1.251 | 1.156 | 9.81 | 4.864 |
| A4c | 0.8 | 6.46 | 7.65 | 3.70 | 1.764 | 1.232 | 1.138 | 5.88 | 4.764 |
| A4d | 1.5 | 6.66 | 7.98 | 11.2 | 5.889 | 1.346 | 1.240 | 40.4 | 5.277 |
| A4e | 2.5 | 7.14 | 8.63 | 19.2 | 11.72 | 1.502 | 1.382 | 93.3 | 6.096 |
| N3a | 0.4 | 6.50 | 9.34 | 2.54 | 5.195 | 3.083 | 2.582 | 2.66 | 20.42 |
| N3b | 0.8 | 6.50 | 9.41 | 6.98 | 14.04 | 3.138 | 2.628 | 15.1 | 20.11 |
| N3c | 0.8 | 6.50 | 9.43 | 8.31 | 16.51 | 3.158 | 2.645 | 19.5 | 19.86 |
| N3d | 0.8 | 6.50 | 9.37 | 5.32 | 10.51 | 3.106 | 2.602 | 8.81 | 19.76 |
| N4a | 0.4 | 6.50 | 9.35 | 4.36 | 7.885 | 3.093 | 2.591 | 5.03 | 18.10 |
| N4b | 0.8 | 6.50 | 9.44 | 9.50 | 17.42 | 3.161 | 2.648 | 20.6 | 18.33 |
| N4c | 0.8 | 6.50 | 9.39 | 7.15 | 12.82 | 3.118 | 2.612 | 11.8 | 17.93 |
| P3a | 0.4 | 8.22 | 9.81 | 0.69 | 0.928 | 1.644 | 1.522 | 0.88 | 13.51 |
| P3b | 0.8 | 8.22 | 9.84 | 2.17 | 2.864 | 1.668 | 1.543 | 6.17 | 13.20 |
| P3c | 0.8 | 8.22 | 9.85 | 2.71 | 3.520 | 1.678 | 1.552 | 8.53 | 12.97 |
| P3d | 0.8 | 8.22 | 9.83 | 1.70 | 2.220 | 1.655 | 1.533 | 3.78 | 13.03 |
| P3e | 1.5 | 8.30 | 10.0 | 6.59 | 8.605 | 1.769 | 1.635 | 33.6 | 13.07 |
| P3f | 2.5 | 8.90 | 10.9 | 13.2 | 19.67 | 2.005 | 1.848 | 90.9 | 14.86 |
| P4a | 0.4 | 8.22 | 9.82 | 1.66 | 1.735 | 1.649 | 1.527 | 2.11 | 10.47 |
| P4b | 0.8 | 8.22 | 9.86 | 3.98 | 4.203 | 1.682 | 1.557 | 10.3 | 10.56 |
| P4c | 0.8 | 8.26 | 9.87 | 3.02 | 3.171 | 1.664 | 1.540 | 6.16 | 10.49 |
| P4d | 1.5 | 8.42 | 10.2 | 9.26 | 10.58 | 1.805 | 1.667 | 43.0 | 11.42 |
| P4e | 2.5 | 9.14 | 11.2 | 15.9 | 22.63 | 2.068 | 1.904 | 103 | 14.24 |
| Model | e | Q | ||
|---|---|---|---|---|
| A3a | 0.99 | 0.003 | 3.4 | 0.04 |
| A3b | 0.96 | 0.020 | 3.3 | 0.26 |
| A3c | 0.96 | 0.027 | 3.2 | 0.36 |
| A3d | 0.98 | 0.012 | 3.3 | 0.16 |
| A3e | 0.87 | 0.095 | 2.9 | 1.45 |
| A3f | 0.75 | 0.212 | 2.5 | 4.20 |
| A4a | 0.98 | 0.007 | 3.3 | 0.09 |
| A4b | 0.94 | 0.031 | 3.2 | 0.42 |
| A4c | 0.96 | 0.019 | 3.2 | 0.25 |
| A4d | 0.85 | 0.115 | 2.9 | 1.83 |
| A4e | 0.73 | 0.229 | 2.5 | 4.77 |
| N3a | 0.98 | 0.008 | 3.1 | 0.31 |
| N3b | 0.93 | 0.042 | 2.8 | 1.73 |
| N3c | 0.91 | 0.053 | 2.7 | 2.25 |
| N3d | 0.96 | 0.025 | 2.8 | 1.03 |
| N4a | 0.97 | 0.015 | 2.9 | 0.57 |
| N4b | 0.91 | 0.055 | 2.7 | 2.40 |
| N4c | 0.95 | 0.033 | 2.8 | 1.39 |
| P3a | 0.99 | 0.003 | 3.2 | 0.07 |
| P3b | 0.96 | 0.019 | 3.1 | 0.48 |
| P3c | 0.94 | 0.026 | 3.0 | 0.66 |
| P3d | 0.97 | 0.012 | 3.1 | 0.30 |
| P3e | 0.87 | 0.094 | 2.8 | 2.69 |
| P3f | 0.72 | 0.219 | 2.4 | 8.44 |
| P4a | 0.98 | 0.007 | 3.2 | 0.16 |
| P4b | 0.94 | 0.032 | 3.1 | 0.81 |
| P4c | 0.96 | 0.019 | 3.1 | 0.48 |
| P4d | 0.83 | 0.118 | 2.7 | 3.53 |
| P4e | 0.68 | 0.242 | 2.3 | 9.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franceschetti, K.; Del Zanna, L.; Soldateschi, J.; Bucciantini, N. Numerical Equilibrium Configurations and Quadrupole Moments of Post-Merger Differentially Rotating Relativistic Stars. Universe 2022, 8, 172. https://doi.org/10.3390/universe8030172
Franceschetti K, Del Zanna L, Soldateschi J, Bucciantini N. Numerical Equilibrium Configurations and Quadrupole Moments of Post-Merger Differentially Rotating Relativistic Stars. Universe. 2022; 8(3):172. https://doi.org/10.3390/universe8030172
Chicago/Turabian StyleFranceschetti, Kevin, Luca Del Zanna, Jacopo Soldateschi, and Niccolò Bucciantini. 2022. "Numerical Equilibrium Configurations and Quadrupole Moments of Post-Merger Differentially Rotating Relativistic Stars" Universe 8, no. 3: 172. https://doi.org/10.3390/universe8030172
APA StyleFranceschetti, K., Del Zanna, L., Soldateschi, J., & Bucciantini, N. (2022). Numerical Equilibrium Configurations and Quadrupole Moments of Post-Merger Differentially Rotating Relativistic Stars. Universe, 8(3), 172. https://doi.org/10.3390/universe8030172






