Late Time Acceleration of the Universe from Quantum Gravity

Abstract

We show that the accelerating expansion phase of the universe can emerge from the group field theory formalism, a candidate theory of quantum gravity. The cosmological evolution can be extracted from condensate states using the mean field approximation, in a form of modified FLRW equations. By introducing an effective equation of state w, we can reveal the relevant features of the evolution and show that, with the proper choice of the parameters, w will approach $-1$, leading to an accelerating phase dominated by the cosmological constant effectively.

1. Introduction

Since its discovery [1,2], the accelerating expansion of our universe remains a challenge to theoretical physics. One way to achieve the acceleration is to introduce dark energy, whose equation of state is close to $-1$ [3]. The simplest candidate would be the cosmological constant $\Lambda$ [4], but the smallness of its observed value [5], compared to the theoretical expectations from the vacuum energy of particle physics [6] or from the renormalisation flow of couplings in general relativity (GR) [7], make it difficult to find a compelling origin of $\Lambda$.

Another route, besides the more particle-theoretic approach, is to modify gravity theory [3]. In particular, the quantum gravity effects can be viewed as modifications to GR at the effective level. For example, the acceleration of the universe can be reproduced within the formalism of an asymptotically safe cosmology [8], of the Dvali–Gabadadze–Porrati braneworld model [9], and of condensate cosmology in group field theory (GFT) [10], without the need for dark energy or the cosmological constant. On the other hand, even if some dark energy fields do exist, their behaviour may be subject to quantum gravity effects; for instance, some future singularities could be avoided [11].

In this work, we also followed this approach. By summarizing the main results obtained in [10], we show that in GFT condensate cosmology, the late time acceleration of the universe’s expansion will emerge naturally, without introducing any dark energy field that may have mysterious properties such as negative pressure.

As a candidate theory of quantum gravity, instead of the familiar spacetime degrees of freedom, GFT provides more abstract, non-spatiotemporal entities, from which the continuum spacetime should emerge [12,13,14]. Furthermore, the cosmological evolution can be extracted from suitably constructed condensate states, which include a large number of quanta to recover the continuum limit [15,16,17,18,19,20,21,22]. In this formalism, the universe can be viewed as a quantum fluid constituted by GFT quanta, and its dynamics follows from the fundamental GFT theory through a hydrodynamic approximation. Various works have been performed in this direction; for example, using the GFT condensate, one can derive the modified FLRW equation [16], a varying Newton constant G [23], and the inflationary phase without the need for inflaton [24]. In this report, we summarise the main results obtained recently in [10], where we made a further step and showed that, using the GFT condensate, it is also possible to reproduce a long-lasting acceleration phase in our cosmological expansion at late times.

The report is organised as follows. In Section 2, we briefly review the basics of the GFT formalism and its relation to cosmology. The dynamics and the modified FLRW equation are given in Section 3, where we also introduce the effective equation of state to make our discussion more explicit. Section 4 presents our main result, that a long-lasting accelerated expansion at the late time can be reproduced in our model, of purely quantum gravity origin. Finally, in Section 5, we give a brief summary of our results.

2. Condensate Cosmology in GFT

For the emergence of $4d$ spacetime, one usually chooses the GFT field to be a map over four copies of the $SU\left(2\right)$ group, $\phi :SU{\left(2\right)}^4\to \mathbb{C},\phi \left(g_v\right)=\phi (g_1,g_2,g_3,g_4)$ [12]. Geometrically, to associate the basic quanta of our theory with a tetrahedron, we further require that the field $\phi \left(g_v\right)$ be right invariant $\phi \left(g_{v}h\right)=\phi (g_{1}h,g_{2}h,g_{3}h,g_{4}h)=\phi \left(g_v\right),\forall h\in SU\left(2\right)$ [12]. Furthermore, since the spacetime is emergent, specifically there is no time to start with, one usually needs a free massless scalar field as a relational clock to track the evolution; this way, the field $\phi (g_v,\varphi )$ becomes time dependent.

The right invariance of $\phi (g_v,\varphi )$ under $SU\left(2\right)$ enables us to project the field using the Peter–Weyl decomposition onto the complete and orthonormal basis of $L^2(SU{\left(2\right)}^4/SU\left(2\right))$, the space of square integrable functions over quotient space $SU{\left(2\right)}^4/SU\left(2\right)$. Such a basis can be given by the spin network vertex functions ${\kappa }_{\overrightarrow{x}}\left(g_v\right)$, which are associated graphically with a spin network four-vertex labelled by $\overrightarrow{x}=(\overrightarrow{j},\overrightarrow{m},\iota )$, i.e., a node with $d=4$ open links associated with four spins $\overrightarrow{j}=(j_1,j_2,j_3,j_4)$, together with angular momentum projections $\overrightarrow{m}$ and the intertwiner quantum number $\iota$ associated instead with the node itself [25]. One thing to be noted is that these quantum numbers characterise the geometrical properties of the tetrahedron, and in particular, each spin label $j_i$ determines the area of the associated face [25,26].

More explicitly, in the second quantised form, the field operators can be written as:

$$\begin{array}{c}\hfill \widehat{\phi }(g_v,\varphi )={\displaystyle \sum _{\overrightarrow{x}}}{\widehat{c}}_{\overrightarrow{x}}\left(\varphi \right){\kappa }_{\overrightarrow{x}}\left(g_v\right),{\widehat{\phi }}^{†}(g_v,\varphi )={\displaystyle \sum _{\overrightarrow{x}}}{\widehat{c}}_{\overrightarrow{x}}^{†}\left(\varphi \right){\overline{\kappa }}_{\overrightarrow{x}}\left(g_v\right),\end{array}$$

(1)

where ${\widehat{c}}_{\overrightarrow{x}}\left(\varphi \right)$ and ${\widehat{c}}_{\overrightarrow{x}}^{†}\left(\varphi \right)$ are the annihilation and creation operator, respectively.

Having the basic operators in hand, the next step would be to find a suitable state for the spacetime of interest, at least approximately. In our case, the homogeneous universe at a given time can be approximated by the coherent peaked state (CPS), which is constituted by a large number of quanta concentrated in a fixed relational time ${\varphi }_0$ [16,22]:

$$\begin{array}{c}\hfill |{\sigma }_{\epsilon };{\varphi }_0,{\pi }_0\rangle =\mathcal{N}\left(\sigma \right)exp\left(\int {\left(\mathrm{d}g\right)}^4\mathrm{d}\varphi {\eta }_{\epsilon }(\varphi -{\varphi }_0,{\pi }_0)\tilde{\sigma }(g_v,\varphi ){\widehat{\phi }}^{†}(g_v,\varphi )\right)|0\rangle ,\end{array}$$

(2)

with $|0\rangle$ the vacuum state, defined by $\widehat{\phi }(g_v,\varphi )|0\rangle =0$ for all $g_v$ and $\varphi$, and $\mathcal{N}\left(\sigma \right)$ a suitable normalisation factor. Peaking function ${\eta }_{\epsilon }(\varphi -{\varphi }_0,{\pi }_0)$ is peaked around ${\varphi }_0$ with a typical width given by $\epsilon$, and the fluctuations of the operator corresponding to the conjugate momentum of the scalar field $\varphi$ are controlled by ${\pi }_0$. We call $\tilde{\sigma }(g_v,\varphi )$ the reduced condensate wave function and assume that it does not modify the peaking property of the CPS [22].

The wave function $\tilde{\sigma }(g_v,\varphi )$ can be decomposed using the Peter–Weyl decomposition as well. For the emerged universe to be isotropic, we require the individual quanta to be as isotropic as possible, enforcing $\tilde{\sigma }(g_v,\varphi )$ to only have support over equilateral tetrahedra [16], for which the area of the four faces is equal. Since each area is determined by the associated spin $j_i$ of the face, we see that only the coefficients with $j_1=j_2=j_3=j_4=j$ survive in the decomposition [16].

$$\begin{array}{c}\hfill \tilde{\sigma }(g_v,\varphi )={\displaystyle \sum _j}{\tilde{\sigma }}_j\left(\varphi \right){\overline{\mathcal{I}}}_{\overrightarrow{m}}^{j,{\iota }_{+}}{\mathcal{I}}_{\overrightarrow{n}}^{j,{\iota }_{+}}{(2j+1)}^2{\displaystyle \prod _{l=1}^4}{D}_{m_l{n}_l}^{j_l}\left(g_l\right),\end{array}$$

(3)

where we write j for $\overrightarrow{j}=(j_1,j_2,j_3,j_4)=(j,j,j,j)$, ${\mathcal{I}}_{\overrightarrow{m}}^{j,{\iota }_{+}}$ is the intertwiner labelled by $\iota$, and $D_{m_l{n}_l}^{j_l}\left(g_l\right)$ are the Wigner matrix functions for $SU\left(2\right)$.

3. Volume Dynamics and Equation of State

The decomposition (3) indicates that the time dependence of the condensate is only encoded in ${\sigma }_j\left(\varphi \right)$; hence, effectively, the dynamics of the condensate can be given by the following action:

$$\begin{array}{ccc}\hfill S(\overline{\tilde{\sigma }},\tilde{\sigma })& =\hfill & \int \mathrm{d}{\varphi }_0\left\{{\displaystyle \sum _j}\left[{\overline{\tilde{\sigma }}}_j\left({\varphi }_0\right){\tilde{\sigma }}_j^{″}\left({\varphi }_0\right)-2\mathrm{i}{\tilde{\pi }}_0{\overline{\tilde{\sigma }}}_j\left({\varphi }_0\right){\tilde{\sigma }}_j^{\prime }\left({\varphi }_0\right)-{\xi }_j^2{\overline{\tilde{\sigma }}}_j\left({\varphi }_0\right){\tilde{\sigma }}_j\left({\varphi }_0\right)\right]+U(\overline{\tilde{\sigma }},\tilde{\sigma })\right\},\end{array}$$

(4)

where ${\displaystyle {\tilde{\pi }}_0=\frac{{\pi }_0}{\epsilon {\pi }_0^2-1}}$, ${\xi }_j$ is an effective parameter encoding the details of the kinetic term of the fundamental GFT action (in the isotropic restriction), and ${}^{\prime }$ denotes the derivatives with respect to ${\varphi }_0$. Finally, from a rather phenomenological approach, the interaction kernel $U(\overline{\tilde{\sigma }},\tilde{\sigma })$ can be modelled in a simple, rather general form [24]:

$$\begin{array}{c}\hfill U(\overline{\tilde{\sigma }},\tilde{\sigma })={\displaystyle \sum _j}\left(\frac{2{\lambda }_j}{n_j}|{\tilde{\sigma }}_j\left({\varphi }_0\right){|}^{n_j}+\frac{2{\mu }_j}{n_j^{\prime }}{\left|{\tilde{\sigma }}_j\left({\varphi }_0\right)\right|}^{n_j^{\prime }}\right),\end{array}$$

(5)

where ${\lambda }_j$ and ${\mu }_j$ are interaction couplings corresponding to each mode j satisfying that $|{\mu }_j|\ll |{\lambda }_j|\ll |{\xi }_j^2-{\tilde{\pi }}_0^2|$, and we assumed that the constants $n_j^{\prime }>n_j>2$.

Varying the action (4) with respect to ${\overline{\tilde{\sigma }}}_j$, we can obtain the equation of motion [22,24]. For a purpose that will be clear later, we can decompose ${\tilde{\sigma }}_j\left(\varphi \right)={\rho }_j\left(\varphi \right)exp\left[\mathrm{i}{\theta }_j\left(\varphi \right)\right]$ into module ${\rho }_j\left(\varphi \right)$ and phase ${\theta }_j\left(\varphi \right)$, then the equation of motion splits into the imaginary and real part, respectively. The imaginary part corresponds to a conserved quantity:

$$\begin{array}{c}\hfill Q_j=({\theta }_j^{\prime }-{\tilde{\pi }}_0){\rho }_j^2,\end{array}$$

(6)

whose derivative vanishes, $Q_j^{\prime }=0$. Then, the real part becomes [22,24]:

$$\begin{array}{c}\hfill {\rho }_j^{″}-\frac{Q_j^2}{{\rho }_j^3}-m_j^2{\rho }_j+{\lambda }_j{\rho }_j^{n_j-1}+{\mu }_j{\rho }_j^{n_j^{\prime }-1}=0,\end{array}$$

(7)

where ${\displaystyle m_j^2={\xi }_j^2-{\tilde{\pi }}_0^2}$. This equation can be integrated once directly, providing another conserved quantity, which corresponds to the “clock-time translation” invariance of the system [16,22,24],

$$\begin{array}{c}\hfill E_j=\frac{1}{2}{\left({\rho }_j^{\prime }\right)}^2+\frac{Q_j^2}{2{\rho }_j^2}-\frac{1}{2}{m}_j^2{\rho }_j^2+\frac{{\lambda }_j}{n_j}{\rho }_j^{n_j}+\frac{{\mu }_j}{n_j^{\prime }}{\rho }_j^{n_j^{\prime }}.\end{array}$$

(8)

Now, we are in a position to extract observables from the condensates. In the condensate, for each equilateral tetrahedron characterised by mode j, we can associate a volume ${\mathcal{V}}_j\propto l_p^3{j}^{3/2}$, and the module square $|{\sigma }_j{|}^2={\rho }_j^2$ gives the number of such tetrahedra. Hence, the total volume of the universe can be approximated by (ignoring the quantum fluctuations) [16,22]:

$$\begin{array}{c}\hfill \mathcal{V}\left({\varphi }_0\right)\approx {\displaystyle \sum _j}{\mathcal{V}}_j{\rho }_j{\left({\varphi }_0\right)}^2.\end{array}$$

(9)

Using Equations (7) and (8), we obtain the modified FLRW equations [16]:

$${\left.(\frac{{\mathcal{V}}^{\prime }}{3\mathcal{V}}\right)}^2={\left[\frac{2{\sum }_j{\mathcal{V}}_j\sqrt{2E_j{\rho }_j^2 - Q_j^2 + m_j^2{\rho }_j^4 - \frac{2}{n_j}{\lambda }_j{\rho }_j^{n_j+2}-\frac{2}{n_j^{\prime }}{\mu }_j{\rho }_j^{n_j^{\prime }+2}}}{3{\sum }_k{\mathcal{V}}_k{\rho }_k^2}\right]}^2,$$

(10)

$$\frac{{\mathcal{V}}^{″}}{\mathcal{V}}=\frac{2{\sum }_j{\mathcal{V}}_j\left[2E_j + 2m_j^2{\rho }_j^2 - \left(1 + \frac{2}{n_j}\right){\lambda }_j{\rho }_j^{n_j} - \left(1 + \frac{2}{n_j^{\prime }}\right){\mu }_j{\rho }_j^{n_j^{\prime }}\right]}{{\sum }_k{\mathcal{V}}_k{\rho }_k^2}.$$

(11)

In the free case where ${\lambda }_j={\mu }_j=0$, the usual FLRW equation can be reproduced when the total volume is large [16].

In a homogeneous and isotropic universe, the modified FLRW Equations (10) and (11) are enough to track the evolution of our universe. However, the relevant features of the dynamics can be extracted more easily from a deduced quantity, the effective equation of state $w=-1-2\dot{H}/\left(3H^2\right)$, where H is the Hubble parameter and the dot represents the derivative with respect to the co-moving time t [3]. In relational language, w can be rewritten as [10]:

$$w=3-\frac{2\mathcal{V}{\mathcal{V}}^{″}}{{\left({\mathcal{V}}^{\prime }\right)}^2},$$

(12)

where $\mathcal{V}$ is the total volume and ${}^{\prime }$ indicates the derivative with respect to the relational time $\varphi$, and we chose the time gauge, in which the volume $\mathcal{V}=a^3$ for scale factor a; hence, there is no temporal direction in the tetrahedron as the building block of the universe; all of the normal vectors to each face of the tetrahedron are orthogonal to the time direction.

In the following, we discuss the late time cosmological expansion using the effective equation of state (12).

First of all, we see that even with only a single mode, we can already obtain useful cosmological results from our model. For example, the classical limit emerges already in the free case with only one mode, where, for a large volume, $w=1$ is a constant, corresponding to the equation of state of a free massless scalar field, the one we introduced as the relational time. In fact, substituting $w=1$ back into its definition (12), we obtain:

$$\frac{{\mathcal{V}}^{″}}{\mathcal{V}}-{\left(\frac{{\mathcal{V}}^{\prime }}{\mathcal{V}}\right)}^2=\frac{\mathcal{V}{\mathcal{V}}^{″}-{\left(\mathcal{V}\right)}^2}{{\mathcal{V}}^2}=\frac{\mathrm{d}}{\mathrm{d}\varphi }\left(\frac{{\mathcal{V}}^{\prime }}{\mathcal{V}}\right)=0;$$

hence, ${\mathcal{V}}^{\prime }/\mathcal{V}=const$, which characterises the FLRW equation using the relational language in the presence of a free massless field [16]. Furthermore, if we take into account the interaction term, by adjusting the value of couplings $\lambda$ and $\mu$, one can obtain a long-lasting inflationary phase and a cyclic universe [24].

In the next section, we consider the case where multiple modes contribute.

4. Late Time Acceleration of the Universe

In general, there is an early time acceleration phase in our model, dominated by the free parameters of the condensate, but such a phase ends quickly, no matter whether we consider only a single mode [23] or multiple modes [10]. When including interactions, however, the phase of the late time acceleration will emerge and could be long lasting. In particular, with two interactions, it is possible to combine the inflation and late time acceleration phase together [10], but for simplicity in this report, we only consider the case where each mode has only one interaction term and setting ${\mu }_j=0$ in Equations (7) and (8) for example. It should be emphasised again that here, we present a summary of our previous results; for more, details please refer to [10].

When ${\rho }_j$ is large, since $n_j>2$ and ${\mu }_j=0$, we see that the $\lambda$ term dominates in Equation (8), which can be approximated to:

$$\begin{array}{c}\hfill {\rho }_j^{\prime }\left(\varphi \right)=\sqrt{\frac{-2{\lambda }_j}{n_j}}\rho {\left({\varphi }_j\right)}^{\frac{n_j}{2}}.\end{array}$$

(13)

We require ${\lambda }_j<0$ so that ${\rho }_j^{\prime }$ stays real. Equation (13) can be easily solved, and we obtain:

$$\begin{array}{c}\hfill {\rho }_j\left(\varphi \right)={\left(\frac{2}{n_j - 2}\sqrt{\frac{-2{\lambda }_j}{n_j}}\right)}^{-\frac{2}{n_j - 2}}\frac{1}{{({\varphi }_{j\infty } - \varphi )}^{\frac{2}{n_j-2}}},\end{array}$$

(14)

where ${\varphi }_{j\infty }$ is a constant of integration, determined by initial conditions, and we have approximately [10]:

$$\begin{array}{ccc}\hfill {\varphi }_{j\infty }& =\hfill & -\frac{ln[-{\lambda }_j/\left(2m_j^2\right)]}{(n_j - 2)m_j}+\frac{1}{2m_j}ln\left[\frac{n_j^{\frac{2}{n_j-2}}\left(2m_j^2\right)}{\sqrt{E_j^2+m_j^2{Q}_j^2}}\right].\end{array}$$

(15)

Since for each j, the module ${\rho }_j$ will diverge at $\varphi ={\varphi }_{j\infty }$, the total volume $\mathcal{V}={\sum }_j{V}_j{\rho }_j^2$ will be dominated by the mode with the smallest ${\varphi }_{j\infty }$. Note that for $n_j\le 6$, the divergence of the volume at the finite relational time will not lead to singularities in our model, as the effective energy density of the whole universe will remain finite, as can be seen later [10].

On the other hand, other modes, even sub-dominated, can still modify the universe’s evolution. In fact, adding another mode will change the way that the effective equation of state w approaches its asymptotic value [10]. To see this, we considered the case with two modes, and to save space, we used ${\rho }_{1,2}$ to represent ${\rho }_{j_1,j_2}$ and similarly for other parameters. Keeping in mind that in this report, we set ${\mu }_1={\mu }_2=0$, then at a large volume, w will be dominated by the $\lambda$ terms, as well as the volume. For simplicity, we further assumed that $n_1=n_2=n$, then w will only depend on the ratio $r={\rho }_2/{\rho }_1$ in the large volume limit:

$$\begin{array}{cc}\hfill w& =3-\frac{(2 + n)({\mathcal{V}}_1 + r^2{\mathcal{V}}_2)({\mathcal{V}}_1{\lambda }_1 + r^n{\mathcal{V}}_2{\lambda }_2)}{2\left({\mathcal{V}}_1^2{\lambda }_1 + r^{2+n}{\mathcal{V}}_2^2{\lambda }_2 - 2r^{1+\frac{n}{2}}{\mathcal{V}}_1{\mathcal{V}}_2\sqrt{{\lambda }_1{\lambda }_2}\right)}\hfill \\ & =2-\frac{n}{2}-\left(\frac{n}{2}+1\right)\frac{{\mathcal{V}}_1{\mathcal{V}}_2{r}^2{\left(r^{n/2-1} - \sqrt{{\lambda }_1/{\lambda }_2}\right)}^2}{{\left(\sqrt{{\lambda }_1/{\lambda }_2}{\mathcal{V}}_1 + {\mathcal{V}}_2{r}^{n/2+1}\right)}^2},\hfill \end{array}$$

(16)

which approaches the asymptotic value ${\displaystyle w\to 2-n/2}$ when the universe’s volume is large.

When ${\varphi }_{1\infty }={\varphi }_{2\infty }$, the ratio ${\displaystyle r=\frac{{\rho }_2}{{\rho }_1}={\left(\frac{{\lambda }_1}{{\lambda }_2}\right)}^{\frac{n}{4}-\frac{1}{2}}}$ becomes a constant. Submitting to Equation (16), we obtain a constant equation of state $w=2-n/2$. Further analysis shows that w approaches this asymptotic value from above [10]. While for ${\varphi }_{1\infty }<{\varphi }_{2\infty }$, ${\rho }_1$ diverges before ${\rho }_2$ does, hence $r\to 0$ and w will approach the asymptotic value from below.

The case with $n=6$ is of particular interest since $w=-1$ corresponds to the cosmological constant. Without loss of generality, we can assume ${\varphi }_{1\infty }<{\varphi }_{2\infty }$, then the equation of state (16) can be expanded with respect to small r, and to the next to leading order, we obtain:

$$w=-1-\frac{4{\mathcal{V}}_2}{{\mathcal{V}}_1}{r}^2=-1-\frac{4{\mathcal{V}}_2}{{\mathcal{V}}_1}\frac{{\rho }_2{\left(\varphi \right)}^2}{{\rho }_1{\left(\varphi \right)}^2}.$$

Therefore, $w<-1$ for $\varphi <{\varphi }_{1\infty }$ and corresponds to some kind of phantom energy, whose energy density increases when the universe grows [3,27,28]. This leads us to the so-called phantom analogue of the de Sitter spacetime [29].

A further approximation can be made by noting that at a large volume, we can replace $\varphi$ by ${\varphi }_{1\infty }$ in ${\rho }_2\left(\varphi \right)$,

$${\rho }_2\left(\varphi \right)\to {\rho }_2\left({\varphi }_{1\infty }\right)={\left(\frac{1}{2}\sqrt{\frac{-{\lambda }_2}{3}}\right)}^{-\frac{1}{2}}\frac{1}{{({\varphi }_{2\infty }-{\varphi }_{1\infty })}^{\frac{1}{2}}}.$$

Furthermore, since ${\rho }_1\left(\varphi \right)\to \infty$, the contribution to the total volume from ${\rho }_2$ can be ignored, then the total volume reduces to $\mathcal{V}\approx {\mathcal{V}}_1{\rho }_1^2$, and we obtain:

$$w=-1-\frac{b}{\mathcal{V}},$$

(17)

where ${\displaystyle b=4{\mathcal{V}}_2{\rho }_2^2\left({\varphi }_{1\infty }\right)}$ is a constant. Notice again that since $b>0$, we have $w<-1$, and the phantom divide $w=-1$ is being crossed. Furthermore, as the volume grows, w approaches $w=-1$ fast enough, and the effective energy density of the universe will remain finite; hence, in our model there are no singularities, but a de Sitter spacetime [10]. In fact, the effective energy density ${\rho }_{\psi }$ satisfies the conservation equation ${\dot{\rho }}_{\psi }+3H(1+w){\rho }_{\psi }=0$, which for a large volume can be approximated as:

$$\frac{\mathrm{d}{\rho }_{\psi }}{\mathrm{d}\mathcal{V}}-\frac{b{\rho }_{\psi }}{{\mathcal{V}}^2}=0.$$

We can then solve for ${\rho }_{\psi }$ at a large volume as:

$${\rho }_{\psi }={\rho }_{\psi 0}{\mathrm{e}}^{-\frac{b}{\mathcal{V}}}\approx {\rho }_{\psi 0}-\frac{{\rho }_{\psi 0}b}{\mathcal{V}},$$

(18)

where ${\rho }_{\psi 0}$ is a constant of integration, representing the asymptotic value of ${\rho }_{\psi }$ when $\mathcal{V}\to \infty$. In fact, ${\rho }_{\psi 0}$ serves as the cosmological constant, and in our model, it is possible to show that the smallness of the observed value of ${\rho }_{\psi 0}$ can be related to the fact that the w crosses the phantom divide $w=-1$ only recently [30]; currently, we are working in this direction.

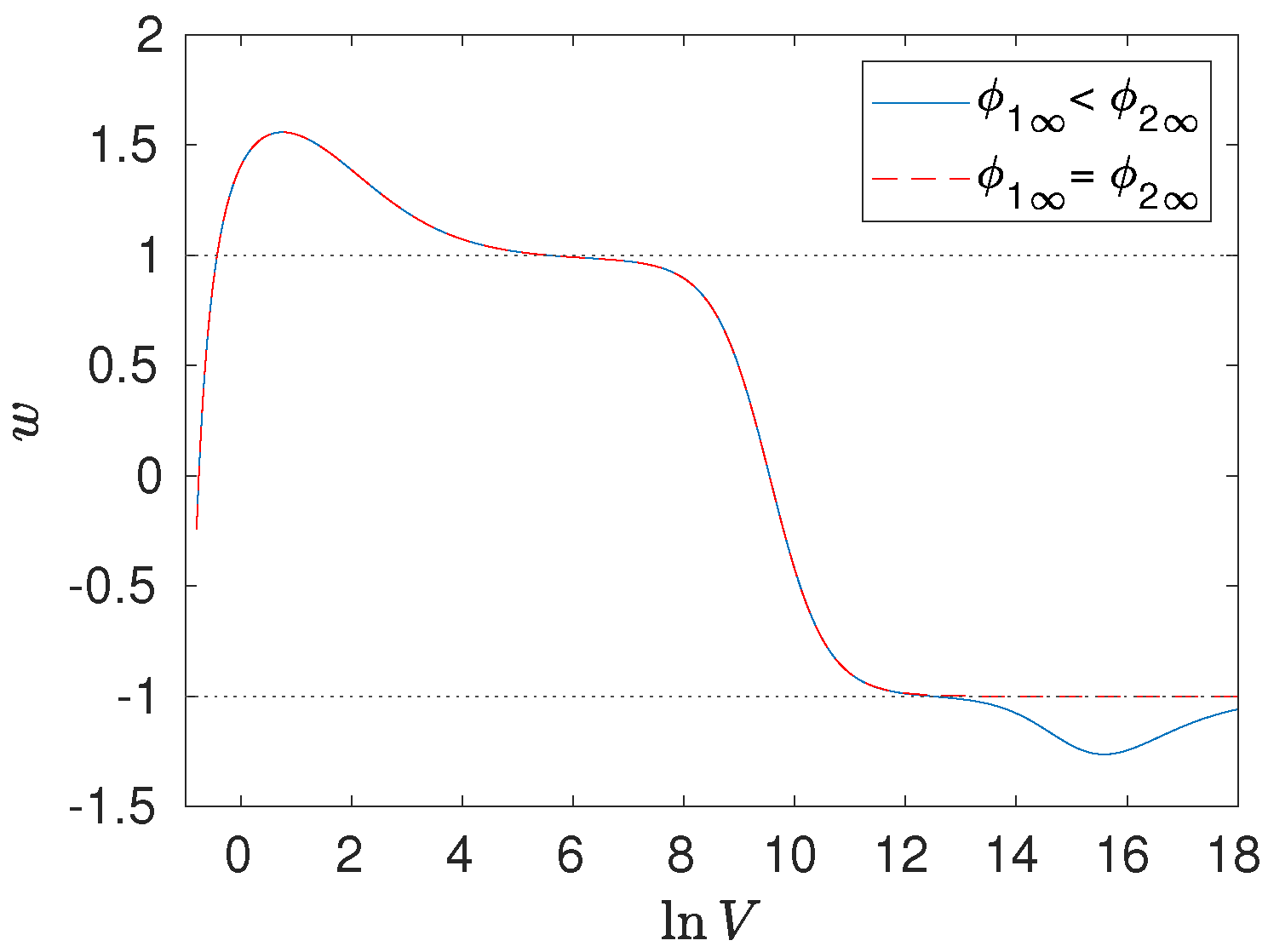
Figure 1 shows the evolution of w in our model [10]. It is clear that in the early universe, when the volume was very small, $w<-1/3$, corresponds to an early acceleration phase. As the volume grows, for ${\varphi }_{1\infty }={\varphi }_{2\infty }$, w decreases when interactions start to dominate and approaches $w=-1$ from above, while for ${\varphi }_{1\infty }<{\varphi }_{2\infty }$, the equation of state w will decreases till it crosses the phantom divide $w=-1$ and then start to increase, reaching its asymptotic value from below. This confirms our analysis in this section.

5. Discussion

This report discusses the possibility to reproduce the late time acceleration phase in the universe’s expansion from a candidate theory of quantum gravity, the group field theory. In this formalism, the universe is constituted by a large number of building blocks, which are excitations of the GFT field. Taking into account the homogeneity, the universe at a given time can be modelled by the CPS, the condensate state peaked around a relational time ${\varphi }_0$. The observables, such as the total volume, can be extracted from the CPS, and in particular, the effective equation of state w can be constructed from the volume and its derivatives.

To obtain the dynamics, we first showed that the wave function $\sigma (g_v,\varphi )$ can be decomposed into different modes ${\sigma }_j\left(\varphi \right)$, and the evolution of the universe can be extracted by considering single or multiple modes. With a suitable choice of the effective action, the equation of motion for the module ${\rho }_j\left(\varphi \right)=\left|{\sigma }_j\left(\varphi \right)\right|$ can be solved approximately at a large volume. We then used the solution (14) to investigate the behaviour of w and found that in the two-mode case with an interaction of order six, at a large volume, w will first decrease, cross the phantom divide $w=-1$, and then increase, coming close to its asymptotic value $w=-1$ from below. Furthermore, in our model, w approaches $w=-1$ fast enough; hence, we will obtain a de Sitter spacetime asymptotically without encountering singularities.

Even though at this stage, it is hard for our model to be connected with cosmological observations, such as the CMB data, there is still some progress along this direction. For example, the inhomogeneities over the FLRW background can be viewed as perturbations over GFT condensates. The power spectrum of the fluctuations are scale invariant to the leading order [31], as one would expect. The dynamics of the scalar perturbations can also be obtained from the underlying quantum gravity effects [32]. Many efforts are certainly needed in these directions.