Variations in Daily Maximum Areas and Longitudinal Widths of Solar Coronal Holes in 2017–2020
Abstract
:1. Introduction
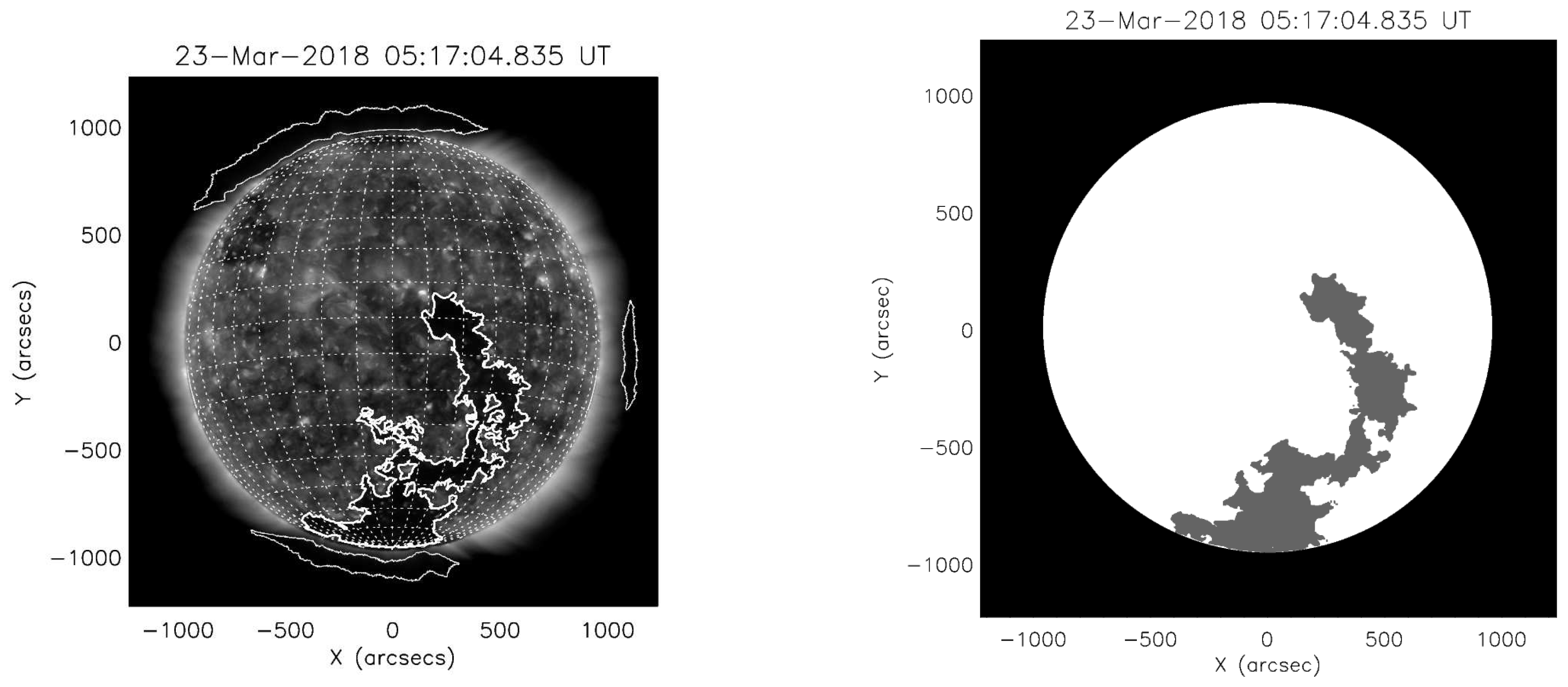
2. Observations and Data Processing
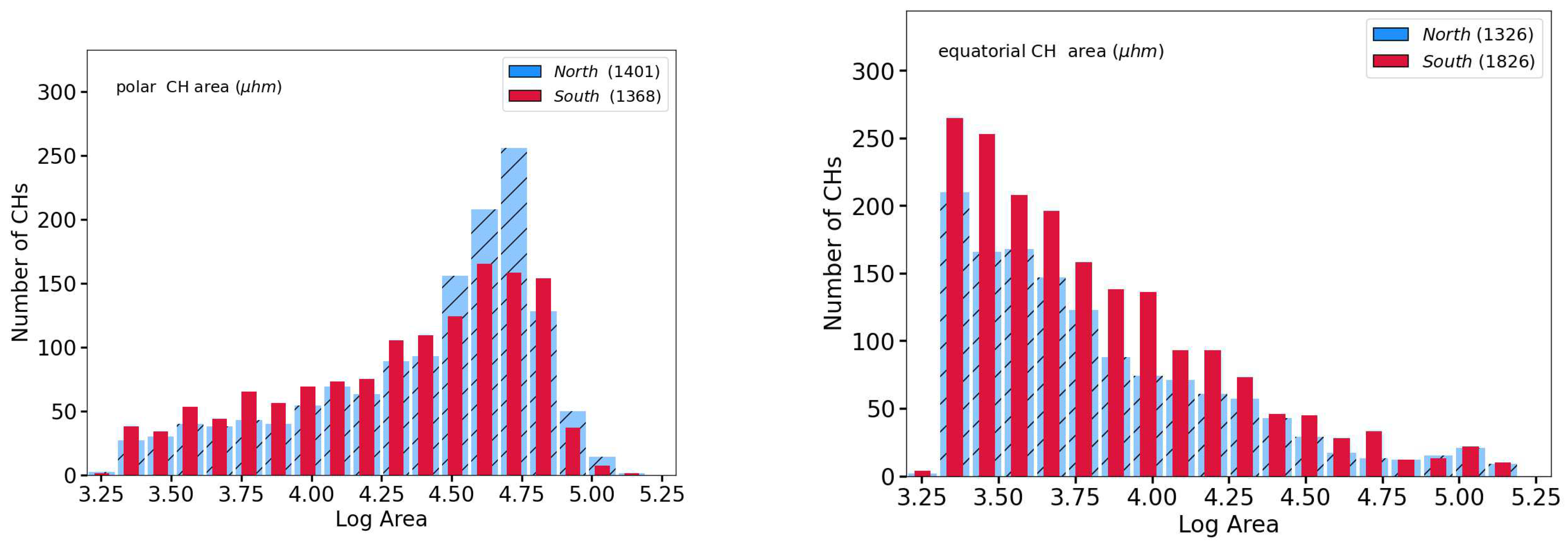
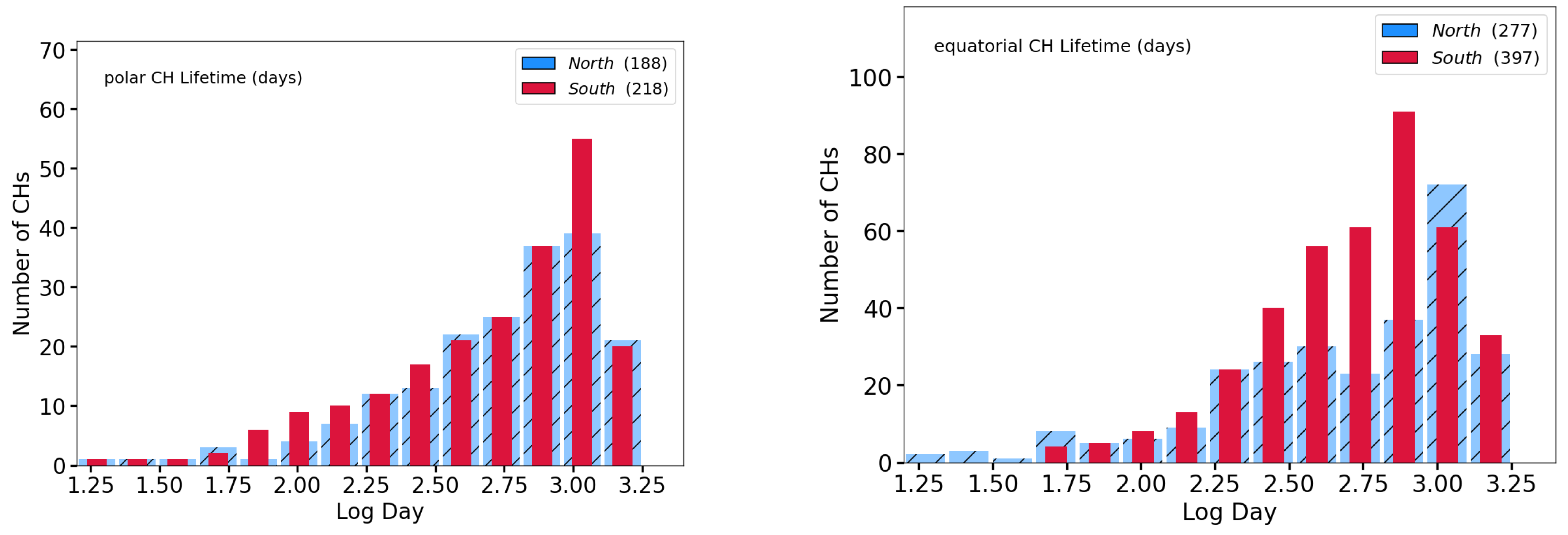
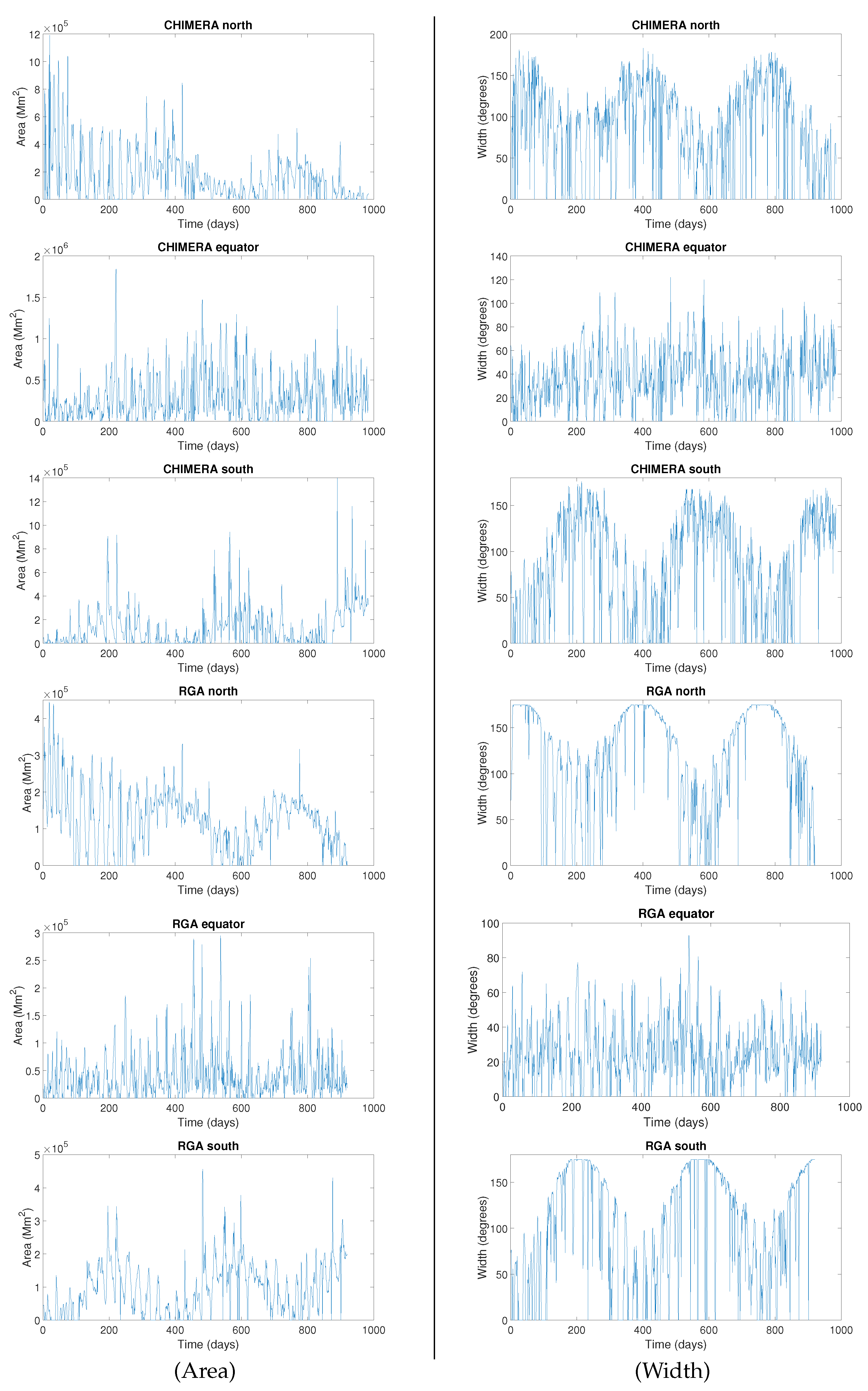
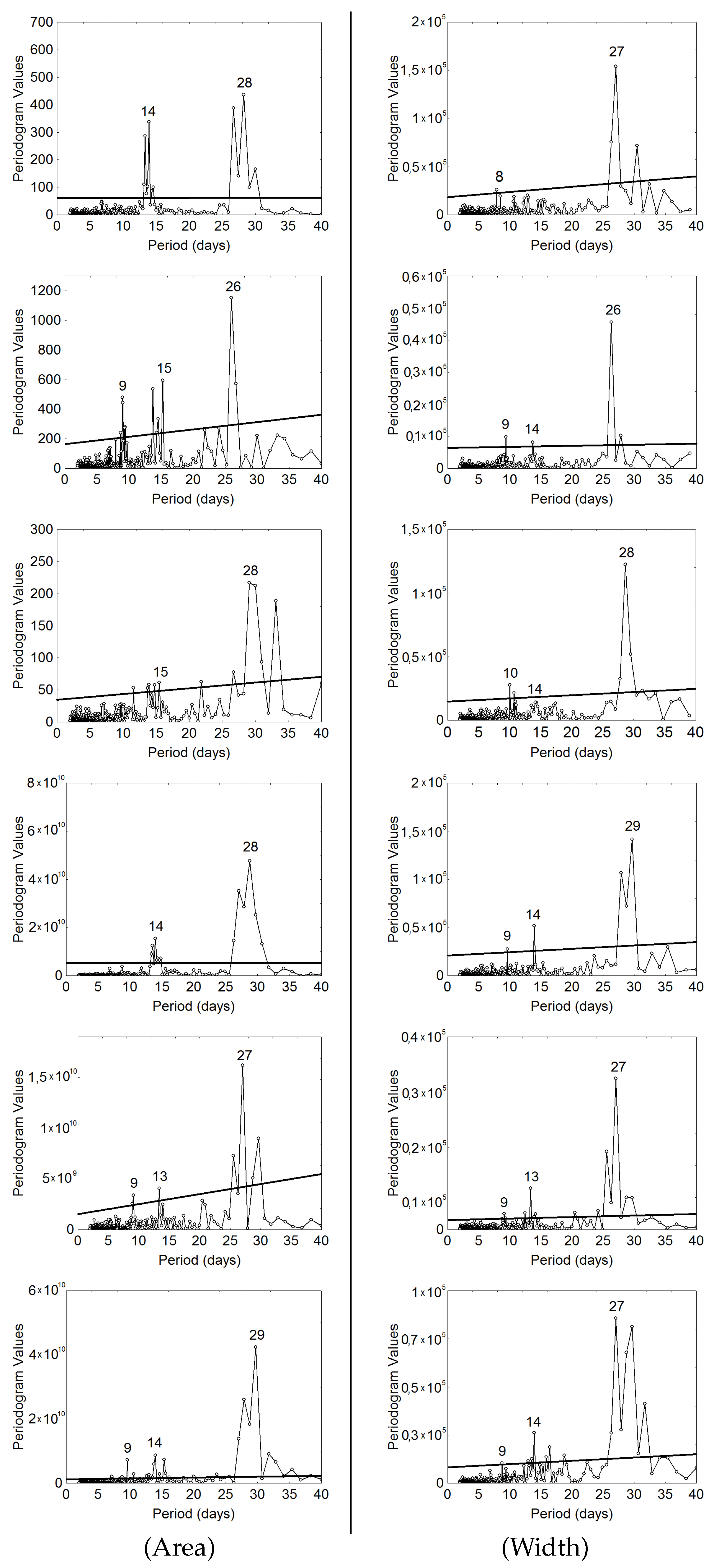
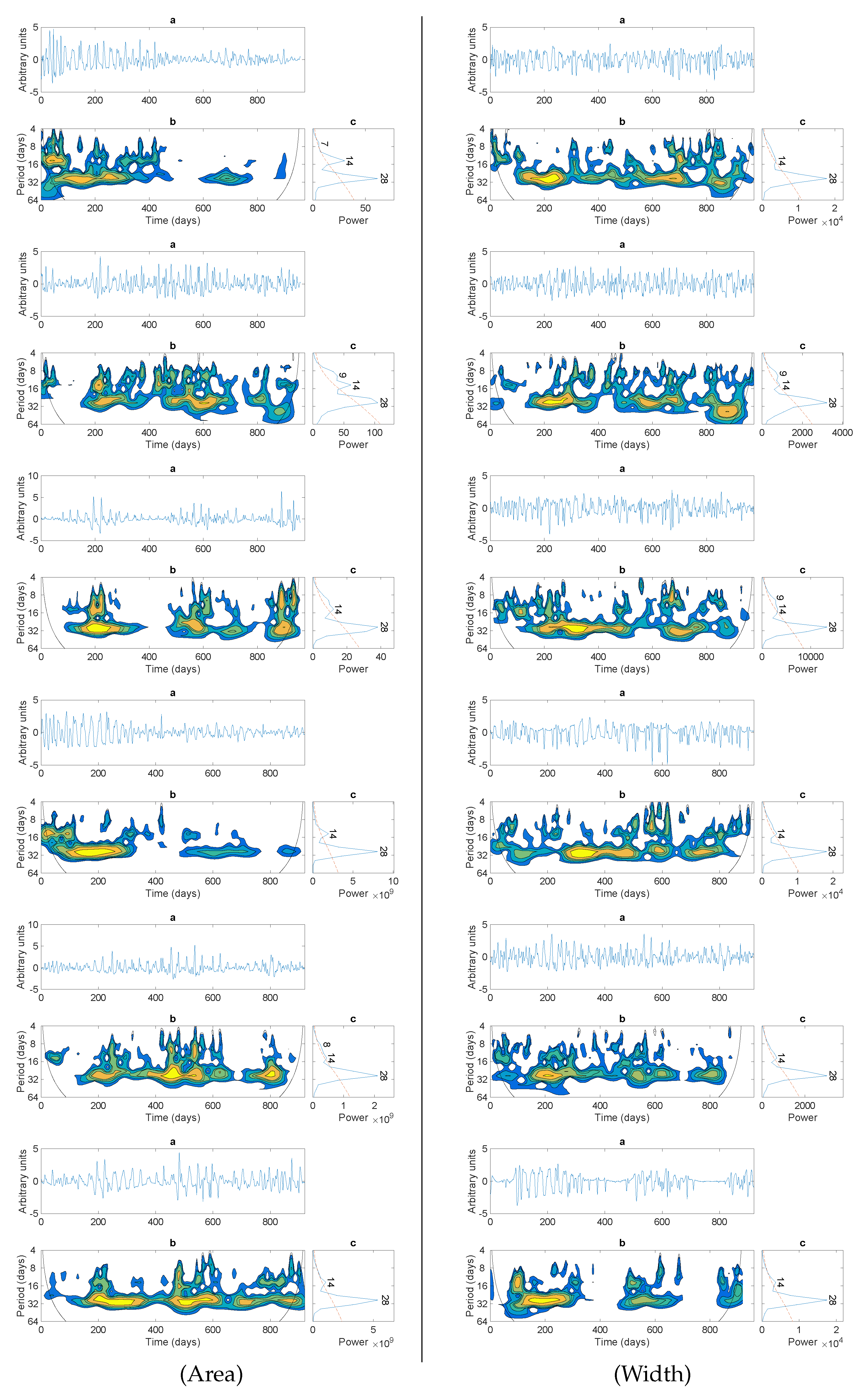
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cranmer, S.R. Coronal Holes. Living Rev. Sol. Phys. 2009, 6, 3. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bale, S.D.; Badman, S.T.; Bonnell, J.W.; Bowen, T.A.; Burgess, D.; Case, A.W.; Cattell, C.A.; Chandran, B.D.G.; Chaston, C.C.; Chen, C.H.K.; et al. Highly structured slow solar wind emerging from an equatorial coronal hole. Nature 2019, 576, 237–242. [Google Scholar] [CrossRef] [PubMed]
- Krieger, A.S.; Timothy, A.F.; Roelof, E.C. A Coronal Hole and Its Identification as the Source of a High Velocity Solar Wind Stream. Sol. Phys. 1973, 29, 505–525. [Google Scholar] [CrossRef]
- Heinemann, S.G.; Jerčić, V.; Temmer, M.; Hofmeister, S.J.; Dumbović, M.; Vennerstrom, S.; Verbanac, G.; Veronig, A.M. A statistical study of the long-term evolution of coronal hole properties as observed by SDO. Astron. Astrophys. 2020, 638, A68. [Google Scholar] [CrossRef]
- Heinemann, S.G.; Temmer, M.; Heinemann, N.; Dissauer, K.; Samara, E.; Jercic, V.; Hofmeister, S.J.; Veronig, A.M. VizieR Online Data Catalog: Coronal hole parameters (Heinemann+, 2019). VizieR Online Data Cat. (Other) 2019, 0580, J/other/SoPh/294. [Google Scholar]
- Heinemann, S.; Pomoell, J.; Temmer, M.; Bourdin, P. Life-time evolution and magnetic structure of coronal holes. In Proceedings of the 43rd COSPAR Scientific Assembly, Sydney, Australia, 28 January–4 February 2021; Volume 43, p. 1024. [Google Scholar]
- Hofmeister, S.J.; Veronig, A.; Reiss, M.A.; Temmer, M.; Vennerstrom, S.; Vršnak, B.; Heber, B. Characteristics of Low-latitude Coronal Holes near the Maximum of Solar Cycle 24. Astrophys. J. 2017, 835, 268. [Google Scholar] [CrossRef] [Green Version]
- Hofmeister, S.J.; Utz, D.; Heinemann, S.G.; Veronig, A.; Temmer, M. Photospheric magnetic structure of coronal holes. Astron. Astrophys. 2019, 629, A22. [Google Scholar] [CrossRef]
- Bagashvili, S.R.; Shergelashvili, B.M.; Japaridze, D.R.; Chargeishvili, B.B.; Kosovichev, A.G.; Kukhianidze, V.; Ramishvili, G.; Zaqarashvili, T.V.; Poedts, S.; Khodachenko, M.L.; et al. Statistical properties of coronal hole rotation rates: Are they linked to the solar interior? Astron. Astrophys. 2017, 603, A134. [Google Scholar] [CrossRef]
- Cadavid, A.C.; Miralles, M.P.; Romich, K. Comparison of the Scaling Properties of EUV Intensity Fluctuations in Coronal Hole and Quiet-Sun Regions. Astrophys. J. 2019, 886, 143. [Google Scholar] [CrossRef] [Green Version]
- Cranmer, S.R.; Winebarger, A.R. The Properties of the Solar Corona and Its Connection to the Solar Wind. Annu. Rev. Astron. Astrophys. 2019, 57, 157–187. [Google Scholar] [CrossRef] [Green Version]
- Cranmer, S.R. Alfven Waves in the Solar Corona and Solar Wind: An Updated Energy Budget. In Proceedings of the American Astronomical Society Meeting Abstracts #235, Honolulu, HI, USA, 4–8 January 2020; Volume 235, p. 149.08. [Google Scholar]
- Nakagawa, Y.; Nozawa, S.; Shinbori, A. Relationship between the low-latitude coronal hole area, solar wind velocity, and geomagnetic activity during solar cycles 23 and 24. Earth Planets Space 2019, 71, 24. [Google Scholar] [CrossRef]
- Hara, H. Nonthermal Motions in a Polar Coronal Hole Measured with Hinode/EIS during an on-Orbit Partial Solar Eclipse on 2017 August 21. Astrophys. J. 2019, 887, 122. [Google Scholar] [CrossRef]
- Mazumder, R.; Bhowmik, P.; Nandy, D. Properties of Coronal Holes in Solar Cycle 21–23 using McIntosh archive. IAU Symp. 2018, 340, 187–188. [Google Scholar] [CrossRef]
- Bravo, S.; Otaola, J.A. Polar Coronal Holes and the Sunspot Cycle—A New Method to Predict Sunspot Numbers. Sol. Phys. 1989, 122, 335–343. [Google Scholar] [CrossRef]
- Hofer, M.Y.; Storini, M. Repeated Structures Found After the Solar Maximum in the Butterfly Diagrams of Coronal Holes. In American Institute of Physics Conference Series; Ten, S.W., Velli, M., Bruno, R., Malara, F., Bucci, B., Eds.; American Institute of Physics: Melville, NY, USA, 2003; Volume 679, pp. 234–237. [Google Scholar] [CrossRef]
- Ikhsanov, R.N.; Tavastsherna, K.S. Latitude-temporal evolution of coronal holes in cycles 21–23. Geomagn. Aeron. 2015, 55, 877–883. [Google Scholar] [CrossRef]
- Stepanian, N.N.; Shtertser, N.I. Polar coronal holes in the solar activity cycle. Adv. Space Res. 2015, 55, 795–797. [Google Scholar] [CrossRef]
- Schou, J.; Scherrer, P.H.; Bush, R.I.; Wachter, R.; Couvidat, S.; Rabello-Soares, M.C.; Bogart, R.S.; Hoeksema, J.T.; Liu, Y.; Duvall, T.L.; et al. Design and Ground Calibration of the Helioseismic and Magnetic Imager (HMI) Instrument on the Solar Dynamics Observatory (SDO). Sol. Phys. 2012, 275, 229–259. [Google Scholar] [CrossRef] [Green Version]
- Scherrer, P.H.; Schou, J.; Bush, R.I.; Kosovichev, A.G.; Bogart, R.S.; Hoeksema, J.T.; Liu, Y.; Duvall, T.L.; Zhao, J.; Title, A.M.; et al. The Helioseismic and Magnetic Imager (HMI) Investigation for the Solar Dynamics Observatory (SDO). Sol. Phys. 2012, 275, 207–227. [Google Scholar] [CrossRef] [Green Version]
- Garton, T.M.; Gallagher, P.T.; Murray, S.A. Automated coronal hole identification via multi-thermal intensity segmentation. J. Space Weather Space Clim. 2018, 8, A02. [Google Scholar] [CrossRef]
- Wang, Q.; Song, X.; Jiang, Z. An Improved Image Segmentation Method Using Three-dimensional Region Growing Algorithm. In Proceedings of the 2013 International Conference on Information Science and Computer Applications, Changsha, China, 8–9 November 2013; Atlantis Press: Amsterdam, The Netherlands, 2013; pp. 148–152. [Google Scholar] [CrossRef]
- Tlatov, A.G.; Vasil’eva, V.V.; Makarova, V.V.; Otkidychev, P.A. Applying an Automatic Image-Processing Method to Synoptic Observations. Sol. Phys. 2014, 289, 1403–1412. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A 1998, 454, 903–998. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef] [Green Version]
- Hiremath, K.M.; Hegde, M. Rotation Rates of Coronal Holes and their Probable Anchoring Depths. Astrophys. J. 2013, 763, 137. [Google Scholar] [CrossRef] [Green Version]
- Obridko, V.N.; Shelting, B.D. Structure of the Heliospheric Current Sheet derived for the interval 1915–1916. Sol. Phys. 1999, 184, 187–200. [Google Scholar] [CrossRef]
- Vasil’Eva, V.V.; Makarov, V.I.; Tlatov, A.G. Rotation Cycles of the Sector Structure of the Solar Magnetic Field and Its Activity. Astron. Lett. 2002, 28, 199–205. [Google Scholar] [CrossRef]
- Fossat, E.; Boumier, P.; Corbard, T.; Provost, J.; Salabert, D.; Schmider, F.X.; Gabriel, A.H.; Grec, G.; Renaud, C.; Robillot, J.M.; et al. Asymptotic g modes: Evidence for a rapid rotation of the solar core. Astron. Astrophys. 2017, 604, A40. [Google Scholar] [CrossRef] [Green Version]
- Efremov, V.I.; Parfinenko, L.D.; Solov’ev, A.A. Global long-term oscillations of the Sun observed by SORCE, SOHO and SDO. Astrophys. Space Sci. 2018, 363, 257. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riehokainen, A.; Smirnova, V.; Solov’ev, A.; Tlatov, A.; Zhivanovich, I.; Al-Hamadani, F.; Strekalova, P. Variations in Daily Maximum Areas and Longitudinal Widths of Solar Coronal Holes in 2017–2020. Universe 2022, 8, 158. https://doi.org/10.3390/universe8030158
Riehokainen A, Smirnova V, Solov’ev A, Tlatov A, Zhivanovich I, Al-Hamadani F, Strekalova P. Variations in Daily Maximum Areas and Longitudinal Widths of Solar Coronal Holes in 2017–2020. Universe. 2022; 8(3):158. https://doi.org/10.3390/universe8030158
Chicago/Turabian StyleRiehokainen, Alexandr, Victoria Smirnova, Alexander Solov’ev, Andrey Tlatov, Ivan Zhivanovich, Firas Al-Hamadani, and Polina Strekalova. 2022. "Variations in Daily Maximum Areas and Longitudinal Widths of Solar Coronal Holes in 2017–2020" Universe 8, no. 3: 158. https://doi.org/10.3390/universe8030158
APA StyleRiehokainen, A., Smirnova, V., Solov’ev, A., Tlatov, A., Zhivanovich, I., Al-Hamadani, F., & Strekalova, P. (2022). Variations in Daily Maximum Areas and Longitudinal Widths of Solar Coronal Holes in 2017–2020. Universe, 8(3), 158. https://doi.org/10.3390/universe8030158





