Warm Dark Matter Galaxies with Central Supermassive Black Holes
Abstract
1. Introduction and Results
- (i)
- We find that takes large positive values in the inner regions as implied by Equation (28), then decreases until vanishing at , and becomes negative for , as shown by our detailed resolution of the Thomas–Fermi equation (Section 3.3 and Figure 1). Therefore, is precisely the transition between the quantum and classical DM behaviors; plays the role of the quantum DM radius of the galaxy for galaxies exhibiting a central black hole. Namely, inside , the WDM gas is a self-gravitating quantum gas, while for the WDM gas is a self-gravitating classical Boltzmann gas. The size of the quantum WDM core turns to be smaller for increasing galaxy masses and black hole masses. WDM inside a small core of radius is in a quantum gas high-density state, namely a Fermi nearly degenerate state with nearly constant density . For the three representative families of galaxy solutions we find here, the values of and are given by Equations (75)–(77). The density is orders of magnitude larger than its values for , where the WDM is in the classical Boltzmann regime. runs between 0.07 and 1.90 pc for galaxies with virial masses from to (as shown in Section 3.3). In any case, is much larger than the Schwarzschild radius of the central black hole, which runs from to pc.This is an important result: in the vicinity of the central black hole, the fermionic WDM is always in a quantum regime, while far from the central black hole, the WDM follows a classical Boltzmann regime [12]. This is natural to understand: the strong attractive gravitational force near the central BH compacts the WDM, and its high density makes it to behave quantum mechanically. On the contrary, far from the BH, the gravitational forces are weak, the WDM is diluted, and it is then described by a classical Boltzmann gas. Ultracompact dwarf galaxies also exhibit WDM in a quantum regime [9,10,12].
- (ii)
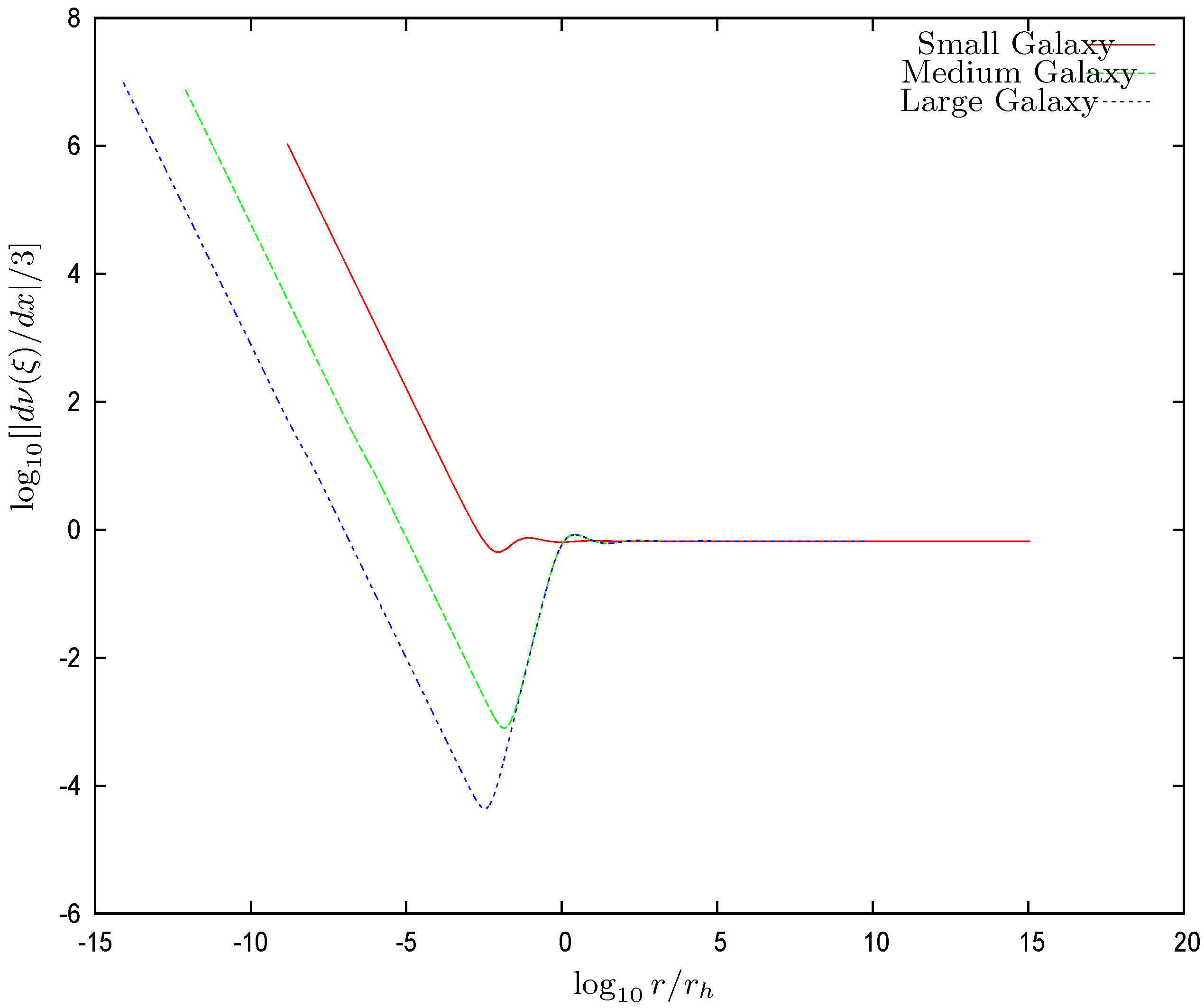
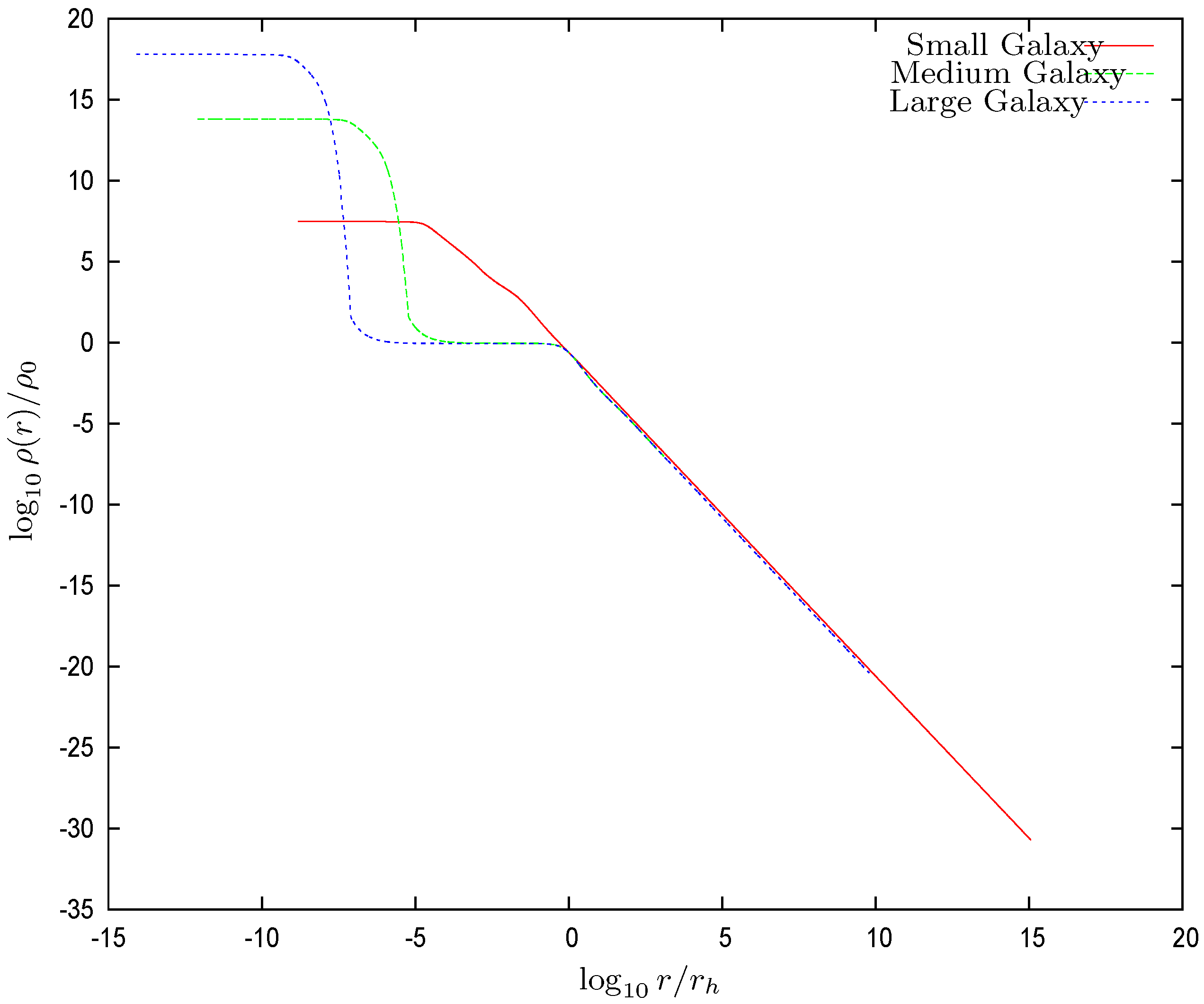
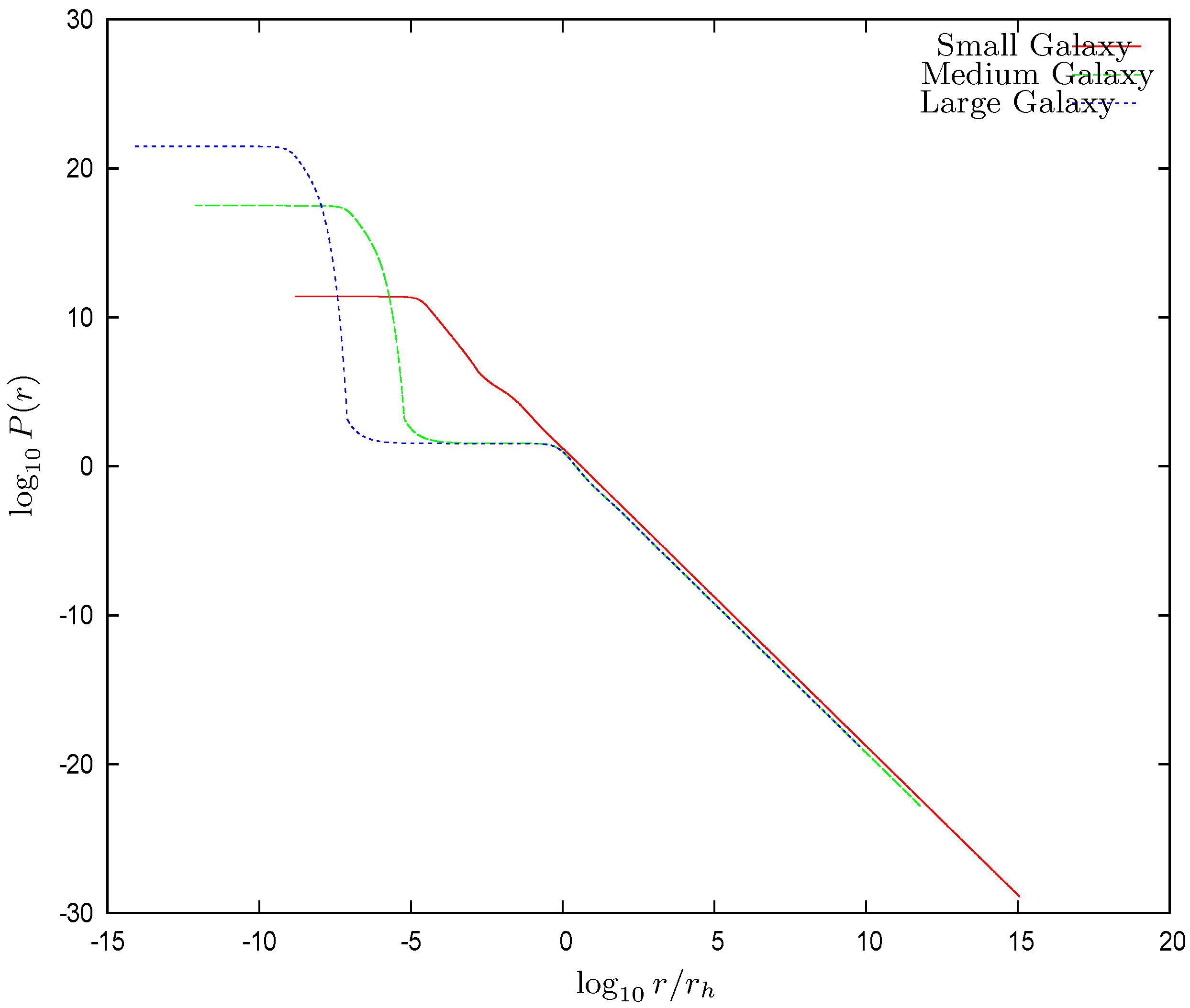
- In addition, the black hole has an influence radius . In the vicinity of the black hole, the gravitational force, due to the black hole, is larger than the gravitational force exerted by the dark matter. The influence radius of the black-hole is defined as the radius where both forces are of equal strength. Both forces point inward and always sum up. turns out to be larger than the radius where the chemical potential vanishes, . The region is dominated by the central black hole, and the WDM exhibits there a classical behavior. For , we see from Figure 1 and Figure 2 that both and (or equivalently, the dimensionless potential and its derivative , x= ln ), follow the behavior dictated by the central black hole Equation (32), which produce straight lines on the left part of the logarithmic plots Figure 1 and Figure 2. Consistently, for and are dominated by the WDM and exhibit a similar behavior to that of the Thomas–Fermi solutions without a central black hole [9,10,11,12].Figure 3 shows that the local density behavior is dominated by the black hole for . For , the WDM gravitational field dominates over the black hole field, and the galaxy core shows up. For medium and large galaxies, the core is seen as a plateau. At the same time, the chemical potential is negative for , and the WDM is a classical Boltzmann gas in this region.The surface densityhas the remarkable property of being nearly constant and independent of luminosity in different galactic systems (spirals, dwarfs irregular and spheroidal, and ellipticals) spanning over 14 magnitudes in luminosity and over different Hubble types [36,37]. It is therefore a useful physical characteristic scale in terms of which galaxy magnitudes are expressed.
- (iii)
- We find the main galaxy magnitudes as the halo radius , halo mass , black hole mass , velocity dispersion, circular velocity, density, pressure and phase space density. Analytic formulae are derived for them and expressed in terms of the reference surface density . Moreover, we can express the black hole mass asbeing the dimensionless central radius and the 2nd momentum of the distribution function Equation (21). The black hole mass grows when grows. Notice that does not simply grow linearly with due to the presence of the factor .
- (iv)
- We find in this approach explicit realistic galaxy solutions with central supermassive black holes and analyze three representative families of them: small size (mass) galaxies, intermediate size (mass) galaxies, and large size (mass) galaxies.For a fixed value of the surface density , the solutions are parametrized by two truly physical parameters: the dimensionless central radius and the constant A characteristic of the chemical potential behavior Equation (32) at the center . The dimensionless central radius is explicated in Equation (28). This is the ratio of the relevant physical parameters which appear in the chemical potential at the center. The constant A is truly physical too and characterizes the boundary condition of the chemical potential at the center in the presence of the central supermassive black hole, Equation (32). In the absence of the central SMBH: , and the boundary condition at the center without BH, is recovered.
- (v)
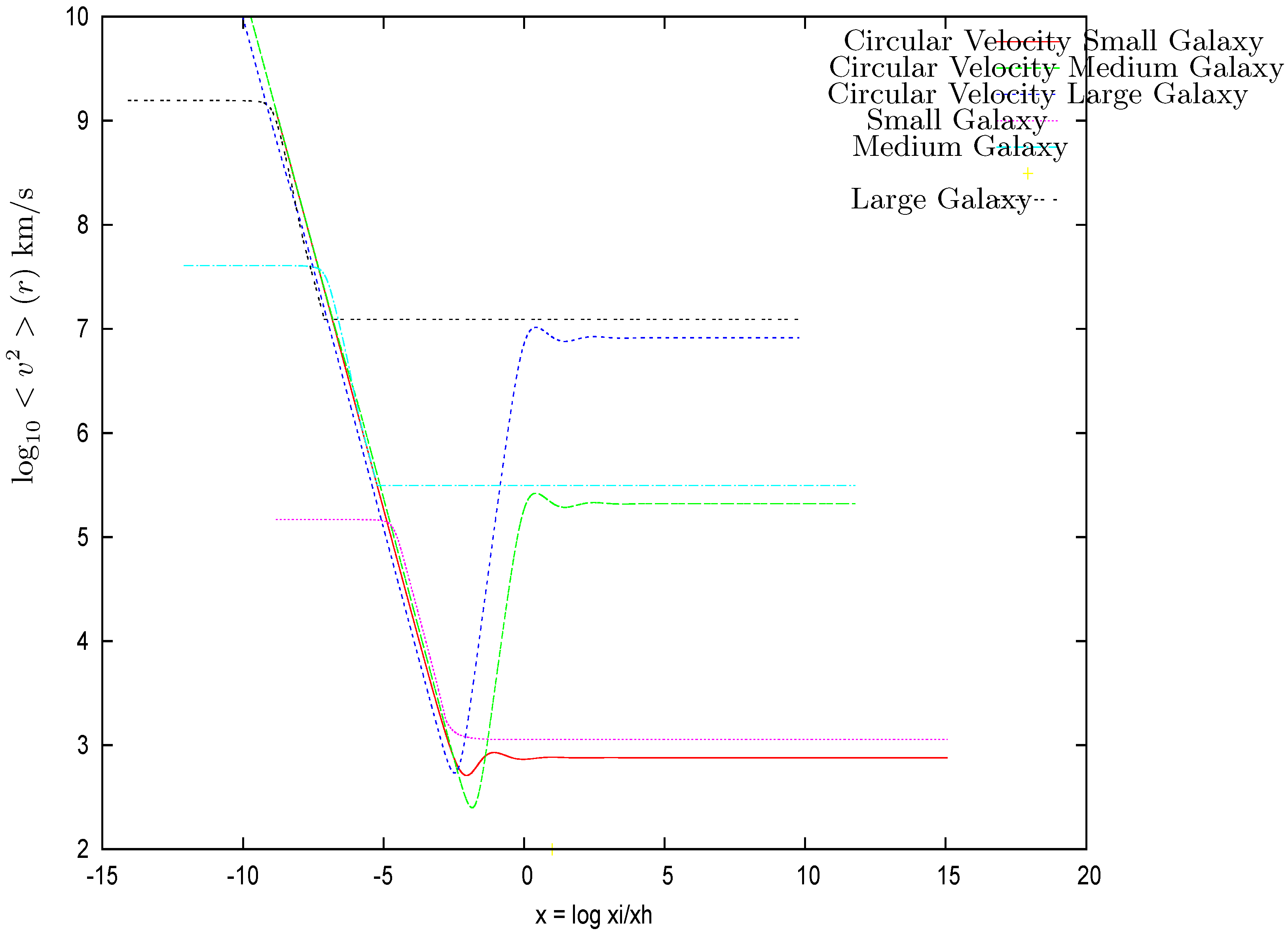
- We find from our extensive numerical calculations that the halo is thermalized at the uniform temperature and matches the circular temperature by . This picture is similar to the picture found in the absence of the central black hole which follows from the observed density profiles in the Eddington-like approach to galaxies [13]. We obtain here in the Thomas–Fermi approach and in the presence of a central supermassive black hole that the halo is thermalized at a uniform temperature inside , which tends to the circular temperature at as illustrated in Figure 4. The circular temperature is defined in terms of the circular velocity as . The circular temperature is discussed in Section 3. We introduce the circular temperature in terms of the circular (virial) velocity in the same way the temperature is defined in terms of the velocity dispersion . The circular velocity is defined and found in Section 2. Near the central black hole, the space dependent temperature is given by an equipartition and the virial theorem, as shown by Equations (68)–(70).
- (vi)
- (vii)
- We find in Equations (75)–(77) the WDM mass inside the quantum galaxy radius . represents only a small fraction of the halo or virial mass of the galaxy but it is a significant fraction of the black hole mass . We see from Equations (75)–(77) that amounts to 20% of for the medium and large galaxies and 45% for the small galaxy.
- (viii)
- We also measure the classical and quantum gas character of the galaxy plus the black hole system by means of the ratio between the particle de Broglie wavelength and the average interparticle distance. For , the system is of a classical dilute nature while for , it is a macroscopic quantum system. We find in terms of the surface density and momenta of the gravitational or chemical potential in dimensionless units Equations (80) and (81). Figure 5 shows vs. for the three representative galaxy solutions. The transition from the quantum to the classical regime occurs precisely at the same point where the chemical potential vanishes (see Figure 1), as it must be, showing the consistency and powerful of our treatment. This point defines the transition from the quantum to the classical behavior.
- (ix)
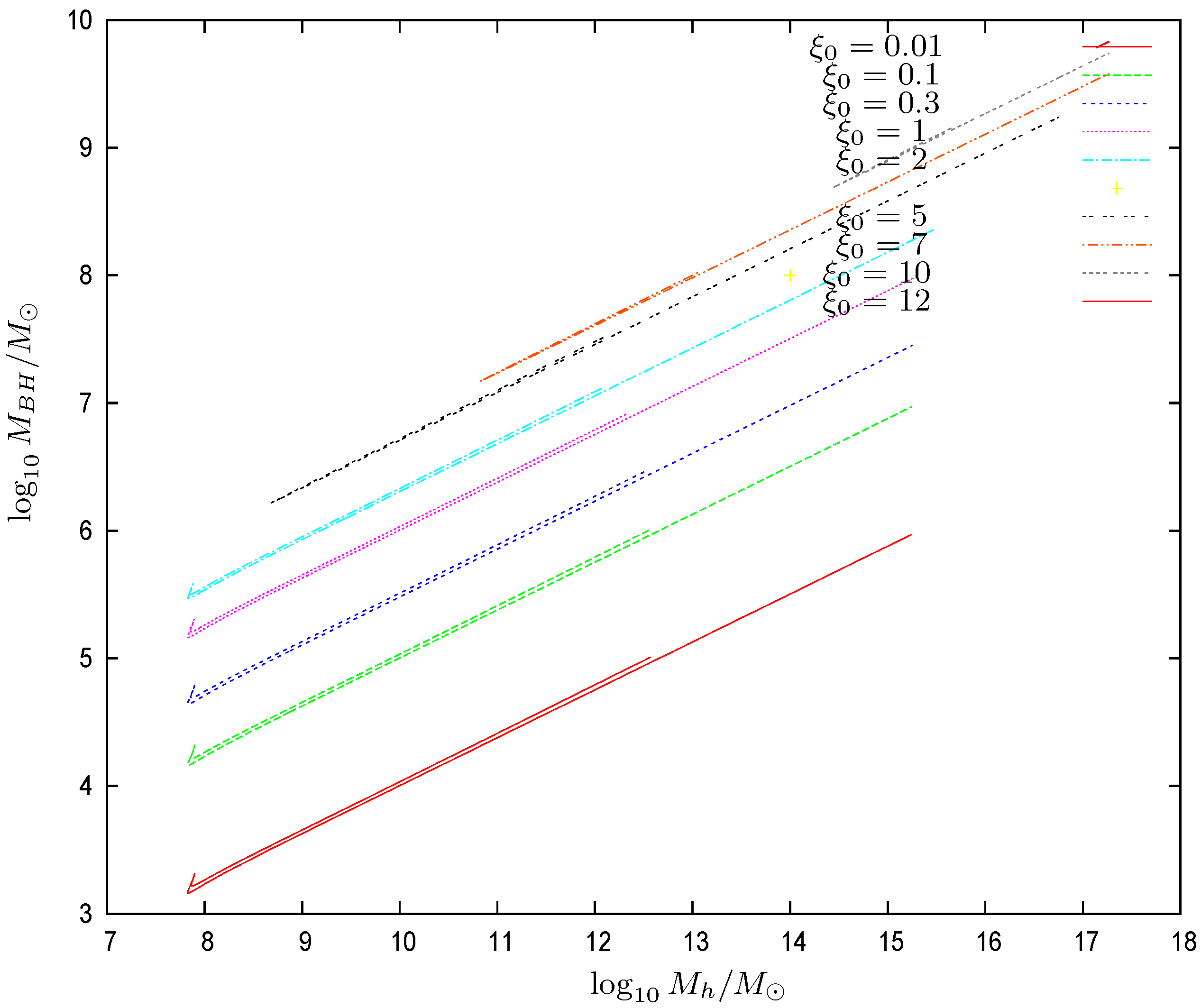
- There is an important qualitative difference between galaxy solutions with a black hole (), and galaxy solutions without a black hole (). In the absence of the central black hole, the halo mass reaches the minimal value Equation (82), which is the degenerate quantum limit at zero temperature [9,10,12]. In the presence of a central black hole, we find that the minimal temperature is always non-zero and that the halo mass takes as a minimal valueThe presence of the supermassive black hole heats up the dark matter gas and prevents it from becoming an exact degenerate gas at zero temperature. The minimal galaxy mass and size and most compact galaxy state with a central black hole is a nearly degenerate state at very low but non-zero temperature as seen from Equation (84). All matter studied in this paper is dark matter, and the only DM interaction is the gravitational interaction. The presence of the black hole naturally makes the DM particles acquire a higher velocity (and thus, a higher associated temperature), and in this sense, the SMBH does “heat” the dark matter around it. Gravitation self-consistently acts on such DM, and the SMBH adds too to such gravitational action. This is a very clean physical process, with a clean framework and clean conclusive results.This situation is clearly shown in Figure 6. The value of with a central black hole is times larger than without the black hole. Notice that the small galaxy solution Equation (75) is just 11% larger in halo mass than the minimal galaxy Equation (83) with a central black hole. We conclude that galaxies possessing a central black hole are in the dilute Boltzmann regime because of their large mass [12]. On the contrary, compact galaxies, in particular, ultracompact galaxies in the quantum regime [12], cannot harbor central black holes because the minimal galaxy mass with central black hole Equation (83) is always larger than . In other words, galaxies with masses , namely ultracompact dwarfs, necessarily do not possess central black holes.The mass of the supermassive black hole monotonically increases with the central radius or equivalently the dimensionless one at fixed A. In addition, for , that is, for small supermassive black holes, and all A, the galaxy parameters, such as halo mass , halo radius , virial mass and galaxy temperature , become independent of , showing a limiting galaxy solution. Only the BH mass depends on in this regime.Figure 7displays our results for . Figure 8 displays our results for the black hole mass vs. the halo mass . We see that is a two-valued function of . For each value of , there are two possible values for , which are quite close to each other. This two-valued dependence on is a direct consequence of the dependence of on A shown in Figure 6. The branch points on the left in Figure 8 correspond to the minimal galactic halo mass Equation (83) when the central supermassive black hole is present. At fixed , as shown in Figure 8, the central black hole mass scales with the halo mass aswhere is an increasing function of . We plot in Figure 9 the halo galaxy mass vs. the galaxy temperature . The halo mass grows when increases. Colder galaxies are smaller. Warmer galaxies are larger. We see at the branch points in Figure 9 the minimal galaxy temperature in Equation (84) when a supermassive black hole is present.We find galaxy solutions with central black holes for arbitrarily small values of and a correspondingly, arbitrarily small central BH mass. There is no minimal central BH mass. The only minimal central BH mass possibility is zero (for ).
- (x)
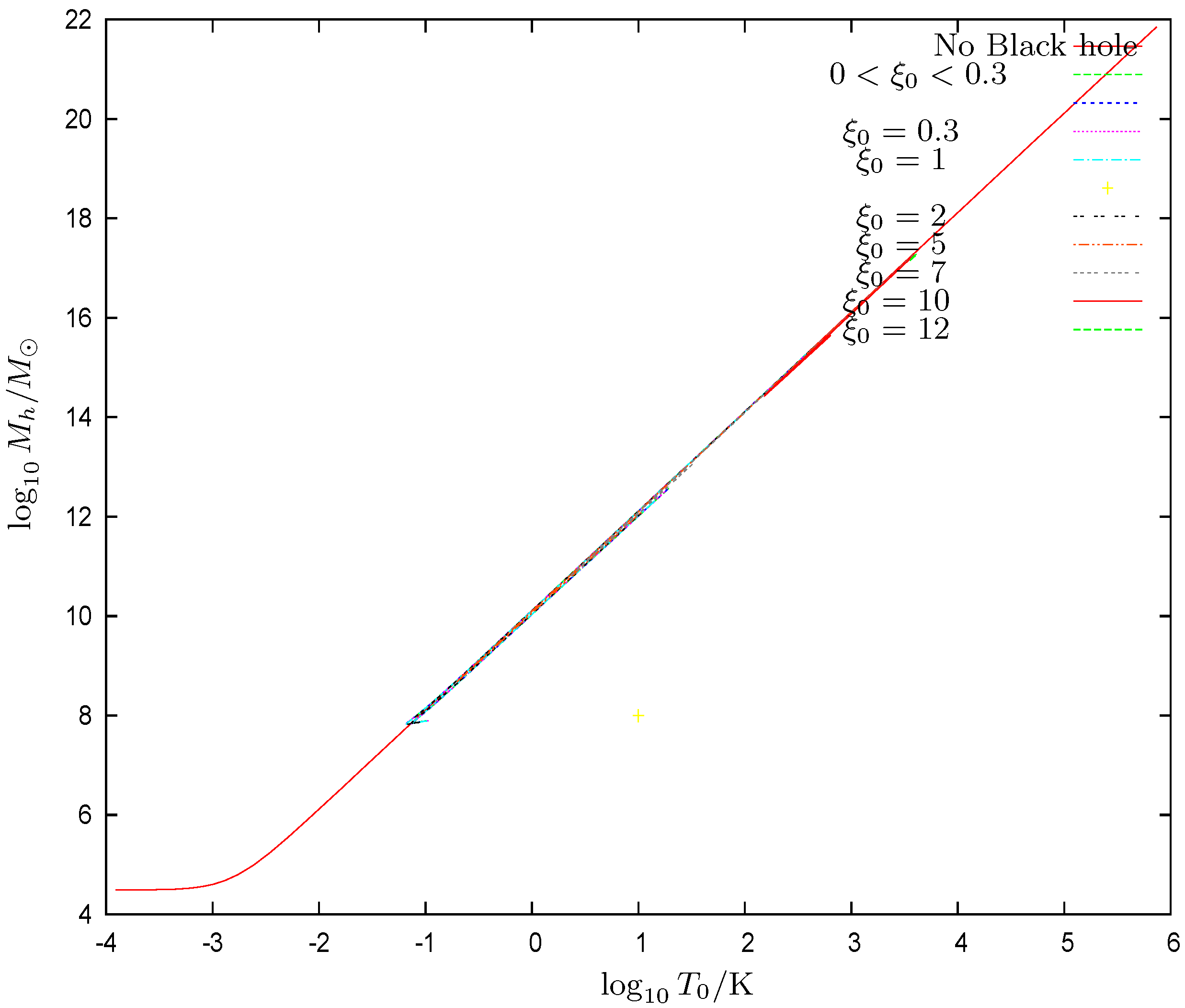
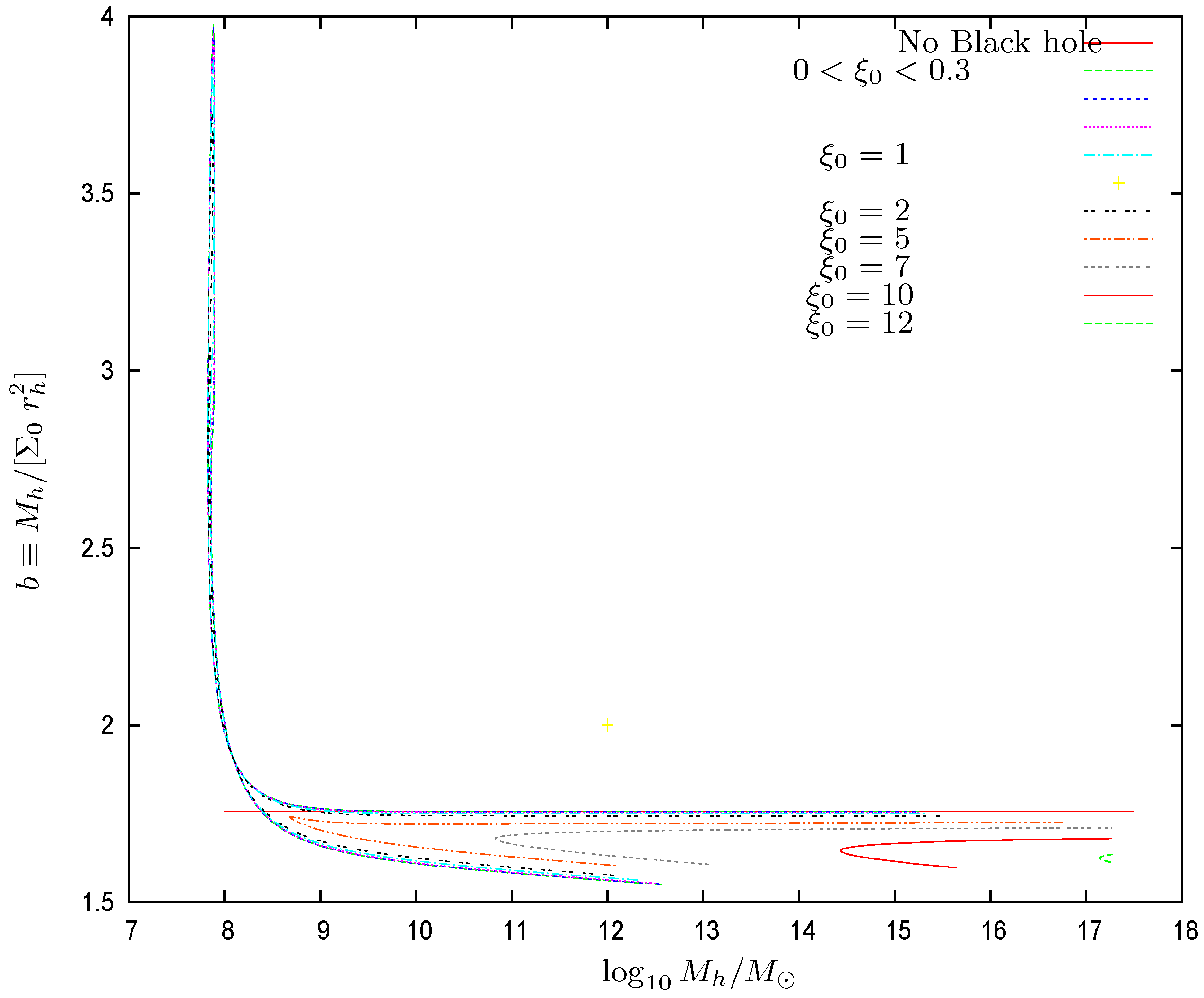
- We find that scales as , which is the same scaling found in the Thomas–Fermi approach to galaxies in the absence of black holes [9,10,12]. We plot in Figure 10 the ordinary logarithm of the halo radius vs. the ordinary logarithm of the halo mass for galaxies with central black holes of many different masses. The halo mass in the absence of a central black hole behaves in the Thomas–Fermi approach as [12]The proportionality factor in this scaling relation is confirmed by the galaxy data [12]. In the presence of a central black hole, we find in the Thomas–Fermi approach an analogous relationwhere the coefficient b turns to be of order unity. We plot in Figure 11 the coefficient b as a function of the halo mass . We see that, except for halo masses near the minimum halo mass , b in the presence of a central black hole takes values up to 10% below its value in the absence of a central black hole Equation (85). For halo masses near increases, reaching values . For very large halos and central black holes, b could be as small as about . b changes at most by a factor from up to 2 while the halo mass varies by ten orders of magnitude. As shown by Figure 11, b is a two-valued function of . b turns out to be independent of the precise value of the WDM particle mass m, which is due to the fact that the scaling relation Equation (86) as well as Equation (85) apply in the classical Boltzmann regime of the galaxy (). In summary, the scaling relation Equation (86) and the coefficient b turn out to be remarkably robust.
- (xi)
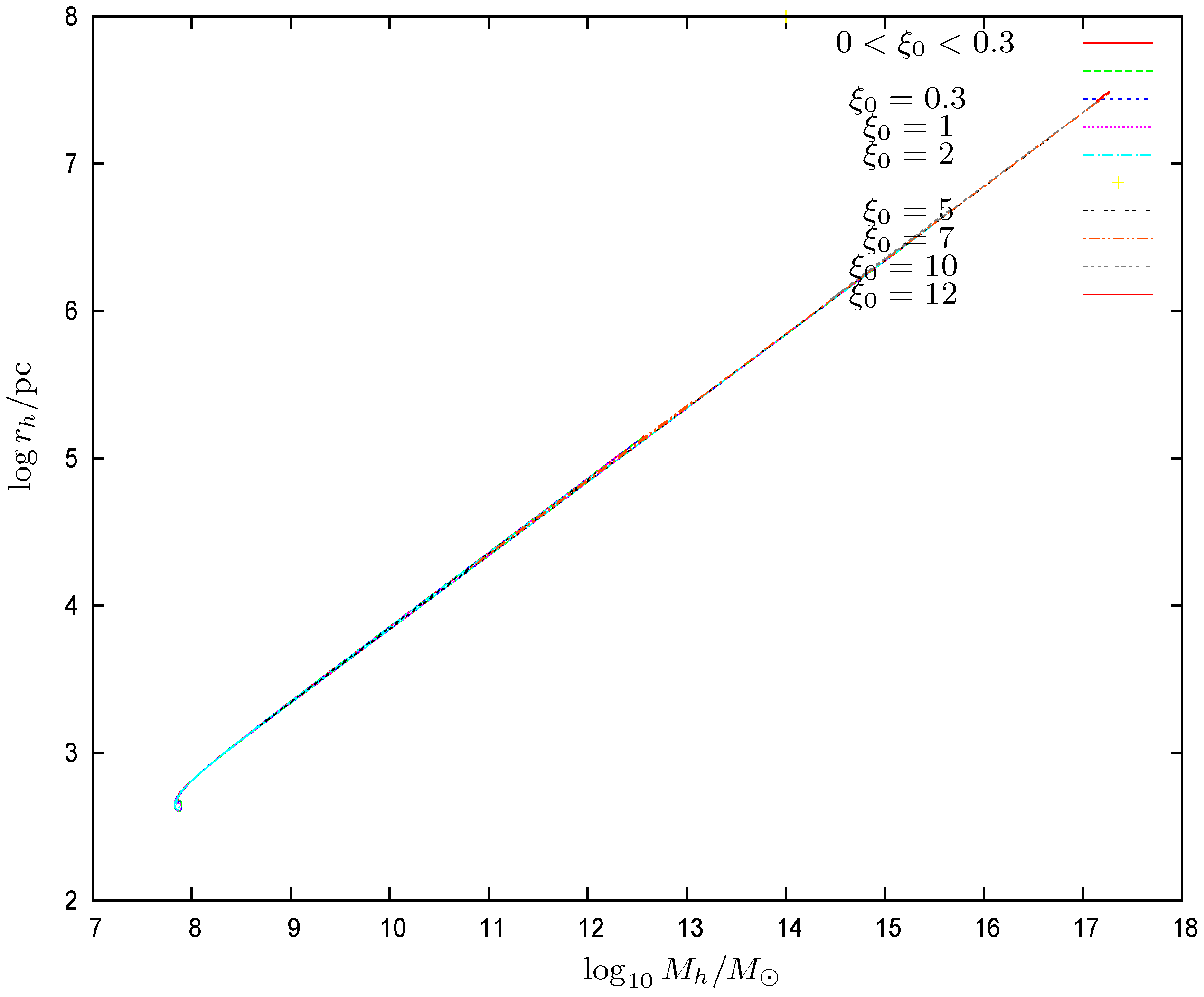
- We plot in Figure 12 the ordinary logarithm of the halo radius versus the ordinary logarithm of the central black hole mass for many galaxy solutions. The halo radius turns out to be a double-valued function of . Remarkably, for fixed scales asThe constant turns out to be a decreasing function of .
- (xii)
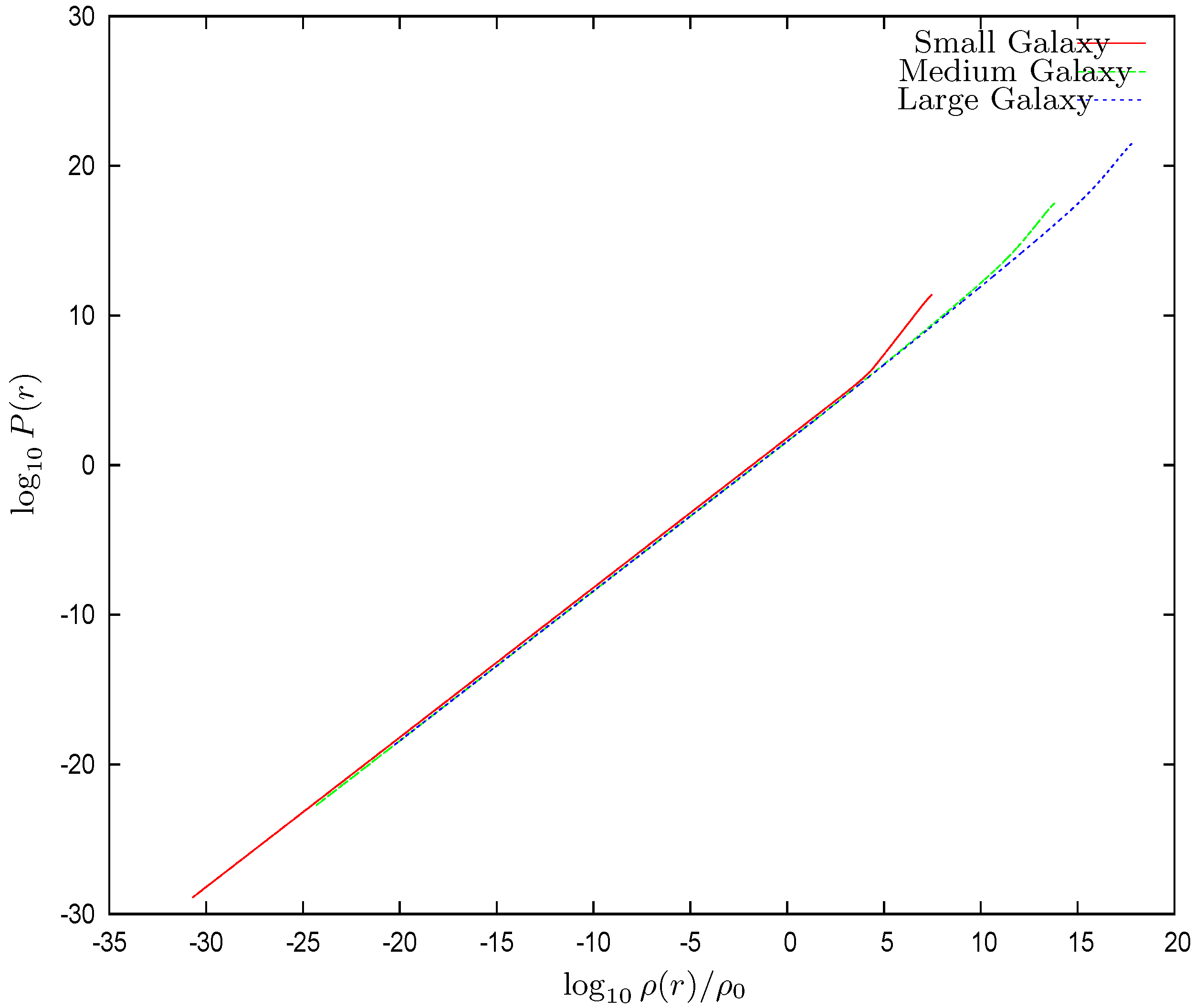
- We find the local pressure as given by Equation (53). In Figure 13, we plot vs. for the three representative galaxy solutions. monotonically decreases with r. The pressure takes huge values in the quantum (high density) region and then it sharply decreases entering the classical (dilute) region . In Figure 14, we plot the derived equation of state vs. for the three galaxy solutions we find here with central SMBH. The three curves almost coincide and are almost straight lines of unit slope. That is, the equation of state is in very good approximation of a perfect gas equation of state , which stems from the fact that galaxies with central black holes have halo masses , Equation (83), and therefore necessarily belong to the dilute Boltzmann classical regime [12]. The equation of state turns out to be a local (r-dependent) perfect gas equation of state because of the gravitational interaction (WDM self-gravitating perfect gas). Indeed, for galaxies with central black holes, the WDM is in a quantum (highly compact) regime inside the quantum radius . However, because is in the parsec scale or smaller (see Equations (75)–(77)), the bulk of the WDM is in the Boltzmann classical regime, which is consistently reflected in the perfect gas equation of state behavior.
2. Galaxy Structure with Central Supermassive Black Holes in the WDM Thomas–Fermi Approach
2.1. Thomas–Fermi Equations with a Central Black Hole
2.2. Central Galactic Black Hole and Its Influence Radius
2.3. Main Physical Magnitudes of the Galaxy plus Central Black Hole System
2.4. Galaxy Properties in the Diluted Boltzmann Regime
3. Explicit Thomas–Fermi Galaxy Solutions with Central Supermassive Black Holes
3.1. Local Thermal Equilibrium in the Galaxy
- For we set
- We find from our extensive numerical calculations that the halo is thermalized at the uniform temperature and matches the circular temperature by . This picture is similar to the picture found in the absence of the central black hole which follows from the observed density profiles in the Eddington-like approach to galaxies [13]. We obtain here in the Thomas–Fermi approach and in the presence of a central supermassive black hole that the halo is thermalized at a uniform temperature inside which matches the circular temperature at (see Figure 4).
- In summary, each galaxy solution with a central black hole depends only on two free parameters: the dimensionless constants and A in Equation (32). We have a two-parameter family of Thomas–Fermi galaxy solutions with a central supermassive black hole parametrized by and A.The black hole mass grows when grows as shown by Equation (45). Notice that does not simply grow linearly with due to the presence of the factorin Equation (45).
3.2. Thomas–Fermi Equations with r-Dependent Temperature Tc(r)
3.3. Examples of Thomas–Fermi Galaxy Solutions with a Central Supermassive Black Hole
- Quantum to classical behavior: The central black hole strongly attracts the WDM and makes its density very high for , where a compact quantum core gets formed. The dimensionless chemical potential vanishes at and becomes negative for . The density drops several orders of magnitude immediately after as shown in Figure 3. is negative for , and the WDM exhibits there a classical Boltzmann behavior while the WDM exhibits a quantum behavior for , where the chemical potential is large and positive. Therefore, the point where the chemical potential vanishes defines the transition from the quantum to classical behavior. In the quantum region , the density exhibits a constant plateau as shown in Figure 3. Notice from Equation (75) that turns to be much larger than the Schwarzschild radius of the central black hole .
- Black hole influence radius : For , the black hole gravitational field dominates over the dark matter gravitational field. The influence radius is defined by Equation (31). The black hole influence radius turns out to be larger than the radius where the chemical potential vanishes, . The region is dominated by the central black hole and the WDM exhibits there a classical behavior. For , we see from Figure 1 and Figure 2 that both and follow the behavior dictated by the central black hole. That is, from Equation (32)which produce straight lines on the left part of the logarithmic plots of Figure 1 and Figure 2. and are dominated by the WDM and exhibit a similar behaviour to that of the Thomas–Fermi solutions without a central black hole [9,10,11,12].Figure 3 shows that the local density behavior is dominated by the black hole for . Coherently, for the WDM gravitational field dominates over the black hole field and the galaxy core shows up for in Figure 3. For medium and large galaxies, the core is seen as a plateau. At the same time, the chemical potential is negative for , and the WDM is a classical Boltzmann gas in this region.
- Halo radius : Finally, we see in Figure 3 the tail of the WDM density profile for , which exhibits a similar shape for all three galaxy solutions.
- WDM thermalization: As shown by Figure 4, the velocity dispersion is constant as a function of r, indicating a thermalized WDM with temperatureWDM is thermalized as in the absence of the central black hole [12]. This is consistent with the use of a thermal Fermi–Dirac distribution function for .
- We also plot in Figure 4 the circular velocity given by Equation (58) vs. . For , the circular velocity tends to the velocity dispersion as obtained from the Eddington equation for realistic density profiles [13]. For , the circular velocity grows as in Equation (59) due to the central black hole field.
- WDM inside a small core of radius is in a quantum gas high density state, namely, a Fermi nearly degenerate state with nearly constant density . For the three galaxy solutions, the values of and are given by Equations (75)–(77). Notice that the density is orders of magnitude larger than its values for , where the WDM is in the classical Boltzmann regime.
- We also give in Equations (75)–(77) the WDM mass inside . represents only a small fraction of the halo or virial mass of the galaxy, but it is a significant fraction of the black hole mass . We see from Equations (75)–(77) that amounts to 20% of for the medium and large galaxies and 45% for the small galaxy.
3.4. Quantum Physics in Galaxies
4. Systematic Study of the Thomas–Fermi Galaxy Solutions with a Central Supermassive Black Hole
- We plot in Figure 9 the halo galaxy mass vs. the galaxy temperature . The halo mass grows when increases. Colder galaxies are smaller. Warmer galaxies are larger.
- We find galaxy solutions with central black holes for arbitrarily small values and correspondingly arbitrarily small central BH mass. There is no emergence of a minimal mass for the central black hole.
4.1. Universal Scaling Relations in the Presence of Central Black Holes
4.2. Pressure and Equation of State in the Presence of Central Black Holes
5. Conclusions
- We presented here a novel study of galaxies with central supermassive black holes, which shows itself as fruitful and enlightening. This framework stresses the key role of gravity and warm dark matter in structuring galaxies with their central supermassive black holes and provides correctly the major physical quantities to be first obtained for the galaxy–black-hole system: the masses, sizes, densities, velocity dispersions, and their internal physical states. This also yields a physical and precise characterization of whether they are compact, ultracompact, low density or large dilute galaxies, encompassed with their classical physics and quantum gas physical properties.
- We thus found different regions structuring internally the halo of the galaxy from the vicinity of the supermassive central black hole region to the external regions or virial radius. For all galaxies harboring a central black hole, there is a transition from the quantum to the classical regime going from the more compact inner regions, which are in a quantum gas state, to the classical dilute regions in a Boltzmann-like state. This is accompanied by a decreasing in the local temperature from the central warmer regions to the colder external ones. The SMBH heats the DM near around and prevents it from becoming exactly degenerated at zero temperature. Although the inner DM quantum core is highly compact in a nearly degenerate quantum gas state, it is not at zero temperature. Inside , the halo is thermalized at a uniform or slowly varying local temperature , which tends to the circular temperature at .
- We formulated the problem of galaxy structure with central supermassive black holes in the WDM Thomas–Fermi approach and found the main physical magnitudes and properties of the galaxy plus black hole system. We solved the corresponding equations and boundary conditions, found three representative families of realistic galaxy solutions (small, medium and large size galaxies) with central supermassive black holes, and provided a systematic analysis of the new quantum and classical physics properties of the system. The approach naturally incorporates the quantum pressure of the self-gravitating dark matter fermions, showing its full power and clearness to treat the galaxy plus supermassive black hole system. The realistic astrophysical masses of supermassive black holes are naturally obtained in this framework.
- We found the main important physical differences between galaxies with and without the presence of a central black hole. In the presence of a central black hole, both the quantum and classical behaviors of the dark matter gas do co-exist generically in any galaxy from the compact small galaxies to the dilute large ones, and a novel galaxy halo structure with three regions show up.
- The transition from the quantum to classical regime occurs at the point , where the chemical potential vanishes and which is, in addition, precisely and consistently, the point where the particle wavelength and the interparticle distance are equal (their ratio being a measure of the quantum or classical properties of the system). The quantum radius is larger for the smaller and more compact galaxies and diminishes with increasing galaxy and black hole masses for the large dilute galaxies. The WDM mass inside the quantum galaxy radius represents only a small fraction of the halo mass or virial mass of the galaxy, but it is a significant fraction of the black hole mass . amounts to 20% of for the medium and large galaxies and 45% for the small galaxies.
- The minimal mass that a galaxy should have in order to harbor SMBHs was found, which shows, among other features, why compact or ultracompact galaxies (in the range ) cannot harbor necessarily central black holes.
- Novel universal scaling relations in the presence of a central supermassive black hole were derived: black hole mass , halo radius and halo mass relations. The black hole mass turned out to be a two-valued function of the halo mass and size , and we found the local pressure and equation of state of the galaxy–black-hole system and its different regimes.
- A more detailed quantitative account of the main features and results of this paper is presented in the Introduction, Section 1.
- The circular velocities, galactic rotation curves in the WDM halo with central SMBH are discussed, self-consistently computed and plotted in Section 2, Equations (56)–(59), (63) and (64) and Figure 4 of this paper, together with the obtained velocity dispersions. These results are presented for the three family of galaxy solutions with SMBHs obtained here with this approach: small or dwarf galaxies, medium galaxies and large galaxies. They remarkably encompass the other relevant physical magnitudes obtained for these systems in this paper with the same approach. Toward the central regions, the circular velocity grows as in Equation (59) due to the central black hole field. As seen from Figure 4, the dispersion velocity is constant in the Boltzmann (outer or classical) region and in the quantum (inner or compact) region, indicating WDM thermalization. For , the circular velocity tends to the velocity dispersion. Remarkably, this result confirms the same behavior we obtained independently with a different approach (the inverse problem or the Eddington integral equation for galaxies which we developed in Ref. [13]), namely, given the observed density profiles as input, the velocities, pressure and other galaxy magnitudes are obtained and analyzed as output. The observed density profiles being, by definition, real realistic data, the obtained results from them are valid, realistic magnitudes. Moreover, another robust verification of the kiloelectron volt WDM Thomas–Fermi approach is the 10 independent sets of observational data we used in Ref. [11] for galaxy masses from to . And also for many other different observational data sets [48,49,50,51,52,53,54,55,56,57,58,59,60]. The theoretical and observational rotation curves do agree. In addition, they agree extremely well with the observational rotation curves described by the empirical Burkert profile for (they differ from each other by only percent). These results show the success of the kiloelectron volt WDM Thomas–Fermi approach to correctly describe the galaxy structures.
- We first investigated pure WDM galaxies with their central black holes because DM is, on average, the over-dominant component in galaxies, and it is reasonable then to investigate first the effects of gravity plus WDM. This is thus a first approximation, more precisely the zero order of a first approximation in which the visible matter component, baryons, can be incorporated to provide a most accurate and complete picture. We observed that these zero order results found here are already realistic, very good and robust results, and they set the basis and the direction for improvements and a more complete understanding.
- Baryons will provide corrections to this picture and will allow to study other processes in which ordinary matter naturally plays a role as the gas and star components, but baryons will not change drastically the pure WDM results found here, which are the structural galaxy and black hole properties, masses, sizes, their scaling and relations, density profiles, the classical and quantum natures of the halo regions and their physical, high-density, medium-density or dilute states, the halo thermalization and virialization.
- This predictive theory and the obtained classes of solutions include very well the different galaxy types through their generic and important physical quantitive properties, such as the pressure, density, equation of state, mass, halo structure, and central black holes. Thus, we have primarily three galaxy classes: large dilute galaxies, intermediate galaxies, and small compact galaxies, whatever their astronomical empirical/historical name. The Milky Way galaxy is one of the galaxies in the large dilute galaxy class we found with all the specific properties of this class, mass, structure and central SMBH. Messier 87 is a larger (“supergiant”) galaxy within the large class of galaxies we found, hosting, consequently, a bigger central SMBH (M87).
- As explained in the paper, the central quantum WDM gaz is relevant for the presence of the obtained central non-cusped cores and their correct sizes, and for the presence of the central SMBHs and their realistic mass values without any ad hoc prescription. Recall, for instance, Figure 3 of the paper, which displays the density normalized at the influence radius , vs. for the three family of galaxy solutions with central SMBHs we found, large dilute galaxies, intermediate galaxies, and small compact galaxies, covering the different types of galaxies with their central SMBHs. The Milky Way is within the large dilute galaxy class we found with all the characteristic properties of this class: mass, structure and central SMBH, namely , galaxy mass and . Notice that in the quantum WDM gas region , the density is constant, clearly exhibiting a plateau behavior corresponding to the quantum macroscopic Fermi DM gas behavior in such a region. Figure 3 shows that the local density behavior is dominated by the black hole for . Coherently, for , the WDM gravitational field dominates over the black hole field, and the galaxy core shows up. For medium and large galaxies, such as the Milky Way, the core is seen as a plateau. At the same time, the chemical potential is negative for and the WDM is a Boltzmann gas in this region.The first or primary “signatures” are the set of galactic physical magnitudes and structural properties: sizes, masses, cored density profiles and their correct sizes. In particular, dwarf galaxies appear to be a full quantum macroscopic system. Dwarf galaxies are really interesting to observe in this respect, as tracers of the quantum kiloelctron volt WDM nature in nearly degenerated states, their temperatures and properties. These are important features all found and provided by the same and one single approach, without tailored prescriptions, and without considering different approaches for each of the different computed magnitudes. Therefore, these are all “signatures” for this approach.These results consistently encompass the ones shown in Figure 2: the derivative of the chemical potential vs. for the three families of galaxy solutions with central SMBH. For , the behavior is dictated by the central black hole. For , they are dominated by the WDM and in this region exhibit a similar behavior to the Thomas-Fermi galaxy solutions without a central SMBH [9,10,11,12]. For galaxies with central black holes, the WDM is in a quantum (highly compact) regime inside the quantum radius . Because is in the parsec scale or smaller (see Equations (75)–(77)), the bulk of the WDM is then in the Boltzmann regime, e.g., Figure 13 and Figure 14. In the quantum gas (dense) region, the equation of state becomes steeper than the perfect gas. Notice the huge values of in the quantum (high density) region and its sharp decrease entering the classical (dilute) region , all consistent with the other results we found.
- In all the obtained results, and in the Introduction, we carefully compared the results and solutions we obtained in this paper for galaxy systems with a central black hole and without a central black hole. From our results here, we recover, in particular, the galaxy structures, the cores of quantum WDM and their right sizes, the velocity dispersions, the scaling relations, the equation of state and the other related results in the absence of black holes, which we already discussed in our previous works [9,10,11,12,13] in which the careful check for rotation curves, masses, scaling relations, velocities, are in full agreement with observations for the whole set of properties.Cored density profiles and their right size, halo masses, are in full agreement with the observations. The quantum DM nature in the central regions is not an exotic property: it is the quantum nature of the degenerate or nearly degenerate gaz of DM particles. Interaction is fully gravitational, namely, a self-gravitating and self-consistent WDM gas. The first or primary “ signatures” are, therefore, the set of galactic physical magnitudes and structural properties—the sizes, masses, central cored profiles, velocity distributions, and surface density we found and confronted to real astronomical observations. Other effects, such as the influence of such DM structures, could in turn exert on the propagation of generated gravitational waves, on the accretion processes, which are superimposed effects, or on the secondary dark matter processes or secondary signatures, a problem which would require individual analysis and is clearly beyond the scope of the present paper, which is devoted to the primary dark matter effects, namely the dark matter galactic structures. Those secondary effects, such as the orbits, diffusion and absorption in the different regions and regimes around the BH require the interaction in propagation with other non dark matter components, as electromagnetic effects and accretion plasmas are not the subject of this paper.
- For the primary objectives of obtaining the galaxy structural magnitudes, e.g., the realistic astrophysical masses of the galaxies, the realistic SMBH central masses, their sizes, velocities, cored density and pressure profiles, the Newtonian treatment is largely enough. Recall that the Thomas–Fermi approach is a statistical many body approach. Near the black hole horizon, there will appear effects of spiraling, orbiting, or a glory effect (180 degrees backscattering) but it does not truly affect the properties and magnitudes of the galaxy–black-hole system (and this paper is not devoted to test GR black hole, horizon or baryonic effects). The values of the relevant radii are as follows (besides the halo radius): the quantum galaxy radius , the BH influence radius , and the horizon black hole radius are given by Equations (75)–(77). The horizon radius is always extremely small with respect to the other radii. For galaxies with virial masses from to , runs between and pc, respectively (as shown in Section 3.3), while the horizon radius of the central black hole runs from to pc for such range of galaxy masses, respectively; is larger than :. The important point in order to account for both the realistic galaxy and their central SMBH masses, their sizes, velocities, pressure profiles, density profiles and the core sizes, is the DM nature: kiloelectron volt WDM with its quantum and its relativistic treatment.Newtonian black holes have many common properties with general relativity black holes, and most importantly, they both have the same size. Recall that Newtonian and post-Newtonian approximation have proven to be remarkably effective, even in describing strong-field systems and astrophysical black hole systems (e.g., binary bhs) in spiraling toward a final merger (e.g., Ref. [61] and references therein). Of course, a fully GR treatment is needed to account for a causal space–time structure, central classical space–time curvature singularity, and precise tests of GR of the horizon or of the “no hair theorems”, for which inner orbits at milliparsec (mpc) distances need to be considered but not for the magnitudes of the galactic masses, sizes, or of their central SMBHs. The GR treatment minimally affects the obtained huge mass magnitude values. A high merit of the kiloelectron volt WDM approach is that it accounts naturally (with dark matter only) for the realistic astrophysical masses, sizes, density and velocity profiles, rotation curves, equation of state and structural properties of both galaxies and their central SMBHs.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Analytic Evaluation of the Density and the Pressure
Appendix A.1. The Quantum (High Density) Regime
Appendix A.2. The Classical Boltzmann Regime
References
- de Vega, H.J.; Sánchez, N.G. Model-independent analysis of dark matter points to a particle mass at the keV scale. Mon. Not. R. Astron. Soc. 2010, 404, 885. [Google Scholar] [CrossRef]
- Frontiers, C.; de Vega, H.J.; Sanchez, N.G. Dark matter in galaxies: The dark matter particle mass is about 7 keV. arXiv 2013, arXiv:1304.0759. [Google Scholar]
- Biermann, P.L.; de Vega, H.J.; Sanchez, N.G. Highlights and Conclusions of the Chalonge Meudon Workshop. arXiv 2012, arXiv:1305.7452. [Google Scholar]
- de Vega, H.J.; Falvella, M.C.; Sanchez, N.G. Highlights and Conclusions of the Chalonge 16th Paris Cosmology Colloquium. arXiv 2012, arXiv:1307.1847. [Google Scholar]
- de Vega, H.J.; Sanchez, N.G. Cosmological evolution of warm dark matter fluctuations. II. Solution from small to large scales and keV sterile neutrinos. Phys. Rev. D 2012, 85, 043516–043517. [Google Scholar] [CrossRef]
- Destri, C.; de Vega, H.J.; Sanchez, N.G. Warm dark matter primordial spectra and the onset of structure formation at redshift z. Phys. Rev. D 2013, 88, 083512. [Google Scholar] [CrossRef]
- de Vega, H.J.; Moreno, O.; Guerra, E.M.d.; Medrano, M.R.; Sanchez, N.G. Role of sterile neutrino warm dark matter in rhenium and tritium beta decays. Nucl. Phys. B 2013, 866, 177. [Google Scholar] [CrossRef][Green Version]
- Lello, L.; Boyanovsky, D. Cosmological implications of light sterile neutrinos produced after the QCD phase transition. Phys. Rev. D 2015, 91, 063502. [Google Scholar] [CrossRef]
- Destri, C.; de Vega, H.J.; Sanchez, N.G. Fermionic warm dark matter produces galaxy cores in the observed scales because of quantum mechanics. New Astron. 2013, 22, 39. [Google Scholar] [CrossRef]
- Destri, C.; de Vega, H.J.; Sanchez, N.G. Quantum WDM fermions and gravitation determine the observed galaxy structures. Astrop. Phys. 2013, 46, 14. [Google Scholar] [CrossRef][Green Version]
- de Vega, H.J.; Salucci, P.; Sanchez, N.G. Observational rotation curves and density profiles versus the Thomas–Fermi galaxy structure theory. Mon. Not. R. Astron. Soc. 2014, 442, 2717. [Google Scholar] [CrossRef]
- de Vega, H.J.; Sánchez, N.G. Equation of state, universal profiles, scaling and macroscopic quantum effects in warm dark matter galaxies. Eur. Phys. J. C 2017, 77, 1–19. [Google Scholar] [CrossRef][Green Version]
- de Vega, H.J.; Sánchez, N.G. The dark matter distribution function and halo thermalization from the Eddington equation in galaxies. Int. J. Mod. Phys. A 2016, 31, 1650073. [Google Scholar] [CrossRef]
- Menci, N.; Sanchez, N.G.; Castellano, M.; Grazian, A. Constraining the warm dark matter particle mass through ultra-deep UV luminosity functions at Z= 2. Astrophys. J. 2016, 818, 90. [Google Scholar] [CrossRef]
- Drewes, M.; Lasserre, T.; Merle, A.; Mertens, S.; Adhikari, R.; Bahr, M.; Baur, J.; Behrens, J.; Bezrukov, F.; Bhupal Dev, P.S.; et al. A White Paper on keV Sterile Neutrino Dark Matter. J. Cosmol. Astropart. Phys. 2017, 1, 25. [Google Scholar]
- Dror, J.A.; Elor, G.; McGehee, R. Directly detecting signals from absorption of fermionic dark matter. Phys. Rev. Lett. 2020, 124, 181301. [Google Scholar] [CrossRef]
- Rudakovskyi, A.; Mesinger, A.; Savchenko, D.; Gillet, N. Constraints on warm dark matter from UV luminosity functions of high-z galaxies with Bayesian model comparison. Mon. Not. R. Astron. Soc. 2021, 507, 3046. [Google Scholar] [CrossRef]
- Special Issue “keV Warm Dark Matter in Agreement with Observations in tribute to Hector de Vega”. Universe 2021. Available online: https://www.mdpi.com/journal/universe/special_issues/kWDM (accessed on 1 October 2021).
- Boyanovsky, D.; de Vega, H.J.; Sanchez, N.G. Constraints on dark matter particles from theory, galaxy observations, and N-body simulations. Phys. Rev. D 2008, 77, 043518–063546. [Google Scholar] [CrossRef]
- de Vega, H.J.; Salucci, P.; Sanchez, N.G. The mass of the dark matter particle: Theory and galaxy observations. New Astron. 2012, 17, 653. [Google Scholar] [CrossRef]
- Colín, P.; Valenzuela, O.; Avila-Reese, V. Substructure and halo density profiles in a warm dark matter cosmology. Astrophys. J. 2000, 542, 622. [Google Scholar] [CrossRef]
- Sommer-Larsen, J.; Dolgov, A. Formation of disk galaxies: Warm dark matter and the angular momentum problem. Astrophys. J. 2001, 551, 608. [Google Scholar] [CrossRef]
- Gao, L.; Theuns, T. Lighting the Universe with filaments. Science 2007, 317, 1527. [Google Scholar] [CrossRef] [PubMed]
- Tikhonov, A.V.; Gottlöber, S.; Yepes, G.; Hoffman, Y. The sizes of minivoids in the local Universe: An argument in favour of a warm dark matter model? Mon. Not. R. Astron. Soc. 2009, 399, 1611. [Google Scholar] [CrossRef]
- Zavala, J.; Jing, Y.P.; Faltenbacher, A.; Yepes, G.; Hoffman, Y.; Gottlöber, S.; Catinella, B. The velocity function in the local environment from ΛCDM and ΛWDM constrained simulations. Astrophys. J. 2009, 700, 1779. [Google Scholar] [CrossRef]
- Papastergis, E.; Martin, A.M.; Giovanelli, R.; Haynes, M.P. The velocity width function of galaxies from the 40% ALFALFA survey: Shedding light on the cold dark matter overabundance problem. Astrophys. J. 2011, 739, 38. [Google Scholar] [CrossRef]
- Lovell, M.R.; Eke, V.; Frenk, C.S.; Gao, L.; Jenkins, A.; Theuns, T.; Wang, J.; White, S.D.M.; Boyarsky, A.; Ruchayskiy, O. The haloes of bright satellite galaxies in a warm dark matter universe. Mon. Not. R. Astron. Soc. 2012, 420, 2318. [Google Scholar] [CrossRef]
- Lovell, M.R.; Frenk, C.S.; Eke, V.R.; Jenkins, A.; Gao, L.; Theuns, T. The properties of warm dark matter haloes. Mon. Not. R. Astron. Soc. 2014, 439, 300. [Google Scholar] [CrossRef]
- Anderhalden, D.; Schneider, A.; Macciò, A.V.; Diemand, J.; Bertone, G. Hints on the nature of dark matter from the properties of Milky Way satellites. J. Cosmol. Astropart. Phys. 2013, 3, 14. [Google Scholar] [CrossRef]
- Wyse, R.F.G.; Gilmore, G. Observed properties of dark matter on small spatial scales. IAU Symp. 2007, 244, 44–52. [Google Scholar] [CrossRef]
- van Eymeren, J.; Trachternach, C.; Koribalski, B.S.; Dettmar, R.J. Non-circular motions and the cusp-core discrepancy in dwarf galaxies. Astron. Astrophys. 2009, 505, 1–20. [Google Scholar] [CrossRef]
- de Blok, W.J.G. The Core-Cusp Problem. Adv. Astron. 2010, 2010, 1–15. [Google Scholar] [CrossRef]
- Salucci, P.; Frigerio Martins, C. The mass distribution in Spiral galaxies. EAS Publ. Ser. 2009, 36, 133–140. [Google Scholar] [CrossRef][Green Version]
- Gilmore, G.; Wilkinson, M.U.; Wyse, R.F.G.; Kleyna, J.T.; Koch, A.; Wyn Evans, N.; Grebel, E.K. The observed properties of dark matter on small spatial scales. Astrophys. J. 2007, 663, 948. [Google Scholar] [CrossRef]
- Walker, M.; Penarrubia, J.P. A method for measuring (slopes of) the mass profiles of dwarf spheroidal galaxies. Astrophys. J. 2011, 742, 20. [Google Scholar] [CrossRef]
- Spano, M.; Marcelin, M.; Amram, P.; Carignan, C.; Epinat, B.; Hernandez, O. GHASP: An Hα kinematic survey of spiral and irregular galaxies–V. Dark matter distribution in 36 nearby spiral galaxies. Mon. Not. R. Astron. Soc. 2008, 383, 297. [Google Scholar] [CrossRef]
- Donato, F.; Gentile, G.; Salucci, S.; Frigerio Martins, C.; Wilkinson, M.I.; Gilmore, G.; Grebel, E.K.; Koch, A.; Wyse, R. A constant dark matter halo surface density in galaxies. Mon. Not. R. Astron. Soc. 2009, 397, 1169. [Google Scholar] [CrossRef]
- Kormendy, J.; Freeman, K.C. Scaling laws for dark matter halos in late-type and dwarf spheroidal galaxies. IAU Symp. Syd. 2004, 220, 377. [Google Scholar] [CrossRef]
- Avila-Reese, V.; Colín, P.; Valenzuela, O.; D’Onghia, E.; Firmani, C. Formation and structure of halos in a warm dark matter cosmology. Astrophys. J. 2001, 559, 516. [Google Scholar] [CrossRef]
- Colín, P.; Valenzuela, O.; Avila-Reese, V. On the structure of dark matter halos at the damping scale of the power spectrum with and without relict velocities. Astrophys. J. 2008, 673, 203. [Google Scholar] [CrossRef]
- Vinas, J.; Salvador-Solé, E.; Manrique, A. Typical density profile for warm dark matter haloes. Mon. Not. R. Astron. Soc. 2012, 424, L6. [Google Scholar]
- Macciò, A.; Paduroiu, S.; Anderhalden, D.; Schneider, A.; Moore, B. Cores in warm dark matter haloes: A Catch 22 problem. Mon. Not. R. Astron. Soc. 2012, 424, 1105. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshits, E.M. Statistical Mechanics; Elsevier: Oxford, UK, 1980. [Google Scholar]
- de Vega, H.J.; Sánchez, N.G. Statistical mechanics of the self-gravitating gas: I. Thermodynamic limit and phase diagrams. Nucl. Phys. B 2002, 625, 409–460. [Google Scholar] [CrossRef]
- Munyaneza, F.; Biermann, P.L. Degenerate sterile neutrino dark matter in the cores of galaxies. Astron. Astrophys. 2006, 458, L9. [Google Scholar] [CrossRef][Green Version]
- Chavanis, P.H. Phase transitions in self-gravitating systems: Self-gravitating fermions and hard-sphere models. Phys. Rev. E 2002, 65, 056123. [Google Scholar] [CrossRef]
- Chavanis, P.H. Phase transitions in self-gravitating systems. Int. J. Mod. Phys. B 2006, 20, 3113. [Google Scholar] [CrossRef]
- McConnachie, A.W. The observed properties of dwarf galaxies in and around the Local Group. Astrophys. J. 2012, 144, 4. [Google Scholar] [CrossRef]
- Menci, N.; Fiore, F.; Lamastra, A. The evolution of active galactic nuclei in warm dark matter cosmology. Astrophys. J. 2013, 766, 110. [Google Scholar] [CrossRef][Green Version]
- Nierenberg, A.M.; Treu, T.; Menci, N.; Lu, Y.; Wang, W. The cosmic evolution of faint satellite galaxies as a test of galaxy formation and the nature of dark matter. Astrophys. J. 2013, 772, 146. [Google Scholar] [CrossRef]
- Pacucci, F.; Mesinger, A.; Haiman, Z. Focusing on warm dark matter with lensed high-redshift galaxies. Mon. Not. R. Astron. Soc. Lett. 2013, 435, L53–L57. [Google Scholar] [CrossRef]
- Salucci, P.; Lapi, A.; Tonini, C.; Gentile, G.; Yegorova, I.; Klein, U. The universal rotation curve of spiral galaxies–II. The dark matter distribution out to the virial radius. Mon. Not. R. Astron. Soc. 2007, 378, 41. [Google Scholar] [CrossRef]
- Simon, J.D.; Geha, M. The kinematics of the ultra-faint Milky Way satellites: Solving the missing satellite problem. Astrophys. J. 2007, 670, 313. [Google Scholar] [CrossRef]
- Simon, J.D.; Geha, M.; Minor, Q.E.; Martinez, G.D.; Kirby, E.N.; Bullock, J.S.; Kaplinghat, M.; Strigari, L.E.; Willman, B.; Choi, P.I.; et al. A complete spectroscopic survey of the milky way satellite Segue 1: The darkest galaxy. Astrophys. J. 2011, 733, 46. [Google Scholar] [CrossRef]
- Wolf, J.; Martinez, J.D.; Bullock, J.B.; Kaplinghat, M.; Geha, M.; Muñoz, R.R.; Simon, J.D.; Avedo, F.F. Accurate masses for dispersion-supported galaxies. Mon. Not. R. Astron. Soc. 2010, 406, 1220. [Google Scholar] [CrossRef]
- Brodie, J.P.; Romanowsky, A.J.; Strader, J.; Forbes, D.A. The relationships among compact stellar systems: A fresh view of ultracompact dwarfs. Astrophys. J. 2011, 142, 199. [Google Scholar] [CrossRef]
- Martinez, G.D.; Minor, Q.E.; Bullock, J.; Kaplinghat, M.; Simon, J.D.; Geha, M. A Complete Spectroscopic Survey of the Milky Way Satellite Segue 1: Dark Matter Content, Stellar Membership, and Binary Properties from a Bayesian Analysis. Astrophys. J. 2011, 738, 55. [Google Scholar] [CrossRef]
- Willman, B.; Strader, J. “Galaxy,” defined. Astrophys. J. 2012, 144, 76. [Google Scholar] [CrossRef]
- Shao, S.; Gao, L.; Theuns, T.; Frenk, C.S. The phase-space density of fermionic dark matter haloes. Mon. Not. R. Astron. Soc. 2013, 430, 2346. [Google Scholar] [CrossRef]
- Watson, C.R.; Li, Z.; Polley, N. Constraining Sterile Neutrino Warm Dark Matter with Chandra Observations of the Andromeda Galaxy. J. Cosmol. Astropart. Phys. 2012, 3, 018. [Google Scholar] [CrossRef]
- Will, C.M. Theory and Experiment in Gravitational Physics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Vega, H.J.; Sanchez, N.G. Warm Dark Matter Galaxies with Central Supermassive Black Holes. Universe 2022, 8, 154. https://doi.org/10.3390/universe8030154
de Vega HJ, Sanchez NG. Warm Dark Matter Galaxies with Central Supermassive Black Holes. Universe. 2022; 8(3):154. https://doi.org/10.3390/universe8030154
Chicago/Turabian Stylede Vega, Hector J., and Norma G. Sanchez. 2022. "Warm Dark Matter Galaxies with Central Supermassive Black Holes" Universe 8, no. 3: 154. https://doi.org/10.3390/universe8030154
APA Stylede Vega, H. J., & Sanchez, N. G. (2022). Warm Dark Matter Galaxies with Central Supermassive Black Holes. Universe, 8(3), 154. https://doi.org/10.3390/universe8030154






