Abstract
We study the stochastic Kardar-Parisi-Zhang equation for kinetic roughening where the time-independent (columnar or spatially quenched) Gaussian random noise is specified by the pair correlation function , d being the dimension of space. The field-theoretic renormalization group analysis shows that the effect of turbulent motion of the environment (modelled by the coupling with the velocity field described by the Kazantsev-Kraichnan statistical ensemble for an incompressible fluid) gives rise to a new nonlinear term, quadratic in the velocity field. It turns out that this “induced” nonlinearity strongly affects the scaling behaviour in several universality classes (types of long-time, large-scale asymptotic regimes) even when the turbulent advection appears irrelevant in itself. Practical calculation of the critical exponents (that determine the universality classes) is performed to the first order of the double expansion in and the velocity exponent (one-loop approximation). As is the case with most “descendants” of the Kardar-Parisi-Zhang model, some relevant fixed points of the renormalization group equations lie in “forbidden zones”, i.e., in those corresponding to negative kinetic coefficients or complex couplings. This persistent phenomenon in stochastic non-equilibrium models requires careful and inventive physical interpretation.
1. Introduction
The Kardar-Parisi-Zhang (KPZ) model was proposed in [1] to describe evolution of an interface that separates a randomly growing substance from the rest of the system. As the interface evolves due to intrinsic dynamics and external disturbances, it becomes progressively “rough”. This joint effect of various deterministic or/and random entries results in what is known as kinetic roughening [2]. Flame fronts, surfaces of tumours or bacterial colonies, and landscape profiles are all examples of interfaces undergoing kinetic roughening; see, e.g., [3] and references therein 1.
The KPZ equation is one of the simplest semi-phenomenological models of kinetic roughening. The model itself is a nonlinear stochastic differential equation for a smoothed height profile of the moving interface. It assumes that the growth is lateral and that its rate is a smooth function of the height gradient. Then, the leading term in the gradient expansion determines the nonlinearity of the KPZ model. Another term, linear in h, incorporates the “surface tension” or the forces of any kind that make the interface smoother [1]. A random noise mimics various microscopic degrees of freedom that can influence the roughening dynamics of the interface.
From physics viewpoints, kinetic roughening is a representative example of non-equilibrium phenomena that occur in a wide variety of complex physical systems evolving due to intrinsic dynamics and undergoing extra disturbances 2. It was argued that it is such competition that gives rise to nontrivial patterns [6,7]. Indeed, many of non-equilibrium systems can evolve to critical states without the fine tuning of control parameters (in contrast to near-equilibrium critical systems). Examples are provided by dissipative driven open systems [8], turbulence [9,10] and, in a more general context, by systems revealing the so-called self-organized criticality, the phenomenon observed in numerous physical, biological, chemical, neural and social systems, etc. [11,12,13,14].
As such systems exhibit universal scaling behaviour, fluctuations of growing surfaces can be viewed as the most pictorial representative for a wide range of phenomena with the same types of critical behaviour (universality classes). Thus, the KPZ model, with its simplest make-up, is customarily referred to as a non-equilibrium analog of the Ising model in equilibrium phase transitions.
That is why an enormous number of papers concerned with the KPZ model is published every year as the KPZ universality class is discovered in new systems or new features of the KPZ model are established [15,16,17,18,19,20,21,22,23,24]. For example, in the recent paper [25], the KPZ universality class has been detected in the morphology of the modern urban skyline observed in the cities throughout the Netherlands.
However, the standard field-theoretic perturbative renormalization group (RG) analysis does not reveal any infrared (IR) attractive fixed points of the RG equations for the KPZ model [26,27] in the physical area of parameters. If an appropriate fixed point does nevertheless exist, it seems to be inaccessible within any kind of perturbative treatment. This point would correspond to the rough phase, or to be precise, to the non-trivial asymptotic behaviour of the interface in the IR range (which implies that times and distances are large in comparison with the characteristic microscopic scales), i.e., to kinetic roughening (or critical scaling).
The functional RG is probably the only existing approach that gives access to that fixed point [28,29,30,31] making it “essentially non-perturbative”.
Other open questions include the random noise interpretation [32,33], the value of the upper critical dimension [3,19,34,35,36,37,38] and its very existence [20,39,40,41,42,43] 3.
All of these facts suggest that instead of a more sophisticated analysis, the KPZ model may need modifications or adjustments that might lead to a drastic change in the RG analysis. It does seem as if the KPZ model may be sensitive to various extensions and modifications; e.g., the simple extension turns the model into one with an infinite number of coupling constants [45,46].
One of the possible modifications consists of choosing a time-independent (spatially quenched or columnar) noise with the correlation function
instead of the white in-time random noise (that differs from (1) by additional Dirac’s function ) that was used in the original KPZ model. Here are the space-time coordinates, the brackets represent an average over many realizations of the randomness4, and d is the dimension of space.
The spatially quenched noise (1) was suggested in [47] to model landscape erosion where non-erodible (“quenched”) regions may be the main reason behind the scaling [48].
The KPZ model is usually considered with a more general form of a quenched disorder that includes dependence on the height of the profile [49,50,51]. This disorder is often used in the study of driven interfaces in random media [52] (also confer [52] for a detailed review of the types of quenched noises). However, the factor is a hard obstacle for analytical approaches [53].
Besides its relative simplicity, the noise (1) also stands aside for its connection with nonuniversality (see [54,55,56] in relation to directed percolation, [57] in relation to erosion of landscapes, and [58] in relation to self-organised criticality).
In this paper we propose to analyse the version of the KPZ equation where the white noise is replaced with the time-independent spatially quenched noise (1). However, one could include the spatially quenched noise in another way, namely, by coupling the conserved KPZ equation (i.e., the modification of the model with conservation law) with the spatially quenched noise [59]. Note that the resulting model is vastly different.
Another possible modification of the KPZ model involves inclusion of the motion of the environment. Critical behaviour of nearly-equilibrium nearly-critical systems can be dramatically affected by the motion of the medium either disappearing altogether or acquiring new unexpected features [60,61,62,63,64,65,66]. Considering that environment motion is almost impossible to exclude in real experimental settings, it is important to account for it while studying critical behaviour.
Recent attempts [67,68,69] revealed that turbulent or random environment (modelled either by stochastic Navier-Stokes equation or by a “rapid-change” Kazantsev-Kraichnan velocity ensemble) dominates scaling and “washes away” the kinetic roughening.
In this paper, we apply the field theoretic RG to a nonlinear non-equilibrium nearly-critical system, subjected to a quenched disorder and turbulent environment. The system is described by the KPZ equation, while the disorder is described by the Gaussian time-independent spatially quenched noise (1). The environment is modelled by the “synthetic” Gaussian ensemble with vanishing correlation time known as the Kazantsev-Kraichnan ensemble [70].
We found out that coupling with the turbulent velocity field leads to an emergence of a new nonlinearity that must be included in the model to make it renormalizable. RG analysis shows that there are six regimes of critical behaviour; critical exponents are calculated for every regime in the leading order of the double expansion in and velocity exponent (one-loop approximation). The most realistic values of parameters ( and ) correspond to the regime where the turbulent advection is irrelevant (in the sense of Wilson) while the new nonlinearity is relevant along with the KPZ nonlinearity.
The plan of the paper is as follows: the problem is described in Section 2; Section 3 details renormalization procedure up to calculation of renormalization constants; fixed points of the RG equation, their stability regions, and corresponding critical exponents are considered in Section 4; Section 5 contains conclusion and discussion of the implications.
2. Formulation of the Problem
Kinetic roughening of growing interfaces can be described by a power law for asymptotic behaviour of the so-called structure functions in the IR range. It could be entered as following:
Here stands for the height of the surface profile (here and below, t and are the time and the space coordinates, respectively), while the averaging is defined as above. The roughness exponent , the dynamical exponent z and the universal scaling functions determine the universality class of the scaling behaviour.
To calculate the critical exponents and z, we perform the RG analysis of the model which consists of the equation for the interface growth and statistical ensemble for the velocity field that models environment motion.
The KPZ model that describes interface growth is a nonlinear differential equation for the field :
Here , , , , and d is the dimension of the space. Summation over repeated tensor indices is implied throughout the paper. The parameter corresponds to the “surface tension”, and (can be either positive or negative) stays by the nonlinear term of the equation. The nonlinearity models lateral growth or decay. Let us first set as a non-trivial that can always be scaled out.
The random noise f is supposed to simulate the processes occurring at small scales (which means the smallness of the noise correlation radius in comparison with the distances we are interested in). So it is reasonable to choose the noise correlation function in the form of a spatial function. A function in time would correspond to a vanishing correlation time which is also a reasonable assumption. Here, however, we choose the spatially quenched noise (1) discussed in Section 1.
This choice violates the Galilean symmetry of the original deterministic equation (the symmetry is preserved for the white in-time noise with ).
Let us proceed with the description of the turbulent motion of the environment (e.g., some fluid). The velocity of the mixing field is represented by the Kazantsev-Kraichnan statistical ensemble (see, e.g., [70]), i.e., the Gaussian distribution with zero mean and the pair correlation function of the form 5
Here, is the transverse projector, it reflects the incompressibility of the fluid (); as the wave number, is a positive amplitude. The sharp cutoff serves as an IR regularization.
The advection by the velocity field is provided by the “minimal” replacement
in the Equation (3), where is the Lagrangian (material, or Galilean covariant) derivative. However, as we will shortly see below, in the present model this replacement is not self-sufficient. The coupling to the external velocity field, given by (5), necessarily leads to the emergence of another effective interaction, proportional to a term in the Equation (3).
3. Field Theoretic Formulation and Renormalization of the Model
3.1. Field Theoretic Formulation
According to the general de Dominicis-Janssen theorem (see, e.g., chapter 5 in the monograph [44] and references therein) the stochastic problem (1), (3), (4) can be reformulated as the field theoretic model for an extended set of fields with the action functional , where
is the action functional for the stochastic Equations (1), (3) and (5) at fixed velocity field, while
provides the averaging over the Gaussian velocity statistics defined by Equation (4).
In the Equation (6), the random noise f was integrated out in favor of the auxiliary response Martin-Siggia-Rose field . In the Equation (7), is the kernel of the integral operation inverse to in (4).
The field theoretic Formulation (6) and (7) means that all the correlation, structure and response functions of the original full stochastic problem problem (1), (3), (4) given by the joint averaging over the Gaussian statistics for f and defined by the Equations (1) and (4) can be represented by functional averages over the full set of fields with weight , and with the proper normalization .
All the needed integrations over the arguments and summations over the vector indices are implied for all terms in the expressions for the action functionals (6), (7) and similar expressions below, e.g.,
The parameters serve as the coupling constants (“charges”):
The above relations follow from the dimensional analysis (detailed in Section 3.2); sets the typical ultraviolet (UV) momentum scale.
The expressions for the bare propagators are obtained by considering the terms quadratic in the fields in the action functional (6). The propagators have the following form in the frequency–momentum representation:
The propagators (10) include the amplitudes , . This is not ideal because while we can still proceed with the calculations, critical dimensions for the fixed points of RG equations with coordinates equal to zero will have to be readjusted. Indeed, the propagators that involve bare charges should be treated carefully in the vicinity of trivial renormalized charges, e.g., when a fixed point has coordinates or . Otherwise, the expressions for the critical dimensions naively derived for such points using the standard Formulas (32) can be wrong. To avoid that complication, let us dilate the fields so that the couplings are removed from quadratic terms.
The appropriate choice for the re-scaling is and , i.e., we exchange the set of fields with the set . Additionally, we pass to new charges , .
We arrive at the following action functional:
Note that we did not change notations for the fields and for the operator even though those quantities were dilated.
3.2. UV Divergences and Renormalization
To eliminate UV divergences, the renormalization procedure is applied. Analysis of UV divergences is based on canonical dimensions, see, e.g., [44]. Dynamic models have two independent scales: a time scale and a space scale ; therefore, the canonical dimension of any quantity F is determined by two numbers, namely, by the frequency dimension and by the momentum dimension :
Values of canonical dimensions are found from the requirement that all terms of an action functional be dimensionless with respect to both canonical dimensions; the obvious normalization conditions are
A total canonical dimension is defined by the expression . The factor 2 follows from the fact that in the free theory. All the canonical dimensions for the theory (11) are presented in the Table 1. Parameters , x, will be defined later on.

Table 1.
Canonical dimensions of the fields and the parameters in the theory (11); .
The model is logarithmic (all coupling constants become dimensionless) at , i.e., at , and .
A total dimension of a 1-irreducible Green’s function that involves fields h, fields , and fields is determined by the following expression
In the logarithmic theory, coincides with the formal index of UV divergence of the corresponding Green’s function. Thus, the divergent part of the function and the possible counterterms are polynomials of degree .
In the case of the theory (11), the real divergence index differs from the formal one: . This is due to the fact that the field h enters the action functional only in the form of a spatial derivative.
Considering the last condition, one can list possible counterterms: , (these two are responsible for renormalization of the mean value of h), , , , , (these five already exist in the action functional), (this one vanishes owing to the incompressibility of the fluid), and, finally, which is a new counterterm.
For the model to be renormalizable, the new term must be added to the action functional (11):
The coupling constant corresponding to the new nonlinearity is notated as . The factor appears from the dimensionality considerations.
Up till now we have been considering the KPZ equation with turbulent advection incorporated via the the Lagrangian derivative (5):
It should be stressed that by including a new term into the action functional we effectively changed this equation into another one:
(here notations stand for the fields before re-scaling).
Now that we ensured multiplicative renormalizability of the theory (15), bare fields and parameters can be expressed in terms of their renormalized counterparts:
Here we added the subscript 0 to the fields to differentiate them from the renormalized ones. The renormalization mass is an additional parameter of the renormalized theory while the set are renormalization constants.
The renormalized action has the form
The constants are found from the condition that the corresponding Green’s functions be UV finite in the given order of the perturbation theory.
For the action (19), the relations between the renormalization constants are:
Using MS scheme and one-loop approximation, we arrive at the following results (see [67] for a detailed example of one-loop calculations):
Here for any , where is the area of the unit sphere in d-dimensional space.
4. RG Equation, Fixed Points, Critical Exponents
4.1. RG Equation, RG Functions
The Green’s functions of the theory (11) can be expressed in terms of their renormalized counterparts in the following way:
Here denotes the full set of the bare parameters while e stands for renormalized ones; other arguments (times, momenta etc.) are denoted with the ellipsis. , , are numbers of the respective fields in the function G.
We apply the operator , taken at fixed bare parameters, to both sides of the expression (22) to obtain the basic RG equation:
Here and ; anomalous dimensions , and beta functions , , are so-called RG functions and they are defined in the standard way:
where and . From (18) and (24) the following relations can be obtained:
The corresponding anomalous dimensions in one-loop approximation are (hereafter we omit the notation):
4.2. Fixed Points, Stability Regions
Critical exponents that characterize IR asymptotic behaviour of a system are associated with IR attractive fixed points of the RG equation derived for the corresponding field theory (see, e.g., [44]). Values of the renormalized charges serve as coordinates of the fixed points; they are found from the system of equations for all . Matrix (where f again is a set of charges ) determines the type of fixed point. For IR attractive points, , where is a complete set of eigenvalues of the matrix . The region of system’s parameters where a given point is IR attractive is referred to as an IR stability region of this point.
The system of beta functions (25) reads
The system has the following solutions:
- FP1a (fixed point 1a) with IR stability region .
- FP2 , with IR stability region . Note that this point is actually two points (as there are two roots of the equation ) that share the same stability region.
- FP3 , , with IR stability region (for all four combinations of the roots).
- FP4 , , with IR stability region (for all 4 combinations of the roots).
- FP5 , , with IR stability region (for both roots).
- FP6 , with empty IR stability region (for both roots).
The listed fixed points must be supplemented with the solutions that account for marginal values of the charges. To find them, let us pass to a new set of charges with β—functions that do not involve terms with nontrivial denominators. The appropriate substitution is a set with a system of β—functions:
Additional fixed points include:
- FP1b , arbitrary with IR stability region ;
- FP7 with IR stability region ;
- FP8 with empty IR stability region.
Stability regions on the plane are shown at the Figure 1.
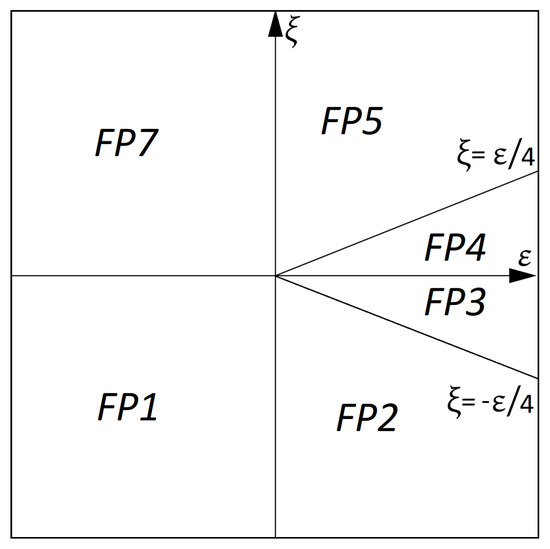
Figure 1.
IR stability regions of the fixed points for the renormalized theory (19).
Let us discuss the stability regions in details. The domain in the lower left part of the graph on the Figure 1 (quadrant III of plane) corresponds to the couple of Gaussian points FP1a and FP1b (their combined stability regions are denoted as FP1 on the Figure 1). This region is related to ordinary diffusion as all the coupling constants in the IR limit tend to zero for the negative and .
The domain denoted FP2 corresponds to the regime where only the KPZ nonlinearity is relevant. As one can see, in this regime, which is consistent with the pure KPZ model (with the spatially quenched noise and without the turbulent mixing) being multiplicatively renormalizable without an extra term in the action functional [71].
Surprisingly, while stability region of the point FP5 also corresponds to the regime where the KPZ nonlinearity is relevant and the turbulent mixing is irrelevant, the coordinate is not trivial for this regime: . That means that the new nonlinearity is relevant even while the turbulent mixing (that induced it in the first place) is “turned off”. It should be noted that it is this regime that corresponds to the Kolmogorov value of the exponent (for either or ).
This is also the case with the regime for the point FP7: the new term determines the IR asymptotic behaviour while both the turbulent mixing and the KPZ nonlinearity are irrelevant.
Finally, in the regimes corresponding to the points FP3 and FP4, both nonlinearities and the turbulent mixing are relevant as all coordinates of the fixed points are nontrivial.
It should be noted that for the regimes that correspond to the regions in the right-hand side of the graph on Figure 1, some coordinates of the fixed points are imaginary while some are negative.
4.3. Critical Exponents
Note that the substitution turns the RG Equation (23) into an equation with constant coefficients
Here and . Canonical scale invariance for the renormalized Green’s function is expressed by the following differential equations:
Here i a is full set of arguments of : . As before, while and stand for canonical dimensions. By combining (29) and (30) to eliminate operator (as is fixed in IR asymptotic) we obtain the equation of critical scaling:
where critical dimensions , , are
Critical exponents and z in the power law (2) are related to critical dimensions in a trivial way: , . This statement, however, is not obvious and requires justification. Indeed, the power law (2) is written for the structure functions that consist of pair correlation functions of the composite fields (“composite operators”). Generally, renormalization of such objects requires additional (sometimes quite complex) analysis. In the present case, however, one can prove (see [67] for a detailed proof in a similar case) that operators are not renormalized and their critical dimensions are given by the equality . The latter is enough to justify the relation for critical exponents.
Critical dimensions for the fixed points FP1–FP7 (one-loop approximation) are presented in Table 2.

Table 2.
Critical dimensions for the fixed points FP1–FP7.
Critical exponent for the point FP2 (the regime of the pure KPZ model) is in agreement with [71] (equation (43)), where the KPZ model with the spatially quenched noise was considered without the turbulent mixing. IR stability region of the point FP6 is empty but it is this point that corresponds to the regime of the pure turbulent mixing. Critical exponents for FP6 related to the velocity field (, ) are in agreement with exponents for Kazantsev-Kraichnan velocity ensemble, see, e.g., equations (2.18)–(2.20) in [72]. All critical exponents for the point FP4 coincide with the ones calculated for nontrivial regime of a system described by the original KPZ model (with the white random noise) and Kazantsev-Kraichnan ensemble, see equation (6.4) in [67].
5. Conclusions and Discussion
We studied the Kardar-Parisi-Zhang (KPZ) model with a time-independent (also referred to as columnar or spatially quenched) random noise and turbulent motion of the environment. The latter was simulated by the Kazantsev-Kraichnan’s “rapid-change” velocity ensemble.
The problem was reformulated as a certain field-theoretic model, and the standard renormalization procedure was applied. It was shown that the original model is not closed with respect to renormalization in the following sense: a new interaction (quadratic in the velocity field) unavoidably appears as a counterterm. The general RG ideology requires this term (that was absent from the initial “naive” formulation of the model) to be included into consideration from the very beginning.
Thus, the original KPZ equation should be generalized not only by the minimal advection replacement (5), but also by adding the new term.
In terms of the Wilsonian RG, the appearance of such a new term can be explained in the following way. The first RG iteration consists of the integration of the band of Fourier modes closest to the UV cut-off. The resulting “effective” stochastic equation (or the corresponding effective action functional) involves infinitely many terms with arbitrarily high powers of fields and their derivatives. Most of them are discarded by dimensionality reasons. In ordinary cases, the remaining terms differ from the original ones only by the change (“renormalization”) of the coefficient parameters. If so, the iteration procedure is infinitely repeated, driving the system to one of the IR attractive fixed points. In our case, the very first iteration gives rise to a new term: in the equation, or in the action functional. This term cannot be discarded, and it will reappear in the subsequent iterations. Thus, it is not forbidden by symmetry or dimensionality reasons, and it is natural to include it into the model from the very beginning. Then, such an extended model will be closed with respect to the renormalization procedure.
For this extended renormalizable field theoretic model, possible types of IR asymptotic behaviour (universality classes) are associated with the fixed points of the corresponding RG equations.
The RG equations, derived for our properly extended model with the new term, have eight fixed points. Two of them are always unstable, while the others can be IR attractive for a certain choice of the spatial dimension d and the velocity exponent . Critical dimensions that describe the IR (long-time, large-distance) asymptotic behaviour of the correlation functions were found in the leading order of the double expansion in and (one-loop approximation). Their values are universal in the sense that they depend only on the spatial dimension d and the parameter .
It turns out, that all the nontrivial scaling regimes correspond to complex or negative fixed points coordinates, which is a feature shared with the majority of models within the KPZ family.
The most realistic values of parameters ( and ) correspond to the point referred to as FP5 in Section 4. In this regime, the advection term appears IR irrelevant (in the sense of Wilson) while the new term is relevant along with the original KPZ nonlinearity. This means that the effect of the turbulent environment manifests itself not as a habitual transfer (advection) but as a certain nonlinear interaction of the velocity field. In other words, the minimal replacement (5) is not internally consistent and thus, is not sufficient to describe the effect of the environment of the scalar field.
This situation has some interesting parallels with the light-light (or photon-photon) scattering, the phenomenon that is absent in the classical electrodynamics, but emerges in the quantum case as a result of interaction with the vacuum fluctuations. To be precise, the situation can roughly be compared with the weak-field limit of the Euler-Heisenberg electrodynamics that involve two terms, quartic in the electromagnetic potential [73]. The simplest interaction term responsible for such phenomenon is a local term quartic in the electromagnetic potential, . It has the necessary canonical dimension but it is forbidden by the gauge symmetry and, therefore, cannot emerge as a counterterm. Similarly, dimensional considerations show that the term can be added to the KPZ equation, no matter what kind of random noise is used. However, if we require the model to be Galilean covariant, such term is forbidden. This happens in the case of the white in-time noise because it respects the Galilean symmetry [70]. On the contrary, in our model, that symmetry is already violated by the spatially quenched noise so the term necessarily results from the renormalization procedure and should be added into the action functional from the very beginning.
However, quartic terms in the QED do appear in the effective action functional due to the radiative corrections. For the first time, they were derived within the Euler-Heisenberg Lagrangian and, for small fields, reduce to the forms and , which are both Lorentz and gauge invariant. Written in terms of the potential , they involve fourth-order derivatives and have a larger canonical dimension in comparison with the classical Lagrangian . This difference is compensated by the dimensional coefficient , where is the electron mass.
Similarly, the effective action for the KPZ model in the Galilean invariant case may include invariant terms, quadratic in the gradients of the velocity field (resulting from the 1-irreducible function ) with a larger canonical dimension and the dimensional coefficient 1/m2.
For the heat transfer equation, an explicit expression for those terms is presented in [74], see equation (50.2) on page 197. They describe dissipation of the mechanical kinetic energy of the fluid into heat and lead to the linear growth of the mean temperature. Note that in the energy balance equation for the fluid they appear with the opposite sign (see, e.g., [10]) providing conservation of the full energy.
It should be stressed that the actual dimensionless parameter in the gradient expansion for the KPZ equation is . In the Galilean invariant case (white in-time noise) the contribution of the new terms to the surface growth rate is suppressed by this parameter, while in the present case (spatially quenched noise) the effect is of order and, therefore, is much more strongly pronounced. Thus, the RG ideology requires that this term be included in the action functional from the very start.
The new term also determines the IR asymptotic behaviour in the regime that corresponds to the fixed point FP7, where both the turbulent mixing and the KPZ nonlinearity are irrelevant.
Now let us briefly comment on the physical interpretation of the negative and imaginary fixed points’ coordinates. Imaginary values of the coordinate correspond to a negative amplitude of the pair correlator for the field h. This has several possible implications. Firstly, it may imply a connection to models constructed within the Doi-Peliti formalism [75,76,77,78,79,80,81] where quadratic terms with negative signs and imaginary random noise can appear [78,79,80,81,82]. Secondly, there is a mapping of the KPZ equation with the white in-time noise onto the one-dimensional Lieb–Liniger model of Bose gas [83,84]. Surprisingly, it is a negative sign of the pair correlator that corresponds to the Bose gas with repulsion [85]. Lastly, such coordinates do not preclude the existence of non-perturbative IR attractive fixed point that remains hidden in perturbative RG analysis. See a more detailed discussion of related issues in [68].
Elsewhere, negative values of kinetic coefficients were sometimes encountered in non-equilibrium stochastic models, especially involving compressible fluids [86,87,88,89]. Complex effective viscosity coefficient is featured in stochastic equations for Langmuir plasma turbulence [90,91] and in a stochastic version of the nonlinear Schrödinger equation [92]. Imaginary fixed points and negative contributions to the diffusivity coefficient were recently obtained in a model of active scalar turbulent convection [93].
Thus, the problem of complex effective values of real physical quantities appears ubiquitous and pervasive in non-equilibrium stochastic problems. The physical interpretation of this persistent phenomenon deserves a careful and systematic analysis and suggests important directions in further investigation. In particular, it is interesting to study more realistic and complex models. As possible generalizations of our present model, non-Gaussian velocity fields with finite correlation time, governed by various types of stochastic Navier-Stokes equations, can be employed.
Another direction to explore was recently suggested in [43] where critical exponents for the KPZ model were obtained for general d by imposing the fractality of the interface. That result brings to mind the earlier work [94] where the exponents were “quantized” due to certain requirements involving an operator product expansion, although the issue of multiscaling was not addressed. By now, multiscaling and multifractals have been observed in a variety of field theoretic models; see, e.g., [72,95,96,97]. One can hope that combined application of functional renormalization group, operator algebras and fractal concept will shed new light to the critical behaviour of growing interfaces and kinetic roughening on the whole.
Author Contributions
All authors contributed equally to this paper. All authors have read and agreed to the published version of the manuscript.
Funding
The work of P.I.K., N.M.G. and N.V.A. was funded by the Russian Foundation for Basic Research (RFBR), project number 20-32-70139. The work of M.M.T. was supported by the RFBR, project number 19-32-60065 and by the Theoretical Physics and Mathematics Advancement Foundation “BASIS” (project number 20-1-4-46-1).
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | To be precise, an equivalent model was introduced much earlier in terms of a vector field in a seminal paper by Forster, Nelson and Stephen [4]. There, among other relevant models, the stochastic d-dimensional generalization of the Burgers equation was studied in connection with problem of long-time tails in hydrodynamic description of fluids. |
| 2 | Giorgio Parisi was awarded the Nobel Prize in Physics 2021 “for the discovery of the interplay of disorder and fluctuations in physical systems from atomic to planetary scales” [5]. |
| 3 | Regarding the upper critical dimension (UCD), it should be noted that in the field theoretic approach to stochastic models analysis, the term “UCD” is used for the dimension above which the critical exponents are given by the mean-field theory [44]. This UCD generally coincides with the logarithmic dimension above which all the interactions become IR irrelevant in the sense of Wilson; see, e.g., Section 1.16 in [44]. In the study of fluctuating surfaces, however, the “UCD” means something different and stands for the dimension below which a surface is rough and above which it is smooth. While the logarithmic dimension can be easily found for a renormalizable model, calculation of thus defined UCD requires significantly more effort. For the KPZ equation, not only there is no consensus on the value of UCD, but even its existence is under a question [3,19,20,34,35,36,37,38,39,40,41,42,43]. |
| 4 | In other words, the random noise is assumed to have Gaussian probability distribution with the correlation function (1). |
| 5 |
References
- Kardar, M.; Parisi, G.; Zhang, Y.-C. Dynamic Scaling of Growing Interfaces. Phys. Rev. Lett. 1986, 56, 889. [Google Scholar] [CrossRef] [PubMed]
- Krug, J.; Spohn, H. Solids far from Equilibrium; Godreche, C., Ed.; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Halpin-Healy, T.; Zhang, Y.-C. Kinetic roughening phenomena, stochastic growth, directed polymers and all that. Aspects of multidisciplinary statistical mechanics. Phys. Rep. 1995, 254, 215. [Google Scholar] [CrossRef]
- Forster, D.; Nelson, D.R.; Stephen, M.J. Long-Time Tails and the Large-Eddy Behavior of a Randomly Stirred Fluid. Phys. Rev. Lett. 1976, 36, 867. [Google Scholar] [CrossRef]
- Giorgio Parisi–Facts–2021. NobelPrize.org. Nobel Prize Outreach AB 2021. Mon. 11 Oct 2021. Available online: https://www.nobelprize.org/prizes/physics/2021/parisi/facts/ (accessed on 14 December 2021).
- Benzi, R.; Parisi, G.; Sutera, A.; Vulpiani, A. A theory of stochastic resonance in climate changes. SIAM J. Appl. Math. 1983, 43, 565. [Google Scholar] [CrossRef]
- Feigenbaum, M.J.; Procaccia, I.; Davidovich, B. Dynamics of Finger Formation in Laplacian Growth Without Surface Tension. J. Stat. Phys. 2001, 103, 973–1007. [Google Scholar] [CrossRef]
- Schmittmann, B.; Zia, R.K.P. Driven diffusive systems: An introduction and recent developments. Phys. Rep. 1998, 301, 5–64. [Google Scholar] [CrossRef]
- Adzhemyan, L.T.; Antonov, N.V.; Vasil’ev, A.N. Quantum field renormalization group in the theory of fully developed turbulence. Usp. Fiz. Nauk 1998, 166, 1257, [In Russian, Engl. Transl.: Phys.-Usp. 1996, 39, 1193.]. [Google Scholar] [CrossRef]
- Adzhemyan, L.T.; Antonov, N.V.; Vasil’ev, A.N. The Field Theoretic Renormalization Group in Fully Developed Turbulence; Gordon & Breach: London, UK, 1999. [Google Scholar]
- Bak, P. How Nature Works: The Science of Self-Organized Criticality; Copernicus: New York, NY, USA, 1996. [Google Scholar]
- Pruessner, G. Self-Organized Criticality: Theory, Models and Characterisation; Cambridge University Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Muñoz, M.A. Colloquium: Criticality and dynamical scaling in living systems. Rev. Mod. Phys. 2018, 90, 031001. [Google Scholar] [CrossRef]
- Marković, D.; Gros, C. Power laws and self-organized criticality in theory and nature. Phys. Rep. 2014, 536, 41. [Google Scholar] [CrossRef]
- Corwin, I. The Kardar-Parisi-Zhang equation and universality class. Random Matrices Theory Appl. 2012, 1, 1130001. [Google Scholar] [CrossRef]
- Takeuchi, K.A. An appetizer to modern developments on the Kardar-Parisi-Zhang universality class. Phys. A 2018, 504, 77. [Google Scholar] [CrossRef]
- Strack, P. Dynamic criticality far from equilibrium: One-loop flow of Burgers-Kardar-Parisi-Zhang systems with broken Galilean invariance. Phys. Rev. E 2015, 91, 032131. [Google Scholar] [CrossRef] [PubMed]
- Niggemann, O.; Hinrichsen, H. Sinc noise for the Kardar-Parisi-Zhang equation. Phys. Rev. E 2018, 97, 062125. [Google Scholar] [CrossRef]
- Katzav, E.; Schwartz, M. Existence of the upper critical dimension of the Kardar-Parisi-Zhang equation. Phys. A 2002, 309, 69. [Google Scholar] [CrossRef]
- Alves, S.G.; Oliveira, T.J.; Ferreira, S.C. Universality of fluctuations in the Kardar-Parisi-Zhang class in high dimensions and its upper critical dimension. Phys. Rev. E 2014, 90, 020103(R). [Google Scholar] [CrossRef] [PubMed]
- Altman, E.; Sieberer, L.M.; Chen, L.; Diehl, S.; Toner, J. Two-dimensional superfluidity of exciton polaritons requires strong anisotropy. Phys. Rev. X 2015, 5, 011017. [Google Scholar] [CrossRef]
- Ji, K.; Gladilin, V.N.; Wouters, M. Temporal coherence of one-dimensional nonequilibrium quantum fluids. Phys. Rev. B 2015, 91, 045301. [Google Scholar] [CrossRef]
- Deligiannis, K.; Squizzato, D.; Minguzzi, A.; Canet, L. Accessing Kardar-Parisi-Zhang universality sub-classes with exciton polaritons (a). EPL (Europhys. Lett.) 2020, 132, 67004. [Google Scholar] [CrossRef]
- Squizzato, D.; Canet, L. Kardar-Parisi-Zhang equation with temporally correlated noise: A nonperturbative renormalization group approach. Phys. Rev. E 2020, 100, 062143. [Google Scholar] [CrossRef]
- Najem, S.; Krayem, A.; Ala-Nissila, T.; Grant, M. Kinetic roughening of the urban skyline. Phys. Rev. E 2020, 101, 050301(R). [Google Scholar] [CrossRef]
- Lässig, M. On the renormalization of the Kardar-Parisi-Zhang equation. Nucl. Phys. B 1995, 448, 559. [Google Scholar] [CrossRef]
- Wiese, K.J. On the perturbation expansion of the KPZ equation. J. Stat. Phys. 1998, 93, 143. [Google Scholar] [CrossRef]
- Canet, L.; Chaté, H.; Delamotte, B.; Wschebor, N. Nonperturbative renormalization group for the Kardar-Parisi-Zhang equation. Phys. Rev. Lett. 2010, 104, 150601. [Google Scholar] [CrossRef] [PubMed]
- Canet, L.; Chaté, H.; Delamotte, B.; Wschebor, N. Nonperturbative renormalization group for the Kardar-Parisi-Zhang equation: General framework and first applications. Phys. Rev. E 2011, 84, 061128. [Google Scholar] [CrossRef] [PubMed]
- Kloss, T.; Canet, L.; Wschebor, N. Nonperturbative renormalization group for the stationary Kardar-Parisi-Zhang equation: Scaling functions and amplitude ratios in 1+1, 2+1, and 3+1 dimensions. Phys. Rev. E 2012, 86, 051124. [Google Scholar] [CrossRef] [PubMed]
- Mathey, S.; Agoritsas, E.; Kloss, T.; Lecomte, V.; Canet, L. Kardar-Parisi-Zhang equation with short-range correlated noise: Emergent symmetries and nonuniversal observables. Phys. Rev. E 2017, 95, 032117. [Google Scholar] [CrossRef]
- Täuber, U.C.; Howard, M.; Vollmayr-Lee, B.P. Applications of field-theoretic renormalization group methods to reaction-diffusion problems. J. Phys. A Math. Gen. 2005, 38, R79. [Google Scholar] [CrossRef]
- Cooper, F.; Dawson, J.F. Auxiliary field loop expansion of the effective action for a class of stochastic partial differential equations. Ann. Phys. 2016, 365, 118. [Google Scholar] [CrossRef]
- Lässig, M.; Kinzelbach, H. Upper critical dimension of the Kardar-Parisi-Zhang equation. Phys. Rev. Lett. 1997, 78, 903. [Google Scholar] [CrossRef]
- Colaiori, F.; Moore, M. Upper critical dimension, dynamic exponent, and scaling functions in the mode-coupling theory for the Kardar-Parisi-Zhang equation. Phys. Rev. Lett. 2001, 86, 3946. [Google Scholar] [CrossRef]
- Fogedby, H.C. Localized growth modes, dynamic textures, and upper critical dimension for the Kardar-Parisi-Zhang Equation in the weak-noise limit. Phys. Rev. Lett. 2005, 94, 195702. [Google Scholar] [CrossRef] [PubMed]
- Fogedby, H.C. Kardar-Parisi-Zhang equation in the weak noise limit: Pattern formation and upper critical dimension. Phys. Rev. E 2006, 73, 031104. [Google Scholar] [CrossRef] [PubMed]
- Fogedby, H.C. Patterns in the Kardar-Parisi-Zhang equation. J. Phys. (Pramana) 2008, 71, 253–262. [Google Scholar] [CrossRef]
- Rodrigues, E.A.; Mello, B.A.; Oliveira, F.A. Growth exponents of the etching model in high dimensions. J. Phys. A Math. Theor. 2015, 48, 035001. [Google Scholar] [CrossRef]
- Castellano, C.; Marsili, M.; Pietronero, L. Nonperturbative renormalization of the Kardar-Parisi-Zhang growth dynamics. Phys. Rev. Lett. 1998, 80, 3527. [Google Scholar] [CrossRef]
- Castellano, C.; Gabrielli, A.; Marsili, M.; Muñoz, M.A.; Pietronero, L. High dimensional behavior of the Kardar-Parisi-Zhang growth dynamics. Phys. Rev. E 1998, 58, R5209. [Google Scholar] [CrossRef]
- Marinari, E.; Pagnani, A.; Parisi, G.; Raćz, Z. Width distributions and the upper critical dimension of Kardar-Parisi-Zhang interfaces. Phys. Rev. E 2002, 65, 026136. [Google Scholar] [CrossRef]
- Gomes-Filho, M.S.; Penna, A.L.A.; Oliveira, F.A. An exact solution for the 2 + 1 Kardar-Parisi-Zhang exponents. Results Phys. 2021, 104, 435. [Google Scholar]
- Vasiliev, A.N. The Field Theoretic Renormalization Group in Critical Behaviour Theory and Stochastic Dynamics; Chapman & Hall/CRC: Boca Raton, FL, USA, 1998; [Translated from the Russian: Institute of Nuclear Physics, Gatchina: St Petersburg, Russian, 1998; ISBN 5-86763-122-2.]. [Google Scholar]
- Pavlik, S.I. Scaling for a growing phase boundary with nonlinear diffusion. J. Exp. Theor. Phys. 1994, 79, 303, [Translated from the Russian: ZhETF 1994, 106, 553.]. [Google Scholar]
- Antonov, N.V.; Vasil’ev, A.N. The quantum-field renormalization group in the problem of a growing phase boundary. J. Exp. Theor. Phys. 1995, 81, 485, [Translated from the Russian: ZhETF 108, 885.]. [Google Scholar]
- Caldarelli, G.; Giacometti, A.; Maritan, A.; Rodriguez-Iturbe, I.; Rinaldo, A. Randomly pinned landscape evolution. Phys. Rev. E 1997, 55, R4865. [Google Scholar] [CrossRef]
- Czirók, A.; Somfai, E.; Vicsek, J. Experimental evidence for self-affine roughening in a micromodel of geomorphological evolution. Phys. Rev. Lett. 1993, 71, 2154. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Kim, J.M. Depinning transition of the quenched Kardar-Parisi-Zhang equation. J. Korean Phys. Soc. 2005, 47, 13. [Google Scholar]
- Jeong, H.; Kahng, B.; Kim, D. Anisotropic surface growth model in disordered media. Phys. Rev. Lett. 1996, 25, 5094. [Google Scholar] [CrossRef]
- Kim, H.-J.; Kim, I.-M.; Kim, J.M. Hybridized discrete model for the anisotropic Kardar-Parisi-Zhang equation. Phys. Rev. E 1998, 58, 1144. [Google Scholar] [CrossRef]
- Hinrichsen, H. Non-equilibrium critical phenomena and phase transitions into absorbing states. Adv. Phys. 2000, 49, 815–958. [Google Scholar] [CrossRef]
- Narayan, O.; Fisher, D.S. Threshold critical dynamics of driven interfaces in random media. Phys. Rev. B 1993, 48, 7030. [Google Scholar] [CrossRef]
- Janssen, H.K. Renormalized field theory of the Gribov process with quenched disorder. Phys. Rev. E 1997, 55, 6253. [Google Scholar] [CrossRef]
- Moreira, A.G.; Dickman, R. Critical dynamics of the contact process with quenched disorder. Phys. Rev. E 1996, 54, R3090. [Google Scholar] [CrossRef]
- Webman, I.; ben Avraham, D.; Cohen, A.; Havlin, S. Dynamical phase transitions in a random environment. Philos. Mag. B 1998, 77, 1401. [Google Scholar] [CrossRef]
- Duclut, C.; Delamotte, B. Nonuniversality in the erosion of tilted landscapes. Phys. Rev. E 2017, 96, 012149. [Google Scholar] [CrossRef] [PubMed]
- Antonov, N.V.; Gulitskiy, N.M.; Kakin, P.I.; Serov, V.D. Effects of turbulent environment and random noise on self-organized critical behavior: Universality versus nonuniversality. Phys. Rev. E 2021, 103, 042106. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, S. Conserved Kardar-Parisi-Zhang equation: Role of quenched disorder in determining universality. Phys. Rev. E 2021, 103, 042102. [Google Scholar] [CrossRef] [PubMed]
- Imaeda, T.; Onuki, A.; Kawasaki, K. Anisotropic spinodal decomposition under shear flow. Progr. Theor. Phys. 1984, 71, 16. [Google Scholar] [CrossRef][Green Version]
- Satten, G.; Ronis, D. Critical phenomena in randomly stirred fluids: Correlation functions, equation of motion, and crossover behavior. Phys. Rev. A 1986, 33, 3415. [Google Scholar] [CrossRef]
- Aronowitz, A.; Nelson, D.R. Turbulence in phase-separating binary mixtures. Phys. Rev. A 1984, 29, 2012. [Google Scholar] [CrossRef]
- Antonov, N.V.; Hnatich, M.; Honkonen, J. Effects of mixing and stirring on the critical behaviour. J. Phys. A Math. Gen. 2006, 39, 7867. [Google Scholar] [CrossRef]
- Antonov, N.V.; Ignatieva, A.A. Critical behaviour of a fluid in a random shear flow: Renormalization group analysis of a simplified model. J. Phys. A Math. Gen. 2006, 39, 13593. [Google Scholar] [CrossRef]
- Antonov, N.V.; Iglovikov, V.I.; Kapustin, A.S. Effects of turbulent mixing on the nonequilibrium critical behaviour. J. Phys. A Math. Theor. 2008, 42, 135001. [Google Scholar] [CrossRef]
- Antonov, N.V.; Kapustin, A.S.; Malyshev, A.V. Effects of turbulent transfer on critical behavior. Theor. Math. Phys. 2011, 169, 1470. [Google Scholar] [CrossRef]
- Antonov, N.V.; Kakin, P.I. Random interface growth in a random environment: Renormalization group analysis of a simple model. Theor. Math. Phys. 2015, 185, 1391. [Google Scholar] [CrossRef]
- Antonov, N.V.; Kakin, P.I.; Lebedev, N.M. The Kardar-Parisi-Zhang model of a random kinetic growth: Effects of a randomly moving medium. J. Phys. A Math. Theor. 2019, 52, 505002. [Google Scholar] [CrossRef]
- Antonov, N.V.; Gulitskiy, N.M.; Kakin, P.I.; Kostenko, M.M. Effects of turbulent environment on the surface roughening: The Kardar-Parisi-Zhang model coupled to the stochastic Navier-Stokes equation. Phys. Scr. 2020, 95, 084009. [Google Scholar] [CrossRef]
- Falkovich, G.; Gawȩdzki, K.; Vergassola, M. Particles and fields in fluid turbulence. Rev. Mod. Phys. 2001, 73, 913. [Google Scholar] [CrossRef]
- Antonov, N.V.; Kakin, P.I.; Lebedev, N.M. Static Approach to Renormalization Group Analysis of Stochastic Models with Spatially Quenched Noise. J. Stat. Phys. 2020, 178, 392. [Google Scholar] [CrossRef]
- Adzhemyan, L.T.; Antonov, N.V.; Vasiliev, A.N. Renormalization group, operator product expansion, and anomalous scaling in a model of advected passive scalar. Phys. Rev. E 1998, 58, 1823. [Google Scholar] [CrossRef]
- Heisenberg, W.; Euler, H. Folgerungen aus der Diracschen Theorie des Positrons. Z. Phys. 1936, 98, 714–732. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Course of Theoretical Physics; Pergamon Press: Oxford, UK, 1987; Volume 6. [Google Scholar]
- Doi, M. Stochastic theory of diffusion-controlled reaction. J. Phys. A 1976, 9, 1479. [Google Scholar] [CrossRef]
- Grassberger, P.; Scheunert, P. Fock-space methods for identical classical objects. Fortschritte Phys. 1980, 28, 547. [Google Scholar] [CrossRef]
- Peliti, L. Path integral approach to birth-death processes on a lattice. J. Phys. (Paris) 1984, 46, 1469. [Google Scholar] [CrossRef]
- Täuber, U.C. Dynamic Phase Transitions in Diffusion-Limited Reactions. Acta Phys. Slovaca 2002, 52, 505. [Google Scholar]
- Täuber, U.C. Scale invariance and dynamic phase transitions in diffusion-limited reactions. Adv. Solid State Phys. 2003, 43, 659. [Google Scholar]
- Täuber, U.C. Field Theory Approaches to Nonequilibrium Dynamics. Lect. Notes Phys. 2007, 716, 295. [Google Scholar]
- Täuber, U.C. Field Theoretic Methods. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2009; Volume 3360, ISBN 978-0-387-30440-3. [Google Scholar]
- Benitez, F.; Duclut, C.; Chaté, H.; Delamotte, B.; Dornic, I.; Muñoz, M.A. Langevin equations for reaction-diffusion processes. Phys. Rev. Lett. 2016, 117, 100601. [Google Scholar] [CrossRef]
- Roberts, J.L.; Claussen, N.R.; Cornish, S.L.; Donley, E.A.; Cornell, E.A.; Wieman, C.E. Controlled collapse of a Bose-Einstein condensate. Phys. Rev. Lett. 2001, 86, 4211. [Google Scholar] [CrossRef]
- Lieb, E.H.; Liniger, W. Exact analysis of an interacting Bose gas. I. The general solution and the ground state. Phys. Rev. 1963, 130, 1605. [Google Scholar] [CrossRef]
- Busiello, G.; De Cesare, L. The critical exponents η and z to second order in ϵ = 2 − d for a Bose system at T = 0. Phys. Lett. 1980, 77, 177. [Google Scholar] [CrossRef]
- Yakhot, V. Ultraviolet dynamic renormalization group: Small-scale properties of a randomly stirred fluid. Phys. Rev. A 1981, 23, 1486–1497. [Google Scholar] [CrossRef]
- Yakhot, V. Large-scale properties of unstable systems governed by the Kuramoto-Sivashinksi equation. Phys. Rev. A 1981, 24, 642–644. [Google Scholar] [CrossRef]
- Sivashinsky, G.; Yakhot, V. Negative viscosity effect in large-scale flows. Phys. Fluids 1985, 28, 1040–1042. [Google Scholar] [CrossRef]
- Avellaneda, M.; Vergassola, M. Scalar transport in compressible flow. Phys. D Nonlinear Phenom. 1997, 106, 148–166. [Google Scholar]
- Pelletier, G. Langmuir turbulence as a critical phenomenon. Part 2. Application of the dynamical renormalization group method. J. Plasma Phys. 1980, 24, 421–443. [Google Scholar] [CrossRef]
- Adzhemyan, L.T.; Vasil’ev, A.N.; Gnatich, M.; Pis’mak, Y.M. Quantum field renormalization group in the theory of stochastic Langmuir turbulence. Theor. Math. Phys. 1989, 78, 260–272. [Google Scholar] [CrossRef]
- Täuber, U.C.; Diehl, S. Perturbative field-theoretical renormalization group approach to driven-dissipative Bose-Einstein criticality. Phys. Rev. X 2014, 4, 021010. [Google Scholar] [CrossRef]
- Antonov, N.V.; Kostenko, M.M. Renormalization Group in the Problem of Active Scalar Advection. J. Math. Sci. 2021, 257, 425–441. [Google Scholar] [CrossRef]
- Lässig, M. Quantized scaling of growing surfaces. Phys. Rev. Lett. 1998, 80, 2366. [Google Scholar] [CrossRef]
- Duplantier, B.; Ludwig, A.W.W. Multifractals, operator-product expansion, and field theory. Phys. Rev. Lett. 1991, 66, 247. [Google Scholar] [CrossRef]
- Eyink, G.L. Lagrangian field theory, multifractals, and universal scaling in turbulence. Phys. Lett. A 1993, 172, 355. [Google Scholar] [CrossRef]
- Altaiskiy, M.; Hnatich, M.; Horvath, D.; Moiseev, S.S. Self-similarity and the renormalization group in hydrodynamic turbulence theory. In Proceedings of the 3rd International Conference, RG’96, Dubna, Russia, 26–31 August 1996; Volume 12, p. 1247. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).