Abstract
We estimate the parameters of the Hybrid Palatini gravity model with the Schwarzschild precession of S-stars, specifically of the S2, S38 and S55 stars. We also take into account the case of bulk mass distribution near the Galactic Center. We assume that the Schwarzschild orbital precession of mentioned S-stars is the same as in General Relativity (GR) in all studied cases. In 2020, the GRAVITY Collaboration detected the orbital precession of the S2 star around the supermassive black hole (SMBH) at the Galactic Center and showed that it is close to the GR prediction. The astronomical data analysis of S38 and S55 orbits showed that, also in these cases, the orbital precession is close to the GR prediction. Based on this observational fact, we evaluated the parameters of the Hybrid Palatini Gravity model with the Schwarzschild precession of the S2, S38 and S55 stars, and we estimated the range of parameters of the Hybrid Palatini gravity model for which the orbital precession is as in GR for all three stars. We also evaluated the parameters of the Hybrid Palatini Gravity model in the case of different values of bulk mass density distribution of extended matter. We believe that proposed method is a useful tool to evaluate parameters of the gravitational potential at the Galactic Center.
1. Introduction
In recent decades, various modified gravity theories have appeared as potential extensions of Einstein’s gravity theory [1]. One of the reasons for a postulation of the mentioned theories is the possibility to exclude the concept of dark energy and dark matter and to explain cosmological and astrophysical data collected at different scales considering further degrees of freedom of the gravitational field. This occurs as a consequence of geometric corrections [2]. Modified gravity theories have to resolve different observations concerning, starting from the Solar system, neutron stars, binary pulsars, spiral and elliptical galaxies and clusters of galaxies, up to the large-scale structure of the Universe [3,4,5,6,7]. In Ref. [3] a cosmological reconstruction (characterized by a very general character) of various modified gravity is given, and, in [4] various formalisms of representatives of standard modified gravity are presented, as well as alternative theoretical approaches. Ref. [5] described stars and cluster of galaxies (spiral and elliptical galaxies), beyond the scope of dark matter, by extending the Hilbert–Einstein action to gravity, and, in [6], the authors discussed observations and experiments, which depicted the fact that GR and the standard model of elementary particles are unable to explain the phenomena behind the dark matter concept. In [7], the chosen cosmological parameters were determined (as accurate cosmological solutions) within the framework of the represented nonlocal gravitational model, which showed satisfactory agreement with experimental observations.
Some Alternative Theories of Gravity.
Let us recall that numerous alternative gravity theories have been proposed (see, e.g., [8,9,10,11,12,13,14,15,16,17,18]). For example, the alternative theories of gravity are discussed in [8]. In [9], the authors introduced extension of the post-Newtonian relativistic theory by additionally considering all relativistic effects, which originated from the presumable existence of a scalar field. Ref. [10] presents a review article, in which the authors discussed specific aspects of 4D massive gravities. In Ref. [11] a numerical solution of the nonlinear Pauli–Fierz theory is given. The proposed solution represents an improvement of the existing solution of GR, which was achieved by including the Vainshtein mechanism. In [12], extended theories of gravity were discussed by taking into account and scalar-tensor gravity in metric and Palatini approaches; the issues, such as inflation, large scale structure, dark energy, dark matter and quantum gravity, were discussed also. Ref. [13] is a review of modified theories of gravity and models of extra dimensions, such as Scalar-Tensor, Einstein–Aether, Bimetric theories, TeVeS, , Horava–Lifschitz gravity, Galileons, Ghost Condensates, Kaluza–Klein, Randall–Sundrum, DGP, higher co-dimension braneworlds as well as the construction of the Parametrized Post-Friedmannian formalism. In the paper [14], the Dvali–Gabadadze–Porrati model (DGP), cascading gravity, ghost-free massive gravity, new mass gravity, Lorentz-violating massive gravity and non-local massive gravity are discussed. The modifications of general relativity, considering galaxy clusters, cosmological perturbations, and N-body simulations, are discussed in [15]. A few observational mass bounds have been established, and among them, the mass bounds from the effects of the Yukawa potential in Ref. [16]. Ref. [17] presents monograph in which the mathematical background is given (for example, conservation laws and symmetries for different theories of gravity), necessary for comparison of methods of perturbations in general relativity; this mathematical introduction enables the building of different modified-gravity theories. In the paper [18], the method for the evaluation of the parameters of the gravitational potential at the Galactic Center, based on the extended gravity models (power-law , general Yukawa-like corrections, scalar-tensor gravity and non-local gravity theories formulated in both metric and Palatini formalism) is given.
Some Alternative Approaches for the Weak Field Limit of Theories of Gravity.
Noteworthy, different alternative approaches for the weak field limit (starting from fourth-order theories of gravity, such as ), have been proposed and considered [19,20,21,22,23,24,25,26,27,28,29,30,31,32]. For example, in Ref. [19] the gravitational microlensing is discussed, considered from the aspect of the weak field limit of fourth-order gravity theory, and, in [20], determination of the mass and the size of dark matter sphere is discussed, based on the -ray emission from the Galactic Center region. Ref. [21] examined the consequences of modified gravity (power-law ) on galactic scales, by performing an analysis of rotational curves. In Ref. [22], the authors discuss the search for general relativistic periastronic shifts, which is limited by the existence of clusters around black hole, which could modify orbits due to classical effects that mask the general relativistic effect. Ref. [23] represents a discussion of solving the problem of dark matter and dark energy (which could be done by considering changing the fundamental law of gravity). Ref. [24] showed that the metric approach of any analytic -gravity model presents a weak field limit (the standard Newtonian potential is corrected by a Yukawa-like term), and [25] considered the limitations of the range parameters that are described by modifications of Newton’s inverse square law of the gravity similar to Yukawa; the results of this study could affect all modified theories of gravity, which include Yukawa-type terms (which are characterized by a range of parameters much larger than the size of the solar system). In [26], a Yukawa-like long-range modified model of gravity (MOG) is discussed. Ref. [27] considered the Modified Newtonian Dynamics, introducing the integration of the equations of motion of Magellanic clouds in a numerical manner. In the paper [28], the limitation of the gravity at Galactic scales, based on the simulation of the S2-like stars orbits, is discussed; it was shown that gravity impacts the simulated orbits in a qualitatively similar way as a bulk distribution of matter in Newton’s gravity. In Ref. [29], an analytic fourth-order theory of gravity (which is non-minimally coupled with a massive scalar field) is applied, to explain deviations of S2 star orbit, by using gravitational potentials derived from modified gravity models in the absence of dark matter. Refs. [30,31] considered an analytical expression for the precession angle (with assumption of a power-law profile of the dark matter density); they calculated the mass of the dark matter in the vicinity of a SMBH at the galaxy center, based on the observations of nonrelativistic precession of the orbits of S0 stars. While, in [32], the authors discuss the physical processes that occurred at the center of the galaxy; the results of this study revealed the mass of the SMBH Sgr A.
Experimental Limits Related to Extended Theories of Gravity.
Also, literature review revealed the presence of some experimental limits related to extended theories of gravity [33,34,35,36,37,38,39,40,41]. In Ref. [33], the authors used cosmography to examine the kinematics of the Universe by a combination of theoretical derivation of cosmological distances and numerical data fitting, while in [34], the authors investigated whether cosmography could be used to ensure information on the cosmological expansion history and discussed the limits of experimentally probing of cosmographic expansion. In Ref. [35], the authors performed cosmographic analyses and discussed the cosmological consequences of and gravities as well as their influence on the cosmography framework. They depicted to the unfavorable degeneracy problem (cosmographic constraints on and cannot be distinguished by theories of GR extensions and dark energy models). In [36], the differences between the Newtonian and relativistic approaches are described, and it is revealed that the relativistic approach presents a more suitable strategy for further probing of modified theories of gravity. In Ref. [37] the generalization of the gravitational action to a function is investigated, as an alternative to the dark matter and dark energy, and the weak field limit of the -gravity is discussed. In [38], the analytical -gravity model is considered, which is characterized by a Yukawa-like modification of the Newtonian potential, and this leads to a modification of particle dynamics. In the paper [39], the authors performed a comparison between the cosmological model and and models; they presented a new approach to breaking degeneration among dark energy models, which was introduced to overcome the limits of standard cosmography. The reference [40] discussed the usage of S-stars observations to constrain a Yukawa-like gravitational potential and considered the fact that deviations from GR are parametrized by the strength of the potential, , and its length scale, . In [41], it is shown that the observing stars orbiting closer to the central gravitational source could allow distinguishing between the black hole and wormhole nature of this object (by observing S2 and S62 stars).
Gravitational Potentials and the Stellar Dynamics.
In this study, the gravitational potentials of self-gravitating structures were investigated by considering the stellar dynamics. Recall that S-stars are the bright stars that move around the Galactic Center [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57] where Sgr A (which presents a compact massive object) is located. The conventional model, used to describe the Galactic Center, considers the SMBH with mass around and an extended mass distribution formed with stellar cluster and dark matter. A spherical shell, where trajectories of bright stars are located, should be characterized by a total mass of bulk distribution, which is significantly smaller compared to the black hole mass. In Ref. [42] measurements of the accelerations for three stars located ∼0.005 pc from the central radio source Sgr A are discussed; the obtained data revealed the localization of the dark mass to within arcsec of the nominal position of Sgr A. In [43], astrometric and radial velocity measurements, performed by the Keck telescopes, are discussed, as well as the estimated distance () and the galaxy’s local rotation speed. They noticed that increased black hole mass depicted a longer period for the innermost stable orbit and longer resonant relaxation timescales for stars in the vicinity of the black hole. The authors of paper [44] discussed a moderate improvement of the statistical errors of mass and distance to Sgr A, and, in [45], the orbits of 38 stars (among them, the orbit of the S2 star) were determined; all stellar orbits were fitted satisfactorily by a single point mass potential. In Ref. [46], the high resolution astrometric imaging is discussed, which is used to investigate two thirds of the orbit of the star currently closest to the massive black hole candidate SgrA; they authors found that the star was on a bound, highly elliptical Keplerian orbit around SgrA, with an orbital period of 15.2 years and a pericentre distance of only 17 light hours. The authors in [47] considered a massive black hole in the Galactic Center and a nuclear star cluster, by analyzing the size and motion measurements of the radio source Sgr A, which is understood as a massive black hole surrounded by a dense nuclear star cluster. In Ref. [48], the authors examined the behavior of a SMBH by investigating stars with short orbital periods at the center of our galaxy; measurements from the Keck Observatory discovered the star S0-102 orbiting a black hole with a period of less than 15 years. Ref. [49] represents an update of the main conclusions regarding the measurement of mass and distance to Sgr A, derived from data obtained by monitoring stellar orbits in the Galactic Center. In Ref. [50], it is shown that short-period stars orbiting around the SMBH in our Galactic Center can successfully be used to probe the gravitational theory in a strong regime. In [51], the behavior of the star S2, which orbits a SMBH in a short period of time (less than 20 years) is considered; the authors reported on the first binarity limits of S0-2, observed from radial velocity monitoring. The GRAVITY Collaboration [52] discussed the orbit of the S2 star around the massive black hole Sgr A, which is used as probe of the gravitational field in the center of the galaxy; by using different statistical analysis methods, the authors detected the combined gravitational redshift and relativistic transverse Doppler effect for the S2 star and found that the S2 data were not consistent with pure Newtonian dynamics. In [53], they presented the results of the measurement of the (the geometric distance to the Galactic Center), by probing the S2 star, which is orbiting around the SMBH Sgr A. In Ref. [54], the authors examined the prediction of GR (that a star passing near a SMBH shows a relativistic redshift), by using observations of the Galactic Center star S2; a combination of special relativistic- and gravitational-redshift was discovered, which confirms the model of GR and excludes Newtonian’s model. Ref. [55] considered the assumption of the presence of a scalar field structure associated with a black hole at the center of our galaxy. The authors used the results of the orbital perturbation theory to compute the extent to which the orbital parameters of the S2 star change during the orbital period. Ref. [56] introduced a new ways of probing fundamental physics, tracking stars in the Galactic Center; a new way of looking for changes in the fine structure constant was proposed, by using measurements of late-type evolved giant stars from the S-star cluster orbiting a SMBH in our Galactic Center. Ref. [57] reported the first detection of the GR Schwarzschild precession in S2’s orbit.
Ruffini, Argüelles & Rueda [58] discussed a dark matter distribution and proposed that it consists of a dense core and a diluted halo. The dark matter distribution was named as the RAR-model. In 2021, Becerra-Vergara et al. [59] commented this model and concluded that the mentioned model ensures a better fit of bright star trajectories compared to the SMBH model. The properties of bright star trajectories in the gravitational field of a dense core, described by the RAR-model, were discussed in [60]. In such a case, trajectories of stars are ellipses as in Kepler’s two-body problem but with one big difference: instead of their foci, the centers of the ellipses coincide with a Galactic Center, and their orbital periods do not depend on their semi-major axes. Therefore, these properties are not consistent with existing observational data [60]. The orbital precession occurs as a consequence of relativistic effects, as well as due to extended mass distribution, because both effects could cause perturbation of the Newtonian potential. In the first case, the precession induces a prograde pericentre shift, while, in the second case, retrograde shift occurs [61]. In both cases, as a final result, rosette-shaped orbits are obtained [62,63].
In addition to Schwarzschild precession, relativistic frame-dragging due to the spin of SMBH, also known as the Lense-Thirring (LT) effect, could cause orbital precession. The LT precession in the case of several S-stars was studied in references [18,64,65,66,67], and it was found that it is much smaller than Schwarzschild precession [18,65]. The spin of Sgr A was estimated to by the observed distribution of the orbital planes of the S-stars [68]. In this paper, we considered only the solutions of the Hybrid Palatini gravity model for a spherically symmetric and stationary gravitational field, which do not include the SMBH spin. Having this in mind, we did not take into account the LT precession in our calculations for S-stars precession.
In our previous studies, we considered various extended gravity theories and compared theoretical models with astronomical data for different astrophysical scales: the S2 star orbit [28,69,70,71,72,73,74,75,76,77], fundamental plane of elliptical galaxies [78,79,80] and barionic Tully–Fischer relation of spiral galaxies [81]. In this study, as a continuation of our previous paper [18], the parameters of the Hybrid Palatini gravity model will be evaluated by Schwarzschild precession of the S2, S38 and S55 stars. Here, we will also take into account the bulk mass density distribution of extended matter in the Galactic Center and assume that the orbital precession of the S2, S38 and S55 stars are equal to the corresponding GR predictions of 0°.18, 0°.11 and 0°.10 per orbital period, respectively. We use this assumption because the GRAVITY Collaboration detected the orbital precession of the S2 star around the SMBH [57] and showed that it is close to the corresponding prediction of GR. According to data analysis in the framework of Yukawa gravity model in the paper [40], the orbital precessions of the S38 and S55 stars are close to the corresponding prediction of GR for these stars.
The paper is organized in the following way. In Section 2, we present the basics of the Hybrid Palatini theoretical model as well as the model for bulk mass density distribution of extended matter. In Section 3, we evaluate the parameters of the Hybrid Palatini theoretical model by Schwarzschild precession of the S2, S38 and S55 stars and discuss the obtained results. Our concluding remarks are given in Section 4, while Appendix A contains the detailed derivation of gravitational potential in the weak field limit for this gravity model.
2. Theory
In this article, we found constraints on the parameters of the Hybrid Palatini gravity model with request that the obtained values of orbital precession angles are the same as in GR but for different values of mass density of matter. We used a weak field limit for the Hybrid Palatini gravitation potential. A straightforward extension of GR is gravity, which, instead of the Einstein–Hilbert action (linear in the Ricci scalar R), considers a generic function of R [19,20,21,82,83,84,85].
2.1. Modified Hybrid Palatini Gravity Model
There are two variational principles that one can apply to the Einstein–Hilbert action in order to derive Einstein’s equations: the standard metric variation and the Palatini variation [85,86,87]. The choice of the variational principle is usually referred to as a formalism, and thus one can use the terms metric or second-order formalism and Palatini or first-order formalism. In the Palatini variation, the metric and the connection are assumed to be independent variables, and one varies the action with respect to both of them. This variation leads to Einstein’s equations, under the important assumption that the matter action does not depend on the connection. Both variational principles lead to the same field equation for an action whose Lagrangian is linear in R, for example in the context of GR, but not for a more general action, for example in extended gravities. gravity in the metric formalism is called metric gravity, and gravity in the Palatini formalism is called Palatini gravity. The Palatini variational approach leads to second-order differential field equations, while the resulting field equations in the metric approach are fourth-order coupled differential equations [85,86,87]. There is also a novel approach, the hybrid variation of these theories. It consists of adding, to the metric Einstein–Hilbert Lagrangian, an term constructed within the framework of the Palatini formalism, i.e., purely metric Einstein–Hilbert action is supplemented with metric-affine correction terms constructed as Palatini [88,89,90,91]. The theories are the special limits of the one-parameter class of theories where the scalar field depends solely on the stress energy trace T (Palatini version) or solely on the Ricci curvature R (metric version). Here, we consider the hybrid metric-Palatini gravitational theory. In the general case, the field equations are fourth-order both in the matter and in the metric derivatives. Hybrid metric-Palatini theory provides a unique interpolation between the two a priori completely distinct classes of gravity theories. The aim of this formulation has two-fold benefits: from one side, one wants to describe the extra gravitational budget in a metric-affine formalism; on the other side, one wants to cure the shortcomings emerging in gravity both in metric and Palatini formulations. In particular, hybrid gravity allows to disentangle the metric and the geodesic structures pointing out that further degrees of freedom coming from can be recast as an auxiliary scalar field. An interesting aspect of metric-Palatini theories is the possibility to generate long-range forces without entering into conflict with local tests of gravity. The possibility of expressing these hybrid metric-Palatini theories using a scalar-tensor representation simplifies the analysis of the field equations and the construction of solutions. To obtain deeper insights, see [86,88,89,90,91,92,93].
The Palatini formalism and the metric one are completely different both from a qualitative and from a quantitative viewpoint. In the Palatini formalism, field equations are easily solvable [94]. In this sense, the Palatini formalism is easier to handle and simpler to analyze compared with the corresponding metric formalism. It is clear that any reasonable model of gravity should satisfy the standard solar system tests. It has been shown that, in principle, the Palatini formalism provides a good Newtonian approximation. It is known that on-shell formulation of Palatini gravity coincides with that of same metric gravity [94]. In the paper [95], a class of scalar-tensor theories was proposed including a non-metricity that unifies the metric, Palatini and hybrid metric-Palatini gravitational actions with non-minimal interaction. The authors presented a new approach to scalar-tensor theories of gravity that unifies metric, Palatini and hybrid. Such an approach will encompass, within one family of theories, not only metric but also Palatini scalar-tensor theories of gravity and will be a natural extension of the hybrid metric-Palatini gravity. It is shown that every such theory can be represented on-shell by a purely metric scalar-tensor theories possessing the same solutions for a metric and a scalar field.
Recall that, in the weak field limit (see the Appendix A for detailed explanation), the scalar field behaves as , where M is the mass of the system and r is the interaction length. The leading parameters for Hybrid Palatini gravity are and . The aim of this study was to evaluate these parameters. We can write the modified gravitational potential in the following form [71,89]:
The parameter represents a scaling parameter for gravity interaction and . We measured the parameter in AU (AU is the astronomical unit). The parameter represents the amplitude of the background value of the scalar field and it is dimensionless. Non-zero values of these two parameters, if obtained, would indicate a potential deviation from GR.
2.2. Orbital Precession in Case of Bulk Mass Distribution
In this study, we investigated S2, S38 and S55 stars. Orbital precession of investigated stars is influenced by other stars, gas and dark matter. It is expected that the stars represent the dominant component of the extended galactic mass distribution near the central SMBH. To investigate orbital precession of S-stars, we made two assumptions. First, we suppose the presence of the Hybrid Palatini gravitational potential [71]. The second assumption is a bulk distribution of mass around SMBH in the central regions of our galaxy [77]:
A bulk mass distribution consists of the central black hole of mass [44] and extended mass distribution enclosed within some radius r. is the total mass, including the stellar cluster, interstellar gas and dark matter. To describe the mass density distribution of extended matter, we adopted a double power-law mass density profile [55,96,97]:
where is varied from 2 to 8 and .
In the case of S-stars throughout the whole region, which we investigated, we can choose only one value of power-law exponent: = 1.4.
A combination of the above mentioned formulas enabled us to obtain the following expression for the extended mass distribution:
Note that, in [30,31], the authors used a similar method for estimation of the total dark matter mass near the SMBH at the Galactic Center based on observations of orbital precession of S-stars and derived an analytical expression for the precession angle in the case of a power-law profile of the dark matter density.
The gravitational potential for the extended mass model can be evaluated as [20]:
where is the outer radius for an extended mass distribution of matter. The total gravitational potential is obtained as a sum of the Hybrid Palatini potential for SMBH with mass and potential for extended matter with mass :
Modified gravity potential, similarly to GR, gives precession around SMBH. At the center of the galaxy, around the SMBH, there are invisible sources of mass (clouds of gas, stars and their remnants and a distributed mass in the form of the diffuse dark matter). This additional invisible sources of mass would cause deviation of the total Newtonian gravitational potential [30,31,32]. As a result of both effects, the orbits of S-stars would be unclosed and would precess. If it is assumed that the total potential does not differ significantly from the Newtonian potential, the perturbed potential has the following form:
3. Results and Discussion
In this section, we give the estimation of parameters of the Hybrid Palatini gravity model by Schwarzschild precession of the S2, S38 and S55 stars, with and without taking into account the bulk mass density distribution of extended matter in the Galactic Center. We assume that the orbital precession of the S2, S38 and S55 stars is equal to the GR value. The main reason is that the GRAVITY Collaboration detected the orbital precession of the S2 star and showed that it is close to the GR prediction and that the direction is the same as in GR [57]. The second reason is that, according to astronomical data fitting in Yukawa gravity model, which are presented in the paper [40], the orbital precessions of the S38 and S55 stars are also close to the corresponding prediction of GR for these stars.
Calculation of Orbital Precession of S-Stars
A general expression for apocenter shifts for Newtonian potential and small perturbing potential is given as a solution (in Section III Integration of the equations of motion, Chapter 15 Kepler’s problem) of problem 3, page 40, Equation (1) in the Landau and Lifshitz book [98]. Assuming that a particle moves in slightly perturbed Newtonian potential, Adkins and McDonnell [62] derived an expression that is equivalent to the above mentioned relation from the Landau and Lifshitz book [98] but in an alternative way. It was shown that the expressions are equivalent, and, after that, they calculated apocenter shifts for several examples of perturbing functions.
According to [62], the orbital precession per orbital period, induced by small perturbations to the Newtonian gravitational potential could be evaluated as:
while, in the textbook [98], it was given in the form
where is the perturbing potential, r is related to z via: in Equation (8) (and in Equation (9)), and L is the semilatus rectum of the orbital ellipse with semi-major axis a and eccentricity e:
Equations (8) and (9) are equivalent, i.e., Equation (8) can be obtained from Equation (9) after substitution: .
Dokuchaev and Eroshenko [30,31,32] evaluated relativistic precessions around SMBH in the case of an additional potential due to the presence of dark matter. The precession angle per orbital period is expressed analytically using the hypergeometric function [30,31,32]:
where is the hypergeometric function. This expression is in good agreement with the corresponding expression given in the Landau and Lifshitz book [98]. More details are given in the references [30,31,32]. If one takes the expressions for precession from the books by Danby [99] (Chapter 11 equation 11.5.13) and by Murray and Dermott [100] (Chapter 2, equation 2.165.), one can obtain the same equations as the above Equation (8).
To calculate the precession of the S2, S38 and S55 stars in Hybrid Palatini modified gravity, we assumed that the perturbed potential is of the form:
and it can be used to calculate the precession angle according to Equation (8):
In order to investigate the parameters of the Hybrid Palatini gravity, which, in the case of the extended mass distribution, give the same orbital precession as GR, we graphically presented Equation (8) by adopting different values of the extended mass density and for three different S-stars. In that way, we created the below Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 showing the dependence of orbital precession angle on the gravity parameters and for several extended mass densities and for the following three S-stars: S2, S38 and S55. The observed quantities that are used in this paper are the parameters of the central SMBH in our galaxy as well as the orbital elements for the mentioned stars.
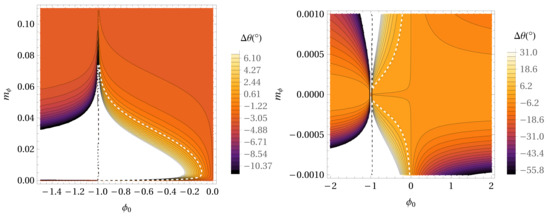
Figure 1.
The precession per orbital period for the - parameter space in the case of the Hybrid Palatini gravity potential with extended mass distribution in the case of the S2 star. The mass density distribution of extended matter is = . With a decreasing value of the precession angle, the colors are darker. Parameter is expressed in AU. The white dashed line depicts the locations in the parameter space where the precession angle has the same value as in GR (0°.18). The right panel represents the same as the left panel but for smaller values of the parameter.
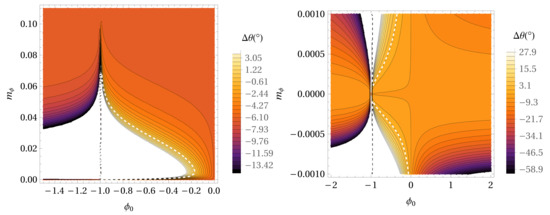
Figure 2.
The same as in Figure 1 but for the values of the mass density distribution of extended matter = . The right panel represents the same as the left panel but for smaller values of the parameter.
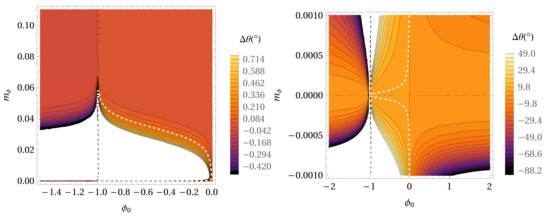
Figure 3.
The precession per orbital period for the - parameter space in the case of the Hybrid Palatini gravity potential without extended mass distribution in the case of the S38 star. With a decreasing value of the precession angle, the colors are darker. Parameter is expressed in AU. The white dashed line depicts the locations in the parameter space where the precession angle has the same value as in GR (0°.11). The right panel represents the same as the left panel but for smaller values of the parameter.
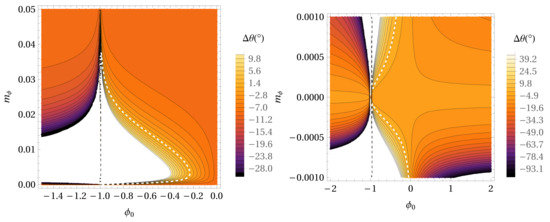
Figure 4.
The same as in Figure 3, but for the mass density distribution = . The right panel represents the same as the left panel but for smaller values of the parameter.
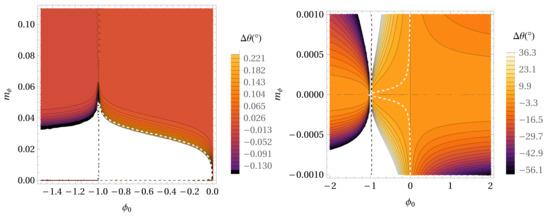
Figure 5.
The precession per orbital period for the - parameter space in the case of the Hybrid Palatini gravity potential without extended mass distribution in the case of the S55 star. With a decreasing value of the precession angle, the colors are darker. Parameter is expressed in AU. The white dashed line depicts the locations in the parameter space where the precession angle has the same value as in GR (0°.10). The right panel represents the same as the left panel but for smaller values of the parameter.
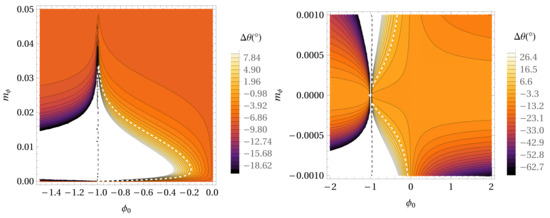
Figure 6.
The same as in Figure 5, but for the mass density distribution = . The right panel represents the same as the left panel but for smaller values of the parameter.
For our calculations, we used the results presented in [49], according to which, the mass of the SMBH of the Milky Way is ; the semi-major axis of the S2 star orbit is , and its eccentricity is ; the semi-major axis of the S38 star orbit is , and its eccentricity is ; and the semi-major axis of the S55 star orbit is , and its eccentricity is .
Figure 1 shows the precession per orbital period for the - parameter space in the case of the Hybrid Palatini gravity potential with extended mass distribution in the case of the S2 star. The mass density distribution of extended matter is = . The white dashed line depicts the locations in the parameter space where the precession angle has the same value as in GR for the S2 star (0°.18). It can be shown that precession of the orbit in the Hybrid Palatini potential is in the same direction as in GR [71], but extended mass distribution produces a contribution to precession in the opposite direction [77].
According to Figure 1 and the formulas for potential in Modified Hybrid Palatini gravity (see denominator in Equation (1)), parameter is between −1 (vertical asymptote) and 0. If the Hybrid Palatini potential reduces to the Newtonian one. The maximal value for is about 0.075 AU and for near 0.005 AU, a maximal value for is obtained, and it is around −0.1 (see left panel). We can see from the right panel that can also take negative values, but when become less than −0.0001, the AU parameter becomes very near 0, and the Hybrid Palatini potential reduces to the Newtonian one. Figure 2 represents the same as Figure 1 but for the values of the mass density distribution of extended matter = . We notice a similar tendency as in previous cases regarding dependence of shape of dashed curve with respect to the values of parameters and . The maximal value for is about 0.065 AU, and for near 0.005 AU, a maximal value for is obtained, and it is around −0.17. If we compare Figure 1 and Figure 2 with the corresponding Figure 4 from paper [18] where we did not take into account the extended mass distribution (maximal value for is about 0.10 AU and for near 0.005 AU, a maximal value for is obtained, and it is around −0.01), then we can conclude that the mass density distribution of extended matter has a strong influence on the gravity parameter and value of the precession angle per orbital period for S2 star. If we increase the value of , we obtain a decrease of the corresponding values of parameters and .
Figure 3 shows the precession per orbital period for the - parameter space in the case of the Hybrid Palatini gravity potential without extended mass distribution in the case of the S38 star. The white dashed line depicts the locations in the parameter space where the precession angle has the same value as in GR for the S38 star (0°.11). The maximal value for is about 0.06 AU, and for near 0.005 AU, a maximal value for is obtained, and it is around −0.01. According to the right panel, we can see that can also take negative values. Figure 4 represent sthe same as Figure 3 but for the mass density distribution = . The maximal value for is less than 0.04 AU, and for near 0.005 AU, a maximal value for is obtained, and it is less than −0.2.
Figure 5 and Figure 6 represent the same as Figure 3 and Figure 4 but for the S55 star (precession angle in GR is 0°.10). If we compare the the estimated parameters of the Hybrid Palatini gravity model of the S2 star with the S38 and S55 stars for the same value of , it can be seen that results are slightly different, i.e., the obtained values for the parameters and are not the same, but they are very close. It appears that parameters of the Hybrid Palatini gravity depend on the scale (the values of the semi-major axes).
According to Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, the mass density distribution of extended matter has significant influence on the values of the precession angle and of the parameters and . We notice that it is not possible to evaluate and in a unique way, if we consider only following two conditions: (1) the orbital precession is prograde as in GR and (2) the value of the precession angle is as in GR. We obtained lines in the - parameter space, and the points of these lines have the coordinates and , which fulfill the above mentioned two requests. If we want to obtain only one unique value of parameters and , we need an additional independent set of observations to combine with these obtained sets of points (, ).
This paper is a continuation of our previous research [80], but we extended our research on the following points:
- (i)
- In this study, we estimated the parameters of the Hybrid Palatini gravity model with the Schwarzschild precession of S-stars. In addition to the S2 star, here, for the first time, we took into account the S38 and S55 stars also. If we compare the estimated parameters of the Hybrid Palatini gravity model of the S2 star with the S38 and S55 stars, it can be seen that the parameters of the Hybrid Palatini gravity depend on the scale of a gravitational system, which, in this case, is the semi-major axis of a stellar orbit.
- (ii)
- In this paper, we considered the orbital precession of the mentioned stars due to additional contributions to the gravitational potential from a bulk distribution of matter. We took into account the different values of bulk mass density distribution of extended matter in the Galactic Center and analyzed their influence on values of parameters and of the Hybrid Palatini gravity model. We concluded that the mass density distribution of extended matter had significant influence on the values of precession angle and of modified gravity parameters. For higher values of , we obtained lower values of gravity parameters and . This paper is also an extension of our previous paper where we investigated the gravity parameters of Yukawa theory and how they change under different values of bulk mass density distribution of extended matter [77]. In this paper, we applied the same procedure but for parameters of the Hybrid Palatini gravity model and we extended it to the S38 and S55 stars.
- (iii)
- We believe that in addition to the most often used S2 star, the S38 and S55 stars are also excellent candidates for probing the gravitational potential around central SMBH and could be also very useful for evaluating accurate parameters of different alternative gravity models.
- (iv)
- In our previous paper [71], where we constrained the parameters of Hybrid Palatini gravity, we used observational data from the VLT and Keck collaborations. The results were obtained by fitting the simulated orbits of S2 star to its observed astrometric positions. Observational data were obtained with relatively large errors, especially at the first stage of monitoring (data were collected for decades). In this paper, we did not fit the observational data but instead we only assumed that the orbital precession of S2 star is equal to the corresponding value predicted by GR because recently the GRAVITY Collaboration claimed that they detected the orbital precession of the S2 star and showed that it is close to the GR prediction [57]. We extended our analysis to the stars S38 and S55 stars because astronomical data analysis of their orbits showed that, also in these cases, orbital precession is close to the GR prediction [40].
4. Conclusions
In this study, we estimated the parameters of the Hybrid Palatini gravity model with the Schwarzschild precession of the S2, S38 and S55 stars. We estimated the parameters with and without taking into account case of bulk mass distribution near Galactic Center. In this study, we were not fitting observation data, but instead we assumed that the Schwarzschild orbital precessions of the S2, S38 and S55 stars are the same as in of GR, i.e., 0°.18, 0°.11 and 0°.10 per orbital period, respectively. We introduced this approximation, since the observed precession angle of S2 star is very close to the GR prediction [57] and according the paper [40] where the authors analyzed observation data in the framework of Yukawa gravity and concluded that the orbital precessions of the S38 and S55 stars were in good agreement to the corresponding prediction of GR for these stars. We had a second reason, i.e., that we should recover the prograde orbital precession of S-stars, as in GR. Our findings indicate that:
- The Modified Hybrid Palatini gravity parameter is between −1 (vertical asymptote) and 0. If , the Hybrid Palatini gravity potential reduces to the Newtonian one.
- For the Hybrid Palatini gravity model (described with two parameters), it is not possible to evaluate both parameters in a unique way, if we consider only the conditions that orbital precession is prograde as in GR and that the value of the precession angle is as in GR. Instead of that, we obtained lines in the - parameter space. The points of these lines have the coordinates and , which fulfilled our two requests (the value of precession as in GR and the precession is prograde as in GR). The white dashed line depicts the locations in the parameter space of these points. If we want to obtain only one value of the parameters and , we need to combine the obtained sets of (, ) with an additional independent set of observations.
- The mass density distribution of extended matter has a significant influence on the values of precession angle and of the modified gravity parameters. Higher values of decrease the corresponding values of parameters and .
- Our analysis shows that the precession of orbit in Hybrid Palatini potential is in the same direction as in GR, but the extended mass distribution produces a contribution to precession in the opposite direction. This means that, for higher mass densities, in order to obtain the same orbital precession as in GR, one has to take the significantly different values of the Hybrid Palatini gravity parameters. In the case when , the Hybrid Palatini gravitational potential reduces to the Newtonian one. However, in order to compensate the effects of extended mass distribution on orbital precession and to obtain the same precession as in GR, has to be larger by an absolute value, thus, causing the larger deviation of the Hybrid Palatini gravitational potential with respect to the Newtonian one.
- If we compare the estimated parameters of the Hybrid Palatini gravity model of the S2 star with the S38 and S55 stars, it can be seen that results are slightly different, i.e., the obtained values for the parameters of the gravity models are not the same, but they are very close. It appears that the parameters of the Hybrid Palatini gravity depend on the scale of a gravitational system, which, in this case, is the semi-major axis of a stellar orbit, in contrast to GR, which is the scale-invariant theory of gravitation. Therefore, we believe that this behavior originates from the deviation of modified gravity from GR.
It is crucial to investigate gravity in the vicinity of very massive compact objects, such as Sgr A, because the environment around these objects is drastically different from that in the Solar System framework or at extragalactic and cosmological scales. The precession of the S stars is a unique opportunity to test gravity at the sub-parsec scale of a few thousand AU because these stars are bright stars and the periods of these stars are relatively short. We believe that it is useful to evaluate the parameters of different alternative modified gravity theories in the vicinity of SMBH with and without extended mass distribution in the metric and Palatini approach. There are various approaches to the construction of the modified gravity theories. In general, one can classify most efforts as modified gravity or introducing exotic matter, such as dark matter and dark energy. The truth, as usual, may lie in between [94].
We hope that using this method and more precise astronomical data will help to evaluate accurate parameters of different alternative gravity models and to obtain gravitational potentials at the Galactic Center.
Author Contributions
All coauthors participated in writing, calculation and discussion of obtained results. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This work is supported by Ministry of Education, Science and Technological Development of the Republic of Serbia. PJ wishes to acknowledge the support by this Ministry through the project contract No. 451-03-9/2021-14/200002. The authors also wish to thank the Center for mathematical modeling and computer simulations in physics and astrophysics of Vinča Institute of Nuclear Sciences.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GR | General Relativity |
| LT | Lense-Thirring |
| SMBH | Supermassive black hole |
Appendix A. Hybrid Palatini Gravity Model
It is important to note that theoretical studies in this field commonly assume c = G = 1 units. However, for practical purposes, i.e., for comparisons with the astronomical observations, it is necessary to recast gravitation potential in appropriate units. Thus, here we derive gravitation potential in weak field limit of the Hybrid Palatini gravity in a form convenient for this purpose.
The action, proposed in the papers by Capozziello et al. (2012,2013) [89,93], Harko et al. (2012) [88] and Borka et al. (2016) [71], is given by:
where , R is the Ricci scalar, presents the Palatini curvature with the independent connection , is the density Lagrangian, and g is the determinant of .
The Palatini curvature is given by the following equations, with the scalar field and potential :
Combination of the Equations (A2)–(A4) resulted in the equation:
Substitution of Equation (A5) into Equation (A2) enabled obtaining the expression for Palatini curvature:
The action is varied respectively to the metric , scalar field and connection , which leads to the following equations:
The Palatini connection is represented by Equation (A9) [101], which is obtained by varied action with respect to the relation , by keeping the metric constant . Equation (A9) implied that the function , and thus the Palatini Tensor and Palatini scalars are given by the following equations:
The trace of Equation (A7) is given in the next relation:
Combination of Equations (A7), (A8), (A10) and (A12), enabled obtaining the metric field equations:
and the trace of Equation (A13) is:
The scalar field equation is obtained by combination of the Equations (A12) and (A14):
We can see that scalar field is governed by the second-order evolution equation, which is an effective Klein–Gordon equation.
Appendix A.1. Equations for Newtonian Limit
In order to derive the Newtonian limit, it is common to write metric as a sum of Minkowski metric and perturbation metric : , , , , [87,101], where c is the speed of light. The paper [87] reviewed the formulation of hybrid metric-Palatini approach and its main achievements in passing the local tests and in applications to astrophysics and cosmology, and, in [101], the gravitational field equations for the modified gravity theory are considered in the framework of the Palatini formalism.
The basic properties of Newtonian limit are: , , . We denote the asymptotic of as and the local perturbation as . Accordingly, Equation (A15) obtained the following shape of linear order:
We neglected the time derivatives of , and thus Equation (A16) can be written in the following way:
where and . It can be shown that the effective mass can be expressed in the form: , where V, and are the potential and its first and second derivatives with respect to , respectively. Solving the Equation (A17), we obtained:
Since the background is Minkowskian, the perturbed Ricci tensor is given by and , (slow motion) [87,101]. Using the following gauge conditions: , where [87], Equation (A13) becomes:
and from this, we obtain:
where is the minimum of potential V [71], and then
where is a characteristic length scale, corresponding to the cosmological background.
By equating , we have:
with an effective potential introduced . The term in Equation (A22) proportional to corresponds to the cosmological background, and it can be neglected on a galactic level [87].
The modified gravitation potential of the Newtonian limit is:
References
- Fischbach, E.; Talmadge, C.L. The Search for Non–Newtonian Gravity; Springer: Berlin/Heidelberg, Germany; New York, NY, USA,, 1999; 305p. [Google Scholar]
- Capozziello, S.; Faraoni, V. Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics; Fundamental Theories of Physics; Springer: Berlin/Heidelberg, Germany, 2011; Volume 170. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. The dark matter problem from f(R) gravity viewpoint. Ann. Phys. 2012, 524, 545. [Google Scholar] [CrossRef]
- Salucci, P.; Esposito, G.; Lambiase, G.; Battista, E.; Benetti, M.; Bini, D.; Boco, L.; Sharma, G.; Bozza, V.; Buoninfante, L.; et al. Einstein, Planck and Vera Rubin: Relevant encounters between the Cosmological and the Quantum Worlds. Front. Phys. 2021, 8, 603190. [Google Scholar] [CrossRef]
- Dimitrijević, I.; Dragović, B.; Koshelev, A.S.; Rakić, Z.; Stanković, J. Cosmological solutions of a nonlocal square root gravity. Phys. Lett. B 2019, 797, 134848. [Google Scholar] [CrossRef]
- Clifton, T. Alternative Theories of Gravity; University of Cambridge: Cambridge, UK, 2006. [Google Scholar]
- Kopeikin, S.; Vlasov, I. Parametrized post-Newtonian theory of reference frames, multipolar expansions and equations of motion in the N-body problem. Phys. Rep. 2004, 400, 209. [Google Scholar] [CrossRef]
- Rubakov, V.A.; Tinyakov, P.G. Infrared-modified gravities and massive gravitons. Phys. Usp. 2008, 51, 759. [Google Scholar] [CrossRef]
- Babichev, E.; Deffayet, C.; Ziour, R. Recovery of general relativity in massive gravity via the Vainshtein mechanism. Phys. Rev. D 2010, 82, 104008. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified gravity and cosmology. Phys. Rep. 2012, 513, 1. [Google Scholar] [CrossRef]
- De Rham, C. Massive Gravity. Living Rev. Relativ. 2014, 17, 7. [Google Scholar] [CrossRef] [PubMed]
- De Martino, I.; De Laurentis, M.; Capozziello, S. Constraining f(R) Gravity by the Large-Scale Structure. Universe 2015, 1, 123–157. [Google Scholar] [CrossRef]
- De Rham, C.; Deskins, J.T.; Tolley, A.J.; Zhou, S.-Y. Massive Gravity. Rev. Mod. Phys. 2017, 89, 025004. [Google Scholar] [CrossRef]
- Petrov, A.N.; Kopeikin, S.M.; Lompay, R.R.; Tekin, B. Metric Theories of Gravity: Perturbations and Conservation Laws; De Gruyter Studies in Mathematical Physics; De Gruyter: Berlin, Germany, 2017; ISBN 9783110351781. [Google Scholar]
- Borka, D.; Borka Jovanović, V.; Capozziello, S.; Zakharov, A.F.; Jovanović, P. Estimating the Parameters of Extended Gravity Theories with the Schwarzschild Precession of S2 Star. Universe 2021, 7, 407. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Nucita, A.A.; Paolis, F.D.; Ingrosso, G. Solar system constraints on Rn gravity. Phys. Rev. D 2006, 74, 107101. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Nucita, A.A.; Paolis, F.D.; Ingrosso, G. Apoastron shift constraints on dark matter distribution at the Galactic Center. Phys. Rev. D 2007, 76, 062001. [Google Scholar] [CrossRef]
- Martins, C.F.; Salucci, P. Analysis of rotation curves in the framework of Rn gravity. Mon. Not. R. Astron. Soc. 2007, 381, 1103. [Google Scholar] [CrossRef]
- Nucita, A.A.; Paolis, F.D.; Ingrosso, G.; Qadir, A.; Zakharov, A.F. Sgr A*: A laboratory to measure the central black hole and stellar cluster parameters. Publ. Astron. Soc. Pac. 2007, 119, 349. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Capozziello, S.; Paolis, F.D.; Ingrosso, G.; Nucita, A.A. The Role of Dark Matter and Dark Energy in Cosmological Models: Theoretical Overview. Space Sci. Rev. 2009, 148, 301. [Google Scholar] [CrossRef]
- Capozziello, S.; Stabile, A.; Troisi, A. A general solution in the Newtonian limit of f(R)-gravity. Mod. Phys. Lett. A 2009, 24, 659. [Google Scholar] [CrossRef]
- Iorio, L. Constraints on the range Λ of Yukawa-like modifications to the Newtonian inverse-square law of gravitation from Solar System planetary motions. JHEP 2007, 10, 041. [Google Scholar] [CrossRef]
- Iorio, L. Putting Yukawa-like Modified Gravity (MOG) on the test in the Solar System. Sch. Res. Exch. 2008, 2008, 238385. [Google Scholar] [CrossRef][Green Version]
- Iorio, L. Galactic orbital motions in the dark matter, modified Newtonian dynamics and modified gravity scenarios. Mon. Not. R. Astron. Soc. 2010, 401, 2012. [Google Scholar] [CrossRef][Green Version]
- Borka, D.; Jovanović, P.; Borka Jovanović, V.; Zakharov, A.F. Constraints on Rn gravity from precession of orbits S2-like stars. Phys. Rev. D 2012, 85, 124004. [Google Scholar] [CrossRef]
- Capozziello, S.; Borka, D.; Jovanović, P.; Borka Jovanović, V. Constraining Extended Gravity Models by S2 star orbits around the Galactic Centre. Phys. Rev. D 2014, 90, 044052. [Google Scholar] [CrossRef]
- Dokuchaev, V.I.; Eroshenko, Y.N. Weighing of the Dark Matter at the Center of the Galaxy. JETP Lett. 2015, 101, 777. [Google Scholar] [CrossRef][Green Version]
- Dokuchaev, V.I.; Eroshenko, Y.N. Weighing of Dark Matter in the Galactic Center: Proceedings of the Seventeenth Lomonosov Conference on Elementary Particle Physics. In Particle Physics at the Year of Light; WSPC: Singapore, 2017; pp. 335–339. [Google Scholar]
- Dokuchaev, V.I.; Eroshenko, Y.N. Physical laboratory at the center of the Galaxy. Phys. Uspekhi 2015, 58, 772. [Google Scholar] [CrossRef]
- Aviles, A.; Gruber, C.; Luongo, O.; Quevedo, H. Cosmography and constraints on the equation of state of the Universe in various parametrizations. Phys. Rev. D 2012, 86, 123516. [Google Scholar] [CrossRef]
- Dunsby, P.K.S.; Luongo, O. On the theory and applications of modern cosmography. Int. J. Geom. Meth. Mod. Phys. 2016, 13, 1630002. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Luongo, O.; Ruggeri, A.C. Cosmographic Constraints and Cosmic Fluids. Galaxies 2013, 1, 216–260. [Google Scholar] [CrossRef]
- De Laurentis, M.; De Martino, I.; Lazkoz, R. Modified gravity revealed along geodesic tracks. Eur. Phys. J. C 2018, 78, 916. [Google Scholar] [CrossRef] [PubMed]
- De Martino, I.; Lazkoz, R.; De Laurentis, M. Analysis of the Yukawa gravitational potential in f(R) gravity I: Semiclassical periastron advance. Phys. Rev. D 2018, 97, 104067. [Google Scholar] [CrossRef]
- De Laurentis, M.; De Martino, I.; Lazkoz, R. Analysis of the Yukawa gravitational potential in f(R) gravity II: Relativistic periastron advance. Phys. Rev. D 2018, 97, 104068. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Extended gravity cosmography. Int. J. Mod. Phys. 2019, 28, 1930016. [Google Scholar] [CrossRef]
- D’addio, A. S-star dynamics through a Yukawa-like gravitational potential. Phys. Dark Universe 2021, 33, 100871. [Google Scholar] [CrossRef]
- De Martino, I.; Della Monica, R. Unveiling the nature of Sgr A* with the geodesic motion of S-stars. arXiv 2021, arXiv:2112.01888. [Google Scholar]
- Ghez, A.M.; Morris, M.; Becklin, E.E.; Tanner, A.; Kremenek, T. The accelerations of stars orbiting the Milky Way’s central black hole. Nature 2000, 407, 349. [Google Scholar] [CrossRef]
- Ghez, A.M.; Salim, S.; Weinberg, N.N.; Lu, J.R.; Do, T.; Dunn, J.K.; Matthews, K.; Morris, M.R.; Yelda, S.; Becklin, E.E.; et al. Measuring distance and properties of the Milky Way’s central supermassive black hole with stellar orbits. Astrophys. J. 2008, 689, 1044. [Google Scholar] [CrossRef]
- Gillessen, S.; Eisenhauer, F.; Fritz, T.K.; Bartko, H.; Dodds-Eden, K.; Pfuhl, O.; Ott, T.; Genzel, R. The orbit of the star S2 around SGR A* from very large telescope and Keck data. Astrophys. J. 2009, 707, L114. [Google Scholar] [CrossRef]
- Gillessen, S.; Eisenhauer, F.; Trippe, S.; Alexander, T.; Genzel, R.; Martins, F.; Ott, T. Monitoring stellar orbits around the massive black hole in the Galactic Center. Astrophys. J. 2009, 692, 1075. [Google Scholar] [CrossRef]
- Schodel, R.; Ott, T.; Genzel, R.; Hofmann, R.; Lehnert, M.; Eckart, A.; Mouawad, N.; Alexander, T.; Reid, M.J.; Lenzen, R.; et al. Closest star seen orbiting the supermassive black hole at the Centre of the Milky Way. Nature 2002, 419, 694. [Google Scholar] [CrossRef] [PubMed]
- Genzel, R.; Eisenhauer, F.; Gillessen, S. The Galactic Center massive black hole and nuclear star cluster. Rev. Mod. Phys. 2010, 82, 3121. [Google Scholar] [CrossRef]
- Meyer, L.; Ghez, A.M.; Schödel, R.; Yelda, S.; Boehle, A.; Lu, J.R.; Do, T.; Morris, M.R.; Becklin, E.E.; Matthews, K. The Shortest-Known-Period Star Orbiting Our Galaxy’s Supermassive Black Hole. Science 2012, 338, 84. [Google Scholar] [CrossRef] [PubMed]
- Gillessen, S.; Plewa, P.M.; Eisenhauer, F.; Sari, R.E.; Waisberg, I.; Habibi, M.; Pfuhl, O.; George, E.; Dexter, J.; von Fellenberg, S.; et al. An Update on Monitoring Stellar Orbits in the Galactic Center. Astrophys. J. 2017, 837, 30. [Google Scholar] [CrossRef]
- Hees, A.; Do, T.; Ghez, A.M.; Martinez, G.D.; Naoz, S.; Becklin, E.E.; Boehle, A.; Chappell, S.; Chu, D.; Dehghanfar, A.; et al. Testing General Relativity with Stellar Orbits around the Supermassive Black Hole in Our Galactic Center. Phys. Rev. Lett. 2017, 118, 211101. [Google Scholar] [CrossRef]
- Chu, D.S.; Do, T.; Hees, A.; Ghez, A.; Naoz, S.; Witzel, G.; Sakai, S.; Chappell, S.; Gautam, A.K.; Lu, J.R.; et al. Investigating the Binarity of S0-2: Implications for Its Origins and Robustness as a Probe of the Laws of Gravity around a Supermassive Black Hole. Astrophys. J. 2018, 854, 12. [Google Scholar] [CrossRef]
- GRAVITY Collaboration; Abuter, R.; Amorim, A.; Anugu, N.; Bauböck, M.; Benisty, M.; Berger, J.P.; Blind, N.; Bonnet, H.; Brandner, W.; et al. Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2018, 615, L15. [Google Scholar] [CrossRef]
- GRAVITY Collaboration; Abuter, R.; Amorim, A.; Bauböck, M.; Berger, J.P.; Bonnet, H.; Brandner, W.; Clénet, Y.; Du Foresto, V.C.; Vincent, F.; et al. A geometric distance measurement to the Galactic center black hole with 0.3% uncertainty. Astron. Astrophys. 2019, 625, L10. [Google Scholar]
- Do, T.; Hees, A.; Ghez, A.; Martinez, G.D.; Chu, D.S.; Jia, S.; Sakai, S.; Lu, J.R.; Gautam, A.K.; O’neil, K.K.; et al. Relativistic redshift of the star S0-2 orbiting the Galactic Center supermassive black hole. Science 2019, 365, 664. [Google Scholar] [CrossRef]
- GRAVITY Collaboration; Amorim, A.; Bauböck, M.; Benisty, M.; Berger, J.P.; Clénet, Y.; Forest, V.C.d.; de Zeeuw, T.; Dexter, J.; Duvert, G.; et al. Scalar field effects on the orbit of S2 star. Mon. Not. R. Astron. Soc. 2019, 489, 4606. [Google Scholar]
- Hees, A.; Do, T.; Roberts, B.M.; Ghez, A.M.; Nishiyama, S.; Bentley, R.O.; Gautam, A.K.; Jia, S.; Kara, T.; Lu, J.R.; et al. Search for a Variation of the Fine Structure Constant around the Supermassive Black Hole in Our Galactic Center. Phys. Rev. Lett. 2020, 124, 081101. [Google Scholar] [CrossRef] [PubMed]
- GRAVITY Collaboration; Abuter, R.; Amorim, A.; Bauböck, M.; Berger, J.P.; Bonnet, H.; Brandner, W.; Cardoso, V.; Clénet, Y.; de Zeeuw, P.T.; et al. Detection of the Schwarzschild precession in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2020, 636, L5. [Google Scholar] [CrossRef]
- Ruffini, R.; Argüelles, C.R.; Rueda, J.A. On the core-halo distribution of dark matter in galaxies. Mon. Not. R. Astron. Soc. 2015, 451, 622. [Google Scholar] [CrossRef]
- Becerra-Vergara, E.A.; Argüelles, C.R.; Krut, A.; Rueda, J.A.; Ruffini, R. Hinting a dark matter nature of Sgr A* via the S-stars. Mon. Not. R. Astron. Soc. 2021, 505, L64. [Google Scholar] [CrossRef]
- Zakharov, A.F. Testing the Galactic Centre potential with S-stars. Mon. Not. R. Astron. Soc. Lett. 2021. [Google Scholar] [CrossRef]
- Rubilar, G.F.; Eckart, A. Periastron shifts of stellar orbits near the Galactic Center. Astron. Astrophys. 2001, 374, 95. [Google Scholar] [CrossRef]
- Adkins, G.S.; McDonnell, J. Orbital precession due to central-force perturbations. Phys. Rev. D 2007, 75, 082001. [Google Scholar] [CrossRef]
- Weinberg, N.N.; Milosavljević, M.; Ghez, A.M. Stellar dynamics at the Galactic Center with an extremely large telescope. Astrophys. J. 2005, 622, 878. [Google Scholar] [CrossRef]
- Peißker, F.; Eckart, A.; Zajaček, M.; Michal, A.; Ali, B.; Parsa, M. S62 and S4711: Indications of a Population of Faint Fast-moving Stars inside the S2 Orbit-S4711 on a 7.6 yr Orbit around Sgr A*. Astrophys. J. 2020, 899, 50. [Google Scholar] [CrossRef]
- Iorio, L. The Short-period S-stars S4711, S62, S4714 and the Lense-Thirring Effect due to the Spin of Sgr A*. Astrophys. J. 2020, 904, 186. [Google Scholar] [CrossRef]
- Iorio, L. On the 2PN Pericentre Precession in the General Theory of Relativity and the Recently Discovered Fast-Orbiting S-Stars in Sgr A*. Universe 2021, 7, 37. [Google Scholar] [CrossRef]
- Gainutdinov, R.; Baryshev, Y. Relativistic Effects in Orbital Motion of the S-Stars at the Galactic Center. Universe 2020, 6, 177. [Google Scholar] [CrossRef]
- Fragione, G.; Loeb, A. An Upper Limit on the Spin of Sgr A* Based on Stellar Orbits in Its Vicinity. Astrophys. J. Lett. 2020, 901, L32. [Google Scholar] [CrossRef]
- Borka, D.; Jovanović, P.; Borka Jovanović, V.; Zakharov, A.F. Constraining the range of Yukawa gravity interaction from S2 star orbits. J. Cosmol. Astropart. Phys. 2013, 11, 081101. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Borka, D.; Borka Jovanović, V.; Jovanović, P. Constraints on Rn gravity from precession of orbits of S2-like stars: A case of a bulk distribution of mass. Adv. Space Res. 2014, 54, 1108. [Google Scholar] [CrossRef]
- Borka, D.; Capozziello, S.; Jovanović, P.; Borka Jovanović, V. Probing hybrid modified gravity by stellar motion around Galactic Center. Astropart. Phys. 2016, 79, 41. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Jovanović, P.; Borka, D.; Borka Jovanović, V. Constraining the range of Yukawa gravity interaction from S2 star orbits II: Bounds on graviton mass. J. Cosmol. Astropart. Phys. 2016, 5, 45. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Jovanović, P.; Borka, D.; Borka Jovanović, V. Constraining the range of Yukawa gravity interaction from S2 star orbits III: Improvement expectations for graviton mass bounds. J. Cosmol. Astropart. Phys. 2018, 2018, 50. [Google Scholar] [CrossRef]
- Zakharov, A.F.; Jovanović, P.; Borka, D.; Borka Jovanović, V. Different Ways to Estimate Graviton Mass. Int. J. Mod. Phys. Conf. Ser. 2018, 47, 1860096. [Google Scholar] [CrossRef]
- Dialektopoulos, K.F.; Borka, D.; Capozziello, S.; Borka Jovanović, V.; Jovanović, P. Constraining nonlocal gravity by S2 star orbits. Phys. Rev. D 2019, 99, 044053. [Google Scholar] [CrossRef]
- Borka Jovanović, V.; Jovanović, P.; Borka, D.; Capozziello, S.; Gravina, S.; D’Addio, A. Constraining scalar-tensor gravity models by S2 star orbits around the Galactic Center. Facta Univ. Ser. Phys. Chem. Tech. 2019, 17, 11–20. [Google Scholar] [CrossRef]
- Jovanović, P.; Borka, D.; Borka Jovanović, V.; Zakharov, A.F. Influence of bulk mass distribution on orbital precession of S2 star in Yukawa gravity. Eur. Phys. J. D 2021, 75, 145. [Google Scholar] [CrossRef]
- Borka Jovanović, V.; Capozziello, S.; Jovanović, P.; Borka, D. Recovering the fundamental plane of galaxies by f(R) gravity. Phys. Dark Universe 2016, 14, 73. [Google Scholar] [CrossRef]
- Capozziello, S.; Borka Jovanović, V.; Borka, D.; Jovanović, P. Constraining theories of gravity by fundamental plane of elliptical galaxies. Phys. Dark Universe 2020, 29, 100573. [Google Scholar] [CrossRef]
- Borka Jovanović, V.; Borka, D.; Jovanović, P.; Capozziello, S. Possible effects of hybrid gravity on stellar kinematics in elliptical galaxies. Eur. Phys. J. D 2021, 75, 149. [Google Scholar] [CrossRef]
- Capozziello, S.; Jovanović, P.; Borka Jovanović, V.; Borka, D. Addressing the missing matter problem in galaxies through a new fundamental gravitational radius. J. Cosmol. Astropart. Phys. 2017, 6, 44. [Google Scholar] [CrossRef]
- Clifton, T.; Barrow, J.D. The power of general relativity. Phys. Rev. D 2005, 72, 103005. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Troisi, A. Gravitational lensing in fourth-order gravity. Phys. Rev. D 2006, 73, 104019. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Troisi, A. Low surface brightness galaxy rotation curves in the low energy limit of Rn gravity: No need for dark matter? Mon. Not. R. Astron. Soc. 2007, 375, 1423. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) theories of gravity. Rev. Mod. Phys. 2010, 82, 451. [Google Scholar] [CrossRef]
- Olmo, G.J. Palatini Approach to Modified Gravity: f(R) Theories and Beyond. Int. J. Mod. Phys. D 2011, 20, 413. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Hybrid Metric-Palatini Gravity. Universe 2015, 1, 199–238. [Google Scholar] [CrossRef]
- Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Metric-Palatini gravity unifying local constraints and late-time cosmic acceleration. Phys. Rev. D 2012, 85, 084016. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Galactic rotation curves in hybrid metric-Palatini gravity. Astropart. Phys. 2013, 35, 65. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Cosmology of hybrid metric-Palatini f(X)-gravity. JCAP 2013, 1304, 011. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Lobo, F.S.N.; Olmo, G.J. Hybrid modified gravity unifying local tests, galactic dynamics and late-time cosmic acceleration. Int. J. Mod. Phys. D 2013, 22, 1342006. [Google Scholar] [CrossRef]
- Koivisto, T.S. Cosmology of modified (but second order) gravity. AIP Conf. Proc. 2010, 1206, 79. [Google Scholar]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Wormholes supported by hybrid metric-Palatini gravity. Phys. Rev. D 2012, 86, 127504. [Google Scholar] [CrossRef]
- Allemandi, G.; Borowiec, A.; Francaviglia, M.; Odintsov, S.D. Dark energy dominance and cosmic acceleration in first-order formalism. Phys. Rev. D 2005, 72, 063505. [Google Scholar] [CrossRef]
- Borowiec, A.; Kozak, A. New class of hybrid metric-Palatini scalar-tensor theories of gravity. J. Cosmol. Astropart. Phys. 2020, 07, 003. [Google Scholar] [CrossRef]
- Genzel, R.; Ott, T.; Eisenhauer, F.; Hofmann, R.; Alexander, T.; Sternberg, A.; Lenzen, R.; Lacombe, F.; Rouan, D.; Renzini, A.; et al. The Stellar Cusp Around the Supermassive Black Hole in the Galactic Center. Astrophys. J. 2003, 594, 812. [Google Scholar] [CrossRef]
- Preto, M.; Saha, P. On Post-Newtonian Orbits and the Galactic-Center Stars. Astrophys. J. 2009, 703, 1743. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Mechanics; Butterworth-Heinemann: Oxford, UK, 1976. [Google Scholar]
- Danby, J.M.A. Fundamental of Celestial Mechanics; Macmillan: New York, NY, USA, 1962. [Google Scholar]
- Murray, C.D.; Dermott, S.F. Solar System Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Wu, J.; Li, G.; Harko, T.; Liang, S.D. Palatini formulation of f(R,T) gravity theory, and its cosmological implications. Eur. Phys. J. C 2018, 78, 430. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).