Abstract
For a pure SU(2) Yang–Mills theory in 4D, we revisit the spatial (3D), ball-like region of radius in its bulk subject to the pressureless, deconfining phase at , where denotes the critical temperature for the onset of the deconfining–preconfining phase transition. Such a region possesses finite energy density and represents the self-intersection of a figure-eight shaped center-vortex loop if a BPS monopole of core radius ∼, isolated from its antimonopole by repulsion externally invoked through a transient shift of (anti)caloron holonomy (pair creation), is trapped therein. The entire soliton (vortex line plus region of self-intersection of mass containing the monopole) can be considered an excitation of the pressureless and energyless ground state of the confining phase. Correcting an earlier estimate of , we show that the vortex-loop self-intersection region associates to the central part of a(n) (anti)caloron and that this region carries one unit of electric U(1) charge via the (electric-magnetic dually interpreted) charge of the monopole. The monopole core quantum vibrates at a thermodynamically determined frequency and is unresolved. For a deconfining-phase plasma oscillation about the zero-pressure background at , we compute the lowest frequency within a neutral and homogeneous spatial ball (no trapped monopole) in dependence of its radius . For a comparison of with reveals that the neutral plasma oscillates much slower than the same plasma driven by the oscillation of a monopole core.
1. Introduction
The thermodynamical phase structure of a single SU(2) Yang-Mills theory (electric-magnetic dually interpreted with respect to U(1) ⊂ SU(2)), comprising deconfining and preconfining thermal ground states of finite energy densities and (partially) massive gauge-field excitations as well as an energyless and pressureless confining ground state, suggests the existence of a solitonic, stable particle with intriguing yet familiar properties. Immersed into the confining ground state [1], the figure-eight configuration of a self-intersecting center-vortex loop acquires its two-fold degenerate magnetic moment by a quantised electric current, composed of a chain of alternating monopoles and antimonopoles [2]. The mass of this soliton mainly arises from deconfining energy density within the self-intersection region of the vortex loop, idealised to be a spherical blob of radius . At a temperature , where is the boundary1 of the deconfining phase, the pressure vanishes with positive slope (stable particle) [1]. The electric charge of this region is carried by a trapped BPS monopole of mass which is not resolved thermodynamically and orginated by large-holonomy (anti)caloron dissociation (pair creation) [3]. The monopole’s core fluctuates and is quantum initiated [1] to breathe at a certain frequency [4,5].
It is tempting to interpret this quantum soliton as the electron (or an idealised charged lepton void of weak decay) (see, however, [6] for an interesting, extended field configuration mapping Minkowski to the internal space and argued to describe the electron’s quantum numbers on the classical level in terms of topological charges). In the present paper (see also [7]), we realise Louis de Broglie’s ideas on the (quantum) thermodynamics of the isolated particle in its rest frame [8,9] subject to internal, spatially homogeneous ‘clock ticks’ at rate . According to de Broglie, such a spatially localised (within a 3D ball-like volume), time-periodic phenomenon prescribes the soliton mass via . By Lorentz-boosting the standing wave of the particle at rest to a propagating wave (particle at spatial momentum p), this implies the well-known matter wavelength —the starting point for the development of wave mechanics [10,11,12,13]. The probabilistic interpretation of the locus of electric charge in terms of the wavefunction’s squared amplitude [14] matches with the fact that the periodically breathing, unresolved monopole core is displaced frequently and undeterministically by a local engagement with ℏ (and an external field, e.g., in a hydrogen atom) throughout the self-intersection region of the vortex. The free solitons’s apparent structurelessness, as inferred from collider experiments, is due to the thermal nature of the self-intersection region (maximum entropy): Electric monopole charges equally likely occur at any spatial point within volume ∼, which is, in turn, immersed into the ground state of the confining phase—a condensate of shrunk-to-points center-vortex loops void of pressure and energy density [1]. (On the scale of rest mass , the non-self-intersecting, spatial center-vortex loop is massless and prone to curve shrinking [1,15].)
In the present paper, we discuss a few amendments to [7], where the above-sketched model for a charged lepton (idealised to be stable against weak decay) was introduced, and we address oscillation physics about temperature of a neutral plasma ball to conclude that the contributions to the quantum mass of the soliton from low-lying frequencies of such spherically symmetric breathing modes are negligible. In Section 2, we correct the values of and the monopole mass as well as the ratio based on the monopole mass formula:
where [1,3,16,17,18,19,20,21,22], and is the value of the effective gauge coupling at [1]. In writing Equation (1), we assume that the spatial asymptotics of the monopole’s (or adjoint Higgs) field is determined by temperature alone, reflecting the fact that the maximum holonomy of the originating, dissociated (anti)caloron is enforced externally and not influenced by the ensemble’s spatial finite-range correlations encoded in the value of . The ratio is substantially smaller than erroneously estimated in [7]: Instead of , we now have . Here, represents the modulus of the adjoint and inert scalar field of the deconfining phase (spatially coarse-grained, densely packed (anti)caloron centers [1]), and denotes the Yang–Mills scale. The length scale , therefore, sets the resolution for the SU(2) gauge-field theory prescribed by the quantum behavior of (anti)caloron centers [1]. In the present paper, we show that . Therefore, the blob of center-vortex self-intersection2 does not per se represent infinite-volume thermodynamics [1]. Rather, it is deeply contained within the central (quantum) region of the accomodating caloron or anticaloron: . We will argue, however, that as far as the derivation of soliton properties is concerned, the thermodynamical results in [1] still apply. Interestingly, the smallness of excludes the possibility of trapping two or more monopoles or antimonopoles within one and the same blob: they would have to be provided by two or more dissociating (anti)calorons but the blob only contains the central part of a single (anti)caloron. In addition to a re-visit of the physics of the self-intersection region at temperature in a spatial center-vortex loop, we also discuss, in Section 3, the lowest radial oscillation of a neutral deconfining plasma ball of radius which does not trap a monopole. Computing the associated frequency requires the determination of longitudinal sound speed at . We obtain . Note that in spite of , where conformal-symmetry breaking effects due to the Yang–Mills scale are large, this value is close to the ultra-relativistic-gas limit . To exclude that there are sizable corrections to the left-hand side of Equation (5) due to plasma-breathing effects just above the threshold we compare and at and find . Finally, in Section 4, we summarise our work and comment on future developments.
2. Self-Intersection Region of a Figure-Eight Shaped Center-Vortex Loop
In [7], a model of the free electron was proposed which relies on the phase structure and thermodynamical quantities of SU(2) Yang–Mills thermodynamics, the nature of the excitations in the confining phase [23], and the work in [4,5] on the perturbed BPS monopole. In [23], an operator—the ’t Hooft loop—was defined nonlocally for pure SU(N) Yang–Mills theory. The ’t Hooft loop is dual in nature relative to the (spatial) Wilson loop. Its action creates one unit of magnetic flux with respect to the maximal Abelian subgroub U(1) SU(N), as expressed by a phase change through a root of unity in the Wilson loop linking to it. In the confining phase of SU(2), such a flux line occurs as the zero-core-size limit of the Abrikosov–Nielsen–Olesen vortex of winding number unity and, thus, is massless, causing ’t Hooft loop to acquire a finite, spatially homogeneous expectation. Moreover, no explicit isolated charges with respect to U(1) ⊂ SU(2)3, which could serve as flux sources or sinks, are tolerated by the pressureless confining ground state, composed of shrunk-to-points single center-vortex loops [1]. Therefore, a given, static vortex line, viewed as a 1D object in 3D space, has to form a closed loop. However, the self-intersection in a center-vortex loop locally represents a strong distortion of confining order (the ’t Hooft loop representing the order parameter), reinstating a region of pressureless, deconfining phase wherein an isolated charge—a BPS monopole or antimonopole—may lead a shielded longtime existence. The responses of such a classical BPS (anti)monopole to a spherically symmetric initial perturbation and the spectrum of normal modes were investigated in [4,5], respectively. As a result, it was found that the asymptotic state of oscillation is determined by a frequency given by the mass of the two off-Cartan modes in the adjoint Higgs model that the monopole lives in. (In a thermal situation, this adjoint Higgs model is the pure Yang–Mills theory with the -component of the gauge field, for which its value at spatial infinity determines the nontrivial (anti)caloron holonomy, playing the role of the Higgs field for the spatial components [20,21,22].)
We now revise the implications of the incorrect monopole mass formula in [7] (Equation (18) of [7]). Moreover, we point out an error in Equation (21) of [7] which requires a conceptual reinterpretation of the physics of the self-intersection region. The mass of a BPS monopole is defined as the spatial integral of the 00-component of the energy-momentum tensor on its field configuration with winding number one in [24]. It reads as follows.
Here, e denotes the defining gauge coupling of the adjoint Higgs model (or the fundamental, thermalised pure SU(2) Yang–Mills theory), and is the spatially asymptotic modulus of the Higgs field. Only (anti)calorons of scale parameter close to contribute to the emergence of the thermal ground state in the deconfining phase. Therefore, the gauge coupling e can be interpreted as the effective one [1].
Assuming that the monopole was liberated by the dissociation of a maximum-holonomy caloron at , we have the following [1,3].
In writing the maximum nontrivial holonomy value of , we assume that this (externally imposed, pair creation) spatial asymptote solely depends on temperature and is not influenced by the spatial finite-range correlations imposed by the trivial-holonomy (anti)caloron constituting the thermal ground-state estimate. Being a quantum soliton of circular frequency , the electron’s rest mass is determined by a monopole-core oscillation [8,9]. This frequency was found to be equal to the mass of the two off-Cartan modes in the adjoint Higgs model containing the BPS monopole [4,5].
Alternatively, assuming a conserved energy content of the approximately ball-like self-intersection region of radius (the contribution of the two vortex loops is negligible [1], and is denoted as in [7])—trapping a quantum non-initialised, static BPS monopole of mass and constituted by a deconfining SU(2) Yang–Mills plasma of energy density —one derives the following equation [7].
Note that the left-hand side describes the soliton mass by a situation of an initialised monopole and its covibrating quantum surroundings—all captured by a multiplication of the frequency with the quantum of action ℏ after the oscillation was triggered by monopole interaction with the thermal ground state and its excitations—while the right-hand side describes the energy balance of the system before such an initialisation has occurred. Energy conservation implies the equality of these two expressions. Notice that entails that the Yang–Mills scale relates to as follows [7].
Solving Equation (5) for yields the following:
instead of , as obtained in [7]. It is instructive to compute the relative contribution of to , the ratio of the monopole core size to , and the reduced Compton wave length to the thermodynamical resolution scale . Note that [4,5]. One has the following.
Therefore, a hypothetically static, classical monopole would not contribute sizably to the mass of the region of self-intersection. Rather, it is the phenomenon of oscillation, expressing a strong interdependence between the unresolved monopole and its quantum environment that gives rise to the mass of this region. The region’s radius is about 50-times larger than the radius of the monopole core, and the monopole core intrinsically is far from being resolved. Therefore, it is safe to say that the quantum-induced motion of the monopole is not influenced by the boundary. This boundary is the surface where the plasma of the self-intersection region transmutes into a thin fuzzy/turbulent shell of preconfining phase adjacent to a surrounding of pressureless confining ground state, which is composed of condensed single and shrunk-to-points center vortices [1]. Interestingly, radius compares to the spatial coarse-graining scale as follows.
A simple calculational error in Equation (22) of [7] has produced a value much larger than unity. The correct result of Equation (9) implies that the “thermodynamics” we discussed so far actually occurs deep within the center of a(n) (anti)caloron of scale parameter . Since we have the following:
Figure 1 suggests that the scale parameter integral, defining the phase of [1], does not quite saturating a harmonic dependence on Euclidean time when cut off at . However, our above discussion on the right-hand side of Equation (5) assumes that such a saturation occurs within the volume . Hence, the right-hand side of Equation (5) only yields an approximate account of the distorted thermodynamics within the self-intersection region: the monopole is always close to the locus of action at the inmost point of the caloron or anticaloron, rendering this region a jittery object even within its deep bulk.
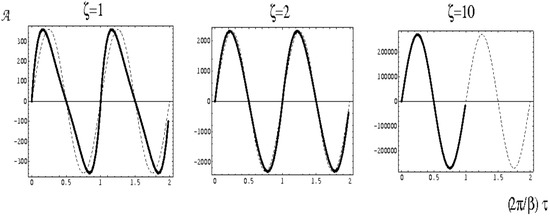
Figure 1.
Saturation towards a harmonic Euclidean time dependence of the contributions of Harrington–Shepard calorons to the field-strength correlation defining the phase of the field as a function of the scaled cutoff for the instanton-scale-parameter integration. Cutting off at suggests that there are (mild) deviations from a harmonic dependence. Figure taken from [25].
Still, the link between a hypothetically static monopole and its surroundings—described by infinite-volume thermodynamics—to the quantum-induced mass of the containing region due to oscillation is self-consistently made via Equation (5) by energy conservation, and reasonable estimates of and the critical temperature keV [7] ( [1]) should yet be possible.
3. Lowest Spherically Symmetric Breathing Mode
Spherically symmetric oscillations of the deconfining plasma temperature are not only driven by internally induced monopole oscillations but interfere with spatially homogeneous, coherent plasma oscillations due to external distortions of the initial temperature: . At the same, radius of these two oscillation modes should be compared in terms of their frequencies and , respectively, in order to judge whether mass of the self-intersection region, arising from monopole-driven oscillation, is influenced sizably by the contribution of a global, oscillatory temperature distortion. Moreover, a neutral plasma ball of radius is subject to thermodynamics at face value. Since such a (distorted) macrocopic ball is expected to radiate electromagnetically on top of its weak black-body evaporation, diagnosing a lower frequency cutoff in the excess spectrum would allow the unique extraction of plasma-ball radius and, hence, of the energy content of the ball.
Let us, thus, compute the frequency of the lowest spherically symmetric breathing mode of a deconfining SU(2) Yang–Mills plasma ball of homogeneous energy density and pressure P, for which its temperature oscillates about . Surface effects, arising from the transition between the deconfining (bulk) and the confining (exterior of ball) phases can be neglected for a sufficiently large ball mass , and the expression for reads as follows [26,27]:
where the dimensionless quantities (longitudinal sound velocity) and ( in units of the inverse Yang–Mills scale ) are defined as follows:
and . In Equation (12), the employments of the one-loop pressure and of the one-loop energy density are excellent approximations (modified by higher-loop corrections on the 1%-level [1]). Amusingly, an estimate of by virtue of a linearisation of the force–balance equation about the stable point and an appeal to energy conservation of the following:
replaces the factor of in Equation (11) by a factor of three. For and , we have the following [1]:
where
Taking into account implicit (via ) and explicit dependences of and on and employing the evolution equation for the mass of off-Cartan gauge modes as a function of temperature [1]:
one derives the following:
where the following is the case.
Substituting Equation (17) into Equation (12) at , we numerically obtain the following.
For Equation (11), this yields the following.
Let us now compare the monopole-core induced frequency of the self-intersection region of the figure-eight shaped center-vortex loop (model of the electron) with at one and the same radius:
see Equation (7). For , this yields the following:
such that the following is the case.
Such a large ratio is natural since the oscillation in the self-intersection region—quantum initiated by caloron or anticaloron action—is induced by the classical dynamics of a monopole core [4,5] for which its radius matches the reduced Compton wave length , while the lowest symmetric breathing mode of the neutral deconfining ball is a consequence of longitudinal sound propagation in an approximate bulk thermodynamics. This bulk associates with being comparable to the Bohr radius [7].
Equation (20) is the more reliable the larger is. Isotropy breaking effects, which associate with the neglected surface dynamics of the ball and/or the excitation of spherically non-symmetric oscillation states, cause this surface to (electromagnetically) radiate with a spectrum that is cut off towards the infrared at a frequency of about , corresponding to wave length .
4. Summary and Discussion
This paper’s main purpose was to compare two situations in which a ball-like region of deconfining phase in SU(2) Yang-Mills thermodynamics oscillates about the zero of the pressure at temperature : (i) the charged self-intersection region of a figure-eight shaped, solitonic center-vortex loop (a model of the electron) containing an internally quantum-perturbed BPS monopole, for which its classical core dynamics drives this oscillation of (circular) frequency (up to a factor ℏ coincident with the rest energy of the soliton [8,9]); and (ii) the homogeneous, neutral region being perturbed externally such that a lowest spherically symmetric oscillatory excitation of (circular) frequency is excited thanks to a finite longitudinal speed of sound . At the same radius, , we obtain . This hierarchy relates to the very different causes of oscillation in either case and assures that the right-hand side of the mass formula Equation (5) for an oscillation in the sense of (i) does not receive any sizable contributions from an oscillation in the sense of (ii).
Secondly, we have observed a numerical error in [7] concerning the estimate of the system radius in terms of the spatial coarse-graining scale at . The correct result states that finite-size corrections to infinite-volume thermodynamics cannot be excluded at face value since the region of self-intersection actually is contained deeply within the ball of spatial coarse-graining invoked in the derivation of the effective theory [1]. However, the asymptotic harmonic time dependence of the integrated field-strength correlation [1], required for the introduction of the field , is approximately saturated when cutting the instanton-scale-parameter integration off at already.
The present work only represents a first step in studying the plasma dynamics of a ball-like region of deconfining phase at . More realistically, the physics of the boundary shell, repesenting the transitions from the deconfining via the preconfining to the confining phases, should be taken into account. Moreover, we did not address evaporation physics (in adiabatic approximation: emission of non-intersecting and self-intersecting center-vortex loops and, assuming a mixing with an SU(2) Yang–Mills theory of much lower scale, electromagnetic modes from the surface of this shell in terms of thermal spectra) in the case of macroscopically sized balls (see [28]) and how this process affects oscillation dynamics. Last but not least, a thorough discussion of (delocalised) spin in terms of the center-flux along the figure-eight shaped vortex line and the emergence of the electric Coulomb field [29] throughout the confining-phase exterior to the blob of vortex-line self-intersection needs to be realised. The latter represents a small contribution to the soliton mass [7] and should manifest polarised dipole densities in (anti)caloron peripheries [1,30].
Our results on the spherically symmetric oscillations of the homogeneous and macroscopic plasma could be relevant in the description of certain, quasi-stabilised, compact and radiating objects created within atmospheric discharges and for plasma diagnostics in terrestial fusion experiments.
Author Contributions
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to acknowledge a useful conversation with Anton Plech. Discussions with Manfried Faber on common themes and differences of his and the here-proposed soliton model are gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | For the sake of pointing out classical vs. quantum physics in association with (anti)calorons, we alternate between SI and natural units in this introduction, and from Section 2 onward, we exclusively work in natural units where the speed of light in vacuum, Planck’s (reduced) quantum of action, and Boltzmann’s constant are all set equal to unity: . |
| 2 | The radius is denoted in [7]. |
| 3 | In physics models, charges and fluxes with respect to U(1) ⊂ SU(2) need to be interpreted in an electric-magnetically dual manner [1]. |
References
- Hofmann, R. The Thermodynamics of Quantum Yang–Mills Theory: Theory and Application, 2nd ed.; World Scientific: Singapore, 2016. [Google Scholar]
- Del Debbio, L.; Manfried, F.; Greensite, J.; Olejnik, S. Center dominance, center vortices, and confinement. In Proceedings of the NATO Advanced Research Workshop on Theoretical Physics: New Developments in Quantum Field Theory, Zakopane, Poland, 14–20 June 1997; Volume 6, p. 47. [Google Scholar]
- Diakonov, D.; Gromov, N.; Petrov, V.; Slizovskiy, S. Quantum weights of dyons and of instantons with nontrivial holonomy. Phys. Rev. D 2004, 70, 036003. [Google Scholar] [CrossRef] [Green Version]
- Fodor, G.; Racz, I. What Does a Strongly Excited ’t Hooft-Polyakov Magnetic Monopole Do? Phys. Rev. Lett. 2004, 92, 151801. [Google Scholar] [CrossRef] [Green Version]
- Forgacs, P.; Volkov, M.S. Resonant Excitations of the ’t Hooft-Polyakov Monopole. Phys. Rev. Lett. 2004, 92, 151802. [Google Scholar] [CrossRef] [Green Version]
- Faber, M. A model for topological fermions. Few Body Syst. 2001, 30, 149. [Google Scholar] [CrossRef] [Green Version]
- Hofmann, R. The isolated electron: De Broglie’s “hidden” thermodynamics, SU(2) Quantum Yang-Mills theory, and a strongly perturbed BPS monopole. Entropy 2017, 19, 575. [Google Scholar] [CrossRef] [Green Version]
- De Broglie, L. Recherches sur la Theorie Des Quanta. Annales de Physique 1925, 10, 4925. [Google Scholar] [CrossRef] [Green Version]
- De Broglie, L. The thermodynamics of the isolated particle. Great Probl. Sci. 1964, 17, 1. [Google Scholar]
- Schrödinger, E. Quantisierung als Eigenwertproblem I. Ann. Phys. 1926, 79, 361. [Google Scholar] [CrossRef]
- Schrödinger, E. Quantisierung als Eigenwertproblem II. Ann. Phys. 1926, 79, 489. [Google Scholar] [CrossRef]
- Schrödinger, E. Quantisierung als Eigenwertproblem III. Ann. Phys. 1926, 80, 437. [Google Scholar] [CrossRef]
- Schrödinger, E. Quantisierung als Eigenwertproblem IV. Ann. Phys. 1926, 81, 109. [Google Scholar] [CrossRef]
- Born, M. Zur Quantenmechanik der Stoßvorgänge. Z. Phys. 1926, 37, 863. [Google Scholar] [CrossRef]
- Moosmann, J.; Hofmann, R. Evolving center-vortex loops. ISRN Math. Phys. 2012, 2012, 236783. [Google Scholar] [CrossRef] [Green Version]
- Nahm, W. A simple formalism for the BPS monopole. Phys. Lett. B 1980, 90, 413. [Google Scholar] [CrossRef] [Green Version]
- Nahm, W. All self-dual multimonopoles for arbitrary gauge groups. In CERN Preprint TH-3172; CERN: Geneva, Switzerland, 1981. [Google Scholar]
- Nahm, W. The Construction of all Self-dual Multimonopoles by the ADHM Method. In Monopoles in Quantum Field Theory; Craigie, N., Ed.; World Scientific: Singapore, 1982; p. 87. [Google Scholar]
- Nahm, W. Self-dual monopoles and calorons. In Group Theoretical Methods in Physics; Springer: Berlin/Heidelberg, Germany, 1983; p. 189. [Google Scholar]
- Kraan, T.C.; Van Baal, P. Exact, T-duality, between calorons, Taub-NUTspaces. Phys. Lett. B 1998, 428, 268. [Google Scholar] [CrossRef] [Green Version]
- Kraan, T.C.; Van Baal, P. Periodic instantons with non-trivial holonomy. Nucl. Phys. B 1998, 533, 627. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.; Lu, C. SU(2) calorons and magnetic monopoles. Phys. Rev. D 1998, 58, 025011. [Google Scholar] [CrossRef] [Green Version]
- ’t Hooft, G. On the phase transition towards permanent quark confinement. Nucl. Phys. B 1978, 138, 1. [Google Scholar] [CrossRef]
- Prasad, M.K.; Sommerfield, C.M. Exact Classical Solution for the ’t Hooft Monopole and the Julia-Zee Dyon. Phys. Rev. Lett. 1975, 35, 760. [Google Scholar] [CrossRef]
- Herbst, U.; Hofmann, R. Emergent Inert Adjoint Scalar Field in SU(2) Yang-Mills Thermodynamics due to Coarse-Grained Topological Fluctuations. ISRN High Energy Phys. 2012, 2012, 373121. [Google Scholar] [CrossRef] [Green Version]
- Hartl, G.V.; Hu, M.; Sader, J.E. Softening of the symmetry breaking mode in gold particles by laser-induced heating. J. Phys. Chem. B 2003, 107, 7472. [Google Scholar] [CrossRef]
- Lamb, H. On the vibrations of an elastic sphere. Proc. Lond. Math. Soc. 1882, 13, 189. [Google Scholar] [CrossRef] [Green Version]
- Giacosa, F.; Hofmann, R. Bursts of low-energy electron-positron pairs in TeV-range collider physics. Mod. Phys. Lett. A 2009, 24, 1937. [Google Scholar] [CrossRef] [Green Version]
- Faber, M. A Geometric Model in 3+1D Space-Time for Electrodynamical Phenomena. Universe 2022, 8, 73. [Google Scholar] [CrossRef]
- Grandou, T.; Hofmann, R. Thermal ground state and nonthermal probes. Adv. Math. Phys. 2015, 2015, 197197. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).