Pulsar Glitches: A Review
Abstract
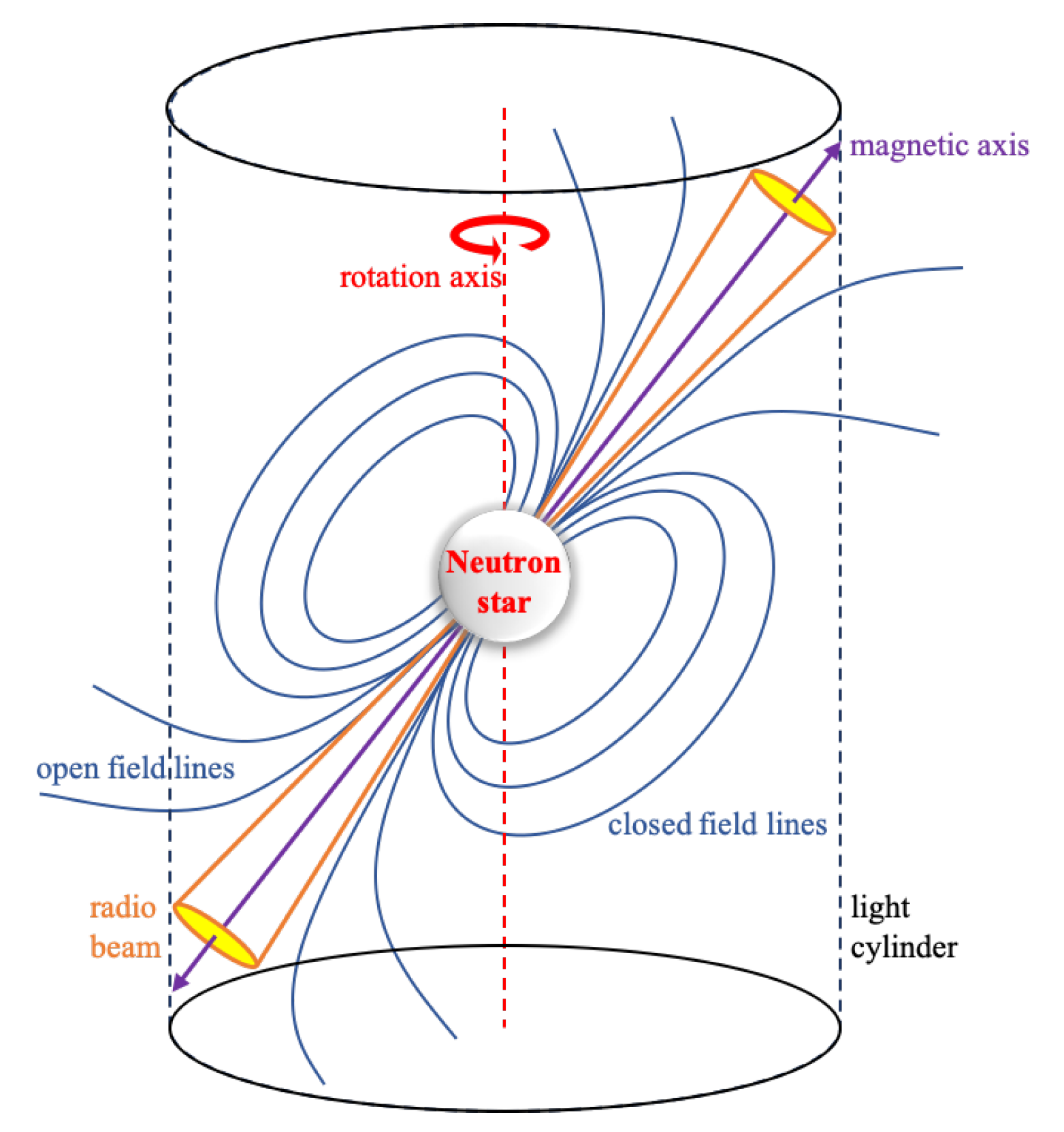
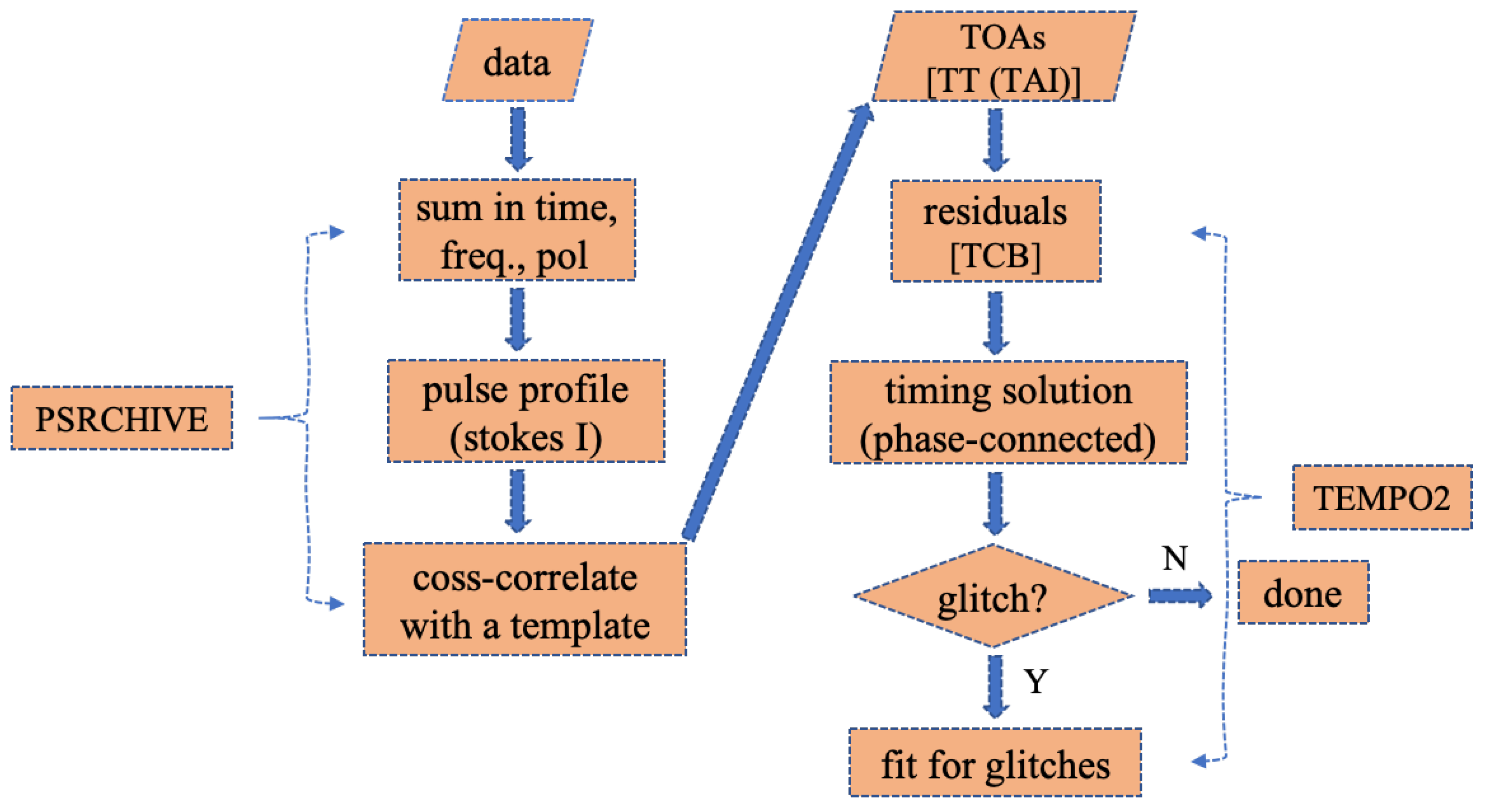
1. Searching for Pulsar Glitches
2. Properties of Pulsar Glitches
- Given the limited resources available to observatories and the large numbers of pulsars, timing observations of some pulsars are not carried out around the glitch [75].
- Glitches are too small to be resolved due to being below the present limit of detectability [32].
- Pulsars that exhibit high levels of timing noise may have small glitches that go undetected in the data [49].
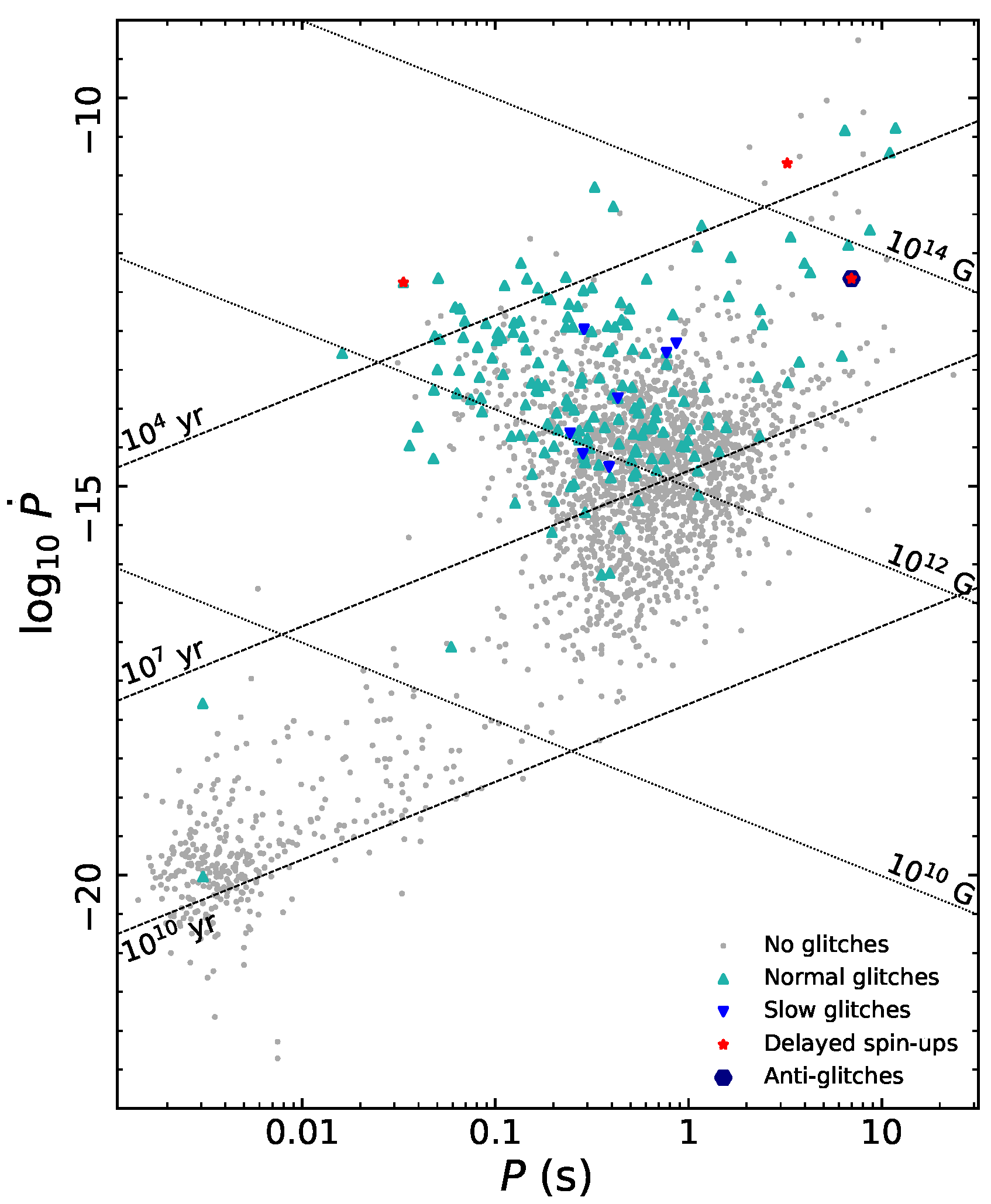
3. Classification of Glitches
3.1. Normal Glitches
3.2. Slow Glitches
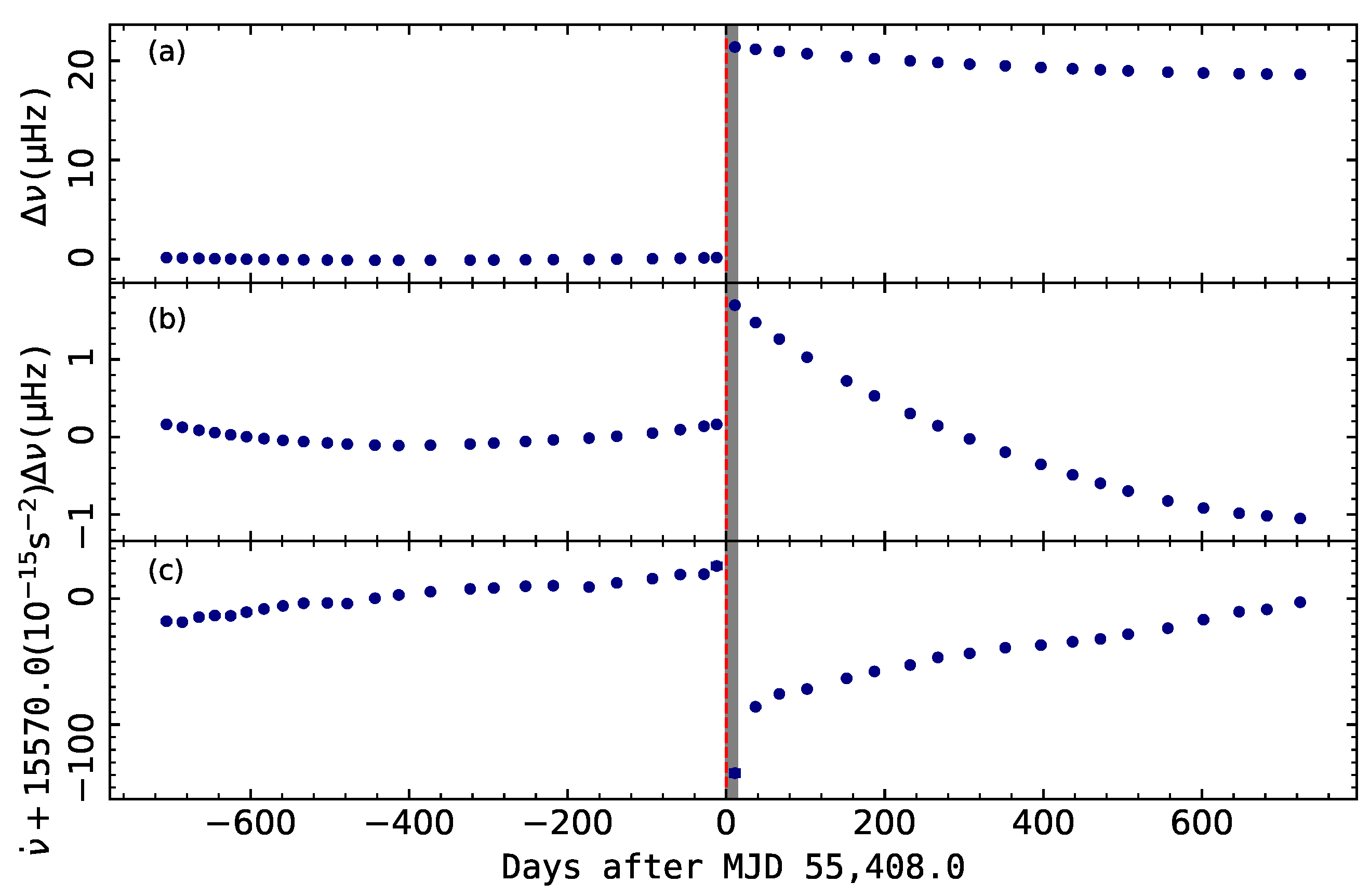
3.3. Delayed Spin-Ups
3.4. Anti-Glitches
4. Models of Pulsar Glitches
4.1. Basics of Superfluid Vortex Dynamics for Neutron Star Rotational Evolution
4.2. Vortex Creep Model
4.3. Crustquake Model
4.4. Vortex Line-Flux Tube Interaction Model
5. Radiative Changes Associated with Glitches
6. Statistics of Glitches
6.1. Glitches Sizes Distributions & Waiting Times
6.2. Glitch Activity
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hewish, A. Pulsars and High Density Physics. Science 1975, 188, 1079–1083. [Google Scholar] [CrossRef]
- Hartnett, J.G.; Luiten, A.N. Colloquium: Comparison of astrophysical and terrestrial frequency standards. Rev. Mod. Phys. 2011, 83, 1–9. [Google Scholar] [CrossRef]
- Jenet, F.; Finn, L.S.; Lazio, J.; Lommen, A.; McLaughlin, M.; Stairs, I.; Stinebring, D.; Verbiest, J.; Archibald, A.; Arzoumanian, Z.; et al. The North American Nanohertz Observatory for Gravitational Waves. arXiv 2009, arXiv:0909.1058. [Google Scholar]
- Hobbs, G.; Archibald, A.; Arzoumanian, Z.; Backer, D.; Bailes, M.; Bhat, N.D.R.; Burgay, M.; Burke-Spolaor, S.; Champion, D.; Cognard, I.; et al. The International Pulsar Timing Array project: Using pulsars as a gravitational wave detector. Class. Quantum Gravity 2010, 27, 084013. [Google Scholar] [CrossRef]
- Hobbs, G.; Guo, L.; Caballero, R.N.; Coles, W.; Lee, K.J.; Manchester, R.N.; Reardon, D.J.; Matsakis, D.; Tong, M.L.; Arzoumanian, Z.; et al. A pulsar-based time-scale from the International Pulsar Timing Array. Mon. Not. R. Astron. Soc. 2020, 491, 5951–5965. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G. Binary recycled pulsars: A powerful physical laboratory. Mem. Soc. Astron. Italiana 2010, 81, 258. [Google Scholar]
- Harding, A.K. Pulsar Emission Physics: The First Fifty Years. In Proceedings of the Pulsar Astrophysics the Next Fifty Years; Weltevrede, P., Perera, B.B.P., Preston, L.L., Sanidas, S., Eds.; Cambridge University Press: Cambridge, UK, 2018; Volume 337, pp. 52–57. [Google Scholar] [CrossRef]
- Melrose, D.B.; Rafat, M.Z.; Mastrano, A. Pulsar radio emission mechanisms: A critique. Mon. Not. R. Astron. Soc. 2021, 500, 4530–4548. [Google Scholar] [CrossRef]
- Philippov, A.; Kramer, M. Pulsar Magnetospheres and Their Radiation. Annu. Rev. Astron. Astrophys. 2022, 60, 495–558. [Google Scholar] [CrossRef]
- Gunn, J.E.; Ostriker, J.P. Magnetic Dipole Radiation from Pulsars. Nature 1969, 221, 454–456. [Google Scholar] [CrossRef]
- Narayan, R.; Ostriker, J.P. Pulsar Populations and Their Evolution. Astrophys. J. 1990, 352, 222. [Google Scholar] [CrossRef]
- Van den Heuvel, E.P.J. Pulsar magnetospheres and pulsar death. Science 2006, 312, 539–540. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Tchekhovskoy, A.; Spitkovsky, A.; Li, J.G. Time-dependent 3D magnetohydrodynamic pulsar magnetospheres: Oblique rotators. Mon. Not. R. Astron. Soc. 2013, 435, L1–L5. [Google Scholar] [CrossRef]
- Ruderman, M.A.; Sutherland, P.G. Theory of pulsars: Polar gaps, sparks, and coherent microwave radiation. Astrophys. J. 1975, 196, 51–72. [Google Scholar] [CrossRef]
- Arons, J. Pair creation above pulsar polar caps: Geometrical structure and energetics of slot gaps. Astrophys. J. 1983, 266, 215–241. [Google Scholar] [CrossRef]
- Daugherty, J.K.; Harding, A.K. Compton Scattering in Strong Magnetic Fields. Astrophys. J. 1986, 309, 362. [Google Scholar] [CrossRef]
- Sturrock, P.A. A Model of Pulsars. Astrophys. J. 1971, 164, 529. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.; Pines, D. Electrical Conductivity of Neutron Star Matter. Nature 1969, 224, 674–675. [Google Scholar] [CrossRef]
- Goldreich, P.; Reisenegger, A. Magnetic Field Decay in Isolated Neutron Stars. Astrophys. J. 1992, 395, 250. [Google Scholar] [CrossRef]
- Tauris, T.M.; Manchester, R.N. On the Evolution of Pulsar Beams. Mon. Not. R. Astron. Soc. 1998, 298, 625–636. [Google Scholar] [CrossRef]
- Tong, H. Pulsar braking: Magnetodipole vs. wind. Sci. China Phys. Mech. Astron. 2016, 59, 5752. [Google Scholar] [CrossRef][Green Version]
- Lorimer, D.; Kramer, M. Handbook of Pulsar Astronomy; Cambridge University Press: Cambridge, UK, 2005; Volume 4. [Google Scholar]
- Kramer, M.; Xilouris, K.M.; Camilo, F.; Nice, D.J.; Backer, D.C.; Lange, C.; Lorimer, D.R.; Doroshenko, O.; Sallmen, S. Profile Instabilities of the Millisecond Pulsar PSR J1022+1001. Astrophys. J. 1999, 520, 324–334. [Google Scholar] [CrossRef]
- Bansal, K.; Taylor, G.B.; Stovall, K.; Dowell, J. Detection of Echoes in PSR B1508+55 at Frequencies below 100 MHz Using the LWA1. Astrophys. J. 2020, 892, 26. [Google Scholar] [CrossRef]
- Edwards, R.T.; Hobbs, G.B.; Manchester, R.N. TEMPO2, a new pulsar timing package—II. The timing model and precision estimates. Mon. Not. R. Astron. Soc. 2006, 372, 1549–1574. [Google Scholar] [CrossRef]
- D’Alessandro, F. Rotational irregularities in pulsars—A review. Astrophys. Space Sci. 1996, 246, 73–106. [Google Scholar] [CrossRef]
- Radhakrishnan, V.; Manchester, R.N. Detection of a Change of State in the Pulsar PSR 0833-45. Nature 1969, 222, 228–229. [Google Scholar] [CrossRef]
- Reichley, P.E.; Downs, G.S. Observed Decrease in the Periods of Pulsar PSR 0833-45. Nature 1969, 222, 229–230. [Google Scholar] [CrossRef]
- Basu, A.; Shaw, B.; Antonopoulou, D.; Keith, M.J.; Lyne, A.G.; Mickaliger, M.B.; Stappers, B.W.; Weltevrede, P.; Jordan, C.A. The Jodrell bank glitch catalogue: 106 new rotational glitches in 70 pulsars. Mon. Not. R. Astron. Soc. 2022, 510, 4049–4062. [Google Scholar] [CrossRef]
- Lower, M.E.; Johnston, S.; Dunn, L.; Shannon, R.M.; Bailes, M.; Dai, S.; Kerr, M.; Manchester, R.N.; Melatos, A.; Oswald, L.S.; et al. The impact of glitches on young pulsar rotational evolution. Mon. Not. R. Astron. Soc. 2021, 508, 3251–3274. [Google Scholar] [CrossRef]
- Manchester, R.N.; Hobbs, G.B.; Teoh, A.; Hobbs, M. The Australia Telescope National Facility Pulsar Catalogue. Astron. J. 2005, 129, 1993–2006. [Google Scholar] [CrossRef]
- Espinoza, C.M.; Lyne, A.G.; Stappers, B.W.; Kramer, M. A study of 315 glitches in the rotation of 102 pulsars. Mon. Not. R. Astron. Soc. 2011, 414, 1679–1704. [Google Scholar] [CrossRef]
- Arumugam, S.; Desai, S. Classification of Pulsar Glitch Amplitudes using Extreme Deconvolution. arXiv 2022, arXiv:2206.02751. [Google Scholar]
- Hotan, A.W.; van Straten, W.; Manchester, R.N. PSRCHIVE and PSRFITS: An Open Approach to Radio Pulsar Data Storage and Analysis. Publ. Astron. Soc. Aust. 2004, 21, 302–309. [Google Scholar] [CrossRef]
- Hobbs, G.B.; Edwards, R.T.; Manchester, R.N. TEMPO2, a new pulsar-timing package—I. An overview. Mon. Not. R. Astron. Soc. 2006, 369, 655–672. [Google Scholar] [CrossRef]
- Taylor, J.H.; Fowler, L.A.; McCulloch, P.M. Measurements of general relativistic effects in the binary pulsar PSR1913 + 16. Nature 1979, 277, 437–440. [Google Scholar] [CrossRef]
- Luo, J.; Ransom, S.; Demorest, P.; Ray, P.S.; Archibald, A.; Kerr, M.; Jennings, R.J.; Bachetti, M.; van Haasteren, R.; Champagne, C.A.; et al. PINT: A Modern Software Package for Pulsar Timing. Astrophys. J. 2021, 911, 45. [Google Scholar] [CrossRef]
- Freire, P.C.C.; Ridolfi, A. An algorithm for determining the rotation count of pulsars. Mon. Not. R. Astron. Soc. 2018, 476, 4794–4805. [Google Scholar] [CrossRef]
- Phillips, C.; Ransom, S. Algorithmic Pulsar Timing. Astron. J. 2022, 163, 84. [Google Scholar] [CrossRef]
- Melatos, A.; Dunn, L.M.; Suvorova, S.; Moran, W.; Evans, R.J. Pulsar Glitch Detection with a Hidden Markov Model. Astrophys. J. 2020, 896, 78. [Google Scholar] [CrossRef]
- Dunn, L.; Melatos, A.; Suvorova, S.; Moran, W.; Evans, R.J.; Osłowski, S.; Lower, M.E.; Bailes, M.; Flynn, C.; Gupta, V. Systematic upper limits on the size of missing pulsar glitches in the first UTMOST open data release. Mon. Not. R. Astron. Soc. 2022, 512, 1469–1482. [Google Scholar] [CrossRef]
- Singha, J.; Basu, A.; Krishnakumar, M.A.; Joshi, B.C.; Arumugam, P. A real-time automated glitch detection pipeline at Ooty Radio Telescope. Mon. Not. R. Astron. Soc. 2021, 505, 5488–5496. [Google Scholar] [CrossRef]
- Zou, W.Z.; Wang, N.; Wang, H.X.; Manchester, R.N.; Wu, X.J.; Zhang, J. Unusual glitch behaviours of two young pulsars. Mon. Not. R. Astron. Soc. 2004, 354, 811–814. [Google Scholar] [CrossRef][Green Version]
- Kou, F.F.; Yuan, J.P.; Wang, N.; Yan, W.M.; Dang, S.J. The spin-down state change and mode change associated with glitch activity of PSR B2035+36. Mon. Not. R. Astron. Soc. 2018, 478, L24–L28. [Google Scholar] [CrossRef]
- Ge, M.Y.; Zhang, S.N.; Lu, F.J.; Li, T.P.; Yuan, J.P.; Zheng, X.P.; Huang, Y.; Zheng, S.J.; Chen, Y.P.; Chang, Z.; et al. Discovery of Delayed Spin-up Behavior Following Two Large Glitches in the Crab Pulsar, and the Statistics of Such Processes. Astrophys. J. 2020, 896, 55. [Google Scholar] [CrossRef]
- Zhang, X.; Shuai, P.; Huang, L.; Chen, S.; Du, Y. X-ray Observation of the 2017 November Glitch in the Crab Pulsar. Astrophys. J. 2018, 866, 82. [Google Scholar] [CrossRef]
- Cong, Z.; Qian, X.; Na, W.; Binbin, X. The Prime Focus Receiver Positioner Design of the Xinjiang QiTai 110 m Radio Telescope. Astron. Res. Technol. 2017, 14, 172–178. [Google Scholar]
- Qian, L.; Yao, R.; Sun, J.; Xu, J.; Pan, Z.; Jiang, P. FAST: Its Scientific Achievements and Prospects. Innovation 2020, 1, 100053. [Google Scholar] [CrossRef]
- Yuan, J.P.; Wang, N.; Manchester, R.N.; Liu, Z.Y. 29 glitches detected at Urumqi Observatory. Mon. Not. R. Astron. Soc. 2010, 404, 289–304. [Google Scholar] [CrossRef]
- Dang, S.J.; Yuan, J.P.; Manchester, R.N.; Li, L.; Wang, N.; Wang, J.B.; Hobbs, G.; Liu, Z.Y.; Kou, F.F. Results of 12 yr of Pulsar Timing at Nanshan. I. Astrophys. J. 2020, 896, 140. [Google Scholar] [CrossRef]
- Yuan, J.P.; Manchester, R.N.; Wang, N.; Zhou, X.; Liu, Z.Y.; Gao, Z.F. A Very Large Glitch in PSR B2334+61. Astrophys. J. Lett. 2010, 719, L111–L115. [Google Scholar] [CrossRef]
- Liu, Y.L.; Yuan, J.P.; Wang, J.B.; Liu, X.W.; Wang, N.; Yuen, R. Timing irregularities of PSR J1705-1906. Astrophys. Space Sci. 2018, 363, 96. [Google Scholar] [CrossRef]
- Zhou, S.Q.; Gügercinoğlu, E.; Yuan, J.P.; Ge, M.Y.; Yu, C.; Zhang, C.M.; Zhang, J.; Feng, Z.W.; Ye, C.Q. New pulse profile variability associated with the glitch of PSR J0738-4042. arXiv 2022, arXiv:2205.08296. [Google Scholar] [CrossRef]
- Yuan, J.P.; Wang, N.; Liu, Z.Y.; Wang, J.B. Pulsar timing with the DFB at Nanshan. In Proceedings of the Neutron Stars and Pulsars: Challenges and Opportunities after 80 Years; van Leeuwen, J., Ed.; Cambridge University Press: Cambridge, UK, 2013; Volume 291, pp. 574–576. [Google Scholar] [CrossRef]
- Wang, N.; Yuan, J.P.; Liu, Z.Y.; Wang, J.B.; Zhu, C. Recent Progress on Pulsar Observations at Nanshan. In Proceedings of the International Journal of Modern Physics Conference Series, Athens, Greece, 9–15 June 2013; Volume 23, pp. 152–156. [Google Scholar] [CrossRef]
- Zou, W.Z.; Wang, N.; Manchester, R.N.; Urama, J.O.; Hobbs, G.; Liu, Z.Y.; Yuan, J.P. Observations of six glitches in PSR B1737-30. Mon. Not. R. Astron. Soc. 2008, 384, 1063–1068. [Google Scholar] [CrossRef]
- Yuan, J.P.; Manchester, R.N.; Wang, N.; Wang, J.B.; Zhou, X.; Yan, W.M.; Liu, Z.Y. Pulse profiles and timing of PSR J1757-2421. Mon. Not. R. Astron. Soc. 2017, 466, 1234–1241. [Google Scholar] [CrossRef]
- Wang, N.; Wu, X.J.; Manchester, R.N.; Zhang, J.; Lyne, A.G.; Yusup, A. A Large Glitch in the Crab Pulsar. Chin. J. Astron. Astrophys. 2001, 1, 195–199. [Google Scholar] [CrossRef]
- Yuan, J.; Li, L.; Liu, Z.; Wang, J.; Wang, N. Timing Observations of 20 Pulsars. In Proceedings of the Frontiers in Radio Astronomy and FAST Early Sciences Symposium, Guiyang, China, 29–31 July 2015; Volume 502, p. 13. [Google Scholar]
- Wang, J.; Wang, N.; Tong, H.; Yuan, J. Recent glitches detected in the Crab pulsar. Astrophys. Space Sci. 2012, 340, 307–315. [Google Scholar] [CrossRef][Green Version]
- Liu, J.; Yan, Z.; Yuan, J.P.; Zhao, R.S.; Huang, Z.P.; Wu, X.J.; Wang, N.; Shen, Z.Q. One large glitch in PSR B1737-30 detected with the TMRT. Res. Astron. Astrophys. 2019, 19, 073. [Google Scholar] [CrossRef]
- Liu, J.; Wang, H.G.; Yan, Z.; Shen, Z.Q.; Tong, H.; Huang, Z.P.; Zhao, R.S. Pulse Profile Variations Associated with the Glitch of PSR B2021+51. Astrophys. J. 2021, 912, 58. [Google Scholar] [CrossRef]
- Liu, J.; Wang, H.G.; Shen, Z.Q.; Yan, Z.; Tong, H.; Huang, Z.P.; Zhao, R.S. Pulse Profile Variations Associated with Two Glitches of PSR B1822-09. Astrophys. J. 2022, 931, 103. [Google Scholar] [CrossRef]
- Liu, J.; Yan, Z.; Shen, Z.Q.; Huang, Z.P.; Zhao, R.S.; Wu, Y.J.; Yuan, J.P.; Wu, X.J. New timing measurement results of 16 pulsars. Publ. Astron. Soc. Jpn. 2020, 72, 70. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Ge, M.Y.; Lu, F.J.; Tuo, Y.L.; Song, L.M.; Zhang, S.N.; Wang, L.J.; Zheng, S.J.; Yan, L.L. Invariable X-ray Profile and Flux of the Crab Pulsar during Its Two Glitches. Astrophys. J. 2022, 932, 11. [Google Scholar] [CrossRef]
- Xu, Y.H.; Yuan, J.P.; Lee, K.J.; Hao, L.F.; Wang, N.; Wang, M.; Yu, M.; Li, Z.X.; Yue, Y.L.; Liu, Z.Y.; et al. The 2016 glitch in the Vela pulsar. Astrophys. Space Sci. 2019, 364, 11. [Google Scholar] [CrossRef]
- Luo, J.T.; Gao, Y.P.; Yang, T.G.; Zhao, C.S.; Tong, M.L.; Rao, Y.N.; Li, Y.F.; Li, B.; Zhu, X.Z.; Qiao, H.H.; et al. Pulsar timing observations with Haoping Radio Telescope. Res. Astron. Astrophys. 2020, 20, 111. [Google Scholar] [CrossRef]
- Han, J.L.; Wang, C.; Wang, P.F.; Wang, T.; Zhou, D.J.; Sun, J.H.; Yan, Y.; Su, W.Q.; Jing, W.C.; Chen, X.; et al. Project design and pulsar discoveries. Res. Astron. Astrophys. 2021, 21, 107. [Google Scholar] [CrossRef]
- Yu, M.; Manchester, R.N.; Hobbs, G.; Johnston, S.; Kaspi, V.M.; Keith, M.; Lyne, A.G.; Qiao, G.J.; Ravi, V.; Sarkissian, J.M.; et al. Detection of 107 glitches in 36 southern pulsars. Mon. Not. R. Astron. Soc. 2013, 429, 688–724. [Google Scholar] [CrossRef]
- Janssen, G.H.; Stappers, B.W. 30 glitches in slow pulsars. Astron. Astrophys. 2006, 457, 611–618. [Google Scholar] [CrossRef]
- Millhouse, M.; Melatos, A.; Howitt, G.; Carlin, J.B.; Dunn, L.; Ashton, G. An updated glitch rate law inferred from radio pulsars. Mon. Not. R. Astron. Soc. 2022, 511, 3304–3319. [Google Scholar] [CrossRef]
- McKee, J.W.; Janssen, G.H.; Stappers, B.W.; Lyne, A.G.; Caballero, R.N.; Lentati, L.; Desvignes, G.; Jessner, A.; Jordan, C.A.; Karuppusamy, R.; et al. A glitch in the millisecond pulsar J0613-0200. Mon. Not. R. Astron. Soc. 2016, 461, 2809–2817. [Google Scholar] [CrossRef]
- Yu, M.; Liu, Q.J. On the detection probability of neutron star glitches. Mon. Not. R. Astron. Soc. 2017, 468, 3031–3041. [Google Scholar] [CrossRef]
- Jankowski, F.; Bailes, M.; van Straten, W.; Keane, E.F.; Flynn, C.; Barr, E.D.; Bateman, T.; Bhandari, S.; Caleb, M.; Campbell-Wilson, D.; et al. The UTMOST pulsar timing programme I: Overview and first results. Mon. Not. R. Astron. Soc. 2019, 484, 3691–3712. [Google Scholar] [CrossRef]
- Shaw, B.; Keith, M.J.; Lyne, A.G.; Mickaliger, M.B.; Stappers, B.W.; Turner, J.D.; Weltevrede, P. The slow rise and recovery of the 2019 Crab pulsar glitch. Mon. Not. R. Astron. Soc. 2021, 505, L6–L10. [Google Scholar] [CrossRef]
- Shaw, B.; Stappers, B.W.; Weltevrede, P. Resolving discrete pulsar spin-down states with current and future instrumentation. Mon. Not. R. Astron. Soc. 2018, 475, 5443–5459. [Google Scholar] [CrossRef]
- Wong, T.; Backer, D.C.; Lyne, A.G. Observations of a Series of Six Recent Glitches in the Crab Pulsar. Astrophys. J. 2001, 548, 447–459. [Google Scholar] [CrossRef][Green Version]
- Espinoza, C.M.; Antonopoulou, D.; Stappers, B.W.; Watts, A.; Lyne, A.G. Neutron star glitches have a substantial minimum size. Mon. Not. R. Astron. Soc. 2014, 440, 2755–2762. [Google Scholar] [CrossRef]
- Hobbs, G.; Lyne, A.G.; Joshi, B.C.; Kramer, M.; Stairs, I.H.; Camilo, F.; Manchester, R.N.; D’Amico, N.; Possenti, A.; Kaspi, V.M. A very large glitch in PSR J1806-2125. Mon. Not. R. Astron. Soc. 2002, 333, L7–L10. [Google Scholar] [CrossRef][Green Version]
- Younes, G.; Ray, P.S.; Baring, M.G.; Kouveliotou, C.; Fletcher, C.; Wadiasingh, Z.; Harding, A.K.; Goldstein, A. A Radiatively Quiet Glitch and Anti-glitch in the Magnetar 1E 2259+586. Astrophys. J. Lett. 2020, 896, L42. [Google Scholar] [CrossRef]
- Cognard, I.; Backer, D.C. A Microglitch in the Millisecond Pulsar PSR B1821-24 in M28. Astrophys. J. Lett. 2004, 612, L125–L127. [Google Scholar] [CrossRef]
- Antonopoulou, D.; Espinoza, C.M.; Kuiper, L.; Andersson, N. Pulsar spin-down: The glitch-dominated rotation of PSR J0537-6910. Mon. Not. R. Astron. Soc. 2018, 473, 1644–1655. [Google Scholar] [CrossRef]
- Ferdman, R.D.; Archibald, R.F.; Gourgouliatos, K.N.; Kaspi, V.M. The Glitches and Rotational History of the Highly Energetic Young Pulsar PSR J0537-6910. Astrophys. J. 2018, 852, 123. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Espinoza, C.M.; Arzoumanian, Z.; Enoto, T.; Tamba, T.; Antonopoulou, D.; Bejger, M.; Guillot, S.; Haskell, B.; Ray, P.S. Return of the Big Glitcher: NICER timing and glitches of PSR J0537-6910. Mon. Not. R. Astron. Soc. 2020, 498, 4605–4614. [Google Scholar] [CrossRef]
- Dodson, R.; Lewis, D.; McCulloch, P. Two decades of pulsar timing of Vela. Astrophys. Space Sci. 2007, 308, 585–589. [Google Scholar] [CrossRef]
- Lyne, A.G.; Pritchard, R.S.; Graham Smith, F. 23 years of Crab pulsar rotational history. Mon. Not. R. Astron. Soc. 1993, 265, 1003–1012. [Google Scholar] [CrossRef]
- Dib, R.; Kaspi, V.M. 16 year of RXTE Monitoring of Five Anomalous X-ray Pulsars. Astrophys. J. 2014, 784, 37. [Google Scholar] [CrossRef]
- Olausen, S.A.; Kaspi, V.M. The McGill Magnetar Catalog. Astrophys. J. Suppl. Ser. 2014, 212, 6. [Google Scholar] [CrossRef]
- Jawor, J.A.; Tauris, T.M. Modelling spin evolution of magnetars. Mon. Not. R. Astron. Soc. 2022, 509, 634–657. [Google Scholar] [CrossRef]
- Chukwude, A.E.; Urama, J.O. Observations of microglitches in Hartebeesthoek Radio Astronomy Observatory radio pulsars. Mon. Not. R. Astron. Soc. 2010, 406, 1907–1917. [Google Scholar] [CrossRef]
- Serim, M.M.; Şahiner, Ş.; Ćerri-Serim, D.; Inam, S.Ć.; Baykal, A. Discovery of a glitch in the accretion-powered pulsar SXP 1062. Mon. Not. R. Astron. Soc. 2017, 471, 4982–4989. [Google Scholar] [CrossRef]
- Palfreyman, J.; Dickey, J.M.; Hotan, A.; Ellingsen, S.; van Straten, W. Alteration of the magnetosphere of the Vela pulsar during a glitch. Nature 2018, 556, 219–222. [Google Scholar] [CrossRef]
- Dodson, R.G.; McCulloch, P.M.; Lewis, D.R. High Time Resolution Observations of the January 2000 Glitch in the Vela Pulsar. Astrophys. J. Lett. 2002, 564, L85–L88. [Google Scholar] [CrossRef]
- Howitt, G.; Haskell, B.; Melatos, A. Hydrodynamic simulations of pulsar glitch recovery. Mon. Not. R. Astron. Soc. 2016, 460, 1201–1213. [Google Scholar] [CrossRef]
- Urama, J.O. Glitch monitoring in PSRs B1046-58 and B1737-30. Mon. Not. R. Astron. Soc. 2002, 330, 58–62. [Google Scholar] [CrossRef][Green Version]
- Zubieta, E.; Missel, R.; Sosa Fiscella, V.; Lousto, C.O.; del Palacio, S.; López Armengol, F.G.; García, F.; Combi, J.A.; Wang, L.; Combi, L.; et al. First results of the glitching pulsars monitoring program at the Argentine Institute of Radioastronomy. arXiv 2022, arXiv:2210.03770. [Google Scholar]
- Flanagan, C.S. Rapid recovery of the Vela pulsar from a giant glitch. Nature 1990, 345, 416–417. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.; Pines, D.; Ruderman, M. Spin Up in Neutron Stars: The Future of the Vela Pulsar. Nature 1969, 224, 872–874. [Google Scholar] [CrossRef]
- Buchner, S.; Flanagan, C. The Vela Double Glitch. In Proceedings of the Radio Pulsars: An Astrophysical Key to Unlock the Secrets of the Universe, American Institute of Physics Conference Series. Sardinia, Italy, 10 October 2010; Burgay, M., D’Amico, N., Esposito, P., Pellizzoni, A., Possenti, A., Eds.; 2011; Volume 1357, pp. 113–116. [Google Scholar] [CrossRef]
- Anderson, P.W.; Itoh, N. Pulsar glitches and restlessness as a hard superfluidity phenomenon. Nature 1975, 256, 25–27. [Google Scholar] [CrossRef]
- Gügercinoğlu, E.; Ge, M.Y.; Yuan, J.P.; Zhou, S.Q. Glitches in four gamma-ray pulsars and inferences on the neutron star structure. Mon. Not. R. Astron. Soc. 2022, 511, 425–439. [Google Scholar] [CrossRef]
- Zhou, S.Q.; Zhou, A.A.; Zhang, J.; Liu, M.Q.; Liu, H.Y.; Zhang, L.; Feng, Z.W.; Zhu, X.D.; Wu, D. A very large slow glitch in PSR J1602-5100. Astrophys. Space Sci. 2019, 364, 173. [Google Scholar] [CrossRef]
- Singha, J.; Joshi, B.C.; Bandyopadhyay, D.; Grover, H.; Desai, S.; Arumugam, P.; Banik, S. Pulsar timing irregularities and the Neutron Star interior in the era of SKA: An Indian Outlook. J. Astrophys. Astron. 2022, 43, 81. [Google Scholar] [CrossRef]
- Shabanova, T.V. An unusual glitch signature in the pulsar PSR B1822-09. Astron. Astrophys. 1998, 337, 723–728. [Google Scholar]
- Shabanova, T.V. Two classes of glitches in the pulsar B1822-09. Astron. Rep. 2009, 53, 465–471. [Google Scholar] [CrossRef]
- Alpar, M.A.; Cheng, K.S.; Pines, D. Vortex Creep and the Internal Temperature of Neutron Stars: Linear and Nonlinear Response to a Glitch. Astrophys. J. 1989, 346, 823. [Google Scholar] [CrossRef]
- Eya, I.O.; Urama, J.O.; Chukwude, A.E. Angular Momentum Transfer and Fractional Moment of Inertia in Pulsar Glitches. Astrophys. J. 2017, 840, 56. [Google Scholar] [CrossRef]
- Link, B.; Epstein, R.I. Thermally Driven Neutron Star Glitches. Astrophys. J. 1996, 457, 844. [Google Scholar] [CrossRef][Green Version]
- Hobbs, G.; Lyne, A.G.; Kramer, M.; Martin, C.E.; Jordan, C. Long-term timing observations of 374 pulsars. Mon. Not. R. Astron. Soc. 2004, 353, 1311–1344. [Google Scholar] [CrossRef]
- Boynton, P.E.; Groth, E.J.; Hutchinson, D.P.; Nanos, G.P.J.; Partridge, R.B.; Wilkinson, D.T. Optical Timing of the Crab Pulsar, NP 0532. Astrophys. J. 1972, 175, 217. [Google Scholar] [CrossRef]
- Lyne, A.G.; Smith, F.G.; Pritchard, R.S. Spin-up and recovery in the 1989 glitch of the Crab pulsar. Nature 1992, 359, 706–707. [Google Scholar] [CrossRef]
- Shaw, B.; Lyne, A.G.; Stappers, B.W.; Weltevrede, P.; Bassa, C.G.; Lien, A.Y.; Mickaliger, M.B.; Breton, R.P.; Jordan, C.A.; Keith, M.J.; et al. The largest glitch observed in the Crab pulsar. Mon. Not. R. Astron. Soc. 2018, 478, 3832–3840. [Google Scholar] [CrossRef]
- Woods, P.M.; Kaspi, V.M.; Thompson, C.; Gavriil, F.P.; Marshall, H.L.; Chakrabarty, D.; Flanagan, K.; Heyl, J.; Hernquist, L. Changes in the X-ray Emission from the Magnetar Candidate 1E 2259+586 during Its 2002 Outburst. Astrophys. J. 2004, 605, 378–399. [Google Scholar] [CrossRef]
- Ge, M.; Yang, Y.P.; Lu, F.; Zhou, S.; Ji, L.; Zhang, S.; Zhang, B.; Zhang, L.; Wang, P.; Lee, K.; et al. A giant glitch from the magnetar SGR J1935+2154 before FRB 200428. arXiv 2022, arXiv:2211.03246. [Google Scholar]
- Manchester, R.N. Pulsar glitches and their impact on neutron-star astrophysics. arXiv 2018, arXiv:1801.04332. [Google Scholar]
- Younes, G.; Baring, M.G.; Harding, A.K.; Enoto, T.; Wadiasingh, Z.; Pearlman, A.B.; Ho, W.C.G.; Guillot, S.; Arzoumanian, Z.; Borghese, A.; et al. Magnetar spin-down glitch clearing the way for FRB-like bursts and a pulsed radio episode. arXiv 2022, arXiv:2210.11518. [Google Scholar]
- Gügercinoǧlu, E.; Alpar, M.A. The largest Crab glitch and the vortex creep model. Mon. Not. R. Astron. Soc. 2019, 488, 2275–2282. [Google Scholar] [CrossRef]
- Archibald, R.F.; Kaspi, V.M.; Ng, C.Y.; Gourgouliatos, K.N.; Tsang, D.; Scholz, P.; Beardmore, A.P.; Gehrels, N.; Kennea, J.A. An anti-glitch in a magnetar. Nature 2013, 497, 591–593. [Google Scholar] [CrossRef]
- Ray, P.S.; Guillot, S.; Ho, W.C.G.; Kerr, M.; Enoto, T.; Gendreau, K.C.; Arzoumanian, Z.; Altamirano, D.; Bogdanov, S.; Campion, R.; et al. Anti-glitches in the Ultraluminous Accreting Pulsar NGC 300 ULX-1 Observed with NICER. Astrophys. J. 2019, 879, 130. [Google Scholar] [CrossRef]
- Ducci, L.; Pizzochero, P.M.; Doroshenko, V.; Santangelo, A.; Mereghetti, S.; Ferrigno, C. Properties and observability of glitches and anti-glitches in accreting pulsars. Astron. Astrophys. 2015, 578, A52. [Google Scholar] [CrossRef]
- Şaşmaz Muş, S.; Aydın, B.; Göğüş, E. A glitch and an anti-glitch in the anomalous X-ray pulsar 1E 1841-045. Mon. Not. R. Astron. Soc. 2014, 440, 2916–2921. [Google Scholar] [CrossRef]
- Içdem, B.; Baykal, A.; Inam, S.Ç. RXTE timing analysis of the anomalous X-ray pulsar 1E 2259+586. Mon. Not. R. Astron. Soc. 2012, 419, 3109–3114. [Google Scholar] [CrossRef]
- Pintore, F.; Bernardini, F.; Mereghetti, S.; Esposito, P.; Turolla, R.; Rea, N.; Coti Zelati, F.; Israel, G.L.; Tiengo, A.; Zane, S. The variable spin-down rate of the transient magnetar XTE J1810-197. Mon. Not. R. Astron. Soc. 2016, 458, 2088–2093. [Google Scholar] [CrossRef]
- Vurgun, E.; Chakraborty, M.; Güver, T.; Göğüş, E. Variable absorption line in XTE J1810-197. New Astron. 2019, 67, 45–52. [Google Scholar] [CrossRef]
- An, H.; Archibald, R. X-ray Timing Studies of the Low-field Magnetar CXOU J164710.2-455216. Astrophys. J. Lett. 2019, 877, L10. [Google Scholar] [CrossRef]
- Tong, H. The Anti-glitch of Magnetar 1E 2259+586 in the Wind Braking Scenario. Astrophys. J. 2014, 784, 86. [Google Scholar] [CrossRef]
- Huang, Y.F.; Geng, J.J. Anti-glitch Induced by Collision of a Solid Body with the Magnetar 1E 2259+586. Astrophys. J. Lett. 2014, 782, L20. [Google Scholar] [CrossRef]
- Garcia, F.; Ranea-Sandoval, I.F. A simple mechanism for the anti-glitch observed in AXP 1E 2259+586. Mon. Not. R. Astron. Soc. 2015, 449, L73–L76. [Google Scholar] [CrossRef]
- Howitt, G.; Melatos, A. Antiglitches in accreting pulsars from superfluid vortex avalanches. Mon. Not. R. Astron. Soc. 2022, 514, 863–874. [Google Scholar] [CrossRef]
- Hu, Y.M.; Pitkin, M.; Heng, I.S.; Hendry, M.A. Glitch or Anti-glitch: A Bayesian View. Astrophys. J. Lett. 2014, 784, L41. [Google Scholar] [CrossRef][Green Version]
- Pines, D.; Shaham, J.; Ruderman, M.A. Neutron Star Structure from Pulsar Observations. In Proceedings of the Physics of Dense Matter; Hansen, C.J., Ed.; Springer: Dordrecht, The Netherlands, 1974; Volume 53, p. 189. [Google Scholar]
- Bisnovatyi-Kogan, G.S. A pulsar as a neutron star and weak interaction. Radiophys. Quantum Electron. 1970, 13, 1441–1444. [Google Scholar] [CrossRef]
- Warszawski, L.; Melatos, A. A cellular automaton model of pulsar glitches. Mon. Not. R. Astron. Soc. 2008, 390, 175–191. [Google Scholar] [CrossRef]
- Warszawski, L.; Melatos, A. Gross-Pitaevskii model of pulsar glitches. Mon. Not. R. Astron. Soc. 2011, 415, 1611–1630. [Google Scholar] [CrossRef]
- Warszawski, L.; Melatos, A.; Berloff, N.G. Unpinning triggers for superfluid vortex avalanches. Phys. Rev. B 2012, 85, 104503. [Google Scholar] [CrossRef]
- Warszawski, L.; Melatos, A. Knock-on processes in superfluid vortex avalanches and pulsar glitch statistics. Mon. Not. R. Astron. Soc. 2013, 428, 1911–1926. [Google Scholar] [CrossRef]
- Khomenko, V.; Haskell, B. Modelling Pulsar Glitches: The Hydrodynamics of Superfluid Vortex Avalanches in Neutron Stars. Publ. Astron. Soc. Aust. 2018, 35, e020. [Google Scholar] [CrossRef]
- Lönnborn, J.R.; Melatos, A.; Haskell, B. Collective, glitch-like vortex motion in a neutron star with an annular pinning barrier. Mon. Not. R. Astron. Soc. 2019, 487, 702–710. [Google Scholar] [CrossRef]
- Howitt, G.; Melatos, A.; Haskell, B. Simulating pulsar glitches: An N-body solver for superfluid vortex motion in two dimensions. Mon. Not. R. Astron. Soc. 2020, 498, 320–331. [Google Scholar] [CrossRef]
- Tsakadze, J.S.; Tsakadze, S.J. Relaxation phenomena at accelaration of rotation of a spherical vessel with helium II and relaxation in pulsars. Phys. Lett. A 1972, 41, 197–199. [Google Scholar] [CrossRef]
- Tsakadze, D.S.; Tsakadze, S.D. “Spontaneous” acceleration of freely rotating helium II and related phenomena in pulsars. Sov. J. Exp. Theor. Phys. Lett. 1975, 22, 139. [Google Scholar]
- Tsakadze, D.S.; Tsakadze, S.D. Simulation of fulsar behavior in a low-temperature laboratory: A Review. Astrophysics 1979, 15, 353–361. [Google Scholar] [CrossRef]
- Tsakadze, J.S.; Tsakadze, S.J. Properties of slowly rotating helium II and the superfluidity of pulsars. J. Low Temp. Phys. 1980, 39, 649–688. [Google Scholar] [CrossRef]
- Larson, M.B.; Link, B. Simulations of glitches in isolated pulsars. Mon. Not. R. Astron. Soc. 2002, 333, 613–622. [Google Scholar] [CrossRef]
- Sidery, T.; Passamonti, A.; Andersson, N. The dynamics of pulsar glitches: Contrasting phenomenology with numerical evolutions. Mon. Not. R. Astron. Soc. 2010, 405, 1061–1074. [Google Scholar] [CrossRef]
- Van Eysden, C.A.; Melatos, A. Spin Down of Superfluid-Filled Vessels: Theory Versus Experiment. J. Low Temp. Phys. 2011, 165, 1–14. [Google Scholar] [CrossRef]
- Van Eysden, C.A.; Melatos, A. Interpreting Superfluid Spin Up Through the Response of the Container. J. Low Temp. Phys. 2012, 166, 151–170. [Google Scholar] [CrossRef][Green Version]
- Xie, Y.; Zhang, S.N. On the Relaxation Behaviors of Slow and Classical Glitches: Observational Biases and Their Opposite Recovery Trends. Astrophys. J. 2013, 778, 31. [Google Scholar] [CrossRef][Green Version]
- Van Eysden, C.A.; Melatos, A. Spin-up of a two-component superfluid: Analytic theory in arbitrary geometry. J. Fluid Mech. 2013, 729, 180–213. [Google Scholar] [CrossRef]
- Van Eysden, C.A.; Melatos, A. Spin-up of a two-component superfluid: Self-consistent container feedback. J. Fluid Mech. 2014, 744, 89–110. [Google Scholar] [CrossRef]
- Graber, V.; Andersson, N.; Hogg, M. Neutron stars in the laboratory. Int. J. Mod. Phys. D 2017, 26, 1730015. [Google Scholar] [CrossRef]
- Alpar, M.A.; Anderson, P.W.; Pines, D.; Shaham, J. Vortex creep and the internal temperature of neutron stars. I—General theory. Astrophys. J. 1984, 276, 325–334. [Google Scholar] [CrossRef]
- Jones, P.B. Rotation of the neutron-dip superfluid in pulsars: Evidence for corotating vortices. Mon. Not. R. Astron. Soc. 1993, 263, 619–627. [Google Scholar] [CrossRef]
- Sedrakian, A.D.; Sedrakian, D.M.; Cordes, J.M.; Terzian, Y. Superfluid Core Rotation in Pulsars. II. Postjump Relaxations. Astrophys. J. 1995, 447, 324. [Google Scholar] [CrossRef]
- Ruderman, M.; Zhu, T.; Chen, K. Neutron Star Magnetic Field Evolution, Crust Movement, and Glitches. Astrophys. J. 1998, 492, 267–280. [Google Scholar] [CrossRef]
- Sedrakian, A.; Cordes, J.M. Vortex-interface interactions and generation of glitches in pulsars. Mon. Not. R. Astron. Soc. 1999, 307, 365–375. [Google Scholar] [CrossRef]
- Pizzochero, P.M. Angular Momentum Transfer in Vela-like Pulsar Glitches. Astrophys. J. Lett. 2011, 743, L20. [Google Scholar] [CrossRef]
- Alpar, M.A.; Nandkumar, R.; Pines, D. Vortex creep and the internal temperature of neutron stars: Timing noise in pulsars. Astrophys. J. 1986, 311, 197–213. [Google Scholar] [CrossRef]
- Jones, P.B. The generation of timing noise by superfluid rotation in pulsars. Mon. Not. R. Astron. Soc. 1990, 246, 364. [Google Scholar]
- Haskell, B. Tkachenko modes in rotating neutron stars: The effect of compressibility and implications for pulsar timing noise. Phys. Rev. D 2011, 83, 043006. [Google Scholar] [CrossRef]
- Melatos, A.; Link, B. Pulsar timing noise from superfluid turbulence. Mon. Not. R. Astron. Soc. 2014, 437, 21–31. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C. Physics of neutron stars. Annu. Rev. Astron. Astrophys. 1979, 17, 415–443. [Google Scholar] [CrossRef]
- Shaham, J. Superfluidity in neutron stars. J. Phys. 1980, 41C2, 9–23. [Google Scholar] [CrossRef]
- Sauls, J. Superfluidity in the interiors of neutron stars. In Timing Neutron Stars; Ögelman, H., van den Heuvel, E.P.J., Eds.; NATO Advanced Study Institute (ASI) Series C; Springer: Çeşme, Turkey, 1989; Volume 262, p. 457. [Google Scholar]
- Pines, D. Pulsar Glitches: To what extent do these probe Crustal Superfluidity, Core-Crust Coupling, and the Equation of State of Dense Neutron Matter? In Proceedings of the Pulsar Timing, General Relativity and the Internal Structure of Neutron Stars, Amsterdam, The Netherlands, 1 January 1999; p. 199. [Google Scholar]
- Haskell, B.; Melatos, A. Models of pulsar glitches. Int. J. Mod. Phys. D 2015, 24, 1530008. [Google Scholar] [CrossRef]
- Haskell, B.; Sedrakian, A. Superfluidity and Superconductivity in Neutron Stars. In Astrophysics and Space Science Library; Rezzolla, L., Pizzochero, P., Jones, D.I., Rea, N., Vidaña, I., Eds.; Springer: Cham, Switzerland; Berlin/Heidelberg, Germany, 2018; Volume 457, p. 401. [Google Scholar] [CrossRef]
- Sedrakian, A.; Clark, J.W. Superfluidity in nuclear systems and neutron stars. Eur. Phys. J. A 2019, 55, 167. [Google Scholar] [CrossRef]
- Alpar, M.A.; Langer, S.A.; Sauls, J.A. Rapid postglitch spin-up of the superfluid core in pulsars. Astrophys. J. 1984, 282, 533–541. [Google Scholar] [CrossRef]
- Alpar, M.A.; Sauls, J.A. On the Dynamical Coupling between the Superfluid Interior and the Crust of a Neutron Star. Astrophys. J. 1988, 327, 723. [Google Scholar] [CrossRef]
- Sedrakian, A.D.; Sedrakian, D.M. Superfluid Core Rotation in Pulsars. I. Vortex Cluster Dynamics. Astrophys. J. 1995, 447, 305. [Google Scholar] [CrossRef]
- Sidery, T.; Alpar, M.A. The effect of quantized magnetic flux lines on the dynamics of superfluid neutron star cores. Mon. Not. R. Astron. Soc. 2009, 400, 1859–1867. [Google Scholar] [CrossRef][Green Version]
- Ashton, G.; Lasky, P.D.; Graber, V.; Palfreyman, J. Rotational evolution of the Vela pulsar during the 2016 glitch. Nat. Astron. 2019, 3, 1143–1148. [Google Scholar] [CrossRef]
- Gügercinoğlu, E.; Alpar, M.A. The 2016 Vela glitch: A key to neutron star internal structure and dynamics. Mon. Not. R. Astron. Soc. 2020, 496, 2506–2515. [Google Scholar] [CrossRef]
- Link, B.; Epstein, R.I.; Baym, G. Superfluid Vortex Creep and Rotational Dynamics of Neutron Stars. Astrophys. J. 1993, 403, 285. [Google Scholar] [CrossRef]
- Gügercinoğlu, E.; Alpar, M.A. Microscopic vortex velocity in the inner crust and outer core of neutron stars. Mon. Not. R. Astron. Soc. 2016, 462, 1453–1460. [Google Scholar] [CrossRef]
- Gügercinoǧlu, E.; Alpar, M.A. Neutron star dynamics under time-dependent external torques. Mon. Not. R. Astron. Soc. 2017, 471, 4827–4831. [Google Scholar] [CrossRef]
- Shibazaki, N.; Lamb, F.K. Neutron Star Evolution with Internal Heating. Astrophys. J. 1989, 346, 808. [Google Scholar] [CrossRef]
- Alpar, M.A. Neutron star dynamics, braking indices and energy dissipation. Adv. Space Res. 1998, 21, 159–166. [Google Scholar] [CrossRef]
- Larson, M.B.; Link, B. Superfluid Friction and Late-Time Thermal Evolution of Neutron Stars. Astrophys. J. 1999, 521, 271–280. [Google Scholar] [CrossRef]
- Alpar, M.A. Pinning and Threading of Quantized Vortices in the Pulsar Crust Superfluid. Astrophys. J. 1977, 213, 527–530. [Google Scholar] [CrossRef]
- Gügercinoğlu, E.; Alpar, M.A. Vortex Creep Against Toroidal Flux Lines, Crustal Entrainment, and Pulsar Glitches. Astrophys. J. Lett. 2014, 788, L11. [Google Scholar] [CrossRef]
- Sourie, A.; Chamel, N. Vortex pinning in the superfluid core of neutron stars and the rise of pulsar glitches. Mon. Not. R. Astron. Soc. 2020, 493, L98–L102. [Google Scholar] [CrossRef]
- Gügercinoğlu, E. Post-glitch exponential relaxation of radio pulsars and magnetars in terms of vortex creep across flux tubes. Mon. Not. R. Astron. Soc. 2017, 469, 2313–2322. [Google Scholar] [CrossRef]
- Yakovlev, D.G.; Pethick, C.J. Neutron Star Cooling. Annu. Rev. Astron. Astrophys. 2004, 42, 169–210. [Google Scholar] [CrossRef]
- Page, D.; Geppert, U.; Weber, F. The cooling of compact stars. Nucl. Phys. A 2006, 777, 497–530. [Google Scholar] [CrossRef]
- Liu, H.Y.; Zhou, S.Q.; Zhang, Y.Q.; Feng, Z.W.; Zhou, X. 30 glitches in 18 radio pulsars. Res. Astron. Astrophys. 2021, 21, 154. [Google Scholar] [CrossRef]
- Seveso, S.; Pizzochero, P.M.; Grill, F.; Haskell, B. Mesoscopic pinning forces in neutron star crusts. Mon. Not. R. Astron. Soc. 2016, 455, 3952–3967. [Google Scholar] [CrossRef]
- Gonzalez, D.; Reisenegger, A. Internal heating of old neutron stars: Contrasting different mechanisms. Astron. Astrophys. 2010, 522, A16. [Google Scholar] [CrossRef]
- Becker, W.; Kramer, M.; Jessner, A.; Taam, R.E.; Jia, J.J.; Cheng, K.S.; Mignani, R.; Pellizzoni, A.; de Luca, A.; Słowikowska, A.; et al. A Multiwavelength Study of the Pulsar PSR B1929+10 and Its X-ray Trail. Astrophys. J. 2006, 645, 1421–1435. [Google Scholar] [CrossRef][Green Version]
- Zharikov, S.V.; Shibanov, Y.A.; Mennickent, R.E.; Komarova, V.N. Possible optical detection of a fast, nearby radio pulsar PSR B1133+16. Astron. Astrophys. 2008, 479, 793–803. [Google Scholar] [CrossRef][Green Version]
- Durant, M.; Kargaltsev, O.; Pavlov, G.G.; Kowalski, P.M.; Posselt, B.; van Kerkwijk, M.H.; Kaplan, D.L. The Spectrum of the Recycled PSR J0437-4715 and Its White Dwarf Companion. Astrophys. J. 2012, 746, 6. [Google Scholar] [CrossRef]
- Rangelov, B.; Pavlov, G.G.; Kargaltsev, O.; Reisenegger, A.; Guillot, S.; van Kerkwijk, M.H.; Reyes, C. Hubble Space Telescope Detection of the Millisecond Pulsar J2124-3358 and its Far-ultraviolet Bow Shock Nebula. Astrophys. J. 2017, 835, 264. [Google Scholar] [CrossRef]
- Guillot, S.; Pavlov, G.G.; Reyes, C.; Reisenegger, A.; Rodriguez, L.E.; Rangelov, B.; Kargaltsev, O. Hubble Space Telescope Nondetection of PSR J2144-3933: The Coldest Known Neutron Star. Astrophys. J. 2019, 874, 175. [Google Scholar] [CrossRef]
- Abramkin, V.; Shibanov, Y.; Mignani, R.P.; Pavlov, G.G. Hubble Space Telescope Observations of the Old Pulsar PSR J0108-1431. Astrophys. J. 2021, 911, 1. [Google Scholar] [CrossRef]
- Abramkin, V.; Pavlov, G.G.; Shibanov, Y.; Kargaltsev, O. Thermal and Nonthermal Emission in the Optical-UV Spectrum of PSR B0950+08. Astrophys. J. 2022, 924, 128. [Google Scholar] [CrossRef]
- Köpp, F.; Horvath, J.E.; Hadjimichef, D.; Vasconcellos, C.A.Z.; Hess, P.O. Internal heating mechanisms in neutron stars. arXiv 2022, arXiv:2208.07770. [Google Scholar]
- Van Riper, K.A.; Epstein, R.I.; Miller, G.S. Soft X-ray Pulses from Neutron Star Glitches. Astrophys. J. Lett. 1991, 381, L47. [Google Scholar] [CrossRef]
- Cheng, K.S.; Li, Y.; Suen, W.M. The Thermal Response of a Pulsar Glitch: The Nonspherically Symmetric Case. Astrophys. J. Lett. 1998, 499, L45–L48. [Google Scholar] [CrossRef]
- Tang, A.P.S.; Cheng, K.S. Thermal X-ray Pulses Resulting from Pulsar Glitches. Astrophys. J. 2001, 549, 1039–1049. [Google Scholar] [CrossRef][Green Version]
- Hui, C.Y.; Cheng, K.S. The Effects of Rotation on Thermal X-ray Afterglows Resulting from Pulsar Glitches. Astrophys. J. 2004, 608, 935–944. [Google Scholar] [CrossRef][Green Version]
- Alpar, M.A.; Chau, H.F.; Cheng, K.S.; Pines, D. Postglitch Relaxation of the Crab Pulsar after Its First Four Major Glitches: The Combined Effects of Crust Cracking, Formation of Vortex Depletion Region and Vortex Creep. Astrophys. J. 1996, 459, 706. [Google Scholar] [CrossRef]
- Alpar, M.A.; Baykal, A. Pulsar braking indices, glitches and energy dissipation in neutron stars. Mon. Not. R. Astron. Soc. 2006, 372, 489–496. [Google Scholar] [CrossRef]
- Alpar, M.A.; Anderson, P.W.; Pines, D.; Shaham, J. Vortex creep and the internal temperature of neutron stars. II. VELA pulsar. Astrophys. J. 1984, 278, 791–805. [Google Scholar] [CrossRef]
- Alpar, M.A.; Chau, H.F.; Cheng, K.S.; Pines, D. Postglitch Relaxation of the VELA Pulsar after Its First Eight Large Glitches: A Reevaluation with the Vortex Creep Model. Astrophys. J. 1993, 409, 345. [Google Scholar] [CrossRef]
- Chau, H.F.; McCulloch, P.M.; Nandkumar, R.; Pines, D. Postglitch Relaxation following the Ninth Glitch of the VELA Pulsar. Astrophys. J. Lett. 1993, 413, L113. [Google Scholar] [CrossRef]
- Akbal, O.; Alpar, M.A.; Buchner, S.; Pines, D. Nonlinear interglitch dynamics, the braking index of the Vela pulsar and the time to the next glitch. Mon. Not. R. Astron. Soc. 2017, 469, 4183–4192. [Google Scholar] [CrossRef]
- Alpar, M.A.; Nandkumar, R.; Pines, D. Vortex creep and the internal temperature of neutron stars: The Crabpulsar and PSR 0525+21. Astrophys. J. 1985, 288, 191–195. [Google Scholar] [CrossRef]
- Alpar, M.A.; Cheng, K.S.; Pines, D.; Shaham, J. The large glitch from PSR 0355+54 and its post-glitch relaxation. Mon. Not. R. Astron. Soc. 1988, 233, 25–31. [Google Scholar] [CrossRef]
- Akbal, O.; Gügercinoğlu, E.; Şaşmaz Muş, S.; Alpar, M.A. Peculiar glitch of PSR J1119-6127 and extension of the vortex creep model. Mon. Not. R. Astron. Soc. 2015, 449, 933–941. [Google Scholar] [CrossRef]
- Pines, D.; Shaham, J.; Alpar, M.A.; Anderson, P.W. Pinned vorticity in rotating superfluids, with application to neutron stars. Prog. Theor. Phys. Suppl. 1980, 69, 376–396. [Google Scholar] [CrossRef]
- Lyne, A.; Hobbs, G.; Kramer, M.; Stairs, I.; Stappers, B. Switched Magnetospheric Regulation of Pulsar Spin-Down. Science 2010, 329, 408. [Google Scholar] [CrossRef] [PubMed]
- Kerr, M.; Hobbs, G.; Johnston, S.; Shannon, R.M. Periodic modulation in pulse arrival times from young pulsars: A renewed case for neutron star precession. Mon. Not. R. Astron. Soc. 2016, 455, 1845–1854. [Google Scholar] [CrossRef]
- Parthasarathy, A.; Shannon, R.M.; Johnston, S.; Lentati, L.; Bailes, M.; Dai, S.; Kerr, M.; Manchester, R.N.; Osłowski, S.; Sobey, C.; et al. Timing of young radio pulsars - I. Timing noise, periodic modulation, and proper motion. Mon. Not. R. Astron. Soc. 2019, 489, 3810–3826. [Google Scholar] [CrossRef]
- Shaw, B.; Stappers, B.W.; Weltevrede, P.; Brook, P.R.; Karastergiou, A.; Jordan, C.A.; Keith, M.J.; Kramer, M.; Lyne, A.G. Long-term rotational and emission variability of 17 radio pulsars. Mon. Not. R. Astron. Soc. 2022, 513, 5861–5880. [Google Scholar] [CrossRef]
- McCulloch, P.M.; Hamilton, P.A.; McConnell, D.; King, E.A. The Vela glitch of Christmas 1988. Nature 1990, 346, 822–824. [Google Scholar] [CrossRef]
- Espinoza, C.M.; Lyne, A.G.; Stappers, B.W. New long-term braking index measurements for glitching pulsars using a glitch-template method. Mon. Not. R. Astron. Soc. 2017, 466, 147–162. [Google Scholar] [CrossRef][Green Version]
- Gügercinoğlu, E.; Köksal, E.; Güver, T. On the Peculiar Rotational Evolution of PSR B0950+08. arXiv 2022, arXiv:2207.04111. [Google Scholar]
- Datta, B.; Alpar, M.A. Implications of the crustal moment of inertia for neutron-star equations of state. Astron. Astrophys. 1993, 275, 210–212. [Google Scholar]
- Ho, W.C.G.; Espinoza, C.M.; Antonopoulou, D.; Andersson, N. Pinning down the superfluid and measuring masses using pulsar glitches. Sci. Adv. 2015, 1, e1500578. [Google Scholar] [CrossRef]
- Pizzochero, P.M.; Antonelli, M.; Haskell, B.; Seveso, S. Constraints on pulsar masses from the maximum observed glitch. Nat. Astron. 2017, 1, 0134. [Google Scholar] [CrossRef]
- Montoli, A.; Antonelli, M.; Pizzochero, P.M. The role of mass, equation of state, and superfluid reservoir in large pulsar glitches. Mon. Not. R. Astron. Soc. 2020, 492, 4837–4846. [Google Scholar] [CrossRef]
- Shang, X.; Li, A. Revisiting the Post-glitch Relaxation of the 2000 Vela Glitch with the Neutron Star Equation of States in the Brueckner and Relativistic Brueckner Theories. Astrophys. J. 2021, 923, 108. [Google Scholar] [CrossRef]
- Epstein, R.I.; Baym, G. Vortex Drag and the Spin-up Time Scale for Pulsar Glitches. Astrophys. J. 1992, 387, 276. [Google Scholar] [CrossRef]
- Jones, P.B. Rotation of the neutron-drip superfluid in pulsars - The Kelvin phonon contribution to dissipation. Mon. Not. R. Astron. Soc. 1992, 257, 501–506. [Google Scholar] [CrossRef]
- Graber, V.; Cumming, A.; Andersson, N. Glitch Rises as a Test for Rapid Superfluid Coupling in Neutron Stars. Astrophys. J. 2018, 865, 23. [Google Scholar] [CrossRef]
- Sourie, A.; Chamel, N.; Novak, J.; Oertel, M. Global numerical simulations of the rise of vortex-mediated pulsar glitches in full general relativity. Mon. Not. R. Astron. Soc. 2017, 464, 4641–4657. [Google Scholar] [CrossRef]
- Gavassino, L.; Antonelli, M.; Pizzochero, P.M.; Haskell, B. A universal formula for the relativistic correction to the mutual friction coupling time-scale in neutron stars. Mon. Not. R. Astron. Soc. 2020, 494, 3562–3580. [Google Scholar] [CrossRef]
- Pizzochero, P.M.; Montoli, A.; Antonelli, M. Core and crust contributions in overshooting glitches: The Vela pulsar 2016 glitch. Astron. Astrophys. 2020, 636, A101. [Google Scholar] [CrossRef]
- Montoli, A.; Antonelli, M.; Magistrelli, F.; Pizzochero, P.M. Bayesian estimate of the superfluid moments of inertia from the 2016 glitch in the Vela pulsar. Astron. Astrophys. 2020, 642, A223. [Google Scholar] [CrossRef]
- Link, B.K.; Epstein, R.I. Mechanics and Energetics of Vortex Unpinning in Neutron Stars. Astrophys. J. 1991, 373, 592. [Google Scholar] [CrossRef]
- Jones, P.B. Motion of Neutron Vortices in the Inner Crust of a Neutron Star. Phys. Rev. Lett. 1997, 79, 792–795. [Google Scholar] [CrossRef]
- Wlazłowski, G.; Sekizawa, K.; Magierski, P.; Bulgac, A.; Forbes, M.M. Vortex Pinning and Dynamics in the Neutron Star Crust. Phys. Rev. Lett. 2016, 117, 232701. [Google Scholar] [CrossRef]
- Link, B.; Levin, Y. Vortex Pinning in Neutron Stars, Slip-stick Dynamics, and the Origin of Spin Glitches. arXiv 2022, arXiv:2208.11494. [Google Scholar]
- Jones, P.B. Amorphous and Heterogeneous Phase of Neutron Star Matter. Phys. Rev. Lett. 1999, 83, 3589–3592. [Google Scholar] [CrossRef]
- Jones, P.B. First-principles point-defect calculations for solid neutron star matter. Mon. Not. R. Astron. Soc. 2001, 321, 167–175. [Google Scholar] [CrossRef][Green Version]
- Bildsten, L.; Epstein, R.I. Superfluid Dissipation Time Scales in Neutron Star Crusts. Astrophys. J. 1989, 342, 951. [Google Scholar] [CrossRef]
- Hirasawa, M.; Shibazaki, N. Vortex Configurations, Oscillations, and Pinning in Neutron Star Crusts. Astrophys. J. 2001, 563, 267–275. [Google Scholar] [CrossRef]
- Avogadro, P.; Barranco, F.; Broglia, R.A.; Vigezzi, E. Quantum calculation of vortices in the inner crust of neutron stars. Phys. Rev. C 2007, 75, 012805. [Google Scholar] [CrossRef]
- Avogadro, P.; Barranco, F.; Broglia, R.A.; Vigezzi, E. Vortex nucleus interaction in the inner crust of neutron stars. Nucl. Phys. A 2008, 811, 378–412. [Google Scholar] [CrossRef]
- Pizzochero, P.M.; Viverit, L.; Broglia, R.A. Vortex-Nucleus Interaction and Pinning Forces in Neutron Stars. Phys. Rev. Lett. 1997, 79, 3347–3350. [Google Scholar] [CrossRef]
- Donati, P.; Pizzochero, P.M. Is there Nuclear Pinning of Vortices in Superfluid Pulsars? Phys. Rev. Lett. 2003, 90, 211101. [Google Scholar] [CrossRef] [PubMed]
- Donati, P.; Pizzochero, P.M. Fully consistent semi-classical treatment of vortex-nucleus interaction in rotating neutron stars. Nucl. Phys. A 2004, 742, 363–379. [Google Scholar] [CrossRef]
- Donati, P.; Pizzochero, P.M. Realistic energies for vortex pinning in intermediate-density neutron star matter. Phys. Lett. B 2006, 640, 74–81. [Google Scholar] [CrossRef]
- Grill, F.; Pizzochero, P. Vortex-lattice interaction in Pulsar Glitches. J. Phys. Conf. Ser. 2012, 342, 012004. [Google Scholar] [CrossRef]
- Kobyakov, D.; Pethick, C.J. Towards a Metallurgy of Neutron Star Crusts. Phys. Rev. Lett. 2014, 112, 112504. [Google Scholar] [CrossRef] [PubMed]
- Kobyakov, D.; Pethick, C.J. Nucleus-nucleus interactions in the inner crust of neutron stars. Phys. Rev. C 2016, 94, 055806. [Google Scholar] [CrossRef]
- Link, B. Dynamics of Quantum Vorticity in a Random Potential. Phys. Rev. Lett. 2009, 102, 131101. [Google Scholar] [CrossRef]
- Antonelli, M.; Haskell, B. Superfluid vortex-mediated mutual friction in non-homogeneous neutron star interiors. Mon. Not. R. Astron. Soc. 2020, 499, 3690–3705. [Google Scholar] [CrossRef]
- Chamel, N.; Haensel, P. Physics of Neutron Star Crusts. Living Rev. Relativ. 2008, 11, 10. [Google Scholar] [CrossRef]
- Lazzari, G.; de Blasio, F.V. Pinning properties of superfluid vortices in the crust of neutron stars. Nuovo C. A Ser. 1995, 108A, 313–321. [Google Scholar] [CrossRef]
- Lazzari, G.; de Blasio, F.V. Vortex pinning with non-spherical nuclei. Z. Fur Phys. A Hadron. Nucl. 1995, 353, 13–14. [Google Scholar] [CrossRef]
- De Blasio, F.V.; Lazzari, G. Pinning mechanism and vortex trap region in neutron star crusts. Z. Fur Phys. A Hadron. Nucl. 1996, 355, 113–116. [Google Scholar] [CrossRef]
- Andersson, N.; Glampedakis, K.; Ho, W.C.G.; Espinoza, C.M. Pulsar Glitches: The Crust is not Enough. Phys. Rev. Lett. 2012, 109, 241103. [Google Scholar] [CrossRef] [PubMed]
- Chamel, N. Crustal Entrainment and Pulsar Glitches. Phys. Rev. Lett. 2013, 110, 011101. [Google Scholar] [CrossRef]
- Li, A. Glitch Crisis or Not: A Microscopic Study. Chin. Phys. Lett. 2015, 32, 079701. [Google Scholar] [CrossRef]
- Delsate, T.; Chamel, N.; Gürlebeck, N.; Fantina, A.F.; Pearson, J.M.; Ducoin, C. Giant pulsar glitches and the inertia of neutron star crusts. Phys. Rev. D 2016, 94, 023008. [Google Scholar] [CrossRef]
- Chamel, N. Entrainment in Superfluid Neutron-Star Crusts: Hydrodynamic Description and Microscopic Origin. J. Low Temp. Phys. 2017, 189, 328–360. [Google Scholar] [CrossRef]
- Sauls, J.A.; Chamel, N.; Alpar, M.A. Superfluidity in Disordered Neutron Stars Crusts. arXiv 2020, arXiv:2001.09959. [Google Scholar]
- Martin, N.; Urban, M. Superfluid hydrodynamics in the inner crust of neutron stars. Phys. Rev. C 2016, 94, 065801. [Google Scholar] [CrossRef]
- Watanabe, G.; Pethick, C.J. Superfluid Density of Neutrons in the Inner Crust of Neutron Stars: New Life for Pulsar Glitch Models. Phys. Rev. Lett. 2017, 119, 062701. [Google Scholar] [CrossRef] [PubMed]
- Durel, D.; Urban, M. Long-wavelength phonons in the crystalline and pasta phases of neutron-star crusts. Phys. Rev. C 2018, 97, 065805. [Google Scholar] [CrossRef]
- Minami, Y.; Watanabe, G. Effects of pairing gap and band gap on superfluid density in the inner crust of neutron stars. Phys. Rev. Res. 2022, 4, 033141. [Google Scholar] [CrossRef]
- Sekizawa, K.; Kobayashi, S.; Matsuo, M. Time-dependent extension of the self-consistent band theory for neutron star matter: Anti-entrainment effects in the slab phase. Phys. Rev. C 2022, 105, 045807. [Google Scholar] [CrossRef]
- Greenstein, G. Superfluid Turbulence in Neutron Stars. Nature 1970, 227, 791–794. [Google Scholar] [CrossRef]
- Peralta, C.; Melatos, A.; Giacobello, M.; Ooi, A. Global Three-dimensional Flow of a Neutron Superfluid in a Spherical Shell in a Neutron Star. Astrophys. J. 2005, 635, 1224–1232. [Google Scholar] [CrossRef]
- Peralta, C.; Melatos, A.; Giacobello, M.; Ooi, A. Transitions between Turbulent and Laminar Superfluid Vorticity States in the Outer Core of a Neutron Star. Astrophys. J. 2006, 651, 1079–1091. [Google Scholar] [CrossRef]
- Melatos, A.; Peralta, C. Superfluid Turbulence and Pulsar Glitch Statistics. Astrophys. J. Lett. 2007, 662, L99–L102. [Google Scholar] [CrossRef][Green Version]
- Andersson, N.; Sidery, T.; Comer, G.L. Superfluid neutron star turbulence. Mon. Not. R. Astron. Soc. 2007, 381, 747–756. [Google Scholar] [CrossRef]
- Mongiovì, M.S.; Russo, F.G.; Sciacca, M. A mathematical description of glitches in neutron stars. Mon. Not. R. Astron. Soc. 2017, 469, 2141–2150. [Google Scholar] [CrossRef]
- Haskell, B.; Antonopoulou, D.; Barenghi, C. Turbulent, pinned superfluids in neutron stars and pulsar glitch recoveries. Mon. Not. R. Astron. Soc. 2020, 499, 161–170. [Google Scholar] [CrossRef]
- Andersson, N.; Comer, G.L.; Prix, R. Are Pulsar Glitches Triggered by a Superfluid Two-Stream Instability? Phys. Rev. Lett. 2003, 90, 091101. [Google Scholar] [CrossRef] [PubMed]
- Mastrano, A.; Melatos, A. Kelvin-Helmholtz instability and circulation transfer at an isotropic-anisotropic superfluid interface in a neutron star. Mon. Not. R. Astron. Soc. 2005, 361, 927–941. [Google Scholar] [CrossRef]
- Sidery, T.; Andersson, N.; Comer, G.L. Waves and instabilities in dissipative rotating superfluid neutron stars. Mon. Not. R. Astron. Soc. 2008, 385, 335–348. [Google Scholar] [CrossRef][Green Version]
- Glampedakis, K.; Andersson, N. Hydrodynamical Trigger Mechanism for Pulsar Glitches. Phys. Rev. Lett. 2009, 102, 141101. [Google Scholar] [CrossRef]
- Andersson, N.; Glampedakis, K.; Hogg, M. Superfluid instability of r-modes in “differentially rotating” neutron stars. Phys. Rev. D 2013, 87, 063007. [Google Scholar] [CrossRef]
- Khomenko, V.; Antonelli, M.; Haskell, B. Hydrodynamical instabilities in the superfluid interior of neutron stars with background flows between the components. Phys. Rev. D 2019, 100, 123002. [Google Scholar] [CrossRef]
- Van Eysden, C.A.; Link, B. Hydrodynamic Stability Analysis of the Neutron Star Core. Astrophys. J. 2018, 865, 60. [Google Scholar] [CrossRef]
- Ruderman, M. Neutron Starquakes and Pulsar Periods. Nature 1969, 223, 597–598. [Google Scholar] [CrossRef]
- Baym, G.; Pines, D. Neutron starquakes and pulsar speedup. Ann. Phys. 1971, 66, 816–835. [Google Scholar] [CrossRef]
- Ogata, S.; Ichimaru, S. First-principles calculations of shear moduli for Monte Carlo-simulated Coulomb solids. Phys. Rev. A 1990, 42, 4867–4870. [Google Scholar] [CrossRef] [PubMed]
- Strohmayer, T.; Ogata, S.; Iyetomi, H.; Ichimaru, S.; van Horn, H.M. The Shear Modulus of the Neutron Star Crust and Nonradial Oscillations of Neutron Stars. Astrophys. J. 1991, 375, 679. [Google Scholar] [CrossRef]
- Baiko, D.A. Shear modulus of neutron star crust. Mon. Not. R. Astron. Soc. 2011, 416, 22–31. [Google Scholar] [CrossRef]
- Zemlyakov, N.A.; Chugunov, A.I. Neutron star inner crust: Reduction of shear modulus by nuclei finite size effect. arXiv 2022, arXiv:2209.05821. [Google Scholar] [CrossRef]
- Alpar, M.A.; Pines, D. Gravitational radiation from a solid-crust neutron star. Nature 1985, 314, 334–336. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Kadau, K. Breaking Strain of Neutron Star Crust and Gravitational Waves. Phys. Rev. Lett. 2009, 102, 191102. [Google Scholar] [CrossRef]
- Hoffman, K.; Heyl, J. Mechanical properties of non-accreting neutron star crusts. Mon. Not. R. Astron. Soc. 2012, 426, 2404–2412. [Google Scholar] [CrossRef]
- Baiko, D.A.; Chugunov, A.I. Breaking properties of neutron star crust. Mon. Not. R. Astron. Soc. 2018, 480, 5511–5516. [Google Scholar] [CrossRef]
- Smoluchowski, R. Frequency of Pulsar Starquakes. Phys. Rev. Lett. 1970, 24, 923–925. [Google Scholar] [CrossRef]
- Cheng, K.S.; Chau, W.Y.; Zhang, J.L.; Chau, H.F. Effects of Evolving Rotating Equilibrium Configurations on the Cooling and Spin-down of Pulsars. Astrophys. J. 1992, 396, 135. [Google Scholar] [CrossRef]
- Gourgouliatos, K.N.; Lander, S.K. Axisymmetric magneto-plastic evolution of neutron-star crusts. Mon. Not. R. Astron. Soc. 2021, 506, 3578–3587. [Google Scholar] [CrossRef]
- Pines, D.; Shaham, J. Microquakes and Macroquakes in Neutron Stars. Nat. Phys. Sci. 1972, 235, 43–49. [Google Scholar] [CrossRef]
- Cutler, C.; Ushomirsky, G.; Link, B. The Crustal Rigidity of a Neutron Star and Implications for PSR B1828-11 and Other Precession Candidates. Astrophys. J. 2003, 588, 975–991. [Google Scholar] [CrossRef]
- Zdunik, J.L.; Bejger, M.; Haensel, P. Deformation and crustal rigidity of rotating neutron stars. Astron. Astrophys. 2008, 491, 489–498. [Google Scholar] [CrossRef]
- Franco, L.M.; Link, B.; Epstein, R.I. Quaking Neutron Stars. Astrophys. J. 2000, 543, 987–994. [Google Scholar] [CrossRef]
- Rencoret, J.A.; Aguilera-Gómez, C.; Reisenegger, A. Revisiting neutron starquakes caused by spin-down. Astron. Astrophys. 2021, 654, A47. [Google Scholar] [CrossRef]
- Gittins, F.; Andersson, N. Modelling neutron star mountains in relativity. Mon. Not. R. Astron. Soc. 2021, 507, 116–128. [Google Scholar] [CrossRef]
- Morales, J.A.; Horowitz, C.J. Neutron Star Crust Can Support A Large Ellipticity. Mon. Not. R. Astron. Soc. 2022, 517, 5610–5616. [Google Scholar] [CrossRef]
- Carter, B.; Quintana, H. Relativistic formulation of the neutron starquake theory of pulsar glitches. Ann. Phys. 1975, 95, 74–89. [Google Scholar] [CrossRef]
- Kojima, Y.; Kisaka, S.; Fujisawa, K. Magneto-elastic equilibrium of a neutron star crust. Mon. Not. R. Astron. Soc. 2021, 506, 3936–3945. [Google Scholar] [CrossRef]
- Ushomirsky, G.; Cutler, C.; Bildsten, L. Deformations of accreting neutron star crusts and gravitational wave emission. Mon. Not. R. Astron. Soc. 2000, 319, 902–932. [Google Scholar] [CrossRef]
- Akbal, O.; Alpar, M.A. Minimum glitch of the Crab pulsar and the crustquake as a trigger mechanism. Mon. Not. R. Astron. Soc. 2018, 473, 621–624. [Google Scholar] [CrossRef]
- Epstein, R.I. Gamma-ray bursts and glitching neutron stars. Phys. Rep. 1988, 163, 155–166. [Google Scholar] [CrossRef]
- Link, B.; Epstein, R.I.; Baym, G. Postglitch Behavior of the Crab Pulsar: Evidence for External Torque Variations. Astrophys. J. Lett. 1992, 390, L21. [Google Scholar] [CrossRef]
- Link, B.; Franco, L.M.; Epstein, R.I. Starquake-induced Magnetic Field and Torque Evolution in Neutron Stars. Astrophys. J. 1998, 508, 838–843. [Google Scholar] [CrossRef]
- Epstein, R.I.; Link, B. Starquake-Induced Glitches in Pulsars. In Astrophysics and Space Science Library; Cheng, K.S., Chau, H.F., Chan, K.L., Leung, K.C., Eds.; Springer: Dordrecht, The Netherlands; Berlin/Heidelberg, Germany, 2000; Volume 254, p. 95. [Google Scholar] [CrossRef]
- Lyne, A.G.; Jordan, C.A.; Graham-Smith, F.; Espinoza, C.M.; Stappers, B.W.; Weltevrede, P. 45 years of rotation of the Crab pulsar. Mon. Not. R. Astron. Soc. 2015, 446, 857–864. [Google Scholar] [CrossRef]
- Giliberti, E.; Antonelli, M.; Cambiotti, G.; Pizzochero, P.M. Incompressible analytical models for spinning-down pulsars. Publ. Astron. Soc. Aust. 2019, 36, e036. [Google Scholar] [CrossRef]
- Giliberti, E.; Cambiotti, G.; Antonelli, M.; Pizzochero, P.M. Modelling strains and stresses in continuously stratified rotating neutron stars. Mon. Not. R. Astron. Soc. 2020, 491, 1064–1078. [Google Scholar] [CrossRef]
- Braithwaite, J. Axisymmetric magnetic fields in stars: Relative strengths of poloidal and toroidal components. Mon. Not. R. Astron. Soc. 2009, 397, 763–774. [Google Scholar] [CrossRef]
- Johnson-McDaniel, N.K.; Owen, B.J. Maximum elastic deformations of relativistic stars. Phys. Rev. D 2013, 88, 044004. [Google Scholar] [CrossRef]
- Peng, C.; Xu, R.X. Pulsar slow glitches in a solid quark star model. Mon. Not. R. Astron. Soc. 2008, 384, 1034–1038. [Google Scholar] [CrossRef]
- Zhou, E.P.; Lu, J.G.; Tong, H.; Xu, R.X. Two types of glitches in a solid quark star model. Mon. Not. R. Astron. Soc. 2014, 443, 2705–2710. [Google Scholar] [CrossRef]
- Lai, X.Y.; Yun, C.A.; Lu, J.G.; Lü, G.L.; Wang, Z.J.; Xu, R.X. Pulsar glitches in a strangeon star model. Mon. Not. R. Astron. Soc. 2018, 476, 3303–3309. [Google Scholar] [CrossRef]
- Wang, W.H.; Lai, X.Y.; Zhou, E.P.; Lu, J.G.; Zheng, X.P.; Xu, R.X. Pulsar glitches in a strangeon star model. II. The activity. Mon. Not. R. Astron. Soc. 2021, 500, 5336–5349. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.; Pines, D. Superfluidity in Neutron Stars. Nature 1969, 224, 673–674. [Google Scholar] [CrossRef]
- Easson, I.; Pethick, C.J. Stress tensor of cosmic and laboratory type-II superconductors. Phys. Rev. D 1977, 16, 275–280. [Google Scholar] [CrossRef]
- Ruderman, M. Neutron Star Crustal Plate Tectonics. III. Cracking, Glitches, and Gamma-Ray Bursts. Astrophys. J. 1991, 382, 587. [Google Scholar] [CrossRef]
- Srinivasan, G.; Bhattacharya, D.; Muslimov, A.G.; Tsygan, A.J. A novel mechanism for the decay of neutron star magnetic fields. Curr. Sci. 1990, 59, 31–38. [Google Scholar]
- Jones, P.B. Neutron superfluid spin-down and magnetic field decay in pulsars. Mon. Not. R. Astron. Soc. 1991, 253, 279. [Google Scholar] [CrossRef]
- Mendell, G. Superfluid Hydrodynamics in Rotating Neutron Stars. I. Nondissipative Equations. Astrophys. J. 1991, 380, 515. [Google Scholar] [CrossRef]
- Ruderman, M. Pulsar Spin, Magnetic Fields, and Glitches. In Astrophysics and Space Science Library; Becker, W., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 357, p. 353. [Google Scholar] [CrossRef]
- Ding, K.Y.; Cheng, K.S.; Chau, H.F. Magnetic Field Decay from the Core of Neutron Stars: Effects of Interpinning of 3P 2 Neutron Superfluid and 1S 0 Proton Superconducting Fluid. Astrophys. J. 1993, 408, 167. [Google Scholar] [CrossRef]
- Jahan-Miri, M. Flux Expulsion and Field Evolution in Neutron Stars. Astrophys. J. 2000, 532, 514–529. [Google Scholar] [CrossRef][Green Version]
- Jones, P.B. Type II superconductivity and magnetic flux transport in neutron stars. Mon. Not. R. Astron. Soc. 2006, 365, 339–344. [Google Scholar] [CrossRef]
- Bransgrove, A.; Levin, Y.; Beloborodov, A. Magnetic field evolution of neutron stars - I. Basic formalism, numerical techniques and first results. Mon. Not. R. Astron. Soc. 2018, 473, 2771–2790. [Google Scholar] [CrossRef]
- Ruderman, M.A. Pulsar Spin-down Induced Phenomena: Heating; Magnetic-field Evolution; Glitches; Pulse-period Modulations. In X-ray Binaries to Gamma-ray Bursts: Jan van Paradijs Memorial Symposium; van den Heuvel, E.P., Kaper, L., Rol, E., Wijers, R.A.M.J., Eds.; Astronomical Society of the Pacific Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 2003; Volume 308, p. 251. [Google Scholar]
- Ruderman, M. A Biography of the Magnetic Field of a Neutron Star. In Electromagnetic Spectrum of Neutron Stars; NATO Advanced Study Institute (ASI) Series B; Springer: Dordrecht, The Netherlands; Berlin/Heidelberg, Germany, 2005; Volume 210, p. 47. [Google Scholar]
- Middleditch, J.; Marshall, F.E.; Wang, Q.D.; Gotthelf, E.V.; Zhang, W. Predicting the Starquakes in PSR J0537-6910. Astrophys. J. 2006, 652, 1531–1546. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Diving below the Spin-down Limit: Constraints on Gravitational Waves from the Energetic Young Pulsar PSR J0537-6910. Astrophys. J. Lett. 2021, 913, L27. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Kuiper, L.; Espinoza, C.M.; Guillot, S.; Ray, P.S.; Smith, D.A.; Bogdanov, S.; Antonopoulou, D.; Arzoumanian, Z.; Bejger, M.; et al. Timing Six Energetic Rotation-powered X-ray Pulsars, Including the Fast-spinning Young PSR J0058-7218 and Big Glitcher PSR J0537-6910. Astrophys. J. 2022, 939, 7. [Google Scholar] [CrossRef]
- Jones, P.B. Post-glitch relaxation in pulsars. Mon. Not. R. Astron. Soc. 2002, 335, 733–740. [Google Scholar] [CrossRef][Green Version]
- Wang, N.; Manchester, R.N.; Pace, R.T.; Bailes, M.; Kaspi, V.M.; Stappers, B.W.; Lyne, A.G. Glitches in southern pulsars. Mon. Not. R. Astron. Soc. 2000, 317, 843–860. [Google Scholar] [CrossRef]
- Sedrakyan, A.D.; Sedrakyan, D.M. Thermal Evolution of Neutron Stars with Internal Heating in the Superfluid Core. Astrophys. J. 1993, 413, 658. [Google Scholar] [CrossRef]
- Pines, D.; Alpar, M.A. Superfluidity in neutron stars. Nature 1985, 316, 27–32. [Google Scholar] [CrossRef]
- Keith, M.J.; Shannon, R.M.; Johnston, S. A connection between radio state changing and glitch activity in PSR J0742-2822. Mon. Not. R. Astron. Soc. 2013, 432, 3080–3084. [Google Scholar] [CrossRef]
- Dang, S.J.; Wang, N.; Wang, H.H.; Yuan, J.P.; Shang, L.H.; Yuen, R.; Ge, M.Y.; Zhou, X.; Wang, S.Q.; Kou, F.F.; et al. Spin-down and emission variations for PSR J0742-2822. Res. Astron. Astrophys. 2021, 21, 042. [Google Scholar] [CrossRef]
- Weltevrede, P.; Johnston, S.; Espinoza, C.M. The glitch-induced identity changes of PSR J1119-6127. Mon. Not. R. Astron. Soc. 2011, 411, 1917–1934. [Google Scholar] [CrossRef]
- Archibald, R.F.; Kaspi, V.M.; Tendulkar, S.P.; Scholz, P. A Magnetar-like Outburst from a High-B Radio Pulsar. Astrophys. J. Lett. 2016, 829, L21. [Google Scholar] [CrossRef]
- Allafort, A.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; Bellazzini, R.; Bonamente, E.; Bottacini, E.; Brandt, T.J.; et al. PSR J2021+4026 in the Gamma Cygni Region: The First Variable γ-Ray Pulsar Seen by the Fermi LAT. Astrophys. J. Lett. 2013, 777, L2. [Google Scholar] [CrossRef]
- Takata, J.; Wang, H.H.; Lin, L.C.C.; Hu, C.P.; Hui, C.Y.; Kong, A.K.H.; Tam, P.H.T.; Li, K.L.; Cheng, K.S. Repeated State Change of Variable Gamma-Ray Pulsar PSR J2021+4026. Astrophys. J. 2020, 890, 16. [Google Scholar] [CrossRef]
- Manchester, R.N.; Hobbs, G. A Giant Glitch in PSR J1718-3718. Astrophys. J. Lett. 2011, 736, L31. [Google Scholar] [CrossRef]
- Espinoza, C.M.; Vidal-Navarro, M.; Ho, W.C.G.; Deller, A.; Chatterjee, S. VLA proper motion constraints on the origin, age, and potential magnetar future of PSR J1734-3333. Astron. Astrophys. 2022, 659, A41. [Google Scholar] [CrossRef]
- Zhu, W.W.; Kaspi, V.M.; McLaughlin, M.A.; Pavlov, G.G.; Ng, C.Y.; Manchester, R.N.; Gaensler, B.M.; Woods, P.M. Chandra Observations of the High-magnetic-field Radio Pulsar J1718-3718. Astrophys. J. 2011, 734, 44. [Google Scholar] [CrossRef]
- Olausen, S.A.; Zhu, W.W.; Vogel, J.K.; Kaspi, V.M.; Lyne, A.G.; Espinoza, C.M.; Stappers, B.W.; Manchester, R.N.; McLaughlin, M.A. X-ray Observations of High-B Radio Pulsars. Astrophys. J. 2013, 764, 1. [Google Scholar] [CrossRef]
- Bransgrove, A.; Beloborodov, A.M.; Levin, Y. A Quake Quenching the Vela Pulsar. Astrophys. J. 2020, 897, 173. [Google Scholar] [CrossRef]
- Yuan, Y.; Levin, Y.; Bransgrove, A.; Philippov, A. Alfvén Wave Mode Conversion in Pulsar Magnetospheres. Astrophys. J. 2021, 908, 176. [Google Scholar] [CrossRef]
- Ng, C.W.; Takata, J.; Cheng, K.S. Observation and Simulation of the Variable Gamma-ray Emission from PSR J2021+4026. Astrophys. J. 2016, 825, 18. [Google Scholar] [CrossRef]
- Alpar, M.A.; Baykal, A. Expectancy of large pulsar glitches: A comparison of models with the observed glitch sample. Mon. Not. R. Astron. Soc. 1994, 269, 849–856. [Google Scholar] [CrossRef]
- Lyne, A.G.; Shemar, S.L.; Smith, F.G. Statistical studies of pulsar glitches. Mon. Not. R. Astron. Soc. 2000, 315, 534–542. [Google Scholar] [CrossRef]
- Wang, N.; Yuan, J. Observational features of pulsar glitches. Sci. China Phys. Mech. Astron. 2010, 53, 3–8. [Google Scholar] [CrossRef]
- Eya, I.O.; Urama, J.O.; Chukwude, A.E. On the distributions of pulsar glitch sizes and the inter-glitch time intervals. Res. Astron. Astrophys. 2019, 19, 089. [Google Scholar] [CrossRef]
- Montoli, A.; Antonelli, M.; Haskell, B.; Pizzochero, P. Statistical Estimates of the Pulsar Glitch Activity. Universe 2021, 7, 8. [Google Scholar] [CrossRef]
- Eya, I.O.; Alhassan, J.A.; Iyida, E.U.; Chukwude, A.E.; Urama, J.O. On the pulsar spin frequency derivatives and the glitch activity. Astrophys. Space Sci. 2022, 367, 28. [Google Scholar] [CrossRef]
- Fuentes, J.R.; Espinoza, C.M.; Reisenegger, A.; Shaw, B.; Stappers, B.W.; Lyne, A.G. The glitch activity of neutron stars. Astron. Astrophys. 2017, 608, A131. [Google Scholar] [CrossRef]
- Ashton, G.; Prix, R.; Jones, D.I. Statistical characterization of pulsar glitches and their potential impact on searches for continuous gravitational waves. Phys. Rev. D 2017, 96, 063004. [Google Scholar] [CrossRef]
- Celora, T.; Khomenko, V.; Antonelli, M.; Haskell, B. The effect of non-linear mutual friction on pulsar glitch sizes and rise times. Mon. Not. R. Astron. Soc. 2020, 496, 5564–5574. [Google Scholar] [CrossRef]
- Haskell, B.; Khomenko, V.; Antonelli, M.; Antonopoulou, D. Crust or core? Insights from the slow rise of large glitches in the Crab pulsar. Mon. Not. R. Astron. Soc. 2018, 481, L146–L150. [Google Scholar] [CrossRef]
- Fuentes, J.R.; Espinoza, C.M.; Reisenegger, A. Glitch time series and size distributions in eight prolific pulsars. Astron. Astrophys. 2019, 630, A115. [Google Scholar] [CrossRef]
- Carlin, J.B.; Melatos, A.; Vukcevic, D. Temporal clustering of rotational glitches in the Crab pulsar. Mon. Not. R. Astron. Soc. 2019, 482, 3736–3743. [Google Scholar] [CrossRef]
- Carlin, J.B.; Melatos, A. Long-term statistics of pulsar glitches triggered by a Brownian stress accumulation process. Mon. Not. R. Astron. Soc. 2020, 494, 3383–3391. [Google Scholar] [CrossRef]
- Carlin, J.B.; Melatos, A. Long-term Statistics of Pulsar Glitches Due to History-dependent Avalanches. Astrophys. J. 2021, 917, 1. [Google Scholar] [CrossRef]
- Melatos, A.; Peralta, C.; Wyithe, J.S.B. Avalanche Dynamics of Radio Pulsar Glitches. Astrophys. J. 2008, 672, 1103–1118. [Google Scholar] [CrossRef]
- Fulgenzi, W.; Melatos, A.; Hughes, B.D. Radio pulsar glitches as a state-dependent Poisson process. Mon. Not. R. Astron. Soc. 2017, 470, 4307–4329. [Google Scholar] [CrossRef]
- Howitt, G.; Melatos, A.; Delaigle, A. Nonparametric Estimation of the Size and Waiting Time Distributions of Pulsar Glitches. Astrophys. J. 2018, 867, 60. [Google Scholar] [CrossRef]
- Melatos, A.; Howitt, G.; Fulgenzi, W. Size-waiting-time Correlations in Pulsar Glitches. Astrophys. J. 2018, 863, 196. [Google Scholar] [CrossRef]
- Melatos, A.; Drummond, L.V. Pulsar Glitch Activity as a State-dependent Poisson Process: Parameter Estimation and Epoch Prediction. Astrophys. J. 2019, 885, 37. [Google Scholar] [CrossRef]
- Carlin, J.B.; Melatos, A. Autocorrelations in pulsar glitch waiting times and sizes. Mon. Not. R. Astron. Soc. 2019, 488, 4890–4896. [Google Scholar] [CrossRef]
- Carlin, J.B.; Melatos, A. Generating quasi-periodic pulsar glitches using a state-dependent Poisson process. Mon. Not. R. Astron. Soc. 2019, 483, 4742–4750. [Google Scholar] [CrossRef]
- Cheng, K.S.; Alpar, M.A.; Pines, D.; Shaham, J. Spontaneous Superfluid Unpinning and the Inhomogeneous Distribution of Vortex Lines in Neutron Stars. Astrophys. J. 1988, 330, 835. [Google Scholar] [CrossRef]
- Link, B.; Epstein, R.I.; Lattimer, J.M. Pulsar Constraints on Neutron Star Structure and Equation of State. Phys. Rev. Lett. 1999, 83, 3362–3365. [Google Scholar] [CrossRef]
- Basu, A.; Char, P.; Nandi, R.; Joshi, B.C.; Bandyopadhyay, D. Glitch Behavior of Pulsars and Contribution from Neutron Star Crust. Astrophys. J. 2018, 866, 94. [Google Scholar] [CrossRef]
- Parmar, V.; Das, H.C.; Kumar, A.; Sharma, M.K.; Patra, S.K. Crustal properties of a neutron star within an effective relativistic mean-field model. Phys. Rev. D 2022, 105, 043017. [Google Scholar] [CrossRef]
- Hobbs, G.; Miller, D.; Manchester, R.N.; Dempsey, J.; Chapman, J.M.; Khoo, J.; Applegate, J.; Bailes, M.; Bhat, N.D.R.; Bridle, R.; et al. The Parkes Observatory Pulsar Data Archive. Publ. Astron. Soc. Aust. 2011, 28, 202–214. [Google Scholar] [CrossRef]
- Abdollahi, S.; Acero, F.; Ackermann, M.; Ajello, M.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; et al. Fermi Large Area Telescope Fourth Source Catalog. Astrophys. J. Suppl. Ser. 2020, 247, 33. [Google Scholar] [CrossRef]
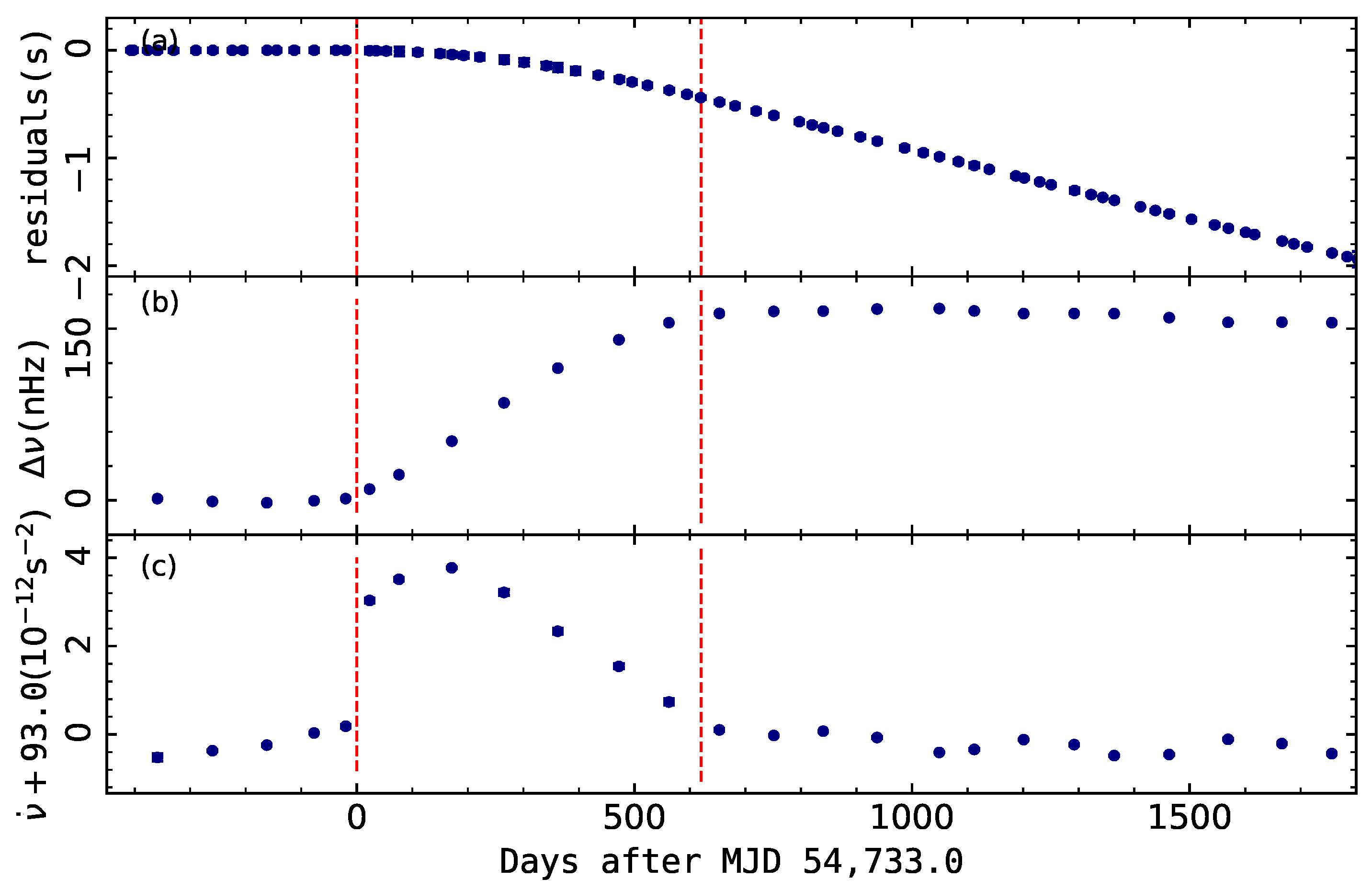

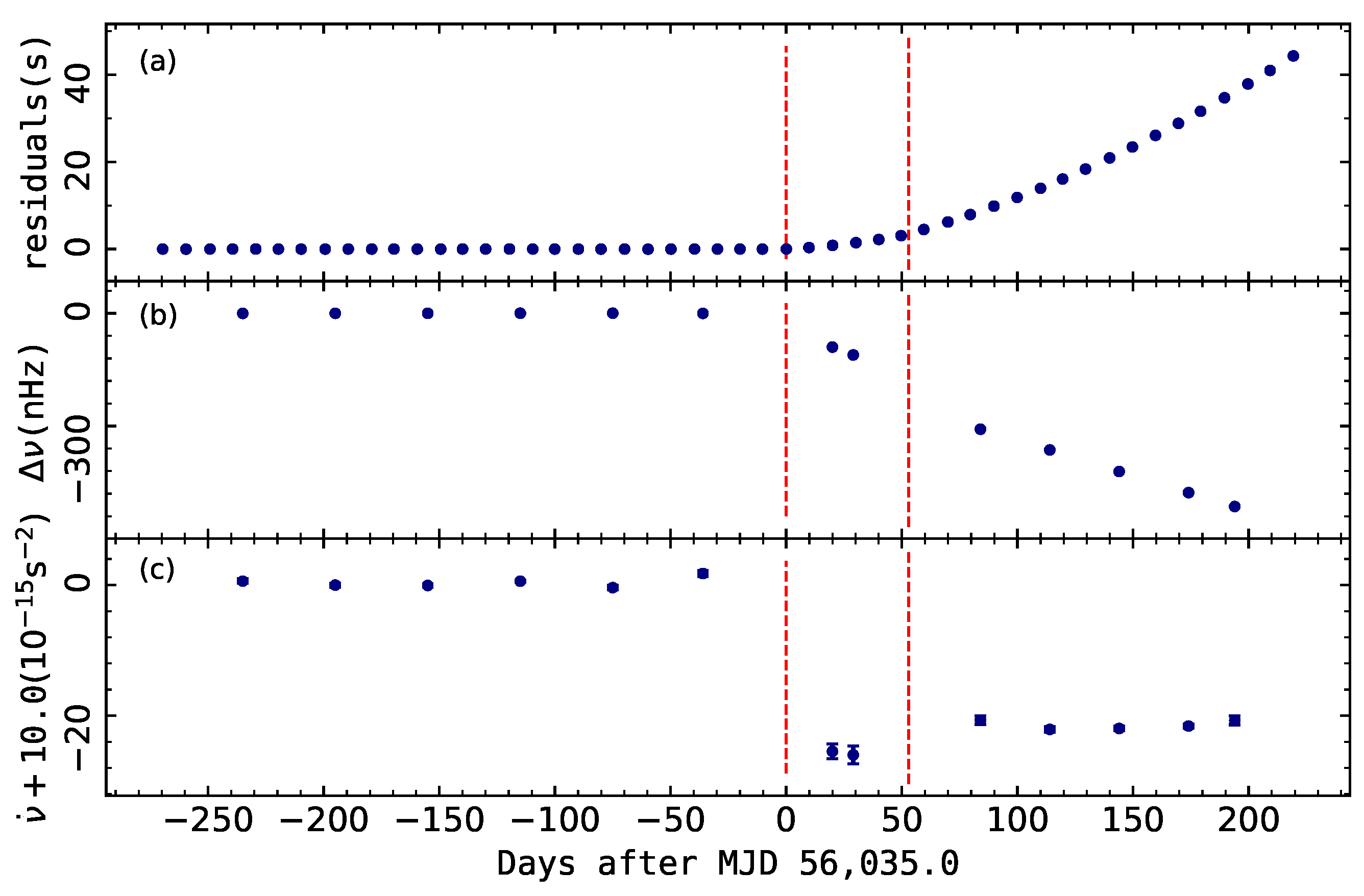
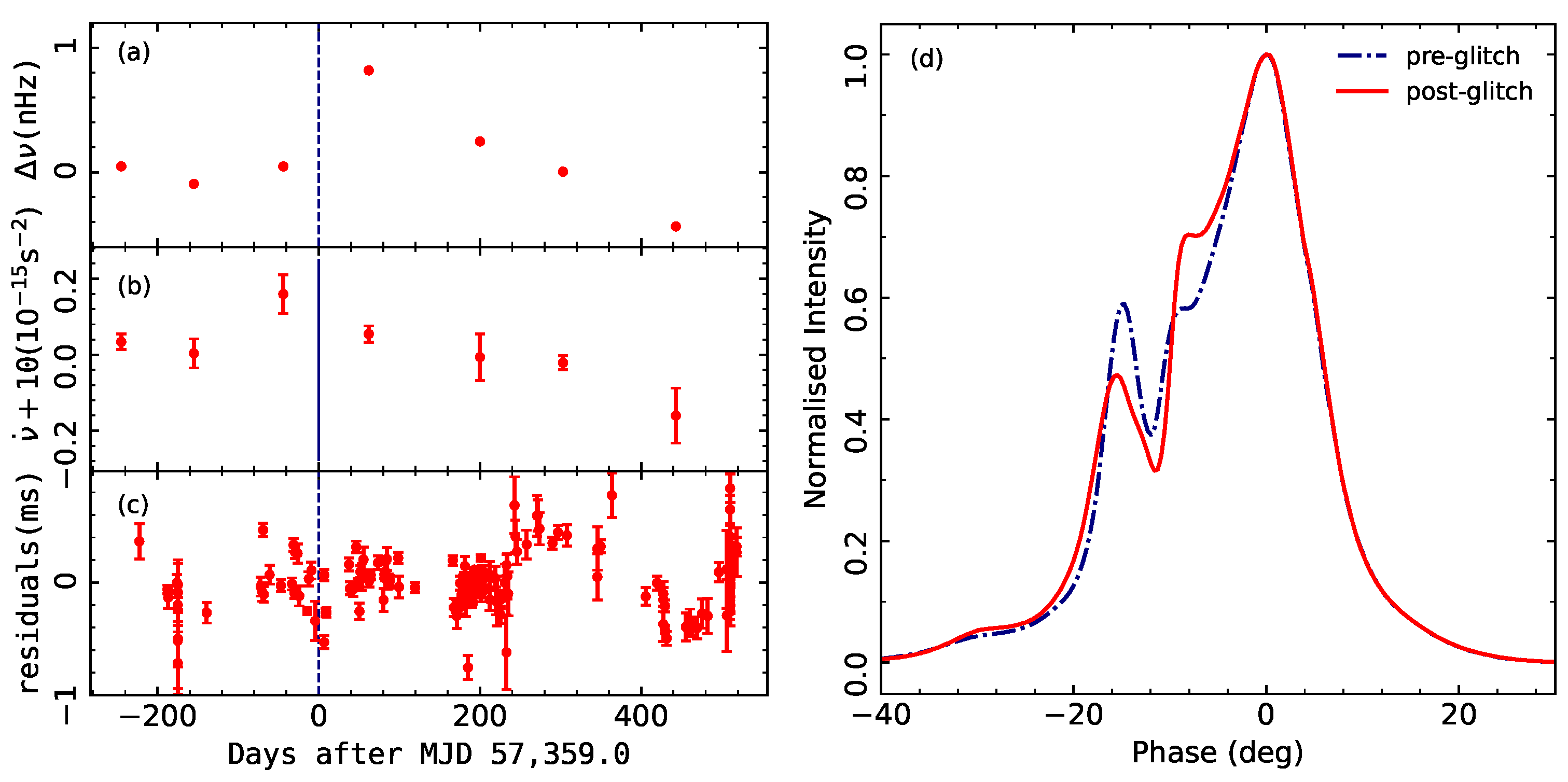


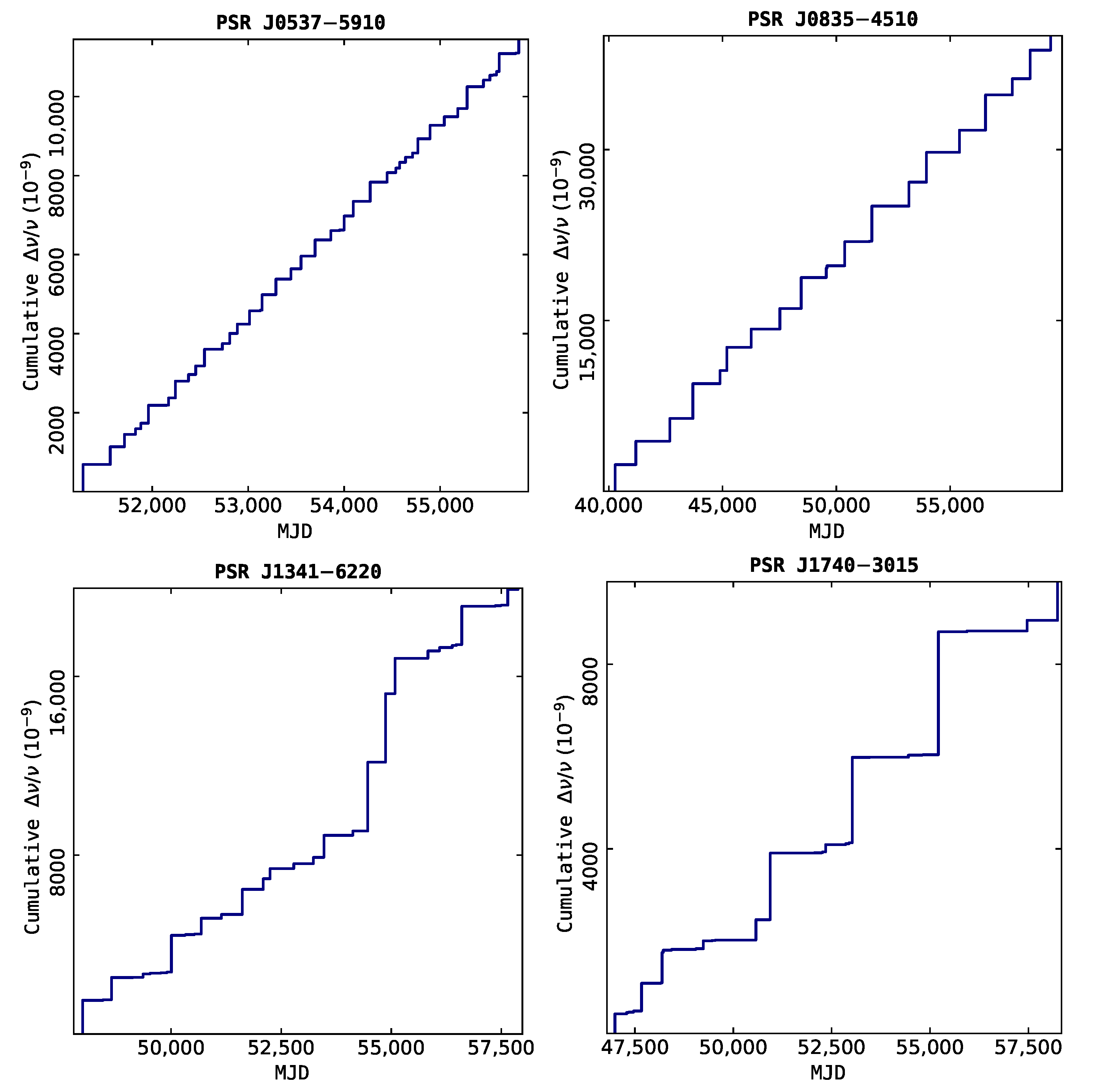
| Telescopes | Location | Diameter | Frequency | Pulsars | Start | No. of Glitches | Ref. |
|---|---|---|---|---|---|---|---|
| NSRT | Nanshan | 26 m | 1.54 GHz | ∼300 | 2000 | 103 | [43,44,49,50,51,52,53,54,55,56,57,58,59,60] |
| TMRT | Shanghai | 65 m | 2.25/4.82/8.60 GHz | ∼100 | 2013 | 5 | [61,62,63,64] |
| Insight-HXMT | Space | – | 1–250 keV | ∼10 | 2017 | 3 | [45,65] |
| KMRT | Yunnan | 40 m | 2.25/4.85 GHz | ∼90 | 2008 | 1 | [66] |
| HRT | Luonan | 40 m | 1.40 GHz | ∼10 | 2014 | 1 | [67] |
| XPNAV-1 | Space | – | 0.5–10 keV | ∼26 | 2016 | 1 | [46] |
| FAST | Pingtang | 500 m | 1.25 GHz | ∼350 | 2016 | – | [68] |
| QTT | Qitai | 110 m | – | – | – | – | [47] |
| JRT | Jingdong | 120 m | – | – | – | – | [48] |
| Pulsar Name (PSR) | P (s) | (kyr) | () | () | () | () | Profile | Ref. |
|---|---|---|---|---|---|---|---|---|
| J0738–4042 | 0.3749 | 4320 | 0.727 | 10 | 0.36(4) | 3(1) | (↓) | [53] |
| J0742–2822 | 0.1667 | 157 | 1.69 | 1400 | 102.73(11) | 2.1(5) | [336,337] | |
| J1119–6127 | 0.4079 | 1.61 | 41 | 23,000 | 9400(300) | 580(14) | [338] | |
| 5740(80) | 79(25) | X(↑) | [339] | |||||
| B1822–09 | 0.7690 | 233 | 6.42 | 45 | 4.08(2) | 0.08(1) | [63] | |
| 7.2(1) | 1.65(7) | [63] | ||||||
| J2021+4026 | 0.2653 | 76.9 | 3.85 | 1200 | <100(–) | 56(9) | (↓) | [340,341] |
| B2021+51 | 0.5291 | 2740 | 1.29 | 8.2 | 0.373(5) | –0.24(3) | (↓) | [62] |
| B2035+36 | 0.6187 | 2180 | 1.69 | 7.5 | 7.7(8) | 67(8) | (↓) | [44] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Gügercinoğlu, E.; Yuan, J.; Ge, M.; Yu, C. Pulsar Glitches: A Review. Universe 2022, 8, 641. https://doi.org/10.3390/universe8120641
Zhou S, Gügercinoğlu E, Yuan J, Ge M, Yu C. Pulsar Glitches: A Review. Universe. 2022; 8(12):641. https://doi.org/10.3390/universe8120641
Chicago/Turabian StyleZhou, Shiqi, Erbil Gügercinoğlu, Jianping Yuan, Mingyu Ge, and Cong Yu. 2022. "Pulsar Glitches: A Review" Universe 8, no. 12: 641. https://doi.org/10.3390/universe8120641
APA StyleZhou, S., Gügercinoğlu, E., Yuan, J., Ge, M., & Yu, C. (2022). Pulsar Glitches: A Review. Universe, 8(12), 641. https://doi.org/10.3390/universe8120641







