Abstract
A rapidly rotating and highly magnetized remnant neutron star (NS; magnetar) could survive from a merger of double NSs and drive a powerful relativistic wind. The early interaction of this wind with the previous merger ejecta can lead to shock breakout (SBO) emission mainly in ultraviolet and soft X-ray bands, which provides an observational signature for the existence of the remnant magnetar. Here, we investigate the effect of an anisotropic structure of the merger ejecta on the SBO emission. It is found that the bolometric light curve of the SBO emission can be broadened, since the SBO can occur at different times for different directions. In more detail, the profile of the SBO light curve can be highly dependent on the ejecta structure and, thus, we can in principle use the SBO light curves to probe the structure of the merger ejecta in future.
1. Introduction
Kilonovae are optical transient emission originating from mergers of double neutron stars (NSs) or NS-black hole (BH) binaries [1,2,3,4,5,6]. The power source of the kilonova emission is conventionally considered to be the radioactive decays of r-process elements, as these elements can be synthesized effectively in the neutron-rich merger ejecta. As an electromagnetic counterpart of the merger-induced GW radiation, kilonova emission can play a very important role in confirming the position, time, redshift, and even the progenitor properties of the mergers. Such effects of kilonovae had been manifested completely in the famous GW170817 event [7], which was accompanied with a kilonova AT2017gfo [8,9,10,11,12,13,14,15,16]. The detailed modeling of the observed kilonovae and as well as their associated gamma-ray burst (GRB) afterglows could further give constraint on the properties of the merger products, especially, when the traditional kilonova model is challenged by the observations.
The nature of the remnant of double NS mergers is one of the most concerned issues in current astrophysical studies. The answer to this mystery would help to constrain the mass limit of NSs and thus the equation of state (EOS) of nuclear matter, which is highly related to the unclear non-perturbative quantum chromodynamics at low energies. However, the confirmation of the nature of merger products is beyond the ability of the current GW detectors, since the detector sensitivities are still higher than the potential GW radiation from the merger products [17]. Therefore, alternatively, it is expected that the electromagnetic counterparts of the GW events can provide other observational signatures for judging the nature of the merger products. Following this consideration, Yu et al. (2013) [18] and Metzger and Piro (2014) [19] investigated the influence of a post-merger NS on the kilonova emission, where the remnant NS is considered to be rapidly rotating and highly magnetized, i.e., a millisecond magnetar. As the most direct effect, the spin-down of the millisecond magnetar can inject energy into the merger ejecta and then enhance the kilonova emission and accelerate the ejecta significantly. Thus, a new name of mergernova was suggested to replace the traditional kilonova in order to reflect the predicted wide range of the emission luminosity that depends on the specific properties of the remnant NS [18]. Using this magnetar-driven mergernova model, Yu et al. (2018) successfully accounted for the relatively high luminosity of AT 2017gfo on the order of ∼ [20], whereas the radioactive kilonova model needs to invoke a too high ejecta mass [21,22,23] (cf., Reference [24] showed this difficulty could be somewhat overcome by considering the 2D radiative transfer elaborately).
Frankly speaking, in view of the complication of mergernova emission, only the information of the luminosity and temperature of the emission is not enough for confirming the existence of a post-merger magnetar. The detailed transfer and transformation of the spin-down energy of the magnetar need to be investigated further [19,20,21,25,26,27,28,29,30,31,32,33,34,35], which could lead to some extra independent observational signatures for the magnetar. Specifically, the energy release from the spinning-down magnetar could be initally in the form of a Poynting flux and gradually transform into a relativistic wind consisting of electron/positron pairs. Once this magnetar wind catches up and collides with the preceding merger ejecta, it will generate a forward shock (FS) propagating into the ejecta and a termination shock (TS) reversely into the continuously injected wind. After a short period, the FS would break out from the ejecta, while the TS is long lasting. So, the primary channel of the energy transfer is the absorption of the TS emission (i.e., a pulsar wind nebula emission) by the merger ejecta. The TS emission can finally leak from the merger ejecta as the ejecta becomes transparent in the related electromagnetic band. As a rsult, a non-thermal emission component can appear in the late phase of the mergernova emission, which has been found in many mergernova candidates including AT2017gfo [26,29,31,32,33,34]. Meanwhile, the breakout of the FS could also cause a rapid soft X-ray flare prior to the primary mergernova emission [25], which is similar to the situation discovered in the supernovae that are suggested to be driven by a magnetar, too [36,37,38]. Generally, this shock breakout (SBO) precursor emission of a mergernova is likely to be outshone by more luminous afterglow emission of the associated GRB. Neverthelss, the observation of GRB 170817A indicates that the nearby GW events are very probably observed off-axis, which can significantly suppress the early afterglow emission and then make the SBO emission emerging.
Therefore, at present, it is necessary to investigate in advance more detailed features of the observational signatures of the magnetar-driven mergernovae, particularly, in expectation of the future discovery of the SBO emission. In theory, the propagation of the FS into the merger ejecta is determined by the radial structure of the merger ejecta. The description of the ejecta structure requires detailed numerical simulations. The first simulation on this topic was performed by Davies et al. [39] with an analytical EOS of nuclear matter and a Newtonian gravity [39], which showed that the ∼ mass of the system can be ejected around the equatorial plane as the dynamical tail of the spiral tidal arms. This result was subsequently reproduced by more simulations [40,41,42,43,44], which further found that (i) the neutrino-energy deposition in the cool outer regions of the tidal arms can enhance the mass loss and (ii) the material at the contact interface between the NSs can be squeezed out, although the tidal ejecta could still be dominant. Subsequently, the consideration of general relativity and more realistic EOSs leads to some new understandings of the formation of the ejecta [45,46,47,48,49,50,51,52,53,54,55]. It is showed that the squeezed component of the ejecta could become dominant over the tidal component [47,48,56], as the squeezed material is effectively heated and accelerated by a shock, spreading into a quasi-isotropic region and owning a velocity higher than that of the tidal component. Then, the collision of the squeezed component with the tidal component would lead to a more complex structure of the ejecta. On the other hand, the simulations also showed that a thick disk of a mass of ∼ can surround the merger remnant and the neutrino emission from both the disk and remnant can drive a hot wind into a funnel shape region in the polar direction [57,58,59,60]. The disk wind component can last for a relatively long timescale due to the viscous heating in the disk, which is further dependent on the lifetime of the remnant NS and the magnetic field configuration of the disk [61,62,63,64]. As the accretion disk finally expands and becomes advection dominated, the wind would become more isotropic and slower until the accretion becomes inefficient [62,64,65,66]. In summary, the properties of the merger ejecta can vary obviously with the angle relative to the symmetric axis of the system, which may leave imprints in the SBO emission. Therefore, in this paper, we revisit the SBO emission by taking into account the anisotropic structure of the merger ejecta.
2. The Model
2.1. Anisotropic Merger Ejecta
As introduced, the material ejected during a merger of double NSs can have different origins, which at least contain three channels including the tidal and squeezed dynamical origins and the disk wind origin. These ejecta components own different masses, velocities, electron fractions, and element compositions, which leads the merger ejecta to be highly anisotropic. In this paper, we adopt the empirical description of the ejecta structure suggested by Kawaguchi et al. [24,67]. While the disk wind is considered to be roughly isotropic, the mass distribution of the dynamical ejecta can exhibit an angular dependence as follows [24,67]:
where represents the density ratio of to and
The above expressions were summarized from the numerical simulations such as those given by [22,49,51,68], which describe the combination of the tidal and squeezed components. The propagation of the magnetar wind-driven FS in the ejecta is highly dependent on the radial distribution of the ejecta mass. According to numerical simulations, we assume as usual that the radial profile of the different ejecta components can be described by power laws as follows [69]
which can be normalized by the masses of the disk wind ejecta and the dynamical ejecta , respectively. This 2D distribution of the density of the merger ejecta in the plane is shown in Figure 1 for the parameter values of Model A listed in Table 1. An axial symmetry around the z-axis is adopted. Here, the maximum radii of the ejecta components are determined by
where and are the corresponding maximum velocities.
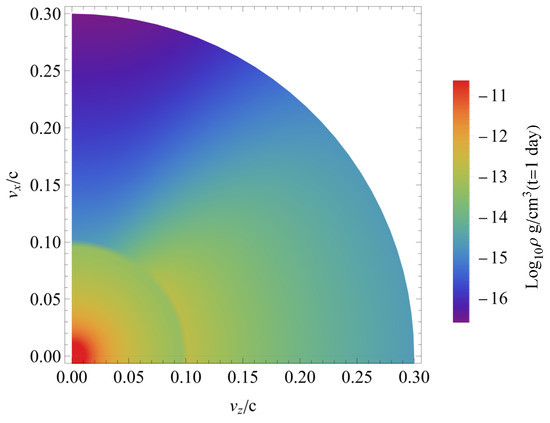
Figure 1.
The density profile employed in our calculations.

Table 1.
Model parameters.
2.2. Magnetar Wind
The remnant NS of a merger event is very likely to be in differential rotation initially, which can lead to the amplification of the magnetic fields of the NS through dynamo mechanisms (e.g., [70,71,72]). As the NS become a magnetar, a powerful relativistic wind can be driven with a luminosity of
where , and are the polar magnetic filed strength, radius, and spin period of the magnetar. Here, the convention is adopted in cgs units. The reference values of the parameters in the above expression are adopted by according to the inference from the shallow-decay and plateau afterglows of GRBs by ascribing these afterglow features to the consequence of a magnetar engine [73,74,75,76]. Nevertheless, the fitting of the mergernova AT2017gfo, which is in counterpart with the GW170817/GRB 170817A event, indicates that the magnetic filed of the remnant NS on a timescale of days could be not much higher than G [20,21], if such a NS indeed played a role in there as supposed. By combining with these two different observational constraints, Yu et al. (2018) suggested that the ultra-high magnetic field of the remnant magnetar could be suppressed drastically by some unclear mechanisms (e.g., hidden by fallback material) at a time of a few hundreds to thousands of seconds [20]. This assumption could also be supported by the discovery of an extremely steep decay following a plateau in some GRB afterglows. In any case, for simplicity, here we would not consider this potential complex in our calculation, and the temporal evolution of the wind luminosity is adopted to be as usual as
where is the spin-down timescale.
2.3. Shock Dynamics and Breakout Emission
As the powerful magnetar wind collides with the merger ejecta, the wind can be shocked by the TS to generate high energy emission, which is absorbed in part by the merger ejecta. Meanwhile, the FS propagates into and finally crosses the ejecta, and its the dynamical evolution can be determined by [25]
where is the shock velocity of the shock front, U is the total internal energy of the shocked region, and is the total luminosity of the thermal emission of merger ejecta. The increase of the swept-up mass can be calculated by
where is the radius of the shock front, is the velocity of the ejecta material in front of the shock, and the mass density is given by Equation (3). Meanwhile, the thermal energy deposited in the shocked material is given by
Here, since the merger ejecta is anisotropic, the above equations should be solved separately for different directions. After the determination of , the evolution of the internal energy accumulated by the shock can be derived from
where and are the volume and pressure of the shock heating region, respectively, and is the bolometric luminosity of the SBO emission. Meanwhile, the evolution of the internal energy excluding the shock-accumulated part, , can be written as (ignoring the radioactivity energy)
where and are the volume and the pressure of the ejecta behind the shock, respectively, and is the bolometric luminosity of the mergernova emission.
Following the approximate one-zone diffusion model in Reference [77], the bolometric luminosity of the SBO emission can be estimated by1
where is the radius at which SBO occurs and is the optical depth of the shell between the radii and . Above , photons can escape from the merger ejecta, because the photon diffusion time in the outside shell is equal to the dynamical time, i.e.,
from which the radius can be derived, where is the opacity. When , the above equation returns to its usual form as . Meanwhile, the bolometric luminosity of the mergernova emission can be given by
where and are the optical depths of shocked and unshocked ejecta. In our calculations, the opacity is adopted to be [33,78]
for and
for , where is the average internal temperature of the related region, k is the Boltzmann constant, is the Stefan–Boltzmann constant, and the values of parameters , , and are listed in Table 1. Here, for the dynamical ejecta, two different opacity values are simply taken for and , in order to reflect the angluar-dependence of the electron faction, which is result of the anisotropic neutrino irradiation from the remnant NS and the disk.
Finally, as photons diffuse and are thermalized continuously, a black-body emission appears at a photosphere of radius with an effective temperature of
where and is taken in our calculation. Then, the emergent net flux at a frequency can be given by using the black-body spectrum as
where h is the Planck constant.
2.4. Integration over the Emission Surface
As illustrated in Figure 2, we adopt coordinates with the z-axis along the symmetric axis of the system and denote the zenith and azimuth angles by and . Then, the specific luminosity for an observer on the line of sight (LOS) of can be obtained by integrating the specific intensity over the visible photosphere as
which is viable for an unresolved emitting source [79,80,81,82], where with and being the unit vectors of the normal of the differential solid angle and the direction of the LOS, respectively. For an ideal black-body surface, the angular distribution of emergent intensities is uniform and, thus, the value of can in principle be derived from Equation(19) to . However, as a more realistic consideration, the hot, expanding ejecta should contain an abundance of free electrons, especially, in the fastest head of dynamical ejecta. In other words, the atmosphere above the photosphere can deviate from the thermal equilibrium and become scattering dominated. In this case, the limb-darkening effect needs to be taken into account, which is widely discussed in the radiation transfer of stellar atmosphere [83,84,85]. Here, we simply consider pure isotropic scattering, which leads the emergent intensities to be different for different directions as [83,84,86]
where2
for and is the Hopf function. This function implies that the intensity emerging from the limb is about of that from the center of the emission source, when the Eddington approximation is taken , which is in fair agreement with the observations of the Sun.
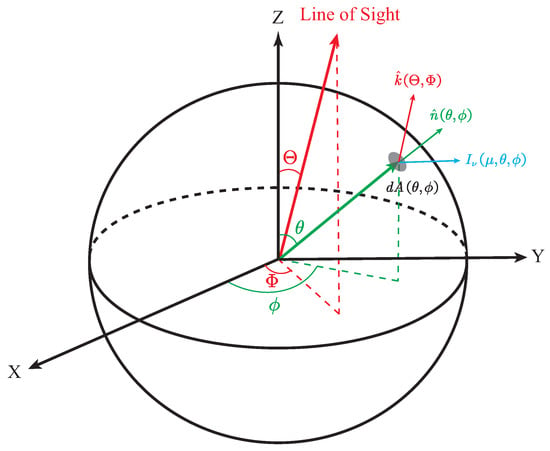
Figure 2.
The sketch of the coordinate system we use, the angles and represent the direction of line of sight, the angles and represent the location of a point in local structure.
3. Results
For the parameter values listed in Table 1, we calculate the light curves of the SBO and mergernova emission, as presented in Figure 3. First of all, the SBO emission is mainly in the UV and soft X-ray bands, while the mergernova emission is in optical, just as found in [25]. In comparison with the GRB afterglow emission, the SBO emission is most likely to be detected in soft X-rays, especially when the GRB jet deviates from the LOS.
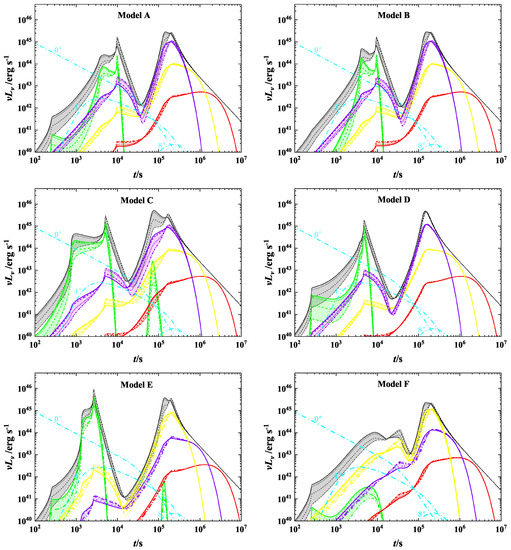
Figure 3.
Multi-band light curves of the magnetar-driven SBO (i.e., the first bump at around s) and mergernova (i.e., the second bump at around s) emission from an anisotropic merger ejecta for parameters listed in Table 1, including 0.1 keV (green), 6 keV (purple), 2 eV (yellow), 0.5 eV (red) and the bolometric ones (black). For a comparison, the GRB X-ray () afterglow is also presented by the cyan dotted–dashed lines for three viewing angles of , and , which are yielded from the afterglowpy [87] for a top-hat jet model with a half-opening angle of , where the typical parameter values as inferred from the GRB 170817A observations are taken as , , , , and . Due to the limb-darkening effect, the SBO emission can slightly vary with the observational directions, as labeled by the solid (), dotted (), dashed (), and dashed–dotted () lines.
The anisotropic structure of the merger ejecta can broaden the bolometric light curve of the SBO emission. This is because the SBO occurs at different times for different directions, and thus, it takes a relatively long period to observe the total SBO emission. In more detail, the harder emission can emerge earlier than the softer emission, since the former corresponds to a smaller SBO radius due to a thin merger ejecta in the polar direction while the latter comes from the thick equatorial ejecta. Such a shift of the highlight on the emission surface is clearly shown in Figure 4. In more detail, the comparison between the different panels shows that the profile of the light curves, in particular, of the increasing phase is highly dependent on the structure parameters of the ejecta, which thus enables us to probe the ejecta structure by observing this SBO emission.
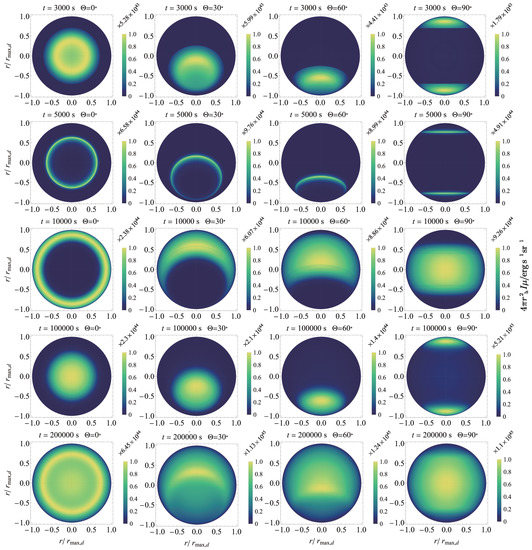
Figure 4.
The intensity distribution on the emission surface for different times (rows) and different viewing angles (columns), for the Model A parameter values.
In addition, the SBO light curves show a slight dependence of the viewing angle. This a result of the limb-darkening effect, which leads to the on-axis observation of an emitting element receiving more intensity than the off-axis observation. Therefore, when the highlight point moves on the emission surface, observers on different directions would detect different light curves, as also shown in Figure 4. Here, it is worth mentioning that this viewing angle-dependence of the SBO emission would be likely to cause a significant difference in the polarization of the emission between different observational directions, although its influence on the light curve profile is unremarkable.
4. Conclusions and Discussion
In this paper, we investigate the influence of the anisotropic structure of merger ejecta on the SBO emission driven by a magnetar wind. In view of the possible suppression of the magnetic field of the magnetar at late time, the early SBO emission (in particular, in the soft X-ray band) can provide an important observational signature for the existence of a remnant magnetar.
It is found that due to the different density distribution in different directions, the occurring time of the SBO can vary with the angle relative to the symmetric axis of the system. This leads to the broadening of the bolometric light curve of the SBO emission, which makes it more possible to be detected. Furthermore, in the future, as some detailed observations can be achieved (e.g., by the Einstein Probe [88]), we can even use the SBO light curve to probe the structure of the merger ejecta, where of course a more realistic structure description must be involved for elaborate modelings. In addition, we also find that the observational SBO emission can be slightly dependent on the viewing angle. This is because the anisotropic structure of the merger ejecta leads to a highlight point moving from the polar to the equatorial direction on the emission surface. This could simultaneously lead to a significant variation in the polarization of the emission for different observational directions, which is worth investigating carefully in the future.
Recently, some fast X-ray transients have been detected and suspected to be powered by a spinning-down magnetar [89,90,91], which could be directly contributed by the dissipating magnetic wind if it is not trapped by thick material [92]. Alternatively, as presented in this paper, even if the magentar wind is surrounded by a merger ejecta, the SBO driven by the magnetar wind could still generate an X-ray transient. In contrast to the highly beamed GRB emission, this SBO emission can in principle be detected at arbitrary directions, which therefore provides a valuable signal for testing the existence of the remnant magnetar. Additionally, in view of the similarity of the mergernovae and superluminous supernovae, such an SBO signal can also be expected to appear in these supernova emission, probably with a relatively longer timescale [37,38].
Author Contributions
Conceptualization, Y.-W.Y.; methodology, G.-L.W., Y.-W.Y. and S.-Z.L.; software, G.-L.W.; validation, G.-L.W., Y.-W.Y. and S.-Z.L.; formal analysis, G.-L.W.; investigation, G.-L.W.; writing—original draft preparation, G.-L.W.; writing—review and editing, Y.-W.Y. and S.-Z.L.; visualization, G.-L.W.; supervision, Y.-W.Y.; project administration, Y.-W.Y.; funding acquisition, Y.-W.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Key R&D Program of China (2021YFA0718500), the National SKA Program of China (2020SKA0120300), and the National Natural Science Foundation of China (grant No. 11833003).
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | Here, the shocked energy is considered to distribute approximately uniformly behind the shock, which is different from [25], where the shocked energy is assumed to be concentrated within a thin shell immediately behind the shock front. |
| 2 | An exact expression of had been given by Mihalas [85] as
|
References
- Li, L.X.; Paczyński, B. Transient Events from Neutron Star Mergers. Astrophys. J. 1998, 507, L59–L62. [Google Scholar] [CrossRef]
- Metzger, B.D.; Martínez-Pinedo, G.; Darbha, S.; Quataert, E.; Arcones, A.; Kasen, D.; Thomas, R.; Nugent, P.; Panov, I.V.; Zinner, N.T. Electromagnetic counterparts of compact object mergers powered by the radioactive decay of r-process nuclei. Mon. Not. R. Astron. Soc. 2010, 406, 2650–2662. [Google Scholar] [CrossRef]
- Roberts, L.F.; Kasen, D.; Lee, W.H.; Ramirez-Ruiz, E. Electromagnetic Transients Powered by Nuclear Decay in the Tidal Tails of Coalescing Compact Binaries. Astrophys. J. 2011, 736, L21. [Google Scholar] [CrossRef]
- Barnes, J.; Kasen, D. Effect of a High Opacity on the Light Curves of Radioactively Powered Transients from Compact Object Mergers. Astrophys. J. 2013, 775, 18. [Google Scholar] [CrossRef]
- Kasen, D.; Badnell, N.R.; Barnes, J. Opacities and Spectra of the r-process Ejecta from Neutron Star Mergers. Astrophys. J. 2013, 774, 25. [Google Scholar] [CrossRef]
- Tanaka, M.; Hotokezaka, K. Radiative Transfer Simulations of Neutron Star Merger Ejecta. Astrophys. J. 2013, 775, 113. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. 2017, 848, L13. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. 2017, 848, L12. [Google Scholar] [CrossRef]
- Arcavi, I.; Hosseinzadeh, G.; Howell, D.A.; McCully, C.; Poznanski, D.; Kasen, D.; Barnes, J.; Zaltzman, M.; Vasylyev, S.; Maoz, D.; et al. Optical emission from a kilonova following a gravitational-wave-detected neutron-star merger. Nature 2017, 551, 64–66. [Google Scholar] [CrossRef]
- Coulter, D.A.; Foley, R.J.; Kilpatrick, C.D.; Drout, M.R.; Piro, A.L.; Shappee, B.J.; Siebert, M.R.; Simon, J.D.; Ulloa, N.; Kasen, D.; et al. Swope Supernova Survey 2017a (SSS17a), the optical counterpart to a gravitational wave source. Science 2017, 358, 1556–1558. [Google Scholar] [CrossRef]
- Cowperthwaite, P.S.; Berger, E.; Villar, V.A.; Metzger, B.D.; Nicholl, M.; Chornock, R.; Blanchard, P.K.; Fong, W.; Margutti, R.; Soares-Santos, M.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/Virgo GW170817. II. UV, Optical, and Near-infrared Light Curves and Comparison to Kilonova Models. Astrophys. J. 2017, 848, L17. [Google Scholar] [CrossRef]
- Evans, P.A.; Cenko, S.B.; Kennea, J.A.; Emery, S.W.K.; Kuin, N.P.M.; Korobkin, O.; Wollaeger, R.T.; Fryer, C.L.; Madsen, K.K.; Harrison, F.A.; et al. Swift and NuSTAR observations of GW170817: Detection of a blue kilonova. Science 2017, 358, 1565–1570. [Google Scholar] [CrossRef] [PubMed]
- Nicholl, M.; Berger, E.; Kasen, D.; Metzger, B.D.; Elias, J.; Briceño, C.; Alexander, K.D.; Blanchard, P.K.; Chornock, R.; Cowperthwaite, P.S.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/Virgo GW170817. III. Optical and UV Spectra of a Blue Kilonova from Fast Polar Ejecta. Astrophys. J. 2017, 848, L18. [Google Scholar] [CrossRef]
- Smartt, S.J.; Chen, T.W.; Jerkstrand, A.; Coughlin, M.; Kankare, E.; Sim, S.A.; Fraser, M.; Inserra, C.; Maguire, K.; Chambers, K.C.; et al. A kilonova as the electromagnetic counterpart to a gravitational-wave source. Nature 2017, 551, 75–79. [Google Scholar] [CrossRef] [PubMed]
- Soares-Santos, M.; Holz, D.E.; Annis, J.; Chornock, R.; Herner, K.; Berger, E.; Brout, D.; Chen, H.Y.; Kessler, R.; Sako, M.; et al. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/Virgo GW170817. I. Discovery of the Optical Counterpart Using the Dark Energy Camera. Astrophys. J. 2017, 848, L16. [Google Scholar] [CrossRef]
- Tanvir, N.R.; Levan, A.J.; González-Fernández, C.; Korobkin, O.; Mandel, I.; Rosswog, S.; Hjorth, J.; D’Avanzo, P.; Fruchter, A.S.; Fryer, C.L.; et al. The Emergence of a Lanthanide-rich Kilonova Following the Merger of Two Neutron Stars. Astrophys. J. 2017, 848, L27. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Search for Post-merger Gravitational Waves from the Remnant of the Binary Neutron Star Merger GW170817. Astrophys. J. 2017, 851, L16. [Google Scholar] [CrossRef]
- Yu, Y.W.; Zhang, B.; Gao, H. Bright “Merger-nova” from the Remnant of a Neutron Star Binary Merger: A Signature of a Newly Born, Massive, Millisecond Magnetar. Astrophys. J. 2013, 776, L40. [Google Scholar] [CrossRef]
- Metzger, B.D.; Piro, A.L. Optical and X-ray emission from stable millisecond magnetars formed from the merger of binary neutron stars. Mon. Not. R. Astron. Soc. 2014, 439, 3916–3930. [Google Scholar] [CrossRef]
- Yu, Y.W.; Liu, L.D.; Dai, Z.G. A Long-lived Remnant Neutron Star after GW170817 Inferred from Its Associated Kilonova. Astrophys. J. 2018, 861, 114. [Google Scholar] [CrossRef]
- Li, S.Z.; Liu, L.D.; Yu, Y.W.; Zhang, B. What Powered the Optical Transient AT2017gfo Associated with GW170817? Astrophys. J. 2018, 861, L12. [Google Scholar] [CrossRef]
- Shibata, M.; Fujibayashi, S.; Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Sekiguchi, Y.; Tanaka, M. Modeling GW170817 based on numerical relativity and its implications. Phys. Rev. D 2017, 96, 123012. [Google Scholar] [CrossRef]
- Metzger, B.D.; Thompson, T.A.; Quataert, E. A Magnetar Origin for the Kilonova Ejecta in GW170817. Astrophys. J. 2018, 856, 101. [Google Scholar] [CrossRef]
- Kawaguchi, K.; Shibata, M.; Tanaka, M. Radiative Transfer Simulation for the Optical and Near-infrared Electromagnetic Counterparts to GW170817. Astrophys. J. 2018, 865, L21. [Google Scholar] [CrossRef]
- Li, S.Z.; Yu, Y.W. Shock Breakout Driven by the Remnant of a Neutron Star Binary Merger: An X-ray Precursor of Mergernova Emission. Astrophys. J. 2016, 819, 120. [Google Scholar] [CrossRef]
- Gao, H.; Ding, X.; Wu, X.F.; Dai, Z.G.; Zhang, B. GRB 080503 Late Afterglow Re-brightening: Signature of a Magnetar-powered Merger-nova. Astrophys. J. 2015, 807, 163. [Google Scholar] [CrossRef]
- Siegel, D.M.; Ciolfi, R. Electromagnetic Emission from Long-lived Binary Neutron Star Merger Remnants. I. Formulation of the Problem. Astrophys. J. 2016, 819, 14. [Google Scholar] [CrossRef]
- Siegel, D.M.; Ciolfi, R. Electromagnetic Emission from Long-lived Binary Neutron Star Merger Remnants. II. Lightcurves and Spectra. Astrophys. J. 2016, 819, 15. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, B.; Lü, H.J.; Li, Y. Searching for Magnetar-powered Merger-novae from Short GRBS. Astrophys. J. 2017, 837, 50. [Google Scholar] [CrossRef]
- Wollaeger, R.T.; Fryer, C.L.; Fontes, C.J.; Lippuner, J.; Vestrand, W.T.; Mumpower, M.R.; Korobkin, O.; Hungerford, A.L.; Even, W.P. Impact of Pulsar and Fallback Sources on Multifrequency Kilonova Models. Astrophys. J. 2019, 880, 22. [Google Scholar] [CrossRef]
- Yu, Y.W.; Chen, A.; Li, X.D. X-ray Transients from the Accretion-induced Collapse of White Dwarfs. Astrophys. J. 2019, 877, L21. [Google Scholar] [CrossRef]
- Ren, J.; Lin, D.B.; Zhang, L.L.; Li, X.Y.; Liu, T.; Lu, R.J.; Wang, X.G.; Liang, E.W. A Pulsar Wind Nebula Embedded in the Kilonova AT 2017gfo Associated with GW170817/GRB 170817A. Astrophys. J. 2019, 885, 60. [Google Scholar] [CrossRef]
- Ren, J.; Dai, Z.G. Broad-band emission from a kilonova ejecta-pulsar wind Nebula system: Late-time X-ray afterglow rebrightening of GRB 170817A. Mon. Not. R. Astron. Soc. 2022, 512, 5572–5579. [Google Scholar] [CrossRef]
- Wu, G.L.; Yu, Y.W.; Zhu, J.P. Does a long-lived remnant neutron star exist after short gamma-ray burst GRB 160821B? Astron. Astrophys. 2021, 654, A124. [Google Scholar] [CrossRef]
- Ai, S.; Zhang, B.; Zhu, Z. Engine-fed Kilonovae (Mergernovae)—I. Dynamical Evolution and Energy Injection / Heating Efficiencies. arXiv 2022, arXiv:2203.03045. [Google Scholar] [CrossRef]
- Kasen, D.; Metzger, B.D.; Bildsten, L. Magnetar-driven Shock Breakout and Double-peaked Supernova Light Curves. Astrophys. J. 2016, 821, 36. [Google Scholar] [CrossRef]
- Liu, L.D.; Gao, H.; Wang, X.F.; Yang, S. Magnetar-driven Shock Breakout Revisited and Implications for Double-peaked Type I Superluminous Supernovae. Astrophys. J. 2021, 911, 142. [Google Scholar] [CrossRef]
- Zhang, Z.D.; Yu, Y.W.; Liu, L.D. The effects of a magnetar engine on the gamma-ray burst-associated supernovae: Application to double-peaked SN 2006aj. arXiv 2022, arXiv:2204.11092. [Google Scholar] [CrossRef]
- Davies, M.B.; Benz, W.; Piran, T.; Thielemann, F.K. Merging Neutron Stars. I. Initial Results for Coalescence of Noncorotating Systems. Astrophys. J. 1994, 431, 742. [Google Scholar] [CrossRef]
- Ruffert, M.; Janka, H.T.; Schaefer, G. Coalescing neutron stars—A step towards physical models. I. Hydrodynamic evolution and gravitational-wave emission. Astron. Astrophys. 1996, 311, 532–566. [Google Scholar]
- Rosswog, S.; Liebendörfer, M.; Thielemann, F.K.; Davies, M.B.; Benz, W.; Piran, T. Mass ejection in neutron star mergers. Astron. Astrophys. 1999, 341, 499–526. [Google Scholar]
- Rosswog, S.; Davies, M.B.; Thielemann, F.K.; Piran, T. Merging neutron stars: Asymmetric systems. Astron. Astrophys. 2000, 360, 171–184. [Google Scholar]
- Ruffert, M.; Janka, H.T. Coalescing neutron stars—A step towards physical models. III. Improved numerics and different neutron star masses and spins. Astron. Astrophys. 2001, 380, 544–577. [Google Scholar] [CrossRef]
- Korobkin, O.; Rosswog, S.; Arcones, A.; Winteler, C. On the astrophysical robustness of the neutron star merger r-process. Mon. Not. R. Astron. Soc. 2012, 426, 1940–1949. [Google Scholar] [CrossRef]
- Piran, T.; Nakar, E.; Rosswog, S. The electromagnetic signals of compact binary mergers. Mon. Not. R. Astron. Soc. 2013, 430, 2121–2136. [Google Scholar] [CrossRef]
- Rosswog, S.; Piran, T.; Nakar, E. The multimessenger picture of compact object encounters: Binary mergers versus dynamical collisions. Mon. Not. R. Astron. Soc. 2013, 430, 2585–2604. [Google Scholar] [CrossRef]
- Bauswein, A.; Goriely, S.; Janka, H.T. Systematics of Dynamical Mass Ejection, Nucleosynthesis, and Radioactively Powered Electromagnetic Signals from Neutron-star Mergers. Astrophys. J. 2013, 773, 78. [Google Scholar] [CrossRef]
- Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Okawa, H.; Sekiguchi, Y.i.; Shibata, M.; Taniguchi, K. Mass ejection from the merger of binary neutron stars. Phys. Rev. D 2013, 87, 024001. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Kiuchi, K.; Kyutoku, K.; Shibata, M.; Taniguchi, K. Dynamical mass ejection from the merger of asymmetric binary neutron stars: Radiation-hydrodynamics study in general relativity. Phys. Rev. D 2016, 93, 124046. [Google Scholar] [CrossRef]
- Foucart, F.; O’Connor, E.; Roberts, L.; Kidder, L.E.; Pfeiffer, H.P.; Scheel, M.A. Impact of an improved neutrino energy estimate on outflows in neutron star merger simulations. Phys. Rev. D 2016, 94, 123016. [Google Scholar] [CrossRef]
- Radice, D.; Galeazzi, F.; Lippuner, J.; Roberts, L.F.; Ott, C.D.; Rezzolla, L. Dynamical mass ejection from binary neutron star mergers. Mon. Not. R. Astron. Soc. 2016, 460, 3255–3271. [Google Scholar] [CrossRef]
- Dietrich, T.; Bernuzzi, S.; Tichy, W. Closed-form tidal approximants for binary neutron star gravitational waveforms constructed from high-resolution numerical relativity simulations. Phys. Rev. D 2017, 96, 121501. [Google Scholar] [CrossRef]
- Dietrich, T.; Ujevic, M.; Tichy, W.; Bernuzzi, S.; Brügmann, B. Gravitational waves and mass ejecta from binary neutron star mergers: Effect of the mass ratio. Phys. Rev. D 2017, 95, 024029. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Hotokezaka, K.; Fromm, S.A.; Bernuzzi, S.; Roberts, L.F. Binary Neutron Star Mergers: Mass Ejection, Electromagnetic Counterparts, and Nucleosynthesis. Astrophys. J. 2018, 869, 130. [Google Scholar] [CrossRef]
- Shibata, M.; Fujibayashi, S.; Sekiguchi, Y. Long-term evolution of neutron-star merger remnants in general relativistic resistive magnetohydrodynamics with a mean-field dynamo term. Phys. Rev. D 2021, 104, 063026. [Google Scholar] [CrossRef]
- Oechslin, R.; Janka, H.T.; Marek, A. Relativistic neutron star merger simulations with non-zero temperature equations of state. I. Variation of binary parameters and equation of state. Astron. Astrophys. 2007, 467, 395–409. [Google Scholar] [CrossRef]
- Dessart, L.; Ott, C.D.; Burrows, A.; Rosswog, S.; Livne, E. Neutrino Signatures and the Neutrino-Driven Wind in Binary Neutron Star Mergers. Astrophys. J. 2009, 690, 1681–1705. [Google Scholar] [CrossRef]
- Perego, A.; Rosswog, S.; Cabezón, R.M.; Korobkin, O.; Käppeli, R.; Arcones, A.; Liebendörfer, M. Neutrino-driven winds from neutron star merger remnants. Mon. Not. R. Astron. Soc. 2014, 443, 3134–3156. [Google Scholar] [CrossRef]
- Martin, D.; Perego, A.; Arcones, A.; Thielemann, F.K.; Korobkin, O.; Rosswog, S. Neutrino-driven Winds in the Aftermath of a Neutron Star Merger: Nucleosynthesis and Electromagnetic Transients. Astrophys. J. 2015, 813, 2. [Google Scholar] [CrossRef]
- Fujibayashi, S.; Sekiguchi, Y.; Kiuchi, K.; Shibata, M. Properties of Neutrino-driven Ejecta from the Remnant of a Binary Neutron Star Merger: Pure Radiation Hydrodynamics Case. Astrophys. J. 2017, 846, 114. [Google Scholar] [CrossRef]
- Siegel, D.M.; Ciolfi, R.; Rezzolla, L. Magnetically Driven Winds from Differentially Rotating Neutron Stars and X-ray Afterglows of Short Gamma-Ray Bursts. Astrophys. J. 2014, 785, L6. [Google Scholar] [CrossRef]
- Fujibayashi, S.; Kiuchi, K.; Nishimura, N.; Sekiguchi, Y.; Shibata, M. Mass Ejection from the Remnant of a Binary Neutron Star Merger: Viscous-radiation Hydrodynamics Study. Astrophys. J. 2018, 860, 64. [Google Scholar] [CrossRef]
- Siegel, D.M.; Metzger, B.D. Three-dimensional GRMHD Simulations of Neutrino-cooled Accretion Disks from Neutron Star Mergers. Astrophys. J. 2018, 858, 52. [Google Scholar] [CrossRef]
- Fernández, R.; Tchekhovskoy, A.; Quataert, E.; Foucart, F.; Kasen, D. Long-term GRMHD simulations of neutron star merger accretion discs: Implications for electromagnetic counterparts. Mon. Not. R. Astron. Soc. 2019, 482, 3373–3393. [Google Scholar] [CrossRef]
- Fernández, R.; Metzger, B.D. Delayed outflows from black hole accretion tori following neutron star binary coalescence. Mon. Not. R. Astron. Soc. 2013, 435, 502–517. [Google Scholar] [CrossRef]
- Just, O.; Bauswein, A.; Ardevol Pulpillo, R.; Goriely, S.; Janka, H.T. Comprehensive nucleosynthesis analysis for ejecta of compact binary mergers. Mon. Not. R. Astron. Soc. 2015, 448, 541–567. [Google Scholar] [CrossRef]
- Kawaguchi, K.; Shibata, M.; Tanaka, M. Diversity of Kilonova Light Curves. Astrophys. J. 2020, 889, 171. [Google Scholar] [CrossRef]
- Kiuchi, K.; Kawaguchi, K.; Kyutoku, K.; Sekiguchi, Y.; Shibata, M.; Taniguchi, K. Sub-radian-accuracy gravitational waveforms of coalescing binary neutron stars in numerical relativity. Phys. Rev. D 2017, 96, 084060. [Google Scholar] [CrossRef]
- Nagakura, H.; Hotokezaka, K.; Sekiguchi, Y.; Shibata, M.; Ioka, K. Jet Collimation in the Ejecta of Double Neutron Star Mergers: A New Canonical Picture of Short Gamma-Ray Bursts. Astrophys. J. 2014, 784, L28. [Google Scholar] [CrossRef]
- Duncan, R.C.; Thompson, C. Formation of Very Strongly Magnetized Neutron Stars: Implications for Gamma-Ray Bursts. Astrophys. J. 1992, 392, L9. [Google Scholar] [CrossRef]
- Price, D.J.; Rosswog, S. Producing Ultrastrong Magnetic Fields in Neutron Star Mergers. Science 2006, 312, 719–722. [Google Scholar] [CrossRef]
- Cheng, Q.; Yu, Y.W. How can Newly Born Rapidly Rotating Neutron Stars Become Magnetars? Astrophys. J. 2014, 786, L13. [Google Scholar] [CrossRef]
- Yu, Y.W.; Cheng, K.S.; Cao, X.F. The Role of Newly Born Magnetars in Gamma-ray Burst X-ray Afterglow Emission: Energy Injection and Internal Emission. Astrophys. J. 2010, 715, 477–484. [Google Scholar] [CrossRef]
- Lyons, N.; O’Brien, P.T.; Zhang, B.; Willingale, R.; Troja, E.; Starling, R.L.C. Can X-ray emission powered by a spinning-down magnetar explain some gamma-ray burst light-curve features? Mon. Not. R. Astron. Soc. 2010, 402, 705–712. [Google Scholar] [CrossRef]
- Lü, H.J.; Zhang, B. A Test of the Millisecond Magnetar Central Engine Model of Gamma-Ray Bursts with Swift Data. Astrophys. J. 2014, 785, 74. [Google Scholar] [CrossRef]
- Lü, H.J.; Zhang, B.; Lei, W.H.; Li, Y.; Lasky, P.D. The Millisecond Magnetar Central Engine in Short GRBs. Astrophys. J. 2015, 805, 89. [Google Scholar] [CrossRef]
- Kasen, D.; Bildsten, L. Supernova Light Curves Powered by Young Magnetars. Astrophys. J. 2010, 717, 245–249. [Google Scholar] [CrossRef]
- Chen, M.H.; Li, L.X.; Lin, D.B.; Liang, E.W. Gamma-Ray Emission Produced by r-process Elements from Neutron Star Mergers. Astrophys. J. 2021, 919, 59. [Google Scholar] [CrossRef]
- Rybicki, G.B. Theoretical Methods of Treating Line Formation Problems in Steady-State Extended Atmospheres. Int. Astron. Union Colloq. 1970, 2, 85–118. [Google Scholar] [CrossRef][Green Version]
- Collins, G.W.I. Further Note on Terminology—Specific Luminosity. Astron. Astrophys. 1973, 26, 315. [Google Scholar]
- Kandel, R.S. Note on Terminology—Specific Luminosity. Astron. Astrophys. 1973, 22, 155. [Google Scholar]
- Rybicki, G.B.; Hummer, D.G. The specific luminosity of a three-dimensional medium in terms of the escape probability. Astrophys. J. 1983, 274, 380–398. [Google Scholar] [CrossRef]
- Hopf, E. Remarks on the Schwarzschild-Milne model of the outer layers of a star. Mon. Not. R. Astron. Soc. 1930, 90, 287–293. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Radiative Transfer; Dover: New York, NY, USA, 1960. [Google Scholar]
- Mihalas, D. Stellar Atmospheres; W.H. Freeman & Co.: San Francisco, CA, USA, 1978; pp. 53–74. [Google Scholar]
- Bronstein, M. Zum Strahlungsgleichgewichtsproblem von Milne. Zeitschrift fur Physik 1929, 58, 696–699. [Google Scholar] [CrossRef]
- Ryan, G.; van Eerten, H.; Piro, L.; Troja, E. Gamma-Ray Burst Afterglows in the Multimessenger Era: Numerical Models and Closure Relations. Astrophys. J. 2020, 896, 166. [Google Scholar] [CrossRef]
- Yuan, W. The Einstein Probe mission. In Proceedings of the 44th COSPAR Scientific Assembly, Athens, Greece, 16–24 July 2022; Volume 44, p. 1966. [Google Scholar]
- Xue, Y.Q.; Zheng, X.C.; Li, Y.; Brandt, W.N.; Zhang, B.; Luo, B.; Zhang, B.B.; Bauer, F.E.; Sun, H.; Lehmer, B.D.; et al. A magnetar-powered X-ray transient as the aftermath of a binary neutron-star merger. Nature 2019, 568, 198–201. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.; Irwin, J.A.; Berger, E.; Nguyen, R. Discovery of Three Candidate Magnetar-powered Fast X-ray Transients from Chandra Archival Data. Astrophys. J. 2022, 927, 211. [Google Scholar] [CrossRef]
- Quirola-Vásquez, J.; Bauer, F.E.; Jonker, P.G.; Brandt, W.N.; Yang, G.; Levan, A.J.; Xue, Y.Q.; Eappachen, D.; Zheng, X.C.; Luo, B. Extragalactic fast X-ray transient candidates discovered by Chandra (2000–2014). Astron. Astrophys. 2022, 663, A168. [Google Scholar] [CrossRef]
- Zhang, B. Early X-ray and Optical Afterglow of Gravitational Wave Bursts from Mergers of Binary Neutron Stars. Astrophys. J. 2013, 763, L22. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).