1. Introduction
In the last years, research in black hole physics has received renewed interest. This is due to the present era of high-precision measurements which have allowed the direct measurement of gravitational waves by LIGO and VIRGO and the image of supermassive black holes by EHT [
1,
2,
3,
4]. However, the black hole interior is riddled with spacetime singularities. To treat this, regular black holes in
D have been proposed (see [
5] and references therein). A good laboratory to study black hole properties is to consider its
counterpart, presented in 1992 by Bañados, Teitelboim, and Zanelli [
6]. The
Einstein–Hilbert’s theory at the classical level is trivial, in the sense that there are no gravitational waves, and any two solutions are locally equivalent. The
-dimensional vacuum has no local degrees of freedom [
7]. Hence, black holes were unexpected since a vacuum solution in
dimensions is necessarily flat. However, by considering a cosmological constant with
, Bañados, Teitelboim, and Zanelli discovered the honored BTZ black holes [
6].
With a strictly negative cosmological constant a
, a BH solution emerges presenting similar properties to the
-dimensional Schwarzschild and Kerr black holes. Remarkably, it admits a no-hair theorem, thus characterizing the solution by its ADM mass, angular momentum, and charge. Likewise, a rotating BTZ BH contains an inner and an outer horizon, analogous to an ergosphere in a Kerr BH. For our aim here, the most important characteristic of the BTZ BH is that it has thermodynamic properties closely analogous to those of realistic four-dimensional ones: a Hawking temperature and an entropy equal to a quarter of its event horizon area, where the surface area is replaced by the BTZ black hole’s disk [
8,
9,
10,
11,
12,
13,
14,
15]. Such notable results in a low dimensional setting strongly suggest that a BH’s statistical mechanics in higher dimensions can be successfully investigated within
-dimensional gravity.
The charged BTZ black hole also presents a singularity at the origin and a regular solution has been presented in ref. [
16]. In the last years, many ways have been used to obtain regular BTZ BHs by considering nonlinear sources, quasi-localized masses, and theories of modified gravity [
17,
18,
19,
20,
21,
22,
23,
24]. However, very recently, a new route to regular black holes has been developed called “black-bounce” spacetimes [
25]. The name is due to the fact that the spacetime neatly interpolates between the standard Schwarzschild black hole and the Morris–Thorne traversable wormhole [
26]. It is important to highlight that the study of traversable wormholes is a topic of great interest in the literature in several contexts [
27,
28,
29,
30,
31,
32,
33]. Beyond this, the geometry is regular everywhere if the “bounce” parameter
a is non-null. Thus, this generalization broadens the known class of regular black holes. Many properties and generalizations of the black-bounce in
have been found, including its rotating and charged counterparts [
34,
35,
36,
37,
38,
39]. However, curiously, up to now, only the case
has been considered.
In this paper, we present the first in a series of papers in which we study black-bounce solutions in dimensions other than D. We will consider the BTZ black-bounce and study its properties. The manuscript is organized as follows. In section two, we apply the Simpson–Visser regularization scheme to the BTZ black hole and analyze its properties. In section three, we study the thermodynamics of the BTZ black-bounce. In section four, we analyze orbits in this spacetime. Finally, in section five, we give the conclusion.
2. Simpson–Visser BTZ Black Hole
The usual solution for the charged BTZ black hole is given by [
6]
The parameter
M is the black hole’s mass,
l is related to the cosmological constant so that
, and
q is the charge. The above solution has, as in the Reissner–Nordström case, horizons and a singularity at
. Recently, a black-bounce was proposed by Simpson and Visser. It is a way to obtain a solution that interpolates between regular black holes and a wormhole. This is controlled by a regulator parameter
a, introduced by replacing
[
25]. We construct here a BTZ black-bounce in the same way. First, we consider the uncharged case, so that the black-bounce metric is obtained from Equation (
1) and given by
To analyze the horizons of the above solution, we note that the radial null curves are given by
Notice that if
we have
and that
. Thus, we identify this region as a (2+1)-dimension traversable wormhole [
26]. In the case when
, we have
and
. This allows us to characterize this case as a one-way wormhole since we have an extremal null throat at
[
25]. Finally, if
, we have
at the location of the horizons, symmetrically placed at
Therefore, the relation between the mass
M and the horizon radius is modified to
The above expressions recover the usual BTZ relation when
. Since
a is a real parameter, the possibility of negative mass regions in this context is disregarded. Such negative mass regions are related to black holes with nontrivial topology [
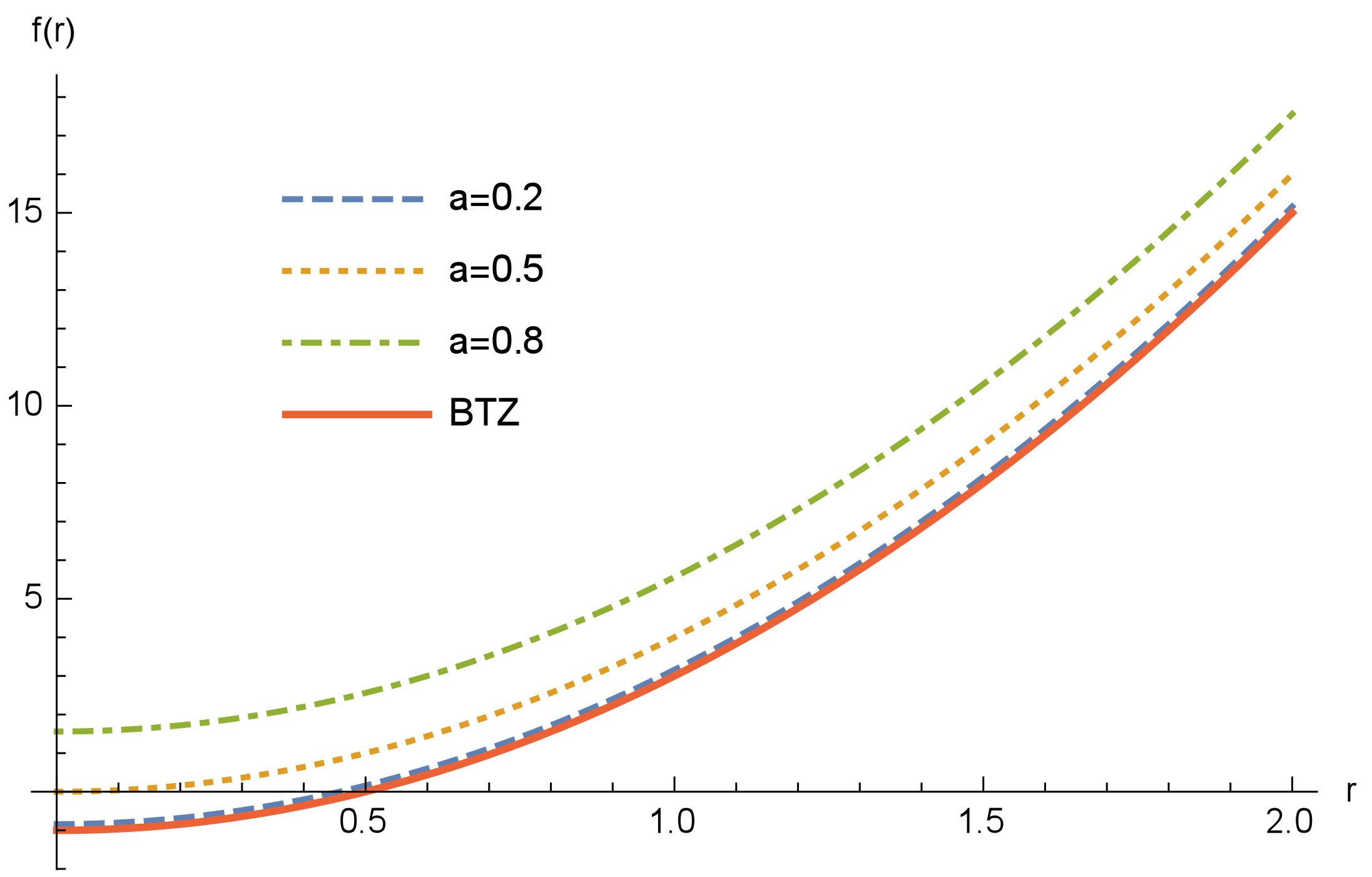
40]. The behavior of the Simpson–Visser BTZ solution is depicted in
Figure 1.
In order to properly discuss the singularities in the present context, we calculate the curvature invariants. The Ricci scalar can be straightforwardly calculated from the metric, which gives us
Note that when
(or alternatively
), we have
, which is the usual result for the BTZ black hole. Moreover, let us highlight that Equation (
5) is always finite, as expected from a regular solution.
The squared Ricci scalar, computed by the contraction
, is written as
while the Kretschmann scalar can be obtained by the contraction
yielding
Both the squared Ricci and the Kretschmann scalars are always finite, independent of the value of
r, and recover the usual BTZ results in the limit when
.
Some comments about the causal structure are necessary. First of all, for the black hole case (
), the Penrose diagram is identical to the one with
. The reason is that the only influence of
a is to change the radius of the horizon. We also have that all the curvature tensors are the same at
. Therefore, the causal structure is the same. The only case worth mentioning is the one-way wormhole (
). In this case, we have that
. Curiously, this is exactly equal to the standard BTZ black hole with
. The Penrose diagram is given in [
41]. The diagram has a null throat at
. The only difference with the Schwarzschild case is that the infinity is now timelike and represented by a vertical line.
3. Energy Conditions
We will now analyze the energy conditions for the matter supporting the Simpson–Visser black hole solution. Due to the bounce regulator parameter a, we must find the regions where the null-energy conditions (NEC, ), weak-energy conditions (WEC, ), strong-energy conditions (SEC, ), and dominant-energy conditions (DEC, ) are satisfied. The index i is for the coordinates, .
The energy density
and the quantities
and
are given by
where
and
stands for the radial pressure and lateral pressure, respectively. Let us notice initially that
is positive everywhere for any nonvanishing bounce parameter
a. Moreover, in order for
(condition present in the NEC, WEC, and SEC), it is required that
. Moreover, the DEC and WEC require that
, which implies
.
For short, the NEC and SEC are satisfied when
, while the WEC and DEC are satisfied when
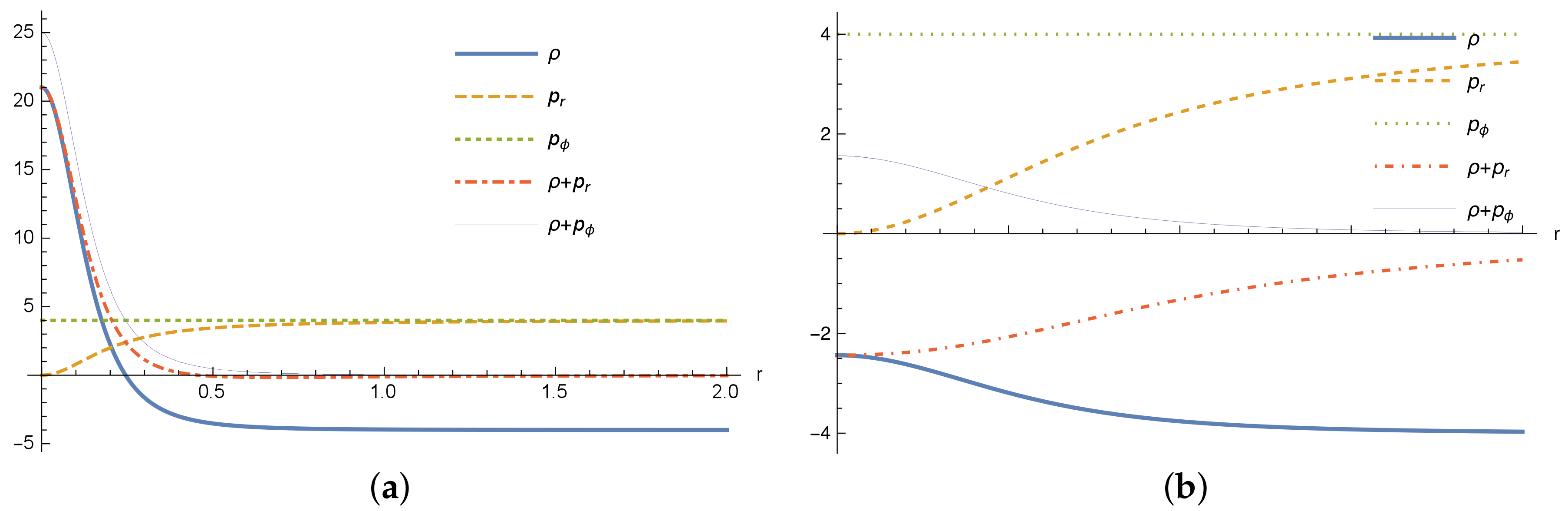
. In
Figure 2, we can see the behavior of the energy density, pressures, and their combination for the present model. The left panel stands for
, which means that we are in the black hole domain, since we are considering
and
. For the right panel, we used the same parameters but with
, so that in this case, we are in the wormhole domain.
Finally, it is important to investigate the state function
by considering a linear equation of state
in order to study what kind of matter would sustain such black holes or wormholes. The state function is given by
From the above equation, we can notice that in the limits when
or
, the state function goes to
(dark energy), which is the usual result for the BTZ black hole. Moreover, the state function can only be positive if the denominator is negative and this occurs only if
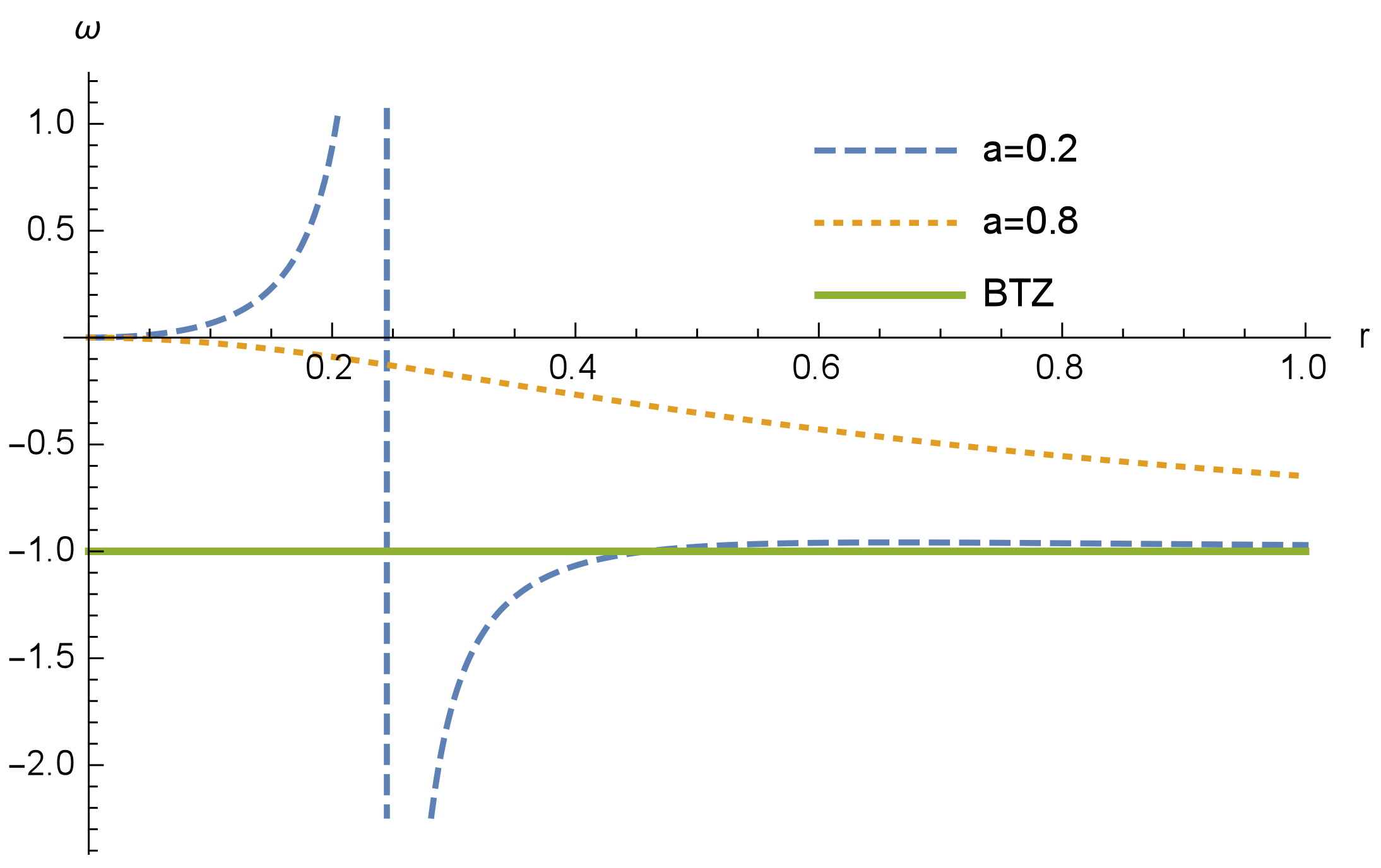
. In
Figure 3, we depict the state function behavior in terms of the radius. We used
and
. For this choice of parameters,
describes a black hole, and we can see that there is a region where it is possible to source this black hole with ordinary matter (
). Moreover, after the discontinuity in the state function given by
, we have regions sourced by phantom (
). For
, we are in the traversable wormhole domain. For this case, we can clearly see from
Figure 3 that the state function is always negative, hence the Simpson–Visser (2 + 1) dimensional wormhole can never be sourced by ordinary matter.
4. Thermodynamics
In possession of the solution for the Simpson–Visser BTZ black hole given by (
2), we are able to study the thermodynamics of the black hole by computing the Hawking’s temperature by means of
, where
is the radius of the horizon. The Hawking temperature for the present model exhibits no modifications in comparison to the usual BTZ black hole case, i.e., the Hawking temperature is given by
, showing the usual linear behavior with the horizon radius.
The entropy of the Simpson–Visser BTZ black hole also remains unmodified in comparison to that of the usual BTZ black hole. Thus, the entropy, given by yields for the present context the usual relation , i.e., twice the perimeter of the black hole. The same occurs with the specific heat, given by , which yields the usual result . Therefore, we can conclude that the proposed modification in the BTZ black hole leads to practically no modification in the thermodynamic parameters.
However, the free energy of the system is slightly changed. The free energy being given by
we obtain for our case
It is convenient to write the above expression for the free energy in terms of the mass
M and the cosmological constant, in order to properly analyze the domains of black hole and wormhole discussed previously. Thus,
From Equation (
12), it is clear that
(
) if
(
), and
when
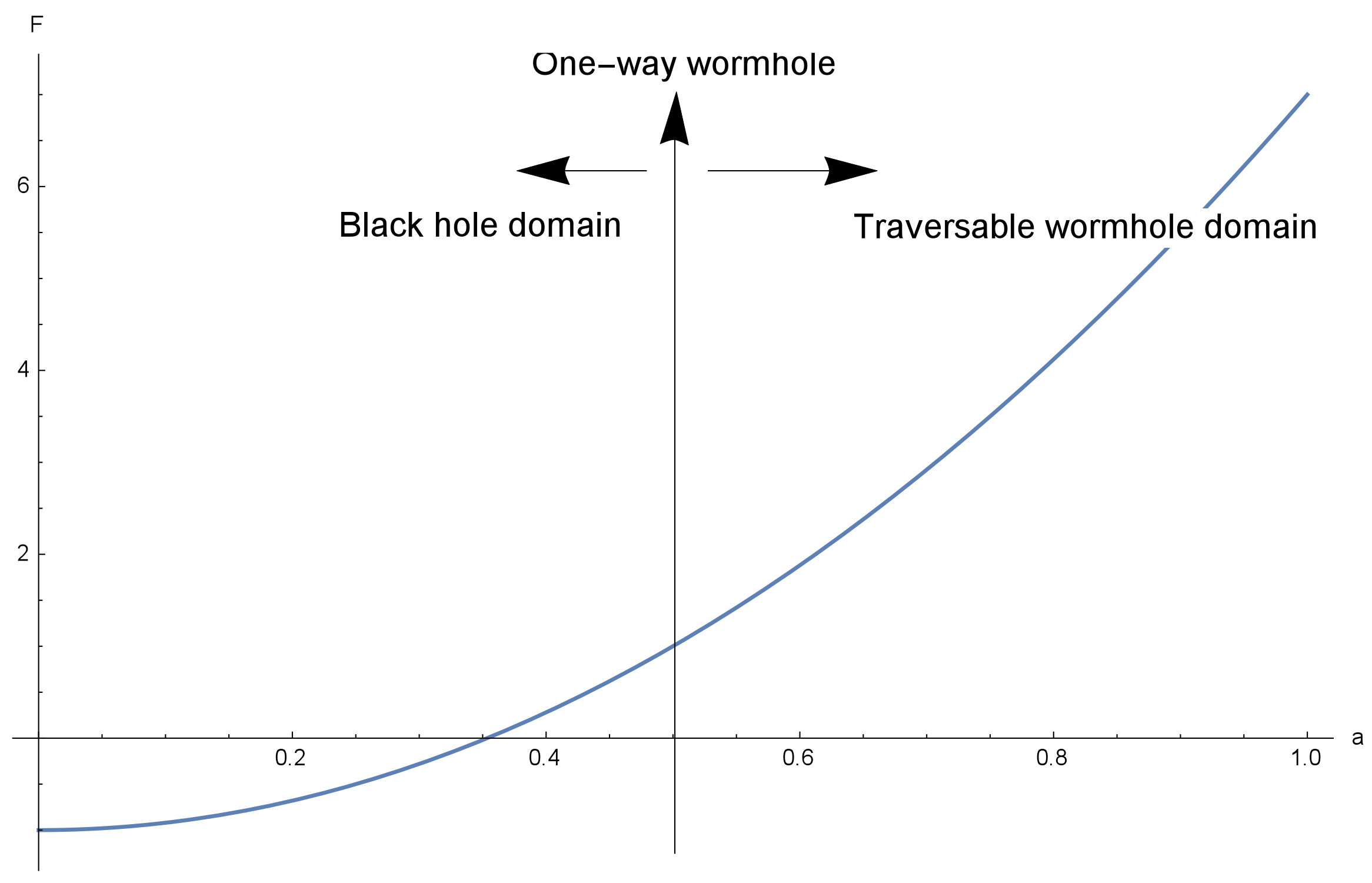
. We can see the behavior of the free energy as a function of the regulator parameter
a depicted in
Figure 4. We used
and
for the plot of
Figure 4. We can see that the black hole domain admits both positive and negative values for the free energy, depending on the value of the regulator parameter
a. On the other hand, the one-way wormhole and the traversable wormhole domain exhibit only positive values for the free energy.
5. Orbits Analysis
Now, let us study the behavior of a test particle around the present modified BTZ black hole. The particle’s geodesic in orbit around a static black hole is given by
where
is the particle’s energy,
L is the angular momentum, and
defines massive (
) particles or massless (
) particles. Thus, the effective potential is written as
The circular geodesics occurs at the points
r satisfying
. Now, we analyze the orbits for both massless and massive particles.
For massless particles, we have the circular orbits occurring at
, i.e.,
Therefore, for massless particles the only solution for
occurs at
. This solution must be disregarded as a physical solution in the present context since this spherical surface is not valid for the location of a photon sphere.
Analogously, for the case of massive particles, we have the circular orbits occurring at
. From Equation (
14), we obtain
Clearly, we have one solution for
at
, which is not valid as an orbit solution for the same reason discussed previously. Moreover, we have four nontrivial solutions, but all of them are complex-valued solutions. This means that these solutions are not physical, since the
r must be a real-valued quantity.
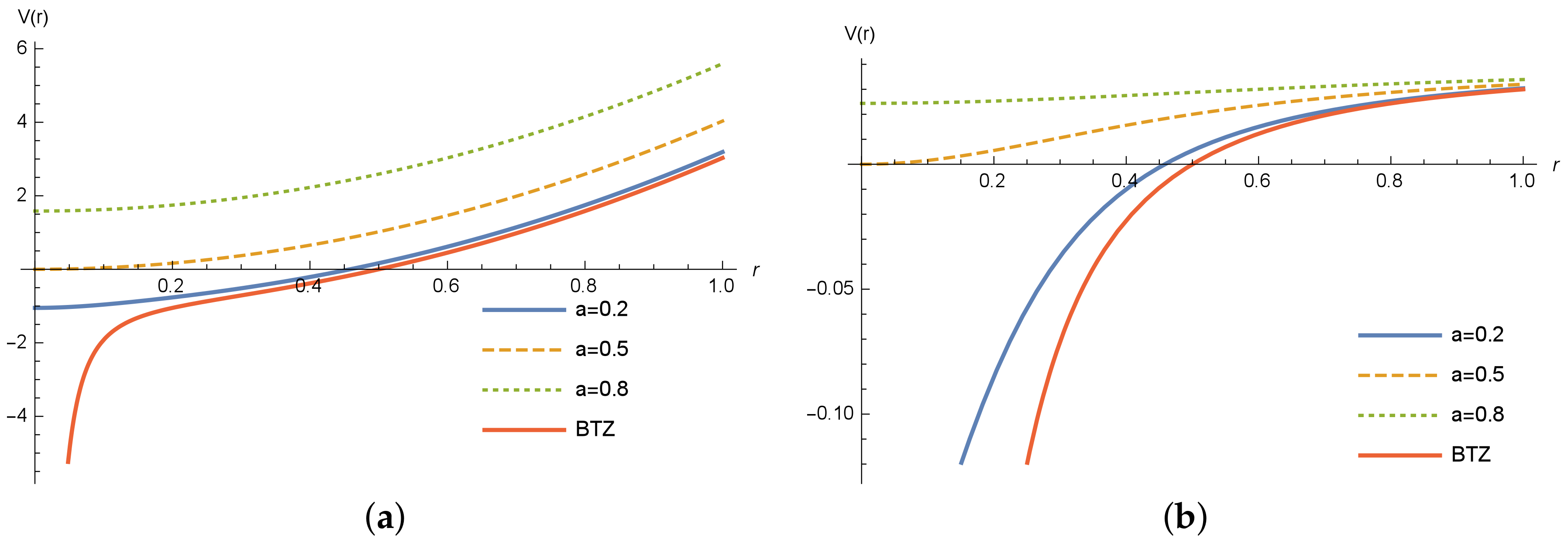
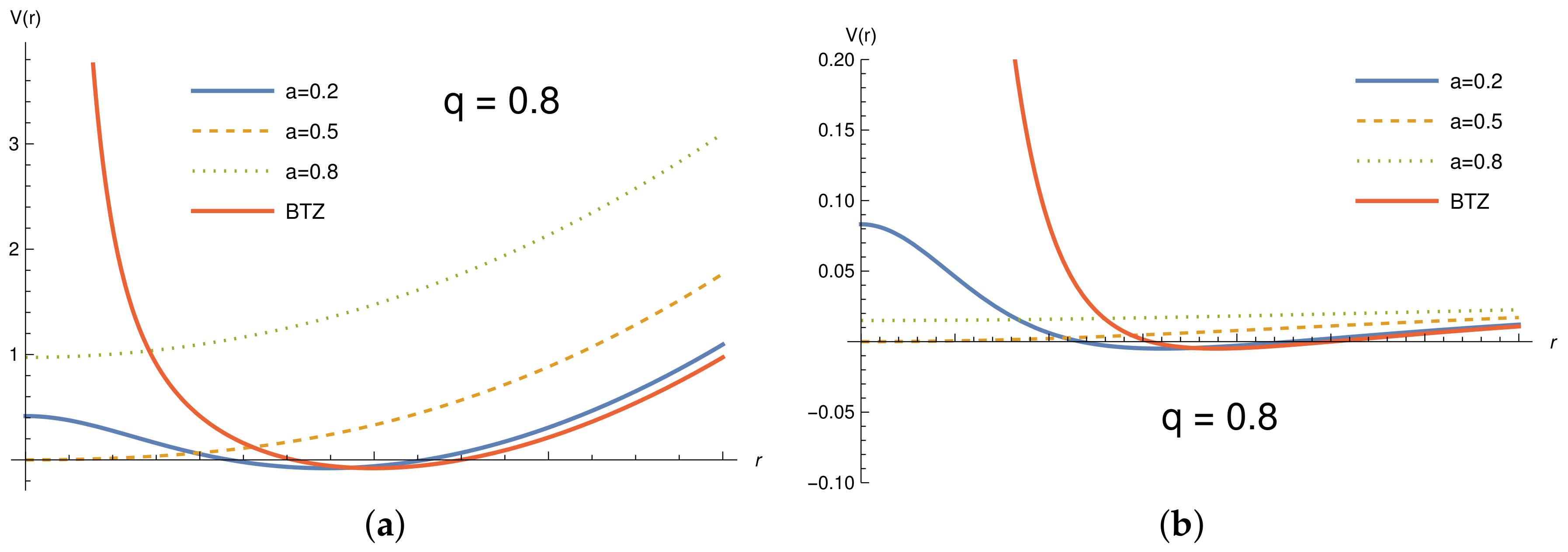
In
Figure 5, we depict the effective potential of massless and massive particles for the Simpson–Visser BTZ black hole. We used for this plot
,
and
, so that for this case,
is a black hole,
is a one-way wormhole, and
is a traversable wormhole.
6. Simpson–Visser Charged BTZ Black Hole
Soon after the Simpson–Visser black-bounce was proposed, the charged version was studied in ref. [
35]. The authors found a solution that interpolated between a regular charged black hole and a charged wormhole. Here, we analyze the case of a charged BTZ black hole under the Simpson–Visser regularization. For this case, the metric is given by (
2) but with
Obviously, when
, we recover the usual expression of
for the charged BTZ black hole. The location of the event horizon
can be obtained by
; however, analytic solutions for
are not easily reachable since
yields a transcendental equation for
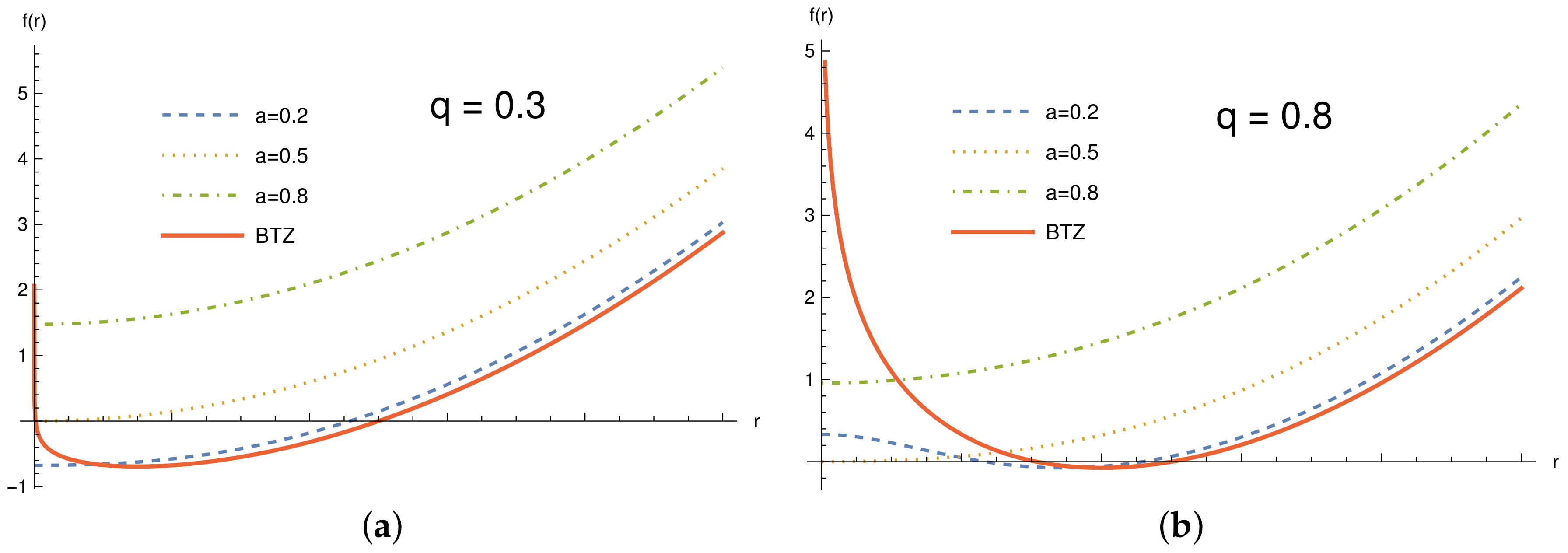
. In order to have a clearer view of the Simpson–Visser charged BTZ black hole, we have plotted the behavior of the
in
Figure 6 for two configurations of charge, namely,
and
.
From the horizon curves, we can obtain the mass of the black hole in terms of the horizon radius as
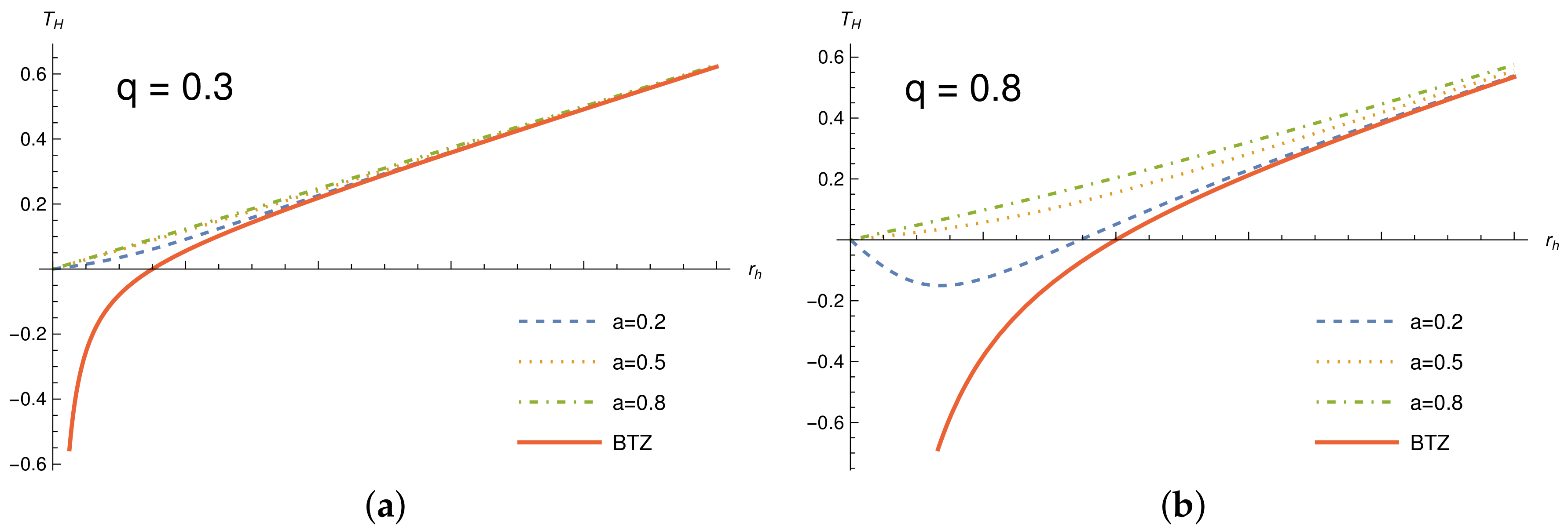
A similar analysis gives us the Hawking temperature for the present case. Differently from the uncharged case, the Simpson–Visser charged BTZ black hole exhibits a different Hawking temperature, given by
The Hawking temperature for the usual charged BTZ black hole is in fact divergent at
. The Simpson–Visser regularization provides a modification in the charge-dependent term which indeed removes the divergence. Moreover, the Hawking temperature vanishes for
and
. We must select the positive solutions, since they provide the possibility of a non-negative horizon radius.
In
Figure 7, we depicted the behavior of the Hawking temperature for the charged Simpson–Visser BTZ black hole for
and
. As we can see, for any
case, we have a vanishing Hawking temperature at the origin and for a large
, the Hawking temperature recovers the linear behavior
. In other words, for a large
, the Hawking temperature no longer sees the presence of the charge.
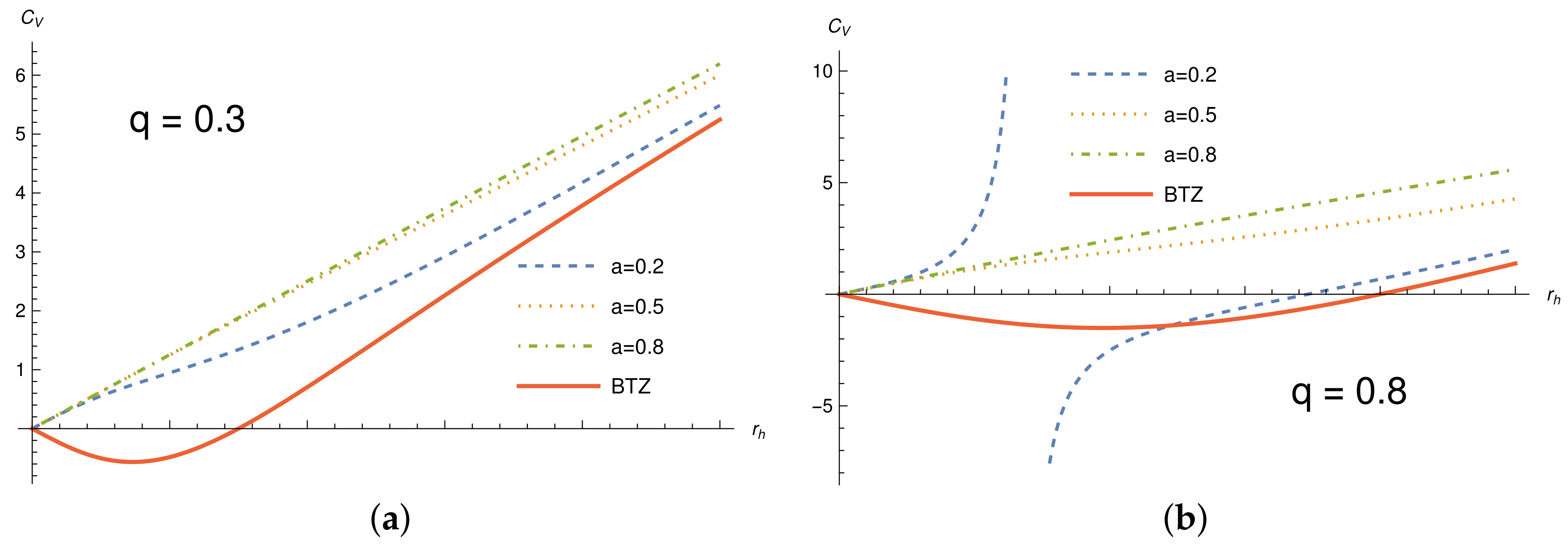
The entropy for the Simpson–Visser charged BTZ black hole, similarly to the uncharged case, presents no modification due to the regularization. Hence, it yields the usual result
. However, the specific heat is modified by the Simpson–Visser regularization, so that,
As it is widely known, the thermodynamic stability of black holes (BTZ black holes for our case) is directly related to the sign of the heat capacity. A positive heat capacity indicates that the system is thermodynamically stable, while its negativity imply a thermodynamic instability. It is possible to obtain the points where Equation (
20) vanishes. Such points are
We must disregard the complex solutions and the negative ones, therefore we have only two physical solutions, namely,
and
. Moreover, notice that the location of
is dependent on the bounce parameter
a. Furthermore, it is clear that we have a divergence in the specific heat when
The divergence in the specific heat indicates a phase transition. As we can see, such phase transition appears as a relation between the bounce parameter and the electric charge. Since
must be a real-valued quantity, from Equation (
22), we reach the condition
for the existence of a phase transition. The behavior of the specific heat can be seen in
Figure 8. We used two values for the charge, namely,
and
, and
.
The free energy is also modified by the bounce parameter, so that
The divergence in the free energy when
is clearly regularized by the bounce parameter. Moreover, the usual charged BTZ result is recovered when
.
Finally, the same analysis performed in the previous section for the orbits of massive and massless particles moving around the uncharged BTZ black hole can be done for the present case as well. By taking the effective potential described by Equation (
14) and replacing
by Equation (
17), we can discuss the orbits for the charged case. For both massive and massless cases, exact solutions for the point where these orbits become stable could not be found. However, graphically, it is possible to see that there are stable orbits for both massive and massless cases. Moreover,
Figure 9 allows us to see that the points where we have stable orbits are sensitive to the bounce parameter and charge.
7. Conclusions
In this manuscript, we applied the procedure proposed by Simpson and Visser to obtain a solution that interpolates between a regular BTZ black hole and a wormhole. Beyond being simple, it opens a new avenue to shed some light on the properties of both wormholes and regular black holes. We considered the charged and uncharged BTZ black holes.
For the uncharged case, we first pointed out that the standard BTZ was already regular. However, when we considered the parameter a, we found a regular BTZ black hole with only one horizon. This is very different from the Schwarzschild case, with two horizons with a radius controlled by the parameter a. We also found that the entropy and Hawking temperature did not depend on a and therefore the behavior was very similar to that of the standard BTZ. We also found that stable orbits were not allowed. Finally, we computed the curvature tensors. We found that they were identical to the standard BTZ at and . For other values of r, we obtained nonconstant values. Therefore, we gained an effective source of the BTZ black hole that did not change its main properties, such as entropy. We found, by studying the energy conditions and the state parameter, that there was a small range of parameters where we could source a black hole with ordinary matter, but wormholes were always sourced by exotic matter.
Next, we studied the charged case. In that case, the BTZ black hole was not regular, and the introduction of the parameter
a regularized it. Differently from the uncharged case, the charged case exhibited modifications due to the parameter
a. We could verify that for the charged case, the bounce parameter
a affected the point where the Hawking temperature vanished. The heat capacity for the charged case was drastically modified by the Simpson–Visser regularization. We could verify that when
, we had a phase transition where the heat capacity changed sign, affecting therefore the stability of the black hole. Moreover, graphically we could see that there were stable orbits for both massive and massless cases.
Figure 9 allowed us to see that the points where we had stable orbits were sensitive to the bounce parameter and charge.
Finally, we should point out that, as far as we know, this is the first time that the Simpson and Visser procedure has been applied to dimensions fewer than . This opens new avenues of study, including cases with dimensions higher than . This is the subject of a future study by us.