Hidden Companions Detected by Asteroseismology. I. Two Kepler Field Non-Eclipsing Binaries
Abstract
1. Introduction
2. Observations
2.1. Kepler Data
2.2. Scuti and Hybrid Variables
3. Time-Frequency Analysis
3.1. Light-Travel Time Effect
3.2. Data Processing Flow
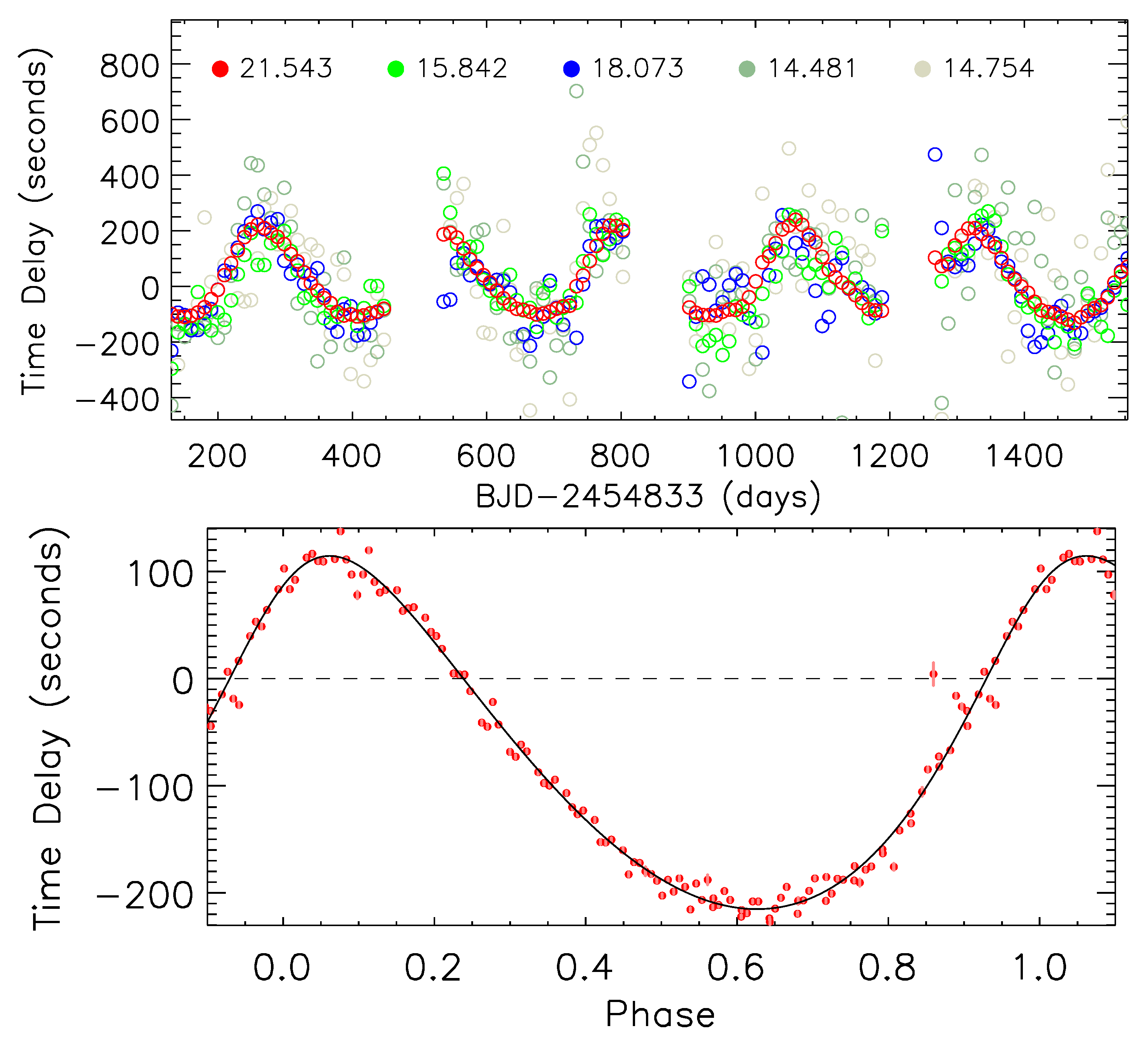
3.3. Orbit Inversion
4. Results and Discussions
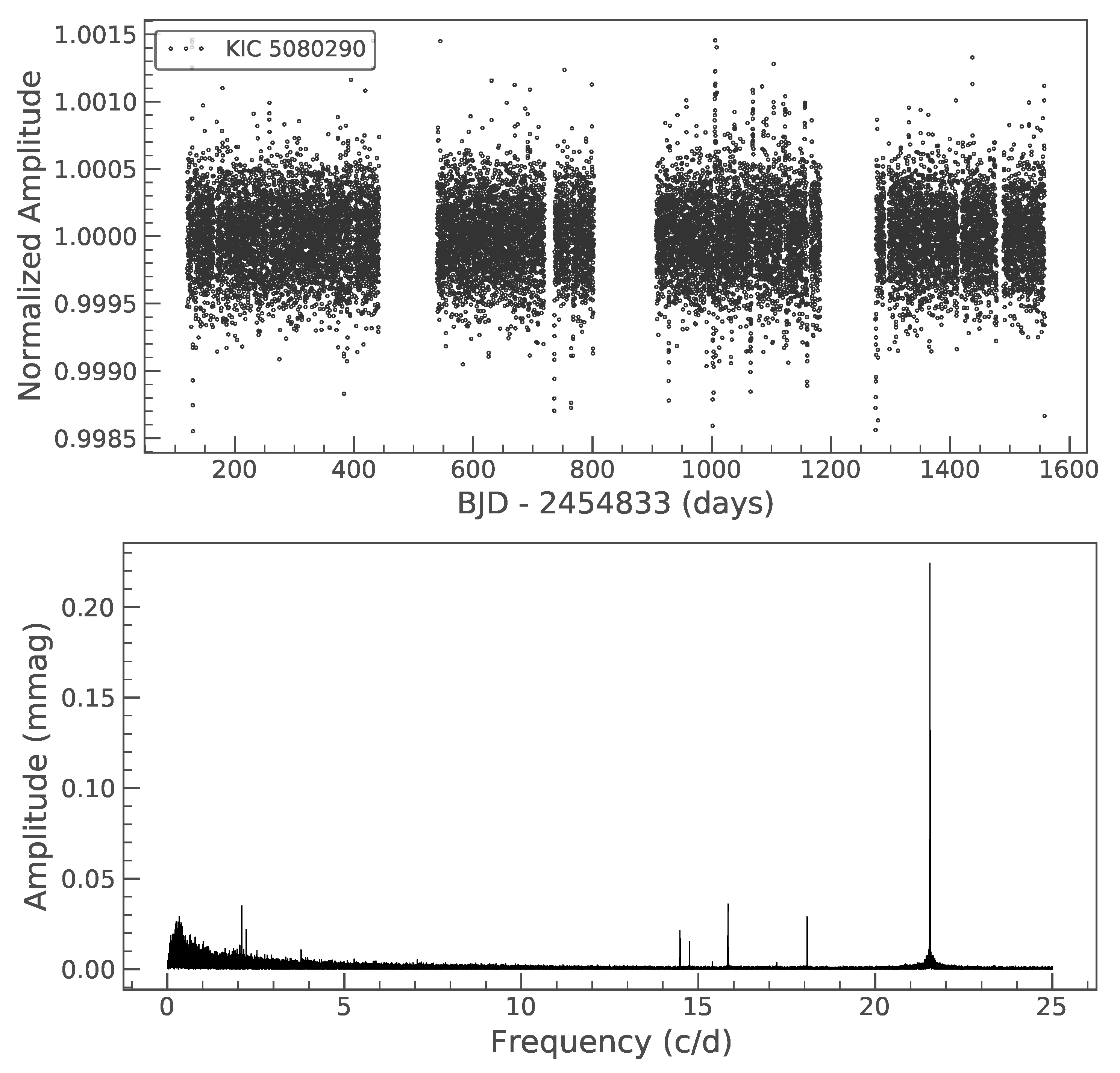
4.1. KIC 5080290
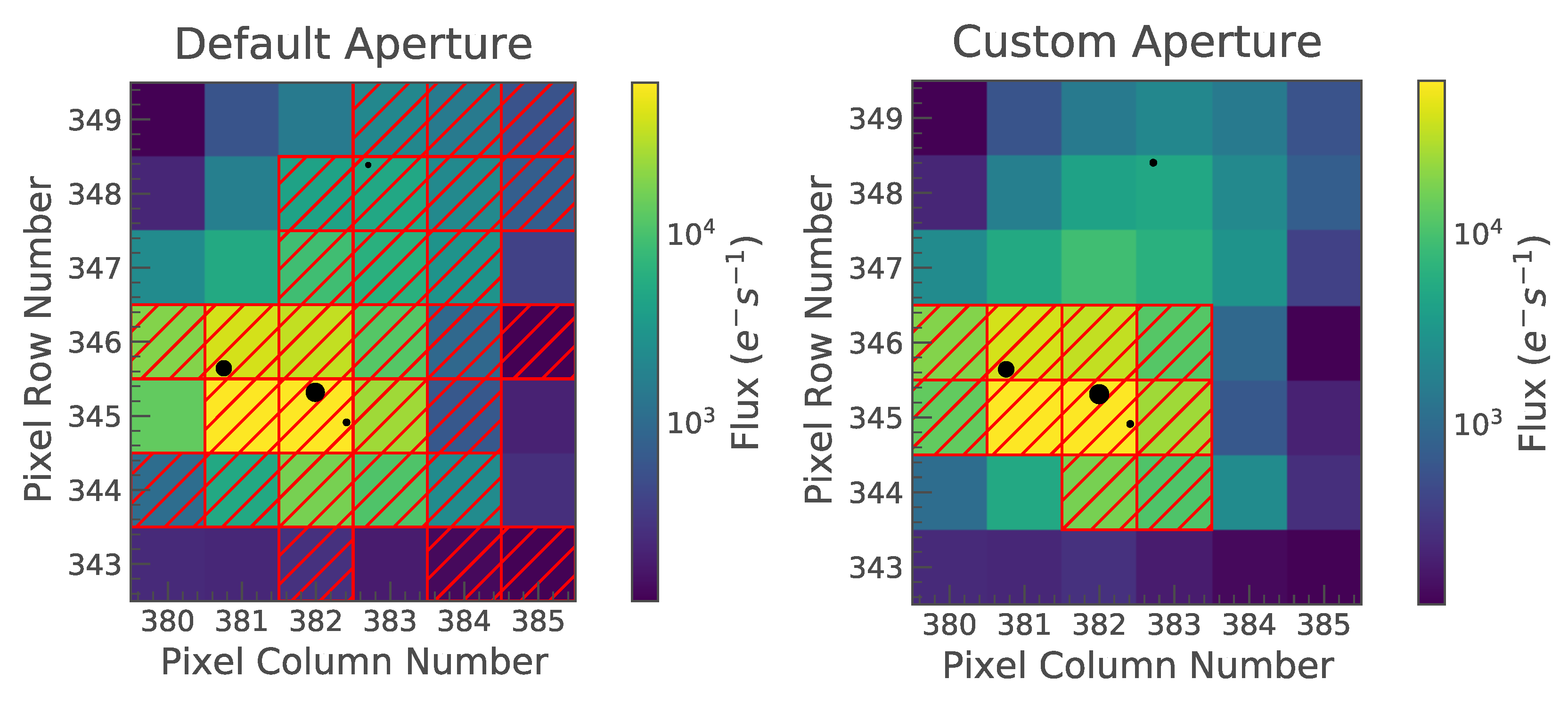
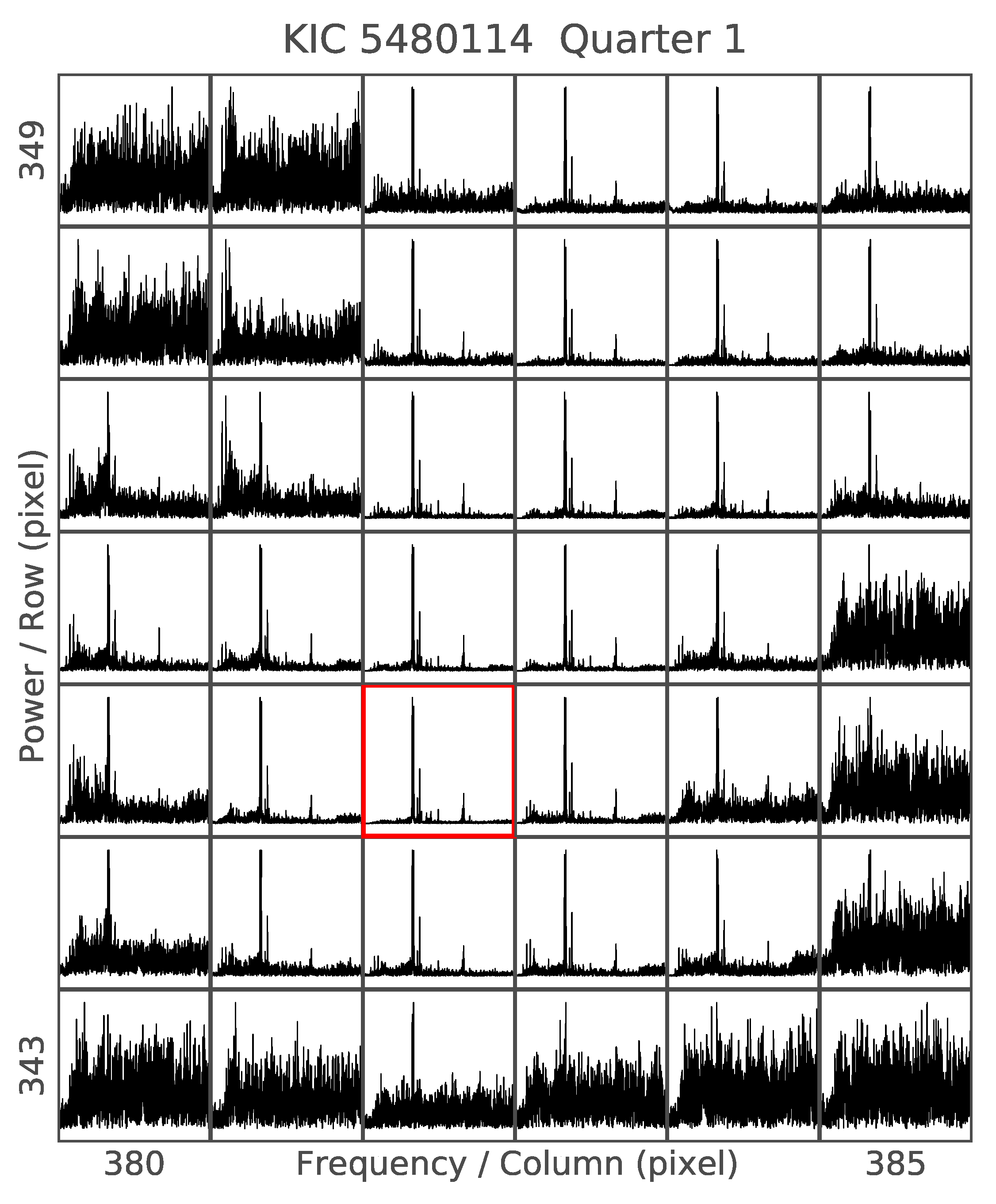
4.2. KIC 5480114
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Breger, M. Delta Scuti and related stars. Publ. Astron. Soc. Pac. 1979, 91, 5. [Google Scholar] [CrossRef]
- Breger, M. δ Scuti stars. Delta Scuti and Related Stars: Reference Handbook and Proceedings of the 6th Vienna Workshop in Astrophysics. Astron. Soc. Pac. Conf. Ser. 2000, 210, 3. Available online: https://www.aspbooks.org/a/volumes/article_details/?paper_id=20138 (accessed on 11 November 2022).
- Rodríguez, E.; López-González, M.J.; López de Coca, P. A revised catalogue of δ Sct stars. Astron. Astrophys. Suppl. Ser. 2000, 144, 469. [Google Scholar] [CrossRef]
- Antoci, V.; Cunha, M.S.; Bowman, D.M.; Murphy, S.J.; Kurtz, D.W.; Bedding, T.R.; Borre, C.C.; Christophe, S.; Daszyńska-Daszkiewicz, J.; Fox-Machado, L.; et al. The first view of δ Scuti and γ Doradus stars with the TESS mission. Mon. Not. R. Astron. Soc. 2019, 490, 4040. [Google Scholar] [CrossRef]
- Balona, L.A. Low frequencies in Kepler δ Scuti stars. Mon. Not. R. Astron. Soc. 2014, 437, 1476. [Google Scholar] [CrossRef]
- Balona, L.A.; Dziembowski, W.A. Kepler observations of δ Scuti stars. Mon. Not. R. Astron. Soc. 2011, 417, 591. [Google Scholar] [CrossRef]
- Bowman, D.M.; Kurtz, D.W.; Breger, M.; Murphy, S.J.; Holdsworth, D.L. Amplitude modulation in δ Sct stars: Statistics from an ensemble study of Kepler targets. Mon. Not. R. Astron. Soc. 2016, 460, 1970. [Google Scholar] [CrossRef]
- Bradley, P.A.; Guzik, J.A.; Miles, L.F.; Uytterhoeven, K.; Jackiewicz, J.; Kinemuchi, K. Results of a search for γ Dor and δ Sct stars with the Kepler spacecraft. Astron. J. 2015, 149, 68. [Google Scholar] [CrossRef]
- Grigahcène, A.; Antoci, V.; Balona, L.; Catanzaro, G.; Daszyńska-Daszkiewicz, J.; Guzik, J.A.; Handler, G.; Houdek, G.; Kurtz, D.W.; Marconi, M.; et al. Hybrid γ Doradus-δ Scuti pulsators: New insights into the physics of the oscillations from Kepler observations. Astrophys. J. Lett. 2010, 713, L192. [Google Scholar] [CrossRef]
- Paparó, M.; Kolláth, Z.; Shobbrook, R.R.; Matthews, J.M.; Antoci, V.; Benkő, J.M.; Park, N.-K.; Mirtorabi, M.T.; Luedeke, K.; Kusakin, A.; et al. The Delta Scuti star 38 Eri from the ground and from space. Mon. Not. R. Astron. Soc. 2018, 477, 4362. [Google Scholar] [CrossRef]
- Pribulla, T.; Rucinski, S.; Matthews, J.M.; Kallinger, T.; Kuschnig, R.; Rowe, J.F.; Guenther, D.B.; Moffat, A.F.J.; Sasselov, D.; Walker, G.A.H.; et al. MOST satellite photometry of stars in the M67 field: Eclipsing binaries, blue stragglers and δ Scuti variables. Mon. Not. R. Astron. Soc. 2008, 391, 343. [Google Scholar] [CrossRef]
- Uytterhoeven, K.; Moya, A.; Grigahcène, A.; Guzik, J.A.; Gutiérrez-Soto, J.; Smalley, B.; Handler, G.; Balona, L.A.; Niemczura, E.; Fox Machado, L.; et al. The Kepler characterization of the variability among A- and F-type stars I. General overview. Astron. Astrophys. 2011, 534, A125. [Google Scholar] [CrossRef]
- Zwintz, K.; Fossati, L.; Ryabchikova, T.; Guenther, D.; Aerts, C.; Barnes, T.G.; Themeßl, N.; Lorenz, D.; Cameron, C.; Kuschnig, R.; et al. Echography of young stars reveals their evolution. Science 2014, 345, 550. [Google Scholar] [CrossRef]
- Walker, G.; Matthews, J.; Kuschnig, R.; Ron, J.; Rucinski, S.; Pazder, J.; Burley, G.; Walker, A.; Skaret, K.; Zee, R.; et al. The MOST asteroseismology mission: Ultraprecise photometry from space. Publ. Astron. Soc. Pac. 2003, 115, 1023. [Google Scholar] [CrossRef]
- Auvergne, M.; Bodin, P.; Boisnard, L.; Buey, J.T.; Chaintreuil, S.; Epstein, G.; Jouret, M.; Lam-Trong, T.; Levacher, P.; Magnan, A.; et al. The CoRoT satellite in flight: Description and performance. Astron. Astrophys. 2009, 506, 411. [Google Scholar] [CrossRef]
- Borucki, W.J.; Koch, D.; Basri, G.; Batalha, N.M.; Brown, T.; Caldwell, D.A.; Caldwell, J.; Christensen-Dalsgaard, J.; Cochran, W.; DeVore, E.; et al. Kepler planet detection mission: Introduction and first results. Science 2010, 327, 977. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.H.; Li, Y.; Lai, X.J.; Wu, T. Asteroseismology of the δ Scuti star HD 50844. Astron. Astrophys. 2016, 593, A69. [Google Scholar] [CrossRef][Green Version]
- Poretti, E.; Michel, E.; Garrido, R.; Lefèvre, L.; Mantegazza, L.; Rainer, M.; Rodríguez, E.; Uytterhoeven, K.; Amado, P.J.; Martín-Ruiz, S.; et al. HD 50844: A new look at δ Scuti stars from CoRoT space photometry. Astron. Astrophys. 2009, 506, 85. [Google Scholar] [CrossRef]
- Bowman, D.M. Amplitude Modulation and Energy Conservation of Pulsation Modes in Delta Scuti Stars. Ph.D. Thesis, University of Central Lancashire, Preston, UK, 2017. [Google Scholar]
- Guo, Z.; Fuller, J.; Shporer, A.; Li, G.; Hambleton, K.; Manuel, J.; Murphy, S.; Isaacson, H. KIC 4142768: An evolved Gamma Doradus/Delta Scuti hybrid pulsating eclipsing binary with tidally excited oscillations. Astrophys. J. 2019, 885, 46. [Google Scholar] [CrossRef]
- Kurtz, D.W.; Saio, H.; Takata, M.; Shibahashi, H.; Murphy, S.J.; Sekii, T. Asteroseismic measurement of surface-to-core rotation in a main-sequence A star, KIC 11145123. Mon. Not. R. Astron. Soc. 2014, 444, 102. [Google Scholar] [CrossRef]
- Saio, H.; Kurtz, D.W.; Takata, M.; Shibahashi, H.; Murphy, S.J.; Sekii, T.; Bedding, T.R. Asteroseismic measurement of slow, nearly uniform surface-to-core rotation in the main-sequence F star KIC 9244992. Mon. Not. R. Astron. Soc. 2015, 447, 3264. [Google Scholar] [CrossRef]
- Schmid, V.S.; Tkachenko, A.; Aerts, C.; Degroote, P.; Bloemen, S.; Murphy, S.J.; Van Reeth, T.; Pápics, P.I.; Bedding, T.R.; Keen, M.A.; et al. KIC 10080943: An eccentric binary system containing two pressure- and gravity-mode hybrid pulsators. Astron. Astrophys. 2015, 584, A35. [Google Scholar] [CrossRef]
- Ou, J.W.; Yang, M.; Zhou, J.L. EPIC 202843107: A close eclipsing binary containing a δ Scuti variable. Res. Astron. Astrophys. 2019, 19, 112. [Google Scholar] [CrossRef]
- Paparó, M.; Benkő, J.M.; Hareter, M.; Guzik, J.A. Unexpected series of regular frequency spacing of δ Scuti stars in the non-asymptotic regime. I. The methodology. Astrophys. J. 2016, 822, 100. [Google Scholar] [CrossRef]
- Paparó, M.; Benkő, J.M.; Hareter, M.; Guzik, J.A. Unexpected series of regular frequency spacing of δ Scuti stars in the non-asymptotic regime. II. Sample-echelle diagrams and rotation. Astrophys. J. Suppl. Ser. 2016, 224, 41. [Google Scholar] [CrossRef]
- García Hernández, A.; Suárez, J.C.; Moya, A.; Monteiro, M.J.P.F.G.; Guo, Z.; Reese, D.R.; Pascual-Granado, J.; Barceló Forteza, S.; Martín-Ruiz, S.; Garrido, R.; et al. Precise surface gravities of δ Scuti stars from asteroseismology. Mon. Not. R. Astron. Soc. 2017, 471, L140. [Google Scholar] [CrossRef]
- García Hernández, A.; Martín-Ruiz, S.; Monteiro, M.J.P.F.G.; Suárez, J.C.; Reese, D.R.; Pascual-Granado, J.; Garrido, R. Observational Δν-ρ Relation for δ Sct Stars using Eclipsing Binaries and Space Photometry. Astrophys. J. Lett. 2015, 811, L29. [Google Scholar] [CrossRef]
- Rodríguez-Martín, J.E.; García Hernández, A.; Suárez, J.C.; Rodón, J.R. Study of the low-order Δν-ρ relation for moderately rotating δ Scuti stars and its impact on their characterization. Mon. Not. R. Astron. Soc. 2020, 498, 1700. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Lin, G.; Chen, Y.; Guo, J. Exploring the helium core of the δ Scuti star COROT 102749568 with asteroseismology. Astrophys. J. 2017, 834, 146. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y. Rotational splitting and asteroseismic modeling of the δ Scuti star EE Camelopardalis. Astrophys. J. 2017, 838, 31. [Google Scholar] [CrossRef]
- Barceló Forteza, S.; Michel, E.; Roca Cortés, T.; García, R.A. Evidence of amplitude modulation due to resonant mode coupling in the δ Scuti star KIC 5892969. Astron. Astrophys. 2015, 579, A133. [Google Scholar] [CrossRef]
- Breger, M.; Montgomery, M.H. Evidence of resonant mode coupling and the relationship between low and high frequencies in a rapidly rotating a star. Astrophys. J. 2014, 783, 89. [Google Scholar] [CrossRef]
- Bedding, T.R.; Murphy, S.J.; Hey, D.R.; Huber, D.; Li, T.; Smalley, B.; Stello, D.; White, T.R.; Ball, W.H.; Chaplin, W.J.; et al. Very regular high-frequency pulsation modes in young intermediate-mass stars. Nature 2020, 581, 147. [Google Scholar] [CrossRef] [PubMed]
- Murphy, S.J.; Moe, M.; Kurtz, D.W.; Bedding, T.R.; Shibahashi, H.; Boffin, H.M.J. Finding binaries from phase modulation of pulsating stars with Kepler: V. Orbital parameters, with eccentricity and mass-ratio distributions of 341 new binaries. Mon. Not. R. Astron. Soc. 2018, 474, 4322. [Google Scholar] [CrossRef]
- Shibahashi, H.; Kurtz, D.W. FM stars: A Fourier view of pulsating binary stars, a new technique for measuring radial velocities photometrically. Mon. Not. R. Astron. Soc. 2012, 422, 738. [Google Scholar] [CrossRef]
- Murphy, S.J.; Bedding, T.R.; Shibahashi, H.; Kurtz, D.W.; Kjeldsen, H. Finding binaries among Kepler pulsating stars from phase modulation of their pulsations. Mon. Not. R. Astron. Soc. 2014, 441, 2515. [Google Scholar] [CrossRef]
- Balona, L.A. Binary star detection using the time-delay method: Application to 34 Kepler objects of interest. Mon. Not. R. Astron. Soc. 2014, 443, 1946. [Google Scholar] [CrossRef]
- Murphy, S.J.; Shibahashi, H.; Bedding, T.R. Finding binaries from phase modulation of pulsating stars with Kepler—IV. Detection limits and radial velocity verification. Mon. Not. R. Astron. Soc. 2016, 461, 4215. [Google Scholar] [CrossRef]
- Murphy, S.J.; Barbara, N.H.; Hey, D.; Bedding, T.R.; Fulcher, B.D. Finding binaries from phase modulation of pulsating stars with Kepler—VI. Orbits for 10 new binaries with mischaracterized primaries. Mon. Not. R. Astron. Soc. 2020, 493, 5382. [Google Scholar] [CrossRef]
- Shibahashi, H.; Kurtz, D.W.; Murphy, S.J. FM stars II: A Fourier view of pulsating binary stars—Determining binary orbital parameters photometrically for highly eccentric cases. Mon. Not. R. Astron. Soc. 2015, 450, 3999. [Google Scholar] [CrossRef]
- Compton, D.L.; Bedding, T.R.; Murphy, S.J.; Stello, D. Binary star detectability in Kepler data from phase modulation of different types of oscillations. Mon. Not. R. Astron. Soc. 2016, 461, 1943. [Google Scholar] [CrossRef][Green Version]
- Bowman, D.M.; Kurtz, D.W. Characterizing the observational properties of δ Sct stars in the era of space photometry from the Kepler mission. Mon. Not. R. Astron. Soc. 2018, 476, 3169. [Google Scholar] [CrossRef]
- Cardoso, J.V.; Hedges, C.; Gully-Santiago, M.; Saunders, N.; Cody, A.M.; Barclay, T.; Hall, O.; Sagear, S.; Turtelboom, E.; et al.; Lightkurve Collaboration Lightkurve: Kepler and TESS time series analysis in Python. Astrophys. Source Code Libr. 2018, ascl:1812.013. [Google Scholar]
- Qian, S.B.; Li, L.J.; He, J.J.; Zhang, J.; Zhu, L.Y.; Han, Z.T. LAMOST views δ Scuti pulsating stars. Mon. Not. R. Astron. Soc. 2018, 475, 478. [Google Scholar] [CrossRef]
- Murphy, S.J.; Hey, D.; Van Reeth, T.; Timothy, R.B. Gaia-derived luminosities of Kepler A/F stars and the pulsator fraction across the δ Scuti instability strip. Mon. Not. R. Astron. Soc. 2019, 485, 2380. [Google Scholar] [CrossRef]
- Roberts, D.H.; Lehar, J.; Dreher, J.W. Time series analysis with CLEAN. I. Derivation of a spectrum. Astron. J. 1987, 93, 968. [Google Scholar] [CrossRef]
- Murphy, S.J.; Shibahashi, H.; Kurtz, D.W. Super-Nyquist asteroseismology with the Kepler Space Telescope. Mon. Not. R. Astron. Soc. 2013, 430, 2986. [Google Scholar] [CrossRef]
- Markwardt, C.B. Non-linear least-squares fitting in IDL with MPFIT. Astron. Data Anal. Softw. Syst. XVIII 2009, 411, 251. [Google Scholar]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1978; Volume 630, p. 105. [Google Scholar] [CrossRef]
- Wright, J.T.; Howard, A.W. Efficient fitting of multiplanet Keplerian models to radial velocity and astrometry data. Astrophys. J. Suppl. Ser. 2009, 182, 205. [Google Scholar] [CrossRef]
- Yang, H.; Liu, J. The flare catalog and the flare activity in the Kepler mission. Astrophys. J. Suppl. Ser. 2019, 241, 29. [Google Scholar] [CrossRef]



| KIC | 5080290 | 5480114 |
|---|---|---|
| Period (days) | 264.89 (05) | 445.02 (17) |
| (s) | 168.79 (39) | 214.15 (49) |
| eccentricity | 0.3674 (39) | 0.3954 (42) |
| (rad) | 3.865 (11) | 0.181 (11) |
| mass function () | 0.0737 (5) | 0.0534 (4) |
| () | ||
| () |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M. Hidden Companions Detected by Asteroseismology. I. Two Kepler Field Non-Eclipsing Binaries. Universe 2022, 8, 614. https://doi.org/10.3390/universe8120614
Yang M. Hidden Companions Detected by Asteroseismology. I. Two Kepler Field Non-Eclipsing Binaries. Universe. 2022; 8(12):614. https://doi.org/10.3390/universe8120614
Chicago/Turabian StyleYang, Ming. 2022. "Hidden Companions Detected by Asteroseismology. I. Two Kepler Field Non-Eclipsing Binaries" Universe 8, no. 12: 614. https://doi.org/10.3390/universe8120614
APA StyleYang, M. (2022). Hidden Companions Detected by Asteroseismology. I. Two Kepler Field Non-Eclipsing Binaries. Universe, 8(12), 614. https://doi.org/10.3390/universe8120614






