N-S Asymmetry and Solar Cycle Distribution of Superactive Regions from 1976 to 2017
Abstract
1. Introduction
2. Data Analysis
2.1. Data Source
2.2. Solar Cycle Distribution of the SARs from 1976 to 2017
2.3. N–S Asymmetry
3. Summary and Discussion
- (i)
- There were 51 SARs during SCs 21–24. Of the 51 SARs, 31 SARs belong to SARs and 20 SARs are SARs. The statistical results show that N/N, N/N and N/N of SARs are 35.5%, 64.5% and 77.4%, respectively, whereas N/N, N/N and N/N for SARs are 50%, 50%, and 100%, respectively, indicating that most of the SARs appeared around the solar maximum, which is very similar to those of strong solar proton events [11], major geomagnetic storms [6] and GLEs [10]. It has been found that stronger storms have the tendency to occur around the solar maximum [9,33]. The SAR that produced the largest FI during each SC always occurred in the descending phase of the SC.
- (ii)
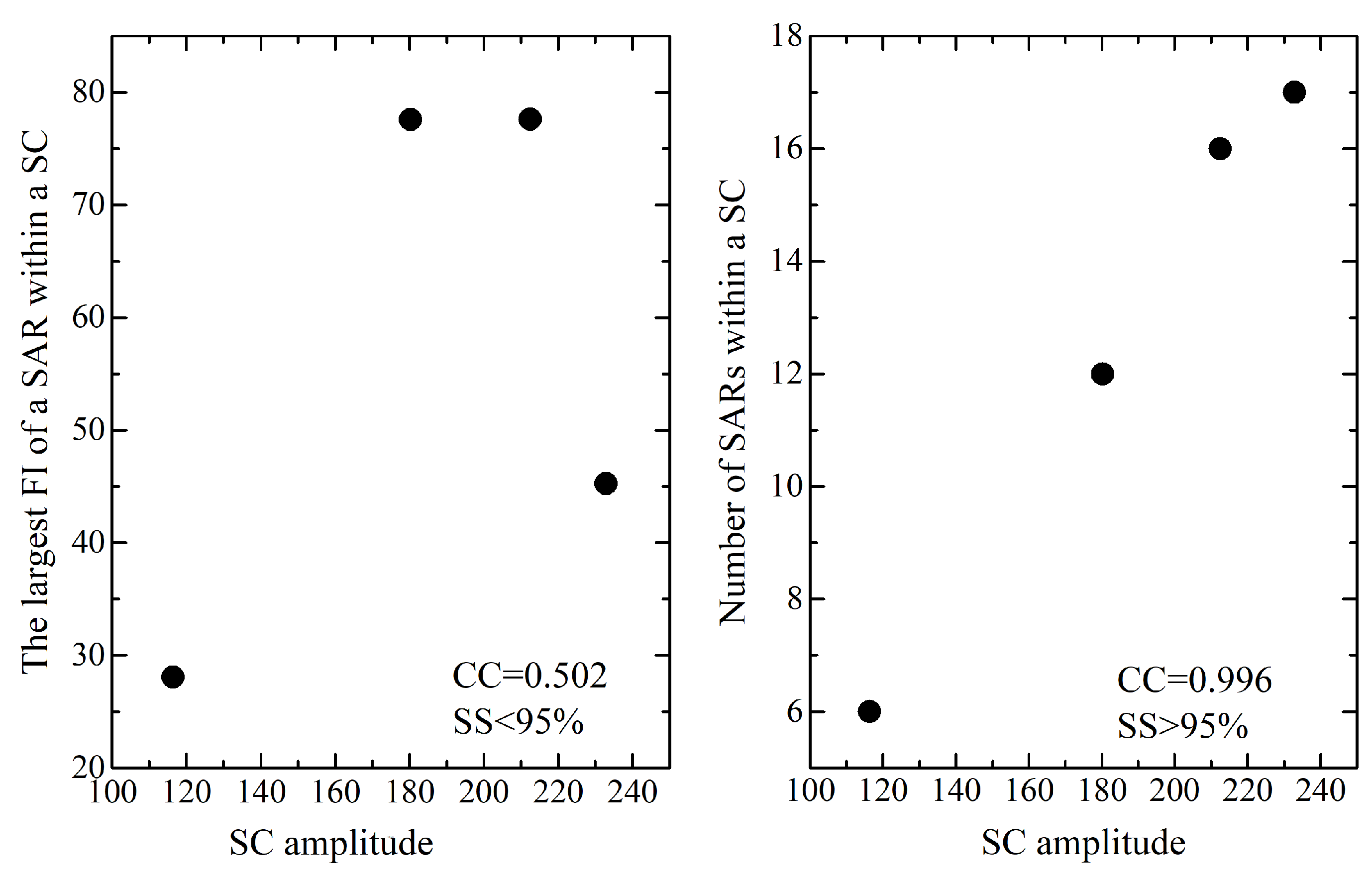
- The number of the SARs during an SC has a good correlation with the SC amplitude, implying that an SC with higher amplitude will have more SARs than that with lower amplitude. However, the largest FI of a SAR during an SC has a poor correlation with the SC amplitude, indicating that a weak SC will have a small number of SARs. However, a weak SC may have a SAR that can produce very strong solar flares. It has been predicted that SC 25 may be a weak SC [34,35,36], implying that the total number of SARs in SC 25 will be small. However, we cannot rule out the possibility that SC 25 may have a SAR that can produce a series of very strong solar activities, including flares and CMEs, and then cause GLEs and even extreme geomagnetic storms.
- (iii)
- N–S asymmetries of both the number and cumulative number of SARs in the two different hemispheres of the sun during the period from SC 21 to SC 24 are significant, i.e., the SARs dominated in the southern hemisphere of the sun during the period from SC 21 to SC 24. This indicated that the extreme solar activities and space weather events during the periods from SC 21 to SC 24 were mainly caused by the SARs in the southern hemisphere of the sun. However, the N–S asymmetry of the SARs during the period from SC 21 to SC 24 is not significant, i.e., the SAR dominated in the different hemispheres by turns for different SCs. N–S asymmetry of the flare indices caused by the SARs from the two different hemispheres of the Sun during the period from SC 21 to SC 24 is inferred to exist. The solar flare activities caused by the SARs with source locations in the southern hemisphere of the sun were much stronger than those caused by the SARs with source locations in the northern hemisphere of the sun during SCs 21–24.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| No. | SC | SAR | Latitude | CL | Date on the Disk | ≥X5.0 Flare | FI | GLE No. | SGSs |
|---|---|---|---|---|---|---|---|---|---|
| yymmdd–mmdd | |||||||||
| 1 | 1092 | N23 | L081 | 780423–0507 | X5.0 | 12.6 | |||
| 2 | 1203 | N18 | L175 | 780708–0721 | 29.9 | ||||
| 3 | 1574 | N17 | L155 | 790214–0225 | 9.2 | ||||
| 4 | 1994 | N06 | L198 | 790916–0927 | 11.6 | ||||
| 5 | 2099 | S14 | L283 | 791105–1112 | 9.5 | ||||
| 6 | 21 | 2776 | N12 | L174 | 801101–1114 | 15.91 | |||
| 7 | 2779 | S11 | L105 | 801105–1119 | X9.0 | 29.03 | |||
| 8 | 3049 | N15 | L153 | 810414–0430 | X5.9 + X5.5 | 17.5 | |||
| 9 | 3234 | S12 | L294 | 810721–0803 | 13.28 | ||||
| 10 | 3390 | S18 | L339 | 811007–1019 | 9.57 | 36 | |||
| 11 | 3576 | S14 | L322 | 820126–0209 | 11.94 | ||||
| 12 | 3763 | S08 | L086 | 820602–0615 | X8.0 + X5.9 | 45.24 | |||
| 13 | 3776 | N13 | L314 | 820611–0624 | 20.94 | ||||
| 14 | 3804 | N14 | L322 | 820708–0722 | X9.8 + X7.1 | 40.47 | −325 nT | ||
| 15 | 4026 | S11 | L078 | 821211–1223 | X12.9 + X5.0 | 25.04 | |||
| 16 | 4474 | S13 | L343 | 840421–0505 | X13.0 | 23.13 | |||
| 17 | 4492 | S10 | L358 | 840518–0531 | X10.1 | 19.87 | |||
| 18 | 22 | 5312 | S31 | L306 | 890106–0120 | 20.64 | |||
| 19 | 5395 | N34 | L256 | 890305–0319 | X15.0 + X6.5 | 55.6 | −589 nT | ||
| 20 | 5533 | S19 | L073 | 890609–0620 | 11.37 | ||||
| 21 | 5629 | S17 | L075 | 890803–0817 | X20.0 | 34.07 | 41 | ||
| 22 | 5669 | S17 | L085 | 890829–0912 | 13.32 | ||||
| 23 | 5698 | S26 | L220 | 890918–0929 | X9.8 | 10.97 | |||
| 24 | 5747 | S27 | L210 | 891014–1027 | X13.0 + X5.7 | 29.87 | 43 + 44 + 45 | −268 nT | |
| 25 | 5852 | S26 | L028 | 891225–1231 | 6.42 | ||||
| 26 | 6063 | N34 | L318 | 900511–0524 | X5.5 + X9.3 | 23.51 | 47 + 48 + 49 + 50 | ||
| 27 | 6471 | S12 | L144 | 910125–0208 | X10.0 | 15.27 | |||
| 28 | 6538 | S23 | L342 | 910305–0317 | X5.5 | 17.08 | |||
| 29 | 6545 | S09 | L287 | 910311–0322 | 16.93 | ||||
| 30 | 6555 | S23 | L188 | 910317–0331 | X9.4 + X5.3 | 32.62 | −298 nT | ||
| 31 | 6659 | N31 | L247 | 910601–0617 | 5(X12.0) + X10.0 | 77.61 | 51 + 52 | ||
| 32 | 6891 | S12 | L184 | 911021–1102 | X6.1 | 20.96 | −254 nT | ||
| 33 | 7321 | S24 | L070 | 921025–1102 | X9.0 | 12.32 | 54 | ||
| 34 | 23 | 8100 | S20 | L352 | 971028–1107 | X9.4 | 12.28 | 55 | |
| 35 | 8307 | N31 | L035 | 980818–0831 | 15.75 | 58 | |||
| 36 | 9077 | N18 | L310 | 000709–0719 | X5.7 | 11.68 | 59 | −301 nT | |
| 37 | 9393 | N18 | L153 | 010324–0404 | X20.0 | 27.84 | −387 nT | ||
| 38 | 9415 | S22 | L359 | 010403–0416 | X5.6 + X14.4 | 27.42 | 60 + 61 | −271 nT | |
| 39 | 10069 | S08 | L299 | 020811–0824 | 8.51 | 64 | |||
| 40 | 10484 | N04 | L354 | 031018–1028 | 6.01 | ||||
| 41 | 10486 | S16 | L284 | 031022–1105 | X5.4 + X17.2 + | 77.56 | 65 + 66 + 67 | (−383nT) + | |
| X10 + X8.3 + X28 | (−353nT) | ||||||||
| 42 | 10488 | N08 | L290 | 031027–1104 | 7.78 | ||||
| 43 | 10720 | N13 | L179 | 050111–0123 | X7.1 | 21.06 | 68 + 69 | ||
| 44 | 10808 | S11 | L230 | 050907–0918 | X17.0 + X5.4 + X6.2 | 46.92 | |||
| 45 | 10930 | S05 | L009 | 061204–1218 | X9.0 + X6.5 | 21.84 | 70 | ||
| 46 | 24 | 11429 | N17 | L081 | 120303–0315 | X5.9 | 11.87 | ||
| 47 | 11520 | S17 | L084 | 120706–0717 | 2.92 | ||||
| 48 | 11944 | S09 | L100 | 140101–0113 | 2.68 | ||||
| 49 | 11967 | S13 | L114 | 140128–0209 | 6.13 | ||||
| 50 | 12192 | S12 | L248 | 141017–1030 | 19.59 | ||||
| 51 | 12673 | S09 | L117 | 170830–0910 | X9.2 + X8.3 | 28.06 | 72 |
References
- Bai, T. Distribution of flares on the sun-Superactive regions and active zones of 1980–1985. Astrophys. J. 1987, 314, 795–807. [Google Scholar] [CrossRef]
- Tian, L.; Liu, Y.; Wang, J. The Most Violent Super-Active Regions in the 22nd and 23rd Cycles. Sol. Phys. 2002, 209, 361–374. [Google Scholar] [CrossRef]
- Chen, A.; Wang, J.; Li, J.; Feynman, J.; Zhang, J. Statistical properties of superactive regions during solar cycles 19–23. A&A 2011, 534, A47. [Google Scholar] [CrossRef]
- Le, G.M.; Liu, G.A.; Zhao, M.X.; Mao, T.; Xu, P.G. Extreme space weather events caused by super active regions during solar cycles 21–24. Res. Astron. Astrophys. 2021, 21, 130. [Google Scholar] [CrossRef]
- Chen, A.; Wang, J. Super-active regions in solar cycle 24. Proc. Int. Astron. Union 2015, 11, 309–314. [Google Scholar] [CrossRef]
- Le, G.M.; Zhao, M.X.; Zhang, W.T.; Liu, G.A. Source Locations and Solar-Cycle Distribution of the Major Geomagnetic Storms (Dst ≤ −100 nT) from 1932 to 2018. Sol. Phys. 2021, 296, 187. [Google Scholar] [CrossRef]
- Richardson, I.G.; Berdichevsky, D.; Desch, M.D.; Farrugia, C.J. Solar-cycle variation of low density solar wind during more than three solar cycles. Geophys. Res. Lett. 2000, 27, 3761–3764. [Google Scholar] [CrossRef]
- Tokumaru, M.; Kojima, M.; Fujiki, K. Solar cycle evolution of the solar wind speed distribution from 1985 to 2008. J. Geophys. Res. Space Phys. 2010, 115, A04102. [Google Scholar] [CrossRef]
- Kilpua, E.K.J.; Olspert, N.; Grigorievskiy, A.; Käpylä, M.J.; Tanskanen, E.I.; Miyahara, H.; Kataoka, R.; Pelt, J.; Liu, Y.D. Statistical study of strong and extreme geomagnetic disturbances and solar cycle characteristics. Astrophys. J. 2015, 806, 272. [Google Scholar] [CrossRef]
- Le, G.M.; Liu, G.A. The Properties of Source Locations and Solar Cycle Distribution of GLEs during 1942–2017. Sol. Phys. 2020, 295, 35. [Google Scholar] [CrossRef]
- Le, G.M.; Zhao, M.X.; Li, Q.; Liu, G.A.; Mao, T.; Xu, P.G. Characteristics of source locations and solar cycle distribution of the strong solar proton events (≥1000 pfu) from 1976 to 2018. Mon. Not. R. Astron. Soc. 2021, 502, 2043–2048. [Google Scholar] [CrossRef]
- Badalyan, O.G. Spatial distribution of the N-S asymmetry of solar activity and its time variations. Astron. Lett. 2012, 38, 51–61. [Google Scholar] [CrossRef]
- Swinson, D.B.; Koyama, H.; Saito, T. Long-term variations in north-south asymmetry of solar activity. Sol. Phys. 1986, 106, 35–42. [Google Scholar] [CrossRef]
- Oliver, R.; Ballester, J.L. The north-south asymmetry of sunspot areas during solar cycle 22. Sol. Phys. 1994, 152, 481–485. [Google Scholar] [CrossRef]
- Joshi, B.; Joshi, A. The North-South Asymmetry of Soft X-ray Flare Index during Solar Cycles 21, 22 and 23. Sol. Phys. 2004, 219, 343–356. [Google Scholar] [CrossRef]
- Ballester, J.L.; Oliver, R.; Carbonell, M. The periodic behaviour of the North-South asymmetry of sunspot areas revisited. A&A 2005, 431, L5–L8. [Google Scholar] [CrossRef]
- Carbonell, M.; Terradas, J.; Oliver, R.; Ballester, J.L. The statistical significance of the North-South asymmetry of solar activity revisited. A&A 2007, 476, 951–957. [Google Scholar] [CrossRef]
- Temmer, M.; Rybák, J.; Bendík, P.; Veronig, A.; Vogler, F.; Otruba, W.; Pötzi, W.; Hanslmeier, A. Hemispheric sunspot numbers Rn and Rs from 1945–2004: Catalogue and N-S asymmetry analysis for solar cycles 18–23. A&A 2006, 447, 735–743. [Google Scholar] [CrossRef]
- Goel, A.; Choudhuri, A.R. The hemispheric asymmetry of solar activity during the last century and the solar dynamo. Res. Astron. Astrophys. 2009, 9, 115–126. [Google Scholar] [CrossRef]
- Li, K.J.; Gao, P.X.; Zhan, L.S. The Long-term Behavior of the North-South Asymmetry of Sunspot Activity. Sol. Phys. 2009, 254, 145–154. [Google Scholar] [CrossRef]
- Li, K.J.; Gao, P.X.; Zhan, L.S.; Shi, X.J.; Zhu, W.W. Relative phase analyses of long-term hemispheric solar flare activity. Mon. Not. R. Astron. Soc. 2010, 401, 342–346. [Google Scholar] [CrossRef]
- Chowdhury, P.; Choudhary, D.P.; Gosain, S. A study of the hemispheric asymmetry of sunspot area during solar cycles 23 and 24. Astrophys. J. 2013, 768, 188. [Google Scholar] [CrossRef]
- Deng, L.H.; Qu, Z.Q.; Yan, X.L.; Wang, K.R. Phase analysis of sunspot group numbers on both solar hemispheres. Res. Astron. Astrophys. 2013, 13, 104–114. [Google Scholar] [CrossRef]
- Feng, S.; Deng, L.H.; Xu, S.C. Long-term hemispheric variation of the flare index. Res. Astron. Astrophys. 2013, 13, 343–350. [Google Scholar] [CrossRef]
- Deng, L.H.; Xiang, Y.Y.; Qu, Z.N.; An, J.M. Systematic regularity of hemispheric sunspot areas over the past 140 years. Astron. J. 2016, 151, 70. [Google Scholar] [CrossRef]
- Zhang, L.; Mursula, K.; Usoskin, I. Consistent long-term variation in the hemispheric asymmetry of solar rotation. A&A 2013, 552, A84. [Google Scholar] [CrossRef]
- Joshi, B.; Bhattacharyya, R.; Pandey, K.K.; Kushwaha, U.; Moon, Y.-J. Evolutionary aspects and north-south asymmetry of soft X-ray flare index during solar cycles 21, 22, and 23. A&A 2015, 582, A4. [Google Scholar] [CrossRef][Green Version]
- Javaraiah, J. North-south asymmetry in small and large sunspot group activity and violation of even-odd solar cycle rule. Astrophys. Space Sci. 2016, 361, 208. [Google Scholar] [CrossRef]
- Chowdhury, P.; Kilcik, A.; Yurchyshyn, V.; Obridko, V.N.; Rozelot, J.P. Analysis of the Hemispheric Sunspot Number Time Series for the Solar Cycles 18 to 24. Sol. Phys. 2019, 294, 142. [Google Scholar] [CrossRef]
- Roy, S.; Prasad, A.; Ghosh, K.; Panja, S.C.; Patra, S.N. Investigation of the Hemispheric Asymmetry in Solar Flare Index during Solar Cycle 21–24 from the Kandilli Observatory. Sol. Phys. 2020, 295, 100. [Google Scholar] [CrossRef]
- Duchlev, P.I. An Estimation of the Long-Term Variation of a North–South Asymmetry of the Long-Lived Solar Filaments. Sol. Phys. 2001, 199, 211–215. [Google Scholar] [CrossRef]
- Li, K.J.; Yun, H.S.; Gu, X.M. Hemispheric Variation in Solar Activity. Astrophys. J. 2001, 554, L115. [Google Scholar] [CrossRef]
- Li, K.J.; Wang, J.X.; Xiong, S.Y.; Liang, H.F.; Yun, H.S.; Gu, X.M. Regularity of the north-south asymmetry of solar activity. A&A 2002, 383, 648–652. [Google Scholar] [CrossRef]
- Singh, A.K.; Bhargawa, A. An early prediction of 25th solar cycle using Hurst exponent. Astrophys. Space Sci. 2017, 362, 199. [Google Scholar] [CrossRef]
- Upton, L.A.; Hathaway, D.H. An Updated Solar Cycle 25 Prediction with AFT: The Modern Minimum. Geophys. Res. Lett. 2018, 45, 8091–8095. [Google Scholar] [CrossRef]
- Jiang, J.; Wang, J.X.; Jiao, Q.R.; Cao, J.B. Predictability of the Solar Cycle over One Cycle. Astrophys. J. 2018, 863, 159. [Google Scholar] [CrossRef]

| SARs | SARs | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| SC | SC Amplitude | N | N | N | N | N | N | N | N |
| 21 | 232.9 | 1 | 8 | 7 | 9 | 4 | 4 | 8 | 8 |
| 22 | 212.5 | 4 | 6 | 10 | 10 | 3 | 3 | 6 | 6 |
| 23 | 180.3 | 5 | 5 | 5 | 10 | 0 | 2 | 2 | 2 |
| 24 | 116.4 | 1 | 1 | 2 | 2 | 3 | 1 | 4 | 4 |
| Total number | N = 11 | N = 20 | N = 24 | N = 31 | N = 10 | N = 10 | N = 20 | N = 20 | |
| SARs | SARs | |||||
|---|---|---|---|---|---|---|
| SC | N | S | N − S | N | S | N − S |
| 21 | 3 | 6 | −3 | 5 | 3 | 2 |
| 22 | 3 | 7 | −5 | 0 | 6 | −5 |
| 23 | 4 | 6 | −2 | 2 | 0 | 2 |
| 24 | 1 | 1 | 0 | 0 | 4 | −4 |
| SC | Ascending Phase | Descending Phase | Total SC | |||
|---|---|---|---|---|---|---|
| 21 | 63.3 | 9.5 | 94.82 | 177.1 | 158.12 | 186.6 |
| 22 | 55.6 | 120.06 | 101.12 | 121.6 | 156.72 | 241.66 |
| 23 | 55.27 | 39.7 | 21.06 | 168.62 | 76.33 | 208.32 |
| 24 | 11.87 | 11.73 | 0 | 47.65 | 11.87 | 59.38 |
| SARs | SARs | |||||
|---|---|---|---|---|---|---|
| SC | N | S | N − S | N | S | N − S |
| 21 | 3 | 6 | −3 | 5 | 3 | 2 |
| 21–22 | 6 | 14 | −8 | 5 | 8 | −3 |
| 21–23 | 10 | 20 | −10 | 7 | 8 | −1 |
| 21–24 | 11 | 21 | −11 | 7 | 12 | −5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, M.-X.; Le, G.-M.; Liu, Y.-H. N-S Asymmetry and Solar Cycle Distribution of Superactive Regions from 1976 to 2017. Universe 2022, 8, 605. https://doi.org/10.3390/universe8110605
Zhao M-X, Le G-M, Liu Y-H. N-S Asymmetry and Solar Cycle Distribution of Superactive Regions from 1976 to 2017. Universe. 2022; 8(11):605. https://doi.org/10.3390/universe8110605
Chicago/Turabian StyleZhao, Ming-Xian, Gui-Ming Le, and Yong-Hua Liu. 2022. "N-S Asymmetry and Solar Cycle Distribution of Superactive Regions from 1976 to 2017" Universe 8, no. 11: 605. https://doi.org/10.3390/universe8110605
APA StyleZhao, M.-X., Le, G.-M., & Liu, Y.-H. (2022). N-S Asymmetry and Solar Cycle Distribution of Superactive Regions from 1976 to 2017. Universe, 8(11), 605. https://doi.org/10.3390/universe8110605










