Astroparticle Constraints from the Cosmic Star Formation Rate Density at High Redshift: Current Status and Forecasts for JWST
Abstract
1. Introduction
2. Methods and Analysis
2.1. Halo Mass Function and Abundance Matching
2.2. Bayesian Analysis
3. Results and Discussion
3.1. Forecasts for JWST
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
| 1 | In fact, one can easily adopt a smooth bending of the luminosity function and set instead the upper limit of integration in Equation (2) just to . For example, [79] empirically suggest to multiply Equation (1) by a factor for . We have checked that in the computation of the cosmic SFR, this produces practically indistinguishable results with respect to our simple treatment. |
References
- Meurer, G.R.; Heckman, T.M.; Calzetti, D. Shedding Light on Dark Matter at Colliders. Int. J. Mod. Phys. 2013, 28, 1330052. [Google Scholar]
- Kahlhoefer, F. Review of LHC dark matter searches. Int. J. Mod. Phys. 2017, 32, 1730006. [Google Scholar] [CrossRef]
- Argyropoulos, S.; Brandt, O.; Haisch, U. Collider Searches for Dark Matter through the Higgs Lens. Symmetry 2021, 13, 2406. [Google Scholar] [CrossRef]
- Aprile, E. et al. [XENON Collaboration] Dark Matter Search Results from a One Ton-Year Exposure of xenon1t. Phys. Rev. Lett. 2018, 121, 111302. [Google Scholar] [CrossRef] [PubMed]
- Bernabei, R.; Belli, P.; Caracciolo, V.; Cerulli, R.; Merlo, V.; Cappella, F.; D’Angelo, A.; Incicchitti, A.; di Marco, A.; Dai, C.J.; et al. DAMA/LIBRA-phase2 results and implications on several dark matter scenarios. Int. J. Mod. Phys. 2020, 35, 2044023. [Google Scholar] [CrossRef]
- Ackermann, M. et al. [The Fermi LAT Collaboration] Limits on dark matter annihilation signals from the Fermi LAT 4-year measurements of the isotropic gamma-ray background. J. Cosmol. Astropart. Phys. 2015, 2015, 8. [Google Scholar] [CrossRef]
- Ackermann, M. et al. [The Fermi LAT Collaboration] The Fermi Galactic Center GeV Excess and Implications for Dark Matter. Astrophys. J. 2017, 840, 43. [Google Scholar] [CrossRef]
- Albert, A. et al. [The Fermi-LAT and DES Collaborations] Searching for Dark Matter Annihilation in Recently Discovered Milky Way Satellites with Fermi-LAT. Astrophys. J. 2017, 834, 110. [Google Scholar] [CrossRef]
- Zornoza, J. Review on Indirect Dark Matter Searches with Neutrino Telescopes. Universe 2021, 7, 415. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D. History of dark matter. Rev. Mod. Phys. 2018, 90, 045002. [Google Scholar] [CrossRef]
- Frenk, C.S.; White, S.D.M. Dark matter and cosmic structure. Ann. Phys. 2012, 524, 507–534. [Google Scholar] [CrossRef]
- Lapi, A.; Danese, L. A Stochastic Theory of the Hierarchical Clustering. I. Halo Mass Function. Astrophys. J. 2020, 903, 117. [Google Scholar] [CrossRef]
- Aghanim, M. et al. [Planck Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493. [Google Scholar] [CrossRef]
- de Blok, W.J.G.; Walter, F.; Brinks, E.; Trachternach, C.; Oh, S.-H.; Kennicutt, R.C., Jr. High-Resolution Rotation Curves and Galaxy Mass Models from THINGS. Astron. J. 2008, 136, 2648. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Bullock, J.S.; Kaplinghat, M. The Milky Way’s bright satellites as an apparent failure of LambdaCDM. Mon. Not. R. Astron. Soc. 2012, 422, 1203–1218. [Google Scholar] [CrossRef]
- Bullock, J.S.; Boylan-Kolchin, M. Small-Scale Challenges to the ΛCDM Paradigm. Annu. Rev. Astron. Astrophys. 2017, 55, 343–387. [Google Scholar] [CrossRef]
- Gentile, G.; Famaey, B.; Zhao, H.; Salucci, P. Universality of galactic surface densities within one dark halo scale-length. Nature 2009, 461, 627–628. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Lelli, F.; Schombert, J.M. Radial Acceleration Relation in Rotationally Supported Galaxies. Phys. Rev. Lett. 2016, 117, 201101. [Google Scholar] [CrossRef]
- El-Zant, A.; Shlosman, I.; Hoffman, Y. Dark Halos: The flattening of the density cusp by dynamical friction. Astrophys. J. 2001, 560, 636. [Google Scholar] [CrossRef]
- Tonini, C.; Lapi, A.; Salucci, P. Angular Momentum Transfer in Dark Matter Halos: Erasing the Cusp. Astrophys. J. 2006, 649, 591. [Google Scholar] [CrossRef]
- Pontzen, A.; Governato, F. Cold dark matter heats up. Nature 2014, 506, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Peirani, S.; Dubois, Y.; Volonteri, M.; Devriendt, J.; Bundy, K.; Silk, J.; Pichon, C.; Kaviraj, S.; Gavazzi, R.; Habouzit, M. Density profile of dark matter haloes and galaxies in the HORIZON-AGN simulation: The impact of AGN feedback. Mon. Not. R. Astron. Soc. 2017, 472, 2153–2169. [Google Scholar] [CrossRef]
- Freundlich, J.; Jiang, F.; Dekel, A.; Cornuault, N.; Ginzburg, O.; Koskas, R.; Lapiner, S.; Dutton, A.; Maccio, A.V. A model for core formation in dark matter haloes and ultra-diffuse galaxies by outflow episodes. Mon. Not. R. Astron. Soc. 2020, 491, 4523–4542. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rev. 2004, 405, 279–390. [Google Scholar] [CrossRef]
- Feng, J.L. Dark Matter Candidates from Particle Physics and Methods of Detection. Annu. Rev. Astron. Astrophys. 2010, 48, 495–545. [Google Scholar] [CrossRef]
- Salucci, P.; Esposito, G.; Lambiase, G.; Battista, E.; Benetti, M.; Bini, D.; Boco, L.; Sharma, G.; Bozza, V.; Buoninfante, L.; et al. Einstein, Planck and Vera Rubin: Relevant encounters between the Cosmological and the Quantum Worlds. Front. Phys. 2021, 8, 603190. [Google Scholar] [CrossRef]
- Kusenko, A. Sterile neutrinos: The dark side of the light fermions. Phys. Rev. 2009, 481, 1–28. [Google Scholar] [CrossRef]
- Adhikari, R.; Agostini, M.; Ky, N.A.; Araki, T.; Archidiacono, M.; Bahr, M.; Baur, J.; Behrens, J.; Bezrukov, F.; Bhupal Dev, P.S.; et al. A White Paper on keV sterile neutrino Dark Matter. J. Cosmol. Astropart. Phys. 2017, 1, 25. [Google Scholar] [CrossRef]
- Bode, P.; Ostriker, J.P.; Turok, N. Halo Formation in Warm Dark Matter Models. Astrophys. J. 2001, 556, 93. [Google Scholar] [CrossRef]
- Lovell, M.R.; Frenk, C.S.; Eke, V.R.; Jenkins, A.; Gao, L.; Theuns, T. The properties of warm dark matter haloes. Mon. Not. R. Astron. Soc. 2014, 439, 300–317. [Google Scholar] [CrossRef]
- Hu, W.; Barkana, R.; Gruzinov, A. Fuzzy Cold Dark Matter: The Wave Properties of Ultralight Particles. Phys. Rev. Lett. 2000, 85, 1158. [Google Scholar] [CrossRef] [PubMed]
- Hui, L.; Ostriker, J.P.; Tremaine, S.; Witten, E. Ultralight scalars as cosmological dark matter. Phys. Rev. D 2017, 95, 043541. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Zavala, J.; Cyr-Racine, F.-Y.; Pfrommer, C.; Bringmann, T.; Sigurdson, K. ETHOS—An effective theory of structure formation: Dark matter physics as a possible explanation of the small-scale CDM problems. Mon. Not. R. Astron. Soc. 2016, 460, 1399–1416. [Google Scholar] [CrossRef]
- Tulin, S.; Yu, H.-B. Dark Matter Self-interactions and Small Scale Structure. Phys. Rep. 2018, 730, 1–57. [Google Scholar] [CrossRef]
- Schneider, A.; Smith, R.E.; Maccio, A.; Moore, B. Non-linear evolution of cosmological structures in warm dark matter models. Mon. Not. R. Astron. Soc. 2012, 424, 684–698. [Google Scholar] [CrossRef]
- Dayal, P.; Mesinger, A.; Pacucci, F. Early Galaxy Formation in Warm Dark Matter Cosmologies. Astrophys. J. 2015, 806, 67. [Google Scholar] [CrossRef]
- Schive, H.-Y.; Chiueh, T.; Broadhurst, T.; Huang, K.-W. Contrasting Galaxy Formation from Quantum Wave Dark Matter, ψDM, with ΛCDM, using Planck and Hubble Data. Astrophys. J. 2016, 818, 89. [Google Scholar] [CrossRef]
- Huo, R.; Kaplinghat, M.; Pan, Z.; Yu, H.-B. Signatures of self-interacting dark matter in the matter power spectrum and the CMB. Phys. Lett. B 2018, 783, 76–81. [Google Scholar] [CrossRef]
- Menci, N.; Grazian, A.; Lamastra, A.; Calura, F.; Castellano, M.; Santini, P. Galaxy Formation in Sterile Neutrino Dark Matter Models. Astrophys. J. 2018, 854, 1. [Google Scholar] [CrossRef]
- Lovell, M.R. Toward a General Parameterization of the Warm Dark Matter Halo Mass Function. Astrophys. J. 2020, 847, 147. [Google Scholar] [CrossRef]
- Romanello, M.; Menci, N.; Castellano, M. The Epoch of Reionization in Warm Dark Matter Scenarios. Universe 2021, 7, 365. [Google Scholar] [CrossRef]
- Kulkarni, M.; Ostriker, J.P. What is the halo mass function in a fuzzy dark matter cosmology? Mon. Not. R. Astron. Soc. 2022, 510, 1425. [Google Scholar] [CrossRef]
- Viel, M.; Becker, G.; Bolton, J.S.; Haehnelt, M.G. Warm dark matter as a solution to the small scale crisis: New constraints from high redshift Lyman-alpha forest data. Phys. Rev. 2013, 88, 043502. [Google Scholar] [CrossRef]
- Irsic, V. New constraints on the free-streaming of warm dark matter from intermediate and small scale Lyman-α forest data. Phys. Rev. 2017, 96, 023522. [Google Scholar]
- Irsic, V. First Constraints on Fuzzy Dark Matter from Lyman-α Forest Data and Hydrodynamical Simulations. Phys. Rev. Lett. 2017, 119, 031302. [Google Scholar] [CrossRef]
- Villasenor, B.; Robertson, B.; Madau, P.; Schneider, E. New Constraints on Warm Dark Matter from the Lyman-α Forest Power Spectrum. arXiv 2022, arXiv:arXiv:2209.14220. [Google Scholar]
- Pacucci, F.; Mesinger, A.; Haiman, Z. Focusing on Warm Dark Matter with Lensed High-redshift Galaxies. Mon. Not. R. Astron. Soc. 2013, 435, L53. [Google Scholar] [CrossRef]
- Menci, N.; Grazian, A.; Castellano, M.; Sanchez, N.G. A Stringent Limit on the Warm Dark Matter Particle Masses from the Abundance of z = 6 Galaxies in the Hubble Frontier Fields. Astrophys. J. 2016, 825, L1. [Google Scholar] [CrossRef]
- Shirasaki, M.; Ishiyama, T.; Ando, S. Virial Halo Mass Function in the Planck Cosmology. Astrophys. J. 2021, 922, 89. [Google Scholar] [CrossRef]
- Sabti, N.; Munoz, J.B.; Blas, D. New Roads to the Small-scale Universe: Measurements of the Clustering of Matter with the High-redshift UV Galaxy Luminosity Function. Astrophys. J. 2022, 928, L20. [Google Scholar] [CrossRef]
- De Souza, R.S.; Mesinger, A.; Ferrara, A.; Haiman, Z.; Perna, R.; Yoshida, N. Constraints on Warm Dark Matter models from high-redshift long gamma-ray bursts. Mon. Not. R. Astron. Soc. 2012, 432, 3218–3227. [Google Scholar] [CrossRef]
- Lapi, A.; Mancuso, C.; Celotti, A.; Danese, L. Galaxy Evolution at High Redshift: Obscured Star Formation, GRB Rates, Cosmic Reionization, and Missing Satellites. Astrophys. J. 2017, 835, 37. [Google Scholar] [CrossRef]
- Barkana, R.; Haiman, Z.; Ostriker, J.P. Constraints on Warm Dark Matter from Cosmological Reionization. Astrophys. J. 2001, 558, 482. [Google Scholar] [CrossRef]
- Lapi, A.; Danese, L. Cold or warm? Constraining dark matter with primeval galaxies and cosmic reionization after Planck. J. Cosmol. Astropart. Phys. 2015, 2015, 3. [Google Scholar] [CrossRef]
- Dayal, P.; Choudhury, T.R.; Bromm, V.; Pacucci, F. Reionization and Galaxy Formation in Warm Dark Matter Cosmologies. Astrophys. J. 2017, 836, 16. [Google Scholar] [CrossRef]
- Carucci, I.P.; Corasaniti, P. Cosmic Reionization History and Dark Matter Scenarios. Phys. Rev. D 2019, 99, 023518. [Google Scholar] [CrossRef]
- Lapi, A.; Ronconi, T.; Boco, L.; Shankar, F.; Krachmalnicoff, N.; Baccigalupi, C.; Danese, L. Astroparticle Constraints from Cosmic Reionization and Primordial Galaxy Formation. Universe 2022, 8, 476. [Google Scholar] [CrossRef]
- Vegetti, S.; Despali, G.; Lovell, M.R.; Enzi, W. Constraining sterile neutrino cosmologies with strong gravitational lensing observations at redshift z∼0.2. Mon. Not. R. Astron. Soc. 2018, 481, 3661. [Google Scholar] [CrossRef]
- Ritondale, E.; Vegetti, S.; Despali, G.; Auger, M.W.; Koopmans, L.V.E.; McKean, J.P. Low-mass halo perturbations in strong gravitational lenses at redshift z∼0.5 are consistent with CDM. Mon. Not. R. Astron. Soc. 2018, 485, 2179. [Google Scholar] [CrossRef]
- Carucci, I.P.; Villaescusa-Navarro, F.; Viel, M.; Lapi, A. Warm dark matter signatures on the 21cm power spectrum: Intensity mapping forecasts for SKA. J. Cosmol. Astropart. Phys. 2015, 2015, 047. [Google Scholar] [CrossRef][Green Version]
- Boyarsky, A.; Drewes, M.; Lasserre, T.; Mertens, S.; Ruchayskiy, O. Sterile neutrino Dark Matter. Prog. Part. Nucl. Phys. 2019, 104, 1–45. [Google Scholar] [CrossRef]
- Chatterjee, A.; Dayal, P.; Choudhury, T.R.; Hutter, A. Ruling out 3 keV warm dark matter using 21 cm EDGES data. Mon. Not. R. Astron. Soc. 2019, 487, 3560–3567. [Google Scholar] [CrossRef]
- Rudakovskyi, A.; Savchenko, D.; Tsizh, M. Can EDGES observation favour any dark matter model? Mon. Not. R. Astron. Soc. 2020, 497, 3393–3399. [Google Scholar] [CrossRef]
- Bringmann, T.; Kahlhoefer, F.; Schmidt-Hoberg, K.; Walia, P. Strong Constraints on Self-Interacting Dark Matter with Light Mediators. Phys. Rev. Lett. 2017, 118, 141802. [Google Scholar] [CrossRef] [PubMed]
- Grand, R.J.J.; White, S.D.M. Dark matter annihilation and the Galactic Centre Excess. Mon. Not. R. Astron. Soc. 2022, 511, L55. [Google Scholar] [CrossRef]
- Weisz, D.R.; Johnson, B.D.; Conroy, C. The Very Faint End of the UV Luminosity Function over Cosmic Time: Constraints from the Local Group Fossil Record. Astrophys. J. 2014, 794, L3. [Google Scholar] [CrossRef][Green Version]
- Weisz, D.R.; Boylan-Kolchin, M. Local Group ultra-faint dwarf galaxies in the reionization era. Mon. Not. R. Astron. Soc. 2017, 469, L83–L88. [Google Scholar] [CrossRef]
- Calabrese, E.; Spergel, D. Ultra-light dark matter in ultra-faint dwarf galaxies. Mon. Not. R. Astron. Soc. 2016, 460, 4397–4402. [Google Scholar] [CrossRef]
- Burkert, A. Fuzzy Dark Matter and Dark Matter Halo Cores. Astrophys. J. 2020, 904, 161. [Google Scholar] [CrossRef]
- Kennedy, R.; Frenk, C.; Cole, S.; Benson, A. Constraining the warm dark matter particle mass with Milky Way satellites. Mon. Not. R. Astron. Soc. 2014, 442, 2487–2495. [Google Scholar] [CrossRef]
- Horiuchi, S.; Humphrey, P.J.; Onorbe, J.; Abazajian, K.N.; Kaplinghat, M.; Garrison-Kimmel, S. Sterile neutrino dark matter bounds from galaxies of the Local Group. Phys. Rev. D 2014, 89, 025017. [Google Scholar] [CrossRef]
- Lovell, M.R.; Bose, S.; Boyarsky, A.; Cole, S.; Frenk, C.S.; Gonzalez-Perez, V.; Kennedy, R.; Ruchayskiy, O.; Smith, A. Satellite galaxies in semi-analytic models of galaxy formation with sterile neutrino dark matter. Mon. Not. R. Astron. Soc. 2016, 461, 60. [Google Scholar] [CrossRef]
- Nadler, E.O.; Birrer, S.; Gilman, D.; Wechsler, R.H.; Du, X.; Benson, A.; Nierenberg, A.M.; Treu, T. Dark Matter Constraints from a Unified Analysis of Strong Gravitational Lenses and Milky Way Satellite Galaxies. Astrophys. J. 2021, 917, 7. [Google Scholar] [CrossRef]
- Newton, O.; Leo, M.; Cautun, M.; Jenkins, A.; Frenk, C.S.; Lovell, M.R.; Helly, J.C.; Benson, A.J.; Cole, S. Constraints on the properties of warm dark matter using the satellite galaxies of the Milky Way. J. Cosmol. Astropart. Phys. 2021, 8, 62. [Google Scholar] [CrossRef]
- Enzi, W.; Murgia, R.; Newton, O.; Vegetti, S.; Frenk, C.; Viel, M.; Cautun, M.; Fassnacht, C.D.; Auger, M.; Despali, G.; et al. Joint constraints on thermal relic dark matter from strong gravitational lensing, the Ly α forest, and Milky Way satellites. Mon. Not. R. Astron. Soc. 2021, 506, 5848. [Google Scholar] [CrossRef]
- Oesch, P.A.; Bouwens, R.J.; Illingworth, G.D.; Labbé, I.; Stefanon, M. The Dearth of z∼10 Galaxies in All HST Legacy Fields—The Rapid Evolution of the Galaxy Population in the First 500 Myr. Astrophys. J. 2018, 855, 105. [Google Scholar] [CrossRef]
- Bouwens, R.J.; Oesch, P.A.; Stefanon, M.; Illingworth, G.; Labbé, I.; Reddy, N.; Atek, H.; Montes, M.; Naidu, R.; Nanayakkara, T.; et al. New Determinations of the UV Luminosity Functions from z∼9 to 2 Show a Remarkable Consistency with Halo Growth and a Constant Star Formation Efficiency. Astron. J. 2021, 162, 47. [Google Scholar] [CrossRef]
- Bouwens, R.J.; Illingworth, G.; Ellis, R.S.; Oesch, P.A.; Stefanon, M. z∼2-9 galaxies magnified by the Hubble Frontier Field Clusters II: Luminosity functions and constraints on a faint end turnover. arXiv 2022, arXiv:2205.11526. [Google Scholar]
- Harikane, Y.; Ouchi, M.; Oguri, M.; Ono, Y.; Nakajima, K.; Isobe, Y.; Umeda, H.; Mawatari, K.; Zhang, Y. A Comprehensive Study on Galaxies at z∼9–17 Found in the Early JWST Data: UV Luminosity Functions and Cosmic Star-Formation History at the Pre-Reionization Epocht. arXiv 2022, arXiv:2208.01612. [Google Scholar]
- Chabrier, G. Galactic Stellar and Substellar Initial Mass Function. Publ. Astron. Soc. Pacific 2003, 115, 763. [Google Scholar] [CrossRef]
- Meurer, G.R.; Heckman, T.M.; Calzetti, D. Dust Absorption and the Ultraviolet Luminosity Density at z∼3 as Calibrated by Local Starburst Galaxies. Astrophys. J. 1999, 521, 64. [Google Scholar] [CrossRef]
- Bouwens, R.J.; Illingworth, G.D.; Oesch, P.A. UV-continuum slopes of >4000 z∼4-8 galaxies from the HUDF/XDF, HUDF09, ERS, CANDELS-South, and CANDELS-North fields. Astrophys. J. 2014, 793, 115. [Google Scholar] [CrossRef]
- Kennicutt, R.C.; Evans, N.J. Star Formation in the Milky Way and Nearby Galaxies. Annu. Rev. Astron. Astrophys. 2012, 50, 531–608. [Google Scholar] [CrossRef]
- Madau, P.; Dickinson, M. Cosmic Star-Formation History. Annu. Rev. Astron. Astrophys. 2014, 52, 415. [Google Scholar] [CrossRef]
- Cai, Z.; Lapi, A.; Bressan, A.; De Zotti, G.; Negrello, M.; Danese, L. A Physical Model for the Evolving Ultraviolet Luminosity Function of High Redshift Galaxies and their Contribution to the Cosmic Reionization. Astrophys. J. 2014, 785, 65. [Google Scholar] [CrossRef]
- Robertson, B.E.; Ellis, R.S.; Furlanetto, S.R.; Dunlop, J.S. Cosmic reionization and early star-forming galaxies: A joint analysis of new constraints from Planck and Hubble Space Telescope. Astrophys. J. 2015, 802, L19. [Google Scholar] [CrossRef]
- Finkelstein, S.L.; D’Aloisio, A.; Paardekooper, J.-P.; Ryan, R., Jr.; Behroozi, P.; Finlator, K.; Livermore, R.; Upton Sanderbeck, P.R.; Dalla Vecchia, C.; Khochfar, S. Conditions for Reionizing the Universe with a Low Galaxy Ionizing Photon Escape Fraction. Astrophys. J. 2019, 879, 36. [Google Scholar] [CrossRef]
- Efstathiou, G. Suppressing the formation of dwarf galaxies via photoionization. Mon. Not. R. Astron. Soc. 1992, 256, 43P–47P. [Google Scholar] [CrossRef]
- Sobacchi, E.; Mesinger, A. How does radiative feedback from an ultraviolet background impact reionization? Mon. Not. R. Astron. Soc. 2013, 432, 3340. [Google Scholar] [CrossRef]
- Diemer, B. COLOSSUS: A Python Toolkit for Cosmology, Large-scale Structure, and Dark Matter Halos. Astrophys. J. Suppl. Ser. 2018, 239, 35. [Google Scholar] [CrossRef]
- Tinker, J.; Kravtsov, A.V.; Klypin, A.; Abazajian, K.; Warren, M.; Yepes, G.; Gottlober, S.; Holz, D.E. Toward a Halo Mass Function for Precision Cosmology: The Limits of Universality. Astrophys. J. 2008, 688, 709. [Google Scholar] [CrossRef]
- Schneider, A.; Smith, R.E.; Reed, D. Halo mass function and the free streaming scale. Mon. Not. R. Astron. Soc. 2013, 433, 1573–1587. [Google Scholar] [CrossRef]
- May, S.; Springel, V. He halo mass function and filaments in full cosmological simulations with fuzzy dark matter. arXiv 2022, arXiv:arXiv:220914886. [Google Scholar]
- Aversa, R.; Lapi, A.; De Zotti, G.; Danese, L. Black Hole and Galaxy Coevolution from Continuity Equation and Abundance Matching. Astrophys. J. 2015, 810, 74. [Google Scholar] [CrossRef]
- Moster, B.P.; Naab, T.; White, S.D.M. EMERGE—An empirical model for the formation of galaxies since z∼10. Mon. Not. R. Astron. Soc. 2018, 477, 1822. [Google Scholar] [CrossRef]
- Cristofari, P.; Ostriker, J.P. Abundance matching for low-mass galaxies in the CDM and FDM models. Mon. Not. R. Astron. Soc. 2019, 482, 4364–4371. [Google Scholar] [CrossRef]
- Behroozi, P.; Wechsler, R.H.; Hearin, A.P.; Conroy, C. UNIVERSEMACHINE: The correlation between galaxy growth and dark matter halo assembly from z = 0–10. Mon. Not. R. Astron. Soc. 2020, 488, 3143–3194. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Kistler, M.D.; Yuksel, H.; Beacom, J.F.; Hopkins, A.M.; Wyithe, J.S.B. The Star Formation Rate in the Reionization Era as Indicated by Gamma-Ray Bursts. Astrophys. J. 2009, 705, L104. [Google Scholar] [CrossRef]
- Gruppioni, C.; Bethermin, M.; Loiacono, F.; Le Fevre, O.; Capak, P.; Cassata, P.; Faisst, A.L.; Schaerer, D.; Silverman, J.; Yan, L.; et al. The ALPINE-ALMA [CII] survey. The nature, luminosity function, and star formation history of dusty galaxies up to z≈6. Astron. Astrophys. 2020, 643, A8. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461. [Google Scholar] [CrossRef]
- Liddle, A.R. How many cosmological parameters? Mon. Not. R. Astron. Soc. 2004, 351, L49. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; Van Der Linde, A. Bayesian measures of model complexity and fit. J. R. Statist. Soc. B 2002, 64, 583. [Google Scholar] [CrossRef]
- Park, J.; Gillet, N.; Mesinger, A.; Greig, B. Properties of reionization-era galaxies from JWST luminosity functions and 21-cm interferometry. Mon. Not. R. Astron. Soc. 2020, 491, 3891. [Google Scholar] [CrossRef]
- Labbe, I.; Bezanson, R.; Atek, H.; Brammer, G.; Coe, D.; Dayal, P.; Feldmann, R.; Forster Schreiber, N.M.; Franx, M.; Geha, M.C.; et al. UNCOVER: Ultra-deep NIRCam and NIRSpec Observations Before the Epoch of Reionization. JWST Propos. Cycle 2021, 1, 2561. [Google Scholar]
- Robertson, B.E. Galaxy Formation and Reionization: Key Unknowns and Expected Breakthroughs by the James Webb Space Telescope. arXiv 2021, arXiv:2110.13160. [Google Scholar] [CrossRef]
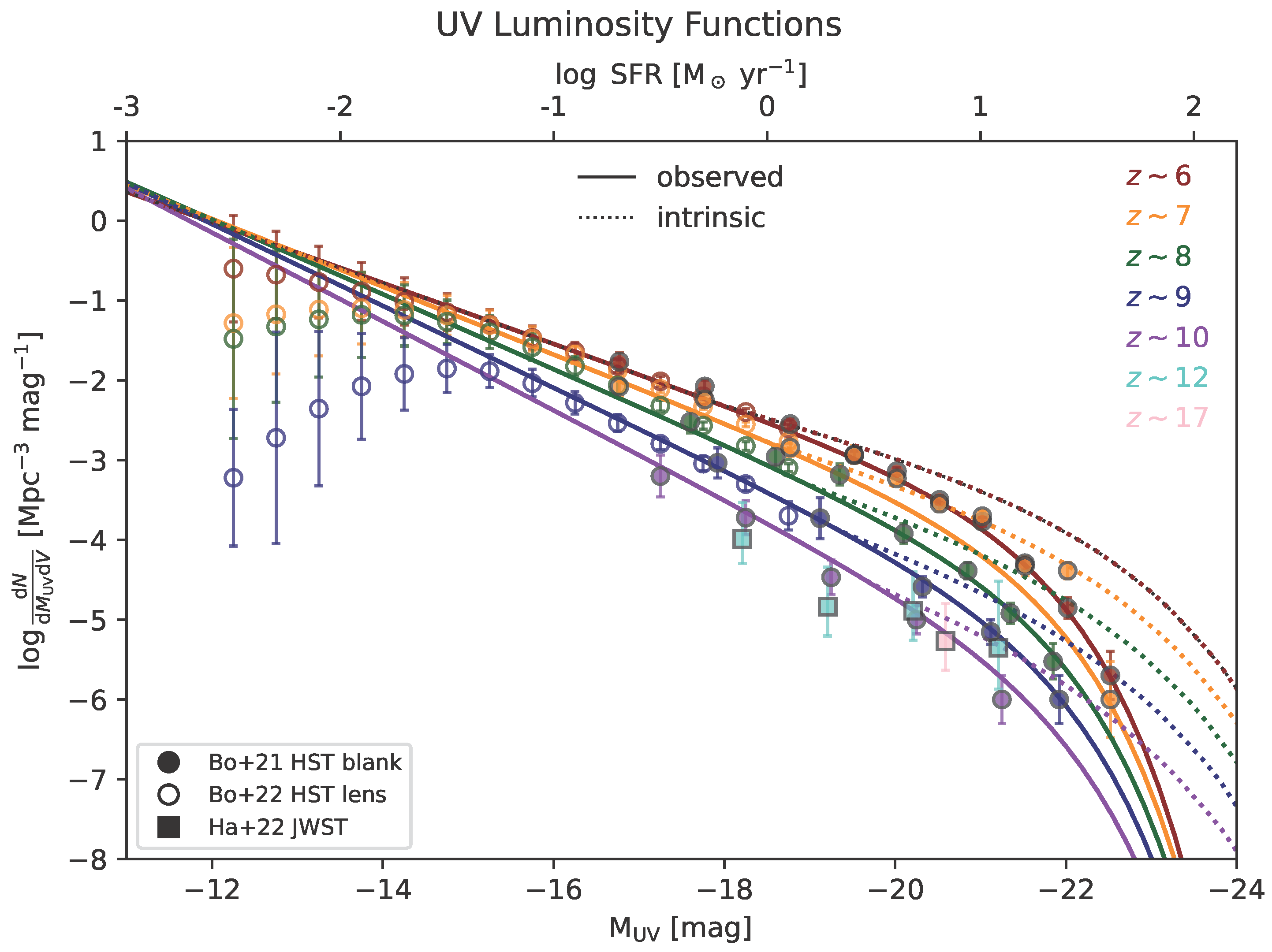
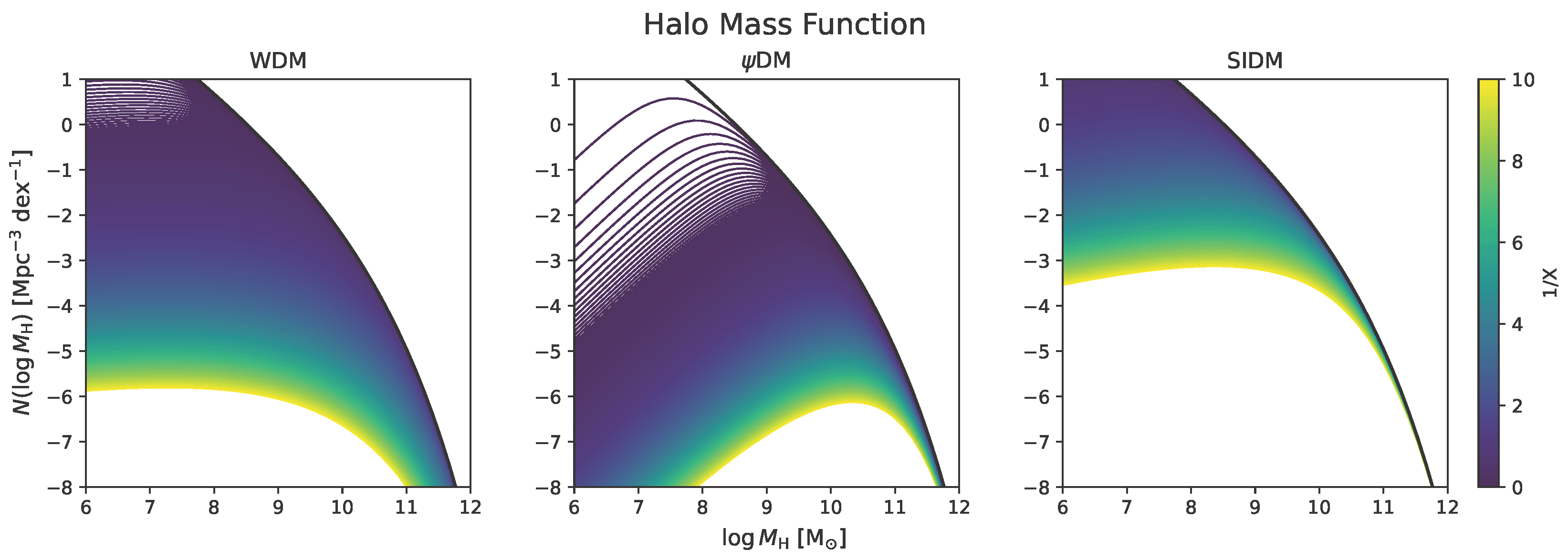
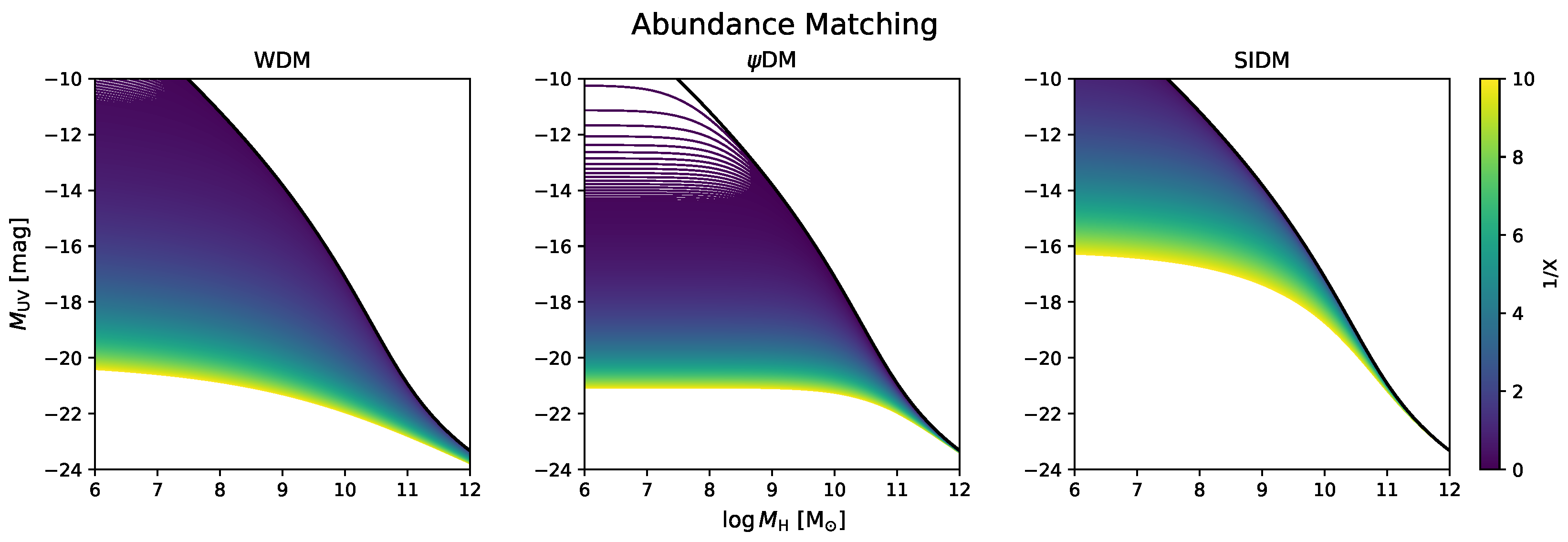
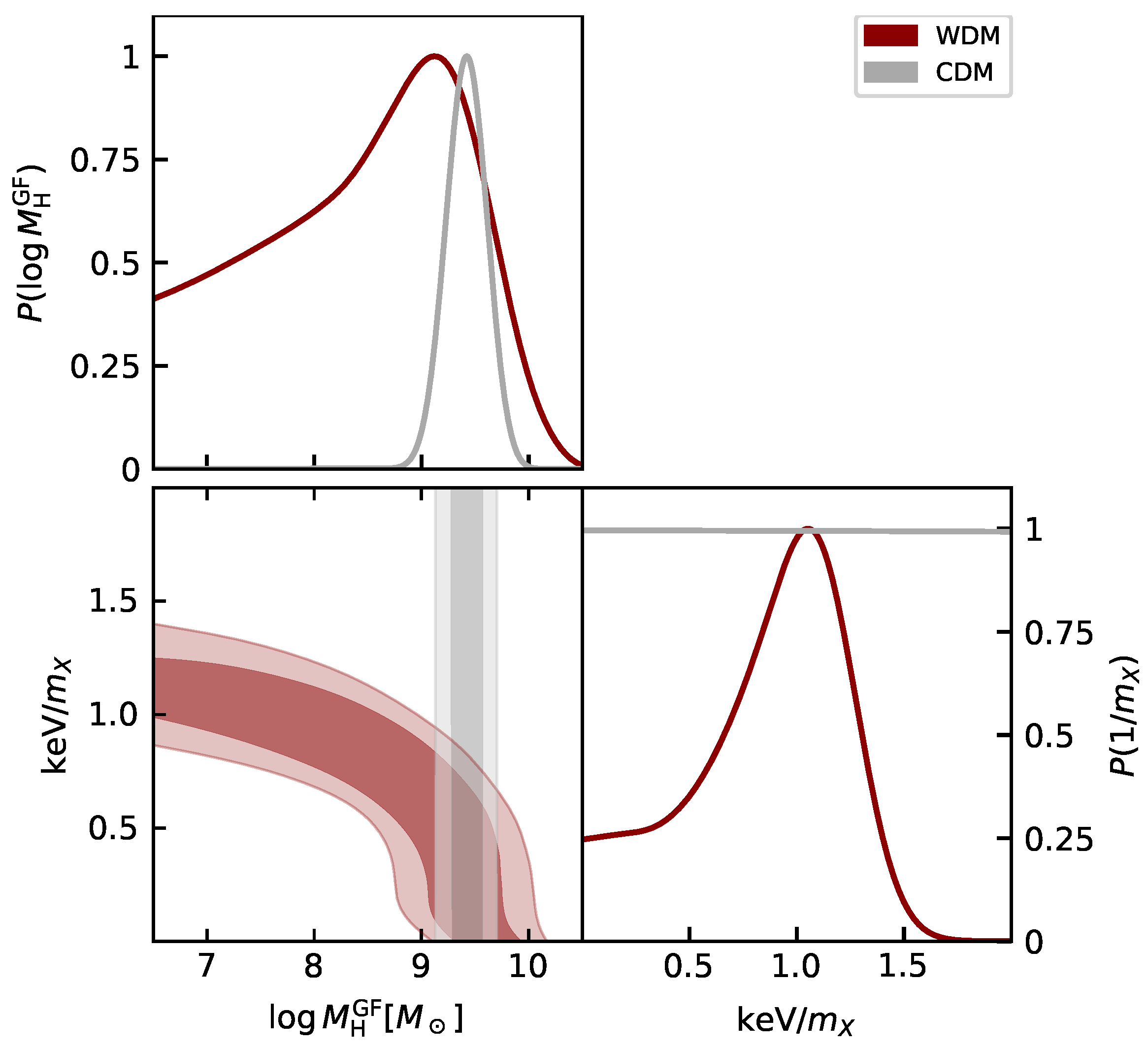
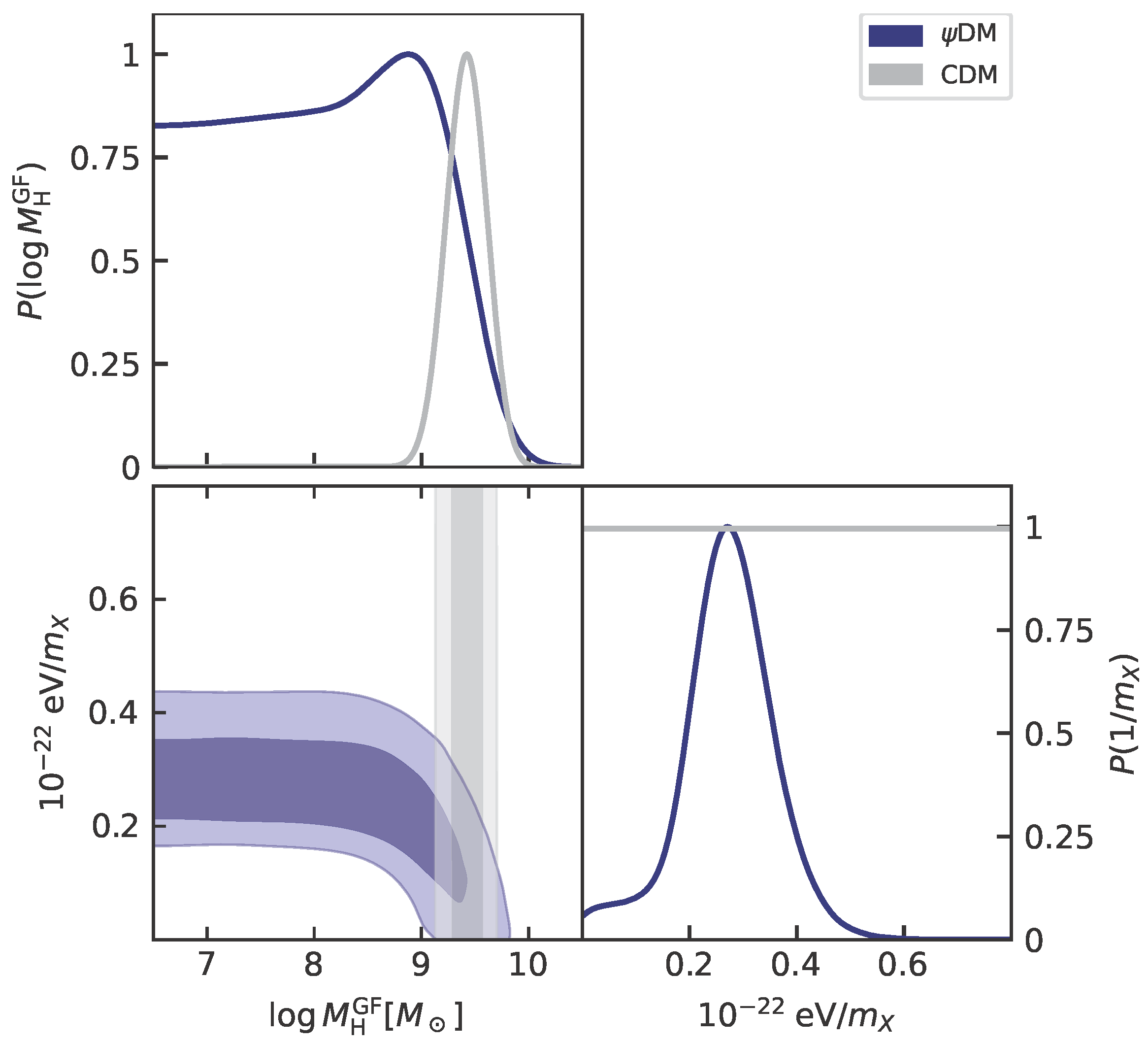
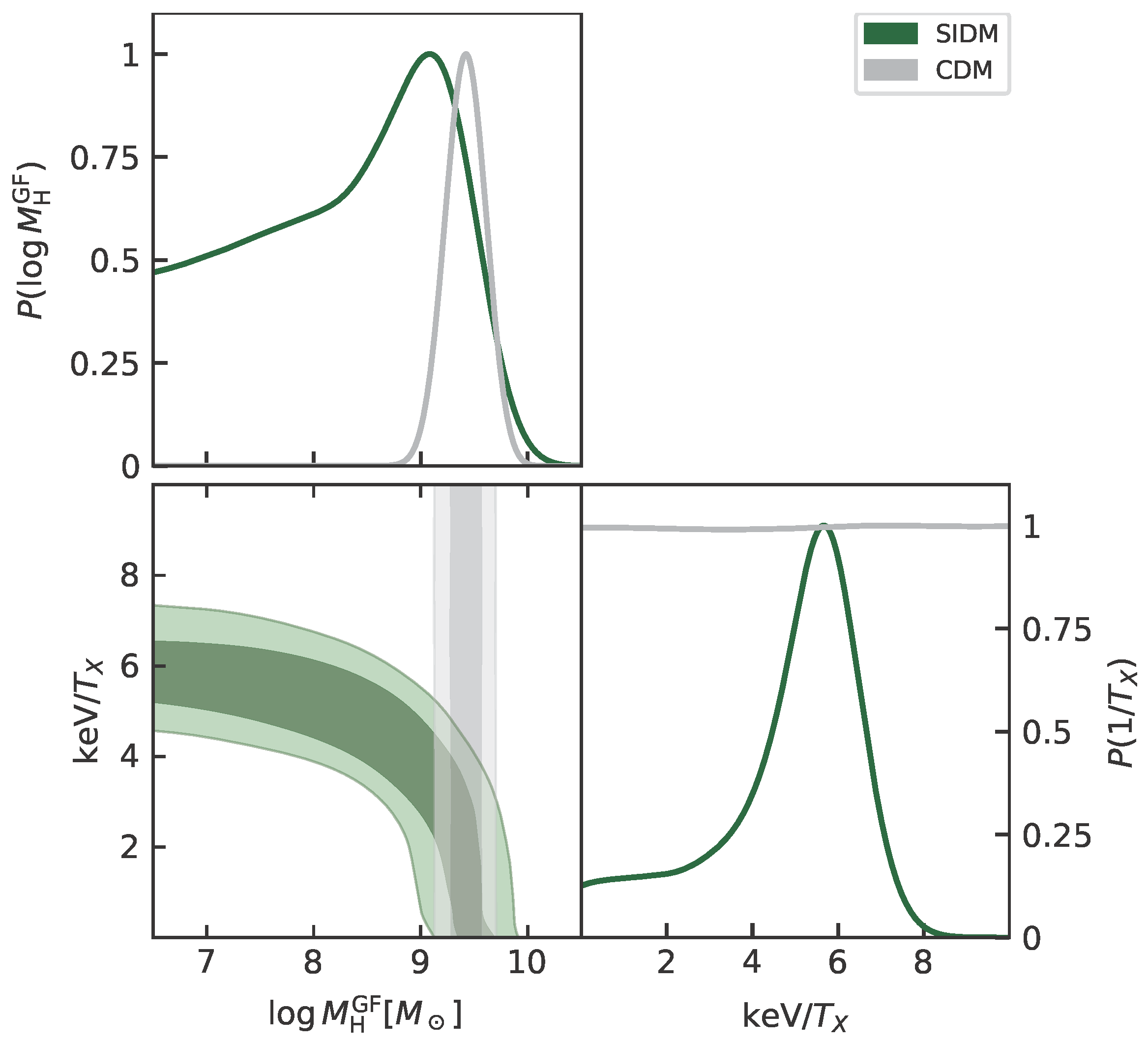
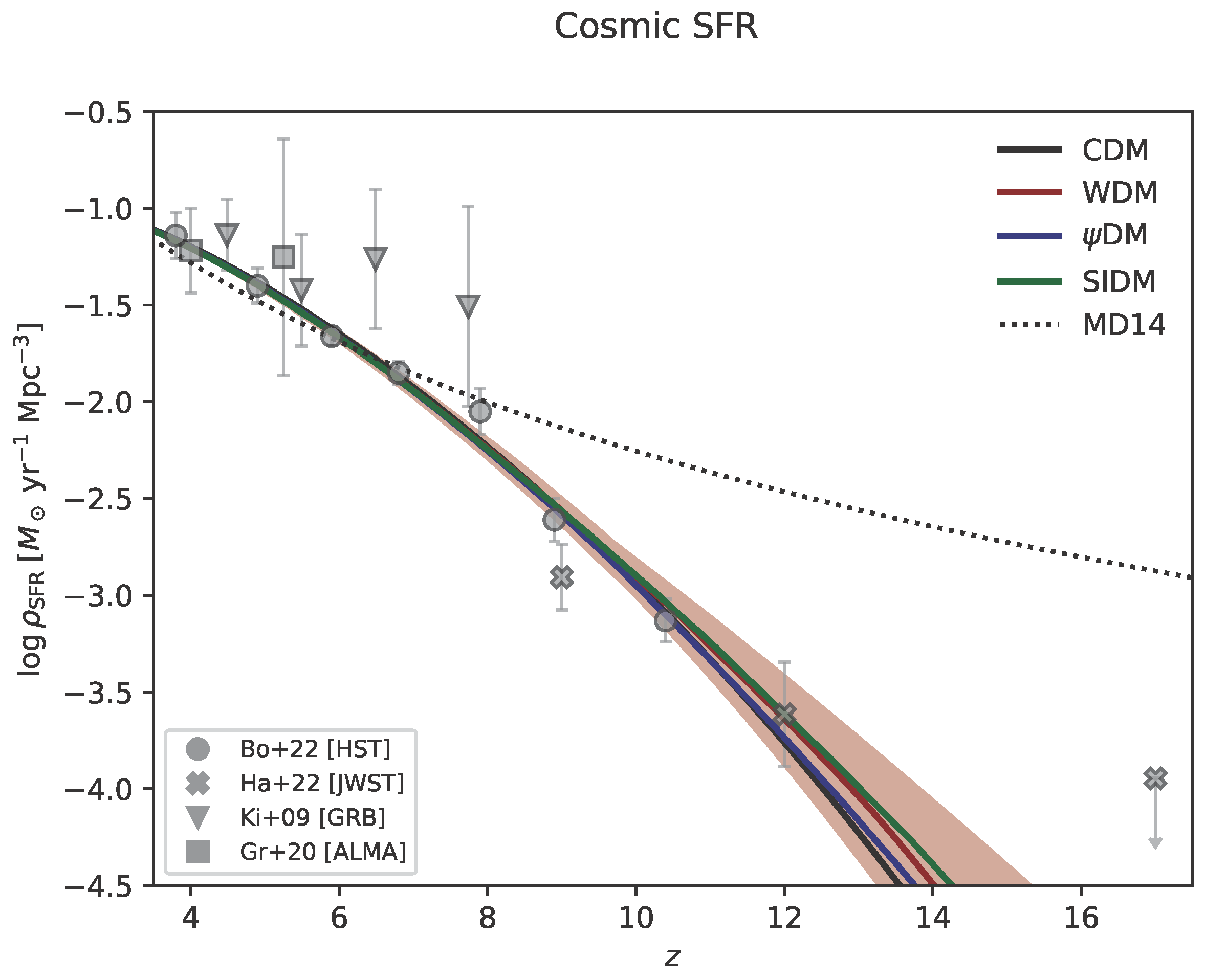
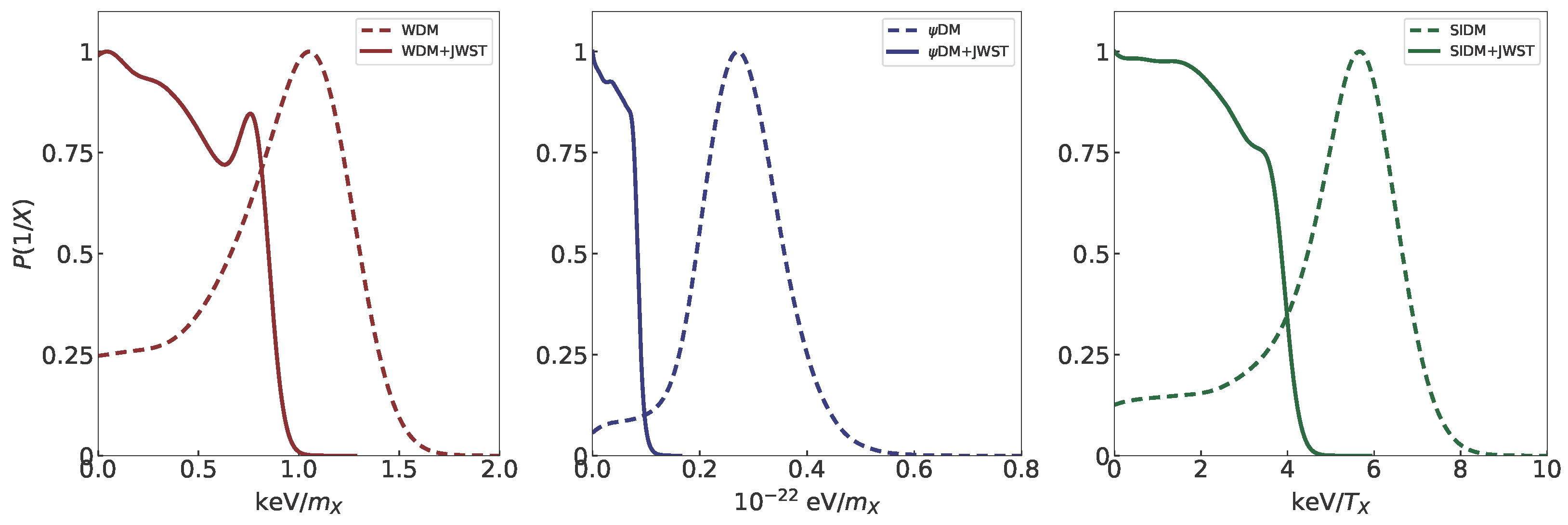
| Scenario | Ref. | ||
|---|---|---|---|
| WDM | [36] | ||
| DM | [38] | ||
| SIDM | [39] |
| Data | Redshifts | Values | Uncertainties | Reference |
|---|---|---|---|---|
| UV LF [HST] | [77,78,79] | |||
| UV LF [JWST] | [80] | |||
| GRB counts [Fermi] | [100] | |||
| (sub)mm LF [ALMA] | [101] |
| Scenario | X | BIC | DIC | |
|---|---|---|---|---|
| CDM | − | |||
| WDM | ||||
| DM | ||||
| SIDM | ||||
| CDM + JWST forecast | − | |||
| WDM + JWST forecast | ||||
| DM + JWST forecast | ||||
| SIDM + JWST forecast |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gandolfi, G.; Lapi, A.; Ronconi, T.; Danese, L. Astroparticle Constraints from the Cosmic Star Formation Rate Density at High Redshift: Current Status and Forecasts for JWST. Universe 2022, 8, 589. https://doi.org/10.3390/universe8110589
Gandolfi G, Lapi A, Ronconi T, Danese L. Astroparticle Constraints from the Cosmic Star Formation Rate Density at High Redshift: Current Status and Forecasts for JWST. Universe. 2022; 8(11):589. https://doi.org/10.3390/universe8110589
Chicago/Turabian StyleGandolfi, Giovanni, Andrea Lapi, Tommaso Ronconi, and Luigi Danese. 2022. "Astroparticle Constraints from the Cosmic Star Formation Rate Density at High Redshift: Current Status and Forecasts for JWST" Universe 8, no. 11: 589. https://doi.org/10.3390/universe8110589
APA StyleGandolfi, G., Lapi, A., Ronconi, T., & Danese, L. (2022). Astroparticle Constraints from the Cosmic Star Formation Rate Density at High Redshift: Current Status and Forecasts for JWST. Universe, 8(11), 589. https://doi.org/10.3390/universe8110589







