Abstract
We consider a consistent with gravity electron based on the overrotating Kerr-Newman (KH) solution and show that the earlier KH electron models proposed by Carter, Israel and López in 1970–1990 should be modified by the Landau-Ginzburg theory, leading to a superconducting electron model consistent with gravity and quantum theory. Truncated by Israel and López, the second sheet of the KN solution is rearranged and represented in a mirror form as a sheet of the positron, so that the modified KN system forms a quantum electron-positron vacuum interacting with gravity. Regularization of the KN black hole solution creates two new important effects leading to a strong gravitational interaction that acts on the Compton scale contrary to the usual Planck scale of Schwarzschild gravity: (A)—gravitational frame-dragging creates two Wilson loops acting at two boundaries of the modified KN solution, and (B)—formation of the flat superconducting core of the regularized KN solution creates a superconducting electron-positron vacuum state. The Landau-Ginzburg model shows that Wilson loops determine phases of two Higgs fields forming superconducting vacuum state of the modified KN solution, quantum vacuum of the electron-positron pairs. The phases of these Higgs fields correspond to two light-like modes of a classical relativistic ring string. We come to the conclusion that the electron models considered by Israel and López are not complete and must be supplemented by a mirror structure that forms a quantum system consistent with QED.
1. Introduction
Two approaches to the problem of interaction between gravity and quantum theory are well known and usually widely discussed: theory of superstrings and loop quantum gravity. Meanwhile, there is a third area of research that has already been discussed over fifty years, and was recently again reactivated. This is the treatment of the elementary quantum particle as an overrotating the Kerr-Newman (KN) solution [1,2,3,4,5,6,7,8,9,10,11,12,13]. Formation of black holes is related with classical gravitational effect of frame-dragging [14], which has not previously been considered in particle physics and, when applied to the problem of interaction between quantum theory and gravity, it leads to two important new consequences:
(A)—the emergence of the topologically non-trivial space-time structure that changes effective scale of the gravitational interaction;
(B)—formation of the Wilson loops of vector potential through gravitational effect of frame-dragging, which creates strong influence of gravity on the particle quantization.
The effects (A) works in the famous Kerr-Newman (KN) solution, which is the well-known solution for a charged and rotating BH, and the effect (B) appears in the regularized KN solution considered as a non-perturbative model of the electron, and possibly other leptons as well.
In 1968, Carter noticed that KN solution has gyromagnetic ratio just the same as that of the Dirac electron [1], which gave rise to two lines in the study of the electron model based on the KN solution: the disk-like and bubble models [3,4,8,15], and the string-like models [5,6,11], based on the analogue of the Kerr singular ring with a string, similar to the Nielsen-Olesen string model in superconductor [16]. These lines were united in the subsequent series of the works [9,10], where the source of the KN electron model was considered as a superconducting bag model with a string formed on the sharp border of the bag-like core.
The KN model of electron is consistent with gravity by nature [2], and these works show, how the known insuperable contradictions between gravity and quantum physics can actually be resolved. 1
As opposed to gravitational radius of the Schwarzschild solution effective zone of gravitational interaction in the KN solution is determined by radius of the Kerr singular ring
which is inverse proportional to mass m and proportional to angular momentum of the Kerr solution One sees that for electron parameters and parameter a is the reduced Compton wave length and the usual arguments on the exclusive role of the Planck length (see for example [17]) turn out to be incorrect when applied to Kerr’s spinning gravity.
Kerr singular ring is the branch line of the KN space into two sheets, and the KN solution with parameters of elementary particles is not really black hole, because (in the dimensionless units) the typical spinning particles have which is condition for disappearance of the black hole horizons, and therefore, the naked singular ring (not covered by horizon) created in 1970s the problem of the physical interpretation of Kerr space.
The energy momentum tensor of the naked Kerr singular ring diverges, and the over-rotating KN solution carries infinite energy. Contrarily to the case of the spherically symmetric gravity, the overrotating KN gravity brings infinite energy on the Compton scale and needs a regularization and even the renormalization similar to QED.
The electromagnetic KN field [2,18] is also unlimited, and being depended on cut-off , it forms a closed Wilson loop of the KN vector potential, which plays important role in formation of the quantum system of electron-positron vacuum.
The cut-off , determines increment of the KN vector potential along the closed Wilson loop [19] that sets balance between gravitational and electromagnetic interaction, and determines the regularized mass of the particle as a result of a nonlinear gravito-electromagnetic interaction.
The overrotating KN solution represents a topologically nontrivial two-folded manifold composed of the “positive” sheet of space, coupled with a mirror “negative” sheet, similarly to the Einstein-Rosen bridge or the wormhole solution.
W.Israel in [3] (1970) formed the KN electron model, truncating “negative” sheet of KN solution, and completing the resulting manifold by a specially selected energy-momentum tensor consistent with the Einstein equations.
López [4] regularized KN solution truncating singular ring (together with “negative” sheet) at the “classical” radius corresponding to the boundary where the energy of electromagnetic field starts compensate the energy of gravitational field. This regularization formed a flat core of the electron as a model of vacuum bubble, which is free from gravitational and electromagnetic field. López’s electron formed a disk with the thickness and the radius equal to the half of the Compton wave length (1), see Figure 1. As a result, core of the regularized electron acquires the flat internal (Minkowskian) metric, retaining the exact external gravitational and electromagnetic field of the KN solution.
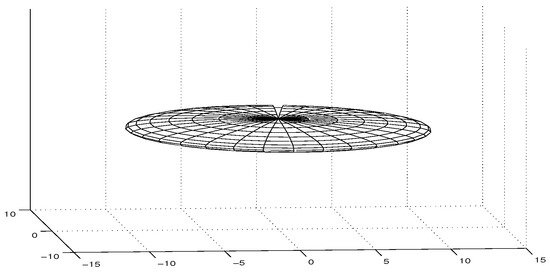
Figure 1.
Disk-like core of the KN electron model is defined unambiguously by form of the Kerr-Newman metric and Kerr’s ellipsoidal coordinate system.
One of the main point of the our consideration of the KN solution is related with the observation that the truncated by W. Israel and C. López “negative” sheet of the KN solution are not unnecessary, and after a small modification (the space reflection with change of the sign of charge), the “negative” sheet starts describe positron, as a counter-part of electron model, and they form, together with electron, the electron-positron vacuum energy, providing strong interaction with the KN gravitational field.
As a result, we arrive to the conclusion that the electron models considered by Israel, as well as by López, are not complete and must be supplemented by the mirror “negative” structure forming a quantum electron-positron system.
This point of view is supported by the Landau-Ginzburg model of the superconducting phase transition, which indicates that the corresponding quantum vacuum core of the KN electron is to be superconducting and core of the KN electron is formed by a strong magnetic coupling of the electron and positron counterparts.
As a result, the KN solution has undergone a transformation that replaces the “negative” sheet with a “mirror” sheet, carrying the opposite charge and current coupled with mirror boundary. Under regularization, the mirror boundary acquires the mirror Wilson line.
Since Wilson lines are integral curves of the strong gravitational and electromagnetic field in a fixed world time t, the evolution of these fields in time is best described in the Kerr-Schild coordinate system. Meanwhile, the relativistic system can also be described by the “proper time s”, where the size of the system is reduced by the Lorentz contraction. We show that the regularized boundary of KN solution represents a classical relativistic ring string taking intermediate position between the string (word time t) and the light-like particle (proper time s) that is created from this string by relativistic contraction. This string-particle correspondence is a copy of the Heisenberg-Schrödinger correspondence in quantum theory and plays very important role in quantum interpretation of the KN electron model.
2. Kerr-Newman Solution in the Kerr-Schild Form
In the Kerr-Schild coordinates, metric of the KN solutions is [2]
where is metric of an auxiliary Minkowski space (signature ), and H is the scalar function which for the KN solution takes the form
and the KN vector potential is
where
and the Kerr angular coordinates are related to Cartesian coordinates as follows
Vector field (), forms Principal Null Congruence of the Kerr solution [2]. Congruence forms a vortex of the null field which propagates analytically from negative sheet of Kerr metric, to positive one, where the ingoing congruence turns into the outgoing field. In equatorial plane, null lines of the Kerr congruence focus on singular ring =0, see Figure 2.
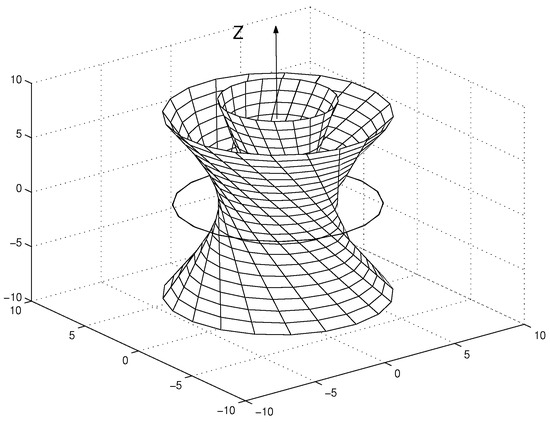
Figure 2.
Two-sheeted Kerr’s congruence passes analytically through the Kerr singular ring from “positive” sheet of KN metric to “negative”.
The “mirror” modification of the KN metric corresponds to a change in the direction of the Kerr congruence on the mirror sheet , when passing through the boundary . The change coupled with a mirror change of the direction of rotation , gives and we have
The metrics on the ingoing and outgoing -sheets become different There is a freedom in choice of the or for the “basic” sheet of space [14]. We take as the “basic” the outgoing field that corresponds to the classical physical picture with the retarded electromagnetic field, and we chose as positive rotation the anticlockwise direction of the Kerr congruence near the Kerr singular ring.
Taking the “mirror sheet” as a sheet of positron, we must also change the sign of the charge, that gives as two vector potentials
acting on the ingoing and outgoing sheets of the KN solution.
3. The Kerr Theorem
Kerr theorem defines two fields of PNC, and in terms of Penrose’s twistor theory [20,21]. Kerr theorem presents two complex analytic solutions of the equation
where F is quadratic holomorphic function of the projective twistor coordinates and
are the null Cartesian coordinates of the auxiliary Minkowski space
In the class of quadratic in Y functions the Kerr theorem gives two analytic solutions of the Equation (9), which correspond to two projective spinor coordinates
which are antipodally conjugate
and the corresponding Weyl spinors and define two antipodal fields of the principal null directions
4. López Electron as a Regularized KN Solution
In regularized by López KN solution, singular region is replaced by a flat core forming interior of the bubble model. The boundary which separates flat core from the external KN gravity is defined unambiguously as a boundary surface where the nonlinear term in (2) is cancelled, and the KN metric becomes flat.
According (3) it corresponds to
(López, 1984 [4]).
The metric at is set flat, and the external KN space is joined continuously with flat interior of the electron core, which corresponds to the Gürsey and Gürses class of the deformed KN metrics [15]. Since r is Kerr’s radial coordinate, (6), the core takes form of a thin ellipsoidal disk (see Figure 1 and Figure 3),which has the thickness and radius determined by the Compton wave length so that the ratio
is the fine structure constant. The small Cartesian distance on Figure 3 works as a cutoff for the regularization of the KN electromagnetic and gravitational fields.
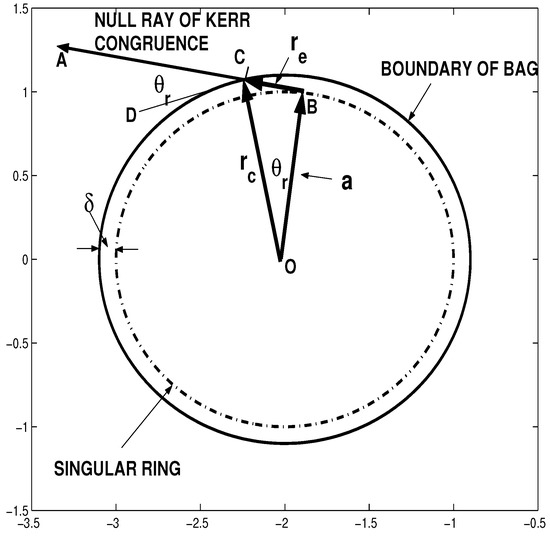
Figure 3.
Kinematic relations for the KN disk in equatorial plane. Null rays of Kerr congruence are tangent to Kerr singular ring and cross border of bag at angle
Since the initial KN manifold is two-sheeted, the López regularization creates also the mirror boundary surface where the nonlinear term in (2) is also cancelled, and metric (2) on the mirror side of the core is also flat,
As shows Figure 3, the original Kerr congruence of the KN solution propagates analytically from the basic sheet of the KN space on the mirror negative sheet, where
Taking into account the above-mentioned reinterpretation of the mirror sheet as a sheet for a positron solution, we perform a space reflection reversing the direction of Kerr congruence and changing the sign of the direction of rotation Then, the transformation relations to Kerr’s coordinates (6) have to be changed, and on the mirror sheet of the KN solution for they take the form
5. Wilson Loops, Quantization and Emergence of the Monopole-Antimonopole Pair
In the regularized KN solution, potential (4) increases strongly near the sharp boundaries of the disk-like core and forms two string-like loops on the borders , which are placed in the equatorial plane at fixed . On the boundary potential is dragged by the lightlike direction and angular component of the potential (4) increases, forming the closed loop
like a smoothed -function with maximal value at the ring string
When integrating over the contour , the Wilson loop gives the phase increment
which, in accordance with the Kerr principal relation
becomes proportional to
We see that phase increment of Wilson line is quantized, similar to phase of the wave function, giving quantum contribution to classical action through “minimal” coupling
To unambiguously determine the we need to put and we obtain ([19]) that the Wilson line gives the electron a quantization condition of angular momentum and also a series of additional quantum solutions, with
The Wilson loop carries the tension energy of the ring string and forms a particle with a spin in the form of a regularized Kerr disk, Figure 3, whose radius is equal to half the Compton wavelength [1,3,4].
In the works [9,19], the boundary of KN disk was formed as a domain wall phase transition in the Ginzburg-Landau field model, where the space inside the disk forms a superconducting vacuum core of the KN bag model, created by a phase transition from the external gravitational solution KN to the vacuum state inside the Kerr disk.
According to Stokes’ theorem, such Wilson loop should generate a magnetic flux
However, we know that a monopole cannot be born alone, and the second Wilson loop should exist with the contour , generating an anti-monopole equal to half of the quantum of the magnetic field , and the Dirac monopole mast be born simultaneously.
Indeed, the similar potential related with the ingoing Kerr congruence, is concentrated on the mirror side of the Kerr space. It is connected with the ingoing Kerr congruence, and at the moment of potential is positioned on the boundary placed in the equatorial plane , forming the ring string along the loop
Integration the Wilson loop with opposite orientation of the contour gives the opposite phase increment
Therefore, contribution of the Wilson loop at the boundary almost completely reduces contribution of the loop at , except for an important asymmetry: integration over the boundary is associated with a retarded vector potential, i.e., with the outgoing “basic” congruence, which generates the gravitational KN field, while the boundary is related with ingoing vector potential and does not contain the electrostatic component
which is usually associated with the mass of electron [22] appearing as the mass term “m” in the Dirac equations and in the expression (3) for KN metric. Therefore, the strong total interaction between the KN gravitational field and two Wilson loops does not manifest itself explicitly in the mass term “m”, but acts non-linearly, increasing the mass by reducing the radius a in the Kerr principal relation (1).
Thus, two Wilson loops generate on two boundaries of the Kerr disk and a magnetically coupled pair consisting of a Dirac monopole and an anti-monopole, that is, a Cooper pair that gives rise to superconducting state in the vacuum core of the Kerr disk.
We should make some reference here to several previous applications of similar ideas in other physical models of elementary particles, not connected with gravitational frame-dragging and KN gravity. First of all we note that the phase increment of this type, similar to the model of Wilson loop, was discussed long ago as a Berry phase, or Pancharatnam-Berry phase, in many models related with classical Bohm-Aharonov magnetic solenoid effect. Second, the close ideas related with classical string models of this type where considered by Frank Wilczek [23], and then, as a 3D non-critical string model of Mezincescu and Townsend [24] and others. Also, the electron vacuum core, and the hidden vacuum magnetic energy of electron-positron vacuum pairs, was considered in the Shulman model [25].
6. Superconducting Core of the KN Solution
Separation of the classical gravity from superconducting core of the KN bag model is performed by the supersymmetric Landau-Ginzburg (LG) domain wall model, see [9,10,26]. The use of supersymmetry is really necessary, because the simpler non-supersymmetric LG models cannot provide the concentration of the Higgs field inside of the bag model and leads to the opposite configuration of the bag, forming the bag as a cavity in a superconductor.
Meanwhile, the simplest LG model, which was used as a phenomenological model of superconductivity in the Nielsen-Olesen string model [16], and in the MIT and SLAC bag models [27,28], can be used to a simplified description of the phase transition between the external KN field and the superconducting state inside the core of the KN electron model.
Lagrangian of the corresponding Nielsen-Olesen field model is
where is covariant derivative, and is the complex Higgs field
The real curved Domain Wall surface considered in [10] is replaced here by a flat one, and we consider interaction of the external KN electromagnetic field with a Higgs field placed inside the superconducting bag.
From Lagrangian (25) we obtain the equations for boundary current
which show that by penetration of the potential in the Higgs vacuum field phase of the Higgs field interacts with potential creating on the bag boundary a superficial current , which penetrates inside the bag on a penetration depth, after that phase of the Higgs field field eats the potential, leading to and r.h.s. of (26) takes the form The resulting equations
can be integrated and give explicit solution for phase of the Higgs field
These important results follow from the famous old paper by Ginzburg and Landau [29], in which for the first time, a connection was established between superconductivity and the quantum wave function of the Schrödinger equation for the simplest case of a flat boundary between superconductivity and an electromagnetic field.
Ginzburg and Landau were the first to use the wave function of the Schrödinger equation to model the superconducting state, and this was the forerunner the fact that superconductivity will play a central role in the structure of elementary particles, and in particular, in the electron structure discussed here. This idea turned out to be extremely fruitful, and was further developed in the close connection between the Higgs mechanism of elementary particle physics and phase transitions in more complex superconducting models.
Finally, the development of the supersymmetric version of the Ginzburg-Landau theory has shown its equivalence to the supersymmetric model of quantum electrodynamics [30], the super-QED model proposed by Wess and Zumino.
Supersymmetric Ginzburg-Landau Model and Two Sides of the KN Disk
In the KN electron model, the discussed above boundary between the exact external KN solution EXT and superconducting core INT represents the oblate ellipsoidal surface shown on Figure 1. It is much more complex then the flat surface, and formation of the phase transition requires the full power of the Supersymmetric Ginzburg-Landau model [30].
As it was shown in [9,10] the boundary should be described by a domain wall, which interpolates between the states EXT and INT and controlled by the superpotential W which must be a holomorphic function of five chiral fields.
In terms of the superfield formalism, two of the chiral fields are the Higgs superfields and and bosonic part of these superfields gives two Higgs fields The relation
shows that the Higgs fields
can have different amplitudes but their phases must be correlated
It was obtained in [10] that the KN bag has also a negative boundary which contributes into the BPS state of the supersymmetric bag model. This boundary is just the mirror boundary corresponding to the in-going fields which fall on the superconducting core of the KN solution before the scattering as ingoing fields.
The coordinate transformations for the mirror sheet (16) are obtained with a space reflection that changes the sign of the Kerr radial coordinate and the direction of rotation In addition, the charge sign is changed that changes the sign of potential energy corresponding to consideration of the mirror sheet as a sheet for a positron. Analogues of the Equations (26)–(28) take the form
where
where the current is created on the boundary related with the ingoing metric based on the Kerr congruence Superconducting core of the KN solution acquires two string-like currents of opposite orientations and two Higgs fields with opposite phases
acting as the left and right light-like modes of the string model.
The Higgs fields and are associated with two superfields of the supersymmetric QED model [30].
7. Emergence of the Classical Ring String Structure
As it was shown in Section 6, the vector potential of Wilson lines creates two surface currents (33) in the core of KN electron model, which are parametrized by the Kerr angular coordinate and have a radius of equal to half of Compton wavelength. These currents turn out to be light-like and generate the model of a closed relativistic ring string, forming a minimal surface in 4d Minkowski space. String model turns out to be very important for compatibility of the nonperturbative KN solution with quantum theory, since it removes contradiction between the extended classical particle and the point particle of quantum theory. Description of the KN electron in the Kerr-Schild coordinate is realised in the word time “t” at a fixed moment , corresponding to image of a closed string placed on the boundary of the KN disk. In quantum theory this corresponds to a state vector in Heisenberg picture. The relativistic ring strings are massless, and their mass-energy is created from their relativistic dynamics. Below we show in Section 7.2 that the length of the relativistic KN string is reduced by the Lorentz contraction, and the KN ring string, which is considered in world time “t” as an extended string of Compton size, is compressed to a point in the proper time “s” coordinates corresponding to Schrödinger state vector of quantum theory.
7.1. Orientifold String
By analogue with the Nielsen-Olesen string model [16], in [6] we considered the Kerr singular ring as a string in the Carter-Israel-López-KN electron model and showed in [11] that this string can have an orientifold structure, which satisfies to equations of motions and constraints corresponding to the classical Nambu-Goto string.
In general, the four-dimensional relativistic bosonic string is 2-dimensional world-sheet embedded in 4-d space-time. It satisfies the wave equation
where are the light-cone parameters, t is the world-sheet time parameter, and is the space-like parameter along the string length. String solution is formed as a sum of the left and right modes obeying the light-cone constraints
At the boundaries phases of the Higgs fields (34) coincide with the left and right null direction of the Kerr congruence and the wave Equation (35) and constraints (36) are satisfied.
The extra factor 2 in (34) reflects peculiarity of the orientifold string, which, as it was shown in [11], is consistent with two-folded structure of the Kerr-Schild geometry. Orientifold forms a parity operator covering the string world-sheet twice: first time as the map and second time as the map in opposite direction.
7.2. Electron as a Quantum Particle
Let us return to the Israel electron model, in which negative sheet of the Kerr solution was truncated but the electromagnetic field was absent and the model was not regularized. In spite of the absence of these components, the Israel model demonstrates very important features of the electron as a quantum particle.
First of all, by representing electron as a disk of the reduced Compton radius (1), Israel’s model shows that this does not contradict the point electron of quantum theory.
Indeed, V. Hamity showed in [31] (1986) that the boundary of Israel’s disk moves at the speed of light, and therefore, an observer at rest will see this boundary compressed to a point due to the Lorentz transformations. Therefore, this known discrepancy is due to the use of different coordinate systems for a strictly relativistic object. The reduced Compton radius of Israel’s electron corresponds to description of Israel’s electron in the Kerr-Schild coordinate system which a fixed world time , that corresponds to Heisenberg picture of quantum theory, while the electron compressed to a point corresponds to its image in relativistically rotating coordinate systems (see [32], par.89, and also [33]), that corresponds to Schrödinger picture of quantum theory.
We see that the Lorentz contraction of the relativistic ring string solves the problems of inconsistency of the extended KN solution, explaining it by the inconsistence of different coordinate systems using for the relativistic light-like particle: the Compton size of the KN disk corresponds to a snapshot picture of the Kerr-Schild coordinate system, or the state vector in the Heisenberg picture at , while the experimental observation of electron as a quantum point corresponds to the Schrödinger picture of the wave function for the light-like relativistic ring string.
Indeed, the Israel model of electron described in the proper time s tells as still more. Truncating the right part of the two-folded KN solution, Israel represents electron as the most elementary string excitation formed only by left mode of the orientifold string. Impact of the right mode is excluded, and Israel’s electron turns into a classical massless relativistic ring string model consisting only from the left half-string excitation. This string has the zero rest mass and satisfies the classical Namby-Goto string equations [11].
Consider this string as a state vector of a quantum particle with Hamiltonian
Following the known Dirac’s approach to linearization of the nonlinear Hamiltonian of this type, we obtain that, for the relativistic string with , Hamiltonian (37) is linearized automatically (without the use of Dirac matrices),
and the Schrödinger equation takes the form
where the momentum operator is divided into a transactional part related to a slow movement of the particle as a whole, and the part associated with circular motion of Kerr’s ring string, parametrized by Kerr’s angular coordinate .
Thus, for a particle at rest, we have , showing that circular motion of the ring string gives the electron an effective rest mass.
Using the Dirac matrices in Cartesian coordinates of the auxiliary Minkowski space of the Kerr-Schild coordinate system, we obtain the Dirac equation in the form
It is convenient to use the Weyl basis, where the Dirac matrices have the form
In this case, the Dirac spinor contains two Weil spinors
In the Weyl basis, the Equations (40) are separated, and two spinors and describe two independent state vectors and which correspond to opposite helicities, i.e., projections of the spin on the direction of momentum .2
As usual, the Heisenberg and Schrödinger state vectors are related by unitary transformation
and we see that factor corresponds to kinetic energy of the ring string rotation. Negative sign of (39) should be related with negative frequencies of the wave function, and gives rise to conjugate relation for co-vector representations of positron
This transformation is singular, which complicates interpretation of and indicates the need of regularization.
8. Wilson Loops of KN Gravity and QED Formalism
8.1. Excess Energy Produces by Wilson Loops, QED and Mass Renormalization
Temporary component of the potential , which concentrated on the Wilson loops, gives the electrostatic part of the electron energy which does not contribute to Wilson loops, since the loops are formed by the condition including only tangent components of Energy of the electrostatic part
when regularizing on the “classical” radius (14) corresponds to observable mass of the electron m, as it was shown for example in [22]. The Wilson loops boundaries and give an additional magnetic contribution to mass-energy of electron—the energy of the interacting with KN gravity electron-positron vacuum pairs.
This shows that López’s regularization requires an additional procedure, known from the QED, as a renormalization of the mass. The rest mass particles m should be formed as the sum
consisting of the excessive mass-energy of the interacting with gravity Wilson lines and the additional hidden contribution , which is reduced during the renormalization process.
8.2. Consistency of Modified KN Structure with QED
The KN solution expressed in Kerr-Schild coordinates is compatible with Heisenberg representation of quantum theory, in which the energy-moment tensor of the KN solution can be obtained in correspondence with the QED (see [35], par. 3.1 ), and takes the form
An analysis of the components in this expression (see also par.89 in [36]) makes it possible to combine quantum theory with gravity through the system of Einstein-Maxwell equations, which in the Kerr-Schild formalism [2] can be presented in the tetrad form as follows
where is the energy-moment tensor (46), presented in the Kerr-Schild tetrad form
The Contributions to created by potentials (19) and (23) on the Wilson loops and are mutually cancelled, for exclusion of the electrostatic (time-) component (24), which plays a special role, being located only on the border It gives after integration the total mass-energy of the electron the mass term m (44), which is usually taken as the mass in the Dirac equation.
Fermionic components in the expression (46), as shown in [37], correspond to orbital part of the current density fluctuations . The vacuum expectation of this sum is zero, since the Dirac electron ring current cancels the oppositely oriented ring current of the positron, forming the vacuum binding energy of the electron-positron pairs.
Alternative, but similar interpretation of these fermionic components in (46) is related to their analogy with Cooper pairs in the Ginzburg-Landau theory of superconductivity (see for example [38]). Comparison with the expression for electron current in QED
shows that the term in (46) is proportional to the density of the electron current and the term is proportional to density of the positron current .
9. Conclusions
The KN electron model, considered initially by Carter, Israel and López, and also by Kerr et al. and Newman et al. in works [1,2,3,4,18] demonstrated explicitly that it carries the strong classical gravitational and electromagnetic fields concentrated on the Compton scale in vicinity of the Kerr singular ring. This result is fundamental and shows that the gravity of the KN solution is strong and requires regularization contrary to the widely held that gravity is the weakest interaction.
Principal novelty of the present treatment of the overrotating KN solution is its modification with respect to the original topologically nontrivial two-sheeted structure. The truncation of the negative sheet of the KN solution used by Israel and López is replaced by the action of the supersymmetric Ginzburg-Landau field model, which regularizes the singular gravitational and electromagnetic fields by phase transition to a superconducting vacuum state that forms the core of the nonperturbative electron model.
The strong gravitational frame-dragging interacts with regularized KN electromagnetic field creating two Wilson loops positioned on two boundaries of the superconducting core attached to the fixed world time . These loops are related with incoming and outgoing Kerr congruences, and in the modified KN solution their action is almost mutually compensated. However, it turns out that these Wilson loops create very the strong indirect gravitational interaction that acts nonlinearly, greatly increasing the mass by reducing the radius a in the basic Kerr relation (1).
Considering the quantum side of the KN electron model, we come to the conclusion that the Kerr-Schild coordinate system allows us to get the most complete nonperturbative description of the electron structure given by the supersymmetric Ginzburg-Landau field model of phase transition, and obtain the superconducting core of the electron in the modified model of KN solution, as well as to give a detailed description of the gravitational interaction through action of the Wilson loops based on the fields at a fixed point of the world time .
The use of world time t is a very important feature of the Kerr-Schild formalism. In the world time t, the surface currents of the Ginzburg-Landau model take the form of an elementary relativistic ring string corresponding to state vector of quantum electron in Heisenberg’s picture of QED. The corresponding Schrödiger state vector is related with unitary transformation, and we obtain that this unitary transformation acts as a relativistic rotation of the elementary ring string, transforming it to a point by the Lorentz contraction. This point electron corresponds to the state vector in the proper time s, which is often used in quantum consideration.
Using the analogy with the KN black hole solution, we can say that, by going from the “t” representation to the “s” representation, the unitary transformation returns the overrotating black hole back to the non-rotating state. This transformation is singular, since the string as well as the core of electron in this case disappear.
We arrive at the main conclusion that the over-rotating Kerr-Newman electron model, initiated by B. Carter in the work [1], and subsequently developed in the work by G.C. Debney, R.P. Kerr and A. Schild [2], and specified in the works by W. Israel [3] and by C. López [4] represents an extremely important progress in the formation of the nonperturbative electron model which answers the questions “What is electron?” and “How to combine gravity with particle physics?”. In the same time we find that these models, at least, are not complete, since they describe a simplified electron model which in many respects is similar to the bare electron described by QED [35].
We obtain that the used by W.Israel and C.López truncation of the negative sheet of the KN solution deprives this model of its mirror side, which is described by the Kerr-Schild metric with ingoing congruence and corresponds to positron. Interaction of the electron with the mirror positron side of KN solution gives the important vacuum contribution in the form of the electron-positron pairs forming the quantum vacuum interacting with gravity through two Wilson loops, carrying the magnetically coupled monopole-antimonopole pairs.
The Ginzburg-Landau field model plays a fundamental role as a base space for elementary excitations of the ring string, generating the wave properties of KN electron, and also as a base space for emergence of Wilson loops creating the superconducting electron-positron vacuum state, leading to a strong interaction of the KN electron with gravity, consistent with QED.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work is a planed research of NSI RAS. The author thanks the staff of the Laboratory of Theoretical Physics, and especially P.S. Kondratenko and L.V. Matveev, and Yu.N. Obukhov for very useful conversations and discussions.
Conflicts of Interest
The author declare that he has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Notes
| 1 | The reason of contradiction between gravity and quantum theory lies in the delusion about weakness of gravity. The strong gravimagnetic effect of the frame-dragging in the over-rotating KN solution shifts the scale of fundamental interaction to Compton level. This fact has been noted in the pioneering works by Carter, Israel and López [1,3,4], but then it was not emphasised and generalized to the fundamental statement that the KN solution with parameters of an electron do indeed implement gravitational interaction on the Compton scale. |
| 2 | Hamiltonian of a particle with definite , (i.e., matrix (38)), does not commute with the matrix , however the operator helicity (the component of spin in direction ) is conserved, see [34]. The Weyl spinors and are the eigenfunctions of the operator , corresponding to two opposite helicities, and we shell relate them with the and state vectors of the ring string. |
References
- Carter, B. Global Structure of the Kerr Family of Gravitational Fields. Phys. Rev. 1968, 174, 1559. [Google Scholar] [CrossRef]
- Debney, G.C.; Kerr, R.P.; Schild, A. Solutions of the Einsein and Einstein-Maxwell Equations. J. Math. Phys. 1969, 10, 1842. [Google Scholar] [CrossRef]
- Israel, W. Source of the Kerr metric. Phys. Rev. D 1970, 2, 641. [Google Scholar] [CrossRef]
- López, C.A. Extended model of the electron in general relativity. Phys. Rev. D 1984, 30, 313. [Google Scholar] [CrossRef]
- Burinskii, A.Y. Microgeons with spin. Sov. Phys. JETP 1974, 39, 193. [Google Scholar]
- Ivanenko, D.D.; Burinskii, A.Y. Gravitational strings in the models of elementary particles. Izv. Vuz. Fiz. 1975, 5, 135. [Google Scholar] [CrossRef]
- Arcos, H.I.; Pereira,J. G. Kerr-Newman solution as a Dirac particle. Gen. Rel. Grav. 2004, 36, 2441. [Google Scholar] [CrossRef]
- Dymnikova, I. Spinning superconducting electrovacuum soliton Phys. Lett. B 2006, 639, 368. [Google Scholar] [CrossRef]
- Burinskii, A. Gravitating lepton bag model. JETP Zh. Eksp. Teor. Fiz. 2015, 148, 228. [Google Scholar] [CrossRef][Green Version]
- Burinskii, A. Source of the Kerr-Newman solution as a supersymmetric domain-wall bubble: 50 years of the problem. Phys. Lett. B 2016, 754, 99. [Google Scholar] [CrossRef]
- Burinskii, A. Orientifold D-String in the Source of the Kerr Spinning Particle. Phys. Rev. D 2003, 68, 105004. [Google Scholar] [CrossRef]
- Schmekel, B.S. Quasi-Local Energy of a Charged Rotating Object Described by the Kerr-Newman Metric. Phys. Rev. D 2019, 100, 124011. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Huang, Y.-T.; O’Connell, D. Kerr Black Holes as Elementary Particles. J. High Energy Phys. 2020, 2020, 46. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation. Part 3; 1973; W.H. Freeman: San Francisco, CA, USA, 2000; ISBN 978-07167-0344-0. [Google Scholar]
- Gürses, M.; Gürsey, F. Lorentz covariant treatment of the Kerr-Schild geometry. J. Math. Phys. 1975, 16, 2385. [Google Scholar] [CrossRef]
- Nielsen, H.B.; Olesen, P. Vortex-line models for dual strings. Nucl. Phys. 1973, 61, 45. [Google Scholar] [CrossRef]
- Baez, J.C. Higher dimensional algebra and planck scale physics. In Physics Meets Philosophy at the Planck Length; Callender, C., Huggett, N., Eds.; Cambridge U. Press: Cambridge, UK, 2001; pp. 177–195. [Google Scholar]
- Newman, E.T.; Couch, E.; Chinnapared, K.; Exton, A.; Prakash, A.; Torrence, R. Metric of a Rotating, Charged Mass. J. Math. Phys. 1965, 6, 918–919. [Google Scholar] [CrossRef]
- Burinskii, A. The Kerr–Newman Black Hole Solution as Strong Gravity for Elementary Particles. Gravit. Cosmol. 2020, 26, 87. [Google Scholar] [CrossRef]
- Penrose,R. Twistor Algebra. J. Math. Phys. 1967, 8, 345. [Google Scholar] [CrossRef]
- Burinskii, A. Wonderful Consequences of the Kerr Theorem. arXiv 2005, arXiv:hep-th/0506006. [Google Scholar]
- Weisskopf, V.F. Recent Developments in the Theory of the Electron. Rev. Mod. Phys. 1949, 21, 305. [Google Scholar] [CrossRef]
- Wilczek, F. Magnetic Flux, Angular Momentum and Statistics. Phys. Rev. Lett. 1982, 48, 1144. [Google Scholar] [CrossRef]
- Mezincescu, L.; Townsend, P. Anions From Strings. Phys. Rev. Lett. 2010, 105, 191601. [Google Scholar] [CrossRef] [PubMed]
- Shulman, M.E. On the Structure of Electrons and Other Charged Leptons. J. High Energy Phys. Gravit. Cosmol. 2017, 3, 503–521. [Google Scholar] [CrossRef][Green Version]
- Burinskii, A. Features of spinning gravity in particle physics: Supersymmetric core of the Kerr-Newman electron. J. Phys. Conf. Ser. 2019, 1275, 012031. [Google Scholar] [CrossRef]
- Chodos, A.J.R.L.; Jaffe, R.L.; Johnson, K.; Thorn, C.B.; Weisskopf, V.F. New extended model of hadrons. Phys. Rev. D 1974, 9, 3471. [Google Scholar] [CrossRef]
- Bardeen, W.A.; Chanowitz, M.S.; Drell, S.D.; Weinstein, M.; Yan, T.M. Heavy quarks and strong binding: A field theory of hadron structure. Phys. Rev. D 1974, 11, 1094. [Google Scholar] [CrossRef]
- Ginzburg, V.L.; Landau, L.D. On the Theory of Superconductivity. Zh. Eksp. Teor. Fiz. 1950, 20, 1064, (English translation in: Landau, L.D. Collected Papers; Pergamon Press: Oxford, UK, 1965; p. 546.). [Google Scholar]
- Wess, J.; Bagger, J. Supersymmetry and Supergravity; Princeton University Press: Princeton, NJ, USA, 1983. [Google Scholar]
- Hamity, V. An “interior” of the Kerr metric. Phys. Lett. A 1976, 56, 77. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics (Volume 2): The Classical Theory of Fields, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2013; ISBN -13 978-0750627689. [Google Scholar]
- Punsly, B. A physical interpretation of the Kerr solution. J. Math. Phys. 1985, 26, 1728. [Google Scholar] [CrossRef]
- Berestetsky, V.B.; Lifshitz, E.M.; Pitaevsky, L.P. Quantum Electrodynamics (Course Of Theoretical Physics, 4); Pergamon: Oxford, UK, 1982. [Google Scholar]
- Akhiezer, A.I.; Berestetskii, V.B. Quantum Electrodynamics; Interscience Publishers: Geneva, Switzerland, 1965. [Google Scholar]
- Bjorken, J.D.; Drell, S.D. Relativistic Quantum Fields v.2; McGraw-Hill Book Company: New York, NY, USA, 1965. [Google Scholar]
- Thirring, W.R. Principles of Quantum Electrodynamics; Academic Press Inc.: New York, NY, USA, 1958. [Google Scholar]
- Beasley, M.R. Notes on the Ginzburg-Landau Theory; ICMR Summer School on Novel Superconductors University of California: Santa Barbara, CA, USA, 2009. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).