Abstract
Probing the polarization of gravitational waves (GWs) would provide evidence of graviton, indicating the quantization of gravity. Motivated by the next generation of gravitational wave detectors, we make an attempt to study the possible helicity coupling of structured lights to GWs. With the analog between gravitational fields and the generic electromagnetic media, we present a 4-vector optical Dirac equation based on the Maxwell theory under the paraxial approximation. It is found that twisted lights propagating in a gravitational field can be viewed as a non-Hermitian system with symmetry. We further demonstrate that the coupling effect between angular momentums of the GWs and twisted lights may make photons undergo both dipole and quadrupole transitions between different orbital-angular-momentum (OAM) eigenstates and lead to some measurable optical features, including the central intensity brightening and macroscopic rotation of the intensity pattern for twisted lights. The former is spin-independent, while the latter is a spin-dependent phenomenon, both of which can be viewed alternatively as the spin-orbital-Hall effect of structured lights in the GWs and can serve as an indicator of the particle nature of GWs.
1. Introduction
The detection of gravitational waves (GW) by the LIGO interferometer fulfilled experimental verification of the last prediction from the linearized Einstein theory of general relativity [1,2]. In the low-energy regime, the canonical quantization of linear perturbations around the Minkowski background yields a massless spin-2 particle called a graviton [3]. Though we believe that long-range gravity is mediated by the graviton, its existence has never been justified experimentally due to its extraordinary weakness. Actually, measuring a graviton is to make sense of the particle nature of GWs according to wave–particle duality at the quantum level, namely, recognizing some particle features by direct or indirect detections [4]. One theoretical possibility was suggested to detect a single graviton by the emission and absorption of gravitons [5,6] and has been revisited by considering the transition between discrete quantum states with different angular momentums [7].
Moreover, the direct detection of gravitational waves by the advanced LIGO interferometer and the advanced Virgo interferometer marks the beginning of the era of gravitational wave astronomy [8,9,10]. These discoveries stimulate the great efforts devoted to develop more advanced optical detection technology. With upgrading to the next-generation interferometers, it is expected to move to design sensitivity and observe ever-increasing numbers of GW sources. The next generation of a GW laser-interferometric GW detector will be upgraded to have unprecedented sensitivity by minimizing various technical noises. One limiting noise arises from mirror thermal noise produced by the Brownian motion of particles in coatings and substrates. Besides physically cooling a mirror, an alternative solution is to change the mode shape of the laser beam inside the interferometer, e.g., resonating the higher-order Laguerre Gauss (LG ) modes in the detector arm cavities to smooth out the thermal noise fluctuations over a bigger portion of the mirror surface [11]. A well-developed technology has made it possible to produce higher-order LG modes with high power output and high mode purity, as required in GW detection [12,13]. Therefore, it would be crucial to understand the wave mechanics of the higher-order LG modes interacting with the passing gravitational wave.
Though wave theory offers a complete classical description of optical phenomena in nature, in most application situations, the typical wavelength of light is much less than the inhomogeneous length scale of the medium, the geometric optics approximation is valid, and the correspondence principle allows us to make a simple analysis in the context of the Hamiltonian dynamics of particles, which can be induced from the dispersion relationship associated with the wave equation. On the other hand, the Maxwell theory encodes intrinsic degrees of freedom—the polarizations associated with rotating electric and magnetic fields, corresponding to the two spin states of photons. In addition, lights can possess two types of orbital angular momentums (OAM)—the intrinsic OAM from the twisted wavefront of structured lights and the extrinsic orbital angular momentum from helical optical paths in inhomogeneous media. It has been realized that the interplay between various optical OAMs—spin–orbit interactions of light (SOI)— will lead to a variety of optical phenomena on subwavelength scales [14,15,16,17]. The important manifestation of the SOI phenomena is the spin-Hall effects in inhomogeneous media arising from the spin–extrinsic OAM interaction, indicating how the intrinsic polarization degrees of freedom affect the light trajectories beyond the geometric optics approximation [18,19,20,21,22,23,24,25].
For light propagation in a gravitational field, the curved space background can be transformed into a linear optical medium, whose optical properties characterized by the effective dielectric tensor are fully specified by the spacetime geometries. A typical example is the deflection of light in gravitational fields; this phenomenon can be illustrated by the correspondence between the refractive index and the scalar gravitational potential. Again, a rotating gravitational field exhibits the optical activity attributed to the vortical dragging vector, corresponding to gyrotropic materials [26,27,28,29]. By this analog, the gravitational spin-Hall effect can be easily understood for lights propagating in curved spacetime [30,31,32,33].
The motivation for this work is two-fold. First, the next generation of GW detectors may provide more information about the polarization modes of GWs. This paper is to explore the spin-orbital-Hall effect of structured light due to GWs, which may potentially reveal more polarization structures of GWs and allow for testing the theory of gravity beyond GR and justifying the particle nature of GWs. Secondly, it would be interesting to seek an alternative mechanism for detecting GWs in the polarization space, which requires a full vector-wave analysis of structured light coupling with GWs on subwavelength scales.
However, it is noted that the current approach for the spin-Hall effect of light is based on the geometrodynamics of spinning particles [20,21,22,23,24], which is not applicable to dealing with structured lights with intrinsic OAMs propagating in an inhomogeneous medium. In this case, full vectorial-wave mechanics is required to describe the behavior of polarized structured lights. In this work, based on the four-vector optical Dirac equation developed by Feng and Wu [34], we investigate the spin-Hall effect of light in GWs, seeking an alternative method to detect GWs. The paper is organized as follows. The optical Dirac equation of paraxial light in linearized gravitational fields is presented in Section 2. We further discuss the dipole and quadrupole interactions of structured light with GWs in Section 3. In Section 4, we present perturbation analyses of the GWs’ signals in two numerical experiments and discuss their physical implications. Finally, we summarize the paper and give concluding remarks in Section 5.
2. Optical Dirac Equation of Paraxial Light in Gravitational Fields
Let us adopt the following 3+1 decomposition, e.g., [35], defining the spatial metric by
and the 3D dragging vector as
The electromagnetic vectors are identified by
where , and is the determinant of . These definitions lead us to the Maxwell equation in a noncovariant form
in which and are related to and by the constitutive equations,
In linearized gravitational wave theory, , , the spacetime background can be approximated adiabatically by an irrotational gravitational field. Thus, , , the electric field and magnetic field are related to the auxiliary fields and simply by the local constitutive equation , . Formally, for a light beam propagating in a gravitational wave, the gravitational field is equivalent to an optical medium with the permittivity and permeability tensors obeying a simple equality relationship with the spatial metric , , which actually corresponds to the spin-degenerate condition in photonic topological insulators [36]. Since the wavelength of light is much less than that of GW, the GW is further assumed to be a static gravitational field. We define a 6-vector, , in this way, the Maxwell equation becomes a Schrödinger-like compact form
As having been discussed by Feng and Wu [34], the Maxwell equation in generic media can be converted to a non-Hermitian -extended Dirac theory for massive fermions. Central to this approach is to perform vectorial analysis on the helicity basis spanned by the transverse basis with respect to a given direction, which can be aligned with the propagation direction of the incident light, e.g., without a loss of generalities, taking the z-axis. In this case, the helicity basis satisfies . The transversality condition places a constraint on the polarization states of photons, implying the field equation, Equation (9), is reducible. It is noted that, under the paraxial approximation, the longitudinal components can be explicitly derived from the transverse condition, and the electromagnetic 6-vector can be reduced to four independent components. Introducing the vector wavefunctions
with the transverse components and in the helicity space and combining and to form a 4-vector we can arrive at the following optical Dirac equation,
in which the effective mass term is
and the momentum components are given in the helicity basis through and ,
where and are the monopoles, is the dipole momentum with the components , and the quadrupoles . The effective momentums, Equation (13), only have surface terms in the transverse plane. It can be seen that Equation (11) describes a non-Hermitian system with PT symmetry [37,38,39] and is similar to the Jackiw–Rebbi model in topological insulators [40,41]. The only difference between the optical Dirac equation, Equation (11), and the Dirac equation for a spin- particle is an extra operation appearing on the momentum term in the former.
Under the geometric optics approximation, keeping the leading term ∼ in Equation (11) yields the energy-eigenvalue equation
where . Equation (14) has two solutions with positive and negative energies. Since the anti-particle of a photon is itself, a photon with negative energy and helicity can be regarded as a mirror photon with positive energy and opposite helicity. According to Equation (14), its solution can be parameterized by , . Accordingly, the positive energy eigenstates with opposite helicities are written as
We consider the positive-energy solutions to Equation (11) only, which can be written by a linear superposition of the two helicity eigenstates in Equation (15),
We define 2-spinor , and we obtain the optical Schrodinger equation
with the complex optical potential
where only the terms of the linear order of are kept as in the linearized gravity theory, clearly, the above equation takes a form similar to the simplest optical model describing the paraxial propagation of light in an inhomogeneous dielectric medium with a complex refractive index [42,43], whereas here, it is emulating a two-component quantum system. The potential from Equation (18) consists of two parts, the real part gives a dipole interaction, while the imaginary part is a non-Hermitian quadrupole interaction corresponding to the optical gain or loss of the medium. On the other hand, the Hamiltonian equation, (17), has been actually decoupled into two independent scalar equations, implying that the spin-up and spin-down states evolve independently, and thereby, no helicity transition occurs. The helicity-dependent quadrupole coupling is an anti-Hermitian conjugate of each other for the spin-up and -down states, which ensures the symmetry of the optical fields and leads to optical chirality.
On a flat space, the optical potential on the right side of Equation (17) vanished due to the spacetime perturbations, and thus Equation (17) reduces to the familiar paraxial equation, which could have family solutions of structured light with OAMs. In the cylindrical coordinates, the paraxial equation has a set of solutions of the Laguerre–Gaussian modes
where n and l are the radial and the azimuthal indices, the order of the model is given by , the constant , is the width of mode, R the radius of the wavefront curvature, and the Gouy phase factor , , here is the beam waist.
3. Dipole and Quadrupole Interaction of Photons and Gravitational Waves
In metric gravity theory, GWs are allowed, at most, to have six polarization modes, including two tensor types (spin-2), two vector types (spin-1) and two scalar types (spin-0) [44,45]. The dipole momentum in Equation (18), is associated with the vector-type excitation. If the incident vector of GWs is at a given direction of in the spherical coordinates with respect to the propagating direction of the light beam, Einstein’s theory only allows for the existence of the tensor polarizations of plus and cross ,
In the case of the incident GW propagating parallel with the light beam, the dipole is identically zero, , as given in the TT gauge. This dipole interaction consists of two contributions, one is , and the other is . The former is from the GW polarization coupled with the OAM density flow of photons , and the latter is from the spin density flow [46].
In the ’helicity basis’, the dipole interaction can be alternatively written by
where
The complex differential operators in the cylindrical coordinates become
where is the orbital angular momentum operator in the z-direction. It is noted that, for the eigenstates , act as the ladder operators to lower/raise OAMs by one unit. Thus, the dipole interaction will make the initial l mode produce two extra modes with the OAM number of and . For the LG modes, , it is not difficult to work out the following ladder relationships for the lowering and raising operators,
where , and ± signs are taken in the meantime on both sides of the equations.
The imaginary part in the complex potential Equation (18) is the helicity-dependent quadrupole interaction. In Einstein gravity, the quadrupole moment can be expressed explicitly as
which are two tensor types associated with the spin-2 excitations, i.e., gravitons. Physically, this quadrupole interaction could be understood as the coupling effect between the helicity of GWs and OAM of twisted lights, which will cause photons to undergo quadrupole transitions by decreasing and increasing the OAMs of two quantum units simultaneously. For the quadrupole coupling , the photon will lose two units of OAMs by emitting a graviton, and conversely, the coupling will cause the photon to gain two units of OAMs by absorbing a graviton. Due to the helicity dependency of the quadrupole interaction, the resulting extra helicity modes would have opposite signs for right and left circularly polarized lights, i.e., an overall phase difference of . Actually, this chirality is due to the ’time-reversal symmetry breaking’ [47]. Recall that, in classical electromagnetism, this breaking is always attributed to the axial property of the magnetic field vector, i.e., even in and odd in , and is manifested by a classical example of the Faraday rotation, in which the polarization plane of a light beam will acquire a rotation angle in a magnetic field aligned with the propagating direction of lights. As we will demonstrate later, this quadrupole coupling effect will also exhibit a new optical activity for polarized twisted lights.
In addition, it should be emphasized here that there exists additional rotation freedom from the GW polarization around , with respect to which the polarizations are defined. Performing a rotation in the transverse plane , (R is a rotation transformation with an angle ), we have .
4. Perturbation Analysis and Numerical Experiments
In the following, we will present two typical ideal experiments to demonstrate the optical features induced by the dipole and quadrupole interaction between structured lights and gravitational waves. We can apply the perturbation theory to solve Equation (17). Since the Laguerre–Gaussian modes form a complete and orthonormal set with respect to the mode indices n and l in the polar plane , we can make a decomposition such that
Substituting this expansion of Equation (26) into Equation (17), we have
where
in which only linear terms in are kept. can be obtained by directly integrating the summation in Equation (27) along the propagating distance z.
Dipole Interaction—Let us consider an incident beam of the Hermite–Gauss mode , which can be written by a superposition of two LG modes with the opposite OAMs, ,
The linear perturbation analysis yields the extra four modes due to the dipole interaction,
with
where L is the optical length of the detector. For each LG mode, it carries ℏ of OAM per photon and has a well-known donut-like intensity profile. Due to the dipole interaction, the induced mode involves one by lowering the OAM of one unit and, consequently, gives rise to the vortex-free Gaussian-like beams of and modes, producing a bright spot in the center. There are two other high-order modes with , each acquiring an extra phase factor but with opposite signs, and thus making a global rotation of the intensity pattern by angle in Equation (31). It is noted that the rotation angle made by the gravitational wave depends on the strain ratio of the cross and plus components—a macroscopic quantity that can be recognized easily if the corresponding signals resulting from GWs are detectable.
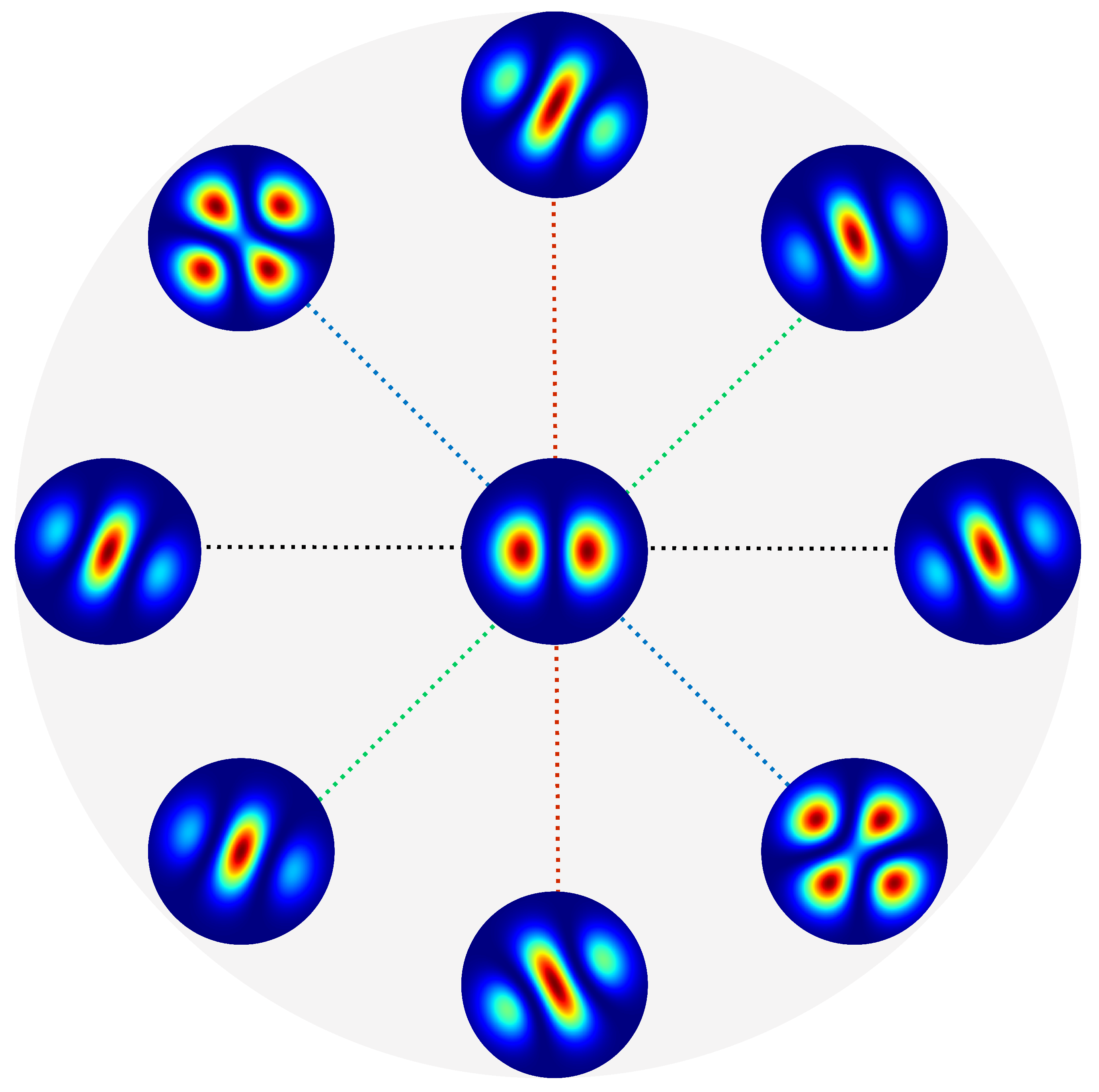
In Figure 1, we illustrate the central intensity brightening and pattern rotation resulting from the dipole effect with an ideal numerical experiment that displays various intensity patterns in different optical-arm orientations. Experimentally, combing the data obtained from the different photodetectors in this network with the theoretical predictions allows for a more accurate estimation of the GW’s physical properties and places more constraints on various gravitational theories.
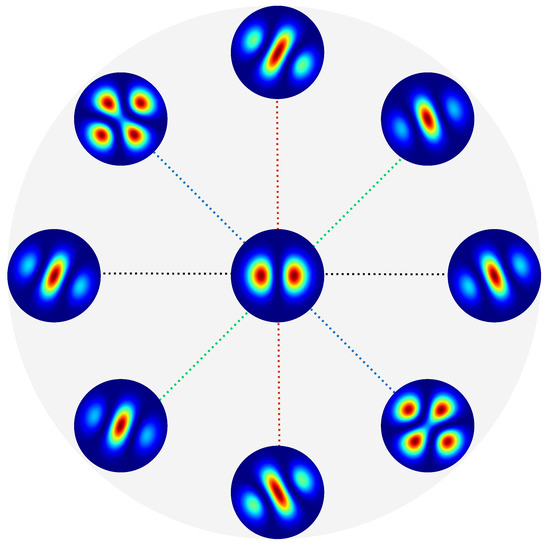
Figure 1.
Demonstration of the dipole signal in the GW polarization experiment. We first set up a laboratory coordinate system; the coordinate origin is located at the light source, a network of photodetectors is uniformly placed on the circle centered on the origin, the radius of the circle is L, the plane is the plane where the photodetectors are located, and its normal direction points to the zenith, set to the z-axis. In our ideal numerical experiment, we make use of eight detectors; the angle between any two adjacent arms is thus . The split light beams injected from the light source are sent to each photodetector along the arms. The incident GW is assumed in the direction of , , and the strains is set to fixed at in the TT gauge. Adopting the Hermite–Gauss mode , which is a superposition of two LG modes with the opposite OAMs, , , the additional dipole signal under the influence of GWs is composed of the vortex-free mode and the vortex modes where the complex dipole momentum has been written as . Given the GW’s strains and incident direction, and vary with the azimuthal angle of the optical arms. The diagram presents the false color intensity profile of the input (at the center) and output (the surrounding frames) light beams, indicating both the central brightening and global rotation of intensity patterns. The normalized transverse intensity pattern for an incident HG mode (upper left), and output excess mixed modes in different angles of , (upper right) (lower left) and (lower right).
Quadrupole Interaction—Since quadrupole interaction is a Hermitian conjugate for opposite spin orientations, we consider a superposition of two Laguerre–Gaussian modes with opposite OAMs of quantum number and with opposite circular polarizations,
where are two 2-vectors for the spin-up and -down states, respectively, and the notation for the LG modes have also been used. The input beam expressed by Equation (32) is an optical vortex with nonuniform polarization, which can be generated by using liquid–crystal converters [48] or spatially varying dielectric gratings [49]. Applying the linear perturbation analysis, we can find an extra vortex-free optical field produced by the GW’s tensor modes,
where
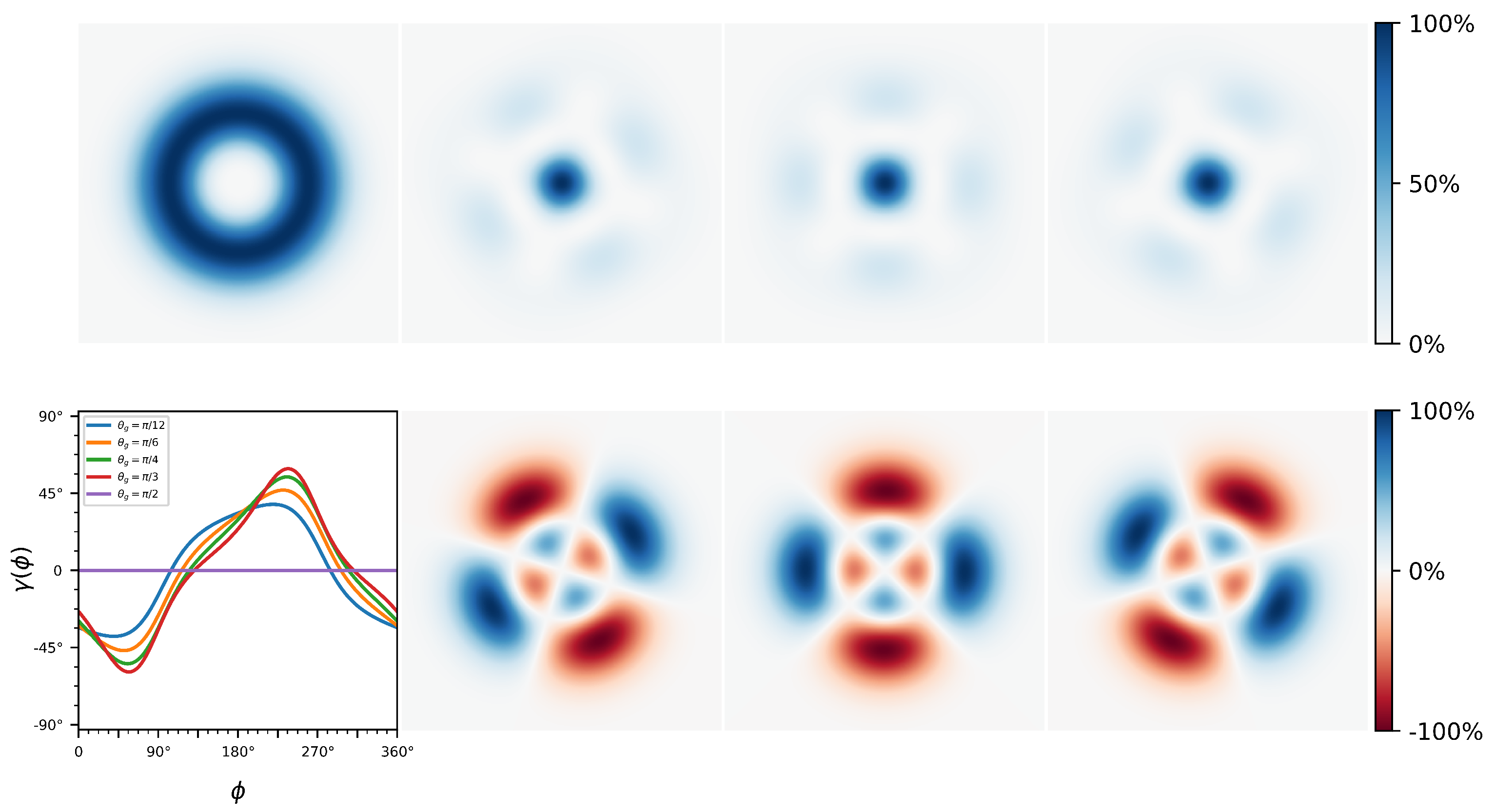
where is given by Equation (31). As indicated in Equation (33), the output beam includes an extra term due to the quadrupole interaction. As a result, the new mode becomes a linear polarization beam with a relative rotation angle and has a Gaussian-like transverse intensity profile, exhibiting both the central intensity brightening and changes in polarization states. Similar to the dipole effect, the output modes also include high-order modes with , and the corresponding intensity pattern will be rotated by an angle that depends on both the GW’s parameters and the direction angle of the lights. We demonstrate the quadrupole effect in Figure 2, where the input light field is assumed to be a single mode with right-circular polarization.
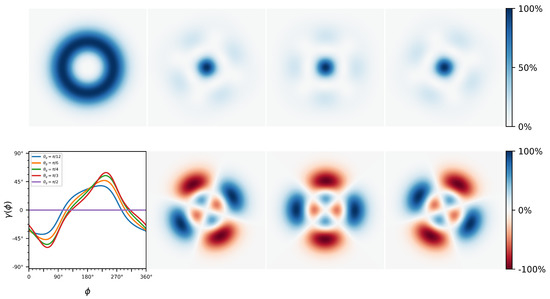
Figure 2.
The quadrupole signal in the GW polarization experiment. The laboratory coordinate system is the same as that described in Figure 1. The incident GW is assumed in the direction of , and the strains are set to . The input light beam adopts the LG mode , whose transverse intensity profile is plotted in the upper right panel. The quadrupole interaction leads to the extra OAM modes . Given the GW’s properties, and are functions of the direction angle of optical arms. In the lower-left panel, are plotted for different incident polar angles as indicated by the legends. Moreover, the right section (2 × 3 frames) illustrates the false color intensity profiles of the extra modes (upper) and the interference pattern between the input mode and the extra modes (lower), at different azimuthal angles of optical arms, from left to right corresponding to , , and respectively.
Since the SAM of photons stays unchanged during the quadrupole transition, the changes in OAMs can be attributed to the helicity-2 gravitons. Taking account of the breaking corresponding to the optical gain or loss, the net effect of the quadrupole process can be interpreted by either emitting or absorbing on-shell gravitons. Given the extreme weakness of the gravity, the momentum or energy transfer is hardly measured by the available technology, however, the precision quantum optical measurements make it possible to detect the AM transfer from gravitons to photons, and hopefully unveil the quantum nature of the gravitation.
5. Discussion
We summarize the paper and make some concluding remarks as follows. Based on the four-vector optical Dirac equation developed by Feng and Wu [34], we investigate a twisted light beam propagating in gravitational waves. We found that the spin–orbit coupling effect between GWs and structured lights will make photons undergo both dipole and quadrupole transitions between different orbital-angular-momentum (OAM) eigenstates, the former being spin-independent and the latter spin-dependent. These coupling effects will produce some measurable optical features in the 2-dimensional intensity distribution of twisted light, significantly the central intensity brightening and macroscopic rotation of the intensity pattern. Moreover, for the spin-dependent quadrupole interaction, it can make the twisted photons with the opposite OAMs and SAMs lose their OAMs and produce a linearly polarized Gaussian light beam, which can be regarded as an alternative spin–orbital Hall effect of light. It offers a possible new way to realize precision measurements of gravitational waves and enables us to explore the polarization modes in 2-dimensional intensity space and extract more information about the physical properties of gravitational waves than the current interferometry experiments.
This paper is focused on gravitational waves in Einstein’s gravity, which only has two polarization modes—cross and plus modes. Obviously, our method can be generalized directly to extended metric gravity theories (e.g., [50,51,52,53,54]), in which there are additional polarization modes, including breathing, longitudinal, vector-x, and vector-y. Depending on various incident-angle responses, these modes will exhibit different features in the 2-dimensional intensity distributions, which will allow us to test and discriminate between a variety of gravitational theories.
Finally, we note that the newly found dipole and quadrupole interactions only exist beyond the plane wave approximation and have been omitted in previous studies, e.g., [55,56]. Therefore, including these coupling effects must be important for precisely quantifying the wave behaviors of the higher-order LG modes in optical cavities for the next generation of GW detectors. As demonstrated in this paper, our approach based on the four-vector optical Dirac equation could provide a first-principle field theory method to study the vector-wave mechanics of structured lights in gravitational fields and can be extended to even more generic optical media.
Author Contributions
Conceptualization, L.F.; methodology, L.F. and Q.W.; software, Q.W. and W.Z.; validation, W.Z.; formal analysis, L.F. and Q.W.; investigation, L.F., Q.W. and W.Z.; writing—original draft preparation, L.F.; writing—review and editing, L.F. and W.Z.; visualization, Q.W.; supervision, L.F.; project administration, L.F.; funding acquisition, L.F. and W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key R&D Program of China through grant 2020YFC2201400 and the Key Program of NFSC through grants 11733010, 11333008 and 12173102.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Tests of General Relativity with GW150914. Phys. Rev. Lett. 2016, 116, 221101. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, S. Photons and Gravitons in Perturbation Theory: Derivation of Maxwell’s and Einstein’s Equations. Phys. Rev. 1965, 138, B988–B1002. [Google Scholar] [CrossRef]
- Parikh, M.; Wilczek, F.; Zahariade, G. Signatures of the quantization of gravity at gravitational wave detectors. Phys. Rev. D 2021, 104, 046021. [Google Scholar] [CrossRef]
- Boughn, S.; Rothman, T. Aspects of graviton detection: Graviton emission and absorption by atomic hydrogen. Class. Quantum Gravity 2006, 23, 5839. [Google Scholar] [CrossRef]
- Rothman, T.; Boughn, S. Can Gravitons be Detected? Found. Phys. 2006, 36, 1801–1825. [Google Scholar] [CrossRef]
- Pitelli, J.P.M.; Perche, T.R. Angular momentum based graviton detector. Phys. Rev. D 2021, 104, 065016. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Binary Black Hole Mergers in the First Advanced LIGO Observing Run. Phys. Rev. X 2016, 6, 041015. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar] [CrossRef]
- Chelkowski, S.; Hild, S.; Freise, A. Prospects of higher-order Laguerre-Gauss modes in future gravitational wave detectors. Phys. Rev. D 2009, 79, 122002. [Google Scholar] [CrossRef]
- Granata, M.; Buy, C.; Ward, R.; Barsuglia, M. Higher-Order Laguerre-Gauss Mode Generation and Interferometry for Gravitational Wave Detectors. Phys. Rev. Lett. 2010, 105, 231102. [Google Scholar] [CrossRef] [PubMed]
- Carbone, L.; Bogan, C.; Fulda, P.; Freise, A.; Willke, B. Generation of High-Purity Higher-Order Laguerre-Gauss Beams at High Laser Power. Phys. Rev. Lett. 2013, 110, 251101. [Google Scholar] [CrossRef] [PubMed]
- Bliokh, K.Y.; Rodríguez-Fortuño, F.J.; Nori, F.; Zayats, A.V. Spin–orbit interactions of light. Nat. Photonics 2015, 9, 796–808. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Nori, F. Transverse and longitudinal angular momenta of light. Phys. Rep. 2015, 592, 1–38. [Google Scholar] [CrossRef]
- Aiello, A.; Banzer, P.; Neugebauer, M.; Leuchs, G. From transverse angular momentum to photonic wheels. Nat. Photonics 2015, 9, 789–795. [Google Scholar] [CrossRef]
- Bliokh, K.Y. Spatiotemporal Vortex Pulses: Angular Momenta and Spin-Orbit Interaction. Phys. Rev. Lett. 2021, 126, 243601. [Google Scholar] [CrossRef]
- Onoda, M.; Murakami, S.; Nagaosa, N. Hall Effect of Light. Phys. Rev. Lett. 2004, 93, 083901. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Frolov, D.Y.; Kravtsov, Y.A. Non-Abelian evolution of electromagnetic waves in a weakly anisotropic inhomogeneous medium. Phys. Rev. A 2007, 75, 053821. [Google Scholar] [CrossRef]
- Liberman, V.S.; Zel’dovich, B.Y. Spin-orbit interaction of a photon in an inhomogeneous medium. Phys. Rev. A 1992, 46, 5199–5207. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Niv, A.; Kleiner, V.; Hasman, E. Geometrodynamics of spinning light. Nat. Photonics 2008, 2, 748–753. [Google Scholar] [CrossRef]
- Bliokh, K.Y. Geometrodynamics of polarized light: Berry phase and spin Hall effect in a gradient-index medium. J. Opt. A Pure Appl. Opt. 2009, 11, 094009. [Google Scholar] [CrossRef]
- Bliokh, K.; Bliokh, Y. Topological spin transport of photons: The optical Magnus effect and Berry phase. Phys. Lett. A 2004, 333, 181–186. [Google Scholar] [CrossRef]
- Duval, C.; Horváth, Z.; Horváthy, P.A. Fermat principle for spinning light. Phys. Rev. D 2006, 74, 021701. [Google Scholar] [CrossRef]
- Ruiz, D.E.; Dodin, I.Y. First-principles variational formulation of polarization effects in geometrical optics. Phys. Rev. A 2015, 92, 043805. [Google Scholar] [CrossRef]
- Carini, P.; Feng, L.L.; Li, M.; Ruffini, R. Phase evolution of the photon in Kerr spacetime. Phys. Rev. D 1990, 46, 5407–5413. [Google Scholar] [CrossRef]
- Feng, L.L.; Lee, W. Gravitomagnetism and the Berry Phase of Photon in a Rotating Gravitational Field. Int. J. Mod. Phys. D 2001, 10, 961–969. [Google Scholar] [CrossRef]
- Mashhoon, B. On the gravitational analogue of Larmor’s theorem. Phys. Lett. A 1993, 173, 347–354. [Google Scholar] [CrossRef]
- Hauck, J.; Mashhoon, B. Electromagnetic waves in a rotating frame of reference. Ann. Phys. 2003, 515, 275–288. [Google Scholar] [CrossRef]
- Oancea, M.A.; Joudioux, J.; Dodin, I.Y.; Ruiz, D.E.; Paganini, C.F.; Andersson, L. Gravitational spin Hall effect of light. Phys. Rev. D 2020, 102, 024075. [Google Scholar] [CrossRef]
- Tamburini, F.; Thidé, B.; Molina-Terriza, G.; Anzolin, G. Twisting of light around rotating black holes. Nat. Phys. 2011, 7, 195–197. [Google Scholar] [CrossRef]
- Shoom, A.A. Gravitational Faraday and spin-Hall effects of light. Phys. Rev. D 2021, 104, 084007. [Google Scholar] [CrossRef]
- Tamburini, F.; Feleppa, F.; Licata, I.; Thidé, B. Kerr-spacetime geometric optics for vortex beams. Phys. Rev. A 2021, 104, 013718. [Google Scholar] [CrossRef]
- Feng, L.; Wu, Q. Four-Vector Optical Dirac Equation and Spin-Orbit Interaction of Structured Light. arXiv 2022, arXiv:2203.14664. [Google Scholar]
- Hanni, R.S. Wave fronts near a black hole. Phys. Rev. D 1977, 16, 933–936. [Google Scholar] [CrossRef]
- Khanikaev, A.B.; Mousavi, S.H.; Tse, W.K.; Kargarian, M.; MacDonald, A.H.; Shvets, G. Photonic topological insulators. Nat. Mater. 2013, 12, 233–239. [Google Scholar] [CrossRef]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947. [Google Scholar] [CrossRef]
- Ashida, Y.; Gong, Z.; Ueda, M. Non-Hermitian physics. Adv. Phys. 2021, 69, 249–435. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Makris, K.G.; Khajavikhan, M.; Musslimani, Z.H.; Rotter, S.; Christodoulides, D.N. Non-Hermitian physics and PT symmetry. Nat. Phys. 2018, 14, 11–19. [Google Scholar] [CrossRef]
- Shen, S.Q. Topological Insulators, Dirac Equation in Condensed Matters; Springer Series in Solid-State Sciences; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Horsley, S.A.R. Indifferent electromagnetic modes: Bound states and topology. Phys. Rev. A 2019, 100, 053819. [Google Scholar] [CrossRef]
- Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Musslimani, Z.H. Beam Dynamics in PT Symmetric Optical Lattices. Phys. Rev. Lett. 2008, 100, 103904. [Google Scholar] [CrossRef] [PubMed]
- Longhi, S. Quantum-optical analogies using photonic structures. Laser Photonics Rev. 2009, 3, 243–261. [Google Scholar] [CrossRef]
- Eardley, D.M.; Lee, D.L.; Lightman, A.P.; Wagoner, R.V.; Will, C.M. Gravitational-Wave Observations as a Tool for Testing Relativistic Gravity. Phys. Rev. Lett. 1973, 30, 884–886. [Google Scholar] [CrossRef]
- Will, C. Theory and Experiment in Gravitational Physics; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Berry, M.V. Optical currents. J. Opt. A Pure Appl. Opt. 2009, 11, 094001. [Google Scholar] [CrossRef]
- Andrews, D.L. Quantum formulation for nanoscale optical and material chirality: Symmetry issues, space and time parity, and observables. J. Opt. 2018, 20, 033003. [Google Scholar] [CrossRef]
- Stalder, M.; Schadt, M. Linearly polarized light with axial symmetry generated by liquid-crystal polarization converters. Opt. Lett. 1996, 21, 1948–1950. [Google Scholar] [CrossRef]
- Bomzon, Z.; Biener, G.; Kleiner, V.; Hasman, E. Radially and azimuthally polarized beams generated by space-variant dielectric subwavelength gratings. Opt. Lett. 2002, 27, 285–287. [Google Scholar] [CrossRef] [PubMed]
- Brans, C.; Dicke, R.H. Mach’s Principle and a Relativistic Theory of Gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Capozziello, S.; Francaviglia, M. Extended theories of gravity and their cosmological and astrophysical applications. Gen. Relativ. Gravit. 2008, 40, 357–420. [Google Scholar] [CrossRef]
- Rosen, N. A theory of gravitation. Ann. Phys. 1974, 84, 455–473. [Google Scholar] [CrossRef]
- Lightman, A.P.; Lee, D.L. New Two-Metric Theory of Gravity with Prior Geometry. Phys. Rev. D 1973, 8, 3293–3302. [Google Scholar] [CrossRef]
- de Rham, C. Massive Gravity. Living Rev. Relativ. 2014, 17, 7. [Google Scholar] [CrossRef] [PubMed]
- Harte, A.I. Optics in a nonlinear gravitational plane wave. Class. Quantum Gravity 2015, 32, 175017. [Google Scholar] [CrossRef]
- Bond, C.; Brown, D.; Freise, A.; Strain, K.A. Interferometer techniques for gravitational-wave detection. Living Rev. Relativ. 2017, 19, 3. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).