A Comprehensive Study of Bright Fermi-GBM Short Gamma-Ray Bursts: II. Very Short Burst and Its Implications
Abstract
1. Introduction
2. Data Reduction
2.1. Sample Selection
2.2. Spectral Fitting
3. Results
3.1. General Results
3.1.1. Result for the CPL Model
3.1.2. Result for the BAND Model
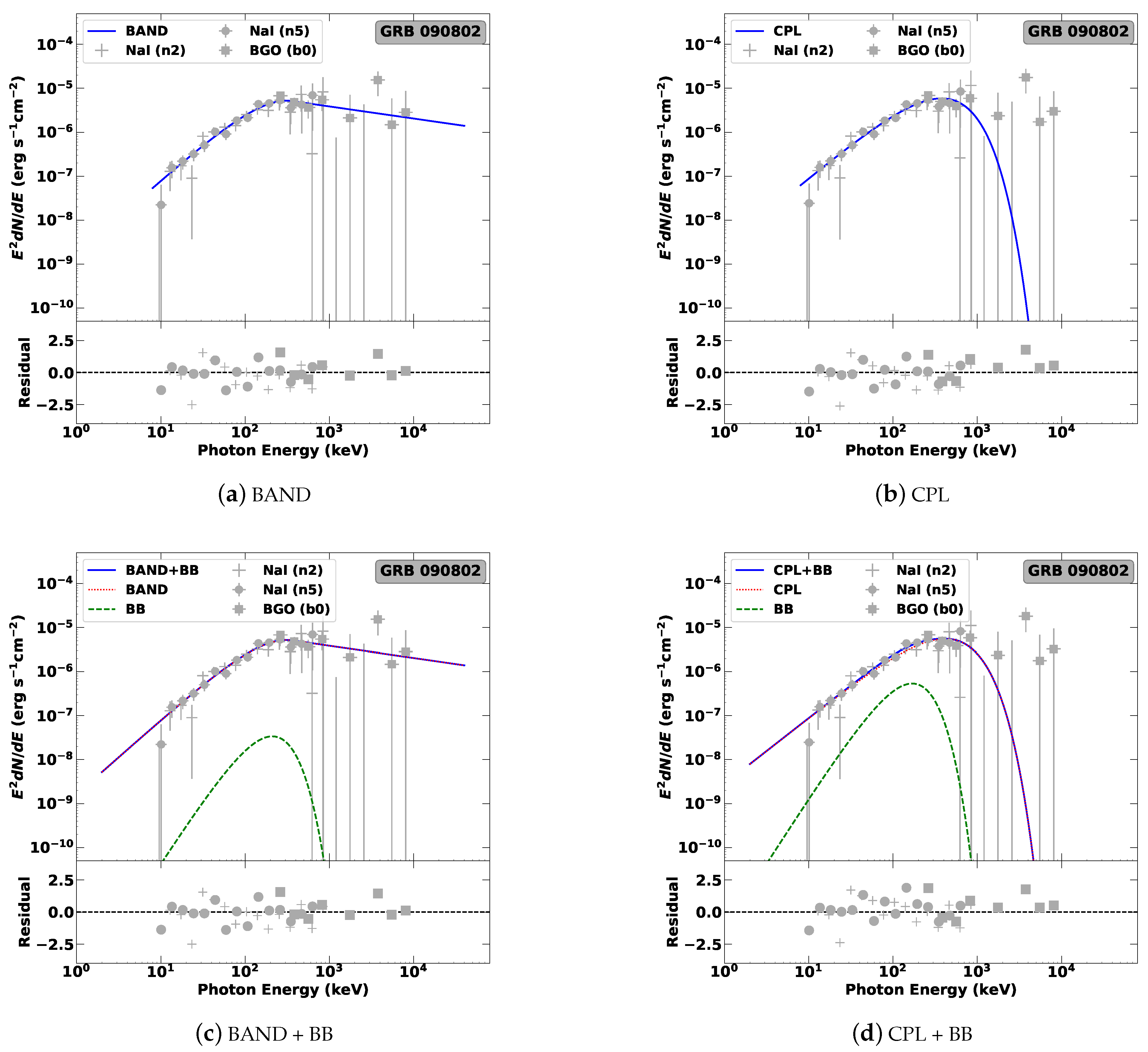
3.1.3. Results for the Models with BB Component
4. Discussion
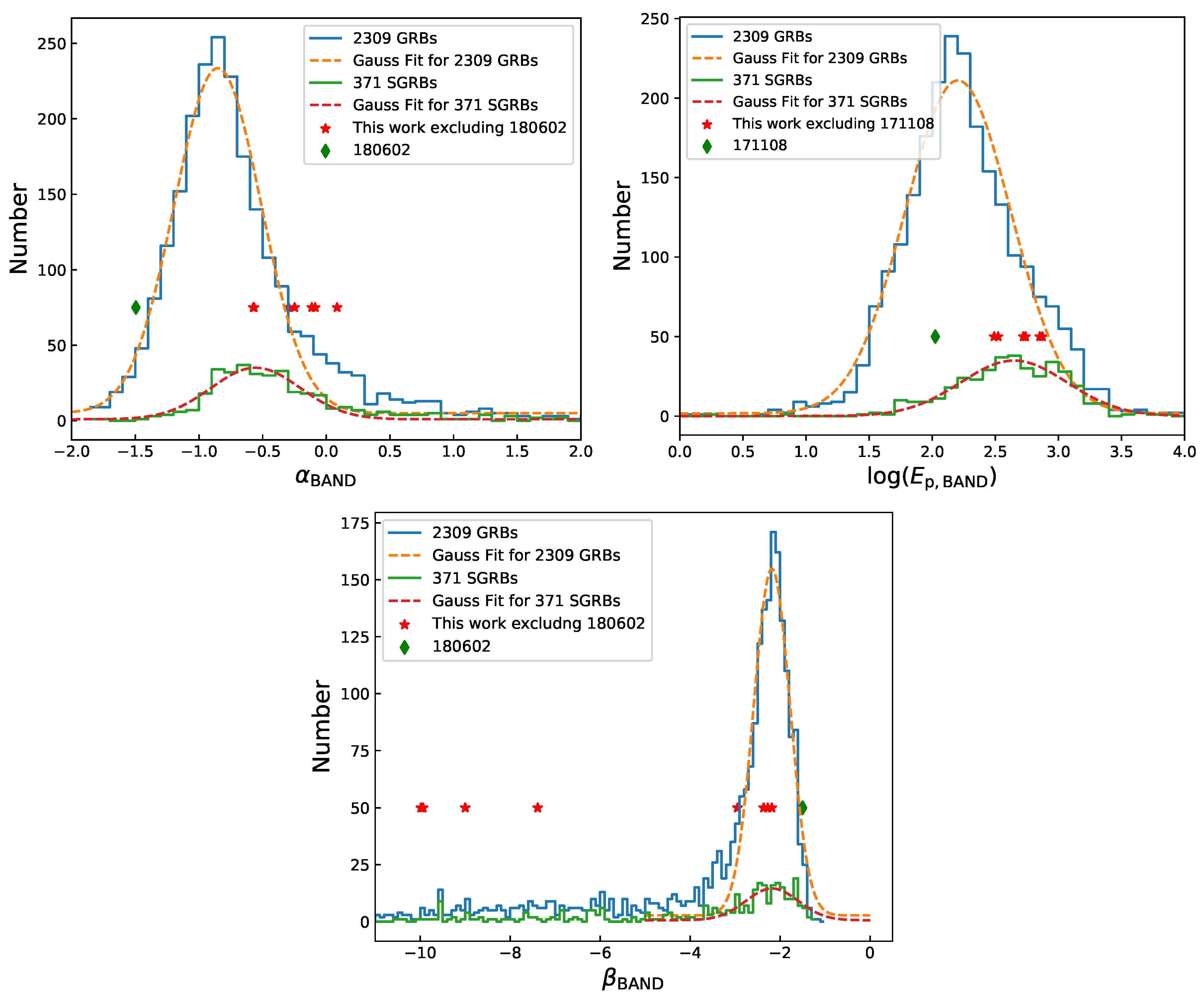
4.1. Does a Very Short GRB Have a Very Hard Spectrum?
4.2. Is There a Common Thermal Component in the Very Short Bursts?
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | https://fermi.gsfc.nasa.gov/ssc/data/access/, accessed on 7 August 2022. |
References
- Woosley, S.E. Gamma-Ray Bursts from Stellar Mass Accretion Disks around Black Holes. Astrophys. J. 1993, 405, 273. [Google Scholar] [CrossRef]
- Paczyński, B. Are Gamma-Ray Bursts in Star-Forming Regions? Astrophys. J. 1998, 494, L45–L48. [Google Scholar] [CrossRef]
- Galama, T.J.; Vreeswijk, P.M.; van Paradijs, J.; Kouveliotou, C.; Augusteijn, T.; Böhnhardt, H.; Brewer, J.P.; Doublier, V.; Gonzalez, J.F.; Leibundgut, B.; et al. An unusual supernova in the error box of the γ-ray burst of 25 April 1998. Nature 1998, 395, 670–672. [Google Scholar] [CrossRef]
- Stanek, K.Z.; Matheson, T.; Garnavich, P.M.; Martini, P.; Berlind, P.; Caldwell, N.; Challis, P.; Brown, W.R.; Schild, R.; Krisciunas, K.; et al. Spectroscopic Discovery of the Supernova 2003dh Associated with GRB 030329. Astrophys. J. 2003, 591, L17–L20. [Google Scholar] [CrossRef]
- Woosley, S.E.; Bloom, J.S. The Supernova Gamma-Ray Burst Connection. Annu. Rev. Astron. Astrophys. 2006, 44, 507–556. [Google Scholar] [CrossRef]
- Fruchter, A.S.; Levan, A.J.; Strolger, L.; Vreeswijk, P.M.; Thorsett, S.E.; Bersier, D.; Burud, I.; Castro Cerón, J.M.; Castro-Tirado, A.J.; Conselice, C.; et al. Long γ-ray bursts and core-collapse supernovae have different environments. Nature 2006, 441, 463–468. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, A.; Ajello, M.; Asano, K.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; et al. Fermi Observations of GRB 090902B: A Distinct Spectral Component in the Prompt and Delayed Emission. Astrophys. J. Lett. 2009, 706, L138–L144. [Google Scholar] [CrossRef]
- Guiriec, S.; Daigne, F.; Hascoët, R.; Vianello, G.; Ryde, F.; Mochkovitch, R.; Kouveliotou, C.; Xiong, S.; Bhat, P.N.; Foley, S.; et al. Evidence for a Photospheric Component in the Prompt Emission of the Short GRB 120323A and Its Effects on the GRB Hardness-Luminosity Relation. Astrophys. J. 2013, 770, 32. [Google Scholar] [CrossRef]
- Tang, Q.-W.; Wang, K.; Li, L.; Liu, R.-Y. Prevalence of Extra Power-Law Spectral Components in Short Gamma-Ray Bursts. Astrophys. J. 2021, 922, 255. [Google Scholar] [CrossRef]
- Zhao, P.-W.; Tang, Q.-W. A Comprehensive Study of Bright Fermi-GBM Short Gamma-ray Bursts: I. Multi-Pulse Lightcurves and Multi-Component Spectra. Universe 2022, 8, 159. [Google Scholar] [CrossRef]
- Zhao, P.-W.; Tang, Q.-W.; Zou, Y.-C.; Wang, K. Detection of a Prompt Fast-variable Thermal Component in the Multipulse Short Gamma-Ray Burst 170206A. Astrophys. J. 2022, 929, 179. [Google Scholar] [CrossRef]
- Arimoto, M.; Asano, K.; Ohno, M.; Veres, P.; Axelsson, M.; Bissaldi, E.; Tachibana, Y.; Kawai, N. High-energy Non-thermal and Thermal Emission from GRB141207A Detected by Fermi. Astrophys. J. 2016, 833, 139. [Google Scholar] [CrossRef]
- Lü, H.-J.; Lü, J.; Zhong, S.-Q.; Huang, X.-L.; Zhang, H.-M.; Lan, L.; Xie, W.; Lu, R.-J.; Liang, E.-W. Extremely Bright GRB 160625B with Multiple Emission Episodes: Evidence for Long-term Ejecta Evolution. Astrophys. J. 2017, 849, 71. [Google Scholar] [CrossRef]
- Hou, S.-J.; Zhang, B.-B.; Meng, Y.-Z.; Wu, X.-F.; Liang, E.-W.; Lü, H.-J.; Liu, T.; Liang, Y.-F.; Lin, L.; Lu, R.-J.; et al. Multicolor Blackbody Emission in GRB 081221. Astrophys. J. 2018, 866, 13. [Google Scholar] [CrossRef]
- Iyyani, S.; Sharma, V. Study of the Prompt Emission of Short Gamma-Ray Bursts Using a Multicolor Blackbody: A Clue to the Viewing Angle. Astrophys. J. Suppl. Ser. 2021, 255, 25. [Google Scholar] [CrossRef]
- Ahlgren, B.; Larsson, J.; Nymark, T.; Ryde, F.; Pe’er, A. Confronting GRB prompt emission with a model for subphotospheric dissipation. Mon. Not. R. Astron. Soc. Lett. 2015, 454, L31–L35. [Google Scholar] [CrossRef]
- Beloborodov, A.M. Sub-photospheric Shocks in Relativistic Explosions. Astrophys. J. 2017, 838, 125. [Google Scholar] [CrossRef]
- Ryde, F.; Yu, H.-F.; Dereli-Bégué, H.; Lundman, C.; Pe’er, A.; Li, L. On the α-intensity correlation in gamma-ray bursts: Subphotospheric heating with varying entropy. Mon. Not. R. Astron. Soc. Lett. 2019, 485, 474–497. [Google Scholar] [CrossRef]
- Lundman, C.; Pe’er, A.; Ryde, F. A theory of photospheric emission from relativistic, collimated outflows. Mon. Not. R. Astron. Soc. Lett. 2013, 428, 2430–2442. [Google Scholar] [CrossRef]
- Meng, Y.-Z.; Liu, L.-D.; Wei, J.-J.; Wu, X.-F.; Zhang, B.-B. The Time-resolved Spectra of Photospheric Emission from a Structured Jet for Gamma-Ray Bursts. Astrophys. J. 2019, 882, 29. [Google Scholar] [CrossRef]
- Meng, Y.-Z.; Geng, J.-J.; Wu, X.-F. The photosphere emission spectrum of hybrid relativistic outflow for gamma-ray bursts. Mon. Not. R. Astron. Soc. Lett. 2022, 509, 6047–6058. [Google Scholar] [CrossRef]
- Lazzati, D.; Begelman, M.C. Non-thermal Emission from the Photospheres of Gamma-ray Burst Outflows. I. High-Frequency Tails. Astrophys. J. 2010, 725, 1137–1145. [Google Scholar] [CrossRef]
- Giannios, G. The peak energy of dissipative gamma-ray burst photospheres. Mon. Not. R. Astron. Soc. Lett. 2012, 422, 3092–3098. [Google Scholar] [CrossRef]
- Vyas, M.; Pe’er, A.; Eichler, D. A Backscattering-dominated Prompt Emission Model for the Prompt Phase of Gamma-Ray Bursts. Astrophys. J. 2021, 908, 9. [Google Scholar] [CrossRef]
- Vyas, M.; Pe’er, A.; Eichler, D. Predicting Spectral Parameters in the Backscattering-dominated Model for the Prompt Phase of GRBs. Astrophys. J. Lett. 2021, 918, L12. [Google Scholar] [CrossRef]
- Guiriec, S.; Kouveliotou, C.; Daigne, F.; Zhang, B.; Hascoët, R.; Nemmen, R.-S.; Thompson, D.-J.; Bhat, P.-N.; Gehrels, N.; Gonzalez, M.-M.; et al. Toward a Better Understanding of the GRB Phenomenon: A New Model for GRB Prompt Emission and its Effects on the New LiNT- Epeak,irest,NT Relation. Astrophys. J. 2015, 807, 148. [Google Scholar] [CrossRef]
- Guiriec, S.; Briggs, M.S.; Connaugthon, V.; Kara, E.; Daigne, F.; Kouveliotou, C.; van der Horst, A.J.; Paciesas, W.; Charles, A.M.; Bhat, P.N.; et al. Time-resolved Spectroscopy of the Three Brightest and Hardest Short Gamma-ray Bursts Observed with the Fermi Gamma-ray Burst Monitor. Astrophys. J. 2010, 725, 225. [Google Scholar] [CrossRef]
- Axelsson, M.; Baldini, L.; Barbiellini, G.; Baring, M.G.; Bellazzini, R.; Bregeon, J.; Brigida, M.; Bruel, P.; Buehler, R.; Caliandro, G.A. GRB110721A: An Extreme Peak Energy and Signatures of the Photosphere. Astrophys. J. Lett. 2012, 757, 31. [Google Scholar] [CrossRef]
- Burgess, J.M.; Preece, R.D.; Ryde, F.; Veres, P.; Mészáros, P.; Connaughton, V.; Briggs, M.; Pe’er, A.; Iyyani, S.; Goldstein, A.; et al. An Observed Correlation between Thermal and Non-thermal Emission in Gamma-Ray Bursts. Astrophys. J. 2014, 784, 43. [Google Scholar] [CrossRef]
- Yu, H.-F.; Dereli-Bégué, H.; Ryde, F. Bayesian Time-resolved Spectroscopy of GRB Pulses. Astrophys. J. 2019, 886, 20. [Google Scholar] [CrossRef]
- Meegan, C.; Lichti, G.; Bhat, P.N.; Bissaldi, E.; Briggs, M.S.; Connaughton, V.; Diehl, R.; Fishman, G.; Greiner, J.; Hoover, A.S.; et al. The Fermi Gamma-ray Burst Monitor. Astrophys. J. 2009, 702, 791–804. [Google Scholar] [CrossRef]
- Ahlgren, B.; Larsson, J.; Ahlberg, E.; Lundman, C.; Ryde, F.; Pe’er, A. Testing a model for subphotospheric dissipation in GRBs: Fits to Fermi data constrain the dissipation scenario. Mon. Not. R. Astron. Soc. Lett. 2019, 485, 474–497. [Google Scholar] [CrossRef]
- Band, D.; Matteson, J.; Ford, L.; Schaefer, B.; Palmer, D.; Teegarden, B.; Cline, T.; Briggs, M.; Paciesas, W.; Pendleton, G.; et al. BATSE Observations of Gamma-Ray Burst Spectra. I. Spectral Diversity. Astrophys. J. 1993, 413, 281. [Google Scholar] [CrossRef]
- Norris, J.P.; Bonnell, J.T.; Kazanas, D.; Scargle, J.D.; Hakkila, J.; Giblin, T.W. Long-Lag, Wide-Pulse Gamma-Ray Bursts. Astrophys. J. 2005, 627, 324. [Google Scholar] [CrossRef]
- Vianello, G.; Lauer, R.J.; Younk, P.; Tibaldo, L.; Burgess, J.M.; Ayala, H.; Harding, P.; Hui, M.; Omodei, N.; Zhou, H. The Multi-Mission Maximum Likelihood framework (3ML). arXiv 2015, arXiv:1507.08343. [Google Scholar]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control. 1974, 19, 716. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461. [Google Scholar] [CrossRef]
- von Kienlin, A.; Meegan, C.A.; Paciesas, W.S.; Bhat, P.N.; Bissaldi, E.; Briggs, M.S.; Burns, E.; Cleveland, W.H.; Gibby, M.H.; Giles, M.M.; et al. The Fourth Fermi-GBM Gamma-Ray Burst Catalog: A Decade of Data. Astrophys. J. 2020, 893, 46. [Google Scholar] [CrossRef]
- Kouveliotou, C.; Meegan, C.A.; Fishman, G.J.; Bhat, N.P.; Briggs, M.S.; Koshut, T.M.; Paciesas, W.S.; Pendleton, G.N. Identification of Two Classes of Gamma-Ray Bursts. Astrophys. J. Lett. 1993, 413, L101. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, B.B.; Virgili, F.J.; Liang, E.W.; Kann, D.A.; Wu, X.F.; Proga, D.; Lv, H.J.; Toma, K.; Mészáros, P.; et al. Discerning the Physical Origins of Cosmological Gamma-ray Bursts Based on Multiple Observational Criteria: The Cases of z = 6.7 GRB 080913, z = 8.2 GRB 090423, and Some Short/Hard GRBs. Astrophys. J. 2009, 703, 1696–1724. [Google Scholar] [CrossRef]
- Burns, E.; Veres, P.; Connaughton, V.; Racusin, J.; Briggs, M.S.; Christensen, N.; Goldstein, A.; Hamburg, R.; Kocevski, D.; McEnery, J.; et al. Fermi GBM Observations of GRB 150101B: A Second Nearby Event with a Short Hard Spike and a Soft Tail. Astrophys. J. 2018, 863, 34. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T.; Narayan, R. Spectra and Light Curves of Gamma-Ray Burst Afterglows. Astrophys. J. 1998, 497, L17–L20. [Google Scholar] [CrossRef]
- Uhm, Z.L.; Zhang, B. Fast-cooling synchrotron radiation in a decaying magnetic field and γ-ray burst emission mechanism. Nat. Phys. 2014, 10, 351. [Google Scholar] [CrossRef]
- Burgess, J.M.; Bégué, D.; Greiner, J.; Giannios, D.; Bacelj, A.; Berlato, F. Gamma-ray bursts as cool synchrotron sources. Nat. Astron. 2020, 4, 174. [Google Scholar]
- Ryde, F. Is Thermal Emission in Gamma-Ray Bursts Ubiquitous? Astrophys. J. 2005, 625, L95–L98. [Google Scholar] [CrossRef]
- Pe’er, A.; Ryde, F.; Wijers, R.A.M.J.; Mészáros, P.; Rees, M.J. A New Method of Determining the Initial Size and Lorentz Factor of Gamma-Ray Burst Fireballs Using a Thermal Emission Component. Astrophys. J. 2007, 664, L1–L4. [Google Scholar] [CrossRef]
- Pe’er, A. Temporal Evolution of Thermal Emission from Relativistically Expanding Plasma. Astrophys. J. 2008, 682, 463–473. [Google Scholar] [CrossRef]
- Bromberg, O.; Mikolitzky, Z.; Levinson, A. Sub-photospheric Emission from Relativistic Radiation Mediated Shocks in GRBs. Astrophys. J. 2011, 733, 85. [Google Scholar] [CrossRef]
- Levinson, A. Observational Signatures of Sub-photospheric Radiation-mediated Shocks in the Prompt Phase of Gamma-Ray Bursts. Astrophys. J. 2012, 756, 174. [Google Scholar] [CrossRef]




| GRB Name | GBM Trigger | (s) | (s) | (s) | Detetor | bkg. Selection (s) |
|---|---|---|---|---|---|---|
| 081229 | bn081229675 | 0.032 | −0.016 | 0.016 | ‘n2’,‘n5’,‘b0’ | [−25, −10], [15, 30] |
| 090802 | bn090802235 | 0.048 | −0.016 | 0.032 | ‘n2’,‘n5’,‘b0’ | [−25, −10], [15, 30] |
| 091126 | bn091126389 | 0.024 | −0.008 | 0.016 | ‘n6’,‘n7’,‘nb’,‘b1’ | [−25, −10], [15, 30] |
| 120616 | bn120616630 | 0.048 | −0.048 | 0 | ‘n3’,‘n7’,‘b0’ | [−25, −10], [15, 30] |
| 160822 | bn160822672 | 0.040 | −0.016 | 0.024 | ‘n9’,‘na’,‘b1’ | [−25, −10], [15, 30] |
| 171108 | bn171108656 | 0.032 | −0.016 | 0.016 | ‘n9’,‘nb’,‘b1’ | [−25, −10], [15, 30] |
| 180103 | bn180103090 | 0.016 | −0.016 | 0 | ‘n4’,‘b0’,‘b1’ | [−25, −10], [15, 30] |
| 180602 | bn180602938 | 0.008 | −0.016 | −0.008 | ‘n0’,‘n1’,‘n3’,‘b0’ | [−25, −10], [15, 30] |
| 190505 | bn190505051 | 0.032 | −0.016 | 0.016 | ‘n0’,‘n1’,‘n3’,‘n5’,‘b0’ | [−25, −10], [15, 30] |
| 201221 | bn201221591 | 0.032 | −0.016 | 0.016 | ‘n6’,‘n7’,‘n9’,‘b1’ | [−25, −10], [15, 30] |
| 1 | AIC/BIC/−ln(L) | 2 | (keV) | (keV) | 3 | |||
|---|---|---|---|---|---|---|---|---|
| 081229 | C | −1741.1/−1729.4/−873.5 | 356 | −0.04 ± 0.43 | 358 ± 184 | - | - | - |
| … | B | −1739.3/−1723.8/−873.7 | 355 | 0.21 ± 0.52 | 290 ± 82 | −2.64 ± 0.80 | - | - |
| … | C2 | −1738.4/−1719.0/−874.2 | 354 | 0.50 ± 1.46 | 443 ± 312 | - | 26 ± 10 | 0.10 |
| … | B2 | −1736.4/−1713.1/−874.2 | 353 | 0.51 ± 1.12 | 443 ± 163 | −8.49 ± 2.87 | 26 ± 10 | 0.11 |
| 090802 | C | −1151.8/−1140.1/−578.9 | 356 | −0.42 ± 0.14 | 376 ± 82 | - | - | - |
| … | B | −1152.3/−1136.7/−580.1 | 355 | −0.30 ± 0.18 | 310 ± 55 | −2.28 ± 0.29 | - | - |
| … | C2 | −1148.0/−1128.5/−579.0 | 354 | −0.49 ± 0.20 | 418 ± 156 | - | 43 ± 27 | 0.04 |
| … | B2 | −1148.3/−1125.0/−580.1 | 353 | −0.30 ± 0.11 | 310 ± 1 | −2.28 ± 0.27 | 54 ± 1 | <0.01 |
| 091126 | C | −2907.7/−2895.2/−1456.8 | 476 | −0.09 ± 0.45 | 711 ± 385 | - | - | - |
| … | C2 | −2910.6/−2889.7/−1460.3 | 474 | 0.95 ± 0.92 | 536 ± 383 | - | 7 ± 1 | 0.02 |
| … | B | −2905.7/−2889.0/−1456.8 | 475 | −0.09 ± 0.41 | 711 ± 192 | −9.98 ± 4.07 | - | - |
| … | B2 | −2908.6/−2883.6/−1460.3 | 473 | 0.95 ± 0.89 | 536 ± 133 | −10.00 ± 2.12 | 7 ± 2 | 0.02 |
| 120616 | C | −895.7/−884.0/−450.8 | 358 | −0.11 ± 0.50 | 744 ± 549 | - | - | - |
| … | B | −893.7/−878.1/−450.8 | 357 | −0.11 ± 0.44 | 746 ± 290 | −9.94 ± 4.20 | - | - |
| … | C2 | −891.9/−872.5/−451.0 | 356 | 3.33 ± 1.51 | 608 ± 221 | - | 40 ± 12 | 0.14 |
| … | B2 | −889.7/−866.4/−450.9 | 355 | −0.04 ± 0.48 | 721 ± 237 | −10.00 ± 0.05 | 4 ± 3 | <0.01 |
| 160822 | C | −1185.8/−1174.2/−595.9 | 355 | −0.59 ± 0.11 | 590 ± 139 | - | - | - |
| … | B | −1187.3/−1171.8/−597.6 | 354 | −0.57 ± 0.11 | 549 ± 98 | −2.36 ± 0.33 | - | - |
| … | C2 | −1187.9/−1168.5/−598.9 | 353 | 0.02 ± 1.25 | 587 ± 426 | - | 19 ± 3 | 0.12 |
| … | B2 | −1189.3/−1166.0/−600.6 | 352 | 0.02 ± 0.73 | 559 ± 124 | −2.44 ± 0.36 | 19 ± 3 | 0.05 |
| 171108 | C | −1724.0/−1712.4/−865.0 | 356 | −0.25 ± 0.22 | 106 ± 20 | - | - | - |
| … | B | −1722.0/−1706.5/−865.0 | 355 | −0.25 ± 0.17 | 106 ± 1 | −9.00 ± 2.28 | - | - |
| … | C2 | −1722.6/−1703.2/−866.3 | 354 | 1.18 ± 1.17 | 126 ± 41 | - | 10 ± 2 | 0.24 |
| … | B2 | −1722.8/−1699.5/−867.4 | 353 | 5.00 ± 0.01 | 122 ± 16 | −3.78 ± 0.76 | 11 ± 1 | 0.62 |
| 180103 | C | −2498.2/−2486.6/−1252.1 | 359 | −0.33 ± 0.43 | 819 ± 519 | - | - | - |
| … | B | −2498.2/−2482.7/−1253.1 | 358 | 0.09 ± 0.63 | 527 ± 188 | −2.18 ± 0.30 | - | - |
| … | C2 | −2495.5/−2476.0/−1252.8 | 357 | −0.67 ± 0.56 | 1847 ± 1861 | - | 90 ± 34 | 0.16 |
| … | B2 | −2495.0/−2471.7/−1253.5 | 356 | 0.24 ± 0.58 | 504 ± 138 | −2.18 ± 0.30 | 2 ± 1 | <0.01 |
| 180602 | C | −3928.5/−3916.0/−1967.3 | 474 | 0.16 ± 0.27 | 420 ± 104 | - | - | - |
| … | C2 | −3924.5/−3903.7/−1967.3 | 472 | 0.16 ± 0.27 | 419 ± 101 | - | 47 ± 1 | <0.01 |
| … | B2 | −3924.5/−3899.5/−1968.2 | 471 | −0.51 ± 0.57 | 315 ± 267 | −1.94 ± 0.45 | 98 ± 14 | 0.85 |
| … | B | −3806.5/−3789.8/−1907.2 | 473 | −1.50 ± 0.27 | 528 ± 82433 | −1.50 ± 0.00 | - | - |
| 190505 | C | −2856.8/−2843.6/−1431.4 | 592 | −0.30 ± 0.20 | 309 ± 80 | - | - | - |
| … | B | −2854.8/−2837.2/−1431.4 | 591 | −0.30 ± 0.19 | 309 ± 44 | −7.39 ± 2.83 | - | - |
| … | C2 | −2852.8/−2830.9/−1431.4 | 590 | −0.38 ± 0.19 | 327 ± 84 | - | 50 ± 30 | 0.04 |
| … | B2 | −2850.8/−2824.4/−1431.4 | 589 | −0.35 ± 0.14 | 322 ± 1 | −9.99 ± 0.39 | 43 ± 1 | 0.12 |
| 201221 | C | −2133.1/−2120.6/−1069.5 | 476 | −0.63 ± 0.14 | 371 ± 105 | - | - | - |
| … | B | −2131.2/−2114.5/−1069.6 | 475 | −0.57 ± 0.17 | 333 ± 72 | −2.95 ± 0.94 | - | - |
| … | C2 | −2132.9/−2112.1/−1071.5 | 474 | −0.83 ± 0.19 | 621 ± 352 | - | 33 ± 7 | 0.10 |
| … | B2 | −2130.9/−2105.9/−1071.5 | 473 | −0.83 ± 0.17 | 622 ± 227 | −9.53 ± 3.83 | 33 ± 7 | 0.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.-Y.; Huang, Y.-L.; Huang, J.-W.; Zhu, Z.; Tang, Q.-W. A Comprehensive Study of Bright Fermi-GBM Short Gamma-Ray Bursts: II. Very Short Burst and Its Implications. Universe 2022, 8, 512. https://doi.org/10.3390/universe8100512
Hu Y-Y, Huang Y-L, Huang J-W, Zhu Z, Tang Q-W. A Comprehensive Study of Bright Fermi-GBM Short Gamma-Ray Bursts: II. Very Short Burst and Its Implications. Universe. 2022; 8(10):512. https://doi.org/10.3390/universe8100512
Chicago/Turabian StyleHu, Ying-Yong, Yao-Lin Huang, Jia-Wei Huang, Zan Zhu, and Qing-Wen Tang. 2022. "A Comprehensive Study of Bright Fermi-GBM Short Gamma-Ray Bursts: II. Very Short Burst and Its Implications" Universe 8, no. 10: 512. https://doi.org/10.3390/universe8100512
APA StyleHu, Y.-Y., Huang, Y.-L., Huang, J.-W., Zhu, Z., & Tang, Q.-W. (2022). A Comprehensive Study of Bright Fermi-GBM Short Gamma-Ray Bursts: II. Very Short Burst and Its Implications. Universe, 8(10), 512. https://doi.org/10.3390/universe8100512








