Nonlinear Charged Black Hole Solution in Rastall Gravity
Abstract
1. Introduction
2. Spherically Symmetric BH Solution
2.1. Nonlinear Charged Spherically Symmetric BH Solution in Rastall’s Theory
2.2. The Physical Properties of the BH Solutions (18)
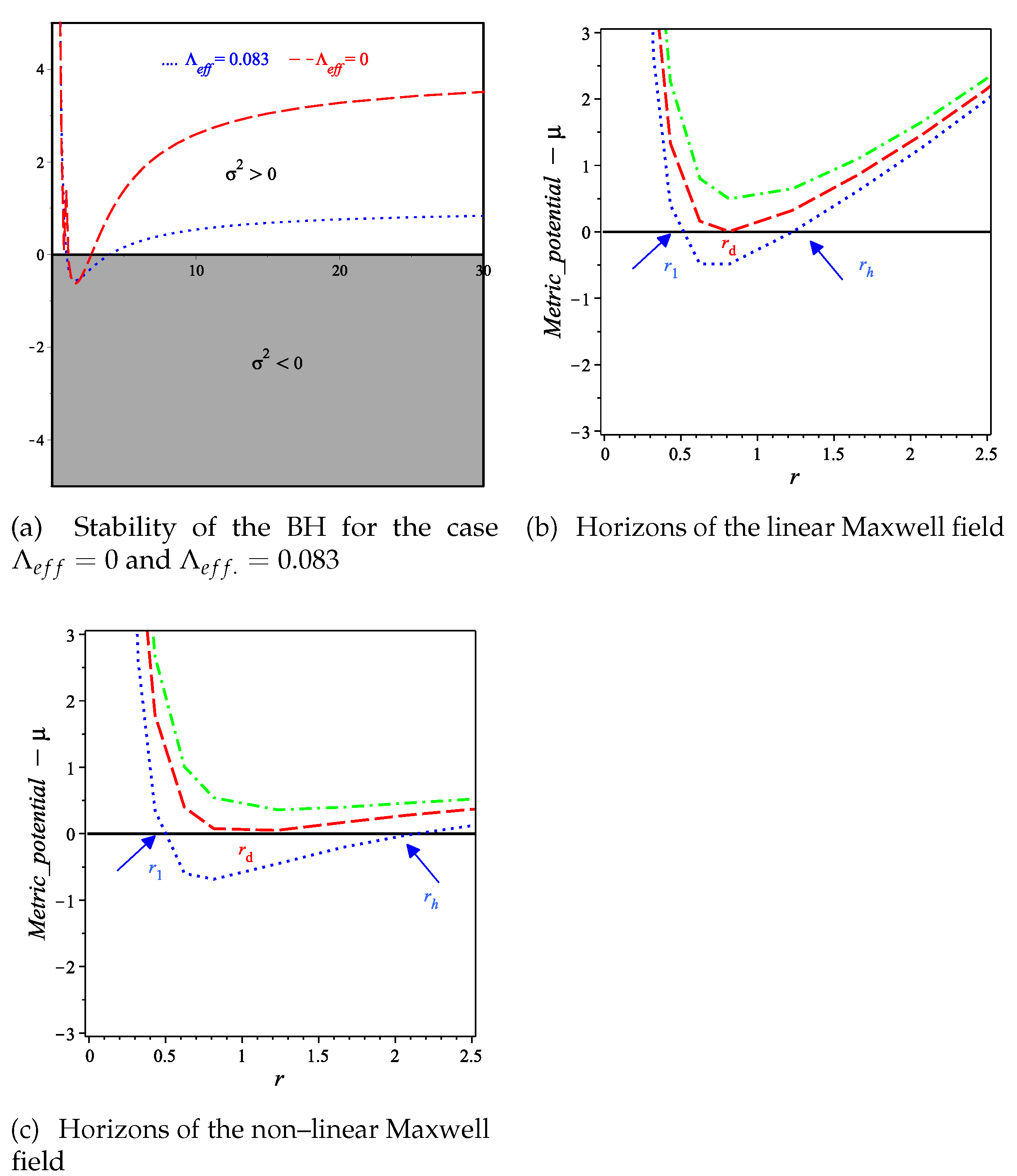
2.3. Stability of Geodesic Motion of BH Given by Equation (19)
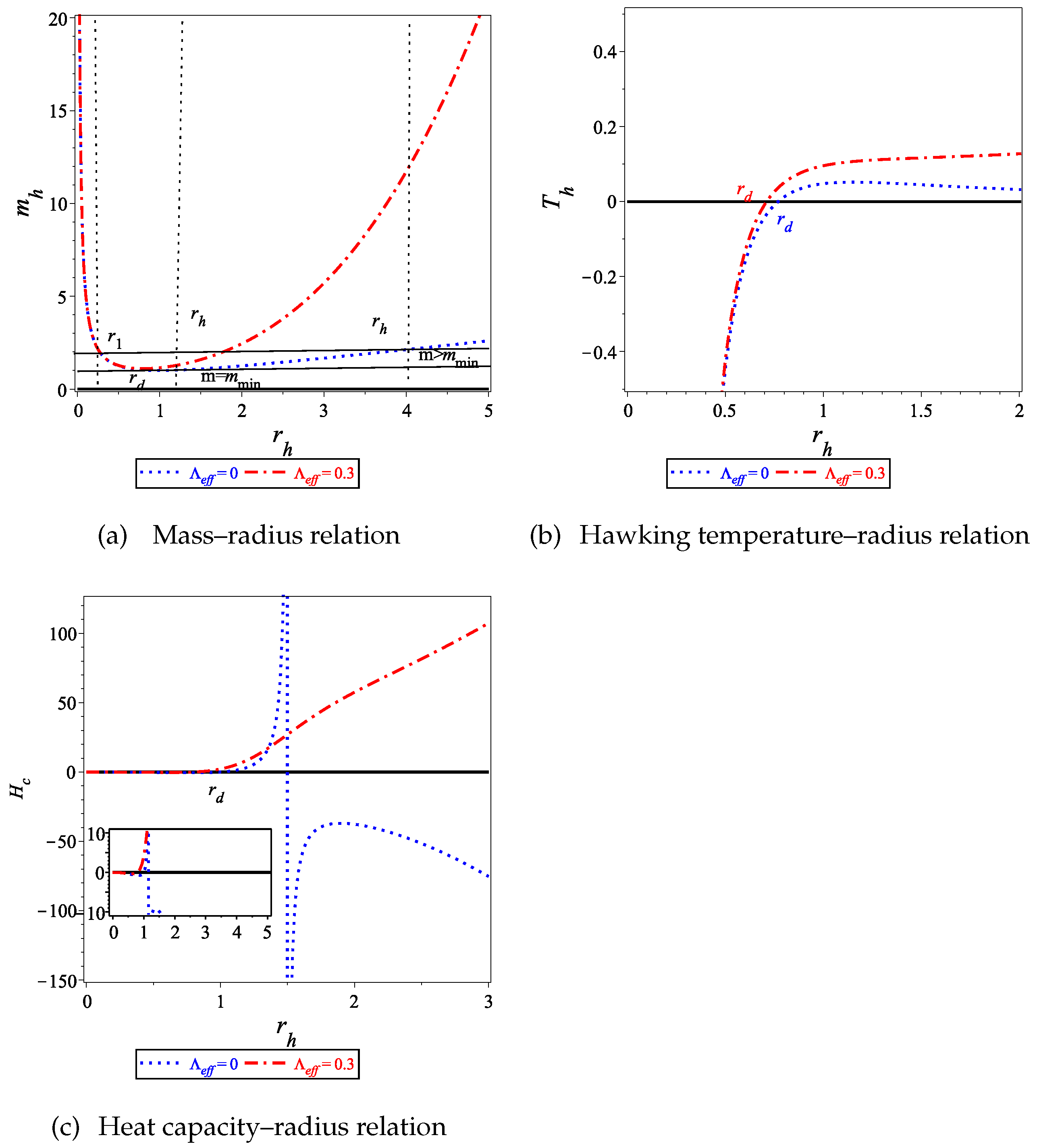
3. The Thermodynamical Properties of the of BH Given by Equation (19)
3.1. First Law of Thermodynamics of the BH Solution (18)
4. Discussion and Conclusions
Funding
Conflicts of Interest
Sample Availability
| 1 | In this study we assume the relativistic units, i.e., . |
| 2 | In the frame of Rastall theory, Reissner−Nordström is a solution since its Ricci scalar has a vanishing value. |
| 3 | The non-vanishing of the trace is an important property in the frame of Rastall’s theory so that the effect of the Rastall parameter may appear unlike Maxwell field theory. |
| 4 | Solution (18) has been checked using Maple software 19. |
| 5 | This result is consistent with what we have done in [57] where the author has shown that the Rastall theory is equivalent to Einstein’s general relativity or equivalent to Einstein’s field equation plus an arbitrary cosmological constant |
References
- Nordström, G. Relativitätsprinzip und gravitation. Phys. Z. 1912, 13, 1126. [Google Scholar]
- Schucking, E.L. On Einstein’s Path; Springer: Berlin/Heidelberg, Germany, 1999; pp. 1–14. [Google Scholar]
- Brans, C.; Dicke, R.H. Mach’s Principle and a Relativistic Theory of Gravitation. Phys. Rev. 1961, 124, 925. [Google Scholar] [CrossRef]
- Dirac, P.A. The Cosmological Constants. Nature 1937, 139, 323. [Google Scholar] [CrossRef]
- Deffayet, C.; Steer, D.A. A formal introduction to Horndeski and Galileon theories and their generalizations. Class. Quant. Grav. 2013, 30, 214006. [Google Scholar] [CrossRef]
- Felice, A.D.; Tsujikawa, S. f(R) Theories. Living Rev. Rel. 2010, 13, 3. [Google Scholar] [CrossRef]
- Elizalde, E.; Nashed, G.G.L.; Nojiri, S.; Odintsov, S.D. Spherically symmetric black holes with electric and magnetic charge in extended gravity: Physical properties, causal structure, and stability analysis in Einstein’s and Jordan’s frames. Eur. Phys. J. 2020, C80, 109. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Hanafy, W.E.; Odintsov, S.D.; Oikonomou, V.K. Thermodynamical correspondence of f(R) gravity in Jordan and Einstein frames. arXiv 2019, arXiv:1912.03897v1. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.F.; Steinhardt, P.J. Essentials of k-essence. Phys. Rev. D 2001, 63, 103510. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Rotating charged black hole spacetimes in quadratic f(R) gravitational theories. Int. J. Mod. Phys. D 2018, 27, 1850074. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Saridakis, E.N. Rotating AdS black holes in Maxwell-f(T) gravity. Class. Quant. Grav. 2019, 36, 135005. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Capozziello, S. Stable and self-consistent compact star models in teleparallel gravity. Eur. Phys. J. C 2020, 80, 969. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Damour, T.; Mukhanov, V.F. k-Inflation. Phys. Lett. B 1999, 458, 209. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.F.; Steinhardt, P.J. Dynamical Solution to the Problem of a Small Cosmological Constant and Late-Time Cosmic Acceleration. Phys. Rev. Lett. 2000, 85, 4438. [Google Scholar] [CrossRef] [PubMed]
- Bronnikov, K.; Clement, G.; Constantinidis, C.; Fabris, J. Structure and stability of cold scalar-tensor black holes. Phys. Lett. A 1998, 243, 121. [Google Scholar] [CrossRef]
- Bronnikov, K.; Clement, G.; Constantinidis, C.; Fabris, J. Cold Scalar-Tensor Black Holes: Causal Structure, Geodesics, Stability. Grav. Cosmol. 1998, 4, 128. [Google Scholar]
- Rastall, P. Generalization of the Einstein Theory. Phys. Rev. D 1972, 6, 3357. [Google Scholar] [CrossRef]
- Fabris, J.C.; Piattella, O.F.; Rodrigues, D.C.; Daouda, M.H. Rastall’s cosmology and its observational constraints. AIP Conf. Proc. 2015, 1647, 50. [Google Scholar] [CrossRef]
- Calogero, S. A kinetic theory of diffusion in general relativity with cosmological scalar field. JCAP 2011, 11, 016. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Energy and momentum of a spherically symmetric dilaton frame as regularized by teleparallel gravity. Annalen Phys. 2011, 523, 450. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Hanafy, W.E. Analytic rotating black-hole solutions in N-dimensional f(T) gravity. Eur. Phys. J. 2017, 77, 90. [Google Scholar] [CrossRef]
- Calogero, S.; Velten, H. Cosmology with matter diffusion. JCAP 2013, 11, 025. [Google Scholar] [CrossRef]
- Velten, H.; Calogero, S. In Proceedings of the 2nd Argentinian-Brazilian Meeting on Gravitation, Relativistic Astrophysics and Cosmology (GRACo II), Buenos Aires, Argentina, 22–25 April 2014; pp. 171–176.
- Koivisto, T. A note on covariant conservation of energy–momentum in modified gravities. Class. Quant. Grav. 2006, 23, 4289. [Google Scholar] [CrossRef]
- Minazzoli, O. Conservation laws in theories with universal gravity/matter coupling. Phys. Rev. D 2013, 88, 027506. [Google Scholar] [CrossRef]
- Almeida, T.S.; Pucheu, M.L.; Romero, C.; Formiga, J.B. From Brans-Dicke gravity to a geometrical scalar-tensor theory. Phys. Rev. D 2014, 89, 064047. [Google Scholar] [CrossRef]
- Chauvineau, B.; Rodrigues, D.C.; Fabris, J.C. Scalar–tensor theories with an external scalar. Gen. Rel. Grav. 2016, 48, 80. [Google Scholar] [CrossRef][Green Version]
- Nashed, G.G.L.; Hanafy, W.E. Non-trivial class of anisotropic compact stellar model in Rastall gravity. Eur. Phys. J. C 2022, 82, 679. [Google Scholar] [CrossRef]
- Övgün, A.; Sakallı, I.; Saavedra, J.; Leiva, C. Shadow cast of noncommutative black holes in Rastall gravity. Mod. Phys. Lett. A 2020, 35, 2050163. [Google Scholar] [CrossRef]
- Gogoi, D.J.; Goswami, U.D. Quasinormal modes of black holes with non-linear-electrodynamic sources in Rastall gravity. Phys. Dark Univ. 2021, 33, 100860. [Google Scholar] [CrossRef]
- Shao, C.-Y.; Hu, Y.; Tan, Y.-J.; Shao, C.-G.; Lin, K.; Qian, W.-L. Dirac quasinormal modes of power-Maxwell charged black holes in Rastall gravity. Mod. Phys. Lett. A 2020, 35, 2050193. [Google Scholar] [CrossRef]
- Gogoi, D.J.; Karmakar, R.; Goswami, U.D. Quasinormal Modes of Non-Linearly Charged Black Holes surrounded by a Cloud of Strings in Rastall Gravity. arXiv 2021, arXiv:2111.00854v1. [Google Scholar] [CrossRef]
- Cai, X.-C.; Miao, Y.-G. Quasinormal modes and spectroscopy of a Schwarzschild black hole surrounded by a cloud of strings in Rastall gravity. Phys. Rev. D 2020, 101, 104023. [Google Scholar] [CrossRef]
- Moradpour, H.; Heydarzade, Y.; Ziaie, C.A.H.; Ghaffari, S. Black hole solutions and Euler equation in Rastall and generalized Rastall theories of gravity. Mod. Phys. Lett. A 2019, 34, 1950304. [Google Scholar] [CrossRef]
- Ziaie, A.H.; Moradpour, H.; Ghaffari, S. Gravitational collapse in Rastall gravity. Phys. Lett. B 2019, 793, 276. [Google Scholar] [CrossRef]
- Oliveira, A.M.; Velten, H.E.S.; Fabris, J.C.; Casarini, L. Neutron stars in Rastall gravity. Phys. Rev. D 2015, 92, 044020. [Google Scholar] [CrossRef]
- Batista, C.E.; Daouda, M.H.; Fabris, J.C.; Piattella, O.F.; Rodrigues, D.C. Rastall cosmology and the ΛCDM model. Phys. Rev. D 2012, 85, 084008. [Google Scholar] [CrossRef]
- Fabris, J.C.; Piattella, O.F.; Rodrigues, D.C.; Batista, C.E.M.; Daouda, M.H. Rastall cosmology. Int. J. Mod. Phys. Conf. Ser. 2012, 18, 67. [Google Scholar] [CrossRef]
- Kanzi, S.; Sakallı, I. GUP modified Hawking radiation in bumblebee gravity. Nucl. Phys. B 2019, 946, 114703. [Google Scholar] [CrossRef]
- Bronnikov, K.; Fabris, J.; Piattella, O.; Santos, E. Static, spherically symmetric solutions with a scalar field in Rastall gravity. Gen. Rel. Grav. 2016, 48, 162. [Google Scholar] [CrossRef]
- Heydarzade, Y.; Moradpour, H.; Darabi, F. Black hole solutions in Rastall theory. Can. J. Phys. 2017, 95, 1253. [Google Scholar] [CrossRef]
- Spallucci, E.; Smailagic, A. Gaussian black holes in Rastall gravity. Int. J. Mod. Phys. D 2017, 27, 1850003. [Google Scholar] [CrossRef]
- Ma, M.-S.; Zhao, R. Noncommutative geometry inspired black holes in Rastall gravity. Eur. Phys. J. C 2017, 77, 629. [Google Scholar] [CrossRef]
- Kumar, R.; Ghosh, S.G. Rotating black hole in Rastall theory. Eur. Phys. J. C 2018, 78, 750. [Google Scholar] [CrossRef]
- Xu, Z.; Hou, X.; Gong, X.; Wang, J. Kerr–Newman-AdS black hole surrounded by perfect fluid matter in Rastall gravity. Eur. Phys. J. C 2018, 78, 513. [Google Scholar] [CrossRef]
- de Mello, E.R.B.; Fabris, J.C.; Hartmann, B. Abelian–Higgs strings in Rastall gravity. Class. Quant. Grav. 2015, 32, 085009. [Google Scholar] [CrossRef]
- Santos, A.; Ulhoa, S. On Gödel-type solution in Rastall’s gravity. Mod. Phys. Lett. A 2015, 30, 1550039. [Google Scholar] [CrossRef]
- Sadeghi, M. Black brane solution in Rastall AdS massive gravity and viscosity bound. Mod. Phys. Lett. A 2018, 33, 1850220. [Google Scholar] [CrossRef]
- Moradpour, H.; Sadeghnezhad, N.; Hendi, S. Traversable asymptotically flat wormholes in Rastall gravity. Can. J. Phys. 2017, 95, 1257. [Google Scholar] [CrossRef]
- Heydarzade, Y.; Darabi, F. Black hole solutions surrounded by perfect fluid in Rastall theory. Phys. Lett. B 2017, 771, 365. [Google Scholar] [CrossRef]
- Graça, J.M.; Lobo, I.P. Scalar QNMs for higher dimensional black holes surrounded by quintessence in Rastall gravity. Eur. Phys. J. C 2018, 78, 101. [Google Scholar] [CrossRef]
- Lobo, I.P.; Moradpour, H.; Graça, J.P.M.; Salako, I. Thermodynamics of black holes in Rastall gravity. Int. J. Mod. Phys. D 2018, 27, 1850069. [Google Scholar] [CrossRef]
- Licata, I.; Moradpour, H.; Corda, C. The commutator algebra of covariant derivative as general framework for extended gravity. The Rastall theory case and the role of the torsion. Int. J. Geom. Meth. Mod. Phys. 2017, 14, 1730003. [Google Scholar] [CrossRef]
- Darabi, F.; Moradpour, H.; Licata, I.; Heydarzade, Y.; Corda, C. Einstein and Rastall theories of gravitation in comparison. Eur. Phys. J. C 2018, 78, 25. [Google Scholar] [CrossRef]
- Caramês, T.; Fabris, J.C.; Piattella, O.F.; Strokov, V.; Daouda, M.H.; Oliveira, A.M. In Proceedings of the II Argentinian-Brazilian Meeting on Gravitation, Astrophysics and Cosmology, Buenos Aires, Argentina, 22–25 April 2014; pp. 81–86.
- Salako, I.G.; Houndjo, M.; Jawad, A. Generalized Mattig’s relation in Brans–Dicke–Rastall gravity. Int. J. Mod. Phys. D 2016, 25, 1650076. [Google Scholar] [CrossRef]
- Visser, M. Rastall gravity is equivalent to Einstein gravity. Phys. Lett. B 2018, 782, 83. [Google Scholar] [CrossRef]
- Rastall, P. A theory of gravity. Can. J. Phys. 1976, 54, 66. [Google Scholar] [CrossRef]
- Capozziello, S.; Gonzalez, P.A.; Saridakis, E.N.; Vasquez, Y. Exact charged black-hole solutions in D-dimensional f(T) gravity: Torsion vs curvature analysis. JHEP 2013, 2, 039. [Google Scholar] [CrossRef]
- Ayon-Beato, E. New regular black hole solution from nonlinear electrodynamics. Phys. Lett. B 1999, 464, 25. [Google Scholar] [CrossRef]
- Salazar, I.H.; García, D.A.; Plebański, J. Duality rotations and type D solutions to Einstein equations with nonlinear electromagnetic sources. J. Math. Phys. 1987, 28, 2171. [Google Scholar] [CrossRef]
- Guo, S.; He, K.-J.; Li, G.-R.; Li, G.-P. The shadow and photon sphere of the charged black hole in Rastall gravity. Class. Quant. Grav. 2021, 38, 165013. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Saridakis, E.N. New rotating black holes in nonlinear Maxwell f(R) gravity. Phys. Rev. D 2020, 102, 124072. [Google Scholar] [CrossRef]
- Prihadi, H.L.; Sakti, M.F.A.R.; Hikmawan, G.; Zen, F.P. Dynamics of charged and rotating NUT black holes in Rastall gravity. Int. J. Mod. Phys. D 2020, 29, 2050021. [Google Scholar] [CrossRef]
- Shahidi, S. osmological implications of Rastall-f(R) theory. Phys. Rev. D 2021, 104, 084033. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Freeman, W.H., Ed.; Macmillan: San Francisco, CA, USA, 1973. [Google Scholar]
- D’Inverno, R.A. Internationale Elektronische Rundschau; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Nashed, G.G.L. Stability of the vacuum non-singular black hole. Chaos Solitons Fractals 2003, 15, 841. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Saridakis, E.N. tability of motion and thermodynamics in charged black holes in f(T) gravity. JCAP 2022, 5, 017. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Nojiri, S. Black holes with Lagrange multiplier and potential in mimetic-like gravitational theory: Multi-horizon black holes. JCAP 2022, 5, 011. [Google Scholar] [CrossRef]
- Hunter, C.J. Action of instantons with a nut charge. Phys. Rev. 1999, 59, 024009. [Google Scholar] [CrossRef]
- Hawking, S.W.; Hunter, C.J.; Page, D.N. NUT charge, anti–de Sitter space, and entropy. Phys. Rev. 1999, 59, 044033. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black Holes and the Second Law. Lett. Nuovo Cim. 1972, 4, 737. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Stationary axisymmetric solutions and their energy contents in teleparallel equivalent of Einstein theory. Astrophys. Space Sci. 2010, 330, 173. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. 1973, 7, 2333. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W. Cosmological event horizons, thermodynamics, and particle creation. Phys. Rev. 1977, 15, 2738. [Google Scholar] [CrossRef]
- Myung, Y.S.; Kim, Y.-W.; Park, Y.-J. Quantum cooling evaporation process in regular black holes. Phys. Lett. 2007, 656, 221. [Google Scholar] [CrossRef]
- Kim, W.; Shin, H.; Yoon, M. Anomaly and Hawking Radiation from Regular Black Holes. J. Korean Phys. Soc. 2008, 53, 1791. [Google Scholar] [CrossRef][Green Version]
- Myung, Y.S.; Kim, Y.-W.; Park, Y.-J. Thermodynamics of regular black hole. Gen. Rel. Grav. 2009, 41, 1051. [Google Scholar] [CrossRef]
- Dymnikova, I.G. De sitter-schwarzschild black hole: Its particlelike core and thermodynamical properties. Int. J. Mod. Phys. D 1996, 5, 529. [Google Scholar] [CrossRef]
- Dymnikova, I. The cosmological term as a source of mass. Class. Quant. Grav. 2002, 19, 725. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Reissner–nordström solutions and energy in teleparallel theory. Mod. Phys. Lett. A 2006, 21, 2241. [Google Scholar] [CrossRef]
- Dymnikova, I. Generic Features of Thermodynamics of Horizons in Regular Spherical Space-Times of the Kerr-Schild Class. Universe 2018, 4, 63. [Google Scholar] [CrossRef]
- Shirafuji, T.; Nashed, G.G.L.; Kobayashi, Y. Equivalence Principle in the New General Relativity. Prog. Theor. Phys. 1996, 96, 933. [Google Scholar] [CrossRef]
- Hayward, S.A. Formation and Evaporation of Nonsingular Black Holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef]
- Nicolini, P.; Smailagic, A.; Spallucci, E. Noncommutative geometry inspired Schwarzschild black hole. Phys. Lett. 2006, 632, 547–551. [Google Scholar] [CrossRef]
- Sharif, M.; Javed, W. Thermodynamics of a Bardeen black hole in noncommutative space. Can. J. Phys. 2011, 89, 1027. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Dymnikova, A.I.G. Nonsingular vacuum cosmologies with a variable cosmological term. Class. Quant. Grav. 2003, 20, 3797. [Google Scholar] [CrossRef]
- Bronnikov, K.; Dymnikova, I.; Galaktionov, E. Multihorizon spherically symmetric spacetimes with several scales of vacuum energy. Class. Quant. Grav. 2012, 29, 095025. [Google Scholar] [CrossRef]
- Nouicer, K. Black hole thermodynamics to all orders in the Planck length in extra dimensions. Class. Quant. Grav. 2007, 24, 6435. [Google Scholar] [CrossRef]
- Dymnikova, I.; Korpusik, M. Thermodynamics of Regular Cosmological Black Holes with the de Sitter Interior. Entropy 2011, 13, 1967. [Google Scholar] [CrossRef]
- Chamblin, A.; Emparan, R.; Johnson, C.V.; Myers, R.C. Charged AdS black holes and catastrophic holography. Phys. Rev. 1999, 60, 064018. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. In Euclidean Quantum Gravity; World Scientific: Singapore, 1975; Volume 43, pp. 199–220. [Google Scholar] [CrossRef]
- Davies, P.C.W. The thermodynamic theory of black holes. Proc. Roy. Soc. Lond. 1977, A353, 499. [Google Scholar] [CrossRef]
- Babichev, E.O.; Dokuchaev, V.I.; Eroshenko, Y.N. Black holes in the presence of dark energy. Phys. Usp. 2013, 56, 1155. [Google Scholar] [CrossRef]
- Wang, P.; Wu, H.; Yang, H.; Yao, F. Extended phase space thermodynamics for black holes in a cavity. JHEP 2020, 9, 154. [Google Scholar] [CrossRef]
- Chaloshtary, S.R.; Zangeneh, M.; Hajkhalili, S.; Sheykhi, A.; Zebarjad, S. Thermodynamics and reentrant phase transition for logarithmic nonlinear charged black holes in massive gravity. Int. J. Mod. Phys. D 2020, 29, 2050081. [Google Scholar] [CrossRef]
- Sajadi, S.; Riazi, N.; Hendi, S. Dynamical and thermal stabilities of nonlinearly charged AdS black holes. Eur. Phys. J. C 2019, 79, 775. [Google Scholar] [CrossRef]
- Yu, S.; Gao, C. Exact black hole solutions with nonlinear electrodynamic field. Int. J. Mod. Phys. D 2020, 29, 2050032. [Google Scholar] [CrossRef]
- Ali, M.S.; Ghosh, S.G. Thermodynamics of rotating Bardeen black holes: Phase transitions and thermodynamics volume. Phys. Rev. D 2019, 99, 024015. [Google Scholar] [CrossRef]
- Caldarelli, M.M.; Cognola, G.; Klemm, D. Thermodynamics of Kerr-Newman-AdS black holes and conformal field theories. Class. Quant. Grav. 2000, 17, 399. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Capozziello, S. Charged spherically symmetric black holes in f(R) gravity and their stability analysis. Phys. Rev. D 2019, 99, 104018. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nashed, G.G.L. Nonlinear Charged Black Hole Solution in Rastall Gravity. Universe 2022, 8, 510. https://doi.org/10.3390/universe8100510
Nashed GGL. Nonlinear Charged Black Hole Solution in Rastall Gravity. Universe. 2022; 8(10):510. https://doi.org/10.3390/universe8100510
Chicago/Turabian StyleNashed, Gamal Gergess Lamee. 2022. "Nonlinear Charged Black Hole Solution in Rastall Gravity" Universe 8, no. 10: 510. https://doi.org/10.3390/universe8100510
APA StyleNashed, G. G. L. (2022). Nonlinear Charged Black Hole Solution in Rastall Gravity. Universe, 8(10), 510. https://doi.org/10.3390/universe8100510






