Extremely Metal-Poor Asymptotic Giant Branch Stars
Abstract
1. Introduction
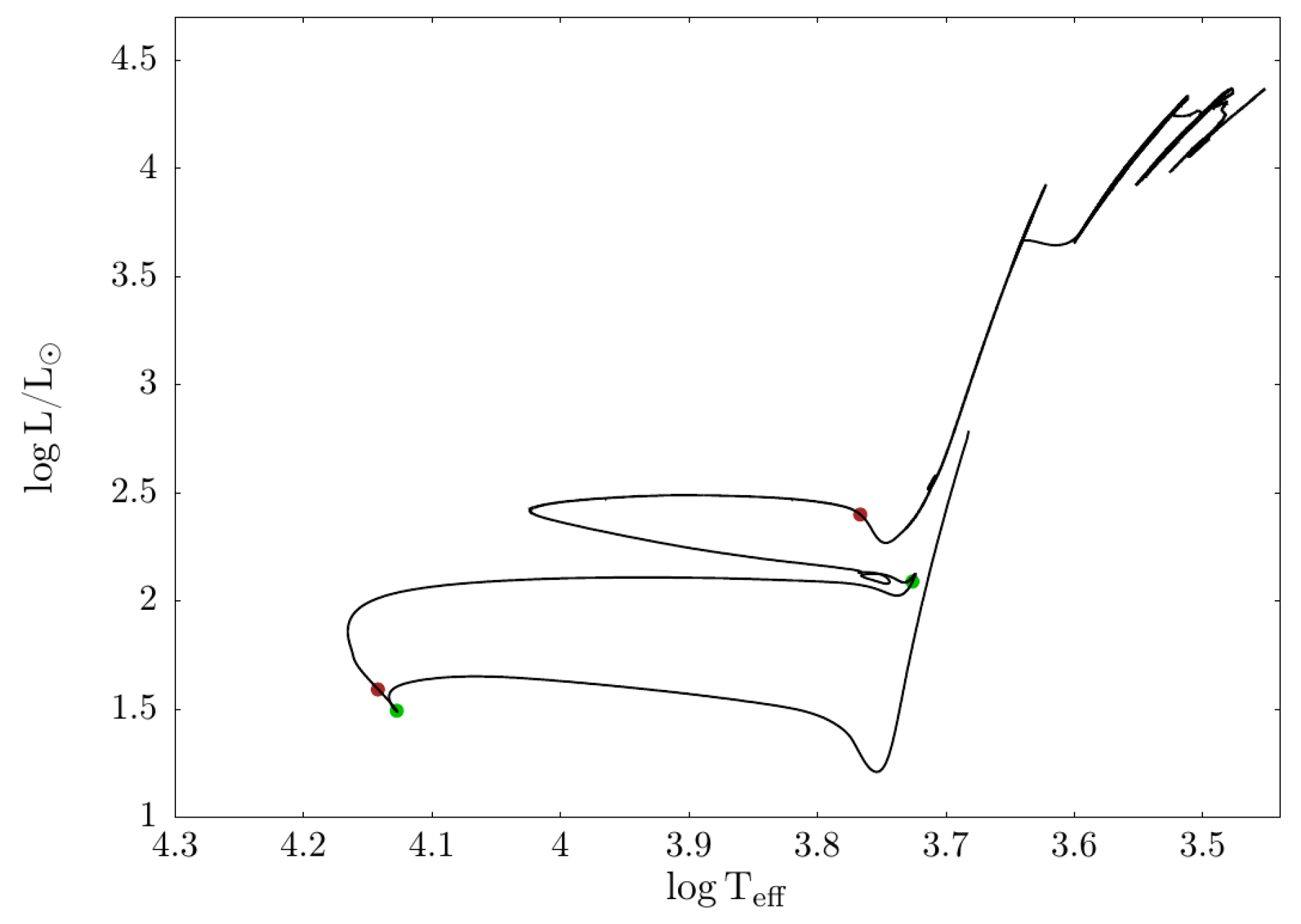
2. Massive AGB Stars
2.1. H- and He-Burning Phases
2.2. The Early Asymptotic Giant Branch and the Second Dredge-Up
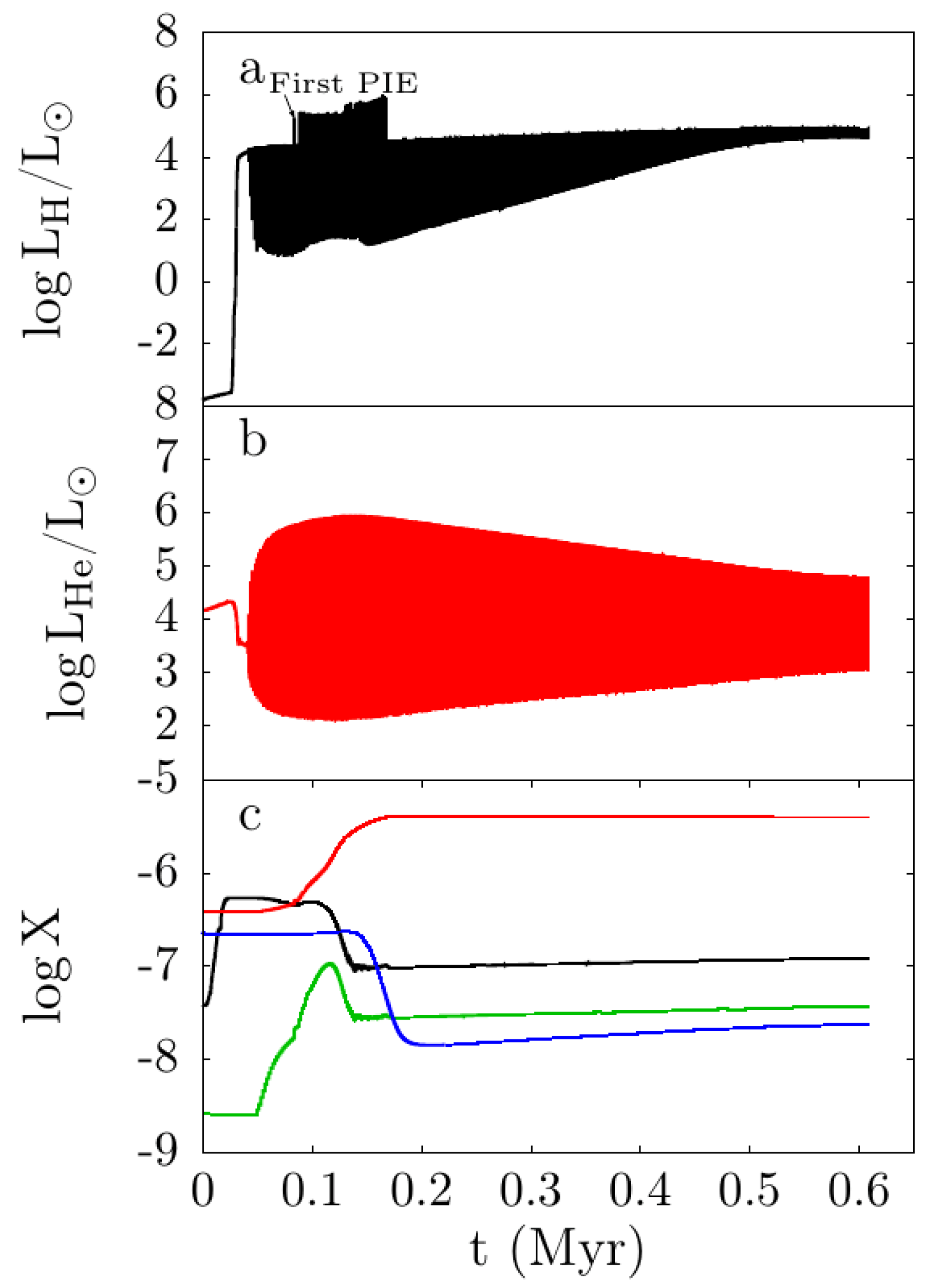
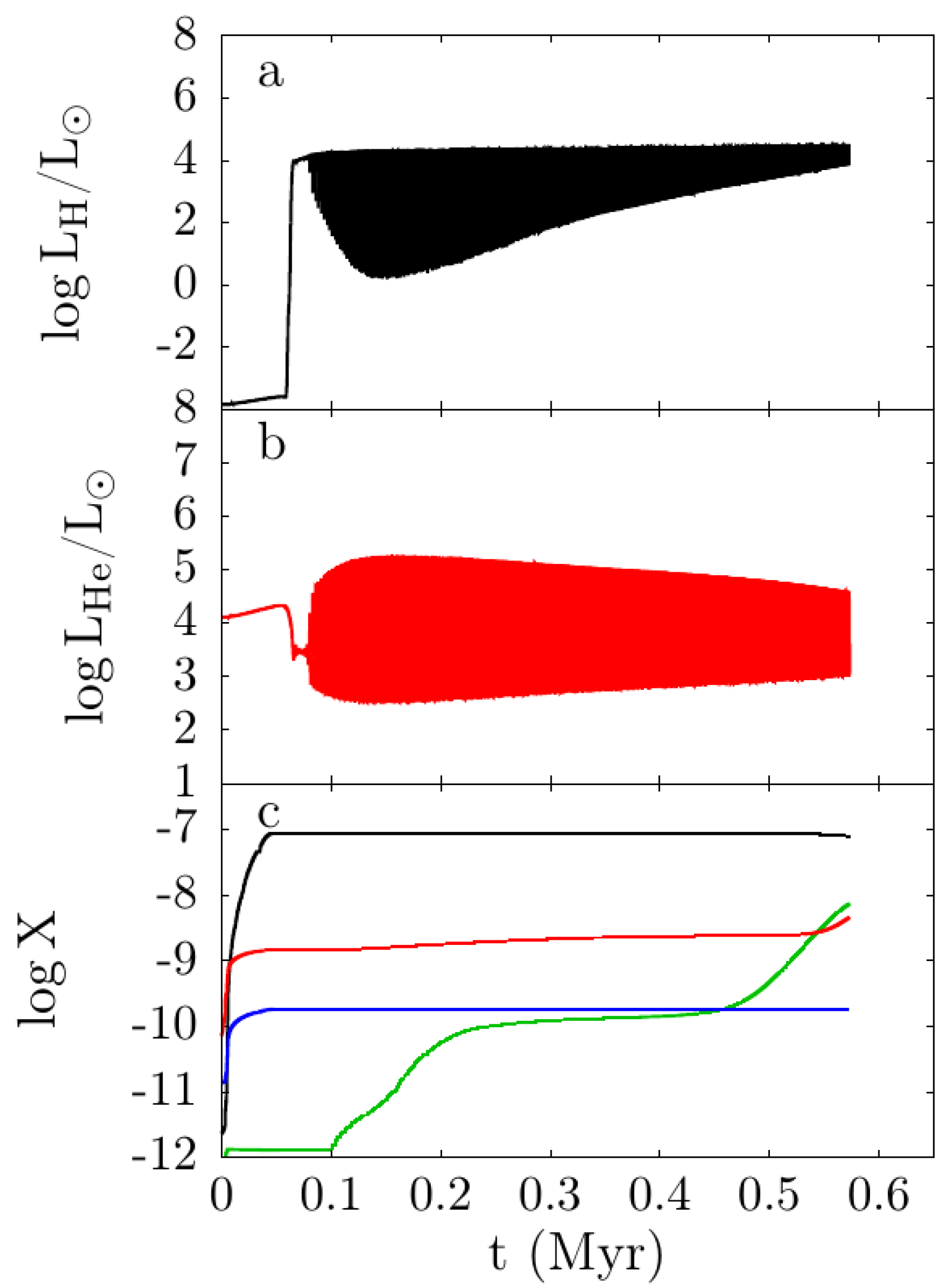
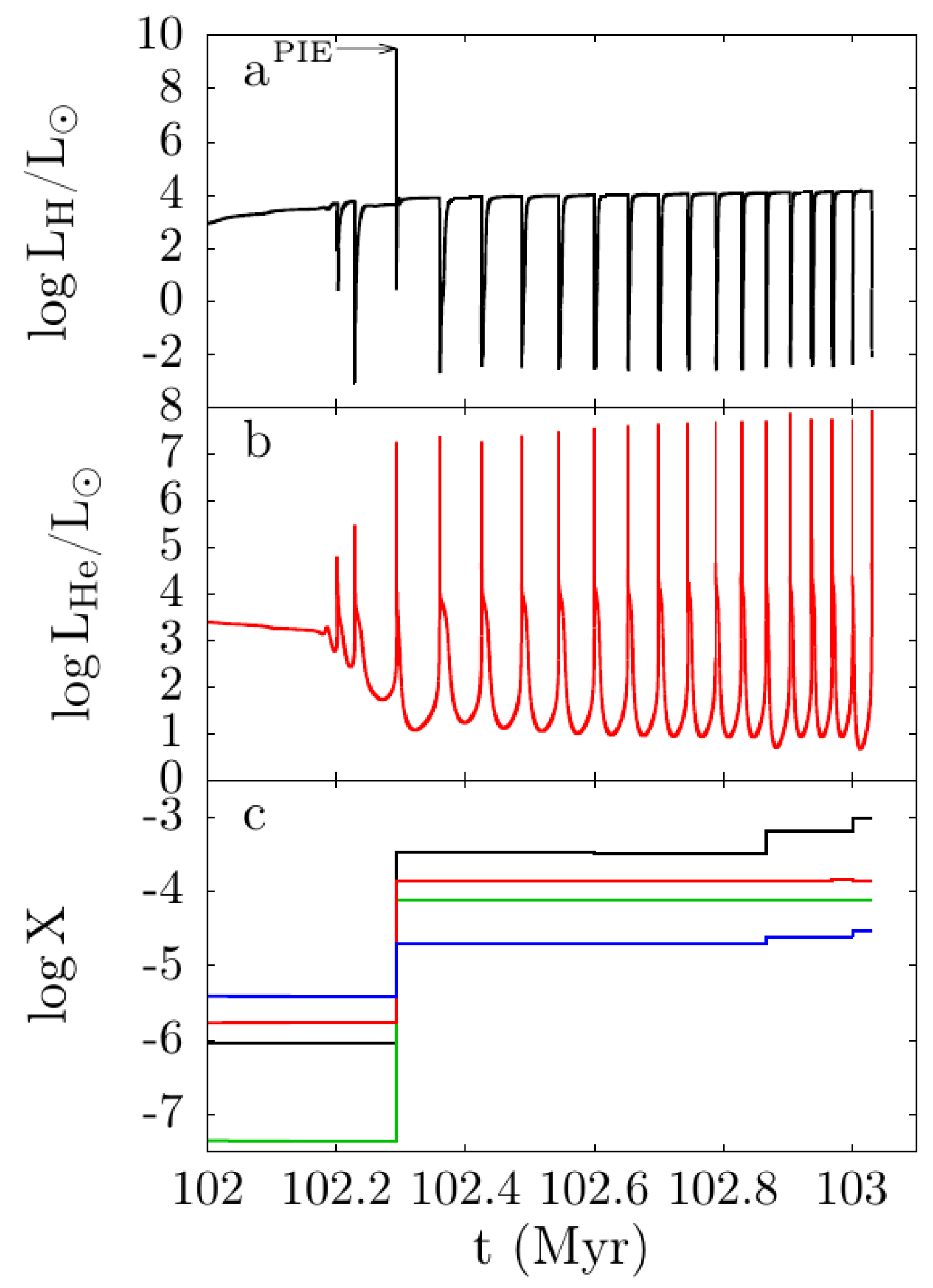
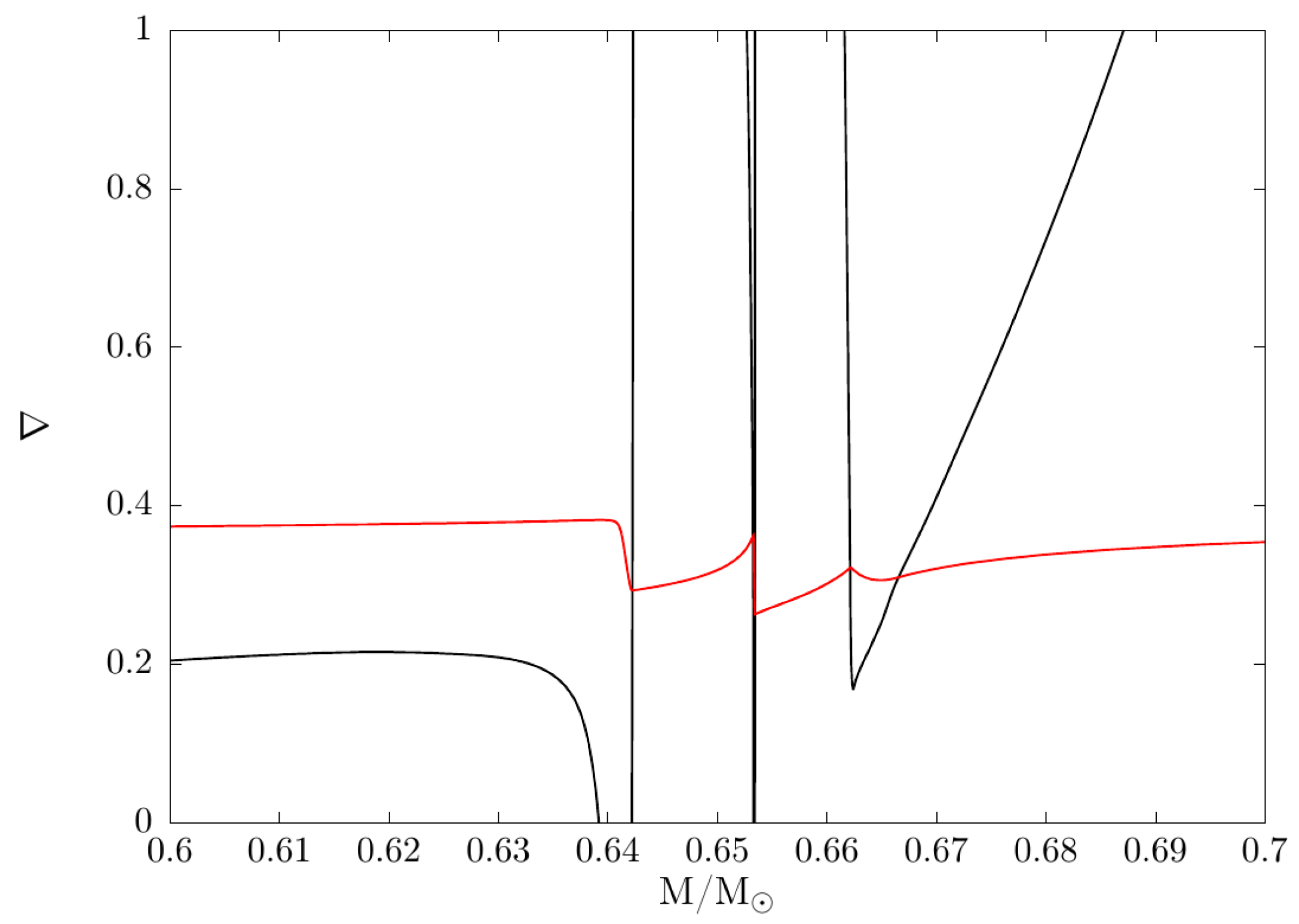
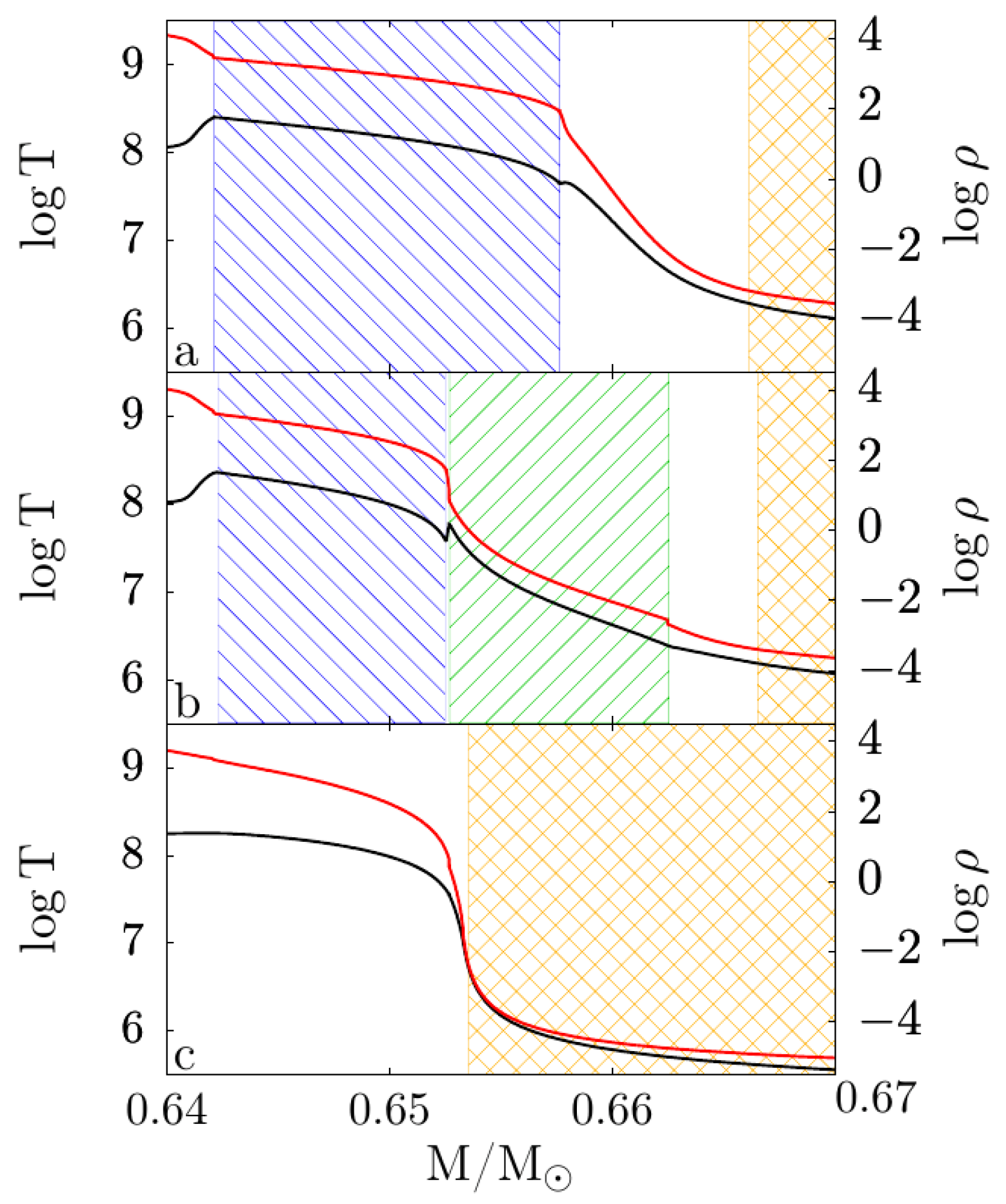
2.3. Thermal Pulses, Proton Ingestion Episodes and Hot Bottom Burning
3. Low-Mass AGB Stars
3.1. From Central-H Burning to E-AGB
3.2. The TP-AGB Phase
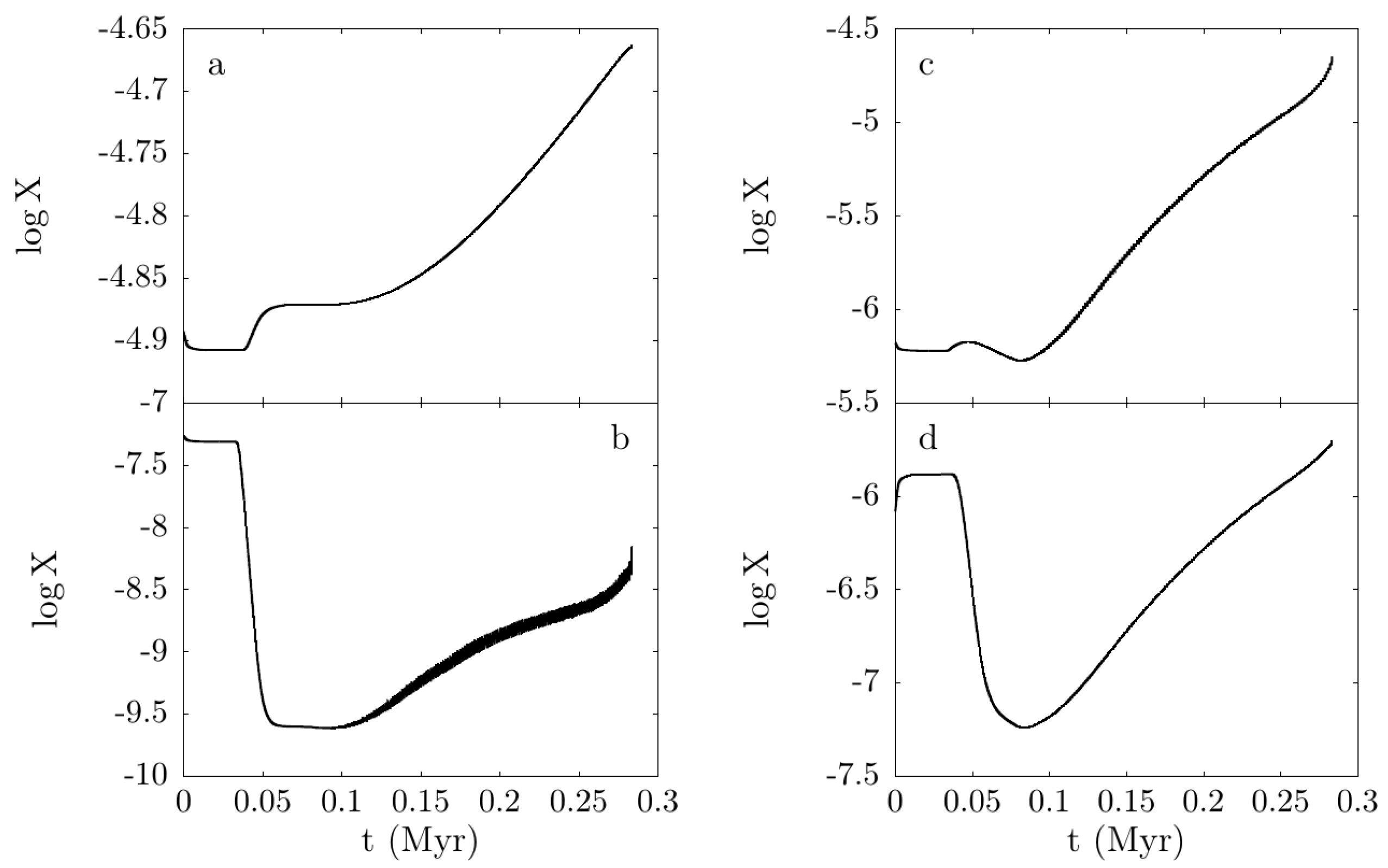
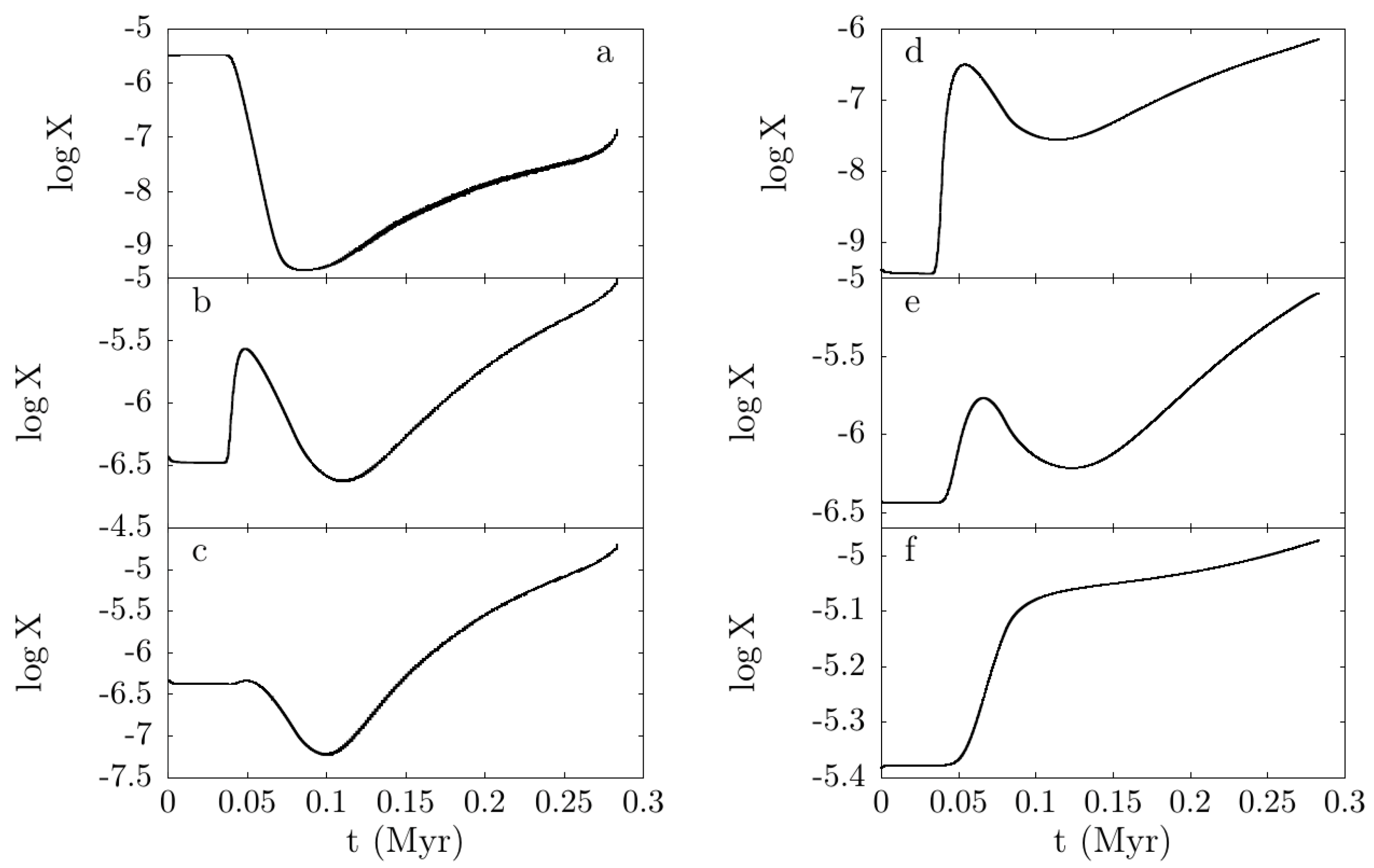
3.3. The Chemistry of the Proton Ingestion Episode
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Zuo, W.; Du, C.; Jing, Y.; Gu, J.; Newberg, H.J.; Wu, Z.; Ma, J.; Zhou, X. The Stellar Metallicity Distribution of the Galactic Halo Based on SCUSS and SDSS Data. Astrophys. J. 2017, 841, 59. [Google Scholar] [CrossRef]
- Marengo, M.; Mullen, J.; Neeley, J.R.; Fabrizio, M.; Marrese, P.M.; Bono, G.; Braga, V.F.; Magurno, D.; Crestani, J.; Fiorentino, G.; et al. Metallicity Distribution of Galactic Halo Field RR Lyræ, and the Effect of Metallicity on Their Pulsation Properties. arXiv 2021, arXiv:2006.09625. [Google Scholar]
- Glover, S.C.O.; Clark, P.C.; Greif, T.H.; Johnson, J.L.; Bromm, V.; Klessen, R.S.; Stacy, A. Open questions in the study of population III star formation. In Low-Metallicity Star Formation: From the First Stars to Dwarf Galaxies; Hunt, L.K., Madden, S.C., Schneider, R., Eds.; Cambridge University Press: Cambridge, UK, 2009; Volume 4, pp. 3–17. [Google Scholar] [CrossRef]
- Saslaw, W.C.; Zipoy, D. Molecular Hydrogen in Pre-galactic Gas Clouds. Nature 1967, 216, 976–978. [Google Scholar] [CrossRef]
- Palla, F.; Salpeter, E.E.; Stahler, S.W. Primordial star formation—The role of molecular hydrogen. Astrophys. J. 1983, 271, 632–641. [Google Scholar] [CrossRef]
- Nakamura, F.; Umemura, M. The Stellar Initial Mass Function in Primordial Galaxies. Astrophys. J. 2002, 569, 549–557. [Google Scholar] [CrossRef]
- Nagakura, T.; Omukai, K. Formation of Population III stars in fossil HII regions: Significance of HD. Mon. Not. R. Astron. Soc. 2005, 364, 1378–1386. [Google Scholar] [CrossRef]
- Johnson, J.L.; Bromm, V. The cooling of shock-compressed primordial gas. Mon. Not. R. Astron. Soc. 2006, 366, 247–256. [Google Scholar] [CrossRef]
- Mattsson, L. The origin of carbon: Low-mass stars and an evolving, initially top-heavy IMF? Astron. Astrophys. 2010, 515, A68. [Google Scholar] [CrossRef][Green Version]
- Bisterzo, S.; Gallino, R.; Straniero, O.; Cristallo, S.; Käppeler, F. The s-process in low-metallicity stars—II. Interpretation of high-resolution spectroscopic observations with asymptotic giant branch models. Mon. Not. R. Astron. Soc. 2011, 418, 284–319. [Google Scholar] [CrossRef]
- Chieffi, A.; Domínguez, I.; Limongi, M.; Straniero, O. Evolution and Nucleosynthesis of Zero-Metal Intermediate-Mass Stars. Astrophys. J. 2001, 554, 1159–1174. [Google Scholar] [CrossRef]
- Straniero, O.; Gallino, R.; Cristallo, S. s process in low-mass asymptotic giant branch stars. Nucl. Phys. A 2006, 777, 311–339. [Google Scholar] [CrossRef]
- Piersanti, L.; Cristallo, S.; Straniero, O. The Effects of Rotation on s-process Nucleosynthesis in Asymptotic Giant Branch Stars. Astrophys. J. 2013, 774, 98. [Google Scholar] [CrossRef]
- Straniero, O.; Dominguez, I.; Piersanti, L.; Giannotti, M.; Mirizzi, A. The Initial Mass-Final Luminosity Relation of Type II Supernova Progenitors: Hints of New Physics? Astrophys. J. 2019, 881, 158. [Google Scholar] [CrossRef]
- Stancliffe, R.J. Does simultaneous solution matter for stellar evolution codes? Mon. Not. R. Astron. Soc. 2006, 370, 1817–1822. [Google Scholar] [CrossRef][Green Version]
- Campbell, S.W.; Lattanzio, J.C. Evolution and nucleosynthesis of extremely metal-poor and metal-free low- and intermediate-mass stars. I. Stellar yield tables and the CEMPs. Astron. Astrophys. 2008, 490, 769–776. [Google Scholar] [CrossRef]
- Suda, T.; Fujimoto, M.Y. Evolution of low- and intermediate-mass stars with [Fe/H] <= −2.5. Mon. Not. R. Astron. Soc. 2010, 405, 177–193. [Google Scholar] [CrossRef]
- Iwamoto, N. Evolution and Nucleosynthesis in Extremely Metal-Poor, Asymptotic Giant Branch Stars. Publ. Astron. Soc. Aust. 2009, 26, 145–152. [Google Scholar] [CrossRef][Green Version]
- Gil-Pons, P.; Doherty, C.L.; Gutiérrez, J.; Campbell, S.W.; Siess, L.; Lattanzio, J.C. Nucleosynthetic yields of Z = 10−5 intermediate-mass stars. Astron. Astrophys. 2021, 645, A10. [Google Scholar] [CrossRef]
- Ventura, P.; Dell’Agli, F.; Romano, D.; Tosi, S.; Limongi, M.; Chieffi, A.; Castellani, M.; Tailo, M.; Lugaro, M.; Marini, E.; et al. Gas and dust from extremely metal-poor AGB stars. Astron. Astrophys. 2021, 655, A6. [Google Scholar] [CrossRef]
- Straniero, O.; Domínguez, I.; Imbriani, G.; Piersanti, L. The Chemical Composition of White Dwarfs as a Test of Convective Efficiency during Core Helium Burning. Astrophys. J. 2003, 583, 878–884. [Google Scholar] [CrossRef]
- Schwarzschild, M.; Härm, R. Thermal Instability in Non-Degenerate Stars. Astrophys. J. 1965, 142, 855. [Google Scholar] [CrossRef]
- Chieffi, A.; Tornambe, A. On the evolution of an intermediate-mass zero-metal star which does not experience thermal instabilities during the double shell burning phase. Astrophys. J. 1984, 287, 745–748. [Google Scholar] [CrossRef]
- Fujimoto, M.Y.; Iben, I.J.; Chieffi, A.; Tornambe, A. Hydrogen and helium burning in zero-metal asymptotic giant branch stars and the existence of thresholds (in core mass and CNO abundance) for the occurrence of helium shell flashes. Astrophys. J. 1984, 287, 749–760. [Google Scholar] [CrossRef]
- Dominguez, I.; Straniero, O.; Limongi, M.; Chieffi, A. Do zero metals intermediate mass stars experience thermal pulses? arXiv 2000, arXiv:astro-ph/astro-ph/9912425. [Google Scholar]
- Lau, H.H.B.; Stancliffe, R.J.; Tout, C.A. The evolution of low-metallicity asymptotic giant branch stars and the formation of carbon-enhanced metal-poor stars. Mon. Not. R. Astron. Soc. 2009, 396, 1046–1057. [Google Scholar] [CrossRef][Green Version]
- Suda, T.; Aikawa, M.; Machida, M.N.; Fujimoto, M.Y.; Iben, I.J. Is HE 0107-5240 A Primordial Star? The Characteristics of Extremely Metal-Poor Carbon-Rich Stars. Astrophys. J. 2004, 611, 476–493. [Google Scholar] [CrossRef]
- Cristallo, S.; Straniero, O.; Lederer, M.T.; Aringer, B. Molecular Opacities for Low-Mass Metal-poor AGB Stars Undergoing the Third Dredge-up. Astrophys. J. 2007, 667, 489–496. [Google Scholar] [CrossRef][Green Version]
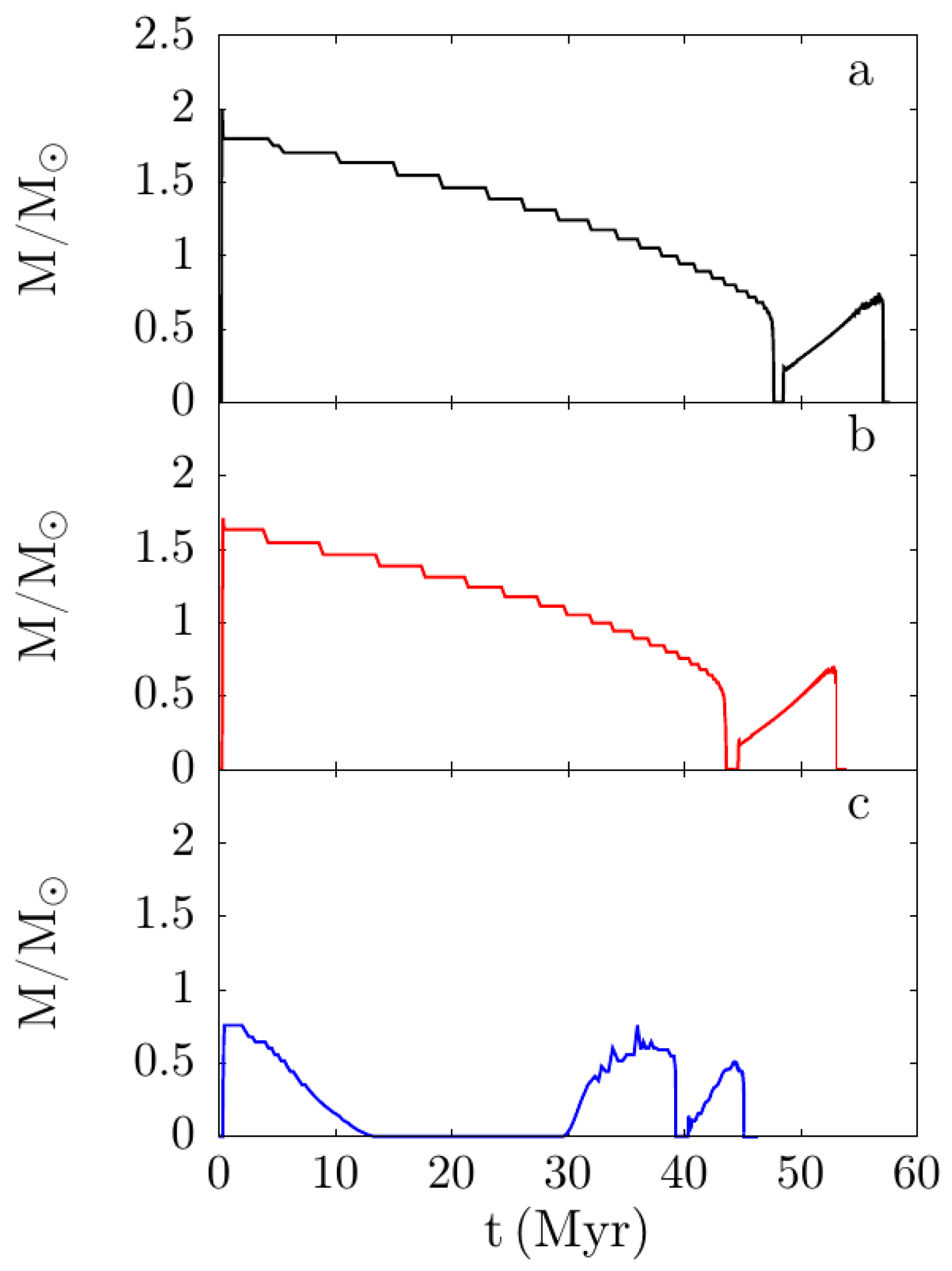
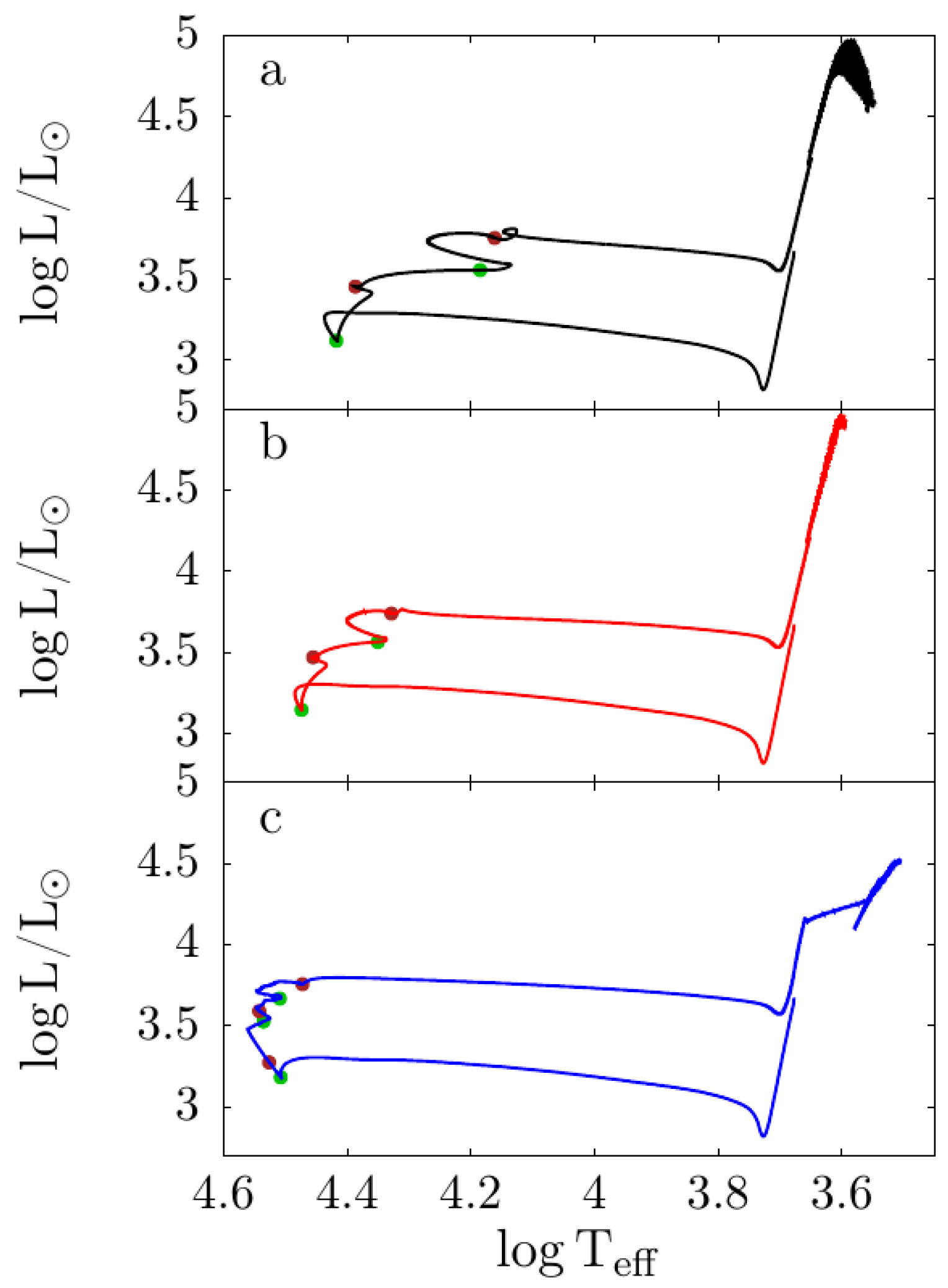
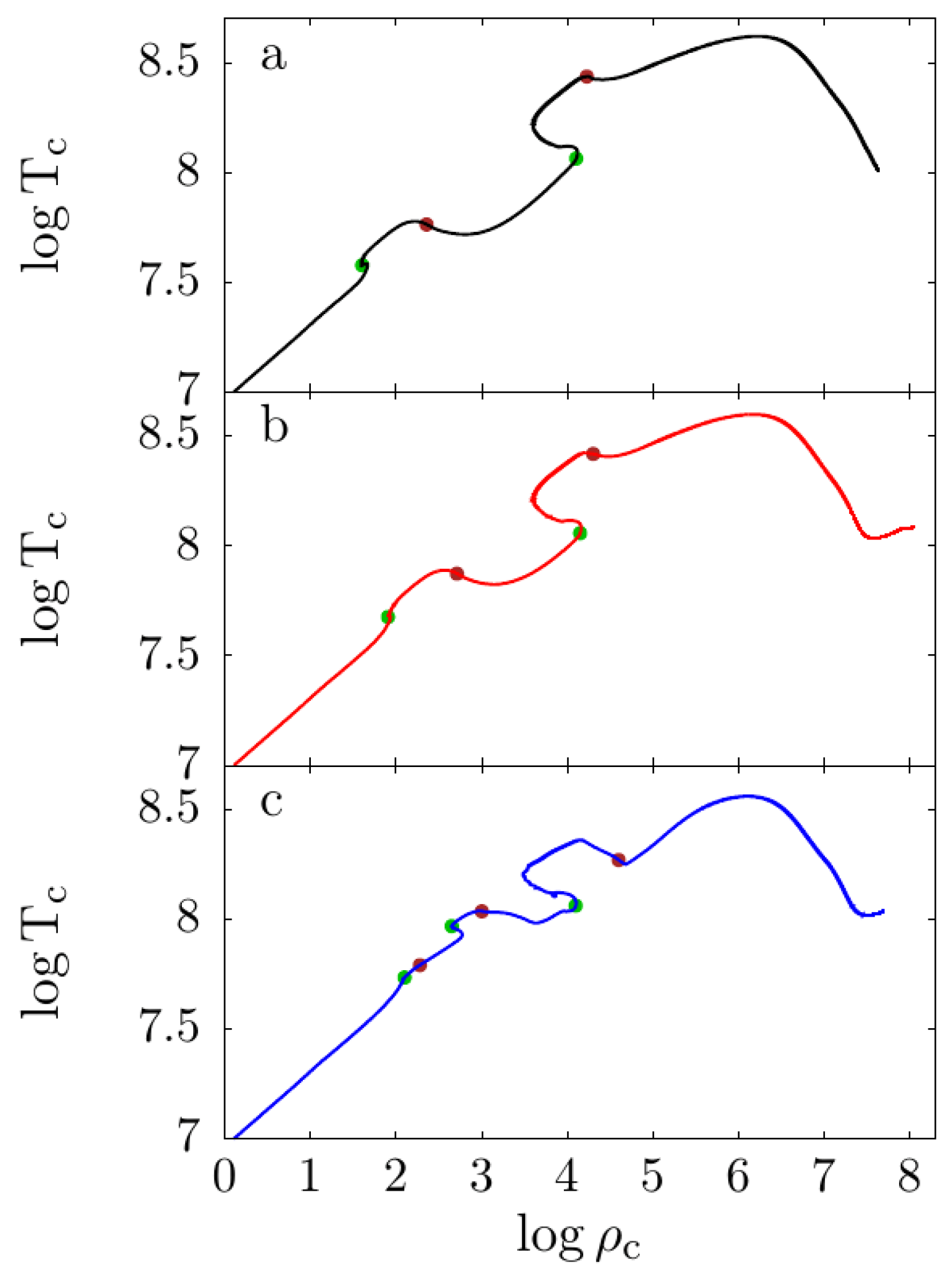
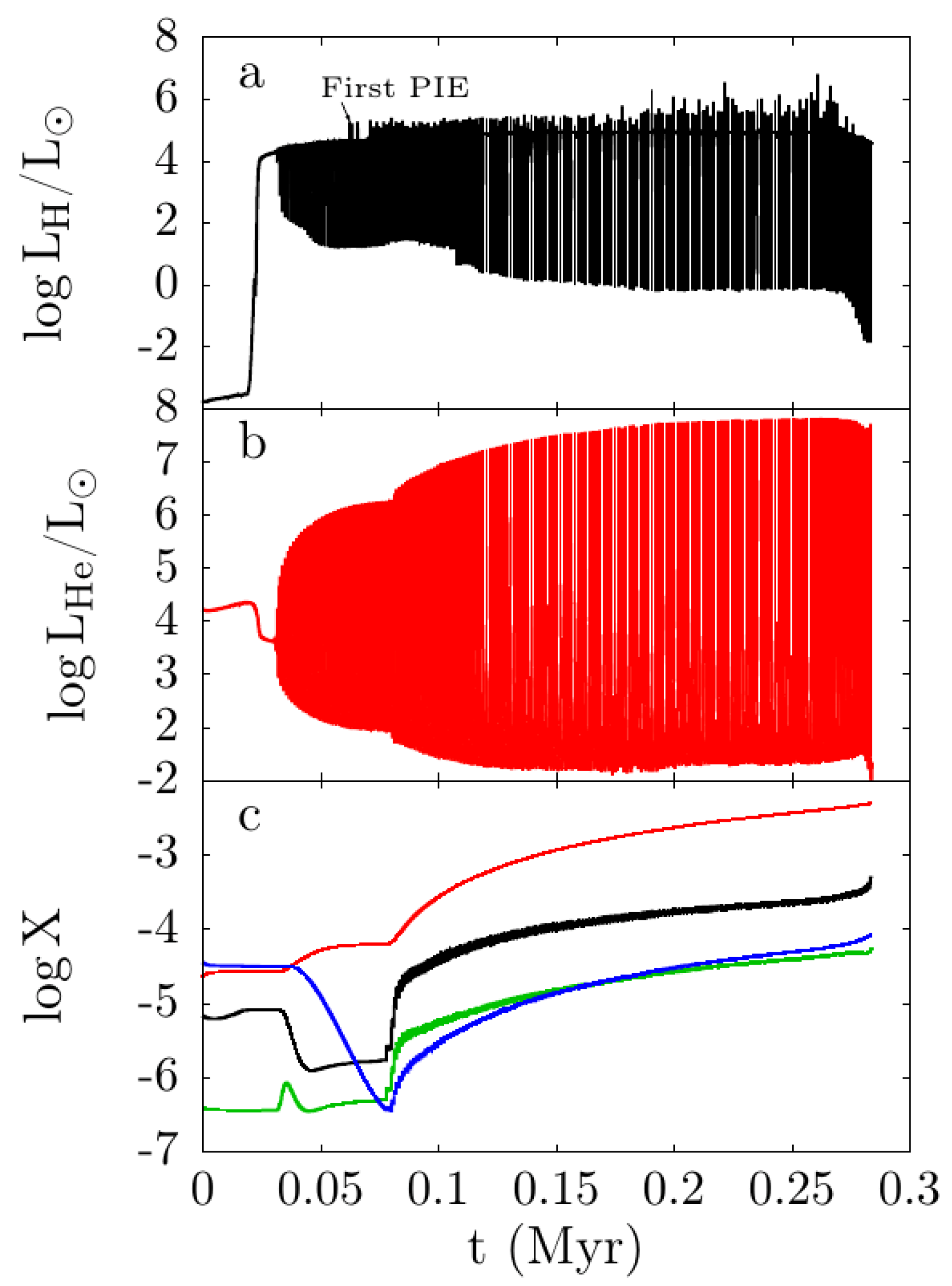
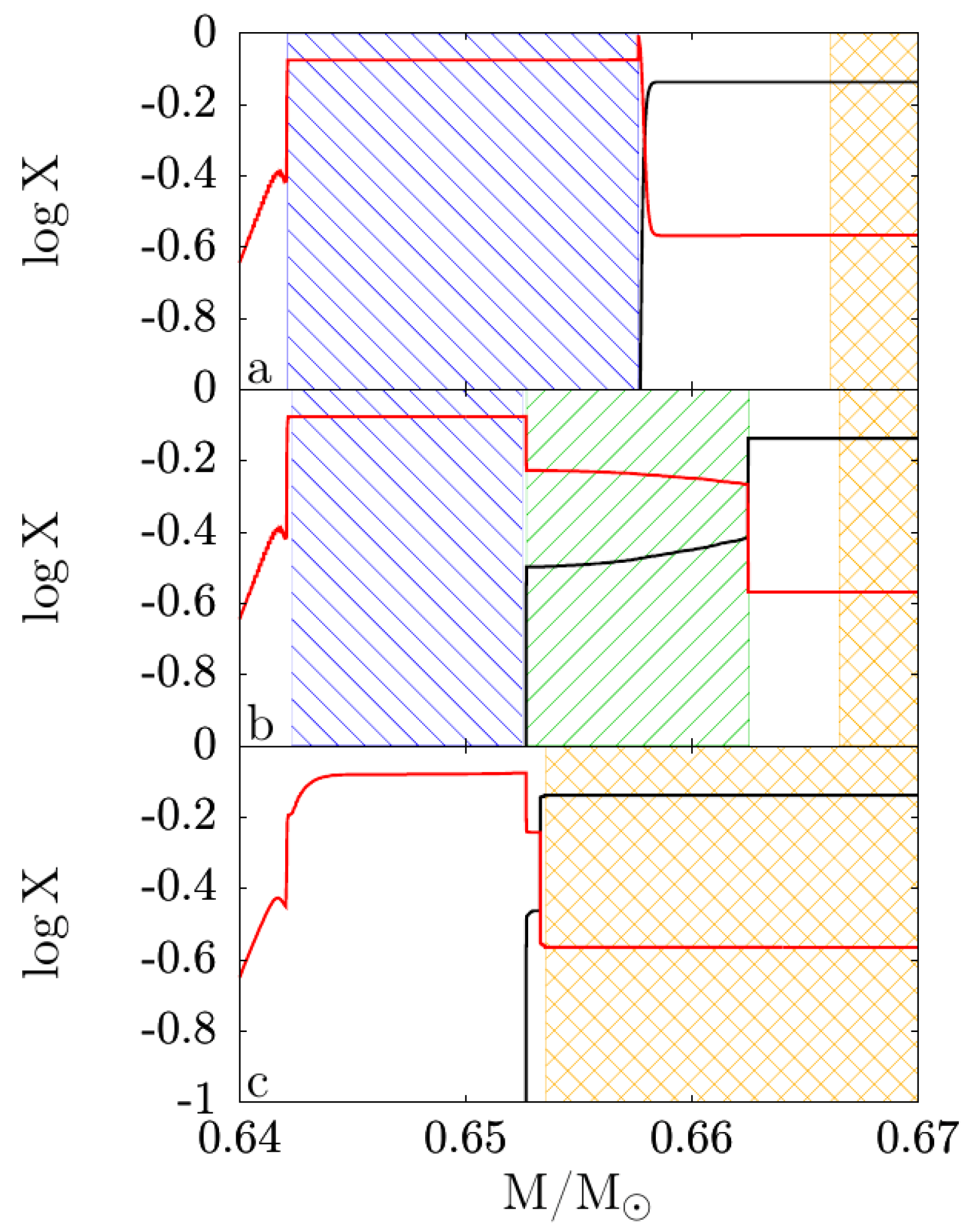
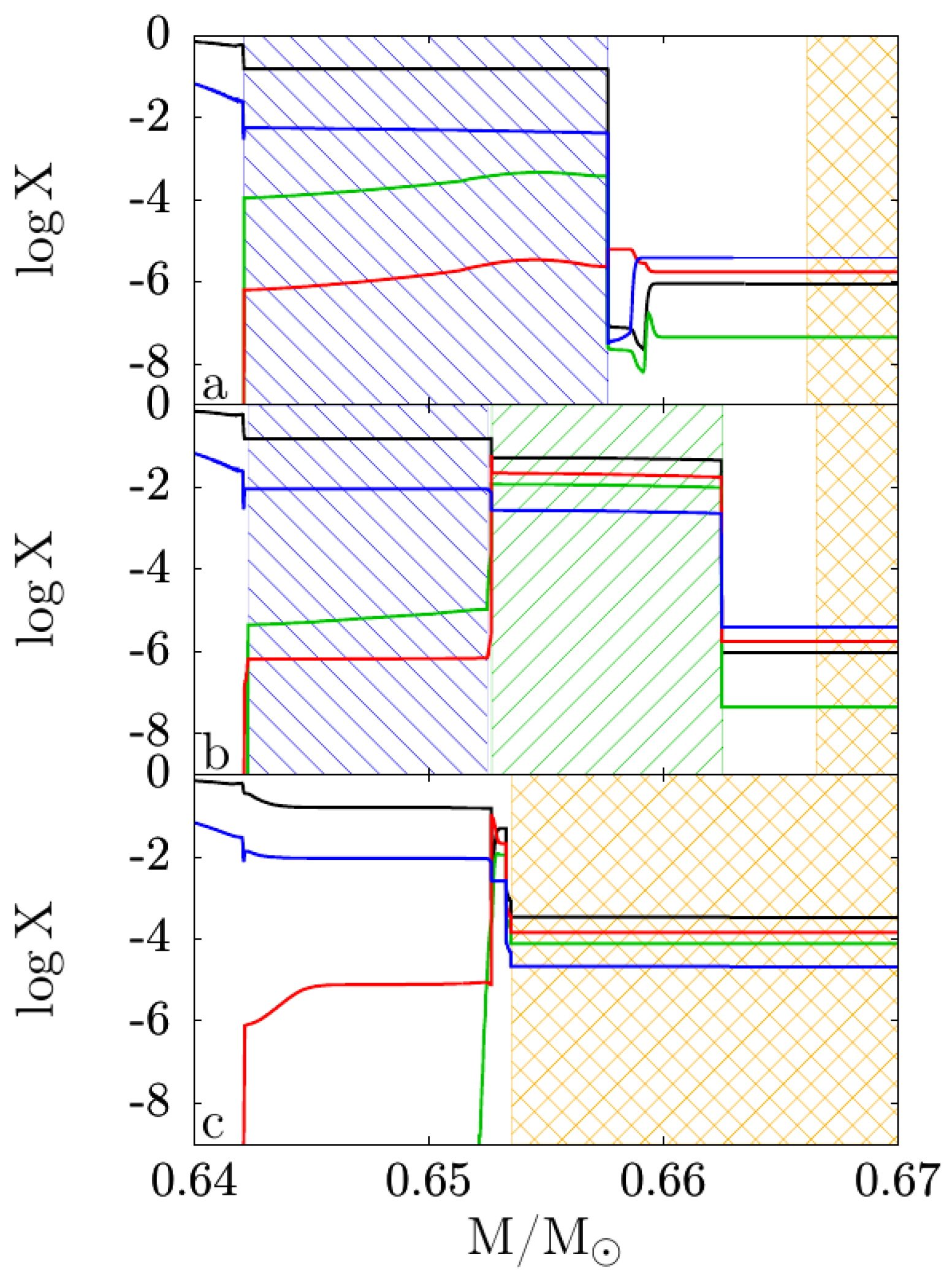
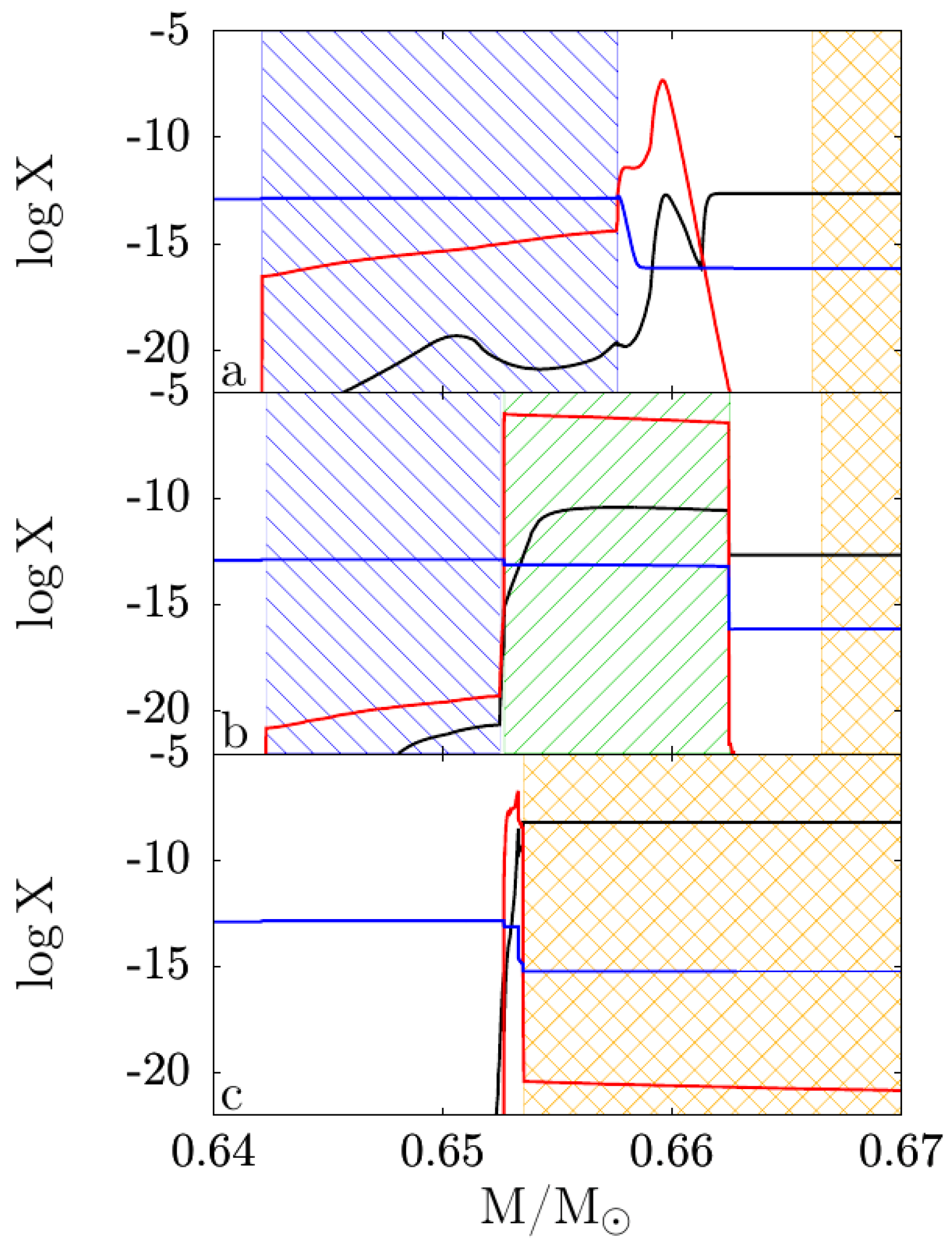
| Z | Pre-Main Sequence (Myr) | Central-H Burning (Myr) | Central-He Burning (Myr) |
|---|---|---|---|
| 0.329 | 47.5 | 8.70 | |
| 0.436 | 43.5 | 8.62 | |
| 0.626 | 38.1 | 6.37 |
| Before | After | Before | After | Before | After | |
|---|---|---|---|---|---|---|
| H | ||||||
| 4He | ||||||
| 12C | ||||||
| 13C | ||||||
| 14N | ||||||
| 16O | ||||||
| CNO | ||||||
| Before | After | Before | After | ||
|---|---|---|---|---|---|
| H | 20Ne | ||||
| 4He | 21Ne | ||||
| 12C | 22Ne | ||||
| 13C | 23Na | ||||
| 14N | 24Mg | ||||
| 16O | 25Mg | ||||
| 7Li | 26Mg | ||||
| 7Be | 26Al | ||||
| 11B | 27Al | ||||
| 15N | 28Si | ||||
| 17O | 29Si | ||||
| 18O | 56Fe | ||||
| 19F | 56Ni to 208Pb |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cirillo, M.; Piersanti, L.; Straniero, O. Extremely Metal-Poor Asymptotic Giant Branch Stars. Universe 2022, 8, 44. https://doi.org/10.3390/universe8010044
Cirillo M, Piersanti L, Straniero O. Extremely Metal-Poor Asymptotic Giant Branch Stars. Universe. 2022; 8(1):44. https://doi.org/10.3390/universe8010044
Chicago/Turabian StyleCirillo, Mario, Luciano Piersanti, and Oscar Straniero. 2022. "Extremely Metal-Poor Asymptotic Giant Branch Stars" Universe 8, no. 1: 44. https://doi.org/10.3390/universe8010044
APA StyleCirillo, M., Piersanti, L., & Straniero, O. (2022). Extremely Metal-Poor Asymptotic Giant Branch Stars. Universe, 8(1), 44. https://doi.org/10.3390/universe8010044






