1. Introduction
There is general agreement that a theoretical study of black holes in a regime where quantum mechanical effects play a role is important for a more complete understanding of General Relativity and/or some modifications of this theme, in its relation to quantum mechanics. But here already, parts of the universal agreement end. How do we introduce quantum mechanics in a black hole? According to one doctrine, when subject to quantum mechanics, even large black holes exhibit problems with
information loss [
1,
2,
3,
4,
5] and
firewalls, Ref. [
6] that can only be understood if one invokes superstring theory and/or AdS/CFT conjectures. However, the result of that is rather sobering: all that can be said about the black hole quantum states seems to be that these will be ‘chaotic’, which almost puts a premature end to all attempts to understand how to characterise these states.
In our approach, we try to be more systematic in pushing the principles of General Relativity a bit further, postponing the need for ‘new Planck scale physics’ to be limited to Planck scale black holes only. This supposes that we should be able to constrain ourselves to black holes whose detailed effects on space-time are limited to structures with dimensions much larger than the Planck length. It seems to be obvious that such black holes should be described by standard General Relativity alone. Quantum mechanical effects would be limited to the effects of Hawking particles, which have low energies, and as such have very limited effects on the global space-time structure, at least when regarded over limited stretches of time. In this paper we show that there are other topological aspects of joining together patches of space-time, and these, in turn, will imply important features of the theory of black holes as well as quantum mechanics itself.
At isolated subregions of space and time, which will be smooth and locally flat at Planckian scales, one should be able to employ ordinary quantum field theoretical methods to address all relevant dynamical structures that may arise. The only thing then left to do is find a systematic way to glue these isolated pieces of information together, so that everything will be clear. Beware, this will be a delicate procedure.
It sounds like an obviously correct starting point: if
A is large enough, for black holes with mass
1 , and size
, one needs the properties of whatever field theory the Standard Model evolves to, up to energy scale
.
This is the regime that we now focus upon. It should be possible to avoid (Super)string theory here. It is the same regime where Hawking radiation becomes exactly calculable, even though it is weak. To derive the existence of Hawking particles, only standard quantum field theories were needed. Yet, in the expression for the Hawking temperature,
we see that thermodynamics (
), Special and General Relativity (
c and
G), and quantum mechanics (
ℏ) all come together.
2 This indicates that, indeed, at some stages of our understanding, known theories can be used in combination, to arrive at statements that continue to be valid
at the Planck scale.
In previous accounts, the author explained how to use the physics of gravitational effects due to particles moving into or out of horizons, to derive dynamical laws for the quantum black hole. Now here, we wish to emphasise that
transformations should be used in order to arrive at more precise, generic results
3. We wish to consider the
quantum data, at specific isolated points in space and time, as seen by different ‘observers’. The observers do not need to ‘measure’ anything, but rather ‘describe’ what they see and experience, in a language that can be understood locally. From a philosophical point of view, this should be the thing to demand: the local language is the best one to use for a local description of the events, so we must be clear about what these local data may say.
It is here that, if one follows the older text books and lecture courses literally, one hits upon the black hole information problem and the firewall problem. According to several authors, these problems imply that the program just sketched above is bound to fail completely. The present author always maintained that this does not need to be so, but it would be a mistake to think that closing one’s eyes for the problems is the appropriate solution. To the contrary, we have to look more carefully at what we are doing.
Suppose that there exists a Hilbert space for all quantum states a black hole can be in. According to our views on the interpretation of quantum mechanics [
8], one has to distinguish
realistic states from
quantum superpositions of realistic states. The mathematical background is summarised in
Appendix A. The realistic
4 states are the states the system can be in when we imagine that these states describe, as accurately as possible, what the most probable truly existing configuration may be. We call those states
beables. Together, the beables form an orthonormal set of vectors in Hilbert space, which can be, but do not have to be, used as a basis. The ‘quantum superpositions’ are all other states we get when we superimpose two or more beables.
In a black hole, the quantum evolution operator will seem to transform beables into quantum superpositions (superimposables). This may sound mysterious, as it is not true in some simpler quantum systems.
5 What this actually means for realism is that every beable evolves into one of many different possible future beables, depending on some very fast fluctuating variables [
9]. As soon as we lose sight of the fast fluctuating variables, the notion of
probability enters. A diffusion process, similar to what was described much earlier by Nelson [
10,
11], takes place. In our theories for quantum realism, summarised in
Appendix A, this tendency is explained. If we could follow each and every one of the fast oscillating variables, we would see that beables evolve into beables, but as soon as we lose sight of the fast variables, we have to deal with probabilities, and probability amplitudes, in accordance with a genuine Schrödinger equation. Explicit models can be constructed for almost any Schrödinger equation one would wish to reproduce. In our recent papers [
9,
12] it is explained how this can be squared with the apparent contradictions with Bell’s theorem [
13] and the CHSH inequalities [
14], by constructing explicit models.
In short, if we start with any particular realistic state of a black hole at time , then determinism tells us that the exact moment, and further details, of the implosion event that has generated the black hole, are completely fixed, but only if one knows exactly also all fast variables. Averaging over the fast variables will smear the implosions over large ranges of the implosion time and all other details, in terms of superpositions of all possible events, leading to expressions to which the usual quantum Schrödinger equation applies, in the usual way. In fact, what we get is a picture of the distant past and the far future of the black hole that is time reversible.
The emergence of superimposed states, where the early implosions and the late explosions occur at superimposed moments in time, also causes superpositions in what we intended to use as our background metric, and this explains why we now avoid the use of a background metric that includes the effects of such events, replacing it by the metric of an eternal black hole. This formalism will get its a posteriori justification later.
Note that time reversibility appears to be totally absent in most scenarios that investigators are finding up to this day. In our work, time reversibility is a central issue. Only if one applies statistical methods in order to handle thermodynamics, time reversibility gets out of sight.
The doctrine called quantum mechanics is merely the vector space representation of deterministic events, as described also in Ref. [
8]. This implies that we can employ quantum mechanics as it usually is, while keeping in mind what it says about reality: the real events taking place follow from studying the beables that maximally overlap with the vector considered. In practice, this is the application of Born’s rule [
15]. As soon as we are unable to specify sufficiently precisely the fastest variables, we recover the usual uncertainty relations, and the standard interpretation of quantum mechanics then applies.
6In the next sections, we discuss a couple of technical issues that are absolutely crucial for understanding the theory that we wish to unfold here. We claim that the firewall problem is an important feature but it can be completely handled by using an important transformation, transforming in-going particles into out-going ones and vice versa [
16]. The effect of this transformation is, that:
A firewall due to an in-going particle may be replaced by out-going particles, and, mutatis mutandis, out-going particles may be replaced by in-going ones. Expanding energy/momenta of in- and out-going particles in spherical harmonics is crucial.
Then,
Section 4 explains the theory in detail, step by step. We see that it is roughly eight precisely shaped jig-saw pieces that have to be put together. The resulting construction is a package deal that has to be accepted entirely, or rejected. There is no possibility in-between. Indeed, one finds numerous publications, in which it was claimed that firewalls [
6] would implicate non-local features in black hole evolution. In our work, this conclusion is sharpened: the only non-locality we arrive at is the new boundary conditions at the horizons, which could be called non-local, in a sense. In
Section 5 we arrive at our conclusion: black holes can be understood best if one also accepts a radical attitude towards the interpretation of quantum mechanics.
Our views on quantum mechanics have been explained elsewhere; they are summarised in
Appendix A. I do realise that many readers will not go along here; they can just ignore this appendix entirely. Although I think they are useful, these insights in what quantum mechanics really is, are not essential for the jig-saw puzzle.
Technical aspects of our calculations are to be found in the references, but these overlap a lot; much of what we need will also be summarised in this paper.
2. The Penrose Diagram
To describe any physical state the black hole might be in, we proceed just the way we are used to in quantum field theory: take a classical solution for the field equations, and then subsequently describe the quantum states in terms of small excitations, using perturbation expansions. The first state we consider is the pure Schwarzschild black hole, where all Standard Model fields take their local vacuum values. This will be a solution of the pure Einstein equations without matter. It is usually written as
As argued and motivated in the previous section, we shall not add the effects of imploding matter or evaporating matter—these will be considered later.
By using different coordinates, one finds that the Schwarzschild solution has an analytic extension beyond the future and the past horizon. Setting
, the Kruskal-Szekeres [
17,
18] coordinates
x and
y are defined by
In these coordinates,
where we see that the horizon singularity at
cancels out.
Note that a point
appears
7 to be mapped onto two points
and
. It is convenient to define coordinates
, with
To understand the resulting picture of the geometry, notice that
x and
y, or equivalently,
and
, are light cone coordinates. As time
t increases,
increases if
x and
y are positive. But if we switch the signs of both
x and
y, Equations (
4) and (
6) stay the same, whereas
decreases as
t increases. This sign flip in the flow of time will be a crucial feature of the theory.
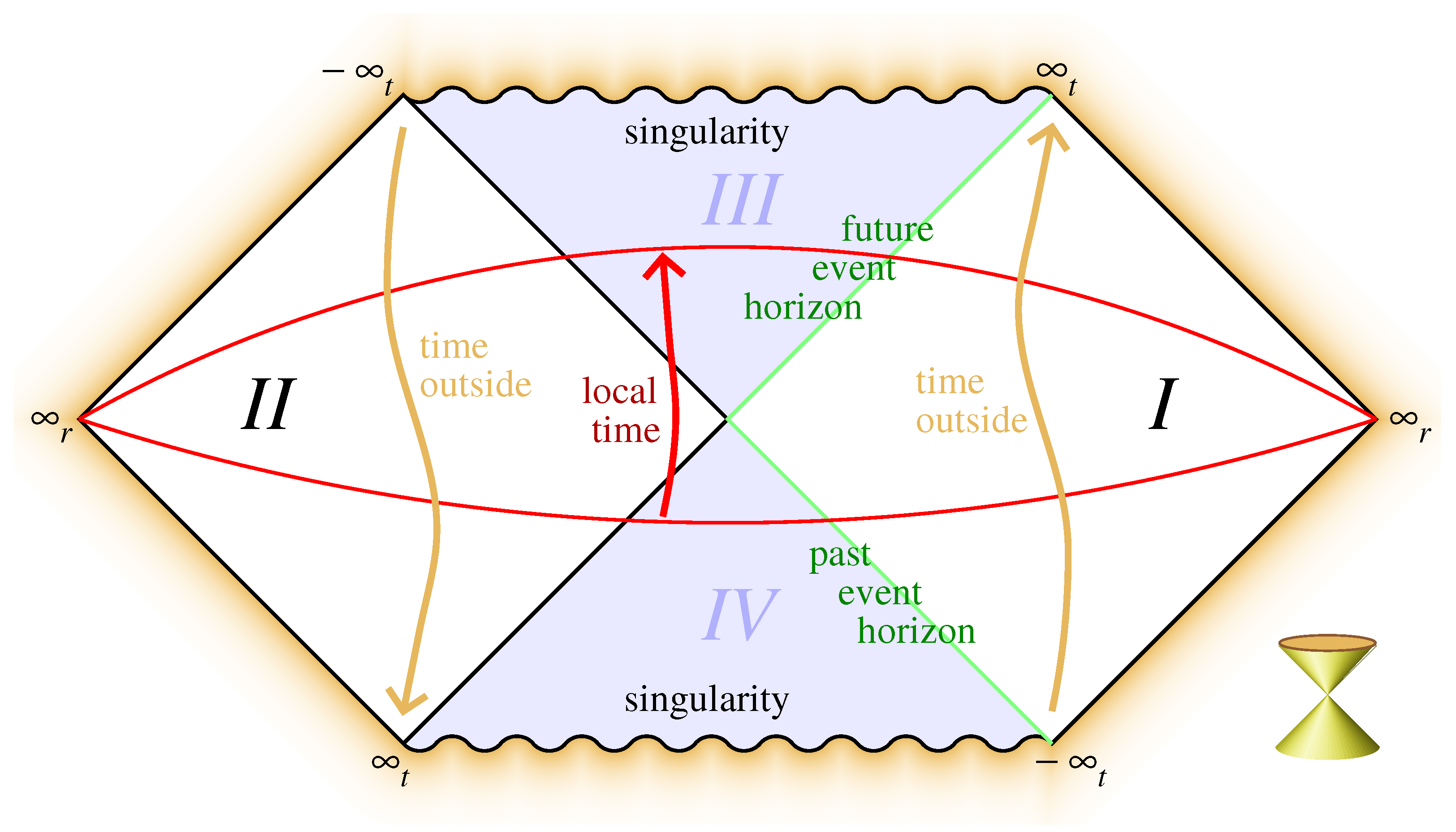
The
Penrose diagram, Figure 1, is obtained if the longitudinal coordinates
r and
t are replaced by these
and
, which include the asymptotic domains of
r and
t.
In
Figure 1, the classically accessible domain is indicated as the diamond shaped region
I. The upward arrow labelled as “time outside” is the arrow of the Schwarzschild time coordinate
t (or
). The radial Schwarzschild coordinate
r (or
) is oriented in the horizontal direction.
Analytic extension generates three other domains, labelled
,
and
. Of these,
and
are of lesser significance. One might now be tempted to consider the states obtained by just adding a finite number of particles to this ‘empty’ configuration, but this does not work exactly as one might expect. This is because
time for an outside observer in region
runs in the opposite direction, see
Figure 1: this is where
x and
y are both negative. Consequently, any particles we might be inclined to add in region
, would contribute
negatively to the total energy obtained as seen by the outside world. That cannot work correctly. In region
, a local observer would be expected to see particles with negative energies. There are no particles with negative energies for a local observer.
To see exactly what has to be done, we first consider the effect of time boosts in the outside regions
I and
. As explained in the previous section, the Schwarzschild solution is invariant under time boosts, like Einstein’s equations themselves. However, the Penrose diagram is not. A time boost for far-away regions in
I and
corresponds to a Lorentz transformation at the origin of the Penrose diagram. The energy eigenstates for the distant observer are Lorentz transformation eigenstates for a local observer near the origin. For small values of the coordinates
and
, a local Lorentz transformation there is generated by the operator
, or in a second quantised system,
We see that, in region
, where
, the local energy density of particles, generated by the Lorentz transformation (
8), is negative
8. One concludes that, if local energies of particles are always positive, then we seem to be talking of negative energy particles as seen by observers in region
.
We now claim that, nevertheless, region
must be assumed to describe the same universe as region
I, since it has an asymptotic region at infinity
9. It would be tempting to side-step this difficulty, but we prefer to face it head-on. In order to compare physical states in the Penrose diagram with physical states in our universe, we must assume that the particles describing the excited states of the system, not only have a lowest energy state, the vacuum, but also a
maximum energy state, to be referred to as the ‘antivacuum’. Then we can simply take region
to be filled almost to the rim with particles, leaving a few holes, which serve as physical particles in region
. We
shift the definition of energy for particles in region
, such that their energies take the values
, where only
represents the locally observed energy of a particle in
. This is exactly the way Dirac introduced the notion of antiparticles.
The reader might wonder how this works out when we add the gravitational forces due to the particles in region . The answer to this is that we only consider particles (in region I), or holes (in region ), with energies that are sufficiently low to allow us to ignore their gravitational back reaction. How this condition works out in detail will become clear soon. As yet, we just declare that gravitational forces will be added as ‘renormalised’ perturbations, in order to cancel the effects of .
The time evolution operator is the operator that describes how particles evolve while occupying states on the Cauchy surface. The Cauchy surface is a space-like surface that propagates in the time direction. For the local observer,
is the space-like coordinate and
is time. In
Figure 1, the Cauchy surface for a
local observer is shown, at two different values for the time coordinate. The arrow at the center indicates the evolution with time. However, this is not the way a Cauchy surface propagates that describes the data as experienced by a
distant observer. She uses the Schwarzschild coordinate
t as her time coordinate. Her Cauchy surfaces, at three different times, are indicated in
Figure 2. Note that these Cauchy surfaces all cross each other at the origin.
Thus, what we found out is how to relate states seen by outside observers, to states observed locally. Cauchy surfaces in region
must be filled or almost filled with local particles, states in region
I are almost empty. It will be important to realise that, near the origin, ‘quantum gravity effects’ might generate curvatures such that, at very tiny distance scales, the conditions ‘almost empty’ or ‘almost filled’ become ill-defined, so that interesting ‘quantum gravity’ effects are to be expected there.
10We believe that our way of handling the events near the origin of the Penrose diagram has big advantages as opposed to proposals where some limits to the
acceleration of particles are proposed, see for instance Rovelli [
19]. Such limits require new physics of a kind that is poorly understood. In the formalism here, particles are not accelerated at all, and the distribution of the physical data on the Cauchy surfaces can be understood directly from flat Minkowski space physics. We do get rapidly varying data near the origin, and these are carefully considered and handled by the firewall transformation, in this paper.
There are still three important issues that need to be considered. First, how can the existence of states with ‘maximal energy’ be reconciled with quantum mechanics? In contrast to standard quantum field theories, the black hole is expected to allow only for a finite number of internal quantum states. Therefore, indeed, one should have expected that there will be a limit to the energies particles in a black hole are allowed to have, so, we should not be surprised to encounter the need for a limit in the allowed energy spectra. Our theory for quantum mechanics has been explained in Refs. [
8,
9,
12]. In this approach, the demand for a maximum in the energy appears to be quite welcome. It is associated to a lower limit for the time step variables
in the classical evolution laws. How this can be squared with Lorentz invariance is not clear, but then, in the Schwarzschild background, Poincaré invariance is indeed violated, so, as yet, there seems to be no direct contradiction.
A typical classical dynamical system is as described in our summary of quantum theory in
Appendix A. We find an almost trivial symmetry
and associated with that,
. In the language of the deterministic system,
does not play any other role than being the inverse of the time steps
. See in particular Equation (
A3); the vacuum is at
and the antivacuum at
, but both these boundaries are totally artificial, they could be displaced in many ways. Fearing that the replacement of the zero energy bound by an
in region
would distort the gravitational interactions is unfounded. We must however remember to renormalise the gravitational force. Then, it is natural to expect that
cannot generate any anomalous gravitational effects.
The second important issue is the occurrence of two asymptotic regions, one in region
I and one in region
. The outside universe, however, has just a single asymptotic region. This problem does not involve only the time coordinate. Our problem is that there are two universes that are connected in the spatial direction.
11Consider the one-particle states. A local observer can put the particle at a point in region I or at the corresponding point, with the same Schwarzschild coordinates, in region . It looks as if the particle in region is a quantum clone of the particle in region I. This jeopardises our quantum mapping procedure. The best way to address this problem is to divide 3-space by an isometry subgroup of the form . This reduction of space is as a boundary condition, since the physical data are now repeated at the other side of the horizon(s), much like the data of a flat space region when mapped on a torus. An important constraint on this boundary condition is that it should not generate any cusp singularities. It was found that this requirement leaves exactly one possibility: is the antipodal mapping.
In ordinary Minkowski space, the antipodal mapping would generate a cusp singularity at the origin of 3-space, which we should not allow. In the Schwarzschild case, the singularity occurs at
, but
that point is singular already, and it is separated from the physically important domain
by a finite distance.
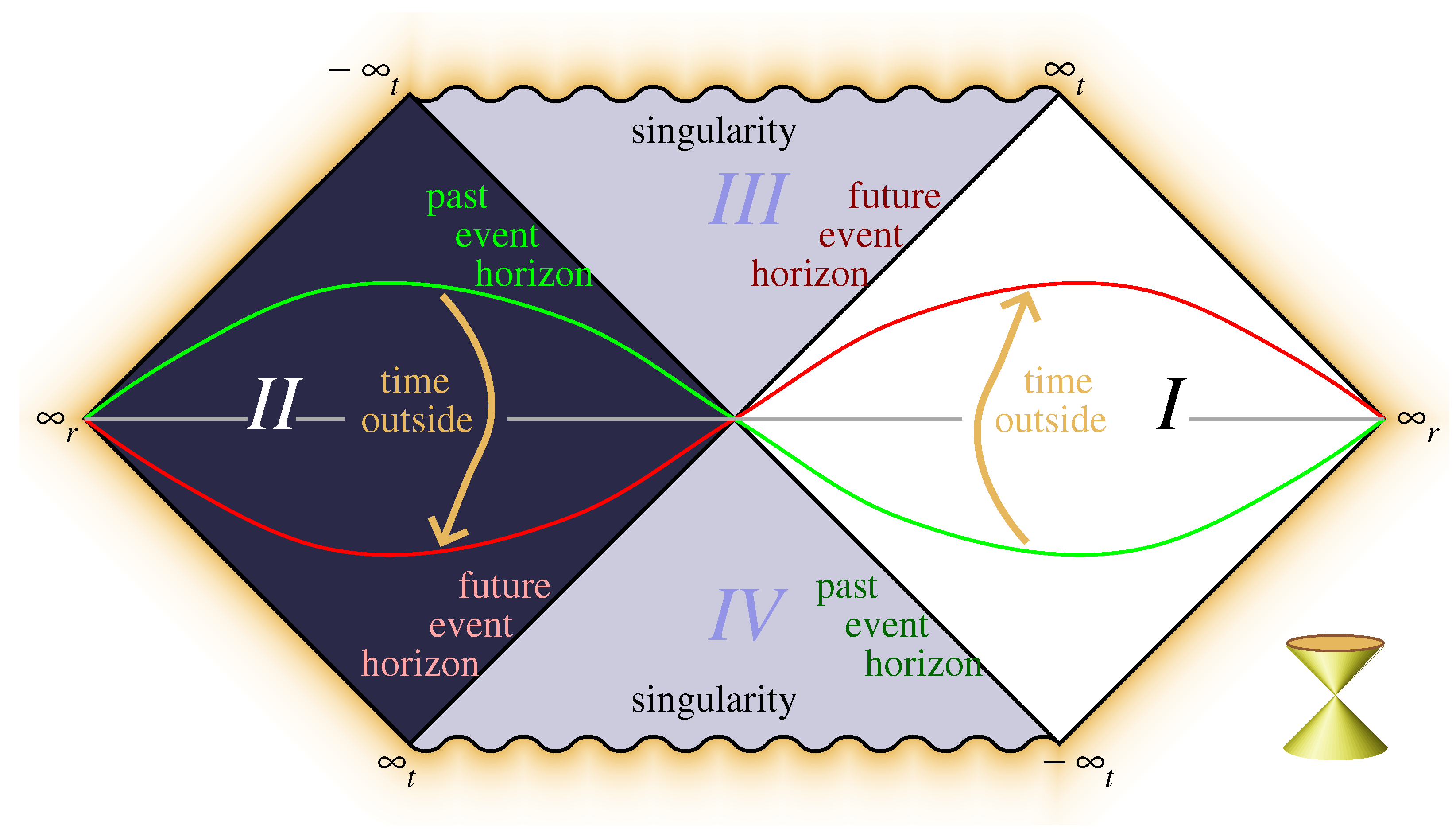
12 In
Figure 1 and
Figure 2, this singularity is on the wavy lines bordering regions
and
; the physical regions are regions
I and
.
We conclude that
region describes the antipodes of region I.13 Since time is also inverted, the
mapping is the
mapping
. Quantum field theory then imposes that the
C replacement (particle ↔ antiparticle) is included, since only
is an exact
symmetry of nature (as far as is known).
Then, there is a third important issue: the firewalls [
6]. We have chosen to use the Penrose diagram at a given moment
in time (
Section 1). At that moment, the Cauchy surface is the grey straight line in
Figure 2. At times later or earlier than that, the Cauchy surface is distorted, not only as a coordinate effect, but also because of curvature caused by gravitational back reactions. Exactly how to handle this situation appropriately, such as when stationary black holes are considered, where we wish to describe energy eigenstates for the external observer, is discussed in the next section.
3. The Firewall Transformation
In the previous section, it is explained that time translations for a distant observer correspond to Lorentz transformations for the local observer. We also explained that we wish to consider only those particle-like excitations whose energies and momenta are small enough to permit us to neglect temporarily their gravitational back reaction. This is almost a contradiction; we have to sharpen our formulations to include the case that particles are boosted to extraordinary high energies. Here we cannot entirely ignore gravity; in contrast, including the gravitational force just here, is possible, and it changes everything; in fact, it becomes the leading effect that dictates how particles will evolve over slightly longer time periods.
This mechanism has been explained in previous publications by the author [
16,
22,
23], but it seems that it still has not been appreciated as we think it should. The gravitational force that is responsible here is relatively easy to compute. Since all particles, after strong Lorentz boosts, behave as almost massless objects moving almost at the speed of light, we may assume as a good start, that the infinite boost limit is appropriate. The precise calculation is all over the literature [
24,
25], but let us first show the hand-waving argument.
Consider a particle going in. At early time
, its energy and momenta are negligible, but when
their gravitational effect aggravates exponentially. It consists of a shift in the same direction as the particle is going.
14 The shift is relatively easy to calculate. Take
as the minus coordinate of some out-going calibration particle. One finds that this particle is shifted by an amount
given by
where
is the solid angle
of the out-going calibration particle, and
the solid angle of the particle going in.
is the momentum of the in-going particle in local coordinates (normalised to the case
). The function
is a Green function, obeying Equation (
9), where
is the angular Laplacian. This equation is a linear relation connecting
and
, and the fact that it is linear allows us to derive new equations linking in- and out-going particles.
It is very convenient to ‘renormalise’ the Equation (
9). Instead of regarding it to relate a
shift to a
modification of the spectrum of in-going particles, we can re-interpret this as a relation connecting the
average position
of
all out-particles, to the
total momentum
of
all particles going in.
These data are dual to one another quantum mechanically, which implies that the entire angular distribution of all in-going particles is now related to the entire distribution of the out-going ones. This enables us to derive a very good approximation for the
black hole time evolution operator[
22].
This discovery also resolves the problem phrased at the beginning of this section, and this goes as follows. The time-dependence of the momentum of in-going particles is determined by repeated Lorentz boosts. Thus, the momentum increases exponentially with time (we talk of time as defined by an external observer). Consequently, the position of a combination of out-going particles also begins with increasing exponentially with time. Actually, the positions are determined by the local velocity of light—as long as the out-particles stay relativistic. As the momentum of an out-particle decreases exponentially in time, it sooner or later becomes non-relativistic and continues to obey standard equations, while moving out and away from the black hole.
As soon as out-going particles have separated from the black hole, we can remove them from the total picture, at which point also the original responsible in-going particle may be discarded. It was the exponential increase of momenta of in-going particles that caused the firewalls there. Thus, we observe that we actually obtained a proper mechanism for removing the firewalls. A firewall due to an in-going particle may be replaced by out-going particles. That’s two flies in one blow: the firewall is removed and a possibly quite accurate evolution operator for the black hole is obtained.
This is one of the reasons for regarding our procedure as a package deal. One cannot understand the role of the firewall without understanding the black hole evolution. But it also comes with the other necessary condition: the identification of the points in region
with the antipodes of region
I. Without such identification, the relation between in- and out particles would not have been unitary—in fact, the violation of unitarity would be huge.
15 The role of the antipodal identification for restoring unitarity in the black hole evolution was further explained in ref. [
23].
The argument for replacing the firewall with out-going particles can also be time-reversed: the out-going particles are the Hawking particles, which must originate near the horizon where they start off with huge amounts of momentum for each particle. What would the effect of these huge momentum values have been on the metric? It is often claimed that the Hawking particles do not cause a firewall when extrapolated to the past. For some reason, earlier researchers had no problem wishing this firewall away. It just could not be there. Now, we claim that Hawking particles can be regarded as decaying firewalls, in the sense that the mechanism described above works both forward in time as backwards, simply because positions and momenta are quantum mechanically dual to one another.
4. The Black Hole Theory as a Package Deal
We are now in a position to put the various pieces for a sound theory together. What we find from various strains of reasoning, is to be regarded as a jig-saw puzzle. Consisting of eight different jig-saw pieces, it is not too difficult to arrange them in a more transparent structure. First of all, it seems that, when phrasing the set of rules to understand how black holes behave, neither quantum mechanics nor general relativity need any major overhauls, other than considering boundary conditions (such as the firewall transformation) more carefully. Below, we show one result that appears to make sense. The overall formulation is more coherent than what we had before, even if some questions have not yet been answered.
We emphasise that the ensuing black hole theory is a package deal; one has to unwrap all entities in the package, read their manuals, and understand how to deal with them, to see the entire picture.
16We have to define a way to characterise all states that together form its Hilbert space, after which we can contemplate the question how these states evolve. At first sight, this seems to be deceptively simple. The situation that we wish to get under control is a black hole with mass , where A is sufficiently large, so that it is well distinguishable from the objects that we allow to move in and out, whose typical energies are of the order of . These particles move in and out at a sufficiently slow rate to ensure that the black hole stays stationary on time scales considerably longer than .
In that case, we claim that, at first approximation, the description of the quantum states of the black hole, in a given stretch of time
17, can be formulated as follows:
- (1)
First, ignore the gravitational fields of the in- and out-going objects altogether. This means that we will be dealing with the space-time of an eternal black hole, as indicated in
Figure 1 and
Figure 2.
- (2)
This Penrose diagram is not yet suitable for our use because it exhibits two external regions, region
I and region
. We need only one such region, and therefore, as explained at the end of
Section 2, we divide space-time by the
isometry of the antipodal mapping; the points
and
are identified. This gives us the correct space-time topology.
- (3)
Regions
I and
however must be glued together smoothly, and the gluing prescription must fit snugly over the entire time period. This means that, as seen from region
I, region
seems to be moving backwards in time, implying that, in region
, also the energies are reversed. Ordinary QFT would not allow this, unless we renormalise the energies in region
: given any small subspace entirely embedded inside region
, this subspace must have a
maximum for the total energy it can contain, and if an outside observer sees a particle with energy
E in region
I, an observer travelling at its antipode in region
, observes an energy
in the same subspace. As seen from region
I, which may be close to the conventional vacuum, region
seems to describe its antipode as being almost full; it is close to its antivacuum. As long as we ignore direct gravitational interactions, this is completely consistent.
18- (4)
However, at the point where the two regions border to one another (at
, or
), the notions of vacuum and antivacuum are ill-defined. We plan not to ignore the gravitational interaction close to the origin, where it matters most. We ignore that only at space-time points sufficiently far separated from the horizons, where all particles have slowed down sufficiently, so that perturbative, renormalised gravity, in combination with Standard Model QFT, is all that is needed to see how these interact. A valid element of the black hole Hilbert space is now defined by concentrating on one Cauchy surface at fixed time only, say
. Left of the origin, where
x and
y are
, our state rapidly approaches the anti-vacuum. At the right, where
and
, the ordinary vacuum is approached. All black hole states are described by specifying how these modes connect at the origin
19. There will always be particles there.
- (5)
The states of the black hole Hilbert space can now be labelled constructively. We must start with one template state; say that this is the state where all fields (except the gravitational metric fields) take their lowest possible energy values in region
I and the highest possible energies in region
. It is not obvious whether this definition would be unique, but in practice, any one state might do as our template state; we go from there to all other states by using creation and annihilation operators. The well-known Bogolyubov transformation [
28,
29] will tell us how to do such constructions.
- (6)
Consider the addition of one particle with inwards momentum in region I. Spectator particles moving out will be dragged inwards by the Shapiro effect. As seen by an observer in region , the spectator particles will be seen to be moved outwards. The rule here is: the entire set of particle data on the Cauchy surface spanned by the past event horizon will be preserved. To be precise: the particle added in region I is seen to move the state there away from the vacuum state, while in the terminology to be applied in region , the same particle moves the state there towards the antivacuum. This sign switch matches the sign switch in our definition of energy in the two regions (after the shift with ), and its associated gravitational force. The firewall transformation tells us that we can remove the in-going particle if we displace all outgoing particles accordingly. This means that the displacement operators for the in-going particles can be identified with the position operators for the out-going particles, and mutatis mutandis we can identify for the in-going particles with the momenta of the out-going ones. This interchange is to be performed whenever the momentum operators become so large that we can no longer ignore their gravitational back reaction effects.
- (7)
A technical feature that was not yet strongly emphasised in this paper, is that the equations for the gravitational shift (Shapiro shift) that in-going particles bring about in the out-going ones—and vice versa—diagonalise if one subjects the in- and out-momenta, as well as the average in- and out positions, to expansions in spherical harmonics.
- (8)
Finally, we have the question how a black hole, with its exotic, antipodal, boundary condition, can ever form—or evaporate completely—and what the rules are here. This question has not yet been addressed, but we can sketch a reasonably plausible scenario, starting from the conventional description of a black hole being formed by matter. The imploding matter will rapidly form a firewall on the past horizon. A firewall transformation will be needed to replace the imploding matter by Hawking particles going out. The question is then, how the antipodal boundary condition is generated. How to formulate this elegantly is not yet known; we had been imagining that first a black hole seed is formed, a Planck-sized black hole, close to where the singularity would arise, before we apply the first firewall transformation.
Now this requires Planck length physics. It could be string theory or any other brand of magic, but this author strongly prefers to avoid ‘magic’. At this scale, quantum effects are large, so we can also think of having a small black hole be created by an intervening gravitational instanton. The instanton could be imagined as a configuration that is obtained by cutting out a small region of space-time in the shape of the interior of an sphere. Subsequently, the antipodes on the sphere are glued together, identified. The topology would be . Such an instanton would be topologically stable for all deformations barring scale transformations. Extra terms in the action would have to prohibit shrinking to a point.
This instanton might also be interpreted as describing directly a microscopic black hole with antipodal boundary conditions, which decays rapidly through Hawking radiation. Subsequently, we can send in more particles by having well-timed particle creation operators act on is quantum state. Thus, a larger black hole is obtained. We have to ensure that, from the earliest stages onwards, the description of the black hole obeys the conditions of the previous seven laws. The mathematical rules will have to be formulated a lot sharper than was done here. We expect that a unified scheme of interacting material objects should be invented, where matter is formed by black holes together with the energy quanta of quantised fields, or perhaps strings. It is tempting to believe that string theory will provide for such an avenue, but even if this were so, the schemes speculated on, up to today, appear to be unsatisfactory to this author.
5. Conclusions
As stated in the introduction, one important motivation for the theoretical study of black holes and their quantum features, was to arrive at new insights concerning physics at the Planck scale.
In our attempts to do things accurately, one of the first things noted is the reversal of time where regions
I and
in the Penrose diagram, are glued together. This is because a time translation for the external observer generates a Lorentz transformation near the center of the diagram. Consequently, if one regards the Penrose diagram after a (long or short) lapse of time, one sees the Cauchy surfaces pivot around the origin, see
Figure 2.
It may sound odd that this time reversal takes place during the entire lifetime of the black hole, which is much longer than the time scale that can be visualised in the diagram. This is because Lorentz transformations form a non-compact group. It also implies that one cannot ignore its consequences. In particular, if one wants to study the stationary modes—the energy eigenstates—of the black hole.
After a strong Lorentz boost, one finds that particles may accumulate towards, or separate from, the centre of the diagram. One of our observations is that the accumulation of particles near the origin may—and should—be transformed away, a procedure described here as the ‘firewall transformation’. It replaced these accumulated in-particles by out particles or vice versa. The procedure works, but there may be an important side effect. We ignored this in earlier papers, but it seems inevitable that, when distant observers send in particles with positive energies, the energies may switch sign as well, when a local observer sees them appearing in region . The sign switch in the energy comes about when one wishes to write the mapping from the familiar world around a black hole to the local world surrounding its horizons, by means of a unitary operation. The time-energy relation in the quantum states, expressed by their phases would ruin unitarity if t changes sign but not E. Particles can make transitions through the wormhole from I to and back (just because of the Shapiro effect), which is why we do not believe that the energy sign flip can be avoided. Total energy must be conserved.
We were forced to speculate on a limiting energy, , so that the particles in region can have positive energies, , while energy conservation is maintained. can be related to the smallest time step, , and this is where deterministic quantum mechanics may enter. Deterministic quantum mechanics leaves some freedom in defining what the smallest time step is, so there may be still some room for speculations concerning the value of . The theory is entirely invariant under .
The state with energy will be called the ‘antivacuum’. The antivacuum in region may actually represent all those particles that filled the black hole during its implosion in the distant past.
As yet in a modest way, our work seems to pay off. Quantum mechanics is likely to demand such a thing as an upper limit for the energy on any compact subset of 3-space—even when disregarding the direct effects of gravity—leading to the notion of an antivacuum. In elementary exercises involving the nature of quantum theory in general, the notion of antivacuum was hinted at, if only to account for the existence of a smallest time scale for defining local interactions. Limits on the energy density of quantum states near the Planck scale have been speculated about a lot; here we see the necessity of this, although the mathematical details are still not quite clear.
How does gravity act in region ? The answer should follow in a straightforward way by analysing the transformations from the asymptotic Minkowski space to the geometry of region , or even simpler, by transforming I to and back. The doctrine demands that we start by ignoring the gravitational effects of the quantum excitations that are being considered, just because the masses and energies of these quantum particles were systematically assumed to be orders of magnitude smaller than that of the black hole itself. As the first step towards further refinement, one can then add the gravitational force perturbatively as one can add the other Standard Model interactions. The non-perturbative aspects of gravity are most acute in the immediate vicinity of the horizons, and those were taken care of accurately by taking the Shapiro shifts into account: the firewall transformation.
We found that in describing interacting beams of particles at Planckian energies, firewalls may be created and subsequently removed by utilising the firewall transformation. A super-Planckian particle may come with the gravitational analogue of a shock wave. General Relativity will allow us to remove this shock wave by a cut-and-paste procedure combined with a local coordinate transformation, after which particles going one way (inwards or outwards) are replaced by particles going in the opposite direction, the rules here being precisely dictated by standard physics.
Needless to say, there are still many questions left: a systematic and complete formalism for the entire set of physical degrees of freedom at Planckian scales, is still missing. Unlike some procedures in string theory and M theory, we insist on maintaining fundamental aspects of locality, which should considerably constrain the amount of freedom we have in constructing our theory. More than half a century ago, physicists had similar difficulties in reconciling quantum mechanics with special relativity. The insight of how to do this right became clear gradually: quantum field theory (QFT). This theory became a beautiful synthesis between simplicity and complexity; the theory was simple enough to enable us to categorise all possible scenarios, and sufficiently complex to allow something as intricate as an entire universe with galaxies, stars, planets and life all controlled by its equations.
We can only hope that the eventual synthesis of quantum mechanics with general relativity will be equally simple and complex to give us an even more detailed understanding.