The Radiative Δ(1600) → γN Decay in the Light-Cone QCD Sum Rules

Abstract

Within the framework of the light-cone QCD sum rules method (LCSR’s), the radiative $\Delta \left(1600\right)\to \gamma N$ decay is studied. In particular, the magnetic dipole moment $G_M^1\left(0\right)$ and the electric quadrupole moment $G_E^1\left(0\right)$ are estimated. We also calculate the ratio $R_{EM}=-\frac{G_E^1\left(0\right)}{G_M^1\left(0\right)}$ and the decay rate. The predicted multipole moments and the decay rate strongly agree with the existing experimental results as well as with the other available phenomenological approaches.

1. Introduction

Today, more than twenty excited baryonic states have been classified within octet and decuplet sectors. The experimental and theoretical study of the electromagnetic properties of these baryonic states and their resonances is one of the main active research areas in nuclear and low-energy particle physics. The electromagnetic transitions within given multiplets provide a possible source of information on the long-range interaction in the domain of quark confinement and represent a possible test for the quantum chromodynamics (QCD) in the low-energy regime.

One of the important electromagnetic properties is the electromagnetic transition form factors, which play an extremely important role in studying the internal structure of baryons, such as size, shape, magnetization, charge, and current distributions [1,2,3].

Recently, there has been increased interest in measuring the electromagnetic structures of the octet and decuplet baryons around their first excitations. Very clean electromagnetic probes for the excitation of these baryons are now available, and their analysis has been performed by various theoretical groups fueled by a large number of experiments planned and already running in several medium-energy hadron and electron accelerator centers including CLAS (Jefferson Lab), MAMI (Mainz), ELSA (Bonn), LEGS (Brookhaven), BATES (MIT), and Spring-8 (Japan) [4,5,6,7,8,9,10,11,12]. Furthermore, polarized beams and targets are now available. These possibilities provide new approaches to the calculation of the ratio of the electric and magnetic dipoles, specifically polarization transfer and beam-target asymmetry.

$N\left(939\right)$ and $\Delta \left(1232\right)$ are the two lowest octet and decuplet baryon states. The reason for studying the nucleon $N\left(939\right)$ to $\Delta \left(1232\right)$ transition is that $\Delta \left(1232\right)$ is a dominant nucleon resonance, so it will be very simple task to identify its properties experimentally through the spin parity selection rules. Moreover, their descriptions and properties play a very important role in our understanding of strong interactions.

$\Delta \left(1232\right)$ has only two decay channels: $\Delta \left(1232\right)\to N\pi$, which is dominant, and $\Delta \left(1232\right)\to \gamma N$, with a branching ratio of less than $1\%$ [13]. Because of the small branching ratio, the electromagnetic transition $\gamma N\leftrightarrows \Delta \left(1232\right)$ at the real photon point has been the subject of intense studies starting from the early 1990s [14,15,16,17,18,19,20].

In recent years, with the energy range expanding and the precision increasing in the electron beam facilities mentioned above, it is possible now to detect the electromagnetic structure of the baryon resonances outside its first resonant region. In light of the current conditions, all theoretical studies and contributions for such baryon resonances will assist in establishing their structural properties. For instance, $\Delta \left(1600\right)$, which is considered the first excited state of $\Delta \left(1232\right)$, can be among those interesting resonances that deserve to be understood. However, it has not been studied in detail so far.

Referring to the Particle Data Group [21], $\Delta \left(1600\right)$ is a three-star resonance that decays likely to $\Delta \left(1600\right)\to N\left(939\right)\pi$, $\Delta \left(1600\right)\to N\left(1440\right)\pi$, and $\Delta \left(1600\right)\to \Delta \left(1232\right)\pi$. For this reason, the electromagnetic properties of $\Delta \left(1600\right)\to \gamma N\left(939\right)$ decay attract much interest both theoretically [22,23] and experimentally [24].

Although the form factors related to the electro-production of this resonance were investigated in the past through a constituent quark model [25], within the last few years, this resonance was involved in the meson–baryon reaction analysis models [26]. Moreover, experiments confirm that the $\Delta \left(1600\right)$ resonance could be extremely important in double pion production in nucleon–nucleon collisions [27]. Furthermore, the $\Delta \left(1600\right)$ resonance has been investigated in lattice QCD simulations [28], QCD sum rules [29], and also a covariant spectator constituent quark model [30]. Very recently, we studied the transition form factors of ${\gamma }^{*}N\to \Delta \left(1600\right)$ for the virtual photon case in the light-cone sum rules method [31].

However, the experimental access for the $\Delta \left(1600\right)$ resonance is still limited; therefore, a theoretical study would be very appropriate. Consequently, in this work, in order to better understand the electromagnetic structure of the $\Delta \left(1600\right)$, the radiative decay $\Delta \left(1600\right)\to \gamma N$ for the real photon case will be studied using the light-cone QCD sum rules (LCSR) method. The magnetic dipole moment $G_M^1\left(0\right)$, electric quadrupole moment $G_E^1\left(0\right)$, the ratio $R_{EM}=-\frac{G_E^1\left(0\right)}{G_M^1\left(0\right)}$, as well as the decay width of this channel will be calculated. With this in mind, the rest of the paper is arranged as follows. In Section 2, the LCSR for the form factors $G_1^1$ and $G_2^1$ of $\Delta \left(1600\right)\to \gamma N$ decay is obtained with the contribution up to twist-4 LCDA. Next, the LCSRs for the magnetic dipole and electric quadrupole moments of the decay are calculated. The numerical analysis of the obtained LCSRs is conducted in Section 3. The last section of this paper contains a summary and concluding remarks.

2. LCSRs for $\Delta \left(\mathbf{1600}\right)\to \mathbf{\gamma }\mathbf{N}$ Decay

As the $\Delta \left(1600\right)$ resonance bears many common properties with the $\Delta \left(1232\right)$ baryon, such as spin and isospin, in order to study the $\Delta \left(1600\right)\to \gamma N$ decay, we will use the LCSR formalism, which was successfully used to study the $\Delta \left(1232\right)\to \gamma N$ decay [23]. In studying the $\Delta \left(1600\right)\to \gamma N$ decay, we will use the notations $G_1^0\left(0\right)$, $G_2^0\left(0\right)$, and ${\Delta }_0$ for the $\Delta \left(1232\right)$, and $G_1^1\left(0\right)$, $G_2^1\left(0\right)$, and ${\Delta }_1$ for $\Delta \left(1600\right)$, respectively.

To investigate the $\Delta \left(1600\right)\to \gamma N$ decay form factors with the LCSR method, it is appropriate to consider the correlation function:

$${\mathsf{\Pi }}^{\mu \nu }(p,q)=i^2\int d^{4}x\int d^{4}y{e}^{ipx+iqy}\langle 0\mid \mathcal{T}\left\{{\eta }^{\mu }\left(x\right)j_{em}^{\nu }\left(y\right)\overline{\eta }\left(0\right)\right\}\mid 0\rangle ,$$

(1)

where ${\eta }^{\mu }$ is the interpolating current with the same quantum numbers for $\Delta \left(1232\right)$ and $\Delta \left(1600\right)$, $\eta$ is the interpolating current for the nucleon, and $j_{em}^{\nu }\left(y\right)$ is the iso-vector part $j_{em}^{\nu (I=1)}=\frac{1}{2}\left(e_u-e_d\right)\left(\overline{u}{\gamma }_{\mu }u-\overline{d}{\gamma }_{\mu }d\right)$, with $e_d=-1/3$ and $e_u=2/3$ being the quark charges.

Because the $\Delta \left(1232\right)$ and $\Delta \left(1600\right)$ states have the same quantum numbers, the interpolating current for these states is also the same and interacts simultaneously with the $\Delta \left(1232\right)$ and $\Delta \left(1600\right)$ states. It is given by the following expression [31]:

$${\eta }^{\mu }\left(x\right)=\frac{1}{\sqrt{3}}{\epsilon }^{abc}\left[2\left(u^a\left(x\right)\mathcal{C}{\gamma }^{\mu }{d}^b\left(x\right)\right)u^c\left(x\right)+\left(u^a\left(x\right)\mathcal{C}{\gamma }^{\mu }{u}^b\left(x\right)\right)d^c\left(x\right)\right],$$

(2)

where $\mathcal{C}$ is the matrix of charge conjugation, while $a,b,c$ are color indices, and ${\epsilon }^{abc}$ is the three-dimensional Levi–Civita symbol.

To construct the LCSRs, we need the distribution amplitudes (DAs) of a photon. According to the LCSR method, operator product expansion (OPE) is obtained near the light cone $x^2\simeq 0$, and the non-perturbative dynamics are parameterized by the LCDAs, which determine the nonlocal operators’ matrix elements among vacuum and one-particle state. The expansion next to the light cone is an expansion in the twist operators instead of an expansion in the mass dimension, as in the traditional QCD sum rules. Twist operator is defined as the difference between the mass dimension and the spin of a traceless and totally symmetric local operator.

Accordingly, the correlation function defined in Equation (1) can be written as follows by introducing the electromagnetic background field of the nucleon $F_{\mu \nu }$:

$${\mathsf{\Pi }}^{\mu \nu }\left(p,q\right)e_{\nu }^{\left(\lambda \right)}=i\int d^{4}x{e}^{ipx}{\langle 0\mid \mathcal{T}\left\{{\eta }^{\mu }\left(x\right)\overline{\eta }\left(0\right)\right\}\mid 0\rangle }_F,$$

(3)

where $e_{\nu }^{\left(\lambda \right)}$ is the four-polarization vector of the emitted photon, $q·e_{\nu }^{\left(\lambda \right)}=0$, and the subscript F means that the vacuum expectation value should be evaluated in the background field $F_{\mu \nu }$.

This correlation function is calculated in two different regions. The hadronic part is calculated in $p^2\simeq m_{{\Delta }_k}^2$ and ${(p+q)}^2\simeq m_N^2$ regions, where $k=0$ and $k=1$ correspond, respectively, to the ground $\Delta \left(1232\right)$ and first $\Delta \left(1600\right)$ radial excitation of the $\Delta$ baryon. On the other hand, the correlation function can be computed in the deep Euclidean region $p^2\ll 0$ and ${(p+q)}^2\ll 0$ using the OPE method in terms of the photon DAs with an increasing twist. The sum rules for the related physical quantities are then obtained by matching the same Lorentz structures of these two representations through a dispersion relation.

By using the procedure mentioned above, the hadronic part is obtained by saturating the above correlation function with complete sets of baryonic states having the same quantum numbers as the interpolating current:

$$\begin{array}{cc}\hfill {\mathsf{\Pi }}^{\mu \nu }\left(p,q\right)e_{\nu }^{\left(\lambda \right)}=& \sum _{s,s^{\prime }}\sum _{k=0}^1\frac{1}{m_{{\Delta }_k}^2-p^2}\frac{1}{m_N^2-p^{\prime 2}}\langle 0\mid {\eta }_{\mu }\left(0\right)\mid {\Delta }_k(p,s)\rangle \times \hfill \\ \hfill & \langle {\Delta }_k(p,s)\mid j_{\nu }^{em}\left(0\right)\mid N(p^{\prime },s^{\prime })\rangle \langle N(p^{\prime },s^{\prime })\mid \overline{\eta }\left(0\right)\mid 0\rangle e_{\nu }^{\left(\lambda \right)},\hfill \end{array}$$

(4)

where s and $s^{\prime }$ are the spins of the ${\Delta }_k$ and nucleon baryons, respectively, $p^{\prime }=p+q$ is the nucleon initial momentum, p is the ${\Delta }_k$ final momenta, and q is the momentum of the emitted photon.

The matrix elements in Equation (4) are parameterized in terms of the residues ${\lambda }_N$ and ${\lambda }_{{\Delta }_k}$:

$$\langle 0\mid {\eta }_{\mu }\left(0\right)\mid {\Delta }_k(p,s)\rangle =\frac{{\lambda }_{{\Delta }_k}}{{\left(2\pi \right)}^2}{u}_{\mu }(p,s),$$

(5)

$$\langle 0\mid \eta \left(0\right)\mid N(p^{\prime },s^{\prime })\rangle =\frac{{\lambda }_N}{{\left(2\pi \right)}^2}u(p^{\prime },s^{\prime }),$$

(6)

where $u_{\mu }(p,s)$ is a Rarita–Schwinger spinor.

On the other hand, the matrix element $\langle {\Delta }_k(p,s)\left|j_{\nu }^{em}\left(0\right)\right|N(p^{\prime },s^{\prime })\rangle$ can be parameterized in terms of a set of form factors as follows:

$$\begin{array}{cc}\hfill \langle {\Delta }_k(p,s)\left|j_{\nu }^{em}\left(0\right)\right|N(p^{\prime },s^{\prime })\rangle =& {\overline{u}}_{\alpha }(p,s){\Gamma }_{\alpha \nu }{\gamma }_{5}u(p^{\prime },s^{\prime }),\hfill \end{array}$$

(7)

Here, the vertex ${\Gamma }_{\alpha \nu }$ defines the six invariant transition form factors $G_1^0\left(0\right)$, $G_1^1\left(0\right)$, $G_2^0\left(0\right)$, $G_2^1\left(0\right)$, $G_3^0\left(0\right)$, and $G_3^1\left(0\right)$:

$$\begin{array}{cc}\hfill {\Gamma }_{\alpha \nu }& =G_1^k\left(0\right)\left(g_{\alpha \nu }\cancel{q}-q_{\alpha }{\gamma }_{\nu }\right)+G_2^k\left(0\right)\left(g_{\alpha \nu }q·\left(p+\frac{q}{2}\right)-q_{\alpha }{\left(p+\frac{q}{2}\right)}_{\nu }\right)\hfill \\ \hfill & +G_3^k\left(0\right)\left(q_{\alpha }{q}_{\nu }-q^2{g}_{\alpha \nu }\right).\hfill \end{array}$$

(8)

Inserting the general expression for the transition matrix elements, and performing a summation over the spins of Rarita–Schwinger spinors with the help of the equation, yields:

$$\begin{array}{cc}\hfill \sum _s{u}_{\mu }^{\left(s\right)}\left(p\right){\overline{u}}_{\nu }^{\left(s\right)}\left(p\right)=& -(\cancel{p}+m_{{\Delta }_k})\left[g_{\mu \nu }-\frac{1}{3}{\gamma }_{\mu }{\gamma }_{\nu }-\frac{2p_{\mu }{p}_{\nu }}{3m_{{\Delta }_k}^2}+\frac{p_{\mu }{\gamma }_{\nu }-p_{\nu }{\gamma }_{\mu }}{3m_{{\Delta }_k}}\right],\hfill \end{array}$$

(9)

For the hadronic side, the correlation function can be expressed as:

$$\begin{array}{cc}\hfill {\mathsf{\Pi }}^{\mu \nu }\left(p,q\right)e_{\nu }^{\left(\lambda \right)}=& -e_{\nu }^{\left(\lambda \right)}\sum _{k=0}^1\frac{{\lambda }_{{\Delta }_k}{\lambda }_N}{(m_{{\Delta }_k}^2-p^2)(m_N^2-p^{\prime 2})}(\cancel{p}+m_{{\Delta }_k})\times \hfill \\ \hfill & \left[g_{\alpha }^{\mu }-\frac{1}{3}{\gamma }^{\mu }{\gamma }_{\alpha }-\frac{2p^{\mu }{p}_{\alpha }}{3m_{{\Delta }_k}^2}+\frac{p^{\mu }{\gamma }_{\alpha }-p_{\alpha }{\gamma }^{\mu }}{3m_{{\Delta }_k}}\right]{\Gamma }^{\alpha \nu }{\gamma }_5(\cancel{p}+\cancel{q}+m_N).\hfill \end{array}$$

(10)

After the necessary contractions, this technique leads us to the hadronic side’s final representation, which contains many independent Lorentz structures $\mathcal{LS}$. Here, it should be noted that these Lorentz structures contain also spin $\frac{1}{2}$ contribution parts. However, in this work, we choose the independent Lorentz structures; in this way, they do not receive contributions from spin minus $\frac{1}{2}$ states. Following [23], we choose:

$$\begin{array}{cc}\hfill {\mathcal{LS}}_1=& 4\left(qp{e}^{\mu }\cancel{q}\cancel{p}{\gamma }_5-ep{q}^{\mu }\cancel{q}\cancel{p}{\gamma }_5\right)-qp\left({\gamma }^{\mu }\neg e\cancel{q}\cancel{p}{\gamma }_5\right),\hfill \\ \hfill {\mathcal{LS}}_2=& q^{\mu }\cancel{e}\cancel{q}\cancel{p}{\gamma }_5,\hfill \end{array}$$

(11)

which contain only the contributions of spin $\frac{3}{2}$ states. With this ordering, the correlation function can be written as:

$$\begin{array}{cc}\hfill {\mathsf{\Pi }}^{\mu \nu }\left(p,q\right)e_{\nu }^{\left(\lambda \right)}=& -\sum _{k=0}^1\frac{{\lambda }_{{\Delta }_k}{\lambda }_N}{\left(m_{{\Delta }_k}^2-p^2\right)\left(m_N^2-p^{\prime 2}\right)}\times \left[\left(\frac{G_1^k\left(0\right)}{16{\pi }^4}\right){\mathcal{LS}}_1+\left(\frac{G_2^k\left(0\right)}{64{\pi }^4}\right){\mathcal{LS}}_2\right].\hfill \end{array}$$

(12)

On the other hand, the correlation function ${\mathsf{\Pi }}^{\mu \nu }(p,q)$ of Equation (1) is to be re-calculated at the deep Euclidean region, where $p^2\ll 0$ and ${(p+q)}^2\ll 0$ by using the OPE in terms of the photon DAs with an increasing twist. For this purpose, we use the explicit expressions of the interpolating currents for both baryons with the spin $J=3/2$ and $J=1/2$. The photon DAs are the main non-perturbative ingredients of LCSRs and they are calculated up to twist-4 [23]. Using the expression for photon DAs given in [23], applying the quark–hadron duality ansatz and performing double Borel transformations with respect to the variable $p^2$, we obtain:

$$\begin{array}{cc}\hfill {\mathsf{\Pi }}^{\mu \nu }\left(p,q\right)e_{\nu }^{\left(\lambda \right)}=& {\mathsf{\Pi }}_1^{\mathit{QCD}}\left(M^2\right){\mathcal{LS}}_1+{\mathsf{\Pi }}_2^{\mathit{QCD}}\left(M^2\right){\mathcal{LS}}_2,\hfill \end{array}$$

(13)

or more explicitly:

$$\begin{array}{cc}\hfill {\mathsf{\Pi }}^{\mu \nu }\left(p,q\right)e_{\nu }^{\left(\lambda \right)}& =(e_u-e_d)\left[-\frac{u\overline{u}}{64{\pi }^4}{M}^4\left(1-e^{-S_0/M^2}\left(1+\frac{S_0}{M^2}\right)\right)+{\mathcal{I}}_1\right]{\mathcal{LS}}_1\hfill \\ \hfill & -\frac{(e_u-e_d)}{{\pi }^2}\langle q\overline{q}\rangle \left[\frac{u}{6}\phi \left(u\right)M^4\left(1-e^{-S_0/M^2}\left(1+\frac{S_0}{M^2}\right)\right)\right.\hfill \\ \hfill & +\left.\frac{u\mathbb{A}\left(u\right)}{8}{M}^2\left(1-e^{-S_0/M^2}\right)+{\mathcal{I}}_2\right]{\mathcal{LS}}_2,\hfill \end{array}$$

(14)

where

$$\begin{array}{cc}\hfill \mathbb{A}\left(u\right)& =40u^2{\overline{u}}^2\left(3\kappa -{\kappa }^{+}+1\right)+8({\zeta }_2^{+}-3{\zeta }_2)\left[u\overline{u}(2+13u\overline{u})\right.\hfill \\ \hfill & +\left.2u^3(10-15u+6u^2)ln\left(u\right)+2{\overline{u}}^3(10-15\overline{u}+6{\overline{u}}^2)ln\left(\overline{u}\right)\right],\hfill \end{array}$$

(15)

$u=\frac{m_{{\Delta }_1}^2}{m_{{\Delta }_1}^2+m_N^2}$, $\overline{u}=1-u$, $\phi \left(u\right)=6\chi \left(\mu \right)u(1-u)$ is the leading photon wave function, $\chi \left(\mu \right)$ is the magnetic susceptibility of the quark condensate, and the expressions for ${\mathcal{I}}_1$ and ${\mathcal{I}}_2$ and the numerical values of the relevant parameters are given in [23].

After calculating both sides of the correlation function, hadronic and QCD, at this point, we matched the coefficients of the chosen structures from both sides of Equations (12) and (13). To suppress the higher states’ contributions and continuum contributions, we applied Borel transformation over the variables $p^2$ and $p^{\prime 2}$; then, we found two coupled sum rule equations for the N and ${\Delta }_k$’s states:

$$\begin{array}{cc}\hfill {\lambda }_{{\Delta }_0}{\lambda }_N{e}^{-{\mu }^2/M^2}\frac{G_1^0\left(0\right)}{32{\pi }^4}+{\lambda }_{{\Delta }_1}{\lambda }_N{e}^{-{\mu }^{\prime 2}/M^2}\frac{G_1^1\left(0\right)}{32{\pi }^4}=& {\mathsf{\Pi }}_1^{\mathit{QCD}}\left(M^2\right),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\lambda }_{{\Delta }_0}{\lambda }_N{e}^{-{\mu }^2/M^2}\frac{G_2^0\left(0\right)}{64{\pi }^4}+{\lambda }_{{\Delta }_1}{\lambda }_N{e}^{-{\mu }^{\prime 2}/M^2}\frac{G_2^1\left(0\right)}{64{\pi }^4}=& {\mathsf{\Pi }}_2^{\mathit{QCD}}\left(M^2\right),\hfill \end{array}$$

(17)

where $M^2$ is the Borel mass parameter, and ${\mathsf{\Pi }}_1^{\mathit{QCD}}\left(M^2\right)$, ${\mathsf{\Pi }}_2^{\mathit{QCD}}\left(M^2\right)$ are the invariant functions of ${\mathcal{LS}}_1$ and ${\mathcal{LS}}_2$ structures, respectively, with ${\mu }^2=\frac{2m_{{\Delta }_0}^2{m}_N^2}{m_{{\Delta }_0}^2+m_N^2}$, and ${\tilde{\mu }}^2=\frac{2m_{{\Delta }_1}^2{m}_N^2}{m_{{\Delta }_1}^2+m_N^2}$.

As can be seen from Equations (16) and (17), there are four unknown decay form factors. Two of them, $G_1^0\left(0\right)$ and $G_2^0\left(0\right)$, belong to $\Delta \left(1232\right)$, and the other two form factors, $G_1^1\left(0\right)$ and $G_2^1\left(0\right)$, correspond to $\Delta \left(1600\right)$. To obtain the decay form factors $G_1^1\left(0\right)$ and $G_2^1\left(0\right)$, we differentiate both sides of Equation (16) with respect to $\frac{d}{d(-1/M^2)}$, and then multiply the original equation by ${\mu }^2$ and then subtract. In the end, we obtain the first decay form factor $G_1^1\left(0\right)$. Similarly, from Equation (17), we can obtain the second decay form factor $G_2^1\left(0\right)$:

$$\begin{array}{cc}\hfill G_1^1\left(0\right)=& \frac{32{\pi }^4}{{\lambda }_{{\Delta }_1}{\lambda }_N({\tilde{\mu }}^2-{\mu }^2)}{e}^{{\tilde{\mu }}^2/M^2}\left({\mu }^2{\mathsf{\Pi }}_1\left(M^2\right)-{{\mathsf{\Pi }}^{\prime }}_1\left(M^2\right)\right),\hfill \\ \hfill G_2^1\left(0\right)=& \frac{64{\pi }^4}{{\lambda }_{{\Delta }_1}{\lambda }_N({\tilde{\mu }}^2-{\mu }^2)}{e}^{{\tilde{\mu }}^2/M^2}\left({\mu }^2{\mathsf{\Pi }}_2\left(M^2\right)-{{\mathsf{\Pi }}^{\prime }}_2\left(M^2\right)\right),\hfill \end{array}$$

(18)

where ${{\mathsf{\Pi }}^{\prime }}_1\left(M^2\right)$ and ${{\mathsf{\Pi }}^{\prime }}_2\left(M^2\right)$ are the first derivatives of ${\mathsf{\Pi }}_1\left(M^2\right)$ and ${\mathsf{\Pi }}_2\left(M^2\right)$ with respect to $\frac{d}{d(-1/M^2)}$.

As already mentioned in the Introduction, since we are considering a decay channel with a real photon, naturally, the terms proportional to $G_3^k$ are equal to zero. Therefore, for analyzing $\Delta \left(1600\right)\to \gamma N$ decay, we need only to know the values of the decay form factors $G_1^1\left(0\right)$ and $G_2^1\left(0\right)$ at $q^2=0$. However, from an experimental point of view, the multipole moments are more helpful than the decay form factors $G_1^1\left(0\right)$ and $G_2^1\left(0\right)$. The relations among the decay form factors $G_1^1\left(0\right)$ and $G_2^1\left(0\right)$, and the multipole moments at $q^2=0$, are given as [20]:

$$\begin{array}{cc}\hfill G_M^1\left(0\right)& =\frac{m_N}{3}\left[(3m_{{\Delta }_1}+m_N)\frac{G_1^1\left(0\right)}{m_{{\Delta }_1}}+(m_{{\Delta }_1}-m_N)G_2^1\left(0\right)\right],\hfill \\ \hfill G_E^1\left(0\right)& =\frac{m_N}{3}\left[(m_{{\Delta }_1}-m_N)\left(\frac{G_1^1\left(0\right)}{m_{{\Delta }_1}}+G_2^1\left(0\right)\right)\right].\hfill \end{array}$$

(19)

3. Numerical Analysis

In the framework of the LCSR strategy discussed in the previous section, the numerical values of the multipole moments of Equation (19) can be obtained via Equation (18). As usual in numerical computations, the LCSR approach incorporates different input parameters that have to be settled. The asymptotic expression for the leading photon wave function $\phi \left(u\right)=6\chi \left(\mu \right)u(1-u)$ is chosen. This choice gives a reasonable result for the proton magnetic moment at a renormalization scale ${\mu }^2=1{\mathrm{GeV}}^2$, with the magnetic susceptibility of the quark condensate $\chi \left(\mu \right)=3.15\pm 0.3Ge{V}^{-2}$ [23]. Furthermore, we take the numerical values for the residues of the baryons with spin $1/2$ and $3/2$, respectively, $|{\lambda }_N{|=\left(2\pi \right)}^2(0.033\pm 0.009)Ge{V}^3$ and $|{\lambda }_{{\Delta }_1}{|=\left(2\pi \right)}^2(0.057\pm 0.0016)Ge{V}^3$, which are given in [22,31,32]. In the numerical computations, one should take an overall current normalization constant $1/\sqrt{3}$. This factor arises in the current normalization of ${\eta }_{{\Delta }_1}$ versus ${\eta }_{{\Delta }_0}$ of Equation (2). The other constants entering the photon DAs can be found in Table 1 of [23].

The LCSR method for the electromagnetic form factors also contains two more unphysical auxiliary parameters: the Borel parameter $M^2$ and the continuum threshold $S_0$. The measurable physical quantities, i.e., the magnetic dipole and electric quadrupole moments, must be independent of these auxiliary parameters. Typically, the continuum threshold indicates the energy scale at which the excited states and continuum begin to add their contribution to the correlation function. There are several approaches to detect this parameter. The method that we have used in this work is to change this parameter in a reasonable range until a Borel window starts to appear and the predictions of the electromagnetic form factors are independent of these unphysical auxiliary parameters [33]. We have varied both the Borel parameter and the continuum threshold in different regions. We found $S_0\approx 2{\mathrm{GeV}}^2$, while the working region for $M^2$ is chosen on the one hand to ensure that the contributions of higher twists are suppressed and on the other hand to keep the contributions of higher states small enough. This work suggests the interval $3{\mathrm{GeV}}^2\le M^2\le 4{\mathrm{GeV}}^2$.

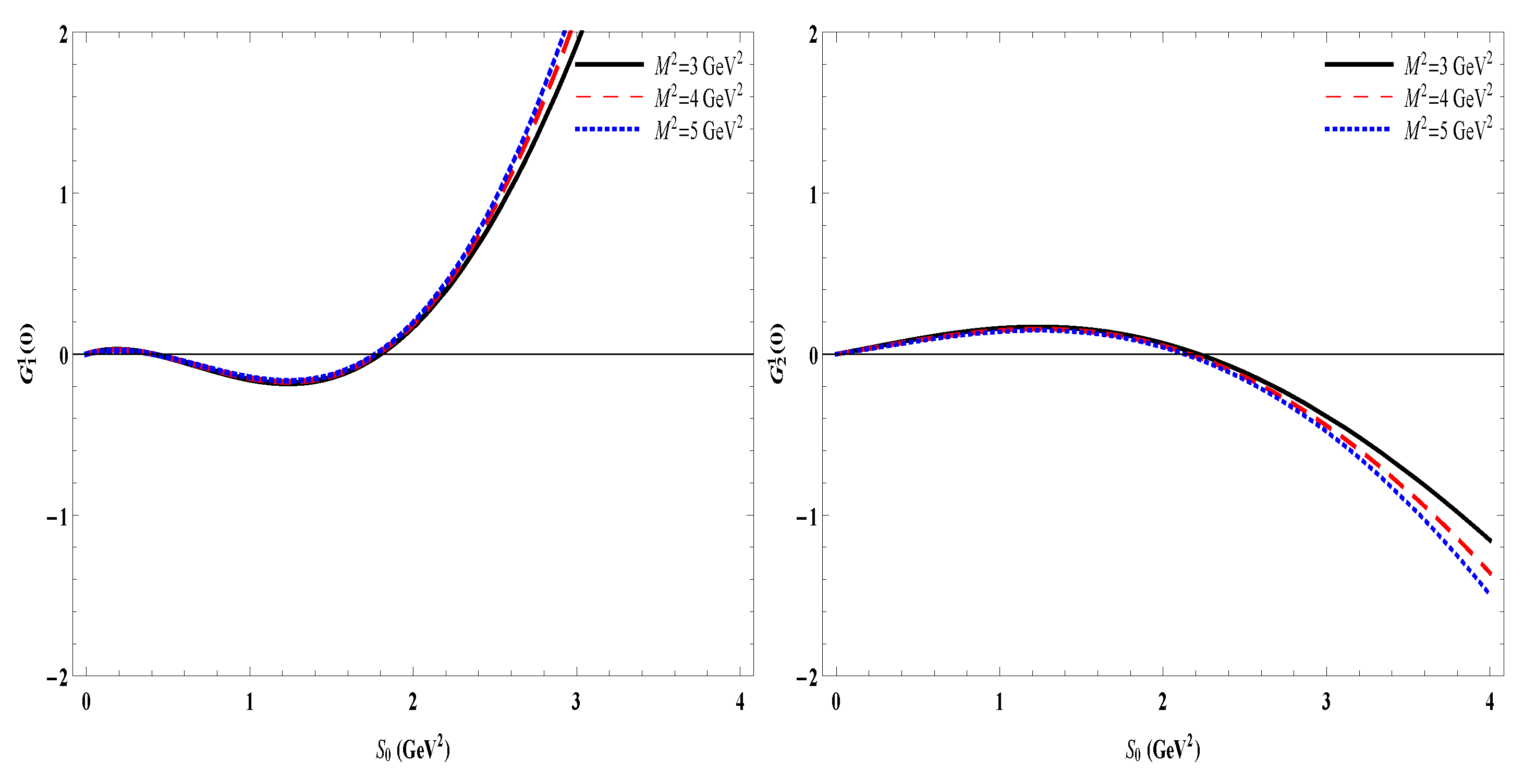
To visualize these working regions, Equation (18) is shown in Figure 1 as a function of the continuum threshold value $S_0$ at different Borel mass parameters $M^2$. We found that both $G_1^1\left(0\right)$ and $G_2^1\left(0\right)$ are relatively stable in the interval when $0{\mathrm{GeV}}^2\le S_0\le 2.2{\mathrm{GeV}}^2$, while both $G_1^1\left(0\right)$ and $G_2^1\left(0\right)$ are unstable when $S_0\ge 2.2{\mathrm{GeV}}^2$. Accordingly, we choose the working region for the continuum threshold to be $1.8{\mathrm{GeV}}^2\le S_0\le 2.2{\mathrm{GeV}}^2$.

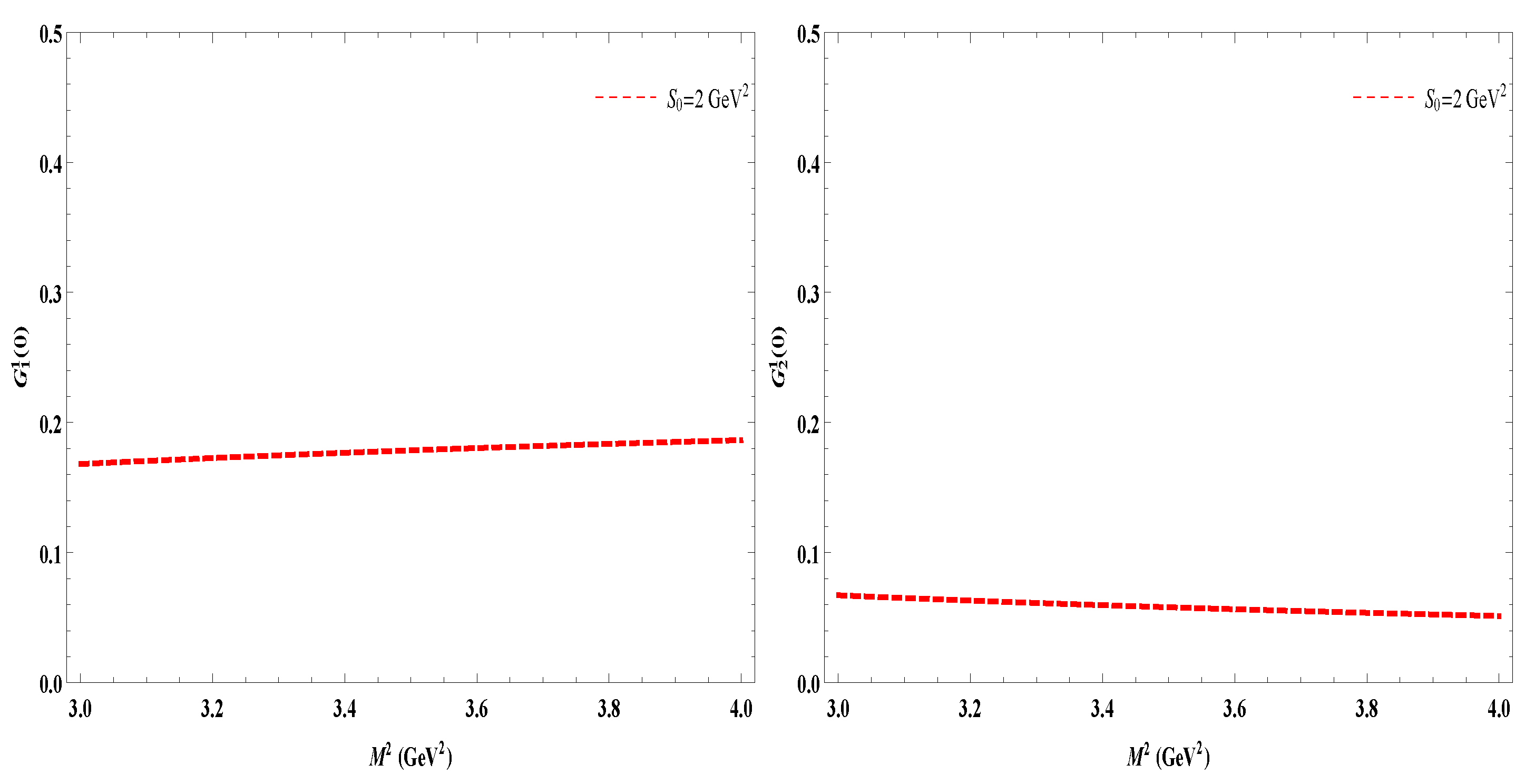
In contrast, in Figure 2, we plotted the LCSR results for the decay form factors $G_1^1\left(0\right)$ and $G_2^1\left(0\right)$ at a fixed value $S_0=2{\mathrm{GeV}}^2$, and for various values of $M^2$. From this figure, it is obvious that both of the decay form factors are stable with respect to the variation of $M^2$. Hence, in the following analysis, the ranges for $S_0$ and $M^2$ discussed above are used. Finally, in Figure 3, we present the dependencies of $G_M^1\left(0\right)$, $G_E^1\left(0\right)$, and $R_{EM}=-\frac{G_E^1\left(0\right)}{G_M^1\left(0\right)}$ on $M^2$ at fixed $S_0=2{\mathrm{GeV}}^2$. The figure shows that the sum rules for $G_M^1\left(0\right)$, $G_E^1\left(0\right)$, and $R_{EM}=-\frac{G_E^1\left(0\right)}{G_M^1\left(0\right)}$ are of negligible dependence on the variation of $M^2$ at fixed value $S_0=2{\mathrm{GeV}}^2$. The obtained numerical values in dimensionless units are $G_M^1\left(0\right)\simeq 0.225$ and $G_E^1\left(0\right)\simeq 0.035$, respectively, while $R_{EM}\left(0\right)\simeq -15\%$.

Our prediction for $G_M^1\left(0\right)\simeq 0.225$ strongly agrees with the theoretical and experimental data $G_M^1\left(0\right)\simeq 0.202$ shown in Table 3 of [30].

In the final part of this section, it is appropriate to present the decay width for the radiative decay under consideration. By considering the decay matrix element in Equation (7) and using the results of Equation (19), one can obtain the following formula for the width of the corresponding decay:

$$\Gamma \left(\Delta \left(1600\right)\to \gamma N\right)=3\frac{\alpha }{32}\frac{{\left(m_{{\Delta }_1}^2-m_N^2\right)}^3}{m_{{\Delta }_1}^3{m}_N^2}\left({\left(G_M^1\left(0\right)\right)}^2+3{\left(G_E^1\left(0\right)\right)}^2\right).$$

(20)

Using the obtained numerical values of the magnetic dipole and electric quadrupole moments as well as the input baryon masses, the result that we obtained for the decay width is $\Gamma \left(\Delta \left(1600\right)\to \gamma N\right)=0.0306$ MeV. Meanwhile, the predicted branching ratio of this channel (for the total decay width, we have used ${\Gamma }_{tot}=250$ MeV [34]) is:

$$BR\left(\Delta \left(1600\right)\to \gamma N\right)=\frac{\Gamma \left(\Delta \left(1600\right)\to \gamma N\right)}{{\Gamma }_{tot}\left(\Delta \left(1600\right)\right)}=0.012\%.$$

(21)

This prediction also agrees well with the experimental data, i.e., $0.001\le BR\le 0.035\%$ [34].

4. Conclusions

In this article, we have studied the $\Delta \left(1600\right)\to \gamma N$ decay within the framework of LCSR’s formalism. We have calculated the magnetic dipole $G_M^1\left(0\right)$, electric quadrupole $G_E^1\left(0\right)$, as well as the ratios $R_{EM}=-\frac{G_E^1\left(0\right)}{G_M^1\left(0\right)}$. Our result for $G_M^1\left(0\right)$ is consistent with the theoretical and experimental data of [30].

To the best of the authors’ knowledge, this is the first study of $\Delta \left(1600\right)\to \gamma N$ decay at the real photon point ($Q^2=0$). By comparing the $G_M^0\left(0\right)=2.59$ of $\Delta \left(1232\right)\to \gamma N$ decay obtained in [23] and our $G_M^1\left(0\right)=0.225$ of $\Delta \left(1600\right)\to \gamma N$ decay, we observe that the magnetic dipole moment for $\Delta \left(1600\right)\to \gamma N$ decay is one order of magnitude smaller compared to the magnetic dipole moment for $\Delta \left(1232\right)\to \gamma N$. This result indicates that the $\Delta \left(1600\right)\to \gamma N$ transition is more localized in the configuration space.

It should be noted here that the main source of uncertainty in the present calculations is due to the choice of the numerical values of the residues $|{\lambda }_N|$ and $|{\lambda }_{{\Delta }_1}|$ and their corresponding masses, as well as the numerical values of parameters in twist-3 and twist-4 DAs, which are known only up to, at best, $50\%$. It is a significant task of its own to calculate these values with high accuracy. Our last remark is that the results obtained would shed light on our knowledge of the interior structures of the resonance $\Delta \left(1600\right)$, and then could be verified through current and future experiments.