Optical Polarimetry for Fundamental Physics
Abstract
:1. Introduction
1.1. VMB beyond First Order QED
1.1.1. Higher Order Corrections
1.1.2. MilliCharged Particles (MCPs)
1.1.3. Axion-Like Particles (ALPs)
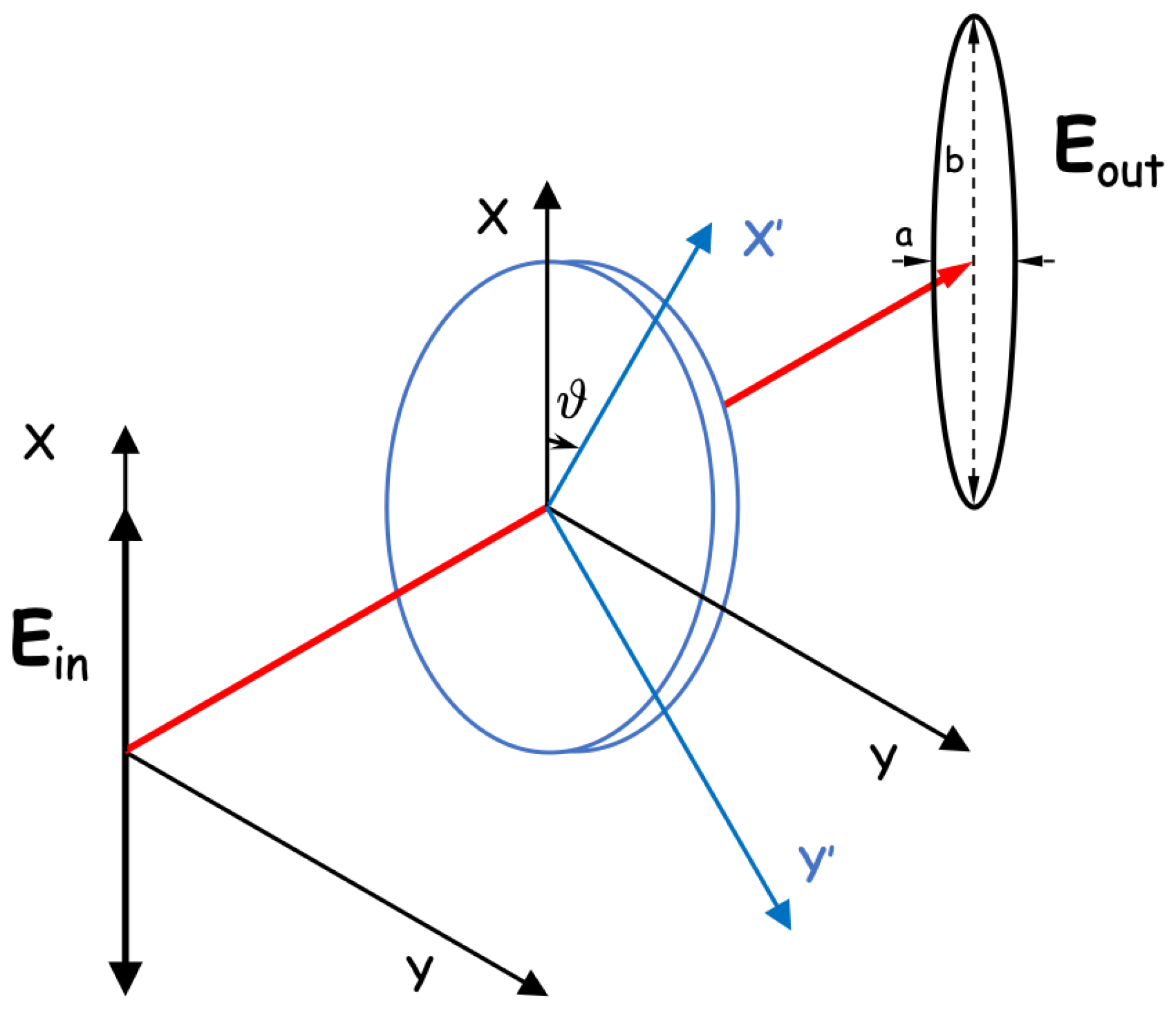
2. Experimental Method
2.1. Systematic Effects
2.2. Noise Considerations
2.3. Expected Detectability of VMB
2.4. Calibration
3. Measuring Vacuum Magnetic Birefringence and Searching for ALPs in Italy: The PVLAS Collaboration
3.1. PVLAS-LNL: Rotating Superconducting Magnet
3.1.1. Infrastructure
3.1.2. Rotating Superconducting Magnet
3.1.3. Rotating Cryostat
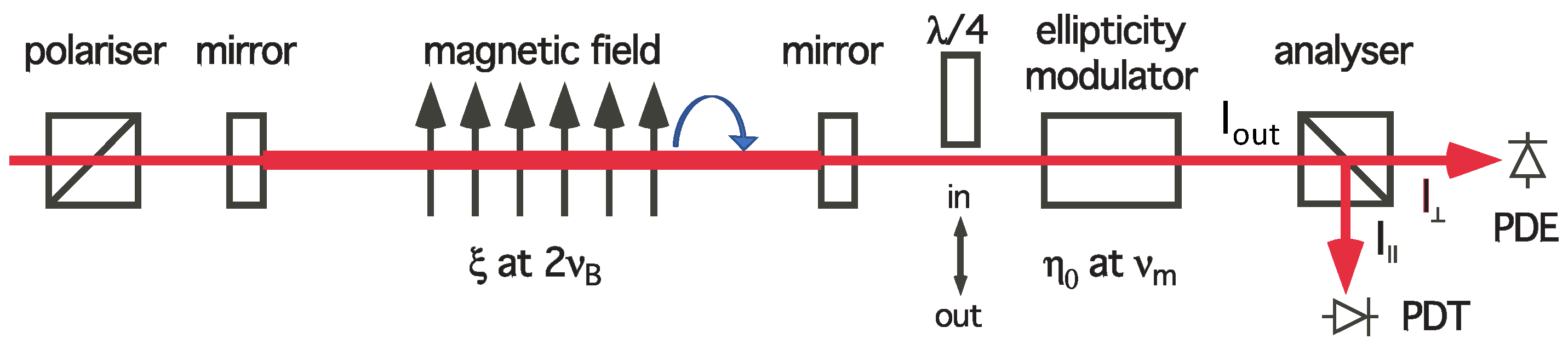
3.1.4. Polarimeter Setup and Results
3.2. PVLAS-FE: Rotating Permanent Magnets
3.2.1. Infrastructure, Optical Bench and Vacuum System
3.2.2. The Rotating Permanent Magnets
3.2.3. Optical Setup
4. Results
4.1. VMB Measurements
4.2. VMD Measurements
4.3. Limits on ALP and MCP Searches with PVLAS-FE
4.4. Future
Author Contributions
Funding
Conflicts of Interest
| 1 | In natural Heaviside-Lorentz units 1 T eV and 1 m eV. |
| 2 | 1 T eV and 1 m eV. |
References
- Ejlli, A.; Della Valle, F.; Gastaldi, U.; Messineo, G.; Pengo, R.; Ruoso, G.; Zavattini, G. The PVLAS experiment: A 25 year effort to measure vacuum magnetic birefringence. Phys. Rep. 2020, 871, 1–74. [Google Scholar] [CrossRef]
- Zavattini, G.; Della Valle, F.; Ejlli, A.; Ruoso, G. A polarisation modulation scheme for measuring vacuum magnetic birefringence with static fields. Eur. Phys. C 2016, 76, 294-1–294-5. [Google Scholar] [CrossRef] [Green Version]
- Ballou, R.; Kunc, Š.; Pengo, R.; Ruoso, G.; Gastaldi, U.; Milotti, E.; Pugnat, P.; Ejlli, A.; Siemko, A.; Zavattini, G.; et al. Letter of Intent to Measure Vacuum Magnetic Birefringence: The VMB@CERN Experiment; Tech. Rep. CERN-SPSC-2018-036, SPSC-I-249; CERN: Geneva, Switzerland, 2018. [Google Scholar]
- Euler, H.; Kockel, B. Über die Streuung von Licht an Licht nach der Diracschen Theorie. Naturwissenschaften 1935, 23, 246–247. [Google Scholar] [CrossRef]
- Euler, H. Über die Streuung von Licht an Licht nach der Diracschen Theorie. Ann. Phys. 1936, 26, 398–448. [Google Scholar] [CrossRef]
- Heisenberg, W.; Euler, H. Folgerungen aus der Diracschen Theorie des Positrons. Z. Phys. 1936, 98, 714–732. [Google Scholar] [CrossRef]
- Weisskopf, V. Über die Elektrodynamik des Vakuums auf Grund der Quantentheorie des Elektrons. Kong. Dan. Vid. Sel. Mat. Fys. Medd. 1936, 14, 1–39. [Google Scholar]
- Karplus, R.; Neuman, M. Non-linear interactions between electromagnetic fields. Phys. Rev. 1950, 80, 380–385. [Google Scholar] [CrossRef]
- Schwinger, J.S. On gauge invariance and vacuum polarization. Phys. Rev. 1951, 82, 664–679. [Google Scholar] [CrossRef]
- Karplus, R.; Neuman, M. The scattering of Light by Light. Phys. Rev. 1951, 83, 776–784. [Google Scholar] [CrossRef]
- Toll, J.S. The Dispersion Relation for Light and Its Applications to Problems Involving Electron Pairs. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1952. [Google Scholar]
- Erber, T. Velocity of Light in a Magnetic Field. Nature 1961, 190, 25–27. [Google Scholar] [CrossRef]
- Klein, J.J.; Nigam, B.P. Birefringence of the vacuum. Phys. Rev. 1964, 135, B1279–B1280. [Google Scholar] [CrossRef]
- Baier, R.; Breitenlohner, P. The Vacuum Refraction Index in the Presence of External Fields. Nuovo Cimento 1967, B47, 117–120. [Google Scholar] [CrossRef]
- Bialynicka-Birula, Z.; Bialynicki-Birula, I. Nonlinear Effects in Quantum Electrodynamics. Photon Propagation and Photon Splitting in External Fields. Phys. Rev. 1970, D2, 2341–2345. [Google Scholar] [CrossRef]
- Adler, S.L. Photon Splitting and Photon Dispersion in a Strong Magnetic Field. Ann. Phys. N. Y. 1971, 67, 599–647. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abbott, D.C.; Abud, A.A.; Abeling, K.; Abhayasinghe, D.K.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; et al. Observation of Light-by-Light Scattering in Ultraperipheral Pb + Pb Collisions with the ATLAS Detector. Phys. Rev. Lett. 2019, 123, 052001-1–052001-21. [Google Scholar] [CrossRef] [Green Version]
- Mignani, R.P.; Testa, V.; Caniulef, D.G.; Taverna, R.; Turolla, R.; Zane, S.; Wu, K. Evidence for vacuum birefringence from the first optical-polarimetry measurement of the isolated neutron star RXJ1856.5-3754. Mon. Not. R. Astron. Soc. 2016, 465, 492–500. [Google Scholar] [CrossRef] [Green Version]
- Capparelli, L.M.; Damiano, A.; Maiani, L.; Polosa, A.D. A note on polarized light from magnetars. Eur. Phys. J. C 2017, 77, 754-1–754-6. [Google Scholar] [CrossRef]
- Born, M. Modified Field Equations with a Finite Radius of the Electron. Nature 1933, 132, 282. [Google Scholar] [CrossRef]
- Born, M.; Infeld, L. Foundations of the New Field Theory. Nature 1933, 132, 1004. [Google Scholar] [CrossRef]
- Born, M.; Infeld, L. Foundations of the New Field Theory. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1934, 144, 425–451. [Google Scholar] [CrossRef]
- Ritus, V.I. Lagrangian of an intensive electromagnetic field and quantum electrodynamics at short distances. Sov. Phys. JETP 1976, 42, 774–782. [Google Scholar]
- Gies, H.; Jaeckel, J.; Ringwald, A. Polarized light propagating in a magnetic field as a probe of millicharged fermions. Phys. Rev. Lett. 2006, 97, 140402-1–140402-4. [Google Scholar] [CrossRef] [Green Version]
- Ahlers, M.; Gies, H.; Jaeckel, J.; Ringwald, A. On the particle interpretation of the PVLAS data: Neutral versus charged particles. Phys. Rev. D 2007, 75, 035011-1–035011-13. [Google Scholar] [CrossRef] [Green Version]
- Tsai, W.-Y.; Erber, T. The propagation of photons in homogeneous magnetic fields: Index of refraction. Phys. Rev. D 1975, 12, 1132–1137. [Google Scholar] [CrossRef]
- Tsai, W.-Y.; Erber, T. Photon pair creation in intense magnetic fields. Phys. Rev. D 1974, 10, 492–499. [Google Scholar] [CrossRef]
- Primakoff, H. Photo-production of neutral mesons in nuclear electric fields and the mean life of the neutral meson. Phys. Rev. 1951, 81, 899. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Pseudoparticles. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef] [Green Version]
- Peccei, R.D.; Quinn, H.R. Constraints imposed by CP conservation in the presence of pseudoparticles. Phys. Rev. D 1977, 16, 1791–1797. [Google Scholar] [CrossRef]
- Weinberg, S. A New Light Boson? Phys. Rev. Lett. 1978, 40, 223–226. [Google Scholar] [CrossRef]
- Wilczek, F. Problem of Strong P and T Invariance in the Presence of Instantons. Phys. Rev. Lett. 1978, 40, 279–282. [Google Scholar] [CrossRef]
- Ringwald, A.; Rosenberg, L.J.; Rybka, G. Axions and Other Similar Particles. Prog. Theor. Exp. Phys. 2020, 2020, 939–952. [Google Scholar]
- Graham, P.W.; Irastorza, I.G.; Lamoreaux, S.K.; Lindner, A.; van Bibber, K.A. Experimental Searches for the Axion and Axion-Like Particles. Ann. Rev. Nucl. Part. Sci. 2015, 65, 485–514. [Google Scholar] [CrossRef] [Green Version]
- Dine, M.; Fischler, W.; Srednicki, M. A simple solution to the strong CP problem with a harmless axion. Phys. Lett. B 1981, 104, 199–202. [Google Scholar] [CrossRef]
- Zhitnitsky, A.R. On Possible Suppression of the Axion Hadron Interactions. Sov. J. Nucl. Phys. 1980, 31, 260. [Google Scholar]
- Kuster, M.; Raffelt, G.; Beltrán, B. (Eds.) Axions: Theory, Cosmology, and Experimental Searches; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Irastorza, I.G.; Redondo, J. New experimental approaches in the search for axion-like particles. Prog. Part. Nucl. Phys. 2018, 102, 89–159. [Google Scholar] [CrossRef] [Green Version]
- Maiani, L.; Petronzio, R.; Zavattini, E. Effects of nearly massless, spin-zero particles on light propagation in a magnetic field. Phys. Lett. B 1986, 175, 359–363. [Google Scholar] [CrossRef] [Green Version]
- Cameron, R.; Cantatore, G.; Melissinos, A.; Ruoso, G.; Semertzidis, Y.; Halama, H.J.; Lazarus, D.M.; Prodell, A.G.; Nezrick, F.; Rizzo, C.; et al. Search for nearly massless, weakly coupled particles by optical techniques. Phys. Rev. D 1993, 47, 3707–3725. [Google Scholar] [CrossRef] [PubMed]
- Sikivie, P. Experimental tests of the invisible axion. Phys. Rev. Lett. 1983, 51, 1415–1417, Erratum in 1984, 52, 695. [Google Scholar] [CrossRef]
- Raffelt, G.; Stodolsky, L. Mixing of the photon with low-mass particles. Phys. Rev. D 1988, 37, 1237–1249. [Google Scholar] [CrossRef] [Green Version]
- Bakalov, D.; Brandi, F.; Cantatore, G.; Carugno, G.; Carusotto, S.; Della Valle, F.; De Riva, A.; Gastaldi, U.; Iacopini, E.; Micossi, P.; et al. The measurement of vacuum polarization: The PVLAS experiment. Hyperfine Interact. 1998, 114, 103–113. [Google Scholar] [CrossRef]
- Zavattini, E.; Zavattini, G.; Ruoso, G.; Raiteri, G.; Polacco, E.; Milotti, E.; Lozza, V.; Karuza, M.; Gastaldi, U.; Di Domenico, G.; et al. New PVLAS results and limits on magnetically induced optical rotation and ellipticity in vacuum. Phys. Rev. D 2008, 77, 032006-1–032006-12. [Google Scholar] [CrossRef] [Green Version]
- Bregant, M.; Cantatore, G.; Carusotto, S.; Cimino, R.; Della Valle, F.; Di Domenico, G.; Gastaldi, U.; Karuza, M.; Lozza, V.; Milotti, E.; et al. Limits on low energy photon-photon scattering from an experiment on magnetic vacuum birefringence. Phys. Rev. D 2008, 78, 032006-1–032006-10. [Google Scholar] [CrossRef] [Green Version]
- Van Bibber, K.; Dagdeviren, N.R.; Koonin, S.E.; Kerman, A.K.; Nelson, H.N. Proposed experiment to produce and detect light pseudoscalars. Phys. Rev. Lett. 1987, 59, 759–762. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoogeveen, F.; Ziegenhagen, T. Production and detection of light bosons using optical resonators. Nucl. Phys. B 1991, 358, 3–26. [Google Scholar] [CrossRef]
- Sikivie, P.; Tanner, D.B.; Van Bibber, K. Resonantly Enhanced Axion-Photon Regeneration. Phys. Rev. Lett. 2007, 98, 172002-1–172002-4. [Google Scholar] [CrossRef] [Green Version]
- Ruoso, G.; Cameron, R.; Cantatore, G.; Melissinos, A.; Semertzidis, Y.; Halama, H.J.; Lazarus, D.M.; Prodell, A.G.; Nezrick, F.; Rizzo, C.; et al. Search for photon regeneration in a magnetic field. Z. Phys. C 1992, 56, 505–508. [Google Scholar] [CrossRef]
- Ehret, K.; Frede, M.; Ghazaryan, S.; Hildebrandt, M.; Knabbe, E.-A.; Kracht, D.; Lindner, A.; List, J.; Meier, T.; Meyer, N.; et al. New ALPS results on hidden-sector lightweights. Phys. Lett. B 2010, 689, 149–155. [Google Scholar] [CrossRef]
- Ballou, R.; Deferne, G.; Finger, M., Jr.; Finger, M.; Flekova, L.; Hosek, J.; Kunc, S.; Macuchova, K.; Meissner, K.A.; Pugnat, P.; et al. New exclusion limits on scalar and pseudoscalar axionlike particles from light shining through a wall. Phys. Rev. D 2015, 92, 092002-1–092002-6. [Google Scholar] [CrossRef] [Green Version]
- Iacopini, E.; Zavattini, E. Experimental method to detect the vacuum birefringence induced by a magnetic field. Phys. Lett. B 1979, 85, 151–154. [Google Scholar] [CrossRef] [Green Version]
- Born, M.; Wolf, E. Principles of Optics, 6th ed.; Pergamon Press: Oxford, UK, 1989. [Google Scholar]
- Cantatore, G.; Della Valle, F.; Milotti, E.; Zavattini, E.; Polacco, E.; Perrone, F.; Rizzo, C.; Zavattini, G.; Ruoso, G. Frequency locking of a Nd:YAG laser using the laser itself as the optical phase modulator. Rev. Sci. Instrum. 1995, 66, 2785–2787. [Google Scholar] [CrossRef] [Green Version]
- De Riva, A.M.; Zavattini, G.; Marigo, S.; Rizzo, C.; Ruoso, G.; Carugno, G.; Onofrio, R.; Carusotto, S.; Papa, M.; Perrone, F.; et al. Very high Q frequency-locked Fabry-Perot cavity. Rev. Sci. Instrum. 1996, 67, 2680–2684. [Google Scholar] [CrossRef] [Green Version]
- Bregant, M.; Cantatore, G.; Della Valle, F.; Ruoso, G.; Zavattini, G. Frequency locking to a high-finesse Fabry-Perot cavity of a frequency doubled Nd:YAG laser used as the optical phase modulator. Rev. Sci. Instrum. 2002, 73, 4142–4144. [Google Scholar] [CrossRef] [Green Version]
- Brandi, F.; Ruoso, G.; Polacco, E. Stress-optic modulator: A novel device for high sensitivity linear birefringence measurements. Meas. Sci. Technol. 2001, 12, 1503–1508. [Google Scholar] [CrossRef]
- Zavattini, G.; Cantatore, G.; Cimino, R.; Di Domenico, G.; Della Valle, F.; Karuza, M.; Milotti, E.; Ruoso, G. On measuring birefringences and dichroisms using Fabry-Pérot cavities. Appl. Phys. B 2006, 83, 571–577. [Google Scholar] [CrossRef]
- Della Valle, F.; Ejlli, A.; Gastaldi, U.; Messineo, G.; Milotti, E.; Pengo, R.; Ruoso, G.; Zavattini, G. The PVLAS experiment: Measuring vacuum magnetic birefringence and dichroism with a birefringent Fabry-Perot cavity. Eur. Phys. J. C 2016, 76, 24-1–24-15. [Google Scholar] [CrossRef] [Green Version]
- Zavattini, G.; Della Valle, F.; Ejlli, E.; Ni, W.-T.; Gastaldi, U.; Milotti, E.; Pengo, R.; Ruoso, G. Intrinsic mirror noise in Fabry-Perot based polarimeters: The case for the measurement of vacuum magnetic birefringence. Eur. Phys. J. C 2018, 78, 585-1–585-16. [Google Scholar] [CrossRef]
- Della Valle, F.; Gastaldi, U.; Messineo, G.; Milotti, E.; Pengo, R.; Piemontese, L.; Ruoso, G.; Zavattini, G. Measurements of vacuum magnetic birefringence using permanent dipole magnets: The PVLAS experiment. New J. Phys. 2013, 15, 053026-1–053026-24. [Google Scholar] [CrossRef] [Green Version]
- Cadène, A.; Berceau, P.; Fouché, M.; Battesti, R.; Rizzo, C. Vacuum magnetic linear birefringence using pulsed fields: Status of the BMV experiment. Eur. Phys. J. D 2014, 68, 16-1–16-7. [Google Scholar] [CrossRef] [Green Version]
- Fan, X.; Kamioka, S.; Inada, T.; Yamazaki, T.; Namba, T.; Asai, S.; Omachi, J.; Yoshioka, K.; Kuwata-Gonokami, M.; Matsuo, A.; et al. The OVAL experiment: A new experiment to measure vacuum magnetic birefringence using high repetition pulsed magnets. Eur. Phys. J. D 2017, 71, 308-1–308-10. [Google Scholar] [CrossRef] [Green Version]
- Rizzo, C.; Rizzo, A.; Bishop, D.M. The Cotton–Mouton effect in gases: Experiment and theory. Int. Rev. Phys. Chem. 1997, 16, 81–111. [Google Scholar] [CrossRef]
- Bregant, M.; Cantatore, G.; Carusotto, S.; Cimino, R.; Della Valle, F.; Di Domenico, G.; Gastaldi, U.; Karuza, M.; Lozza, V.; Milotti, E.; et al. New precise measurement of the Cotton–Mouton effect in helium. Chem. Phys. Lett. 2009, 471, 322–325. [Google Scholar] [CrossRef]
- Cadène, A.; Sordes, D.; Berceau, P.; Fouché, M.; Battesti, R.; Rizzo, C. Faraday and Cotton-Mouton effects of helium at λ = 1064 nm. Phys. Rev. A 2013, 88, 043815-1–043815-11. [Google Scholar] [CrossRef] [Green Version]
- Della Valle, F.; Milotti, E.; Ejlli, A.; Messineo, G.; Piemontese, L.; Zavattini, G.; Gastaldi, U.; Pengo, R.; Ruoso, G. First results from the new PVLAS apparatus: A new limit on vacuum magnetic birefringence. Phys. Rev. D 2014, 90, 092003-1–092003-7. [Google Scholar] [CrossRef] [Green Version]
- Bregant, M.; Cantatore, G.; Carusotto, S.; Cimino, R.; Della Valle, F.; Di Domenico, G.; Gastaldi, U.; Karuza, M.; Milotti, E.; Polacco, E.; et al. A precise measurement of the Cotton-Mouton effect in neon. Chem. Phys. Lett. 2005, 410, 288–292. [Google Scholar] [CrossRef]
- Bregant, M.; Cantatore, G.; Carusotto, S.; Cimino, R.; Della Valle, F.; Di Domenico, G.; Gastaldi, U.; Karuza, M.; Lozza, V.; Milotti, E.; et al. Erratum to ‘Measurement of the Cotton-Mouton effect in krypton and xenon at 1064 nm with the PVLAS apparatus’ [Chem. Phys. Lett. 392 (2004) 276] and ‘A precise measurement of the Cotton-Mouton effect in neon’ [Chem. Phys. Lett. 410 (2005) 288]. Chem. Phys. Lett. 2009, 477, 415. [Google Scholar] [CrossRef]
- Mei, H.H.; Ni, W.T.; Chen, S.J.; Pan, S.S. Measurement of the Cotton-Mouton effect in nitrogen, oxygen, carbon dioxide, argon, and krypton with the Q & A apparatus. Chem. Phys. Lett. 2009, 471, 216–221. [Google Scholar]
- Della Valle, F.; Ejlli, A.; Gastaldi, U.; Messineo, G.; Milotti, E.; Pengo, R.; Piemontese, L.; Ruoso, G.; Zavattini, G. Measurement of the Cotton Mouton effect of water vapour. Chem. Phys. Lett. 2014, 592, 288–291. [Google Scholar] [CrossRef] [Green Version]
- Lukins, P.B.; Ritchie, G.L.D. Vapor-phase Cotton-Mouton effects of methane, methyl chloride, chloroform, and carbon tetrachloride. J. Phys. Chem. 1988, 92, 2013–2015. [Google Scholar] [CrossRef]
- Bregant, M.; Cantatore, G.; Carusotto, S.; Cimino, R.; Della Valle, F.; Di Domenico, G.; Gastaldi, U.; Karuza, M.; Milotti, E.; Polacco, E.; et al. Measurement of the Cotton-Mouton effect in krypton and xenon at 1064 nm with the PVLAS apparatus. Chem. Phys. Lett. 2004, 392, 276–280. [Google Scholar] [CrossRef]
- Cadene, A.; Fouché, M.; Rivere, A.; Battesti, R.; Coriani, S.; Rizzo, A.; Rizzo, C. Circular and linear magnetic birefringences in xenon at λ = 1064 nm. J. Chem. Phys. 2015, 142, 124313-1–124313-10. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.-J.; Mei, H.-H.; Ni, W.-T. Q & A experiment to search for vacuum dichroism, pseudoscalar-photon interaction and millicharged fermions. Mod. Phys. Lett. A 2007, 22, 2815–2831. [Google Scholar]
- Brandi, F.; Della Valle, F.; Micossi, P.; De Riva, A.M.; Zavattini, G.; Perrone, F.; Rizzo, C.; Ruoso, G. Cotton-Mouton effect of molecular oxygen: A novel measurement. J. Opt. Soc. Am. B 1998, 15, 1278–1281. [Google Scholar] [CrossRef]
- Superconducting Magnet Record. CERN Bull. 1982, 28, 1.
- Iacopini, E.; Lazeyras, P.; Smith, B.; Picasso, E.; Polacco, E.; Morpuirgo, M.; Zavattini, E. Experimental Determination of Vacuum Polarization Effects on a Laser Light-Beam Propagating in a Strong Magnetic Field; Tech. Rep. Proposal D2; CERN: Geneva, Switzerland, 1980. [Google Scholar]
- Carusotto, S.; Scuri, F.; Smith, B.; Iacopini, E.; Picasso, E.; Polacco, E.; Lazeyras, P.; Stefanini, F.; Morpuirgo, M.; Zavattini, E. Addendum to the Proposal D2: Experimental Determination of Vacuum Polarization Effects on a Laser Light-Beam Propagating in a Strong Magnetic Field; Tech. Rep. Proposal D2-Add; CERN: Geneva, Switzerland, 1983. [Google Scholar]
- Multilams First Choice in Scientific Experiments. MC®/HCK® News. 13 March 1999. Available online: https://ec.staubli.com/AcroFiles/Catalogues/News/Archiv/Archiv/SZ_News-1999_(en)_hi.pdf (accessed on 31 May 2020).
- Pengo, R.; Petrucci, G.; Marigo, S. An original rotating cryostat for the experiment PVLAS. In Proceedings of the 17th International Cryogenic Engineering Conference (ICEC 17), Bournemouth, UK, 14–17 July 1998; Dew-Hughes, D., Scurlock, R.G., Watson, J.H.P., Eds.; IOP: Bristol, UK, 1998; pp. 851–854. [Google Scholar]
- Claudet, G.; Lacaze, A.; Roubeau, P.; Verdier, J. The design and operation of a refrigerator system using superfluid helium. In Proceedings of the 5th International Cryogenic Engineering Conference (ICEC 5), Kyoto, Japan, 7–10 May 1974; Mendelssohn, K., Ed.; IPC Science and Technology Press: Guildford, UK, 1974; pp. 265–267. [Google Scholar]
- Bakalov, D.; Brandi, F.; Cantatore, G.; Carugno, G.; Carusotto, S.; Della Valle, F.; De Riva, A.M.; Gastaldi, U.; Iacopini, E.; Micossi, P.; et al. Experimental method to detect the magnetic birefringence of vacuum. Quantum Semiclass. Opt. 1998, 10, 239–250. [Google Scholar] [CrossRef]
- Della Valle, F.; Di Domenico, G.; Gastaldi, U.; Milotti, E.; Pengo, R.; Ruoso, G.; Zavattini, G. Towards a direct measurement of vacuum magnetic birefringence: PVLAS achievements. Opt. Commun. 2010, 283, 4194–4198. [Google Scholar] [CrossRef] [Green Version]
- Halbach, K. Design of permanent multipole magnets with oriented rare earth cobalt material. Nucl. Instrum. Methods 1980, 169, 1–10. [Google Scholar] [CrossRef] [Green Version]
- CAST Collaboration. New CAST limit on the axion-photon interaction. Nat. Phys. 2017, 13, 584–590. [Google Scholar] [CrossRef]


















| Species | (Tatm) | (nm) | (mbar) | Ref. |
|---|---|---|---|---|
| He | 1064 | [65] | ||
| 1064 | [66] | |||
| 1064 | [67] | |||
| Ne | 1064 | [68,69] | ||
| Ar | 1064 | [59] | ||
| 1064 | [70] | |||
| HO | 1064 | [71] | ||
| H | 514 | [64] | ||
| CH | 632.8 | [72] | ||
| Kr | 1064 | [69,73] | ||
| Xe | 1064 | [69,73] | ||
| 1064 | [74] | |||
| CH | 632.8 | [70] | ||
| CO | 546 | [64] | ||
| N | 1064 | [70,75] | ||
| CO | 1064 | [70] | ||
| O | 1064 | [76] |
| Cold bore useful diameter | 0.1 m |
| Magnetic field length | 1 m |
| Overall magnet length | 1.3 m |
| Current (corresponding to a central field of 8 T) | 3810 A |
| Max field on the conductor | 8.8 T |
| Field uniformity in the useful bore | ±2.5% |
| Average current density in the winding | 105 A/mm |
| Stored energy | 1.5 MJ |
| Magnetic system design | cylindrical |
| Magnetic field direction | normal to bore axis |
| Overall length | 934 mm |
| Outer diameter | 280 mm |
| Bore diameter | 20 mm |
| Net weight | 450 kg |
| Magnetic material | high coercivity Nd-Fe-B |
| Maximum field intensity | 2.5 T |
| Squared field integral | 5.12 Tm |
| Magnetic field length | 0.82 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zavattini, G.; Della Valle, F. Optical Polarimetry for Fundamental Physics. Universe 2021, 7, 252. https://doi.org/10.3390/universe7070252
Zavattini G, Della Valle F. Optical Polarimetry for Fundamental Physics. Universe. 2021; 7(7):252. https://doi.org/10.3390/universe7070252
Chicago/Turabian StyleZavattini, Guido, and Federico Della Valle. 2021. "Optical Polarimetry for Fundamental Physics" Universe 7, no. 7: 252. https://doi.org/10.3390/universe7070252
APA StyleZavattini, G., & Della Valle, F. (2021). Optical Polarimetry for Fundamental Physics. Universe, 7(7), 252. https://doi.org/10.3390/universe7070252






