Quantum Vacuum Energy of Self-Similar Configurations
Abstract
1. Introduction
2. Self-Similarity as Many-Body Systems on a Regular Smooth Manifold
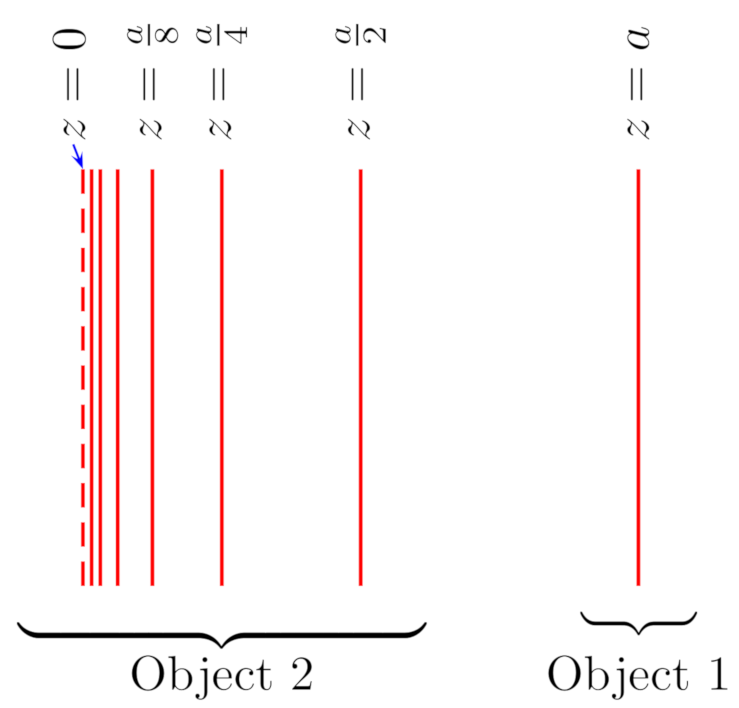
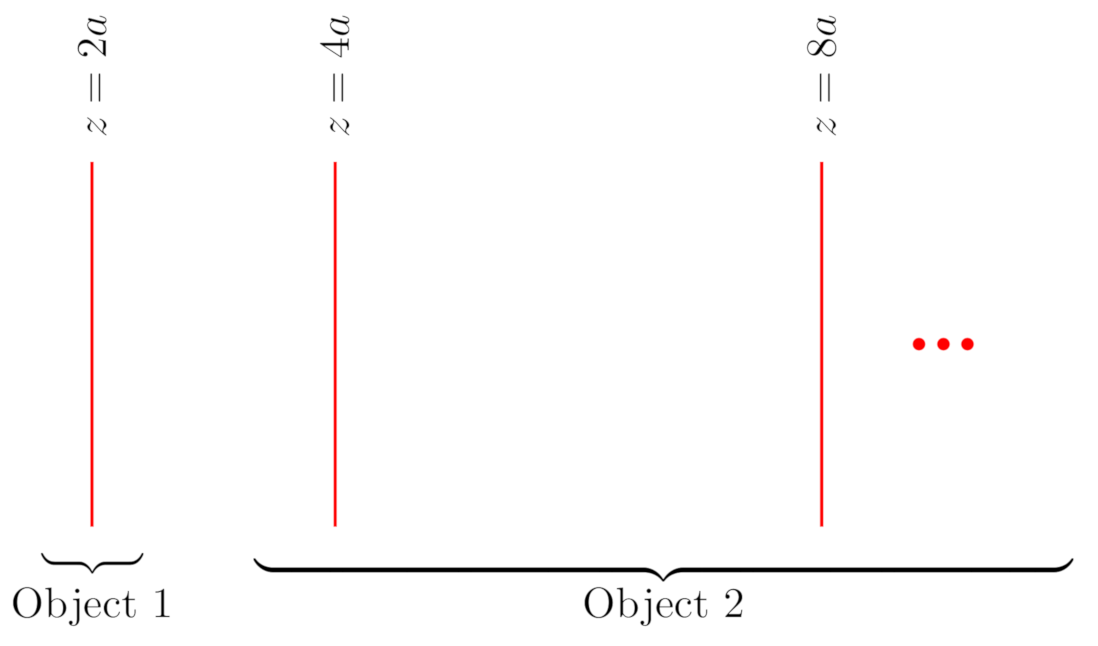
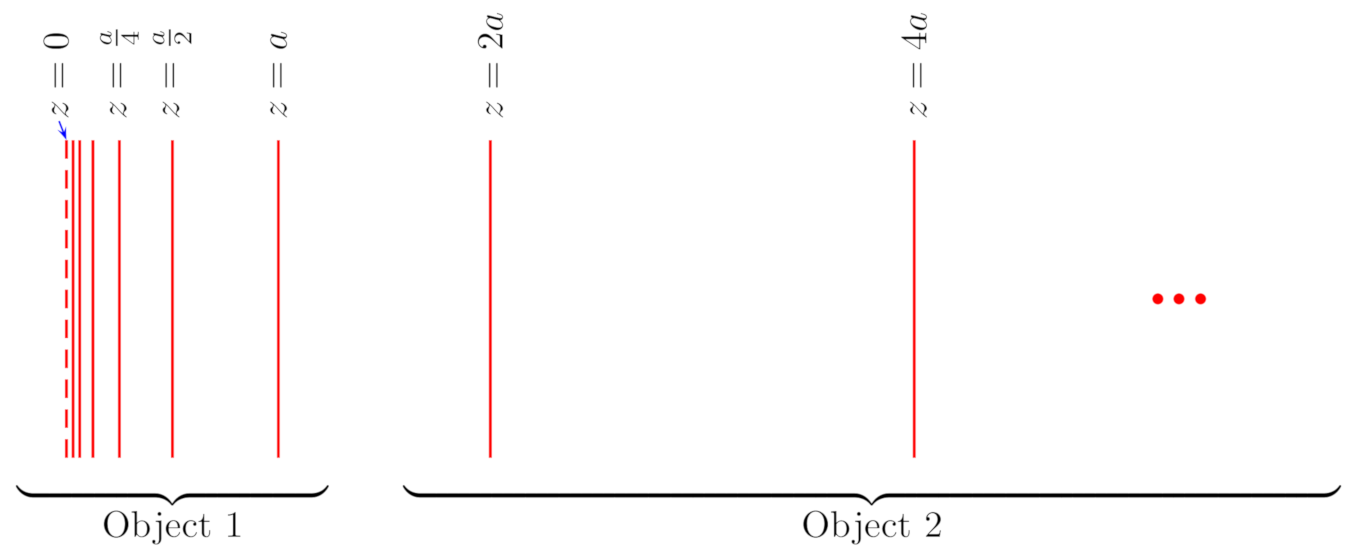
2.1. Self-Similar Parallel Plates
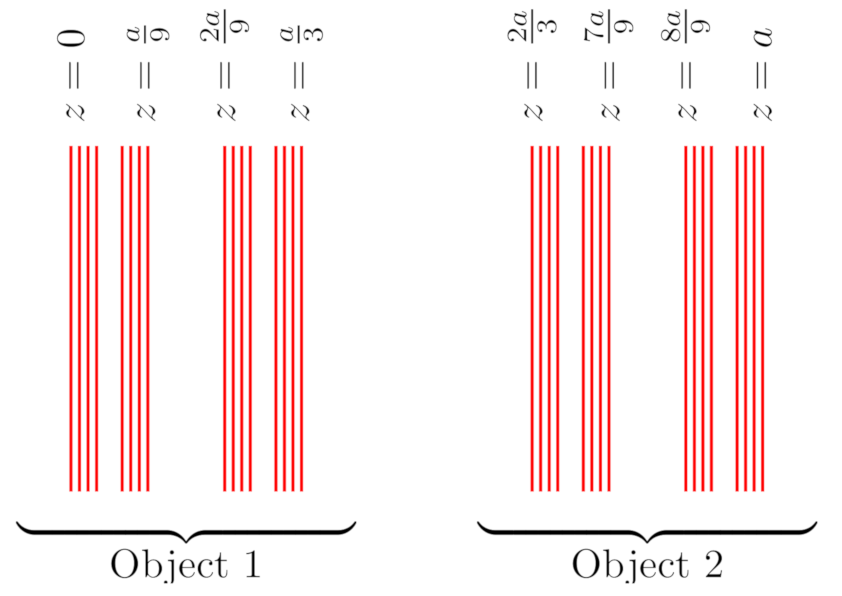
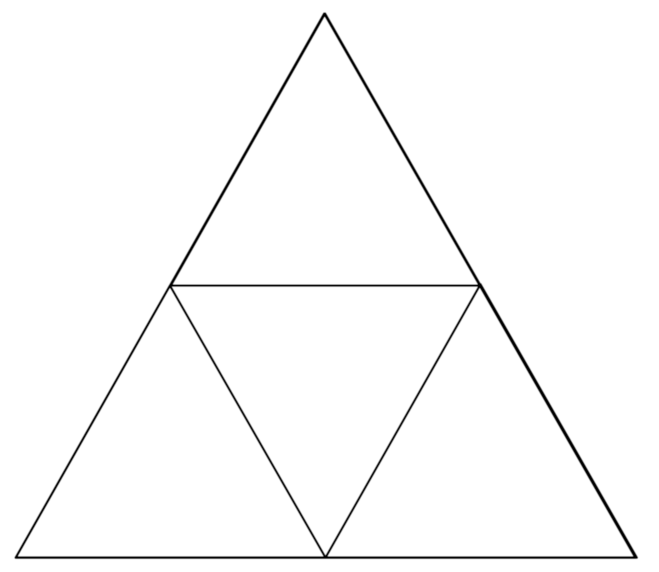
2.2. Sierpinski Triangles
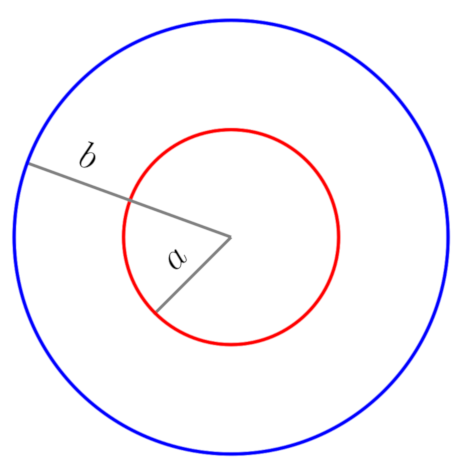
3. Concentric Spheres—Self-Similar Spheres
Inversion
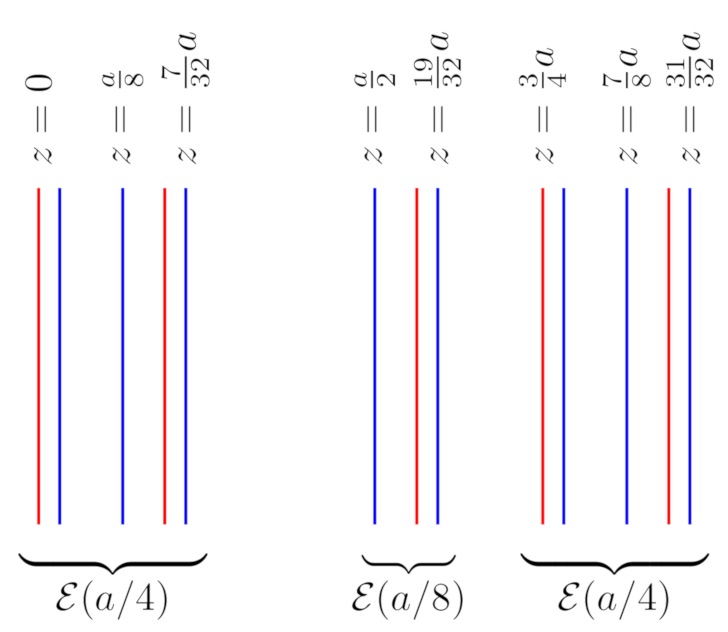
4. Quasi-Periodic Configuration of Plates
5. Spectral Functions, Revisited
6. Self-Similar Manifolds
Example—Casimir Energy of a Sierpinski Triangle
7. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Miloni, P. The Quantum Vacuum; Academic Press, Inc.: London, UK, 1994. [Google Scholar]
- Plunien, G.; Müller, B.; Greiner, W. The Casimir Effect. Phys. Rep. 1986, 134, 87–193. [Google Scholar] [CrossRef]
- Milton, K.A. The Casimir Effect: Physical Manifestations of Zero- Point Energy; World Scientific: Hackensack, NJ, USA, 2001. [Google Scholar]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Bordag, M.; Mohiden, U.; Mostepanenko, V.M. New developments in the Casimir effect. Phys. Rep. 2001, 353, 1–205. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Experiment and theory in the Casimir effect. Contemp. Phys. 2006, 47, 131–144. [Google Scholar] [CrossRef]
- Farina, C. The Casimir effect: Some aspects. Braz. J. Phys. 2006, 36, 1137–1149. [Google Scholar] [CrossRef]
- Lamoreaux, S. The Casimir force: Background, experiments, and applications. Rep. Prog. Phys. 2004, 68, 201–236. [Google Scholar] [CrossRef]
- Kac, M. Can One Hear the Shape of a Drum? Am. Math. Mon. 1966, 73, 1–23. [Google Scholar] [CrossRef]
- Fulling, A. Vacuum Energy as Spectral Geometry. SIGMA 2007, 3, 094. [Google Scholar] [CrossRef][Green Version]
- Shajesh, K.V.; Brevik, I.; Cavero-Peláez, I.; Parashar, P. Casimir energies of self-similar plate configurations. Phys. Rev. D 2016, 94, 065003. [Google Scholar] [CrossRef]
- Shajesh, K.V.; Parashar, P.; Cavero-Peláez, I.; Kocik, J.; Brevik, I. Casimir energy of Sierpinski triangles. Phys. Rev. D 2017, 96, 105010. [Google Scholar] [CrossRef]
- Strichartz, R.S. Differential Equations on Fractals: A Tutorial; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Kigami, J. A harmonic calculus on the Sierpinski spaces. Jpn. J. Ind. Appl. Math. 1989, 6, 259–290. [Google Scholar] [CrossRef]
- Balian, R.; Duplantier, B. Electromagnetic waves near perfect conductors. I. Multiple scattering expansions. Distribution of modes. Ann. Phys. 1977, 104, 300–335. [Google Scholar] [CrossRef]
- Balian, R.; Duplantier, B. Electromagnetic waves near perfect conductors. II. Casimir effect. Ann. Phys. 1978, 112, 165–208. [Google Scholar] [CrossRef]
- Kenneth, O.; Klich, I. Opposites Attract: A Theorem about the Casimir Force. Phys. Rev. Lett. 2006, 97. [Google Scholar] [CrossRef]
- Emig, T.; Graham, N.; Jaffe, R.L.; Kardar, M. Casimir Forces between Compact Objects. I. The Scalar Case. Phys. Rev. D 2008, 77. [Google Scholar] [CrossRef]
- Milton, K.A.; Wagner, J. Multiple scattering methods in Casimir calculations. J. Phys. A 2008, 41. [Google Scholar] [CrossRef]
- Wirzba, A. Quantum mechanics and semiclassics of hyperbolic n-disk scattering systems. Phys. Rep. 1999, 309, 1–116. [Google Scholar] [CrossRef]
- Schaden, M. Irreducible many-body Casimir energies of intersecting objects. EPL 2011, 94. [Google Scholar] [CrossRef]
- Shajesh, K.V.; Schaden, M. Many-body contributions to Green’s functions and Casimir energies. Phys. Rev. D 2011, 83. [Google Scholar] [CrossRef]
- Shajesh, K.V.; Schaden, M. Significance of Many-Body Contributions to Casimir Energies. Int. J. Mod. Phys. Conf. Ser. 2012, 14. [Google Scholar] [CrossRef]
- Hardy, G.H. Divergent Series; Clarendon: Oxford, UK, 1956. [Google Scholar]
- Elizalde, E.; Romeo, A. Essentials of the Casimir effect and its computation. Am. J. Phys. 1991, 59, 711–719. [Google Scholar] [CrossRef]
- Parashar, P.; Milton, K.A.; Shajesh, K.V.; Brevik, I. Electromagnetic δ-function sphere. Phys. Rev. D 2017, 96, 085010. [Google Scholar] [CrossRef]
- NIST Digital Library of Mathematical Functions. Release 1.0.8 of 2014-04-25. Available online: http://dlmf.nist.gov/ (accessed on 3 April 2021).
- Casimir, H.B.G. On the attraction between two perfectly conducting plates. Kon. Ned. Akad. Wetensch. Proc. 1948, 51, 793–795. [Google Scholar]
- Elizalde, E. Ten Physical Applications of Spectral Zeta Functions; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Kirsten, K. Spectral Functions in Mathematic and Physics; Chapman & Hall/CRC: New York, NY, USA, 2002. [Google Scholar]
- Abalo, E.K.; Milton, K.A.; Kaplan, L. Casimir energies of cylinders: Universal function. Phys. Rev. D 2010, 82. [Google Scholar] [CrossRef]
- Milton, K.A.; Schwinger, J. Electromagnetic Radiation: Variational Methods, Waveguides and Accelerators; Springer: Berlin, Germany, 2006. [Google Scholar]
- Schwinger, J.; DeRaad, L.L.J.; Milton, K.A.; Tsai, W.Y. Classical Electrodynamics; Westview Press: New York, NY, USA, 1998. [Google Scholar]
- Weyl, H. Ueber die asymptotische Verteilung der Eigenwerte. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen Mathematisch-Physikalische Klasse 1911, 1911, 110–117. Available online: http://eudml.org/doc/58792 (accessed on 3 April 2021).
- De Gennes, P.G. La Percolation: Un Concept Unifacateur; World Scientific: Singapore, 1976. [Google Scholar]
- Jost, J. Riemannian Geometry and Geometric Analysis; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Boothby, W.M. An Introduction to Differentiable Manifolds and Riemannian Geometry, Revised, 2nd ed.; Academic Press: Berkeley, CA, USA, 2003. [Google Scholar]
- Molchanov, S.A. Diffusion processes and Riemannian geometry. Russ. Math. Surv. 1975, 30, 1–63. [Google Scholar] [CrossRef]
- Derfel, G.; Grabner, P.J.; Vogl, F. Laplace operators on fractals and related functional equations. J. Phys. A Math. Theor. 2012, 45, 463001. [Google Scholar] [CrossRef]
- Fukushima, M.; Shima, T. On a spectral analysis for the Sierpinski gasket. Potential Anal. 1992, 1, 1–35. [Google Scholar] [CrossRef]
- Shima, T. On eigenvalue problems for the random walks on the Sierpinski pre-gaskets. Jpn. J. Ind. Appl. Math. 1991, 127–141. [Google Scholar] [CrossRef]
- Derfel, G.; Grabner, P.J.; Volg, F. The zeta function of the Laplacian on certain Fractals. Trans. Am. Math. Soc. 2008, 360, 881–897. [Google Scholar] [CrossRef]
- Teplyaev, A. Spectral zeta functions of fractals and the complex dynamics of polynomials. Trans. Am. Math. Soc. 2007, 359, 4339–4358. [Google Scholar] [CrossRef]
- Dunne, G. Heat kernels and zeta functions on fractals. J. Phys. A Math. Theor. 2012, 45. [Google Scholar] [CrossRef]
- Kumagai, T. Estimates of transition densities for Brownian motion on nested fractals. Probab. Theory Relat. Fields 1993, 96, 205–224. [Google Scholar] [CrossRef]
- Akkermans, E.; Dunne, G.V.; Teplyaev, A. Physical consequences of complex dimensions of fractals. Eur. Phys. Lett. 2009, 88, 40007. [Google Scholar] [CrossRef]
- Akkermans, E.; Dunne, G.V.; Teplyaev, A. Thermodynamics of Photons on Fractals. Phys. Rev. Lett. 2010, 105, 230407. [Google Scholar] [CrossRef]
- Brossard, J.; Carmona, R. Can one hear the dimension of a fractal? Comm. Math. Phys. 1986, 104, 103–122. [Google Scholar] [CrossRef]
- Lapidus, M.L. Fractal Drum, Inverse Spectral Problems for elliptic operators and a partial resolution of the Weyl-Berry conjecture. Trans. Am. Math. Soc 1991, 325, 465–529. [Google Scholar] [CrossRef]
- Lapidus, M.L.; Pomerance, C. The Riemann Zeta-Function and the One-Dimensional Weyl-Berry Conjecture for Fractal Drums. Proc. Lond. Math. Soc. 1993, 66, 41–69. [Google Scholar] [CrossRef]
- Lapidus, M.L.; Pomerance, C. Counterexamples to the modified Weyl-Berry conjecture on fractal drums. Math. Proc. Camb. Philos. Soc. 1996, 119, 167–178. [Google Scholar] [CrossRef]
| 1 | We assume . |
| 2 | Of course this is a formal definition and must not be understood as a mere difference between two quantities that are, as a matter of fact, infinite. To make sense of it, one must use regularization methods to extract the finite part of such difference. |
| 3 | We do not distinguish for now between global energy and energy density. |
| 4 | Note that, according to our notation, the self-similar structure has a width of now. |
| 5 | Casimir computed this for the first time in 1948 in a completely different manner [28]. |
| 6 | It obeys the heat conduction equation, and once the initial condition is fixed, it obeys the same boundary conditions as . |
| 7 | In the particular case of parallel plates, these two coefficients are infinite, but this is not a problem since the background vacuum needs to be subtracted and contributes with the same terms. |


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cavero-Peláez, I.; Parashar, P.; Shajesh, K.V. Quantum Vacuum Energy of Self-Similar Configurations. Universe 2021, 7, 128. https://doi.org/10.3390/universe7050128
Cavero-Peláez I, Parashar P, Shajesh KV. Quantum Vacuum Energy of Self-Similar Configurations. Universe. 2021; 7(5):128. https://doi.org/10.3390/universe7050128
Chicago/Turabian StyleCavero-Peláez, Inés, Prachi Parashar, and K. V. Shajesh. 2021. "Quantum Vacuum Energy of Self-Similar Configurations" Universe 7, no. 5: 128. https://doi.org/10.3390/universe7050128
APA StyleCavero-Peláez, I., Parashar, P., & Shajesh, K. V. (2021). Quantum Vacuum Energy of Self-Similar Configurations. Universe, 7(5), 128. https://doi.org/10.3390/universe7050128





