Abstract
New observational data and modeling of physical processes constantly appear in the young and rapidly developing branch of science of plasma astrophysics. However, there is a lack of theoretical studies in the field of plasma astrophysics, that could unite the physics of various objects in the Universe, explain the observed phenomena and contribute to the improvement of numerical modeling schemes efficiency. This article makes up for this shortcoming by introducing different models, taking into account the various properties of plasma objects. We present a review of the latest magnetohydrodynamic theories of wave processes in rotating astrophysical plasma, taking into account important and common properties of astrophysical objects as compressibility and stratification.
1. Introduction
Plasma is one of the most common states of objects in the universe. The study of plasma objects outside of the Earth’s atmosphere is the subject of plasma astrophysics. The objects of this scientific field combine the objects of astrophysics (outside the Solar System) and objects of space physics (the Sun). Plasma astrophysics is responsible for the study and description of processes in plasma, contributing to a deeper understanding of the physics of objects in the Universe. The study of plasma unites in itself almost all known objects of the Universe, from small planets to huge clusters of galaxies. A strong advantage of plasma astrophysics is similarity of plasma processes that arise in different astrophysical objects.
Recently, the study of large-scale magnetohydrodynamic (MHD) flows has come to the front due to the development of a number of new research applications in this area. They are dynamics of the solar tachocline [1,2,3,4], accretion of matter onto neutron stars [5,6,7], dynamics of the atmospheres of neutron stars and magnetoactive atmospheres of exoplanets [8]. In this context, the study of various objects contains the development of the basic principles of magnetohydrodynamics.
Theoretical and numerical studies are being actively developed to solve the problems of studying multiscale flows of astrophysical plasma. They are aimed at investigating properties common to a wide range of astrophysical objects. In such studies the fundamentals of geophysical hydrodynamics extended to the presence of a magnetic field. The effects of magnetism are associated with differences in behavior between plasma flows and neutral flows. Moreover, on the largest scales plasma environment is affected by gravity and rotation. The complete system of equations of magnetohydrodynamics for rotating plasma in a gravitational field is a practically unsolvable problem, both for analytical research and for numerical simulation. This article presents approximate models describing the flows of astrophysical plasma on a global scale. Such large-scale models describe waves and turbulence in astrophysical plasma at different spatial and temporal scales. Here we focus on the study of wave processes in a rotating astrophysical plasma with variable density. The results of studies of turbulence in rotating astrophysical plasma are presented in [9,10,11,12].
Studies of variable density effects in MHD models of a rotating astrophysical plasma are used as applications in the study of processes in the solar tachocline [1,2,3,4,13,14,15], stably stratified radioactive regions in star interiors [16], outer liquid core of planets [17], dynamics of astrophysical disks [18,19] and exoplanets [20], oscillations of rotating stars and the Sun [21,22,23]. Including stratification into consideration significantly increases the accuracy of interpretation of observational data of solar magneto-Rossby waves [22,24,25,26]. The discovery of solar Rossby waves by experimental methods initiated the development of models describing large-scale magnetohydrodynamic flows of rotating plasma [27,28,29,30]. Magneto-Rossby waves have an important influence on the solar seasons [23,31,32] and, as a consequence, play a key role in understanding of space weather [33]. Rossby waves also play the crucial role in the emergence of zonal flows in two-dimensional magnetohydrodynamic turbulence and in the Earth’s core [10,34,35]. Note as well the important papers on the study of large-scale Rossby waves in geophysical hydrodynamics [36,37]. In this review we consider four different approaches to variable density flows: two-layer shallow water approximation, Boussinesq approximation, anelastic approximation, shallow water approximation with large-scale compressibility.
1.1. Stratified MHD Flows in Two-Layer Shallow Water Approximation
The shallow water approximation is one of the main magnetohydrodynamic approximations used to study large-scale processes in rotating astrophysical plasma. The magnetohydrodynamic shallow water equations used to describe space and astrophysical plasma are analogous to the shallow water equations in geophysical hydrodynamics. A lot of works have been aimed at studying wave processes in the shallow water approximation [14,15,24,27,36,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52]. Studies of magneto-Rossby waves are of particular interest. Such waves govern the dynamics of the Sun and stars [1,14,15,53,54,55], magnetospheres of exoplanets [8] and accretion disks of neutron stars [6]. Magneto-Rossby waves are analogous to Rossby waves in geophysical hydrodynamics [36,37,49,50,56]. Such waves govern the atmospheric dynamics of planets on a large scale. The first results on the experimental detection of solar Rossby waves [24,25,57] and substantial studies on the development of a nonlinear theory of magneto-Rossby waves [27,58,59,60] are mentioned here.
The MHD shallow water approximation is used to describe flows in a layer of plasma with certain properties. For the shallow water approximation to be applicable, the spatial vertical scale of the flow must be much smaller than the spatial horizontal scale. The MHD shallow water equations are an alternative to the MHD equations for a rotating layer of an incompressible inviscid fluid with a free surface in the gravity field. The system of MHD equations in the shallow water approximation is derived from the system of MHD equations for an incompressible fluid by averaging the equations over the layer height. The layer height is assumed to be small compared to the characteristic horizontal flow scale. The total pressure satisfies the hydrostatic condition [2,38,39,40,61,62,63,64]. External vertical magnetic field plays important role in MHD shallow water equations. Such configuration of magnetic field is typical for neutron stars [45] and exoplanets [8]. The presence of an external vertical magnetic field substantially modifies MHD shallow water equations. These modifications lead to emergence of two new fast linear waves: magneto-Poincare and magnetostrophic [45]. The MHD shallow water equations with an external vertical magnetic field contain a modified divergence-free condition which is a consequence of the equations for the magnetic field [43]. Moreover, a new supplementary equations for the vertical component of magnetic field is added to the system in [43]. It reveal the three-dimensional dynamics of the magnetic field in plasma layer in the external vertical magnetic field. In contrast, in the standart shallow water equations the magnetic field is strictly horizontal.
The derivation of the MHD shallow water equations with stratification and an external magnetic field in the model of two plasma layers with different but constant densities is presented in [28]. This paper has been the first step in including stratification effects in study of waves in a rotating plasma. Within this model, linear magneto-Rossby waves with corrections due to stratification have been obtained. Weakly nonlinear theory of magneto-Rossby waves has been developed: amplitude equations for three interacting waves have been derived and increments of parametric instabilities (decay and amplification) have been obtained. A detailed review of the results on wave processes in an astrophysical plasma in the shallow water approximation can be found in [9]. However, the MHD shallow water equations are two-dimensional. Allowance for the vertical components of the velocity and magnetic field as well as the vertical variation of their horizontal components is not possible in shallow water model. Thus, the system of MHD shallow water equations cannot completely describe a stably and continuously stratified plasma layer, which is an important characteristic of astrophysical plasma flows.
1.2. Stratified MHD Flows in Boussinesq Approximation
The study of three-dimensional wave processes in MHD flows of a stratified rotating plasma in the Boussinesq approximation [29] has been the fundamental step towards real astrophysical flows with a continuous stratification. Magnetic field plays a role of an additional restoring force for waves, along with Coriolis and buoyancy forces. Thus, in contrast to neutral fluid flows, in magnetic flows the solutions contain new types of waves.
In [29] the Boussinesq approximation is used to study MHD flows in stably stratified rotating layer of plasma with linear density profile. The dispersion relations for various types of magnetic inertia–gravity, magnetostrophic, and magneto-Rossby waves have been derived. Restoring mechanisms for these waves are rotation, magnetic field and stratification. The dispersion relation of low-frequency magneto-Rossby mode in horizontal flow approximation becomes similar to the dispersion relation for magneto-Rossby wave in the two-layer shallow water approximation. The dispersion curves for all of the found types of waves have been qualitatively analyzed to ascertain the fulfillment of the phase matching condition. The amplitude equations of three-interacting waves have been derived for all types of interactions. The possible parametric instabilities have been derived, and their growth rates have been found.
Note, that for the Boussinesq approximation to be applicable the density gradient must be proportional only to the temperature gradient and fluid must be incompressible [49].
1.3. Compressible MHD Flows with Stable Stratification in Anelastic Approximation
Compressibility is a significant property of astrophysical plasma flows. It is inherent in practically all observable astrophysical objects. Astroseismology and magnetic field investigations have played crucial role in the first experimental observations of large-scale astrophysical plasma flows. Including effects of compressibility in MHD models of a rotating plasma substantially improve interpretation of astroseismological data, such as the data on the latitude dependence of solar oscillation eigenmodes [22]. Anelastic approximation filters out acoustic waves. Density gradient in this approximation depends not only on pressure gradient but also on temperature gradient [65]. The system of MHD equations in the anelastic approximation describe low Mach number flows. These equations are derived from the MHD equations for compressible plasma by assuming density perturbations to be small.
In [66] anelastic approximation is used to theoretically investigate rotating flows of stably stratified compressible plasma with a linear entropy profile. An additional restoring mechanism, the compressibility, along with the rotation, magnetic field and gravity, lead to emergence of new types of waves. The compressibility effects are represented in the new dispersion equations by the Brunt–Väisälä frequency for compressible stratified flows. This frequency depend not only on initial density profile but also on initial pressure profile. All possible three-wave interactions have been disclosed through a qualitative analysis of the dispersion curves. A system of amplitude equations for interacting waves and the increments of parametric instabilities have been obtained using of the multiscale expansion method.
1.4. MHD Flows in Shallow Water Approximation with Large-Scale Compressibility
Another possibility for studying MHD plasma flows with a variable density in astrophysical processes is using shallow water MHD approximation with a large-scale compressibility [67]. As has been noted, the three-dimensional system of MHD equations for compressible plasma with rotation is quite complicated both for numerical simulations and for a theoretical study. Despite the great increase in computer power there are still some demands in 3D simulations. Nowadays the problems only with computational complexity less than are solvable or can be solved on supercomputers. But such complex 3D simulations as simulation of entire convective solar zone is still demanding and technology that could solve this problem unlikely to appear in the foreseeable future [68]. State-of-art in numerical simulation of compressible magnetohydrodynamic flows can be found in [68,69,70,71,72,73,74]. This fact leads to the need for constant improvement of models based on physical simplification of equations for describing compressible magnetohydrodynamic flows.
In the approximation of large-scale compressibility, two-dimensional equations for height-averaged horizontal velocities and magnetic fields are obtained. Unlike the case of incompressible plasma the mass conservation law is written for a new variable that is a product of the plasma density and plasma layer height. In this case the density varies with horizontal coordinates and all the plasma parameters are constant along the vertical. Therefore, large-scale compressibility approximation significantly differs from the two-layer approximations as well as Boussinesq approximation where plasma is vertically stratified and anelastic approximation where density varies with all three coordinates.
To derive shallow water MHD equations considering large-scale compressibility we average original three-dimensional MHD equations for a compressible plasma over the layer height. The pressure is assumed to be magneto-hydrostatic and the layer height is assumed to be small compared to the characteristic horizontal linear size of the flow [41]. The obtained system generalizes the equations derived in [2,38,39,42,62,63,64]. Eventually, the sound waves in this approximation are eliminated and the density variations become significant on large scales describing the static compressibility effects, in contrast with the case of an incompressible plasma [41,75,76,77]. The derived system describes a broad spectrum of applications in research of astrophysical plasma processes. In the large-scale compressibility approximation the mass conservation law is formulated for a variable that nontrivially depends on the characteristic vertical scale of the flow and the scale of heights at which the density variation becomes significant. The horizontal momentum is taken into consideration more accurately compared with the case of an incompressible fluid [27]. Thus the derived system offers an essential advantage in applying to the space and astrophysical plasma flows research. In [67] two systems of MHD equations in the shallow water approximation in an external vertical magnetic field with large-scale compressibility are presented: the system on f-plane and on -plane. The dispersion relations for linear magneto-Poincare, magnetostrophic, and magneto-Rossby waves in both cases have been introduced by taking into account the large-scale plasma compressibility. A qualitative analysis of the dispersion surfaces for linear waves has been completed. Conclusions about the possibility of three-wave interactions for each type of waves have been made. The three-wave amplitude equations have been derived by the multiscale asymptotic method for all cases of wave phase matching. Parametric instabilities have been considered for each case.
2. Stratified Flows of Rotating Astrophysical Plasma in Two-Layer Magnetohydrodynamic Shallow Water Approximation
In this section stratified rotating flows of astrophysical plasma in the presence of an external vertical magnetic field are discussed. Investigation of hydrodynamics of stratified plasma within the full system of MHD equations causes difficulties both in theoretical analysis and in numerical simulation. A model of n superimposed plasma layers with different densities is an appropriate model for description of continuously stratified plasma [64,78]. We have proposed magnetohydrodynamic equations of stratified plasma in the two-layer shallow water approximation [28]. This model has unique properties due to self-consistent accounting of an external vertical magnetic field and stratification. Two-layer shallow water MHD model is efficient for space and astrophysical plasma in the same way as classical shallow water model in hydrodynamics of a neutral stratified fluid [49,79,80]. Accounting for effects of stratification in MHD models of rotating plasma is significant in analysis of the R-mode oscillations in rotating stars and the Sun [81,82,83]. It improves quality of interpretation of the observational data of large-scale solar Rossby waves [22,23,24,31].
The magnetohydrodynamic equations of stratified plasma in the two-layer shallow water approximation describe flow of a thin layer of plasma with height in gravitational field with external vertical magnetic field , which is divided into two thin layers with heights and and constant but different densities and correspondingly (Figure 1).
Figure 1.
Geometry of two-layer shallow water approximation for stratified flows in an external vertical magnetic field.
Full magnetohydrodynamic system of equation in two-layer shallow water approximation with rotation and an external vertical magnetic field has the following form:
Here index corresponds to the lower layer where , , and , while index corresponds to the upper layer where , , and . The first equation describes variation of height of each plasma layer, the second equation govern horizontal velocities averaged over height, while the third equation describe horizontal magnetic fields averaged over height.
Horizontal dynamics of the magnetic field in the shallow water approximation is significantly modified by an external vertical magnetic field [43]. Equation (1) represent a closed system that is used for analysis of wave processes. The following equations for magnetic field
ensure the divergence-free condition, which is used to specify the correct initial conditions. Additional equations for magnetic field describe the fundamental three-dimensionality and axisymmetry of the magnetic fields in the shallow water approximation. When the external magnetic field is zero, Equation (1) transform into MHD equations for stratified plasma in the two-layer shallow water model [64,78]. When heights and densities of the layers are equal, Equation (1) transform into MHD equations in the single-layer shallow water model with an external vertical magnetic field [43] and at reduce to shallow water MHD equations in the absence of an external magnetic field [2,64,76,84].
The system of Equation (1) is an essential step in the study of astrophysical flows within the shallow water approximation, including not only the external magnetic field and rotation, but also stratification.
The system of two-layer shallow water equations in an external magnetic field is derived from a three-dimensional system of magnetohydrodynamic equations for an incompressible rotating plasma in gravitational field [28]. The equations for both layers are integrated along z coordinate from 0 to for the lower layer and from to for the upper layer, taking into account the boundary conditions and hydrostatic condition for the total pressure. The heights of each layer are assumed to be small in comparison with the characteristic horizontal flow scale.
For the velocity boundary conditions are the impermeability at the bottom and equality of vertical components of velocities in the layers and translate velocities of interlayer and free boundaries. For the magnetic field boundary conditions are equality of vertical components of magnetic filed on interlayer and free boundaries and sum of horizontal components multiplied by correspondent tangent angles. The boundary condition at the bottom is nonzero and equal due to the presence of an external vertical magnetic field. This term is also added to the boundary conditions at interlayer and free boundaries.
After integration, the height-averaged velocities and magnetic fields are introduced in each layer as a sum of average values and fluctuations. Thus, after neglecting terms with fluctuations, magnetohydrodynamic shallow water equations for stratified rotating plasma in a gravitational field in the two-layer model with an external magnetic field are obtained. Detailed derivation of these equations has been made in [28].
For magnetohydrodynamic flows on f-plane, solutions have been found in the form of magneto-Poincaré waves and magnetostrophic waves in the absence of stratification. However, corrections associated with the difference in layer densities have too little effect on the waves and are analytically complex for further analysis, so we have limited ourselves to a detailed study of the magneto-Rossby waves—the waves caused by the latitude dependence of the Coriolis force [80], analogous to Rossby waves neutral fluid dynamics. Thus, within the framework of magnetohydrodynamic equations in two-layer shallow water approximation, we have considered spherical flows to study the effect of stratification on low-frequency magneto-Rossby waves. Accounting for sphericity is made by use of the -plane approximation as well as in neutral fluid dynamics [43]. In this approximation the variations of Coriolis parameter f due to small changes of the latitude are assumed to be small. Thus the parameter f can be expressed in the following form:
where is the angular rotational velocity same for both layers, , and the y coordinate is measured along the latitude in the north direction and is related to by the expression , where r is the sphere radius [79].
Thus two-layer magnetohydrodynamic shallow water equations for a stratified rotating plasma on the -plane in the presence of an external magnetic field take following form:
Two different stationary solutions satisfy the system of Equation (3): a layer at rest with an external vertical magnetic field () and a layer at rest with horizontal magnetic field , (). In both cases an analysis of the magneto-Rossby waves is performed.
2.1. Linear Magneto-Rossby Waves in a Stratified Astrophysical Plasma in Two-Layer Approximation in Presence of an External Vertical Magnetic Field
This section presents solutions of the linearized system of Equation (3) on the background of a stationary state with constant external vertical magnetic field:
Solutions take the form of magneto-Rossby waves. Corrections to them associated with stratification, have been obtained in [28].
The dispersion equation for the waves in stratified rotating plasma in an external vertical magnetic field in two-layer shallow water approximation on a beta-plane has the form:
where
is the perturbation frequency, is the perturbation wave vector, and .
Terms on the right-hand side of the expression (4) represent the effects of stratification in the two-layer model. The terms on the left-hand side of (4) are in the form of a product of two expressions. The expression in the first bracket corresponds to the lower layer, and in the second—to the upper layer. We investigate the effects of stratification on magneto-Rossby waves in two-layer model. Therefore, we search for solution of (4) in form of magneto-Rossby wave in the case of equal densities. Then we assume the difference in densities is small and search for solution of (4) in the form of a correction to the frequency of magneto-Rossby wave related to plasma stratification.
Dispersion Equation (4) at takes the following form:
which yields the following expression for the magneto-Rossby wave in the absence of stratification, whose restoring forces are the Lorentz and Coriolis forces:
It should be noted that the dispersion relation for explicitly includes the heights of both layers. If heights of layers are equal (), dispersion relation (6) describes a magneto-Rossby wave in the single-layer shallow water model [27]:
To take into account effects of stratification () Equation (4) is rewritten in the form
Correction is assumed to be small relative to the frequency . Using the notation for the expression in the right-hand side of (7) and following expressions for resonant frequencies (solutions of the first parentheses in (7) equal to zero):
Correction to the magneto-Rossby wave due to stratification in an external vertical magnetic field is obtained in following form:
Dispersion curve of magneto-Rossby wave in an external vertical magnetic field in two-layer shallow water approximation is illustrated in Figure 2a,b shows the dispersion curve of magneto-Rossby wave in an external vertical magnetic field with correction due to stratification in two-layer shallow water approximation . As can be seen from Figure 2 correction slightly modify the dispersion curve.
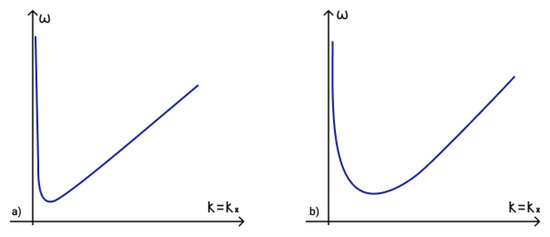
Figure 2.
Dispersion curves of (a) magneto-Rossby wave in an external vertical magnetic field and (b) magneto-Rossby wave in an external vertical magnetic field with correction due to stratification .
Dispersion Equation (5) reduces to the dispersion equation for a layer of neutral fluid of height in the shallow water approximation [80] in the absence of an external magnetic field:
and has a solution in form of a hydrodynamic Rossby wave
The correction due to stratification to a hydrodynamic Rossby wave is also found. The dispersion relation in case of neutral fluid in two-layer model with small difference in densities has the form
Denoting the right-hand side as , the correction as , and taking the condition that into account we have
Dispersion curve of hydrodynamic Rossby wave in two-layer shallow water approximation is illustrated in Figure 3a,b shows the dispersion curve of hydrodynamic Rossby wave with correction due to stratification in two-layer shallow water approximation . As seen from Figure 3, correction slightly modify the dispersion curve.
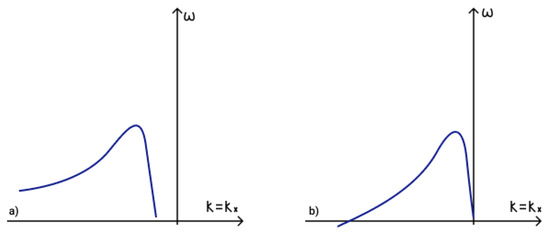
Figure 3.
Dispersion curves of (a) hydrodynamic Rossby wave and (b) hydrodynamic Rossby wave with correction due to stratification .
Summing up, the solution of linearized two-layer shallow water equations with an external vertical magnetic field (3) has been found in the form of a magneto-Rossby wave (6) with a correction (8) due to plasma stratification. Both expression include the parameter related to the effects of sphericity. However, in case of neutral fluid, parameter is absent in expression (12) for correction to hydrodynamic Rossby wave, which describe effects of stratification in case of the absence of magnetic field in two-layer shallow water model.
2.2. Linear Magneto-Rossby Waves in a Stratified Astrophysical Plasma in Two-Layer Approximation in Presence of a Horizontal Magnetic Field
In this subsection we proceed by results of analyzing the flows of a thin stratified plasma layer in shallow water model in -plane approximation in the absence of an external vertical magnetic field. In the case of such magnetic field configuration, Equation (3) have a stationary solution in the form of a horizontal magnetic field:
The dispersion equation for the waves in stratified rotating plasma in a horizontal field in shallow water model on a beta-plane has the following form:
where
is the perturbation frequency, is the perturbation wave vector, and .
Terms on the right-hand side of the expression (13) represent the effects of stratification in the two-layer model. The terms on the left-hand side of (13) are in form of a product of two expressions. The expression in the first bracket corresponds to the lower layer, and in the second—to the upper layer. We investigate the effects of stratification on magneto-Rossby waves in two-layer model. Therefore, we search for solution of (13) in form of magneto-Rossby wave in case of equal densities. Then we assumed the difference in densities is small and search for solution of (13) in form of a correction to the frequency of magneto-Rossby wave related to plasma stratification.
Dispersion Equation (13) in the case of equal magnetic field magnitudes in the layers, and for equal densities () takes the form
The expression of the first term of the product in Equation (14) is a dispersion equation similar to that obtained in a single-layer shallow water model for a layer of plasma with height on the -plane:
It reveals substantial difference between plasma flows in a horizontal and in an external vertical magnetic fields.
The dispersion relation (15) has a solution in the form of a magneto-Rossby wave [27]
whose restoring mechanisms are rotation and magnetic field.
In the particular configuration of a toroidal magnetic field, dispersion relation (16) has the form [14]
To take into account effects of stratification () Equation (13) is rewrited in the following form:
Correction is assumed to be small relative to the frequency . Using notation for the expression on the right-hand side of (17) and following expressions for resonant frequencies (solutions of the first parentheses of dispersion relation (17) being equal zero):
Correction to the magneto-Rossby wave in horizontal magnetic field related to the presence of stratification is obtained in the following form:
The expression (13) describe waves in a layer of neutral fluid of height (9) in case of zero magnetic field () and equal densities (). Its solution has a form of a hydrodynamic Rossby wave (10) with a correction due to stratification (12).
Dispersion curve of magneto-Rossby wave in a horizontal magnetic field in two-layer shallow water approximation is illustrated in Figure 4a,b shows the dispersion curve of magneto-Rossby wave in a horizontal magnetic field with correction due to stratification in two-layer shallow water approximation . As can be seen from Figure 4 correction slightly modify the dispersion curve.
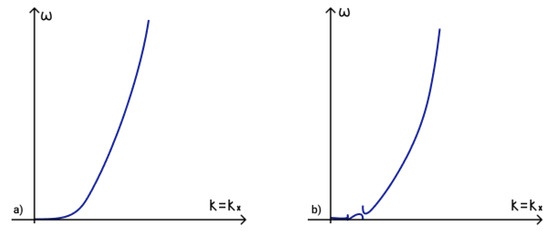
Figure 4.
Dispersion curves of (a) magneto-Rossby wave in a horizontal magnetic field and (b) magneto-Rossby wave in a horizontal magnetic field with correction due to stratification .
Summing up, the solution of linearized two-layer shallow water equations in the absence of an external vertical magnetic field (3) has been found in form of a magneto-Rossby wave (16) with a correction (18) due to plasma stratification. Both expression include the parameter related to the effects of sphericity. Moreover these expressions have substantial difference from those obtained for a configuration with an external vertical magnetic field.
2.3. Three Waves Resonances and Parametric Instabilities in Two-Layer Model for Stratified Astrophysical Plasma
This subsection presents the results of the analysis of the dispersion curves and parametric instabilities of non-linear three-wave interactions of the magneto-Rossby waves in external vertical and horizontal magnetic fields with corrections due to stratification to reveal the fulfillment of the phase-matching condition for three interacting waves with wave vectors , , and frequencies , , [85]:
To determine the fulfilment of the phase-matching condition (19) for three interacting waves it is necessary to analyze dispersion curves. The first term in phase-matching condition (19) determines the point () on a dispersion curve. Term determines the point () on a shifted dispersion curve. The intersection of these two curves determines a point () and reveals the fulfilment of the phase matching condition (19). The dispersion curves in the presence of an external vertical magnetic field are illustrated in Figure 5a, while those for the case of a horizontal magnetic field are illustrated in Figure 5b.
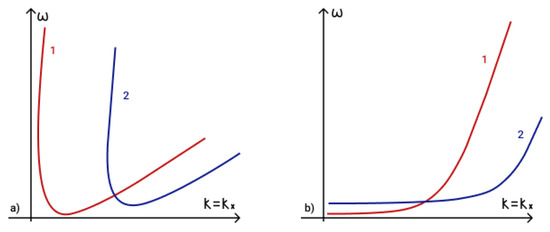
Figure 5.
Phase matching condition for three magneto-Rossby waves in (a) external vertical magnetic field and (b) horizontal magnetic field: 1 — , 2 — .
The intersections of dispersion curves in Figure 5 take place for both magnetic field configurations (an external magnetic field (a) and horizontal magnetic field (b)), which determine the fulfilment of the phase matching condition [86].
To analyze weakly nonlinear wave interactions the asymptotic multiscale expansion method is used. In this article we have restricted ourselves to a schematic description of the method and provide only primary results with references to the coefficients of the amplitude equations and the increments of instability obtained in [28]. The details of the multiscale method in MHD flows of rotating plasma can be found in [27,41,43].
The solution of the equations under study is represented in form of an asymptotic series in the small parameter , which characterizes a weak nonlinearity:
where is the initial equilibrium state, is the solution of the linear system, and is the term describing the quadratic nonlinearity effects. Resonant terms take place in the system in the second order of smallness in . These terms violate the condition of the convergence. Slowly changing amplitudes are introduced to eliminate them. The solution of the equations under study is represented in form of a sum of three interacting waves with slowly changing amplitudes , , and :
where relation between the “slow” (with index 1) and “fast” (with index 0) variables is given by the following relations:
The system of equations in the second order of smallness in derived after representing the solution as (21) has the following form:
where is the linear operator of a linearized system of equations under study dependent on , , , and the right-hand side of the system contains the resonant terms. After applying the compatibility condition [28,43] the resonant terms are eliminated. By successively writing out the terms on the right-hand side proportional to , , and , the system of equations for the amplitudes of three interacting waves satisfying the phase matching condition (19) is obtained:
where is the differential operator with respect to the slow variables
and the coefficients depend only on the initial conditions and interacting wave characteristics.
Note that the system of Equation (24) has a general form for solving various problems of three-wave interactions. Differences related to the geometry of the problem, properties of plasma flows and types of waves are contained precisely in the differential operators and coefficients . Moreover, system of Equation (24) describes two types of the parametric instabilities (amplification and decay) in all cases [27,42]. The main difference consists in the increments of the parametric instabilities and threshold values.
Expressions for coefficients , , and ([28], Equations (50)–(53)) in the presence of an external vertical magnetic field can be logically separated into three groups of terms. Two with similar form are related to the lower and upper layer. Third group include the ratio of densities and represent the effects of stratification in the two-layer shallow water model. These coefficients take form of those obtained in a single-layer shallow water model [80] in case of zero height of one of the layers, equal densities and special condition for the complex wave vector. In a horizontal magnetic field clear difference in expressions is only in coefficients and ([28], p. 61). Other coefficients differ from the corresponding ones found in the case of an external vertical magnetic field only by the components of the eigenvector . Hence, the transition to analogous coefficients in a single-layer shallow water model in a horizontal magnetic field [27] is also take place in this case.
Analysis of the system of Equation (24) in two-layer shallow water model for parametric instabilities of the decay and amplification type presented the following results: the decay of magneto-Rossby wave () into two magneto-Rossby waves () and () with increment of instability ([28], p. 62); the decay of magneto-Rossby wave () into two magneto-Rossby waves () and () with increment of instability ([28], p. 62); the amplification of magneto-Rossby wave () by two magneto-Rossby waves () and () with increment of instability ([28], p. 62); the amplification of magneto-Rossby wave () by two magneto-Rossby waves () and () with increment of instability ([28], p. 62).
Thus in this section linear magneto-Rossby waves and their nonlinear three-wave interactions have been reviewed in MHD shallow water equations in an external magnetic field with stratification in the model of two plasma layers of different but constant densities. Nevertheless, the two-dimensionality of MHD shallow water theory does not allow to describe a stably and continuously stratified plasma layer. The stable and continuous stratification is an important feature of astrophysical flows, so the next section is devoted to a significant step forward in the theory of wave processes in MHD flows of a rotating stratified plasma.
3. Stratified Flows of Rotating Astrophysical Plasma in Boussinesq Approximation
In this section we discuss stably stratified flows of a rotating astrophysical plasma in the Boussinesq approximation with a geometry of a layer as shown on Figure 6. Inertia-gravity waves arise in stratified rotating flows [87,88]. In the geophysical hydrodynamics restoring forces of such waves are Coriolis and buoyancy forces. New types of waves should arise in plasma flows due to the presence of magnetic field as an additional restoring mechanism.
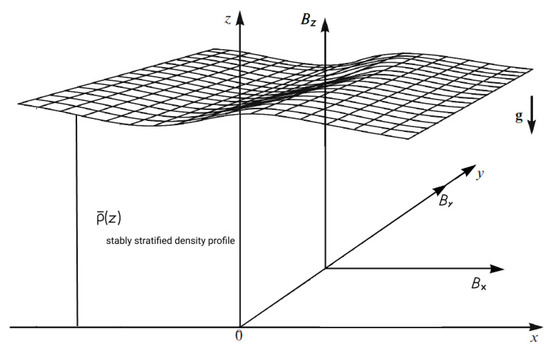
Figure 6.
Geometry of a layer of plasma with stably stratified density profile.
The flow density and temperature variations in Boussinesq approximation must be small and the flow must be buoyancy driven. This way the approximation still correctly describes incompressible fluid, but also includes density variability [89]. In [90] it is shown that the magnetohydrodynamic equations in the Boussinesq approximation represent an incompressible system with temperature gradient being close to the adiabatic temperature gradient and filters out the fast (acoustic) wave processes. In [91] the Boussinesq approximation has been extended by including varying magnetic fields. In the Boussinesq approximation for neutral fluid the fluctuations of pressure are neglected in the equation of state. In the magnetic Boussinesq equations the fluctuations of total pressure (magnetic and thermal) are still considered small. Magnetic Boussinesq approximation is applicable only as long as the horizontal scale of variations is less or one order of the layer height. The Boussinesq approximation is wide-used approximation for investigation of stably stratified flows both in neutral fluid [92,93,94] and in astrophysical plasma [95,96,97]. Three-dimensional MHD equations of rotating stratified plasma in the Boussinesq approximation has the following form:
where is the velocity field, is the magnetic field, f is the Coriolis parameter, is the plasma density, is the density at equilibrium temperature, is the initial density profile providing stable stratification, p is pressure, , and . The first equation of the system is the momentum evolution equation, the second is the magnetic field transport equation, the third is the density evolution equation, and the fourth is the velocity field divergence-free condition. The following notation is introduced: , , .
The system of Equation (26) allows for an analytical study for a stratified plasma layer with an initial stable linear density profile:
where is the Brunt–Väisälä frequency.
In this case density evolution equation (third equation) in (26) is rewritten in the following form:
Thus, the system of Equation (26) together with Equation (27) is used to study stratified flows in two approximations of the Coriolis force: the f-plane approximation and the -plane approximation [29]. Results of this study are discussed below.
3.1. Linear Waves on f-Plane in a Stratified Astrophysical Plasma in Boussinesq Approximation
This subsection presents solutions of the linearized system of Equations (26) and (27) on the background of a stationary state of a layer at rest with constant magnetic field. Coriolis force is taken into account in f-plane approximation, in which Coriolis vector is assumed strictly vertical and constant .
The dispersion relation for waves in a stratified rotating plasma in the Boussinesq approximation on an f-plane has the form
where is the horizontal component of the wave vector. The dispersion Equation (28) has four solutions, which describe two different types of waves with magnetic field, rotation and stratification as their restoring mechanisms. First type is three-dimensional magnetic inertia-gravity waves in the Boussinesq approximation:
In this dispersion relation sign “+” determine wave propagation along the wave vector k and sign “−” — in the direction opposite to k. For the case of zero magnetic field (), this relation describes three-dimensional inertia-gravity waves [98]:
The group velocity of hydrodynamic inertia-gravity wave is perpendicular to the wave vector [98]. Analysis of the dispersion relation (29) has revealed that the presence of a magnetic field breaks this condition. Magnetic inertia-gravity waves propagating only along the vertical component of the wave vector has following dispersion relation
and has only rotation and magnetic field as their restoring mechanisms. The dispersion relation (31) reduces to in the case of zero magnetic field ().
Magnetic inertia-gravity waves propagating in the () plane transform into Alfvén waves with following dispersion relation:
whose dynamics is determined only by magnetic field.
Another solution of (28) determines the second type of waves—three-dimensional magnetostrophic waves:
These waves have no counterpart in the hydrodynamics of a neutral fluid. The dispersion relation for them reduces to zero in the case of zero magnetic field.
Magnetostrophic waves propagating only along the vertical component of the wave vector have the following dispersion relation
and have only rotation and magnetic field as their restoring mechanisms.
Magnetostrophic waves propagating in the plane transform into magnetogravity waves with dispersion relation in the following form:
whose dynamics is determined by stratification and magnetic field. Magnetogravity waves transform to gravitational waves with frequency in the case of zero magnetic field.
The general shape of the dispersion curves for waves on an f-plane for and and are illustrated in Figure 7a,b.
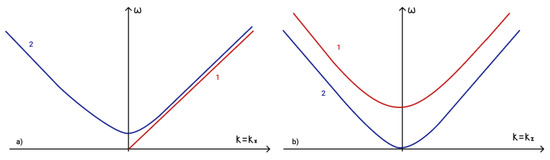
Figure 7.
Dispersion curves for (a) 1—Alfven wave and 2—magnetogravity wave ; (b) 1—magnetic wave with frequency and 2—magnetic wave with frequency
3.2. Linear Waves on -Plane in a Stratified Astrophysical Plasma in Boussinesq Approximation
In this section we proceed by results of analyzing the spherical flows of stably stratified rotating plasma in Boussinesq approximation. Effects of sphericity are taken into account by use of the -plane approximation (2) . This approximation preserves the first order of smallness in the expansion of the Coriolis parameter. The MHD equations of a rotating stratified astrophysical plasma in the Boussinesq approximation with a linear density profile on a -plane has following form
Dispersion equation for waves in a rotating stratified plasma on a -plane in the Boussinesq approximation has been found in the following form:
where and .
In the horizontal flows approximation () the dispersion relation takes form
and has solutions in form of magnetogravity and magneto-Rossby waves. Magnetogravity waves are analogous to those obtained in an f-plane approximation (35). The first type of magneto-Rossby waves has following dispersion relation
and transform into hydrodynamic Rossby waves in the case of zero magnetic field:
The second type of magneto-Rossby waves has following dispersion relation
and disappear in the case of zero magnetic field.
Both types of magneto-Rossby waves have rotation and magnetic field as their restoring mechanisms. Moreover, both of them transform into Alfvén waves in case of propagation strictly along :
Dispersion relation (37) has a low-frequency solution in the form of a three-dimensional magneto-Rossby wave:
which has an additional restoring force — the buoyancy force. The dispersion relation (43) take form similar to that obtained in the shallow water model in case of horizontal flow approximation () [22,41]:
when waves propagate strictly along , they take form of two types of magnetic waves as in an f-plane approximation, (31) and (34).
The general shape of the dispersion curves for waves on an -plane for and are demonstrated in Figure 8.
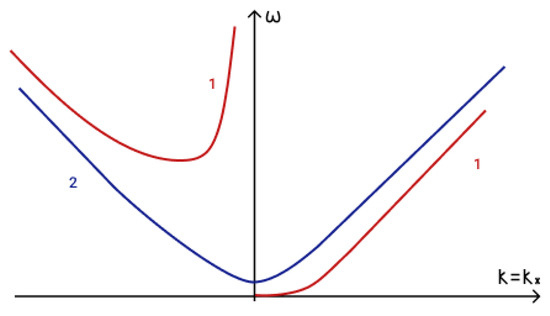
Figure 8.
Dispersion curves for 1—magneto-Rossby wave and 2—magnetogravity wave .
In the case of neutral fluid hydrodynamics (), Equation (37) takes the form
The dispersion relation for three-dimensional low-frequency hydrodynamic Rossby wave obtained in Boussinesq approximation has the following form:
In case of horizontal flows () this dispersion relation determine standard hydrodynamic Rossby wave (40). Note, that three-dimensional Rossby wave in Boussinesq approximation has two restoring mechanisms, namely rotation and stratification, in contrast to standard Rossby wave with rotation only.
3.3. Three Waves Resonances and Parametric Instabilities in Boussinesq Model for Stratified Astrophysical Plasma
This section presents the results of the analysis of the dispersion curves and parametric instabilities of non-linear three-wave interactions of waves in the Boussinesq approximation. The following three-waves interactions that satisfy the phase matching condition (19) are found for waves on f-plane: the emergence of magnetogravity wave (35) due to the interaction of Alfvén wave (32) and magnetogravity wave (Figure 9); the emergence of magnetic wave with frequency (31) due to the interaction of magnetic wave with frequency (34) and magnetic wave with frequency (Figure 10a); the emergence of magnetic wave with frequency due to the interaction of two magnetic waves with frequencies (Figure 10b).
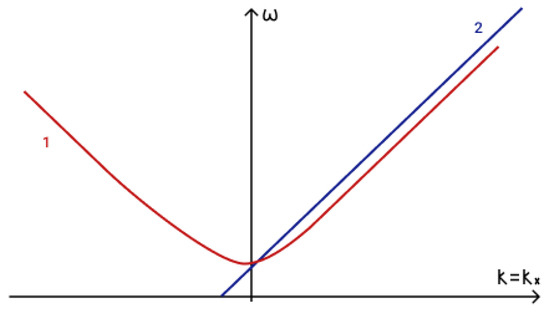
Figure 9.
Phase matching condition for two magnetogravity waves and one Alfvén wave: 1—, 2—.
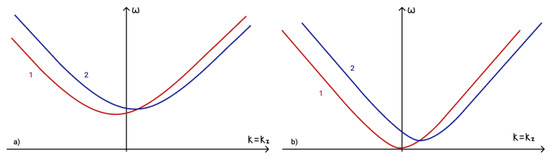
Figure 10.
Phase matching condition for (a) two waves with frequency and one wave with frequency : 1—, 2—; (b) three waves with frequency : 1—, 2—.
Qualitative analysis of dispersion relations of waves on -plane shows the possibility of the following three-waves interactions: three magneto-Rossby waves with frequency interact with each other (Figure 11); two magnetogravity waves (35) interact with magneto-Rossby wave with frequency (Figure 12a) and two magneto-Rossby waves with frequency interact with magnetogravity wave (35) (Figure 12b).
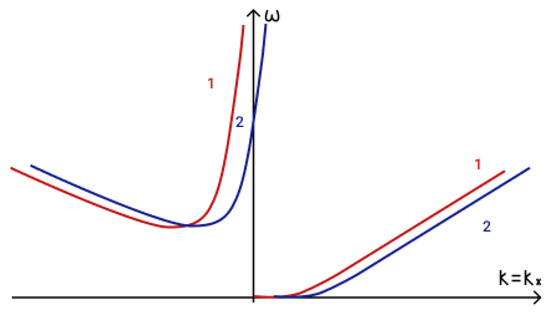
Figure 11.
Phase matching condition for three magneto-Rossby waves: 1—, 2—.
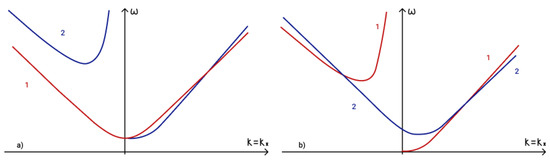
Figure 12.
Phase matching condition for (a) two magnetogravity waves one magneto-Rossby wave: 1—, 2—; (b) two magneto-Rossby waves and one magnetogravity wave: 1 — , 2—.
Moreover an interaction of three magneto-Rossby waves (43) for low-frequency approximation is shown in Figure 13.
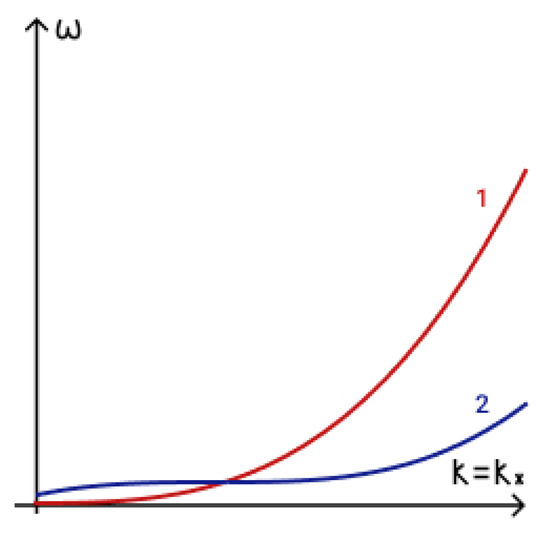
Figure 13.
Phase matching condition for three magneto-Rossby waves in low-frequency approximation: 1—, 2—.
Summing up, the following three-wave interactions have been revealed by use of a qualitative analysis of dispersion curves on f-plane: two magnetogravity waves and one Alfvén wave; two magnetic waves with frequency (31) and a magnetic wave with frequency (34); three magnetic waves with frequency (34). For waves on -plane three-waves interactions are following: three magneto-Rossby waves, two magnetogravity waves and magneto-Rossby wave, two magneto-Rossby waves and magnetogravity wave, three magneto-Rossby waves in low-frequency approximation.
As it was mentioned in Section 2, to analyze weakly nonlinear wave interactions the asymptotic multiscale expansion method is used. The system of amplitude equations for three interacting waves in stratified flows of rotating plasma in Boussinesq approximation has form (24) with coefficients , , , , ([29], Equations (18)–(22)) on f-plane; and , , , , ([29], Equations (52)–(56)] on -plane.
Analysis of this system of equations on an f-plane for parametric instabilities of the decay and amplification type reveals the following configurations: the decay of magnetogravity wave into Alfvén wave and magnetogravity wave ; the decay of magnetic wave into magnetic wave and magnetic wave ; the decay of magnetic wave into two magnetic waves and ; the amplification of magnetogravity wave by Alfvén wave and magnetogravity wave ; the amplification of magnetic wave by magnetic wave and magnetic wave ; the amplification of magnetic wave by two magnetic waves and .
Analysis of parametric instabilities of the decay and amplification type in Boussinesq approximation on a -plane reveals the following configurations: the decay of magneto-Rossby wave either into two magneto-Rossby waves and , or into two magnetogravity waves and ; the decay of magnetogravity wave into two magneto-Rossby waves and ; the decay of low-frequency magneto-Rossby wave into two low-frequency magneto-Rossby waves and ; the amplification of magneto-Rossby wave either by two magneto-Rossby waves and , or by two magnetogravity waves and ; the amplification of magnetogravity wave by two magneto-Rossby waves and ; the amplification of low-frequency magneto-Rossby wave by two low-frequency magneto-Rossby waves and .
The instability increment of decay in all these instabilities is and the amplification factor is .
Thus in this section results on study of linear waves and their nonlinear three-wave interactions in MHD equations for a stratified rotating plasma in Boussinesq approximation have been presented. The Boussinesq approximation is an approximation only for incompressible flows. Moreover its applicability is valid for density gradient proportional only to the temperature gradient [49]. In the next section we discuss compressible rotating astrophysical plasma flows.
4. Compressible Stratified Flows of Rotating Astrophysical Plasma in Anelastic Approximation
In this section we discuss the fundamental role of compressibility in large-scale rotating astrophysical plasma flows with a stable stratification in anelastic approximation of complete MHD system of equations [66]. This approximation filters out acoustic waves. The density gradient in anelastic approximation depends on both pressure and temperature gradients [65] and density perturbations are assumed small. The subject of investigation in MHD model of compressible plasma in the anelastic approximation is low Mach number flows [74,99]. Such flows are characterized by the characteristic time scale exceeding the propagation time of acoustic waves. Volume change of a vertically moving fluid element occurs due to the pressure change. In this way the effects of compressibility are taken into account in anelastic approximation. Geometry of a layer of plasma for study of compressible flows in anelastic approximation is shown on Figure 14.
Figure 14.
Geometry of a layer of plasma with stably stratified entropy (potential temperature) profile.
For the first time the anelastic approximation has been introduced in study on geophysical hydrodynamics [100]. Equations form the above paper have been obtained by use of the multiscale analysis. Some assumptions have been made, namely near-adiabatic distribution of pressure, density and potential temperature, and determination of time scale by the Brunt–Väisälä frequency. After deriving the equations, the author has found that there have been no acoustic waves in them, which was not originally the purpose of the approximation.
This purpose has been first set in [101] in the model of large-scale geophysical hydrodynamic. The absence of acoustic waves could simplify the numerical simulations of heat convection. Possibility of using anelastic approximation in studies of inertia-gravity waves at low Mach numbers has been first declared in [102]. Note also a number of important papers in field of mathematical features of the anelastic approximation in hydrodynamics [103,104,105,106,107].
The anelastic approximation usability in studies of terrestrial convection and geodynamo problems have been mentioned in [108,109,110,111]. Interest in the possibilities of using the approximation in studies of astrophysics and planetary physics has appeared. For these purposes the anelastic approximation has been applied in [112,113] for equations of a neutral fluid. The anelastic approximation for MHD equations has been applied in [114,115,116,117,118,119,120] to study the convection and dynamo on the Sun and in stars.
For more clear understanding of further results, these papers should be noted [65,121]. In [65] has been derived the system of equations in anelastic approximation for a neutral gas. The derivation has been made with introduction of reduced pressure, which is most adequate for astrophysical problems. This method has been extended for MHD equations of rotating plasma flows in [121]. Based on this technique the MHD equations of compressible stratified rotating plasma flows have been derived in [66]:
where variables with bottom index 0 are quantities at initial state and variables with hatches are their perturbations. Here is the plasma density, is the velocity field, is the Coriolis parameter, is the angular velocity vector, p is the pressure, is the gravitational acceleration, is the magnetic field, is <<reduced pressure>> [65,121], and is the potential temperature.
There are crucial differences between the systems of equations in the anelastic (47) and Boussinesq approximations (26). The energy equation in anelastic approximation is written in terms of the potential temperature, not in terms of the density as it is written in Boussinesq approximation. The continuity equation in anelastic approximation includes the initial stratified density profile, while the continuity equation in Boussinesq approximation is reduced to divergence-free condition for the velocity field. The equation of state in anelastic approximation defines the density function as a function of not only the pressure as in Boussinesq approximation, but also of the potential temperature (entropy). Summing up, pressure and density of the fluid change not only due to the buoyancy force, as in Boussinesq approximation, but also due to the potential temperature (entropy) variations.
The derived system of Equation (47) admit an analytical study for a stratified layer of plasma with an initial stable linear entropy profile
The Brunt–Väisälä frequency in compressible stratified astrophysical plasma flows has the following form:
Including compressibility in Equation (49) leads to the Brunt–Väisälä frequency being a function of not only density, but also pressure. The first term in the expression (49) is quite similar to the Brunt–Väisälä frequency in the Boussinesq approximation . The difference contains in the initial density profile that ensures the linearity and stability of the entropy profile (). To present further results in more compact and convenient way the designation of the first term in (49) is made in the following form:
In addition, following redesignations for the potential temperature and the magnetic field are introduced:
Thus, the system of Equation (47) taking into account Equations (49)–(51) is used to study stratified flows of compressible plasma in two approximations of the Coriolis force: the f-plane approximation and the -plane approximation [66]. Results of this study are discussed below.
4.1. Linear Waves on f-Plane in a Stratified Compressible Astrophysical Plasma in Anelastic Approximation
This section presents solutions of the linearized system (47) on the background of a stationary state of layer at rest with constant magnetic field. Coriolis force is taken into account in f-plane approximation, in which Coriolis vector is assumed strictly vertical and constant .
The dispersion equation for waves in rotating compressible stratified plasma in anelastic approximation on an f-plane has the form:
where .
In the case of initial magnetic field configuration in following form , the dispersion Equation (52) transforms into
There are four solutions of this dispersion equation, which describe two types of three-dimensional waves in anelastic approximation. The first type is compressible magnetic inertia-gravity waves with following dispersion relation
which is analogues to the same type of waves in the Boussinesq approximation (29). Fundamental difference between anelastic and Boussinesq magnetic inertia-gravity waves contained in the Brunt–Väisälä frequency in Equation (54). This frequency due to its dependence not only on the initial density abut also on the pressure profiles represents the feature of compressibility as an additional restoring mechanism of the wave, along with rotation, magnetic field and gravity.
In the case of zero magnetic field (), Equation (54) describes three-dimensional inertia-gravity waves in a neutral fluid [98]:
The second type of waves, another solutions of the Equation (53), is three-dimensional magnetostrophic waves in the anelastic approximation:
These waves are quite similar to those obtained in the Boussinesq approximation (33). The difference is the Brunt–Väisälä frequency , which represents the compressibility effects.
Equation (52) in horizontal flow approximation () takes following form
and has two types of waves as its solutions: Alfvén waves (32) and two-dimensional magneto-gravity waves in the anelastic approximation with the dispersion relation in following form:
Expression (58) determines gravity waves in compressible neutral fluid with frequency in the case of zero magnetic field.
Equation (52) in vertical flow approximation () has same solutions as in the Boussinesq approximation (31) and (34).
The general shape of the dispersion curves for waves on an f-plane for and are illustrated in Figure 15a,b.
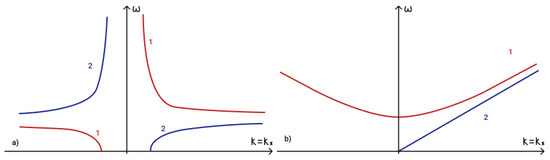
Figure 15.
Dispersion curves for (a) 1—compressible magnetic inertia-gravity wave and 2—compressible magnetostrophic wave ; (b) 1—compressible magnetogravity wave and 2—Alfven wave .
Thus, in the f-plane approximation compressible magneto-gravity, compressible magnetostrophic, and compressible magnetic inertia-gravity waves have been found. The compressibility effects are represented in their dispersion relations by the term with the Brunt–Väisälä frequency. In addition to new type of waves analogous to waves in Boussinesq approximation have been found, such as Alfvén waves and vertical magnetic waves.
4.2. Linear Waves on -Plane in a Stratified Compressible Astrophysical Plasma in Anelastic Approximation
In this section we proceed by results of analyzing the flows of compressible stratified rotating plasma with regard to the effects of sphericity in the -plane approximation (2) (). The system of MHD equations of a compressible stratified rotating plasma in the anelastic approximation on a -plane has the form:
The dispersion equation for waves in rotating compressible stratified plasma in anelastic approximation on -plane has the form:
Consider horizontal flow approximation (). The Equation (60) in this case takes following form:
Expression (61) describes three types of waves, namely compressible magneto-gravity waves analogous to those on an f-plane (58) and magneto-Rossby waves analogous to those in Boussinesq approximation (39) and (41).
For flows with one-dimensional perturbations directed strictly along the poloidal magnetic field component, the Equation (60) transforms into
Expression (62) describes two types of waves: Alfvén waves (42) and magneto-gravity waves with the dispersion relation in the form .
Three-dimensional low-frequency magneto-Rossby waves in anelastic approximation have been found in following form:
Expression (63) includes the effects of compressibility by means of the Brunt–Väisälä frequency . Equation (63) has a form quite similar to the dispersion relation for three-dimensional low-frequency magneto-Rossby waves in the Boussinesq approximation (63). The difference consists not only in the Brunt–Väisälä frequency, but also in in the denominator. There is an additional term related to the density stratification, which zeros out in the case of vertical magnetic field.
The general shape of the dispersion curve of low-frequency magneto-Rossby wave (63) for and is illustrated in Figure 16.
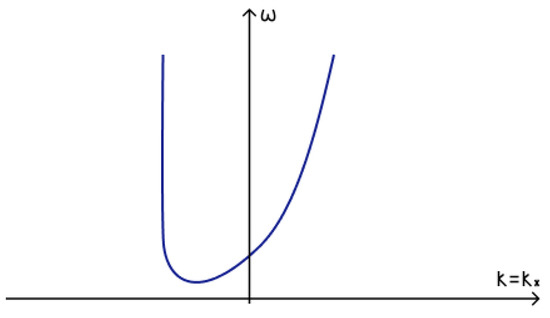
Figure 16.
Dispersion curve of low-frequency magneto-Rossby wave.
Summing up, in -plane approximation compressible magneto-gravity waves and compressible three-dimensional low-frequency magneto-Rossby waves have been found. The compressibility effects are represented in their dispersion relations by means of the Brunt–Väisälä frequency. This frequency in compressible flows includes both initial density and pressure profiles. In addition to the new types of waves, Alfvén waves and magneto-Rossby waves have been found in similar form to the waves in Boussinesq approximation.
4.3. Three Waves Resonances and Parametric Instabilities in Anelastic Model for Compressible Stratified Astrophysical Plasma
This section presents the results of the analysis of dispersion curves and parametric instabilities of non-linear three-wave interactions of waves in the anelastic approximation. For waves on f-plane the following three-waves interactions are found that satisfy the phase matching condition (19): magnetogravity wave occurs (58) due to the interaction of Alfvén wave (32) and magnetogravity wave (Figure 17); magnetic inertia gravity wave occurs (54) due to the interaction of magnetostrophic wave (56) and magnetic inertia gravity wave (Figure 18a); magnetostrophic wave occurs due to the interaction of two magnetic inertia gravity waves (Figure 18b); magnetostrophic wave occurs due to the interaction of magnetic inertia gravity wave and magnetostrophic wave (Figure 18c); magnetic inertia gravity wave occurs due to the interaction of two magnetostrophic waves (Figure 18d); magnetostrophic wave occurs due to the interaction of two magnetostrophic waves (Figure 18e).
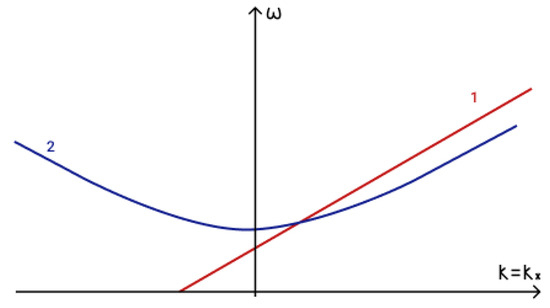
Figure 17.
Phase matching condition for two magnetogravity waves and one Alfvén wave: 1—, 2—.
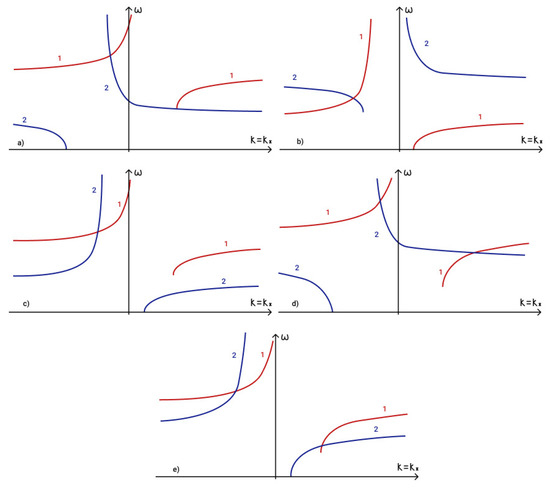
Figure 18.
Phase matching conditions for (a) two magnetic inertia gravity waves and one magnetostrophic wave: 1—, 2—, (b) two magnetic inertia gravity waves and one magnetostrophic wave: 1—, 2—, (c) two magnetostrophic waves and one magnetic inertia gravity wave: 1—, 2—, (d) two magnetostrophic waves and one magnetic inertia gravity wave: 1—, 2—, (e) three magnetostrophic waves: 1—, 2—.
Three-waves interaction of three magneto-Rossby waves in low-frequency approximation for a new type of waves on -plane in anelastic approximation is shown in Figure 19.
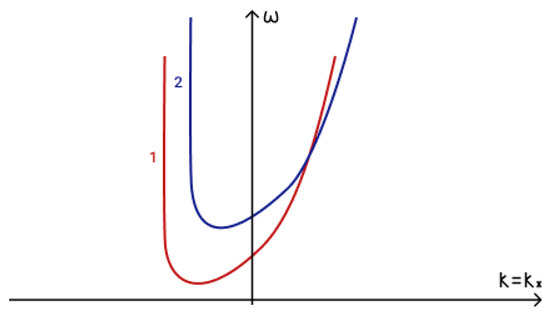
Figure 19.
Phase matching condition for three magneto-Rossby waves in low-frequency approximation: 1 — , 2 — .
As it was mentioned in Section 2, to analyze weakly nonlinear wave interactions the asymptotic multiscale expansion method is used. The system of amplitude equations for three interacting waves in compressible stratified flows of rotating plasma in anelastic approximation has the form (24) with coefficients , , , , ([66], Equations (100)–(104)) on f-plane and , , , , ([66], Equations (112)–(116)) on -plane.
Analysis of this system of equations on an f-plane for parametric instabilities of the decay and amplification type presented the following configurations: the decay/amplification of Alfvén wave into/by two compressible magnetogravity waves and ; the decay/amplification of magnetic wave into/by magnetic wave and magnetic wave ; the decay/amplification of magnetic wave into/by two magnetic waves and ; the decay/amplification of compressible magnetostrophic wave either into/by two compressible magnetic inertia-gravity waves and , or into/by compressible magnetostrophic wave and compressible magnetic inertia-gravity wave , or into/by two compressible magnetostrophic waves ; the decay/amplification of compressible magnetic inertia-gravity wave either into/by compressible magnetic inertia-gravity wave and compressible magnetostrophic wave , or into/by two compressible magnetostrophic waves and .
Analysis of parametric instabilities of the decay and amplification type in anelastic approximation on a -plane presented the following configurations: the decay/amplification of magneto-Rossby wave either into/by two magneto-Rossby waves and , or into/by two compressible magnetogravity waves and ; the decay/amplification of compressible magnetogravity wave into/by two magneto-Rossby waves and ; the decay/amplification of low-frequency compressible magneto-Rossby wave into/by two low-frequency compressible magneto-Rossby waves and .
The instability increment of decay in all these instabilities is and the amplification factor is .
Thus in this section we have presented results on study of linear waves and their nonlinear three-wave interactions in compressible stably stratified rotating plasma in the anelastic approximation. In the next section we discuss two-dimensional rotating flows of compressible plasma in magnetohydrodynamic shallow water model with an external magnetic field.
5. Compressible Flows of Rotating Astrophysical Plasma in Magnetohydrodynamic Shallow Water Approximation
In this section we discuss compressible rotating flows of astrophysical plasma in the presence of an external vertical magnetic field. Such flows are described by magnetohydrodynamic equations in shallow water approximation with large-scale compressibility [67]. To derive the system of MHD equations in the shallow water approximation including large-scale density variations the original three-dimensional MHD equations are averaged over the plasma height. The geometry of a plasma layer is shown in Figure 20. Wherein the pressure is assumed to be hydrostatic and the layer height is assumed to be much less than a characteristic horizontal flow size [41]. The obtained system represents a generalization of the equations derived in [2,38,39,42,62,63,64]. In contrast to the incompressible MHD shallow water equations [41,75,76,77], in the proposed approximation, the sound waves are excluded from consideration and the density varies on large scales describing the effects of static compressibility. It is shown, that the main parameter defining the plasma layer dynamics is a product of the depth-averaged plasma density and layer height. The mass conservation law is formulated for a variable that nontrivially depends on the ratio of the characteristic vertical scale of the flow and the scale of height at which the density variation becomes significant. The horizontal momentum in the equations is taken into consideration more accurately compared to the case of an incompressible fluid [27], which offers a fundamental advantage when applying these equations to the description of space and astrophysical flows. Therefore, the derived system is widely used in applications for the description of an astrophysical plasma processes.
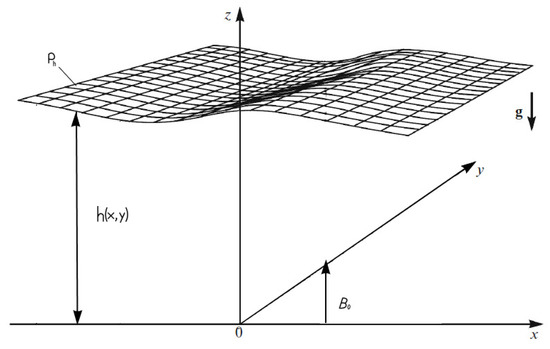
Figure 20.
Geometry of the a layer of compressible plasma.
The system of MHD shallow water equations in an external magnetic field with a large-scale compressibility is derived from a three-dimensional system of MHD equations for compressible rotating plasma in gravitational field, the equation describing the variation of internal energy in adiabatic processes and the Clapeyron equation [67]. The equations are integrated along z axis from 0 to h, taking into account the boundary conditions and hydrostatic condition for the total pressure. The height of the layer is assumed to be small in comparison with the characteristic horizontal flow scale. Upon application of an external vertical magnetic field, the term must be added to the boundary conditions for vertical magnetic field component at each surface. After disregarding terms with fluctuations, the height-averaged density, velocities and magnetic fields are introduced. The product of averaged density and the layer height is introduced as a new variable to close the obtained system of equations. Detailed derivation of these equations can be found in [67].
Thus, the system of MHD equations in shallow water approximation with rotation in an external vertical magnetic field with large-scale compressibility has the following form:
where f is the Coriolis parameter and g is gravity acceleration; g and f are assumed to be constant, is a non-negative monotonically increasing function of l:
In (65) is the plasma density on the free surface, is the total (magnetic and hydrodynamic) plasma pressure on the free surface, is the adiabatic index. The system of Equation (64) is written in terms of the horizontal flow velocities averaged over the layer height and , the height-averaged horizontal magnetic fields and , the height-averaged vertical magnetic field , and the variable l playing the same role as layer height for an incompressible flow. The variable l is explicitly linked to the layer height h:
where is the plasma density averaged over the layer height. represents the scale of height at which the density variations becomes significant:
where is specific heat at constant pressure. If the characteristic scale (67) is much larger than the layer height h (), then the flow may be considered incompressible. The fulfillment of this condition transforms the system of shallow water equations for a compressible plasma (64) to the classical MHD rotating shallow water equations for an incompressible plasma.
The obtained system (64) naturally generalize the MHD shallow water equations derived in [42,43]. The first equation is a consequence of the mass conservation law. The two following equations represent the equations for the momentum. The fourth and the fifth equations describe the variations of the depth-averaged horizontal magnetic field. Compared to the equations in [42], this new system contains new terms caused by the presence of the external vertical magnetic field . The system (64) is supplemented with a new equation for the vertical component of the magnetic field . This equation is obtained by integrating the equation for the third component of the magnetic field in a three-dimensional system. The last equation is an analogue for the divergence-free condition in the three-dimensional MHD system and it can be obtained as a consequence of the equations for the magnetic field. This condition is satisfied identically when the proper initial conditions for the magnetic field are specified.
The presence of an external vertical magnetic field in the thin plasma layer leads to significant changes in the developed system. A new equation for the vertical component of the magnetic field makes it a fundamentally three-component, where the components of magnetic field depend only on horizontal coordinates and time. Equations for the momentum and for the horizontal components of the magnetic field include new terms with the external vertical magnetic field . These new terms define significant changes in the linear waves and weakly nonlinear theory. The equation for the vertical component can be separated from the system, therefore, we can consider the system of the first five equations in linear and weakly nonlinear approximations. It is shown, that in the absence of an external vertical magnetic field, the system transforms to the MHD shallow water equations with the large-scale compressibility derived in [42].
The obtained system has a number of essential differences from the classical shallow water MHD equations. The main parameters defining the interaction of the fluid column with the remaining fluid are height of the flow, horizontal velocities and horizontal magnetic fields. In the system (64) instead of the height of the plasma layer h, a new variable l is used, which depends on the mean density of the plasma column. It allows us to describe the horizontal momentum and magnetic field dynamics more accurately. Therefore, a new variable l contains a dependence from a characteristic horizontal scale and it includes in the equations the effects of the large-scale compressibility. All the equations in the obtained system are written with the new variable, which significantly improves the description of the astrophysical processes.
5.1. Linear Waves on f-Plane in a Compressible Astrophysical Plasma in Magnetohydrodynamic Shallow Water Approximation
This section present solutions of the linearized system of Equation (64) on the background of a stationary state , and in the absence of the vertical magnetic field with a constant horizontal magnetic field , , , . Coriolis force is taken into account in f-plane approximation ().
The dispersion equation for the waves in rotating stratified plasma with large-scale compressibility in an external vertical magnetic field on a f-plane has the following form:
The solutions of Equation (68) are dispersion relations that describe waves equivalent to magneto-Poincare and magnetostrophic waves in an incompressible plasma in an external vertical magnetic field. The dispersion relation for magneto-Poincare waves in compressible plasma in an external vertical magnetic field in shallow water approximation has the form:
In the absence of magnetic field () this relation describe Poincare waves in neutral fluid dynamics.
The dispersion relation for magnetostrophic waves in compressible plasma in an external vertical magnetic field in shallow water approximation has the form:
This type of waves has no counterpart in a neutral fluid dynamics. Note that if the layer height is small compared to the scale height where compressibility effects become important, then the variable transforms to the layer height and the dispersion relations transform to those for an incompressible plasma [45].
The dispersion equation for the waves in rotating stratified plasma with large-scale compressibility in horizontal magnetic field with the stationary solution , , , on f-plane has following form:
The solutions of Equation (72) are dispersion relations describing waves equivalent to magneto-Poincare and magnetostrophic waves in an incompressible plasma in horizontal magnetic field. The dispersion relation for magneto-Poincare waves in horizontal magnetic field in approximation of large-scale compressibility has the form:
In the absence of magnetic field () this relation describes Poincare waves in a neutral fluid dynamics (70). The dispersion relation for magnetostrophic waves in compressible plasma in horizontal magnetic field in shallow water approximation has form:
This type of waves has no counterpart in a neutral fluid dynamics. If the layer height is small compared to the scale height , then the variable transforms to the layer height and the dispersion relations transform to those for an incompressible plasma [44].
The general shape of the dispersion curves for waves on an f-plane in an external vertical magnetic field and in a horizontal magnetic field for and are illustrated in Figure 21.
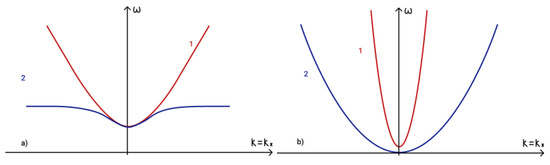
Figure 21.
Dispersion curves for 1—magneto-Poincare and 2—magnetostrophic waves (a) in an external vertical magnetic field and (b) in a horizontal magnetic field.
Dispersion relations for magneto-Poincare (69) and (73) and magnetostrophic (71) and (74) waves in a compressible medium and those in the case of an incompressible plasma ([44,45]) almost match. The differences are in the term with the external magnetic field , which transforms to and in the expression for the square of the velocity of weak disturbances changes to . The latter generally leads to a change in the group velocity of magneto-Poincare and magnetostrophic waves. Compressibility changes the curvature of the dispersion surfaces, with their overall shape remaining analogous to the case of an incompressible plasma [43].
5.2. Linear Waves on -Plane in a Compressible Astrophysical Plasma in Magnetohydrodynamic Shallow Water Approximation
In this section we proceed by results of analyzing the flows of compressible rotating plasma in an external vertical magnetic field in shallow water approximation with regard to the effects of sphericity in the -plane approximation (2) (). The system of MHD equations of compressible rotating plasma in an external vertical magnetic field in shallow water approximation on a -plane has the form:
The system of Equation (75) has a nontrivial stationary solution in the form of a layer with a constant thickness , , . The dispersion equation in this case has the form:
The dispersion relation (76) describes waves in magnetohydrodynamics on the -plane in an external vertical magnetic field with plasma compressibility. In the high-frequency approximation the dispersion relation (76) describes waves analogous to magneto-Poincare waves in a compressible plasma (69). In the low-frequency approximation the dispersion relation (76) describes large-scale Rossby waves for which relation (76) takes the form
The obtained dispersion relation also has a solution of fast magneto-Rossby wave modes in plasma with a large-scale compressibility analogous to those considered in [14] in the incompressible case. This solution lies between high frequency magneto-Poincare mode and the low-frequency slow magneto-Rossby mode (77). Here we primarily discuss slow low-frequency planetary Rossby waves. The dispersion relation ((77) determines waves in the shallow water MHD with a large-scale compressibility propagating eastward. This wave generates due to the shift of the rotating flow because of the Coriolis force changes with latitude.
It follows from (76) that large-scale compressibility in the MHD shallow water equations modifies the dispersion relation in the linear theory. As in the case of waves on the f-plane, the general form of the dispersion curves is retained, while the coefficients in the dispersion relation are modified: the expression (65) appears instead of the expression for the squared velocity of small disturbances in an incompressible layer and the coefficient related to the external vertical magnetic fields changes to compared to the incompressible case [27]. Thus, compressibility changes the group velocity of magneto-Rossby waves. In the limit of an incompressible plasma () the dispersion relation completely transforms to the well-known relation for an incompressible plasma.
The system of equations (75) on the -plane in the absence of an external magnetic field () also has an exact stationary solution , , , , corresponding to the presence of a horizontal magnetic field . The dispersion equation in this case has the form:
The dispersion relation (78) describes waves in magnetohydrodynamics on the -plane in a horizontal magnetic field with plasma compressibility. In the low-frequency approximation the dispersion relation (78) describes large-scale Rossby waves for which relation (78) takes the form
Relation (79) describes MHD Rossby waves in a horizontal magnetic field in the shallow water approximation propagating in the direction.
The general shape of the dispersion curves for waves on an -plane for and is demonstrated in Figure 22.
Figure 22.
Dispersion curves for magneto-Rossby waves in (a) external vertical magnetic field and in (b) horizontal magnetic field.
Thus, in the linear theory for magneto-Rossby waves in a horizontal magnetic field compressibility leads to a new expression for the squared velocity of small disturbances , while the general form of the dispersion relation does not change. Compressibility changes the group velocity of magneto-Rossby waves in a horizontal magnetic field. Note also that instead of the variable h, a new variable l appears in relation (79), which includes the dependence on the mean density of a plasma column. In the approximation of an incompressible plasma , the dispersion relation transforms to a well-known one [27].
5.3. Three Waves Resonances and Parametric Instabilities in Magnetohydrodynamic Shallow Water Model for Compressible Astrophysical Plasma
This section presents the results of the analysis of the dispersion curves and parametric instabilities of non-linear three-wave interactions of waves in magnetohydrodynamic shallow water approximation with large-scale compressibility [67].
The following three-waves interactions satisfying the phase matching condition (19) are found on an f-plane in an external vertical magnetic field and in horizontal magnetic field: three magneto-Poincare waves (69) interaction (Figure 23a and Figure 24a), interaction of two magneto-Poincare waves and one magnetostrophic (71) wave (Figure 23b and Figure 24b), interaction of two magnetostrophic waves and one magneto-Poincare wave (Figure 23c and Figure 24c), and three magnetostrophic waves interaction (Figure 23d and Figure 24d).
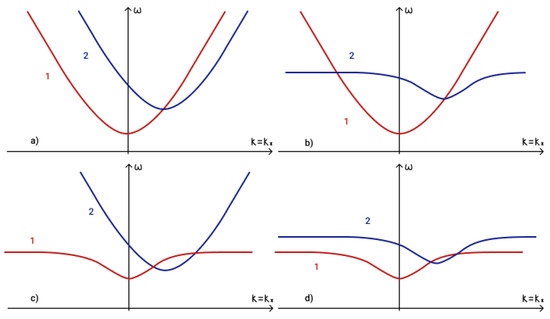
Figure 23.
Phase matching conditions for waves in an external vertical magnetic field, namely for (a) three magneto-Poincare waves: 1—, 2—, (b) two magneto-Poincare and one magnetostrophic waves: 1—, 2—, (c) two magnetostrophic and one magneto-Poincare waves: 1—, 2—, (d) three magnetostrophic waves: 1—, 2—.
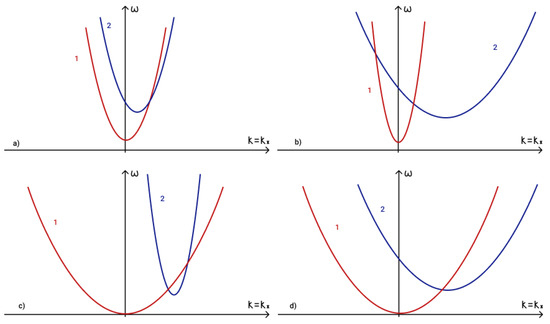
Figure 24.
Phase matching conditions for waves in a horizontal magnetic field, namely for (a) three magneto-Poincare waves: 1—, 2—, (b) two magneto-Poincare and one magnetostrophic waves: 1—, 2—, (c) two magnetostrophic and one magneto-Poincare waves: 1—, 2—, (d) three magnetostrophic waves: 1—, 2—.
In the case of -plane in a vertical magnetic field it is shown (Figure 25a) that there exists an interaction of three magneto-Rossby waves in the presence of large-scale compressibility (77). In horizontal magnetic field there exists interaction (Figure 25b) of three magneto-Rossby waves in the presence of large-scale compressibility (79).
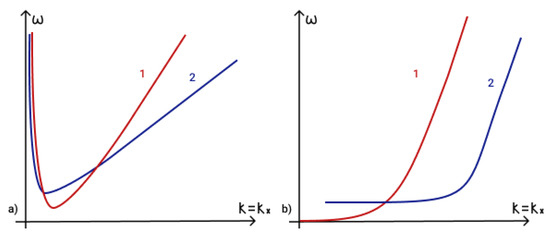
Figure 25.
Phase matching conditions for (a) three magneto-Rossby waves in vertical magnetic field: 1—, 2—, (b) three magneto-Rossby waves in horizontal magnetic field: 1—, 2—.
As in the previous sections, the asymptotic multiscale expansion method is used to analyze weakly nonlinear wave interactions. The system of amplitude equations for three interacting waves in the flows of rotating plasma with a large-scale compressibility has the form (24) with coefficients , , , ([67], Equations (4.12)–(4.13)), on f-plane; , , , Equations (4.23)–(4.25), on -plane in vertical magnetic field; , , , ([67] Equations (4.31)–(4.33)), on -plane in horizontal magnetic field.
Analysis of this system of equations on an f-plane for parametric instabilities presented the following configurations: the decay/amplification of magneto-Poincare wave into/by two magneto-Poincare waves , the decay/amplification of magneto-Poincare wave into/by magneto-Poincare wave and magnetostrophic wave , the decay/amplification of magnetostrophic wave into/by magneto-Poincare wave and magnetostrophic , the decay/ amplification of magnetostrophic wave into/by two magnetostrophic waves .
Analysis of this system of equations on an -plane in vertical magnetic field for parametric instabilities presented the decay/amplification of magneto-Rossby wave into/by two magneto-Rossby waves . Similarly, for the equations in horizontal magnetic field there exists the decay/amplification of magneto-Rossby wave into/by two magneto-Rossby waves
The instability increment of decay in all these instabilities has a similar form: and the amplification factor is , where the coefficients differs for different cases of three-waves interactions.
Thus in this section results have been presented on study of linear waves and their nonlinear three-wave interactions in a rotating layer of plasma in an external vertical magnetic field and in horizontal magnetic field in shallow water approximation with large-scale compressibility.
6. Conclusions
Variable density flows are common and important for most objects in the Universe. Correct accounting of stratification and compressibility allows one to bring theoretical models closer to real objects. Since the aim of plasma astrophysics is to investigate and describe the behaviour of plasma and understand the detailed evolution of different astrophysical objects, the demand for more accurate models taking into account the various properties of plasma objects is high. We have discussed here rotating flows of astrophysical plasma in gravitational field with regard to variable density effects in four different magnetohydrodynamic approximations: two-layer shallow water approximation, Boussinesq approximation, anelastic approximation and shallow water approximation with large-scale compressibility. Below we summarize outcomes of our review.
6.1. Magnetohydrodynamic Two-Layer Shallow-Water Approximation
The magnetohydrodynamic two-layer shallow water equations with an external magnetic field have proposed a model of stratified rotating layer of plasma. In this model a flow of a thin layer of plasma in gravitational field with an external vertical magnetic field is divided into two thin layers with constant but different densities. In a particular case of equal heights and densities of layers the magnetohydrodynamic two-layer shallow water equations transform into single-layer shallow water equations with an external vertical magnetic field. The presence of an external vertical magnetic field in MHD two-layer shallow water equations has revealed three-dimensionality and axisymmetry of the magnetic field despite the two-dimensional nature of the velocity field. Two-layer shallow water MHD equations accept two different solutions, one with an external vertical magnetic field and another (in the absence of an external vertical magnetic field) with a stationary horizontal magnetic field. Dispersion relations in both configurations of magnetic field describe low-frequency magneto-Rossby waves. Characteristics of these waves include effects of stratification in form of modifications to frequencies. These modifications depend on ratio of plasma layers densities. Qualitative analysis of the dispersion curves of low-frequency magneto-Rossby waves has revealed their three-wave interactions in both configurations of magnetic field. The amplitude equations for three interacting waves have been derived by use of the multiscale asymptotic method. Two possible types of parametric instability (decay and amplification) have been investigated and their increments have been obtained.
6.2. Magnetohydrodynamic Boussinesq Approximation
Due to its two-dimensionality, the MHD system of equations in the shallow water approximation cannot adequately describe the case of a stably and continuously stratified layer of plasma. Consequently, the next logical step has been the development of the theory of rotating plasma flows in the Boussinesq approximation. This approximation is widely used for describing stably-stratified flows in astrophysical plasma as well as in geophysical fluid dynamics. Study of wave processes in stratified rotating plasma flows in the Boussinesq approximation has given the following results: obtained the dispersion equations and their solutions for flows on an f-plane, describing waves with Lorentz, buoyancy and Coriolis forces as their restoring mechanisms (three-dimensional magnetic inertia-gravity and magnetostrophic waves). It has also been revealed that group velocity of inertia-gravity wave and its wave vector are not perpendicular to each other in the presence of a magnetic field, as it is in neutral fluid. In the horizontal flows approximation, dispersion relation of magnetic inertia-gravity waves describe Alfvén waves and dispersion relation of magnetostrophic waves describe magnetogravity waves. Moreover new types of waves propagating only along the vertical component of the wave vector have been found, whose dynamics is determined only by rotation and magnetic field. Dispersion relations in -plane approximation have also been obtained. Their solutions have the form of magnetogravity waves and magneto-Rossby waves. Three-dimensional low-frequency magneto-Rossby waves have also been found. In the horizontal flows approximation these waves are analogous to magneto-Rossby waves in MHD shallow water model. Qualitative analysis of the obtained dispersion relations has revealed all three-waves interactions that satisfy the phase-matching condition. The equations that govern the interaction of three waves have been derived by the multiscale asymptotic expansion. Two types of parametric instabilities (decay and amplification) have been revealed, and their increments have been found.
6.3. Magnetohydrodynamic Anelastic Approximation
Another type of density variability is a property of compressibility. Wave processes in compressible stratified rotating flows of astrophysical plasma in an anelastic approximation have been considered. The system of MHD equations in this approximation filters out acoustic waves and describes compressible plasma flows. The waves obtained within the framework of the anelastic approximation have three restoring mechanisms: rotation, magnetic field, and compressibility. The latter is represented in dispersion relations by the terms with the Brunt-Väisälä frequency for compressible flows, which includes the dependence not only on the initial density profile (as in the case of the Boussinesq approximation for incompressible flows), but also on the initial pressure profile. In the f-plane approximation the dispersion relations have been found, which describe the following types of waves: compressible three-dimensional magnetic inertia-gravity waves, three-dimensional magnetostrophic waves, two-dimensional Alfvén waves, two-dimensional compressible magneto-gravity waves and vertical magnetic waves similar to those found in Boussinesq approximation. For spherical flows in -plane approximation a theory of linear waves also has been developed and the dispersion relations have been derived, which describe the following types of waves: two-dimensional compressible magneto-gravity waves, magneto-Rossby waves similar to those found in Boussinesq approximation, one-dimensional Alfvén waves and low-frequency compressible three-dimensional magneto-Rossby waves. By use of qualitative analysis of the dispersion curves all three-waves interactions have been revealed, satisfying the phase-matching condition. The equations that govern the interaction of three waves have been derived by use of the multiscale asymptotic method. Two types of parametric instabilities (decay and amplification) have been investigated, and their increments have been found.
6.4. Magnetohydrodynamic Shallow Water Approximation with Large-Scale Compressibility
The compressibility effects have also been investigated in the shallow water MHD model of a rotating astrophysical plasma in an external magnetic field. In contrast to the MHD equations in anelastic approximation the obtained system with large-scale compressibility is two-dimensional which simplify the plasma modeling procedures. Besides that, the large-scale compressibility approximation allows to describe large-scale horizontal variations of plasma density while it cannot be used for stratified flows. Note that the inclusion of a vertical magnetic field in the consideration allows us to significantly expand the scope of applying the shallow water approximation in plasma astrophysics processes. The three-dimensional equations for a compressible plasma are averaged over the layer height to obtain shallow water MHD equations with a large-scale compressibility. The pressure distribution is assumed to be hydrostatic, the layer height is assumed to be small compared to the characteristic horizontal scale of the flow. This approximation takes into account the pressure dependence on the density variations on the large scales. A -plane approximation is used to consider sphericity effects in the astrophysical plasma processes in the large-scale compressibility approximation. Theory of linear waves on a -plane has been presented. The derived dispersion relations for magneto-Poincare, magnetostrophic and magneto-Rossby waves depend on a new variable, the product of the plasma layer height and the depth-averaged plasma density, and the velocity of weak disturbances. Wherein, the velocity of weak disturbances in both systems on a f-plane and on a -plane are depend on large-scale density variations. Thus, the study of linear waves in the MHD of a rotating plasma with large-scale compressibility has eventually shown that the group velocities of magneto-Poincare, magnetostrophic, and magneto-Rossby waves depend on the value of plasma compressibility. The effects of the large-scale compressibility modify the curvature of the dispersion curves for linear waves in both models. However, it is shown that in the weak nonlinearity limit there exist the same three-wave interactions as in incompressible flows. The changes in the interaction coefficients and in the parametric instability growth rates due to the presence of large scale compressibility are investigated.
Author Contributions
All authors have read and agreed to the published version of the manuscript. The work was equally contributed by all authors.
Funding
This research was funded by the “Basis” Foundation for the Advancement of Theoretical Physics and Mathematics and the Russian Foundation for Basic Research (19-02-00016).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hughes, D.W.; Rosner, R.; Weiss, N.O. The Solar Tachocline; CUP: Cambridge, UK, 2007. [Google Scholar]
- Gilman, P.A. Magnetohydrodynamic shallow water equations for the solar tachocline. Astrophys. J. Lett. 2000, 544, L79. [Google Scholar] [CrossRef]
- Miesch, M.S.; Gilman, P.A. Thin-shell magnetohydrodynamic equations for the solar tachocline. Sol. Phys. 2004, 220, 287–305. [Google Scholar] [CrossRef]
- Dikpati, M.; Gilman, P.A. Analysis of hydrodynamic stability of solar tachocline latitudinal differential rotation using a shallow-water model. Astrophys. J. 2001, 551, 536. [Google Scholar] [CrossRef]
- Inogamov, N.A.; Sunyaev, R. Spread of matter over a neutron star surface during disk accretion. Astron. Lett. 1999, 25, 269. [Google Scholar]
- Inogamov, N.A.; Sunyaev, R.A. Spread of matter over a neutron-star surface during disk accretion: Deceleration of rapid rotation. Astron. Lett. 2010, 36, 848–894. [Google Scholar] [CrossRef]
- Spitkovsky, A.; Levin, Y.; Ushomirsky, G. Propagation of thermonuclear flames on rapidly rotating neutron stars: Extreme weather during type I X-ray bursts. Astrophys. J. 2002, 566, 1018. [Google Scholar] [CrossRef]
- Cho, J.Y. Atmospheric dynamics of tidally synchronized extrasolar planets. Philos. Trans. R. Soc. A 2008, 366, 4477–4488. [Google Scholar] [CrossRef]
- Petrosyan, A.S.; Klimachkov, D.A.; Fedotova, M.A.; Zinyakov, T.A. Shallow water magnetohydrodynamics in plasma astrophysics. Waves, turbulence, and zonal flows. Atmosphere 2020, 11, 314. [Google Scholar] [CrossRef]
- Zinyakov, T.A.; Petrosyan, A.S. Zonal Flows in Two-Dimensional Decaying Magnetohydrodynamic Turbulence on a β-Plane. JETP Lett. 2018, 108, 85–92. [Google Scholar] [CrossRef]
- Zinyakov, T.A.; Petrosyan, A.S. Spectra of Two-Dimensional Decaying Magnetohydrodynamic Turbulence on a β-Plane. JETP Lett. 2020, 111, 76–84. [Google Scholar] [CrossRef]
- Sirazov, R.A.; Petrosyan, A.S. Nonlinear Transformations of the Kinetic and Magnetic Energies in Rotating Magnetohydrodynamic Turbulent Flows. JETP Lett. 2019, 110, 329–335. [Google Scholar] [CrossRef]
- Dikpati, M.; Charbonneau, P. A Babcock-Leighton flux transport dynamo with solar-like differential rotation. Astrophys. J. 1999, 518, 508. [Google Scholar] [CrossRef]
- Zaqarashvili, T.V.; Oliver, R.; Ballester, J.L.; Shergelashvili, B.M. Rossby waves in shallow water magnetohydrodynamics. Astron. Astrophys. 2007, 470, 815–820. [Google Scholar] [CrossRef]
- Zaqarashvili, T.V.; Oliver, R.; Ballester, J.L.; Carbonell, M.; Khodachenko, M.L.; Lammer, H.; Leitzinger, M.; Odert, P. Rossby waves and polar spots in rapidly rotating stars: Implications for stellar wind evolution. Astron. Astrophys. 2011, 532, A139. [Google Scholar] [CrossRef]
- Braithwaite, J.; Spruit, H.C. Magnetic fields in non-convective regions of stars. R. Soc. Open Sci. 2017, 4, 160271. [Google Scholar] [CrossRef] [PubMed]
- Philidet, J.; Gissinger, C.; Lignières, F.; Petitdemange, L. Magnetohydrodynamics of stably stratified regions in planets and stars. Geophys. Astrophys. Fluid Dyn. 2020, 114, 336–355. [Google Scholar] [CrossRef]
- Stone, J.M.; Hawley, J.F.; Gammie, C.F.; Balbus, S.A. Three-dimensional magnetohydrodynamical simulations of vertically stratified accretion disks. Astrophys. J. 1996, 463, 656. [Google Scholar] [CrossRef]
- Lovelace, R.V.E.; Romanova, M.M. Rossby wave instability in astrophysical discs. Fluid Dyn. Res. 2014, 46, 041401. [Google Scholar] [CrossRef][Green Version]
- Batygin, K.; Stanley, S.; Stevenson, D.J. Magnetically controlled circulation on hot extrasolar planets. Astrophys. J. 2013, 776, 53. [Google Scholar] [CrossRef]
- Böning, V.G.; Hu, H.; Gizon, L. Signature of solar g modes in first-order p-mode frequency shifts. Astron. Astrophys. 2019, 629, A26. [Google Scholar] [CrossRef]
- Loeptien, B.; Gizon, L.; Birch, A.C.; Schou, J.; Proxauf, B.; Duvall, T.L.; Bogart, R.S.; Christensen, U.R. Global-scale equatorial Rossby waves as an essential component of solar internal dynamics. Nat. Astron. 2018, 7, 1. [Google Scholar] [CrossRef]
- Dikpati, M.; Belucz, B.; Gilman, P.A.; McIntosh, S.W. Phase Speed of Magnetized Rossby Waves that Cause Solar Seasons. Astrophys. J. 2018, 862, 159. [Google Scholar] [CrossRef]
- McIntosh, S.W.; Cramer, W.J.; Marcano, M.P.; Leamon, R.J. The detection of Rossby-like waves on the Sun. Nat. Astron. 2017, 1, 0086. [Google Scholar] [CrossRef]
- Zaqarashvili, T.V.; Gurgenashvili, E. Magneto-Rossby waves and seismology of solar interior. Front. Astron. Space Sci. 2018, 5, 7. [Google Scholar] [CrossRef]
- Gizon, L.; Fournier, D.; Albekioni, M. Effect of latitudinal differential rotation on solar Rossby waves: Critical layers, eigenfunctions, and momentum fluxes in the equatorial β plane. Astron. Astrophys. 2020, 642, A178. [Google Scholar] [CrossRef]
- Klimachkov, D.A.; Petrosyan, A.S. Rossby waves in the magnetic fluid dynamics of a rotating plasma in the shallow-water approximation. J. Exp. Theor. Phys. 2017, 125, 597–612. [Google Scholar] [CrossRef]
- Fedotova, M.A.; Klimachkov, D.A.; Petrosyan, A.S. The Shallow-Water Magnetohydrodynamic Theory of Stratified Rotating Astrophysical Plasma Flows: Beta-Plane Approximation and magneto-Rossby Waves. Plasma Phys. Rep. 2020, 46, 50. [Google Scholar] [CrossRef]
- Fedotova, M.A.; Petrosyan, A.S. Wave processes in three-dimensional stratified flows of a rotating plasma in the Boussinesq approximation. J. Exp. Theor. Phys. 2020, 131, 337–355. [Google Scholar] [CrossRef]
- Zaqarashvili, T.V.; Albekioni, M.; Ballester, J.L.; Bekki, Y.; Biancofiore, L.; Birch, A.C.; Dikpati, M.; Gizon, L.; Gurgenashvili, E.; Heifetz, E.; et al. Rossby Waves in Astrophysics. Space Sci. Rev. 2021, 217, 1–93. [Google Scholar] [CrossRef]
- Dikpati, M.; Cally, P.S.; McIntosh, S.W.; Heifetz, E. The Origin of the Seasons in Space Weather. Sci. Rep. 2017, 7, 14750. [Google Scholar] [CrossRef]
- Lou, Y.Q. Rossby-type wave-induced periodicities in flare activities and sunspot areas or groups during solar maxima. Astrophys. J. 2000, 540, 1102. [Google Scholar] [CrossRef]
- Dikpati, M.; McIntosh, S.W. Space weather challenge and forecasting implications of Rossby waves. Space Weather 2020, 18, e2018SW002109. [Google Scholar] [CrossRef]
- Tobias, S.M.; Diamond, P.H.; Hughes, D.W. β-plane magnetohydrodynamic turbulence in the solar tachocline. Astrophys. J. Lett. 2007, 667, L113. [Google Scholar] [CrossRef]
- Hori, K.; Jones, C.A.; Teed, R.J. Slow magneto-Rossby waves in the Earth’s core. Geophys. Res. Lett. 2015, 42, 6622–6629. [Google Scholar] [CrossRef]
- Petviashvili, V.I.; Pokhotelov, O.A. Solitary Waves in Plasmas and in the Atmosphere; Gordon and Breach Science Publishers: Reading, UK; Philadelphia, PA, USA, 1992. [Google Scholar]
- Onishchenko, O.G.E.; Pokhotelov, O.A.; Astafieva, N.M. Generation of large-scale eddies and zonal winds in planetary atmospheres. Phys. Uspekhi 2008, 51, 577. [Google Scholar] [CrossRef]
- Karelsky, K.V.; Petrosyan, A.S.; Tarasevich, S.V. Nonlinear dynamics of magnetohydrodynamic flows of a heavy fluid in the shallow water approximation. J. Exp. Theor. Phys. 2011, 113, 530. [Google Scholar] [CrossRef][Green Version]
- Karelsky, K.V.; Petrosyan, A.S.; Tarasevich, S.V. Nonlinear dynamics of magnetohydrodynamic shallow water flows over an arbitrary surface. Phys. Scr. 2013, 155, 014024. [Google Scholar] [CrossRef]
- Karelsky, K.V.; Petrosyan, A.S.; Tarasevich, S.V. Nonlinear dynamics of magnetohydrodynamic flows of a heavy fluid on slope in the shallow water approximation. J. Exp. Theor. Phys. 2014, 119, 311–325. [Google Scholar] [CrossRef]
- Klimachkov, D.A.; Petrosyan, A.S. Nonlinear wave interactions in shallow water magnetohydrodynamics of astrophysical plasma. J. Exp. Theor. Phys. 2016, 122, 832–848. [Google Scholar] [CrossRef]
- Klimachkov, D.A.; Petrosyan, A.S. Nonlinear theory of magnetohydrodynamic flows of a compressible fluid in the shallow water approximation. J. Exp. Theor. Phys. 2016, 123, 520–539. [Google Scholar] [CrossRef]
- Klimachkov, D.A.; Petrosyan, A.S. Parametric instabilities in shallow water magnetohydrodynamics of astrophysical plasma in external magnetic field. Phys. Lett. A 2017, 381, 106–113. [Google Scholar] [CrossRef]
- Zaqarashvili, T.V.; Oliver, R.; Ballester, J.L. Global shallow water magnetohydrodynamic waves in the solar tachocline. Astrophys. J. Lett. 2009, 691, L41. [Google Scholar] [CrossRef]
- Heng, K.; Spitkovsky, A. Magnetohydrodynamic shallow water waves: Linear analysis. Astrophys. J. 2009, 703, 1819. [Google Scholar] [CrossRef]
- Dikpati, M.; McIntosh, S.W.; Bothun, G.; Cally, P.S.; Ghosh, S.S.; Gilman, P.A.; Umurhan, O.M. Role of Interaction between magneto-Rossby Waves and Tachocline Differential Rotation in Producing Solar Seasons. Astrophys. J. 2018, 853, 144. [Google Scholar] [CrossRef]
- Marquez-Artavia, X.; Jones, C.A.; Tobias, S.M. Rotating magnetic shallow water waves and instabilities in a sphere. Geophys. Astrophys. Fluid 2017, 111, 282–322. [Google Scholar] [CrossRef]
- Zaqarashvili, T. Equatorial magnetohydrodynamic shallow water waves in the solar tachocline. Astrophys. J. 2018, 856, 32. [Google Scholar] [CrossRef]
- Vallis, G.K. Atmospheric and Oceanic Fluid Dynamics: Fundamental and Large-Scale Circulation; CUP: Cambridge, UK, 2006. [Google Scholar]
- Zeitlin, V. Geophysical Fluid Dynamics: Understanding (Almost) Everything with Rotating Shallow Water Models; OUP: Oxford, UK, 2018. [Google Scholar]
- Kaladze, T.D.; Horton, W.; Kahlon, L.Z.; Pokhotelov, O.; Onishchenko, O. Zonal flows and magnetic fields driven by large-amplitude Rossby-Alfvén-Khantadze waves in the E-layer ionosphere. J. Geophys. Res. Space Phys. 2013, 118, 7822–7833. [Google Scholar] [CrossRef]
- Balk, A.M. Large-scale quasi-geostrophic magnetohydrodynamics. Astrophys. J. 2014, 796, 143. [Google Scholar] [CrossRef]
- Dikpati, M.; Gilman, P.A.; Chatterjee, S.; McIntosh, S.W.; Zaqarashvili, T.V. Physics of magnetohydrodynamic Rossby waves in the sun. Astrophys. J. 2020, 896, 141. [Google Scholar] [CrossRef]
- Mandal, K.; Hanasoge, S. Properties of solar Rossby waves from normal mode coupling and characterizing its systematics. Astrophys. J. 2020, 891, 125. [Google Scholar] [CrossRef]
- Raphaldini, B.; Medeiros, E.; Raupp, C.F.; Teruya, A.S. A new mechanism for maunder-like solar minima: Phase synchronization dynamics in a simple nonlinear oscillator of magnetohydrodynamic Rossby waves. Astrophys. J. Lett. 2020, 890, L13. [Google Scholar] [CrossRef]
- Onishchenko, O.G.; Pokhotelov, O.A.; Sagdeev, R.Z.; Shukla, P.K.; Stenflo, L. Generation of zonal flows by Rossby waves in the atmosphere. Nonlinear Process. Geophys. 2004, 11, 241–244. [Google Scholar] [CrossRef]
- Liang, Z.C.; Gizon, L.; Birch, A.C.; Duvall, T.L. Time-distance helioseismology of solar Rossby waves. Astron. Astrophys. 2019, 626, A3. [Google Scholar] [CrossRef]
- Raphaldini, B.; Raupp, C.F. Nonlinear dynamics of magnetohydrodynamic Rossby waves and the cyclic nature of solar magnetic activity. Astrophys. J. 2015, 799, 78. [Google Scholar] [CrossRef]
- Raphaldini, B.; Teruya, A.S.; Raupp, C.F.; Bustamante, M.D. Nonlinear Rossby wave—wave and wave—mean flow theory for long-term solar cycle modulations. Astrophys. J. 2019, 887, 1. [Google Scholar] [CrossRef]
- Lou, Y.Q. Nonlinear magnetohydrodynamic waves in a steady zonal circulation for a shallow fluid shell on the surface of a rotating sphere. Astrophys. J. 1987, 322, 862–869. [Google Scholar] [CrossRef]
- Gilman, P.A. Stability of baroclin flows in a zonal magnetic field: Part I. J. Atmos. Sci. 1967, 24, 101–118. [Google Scholar] [CrossRef][Green Version]
- De Sterck, H. Hyperbolic theory of the shallow water magnetohydrodynamics equations. Phys. Plasmas 2001, 8, 3293–3304. [Google Scholar] [CrossRef]
- Dellar, P.J. Dispersive shallow water magnetohydrodynamics. Phys. Plasmas 2003, 10, 581–590. [Google Scholar] [CrossRef]
- Zeitlin, V. Remarks on rotating shallow-water magnetohydrodynamics. Nonlinear Process. Geophys. 2013, 20, 893–908. [Google Scholar] [CrossRef]
- Brown, B.P.; Vasil, G.M.; Zweibel, E.G. Energy conservation and gravity waves in sound-proof treatments of stellar interiors. Part I. Anelastic approximations. Astrophys. J. 2012, 756, 109. [Google Scholar] [CrossRef]
- Fedotova, M.A.; Petrosyan, A.S. Wave Processes in Rotating Compressible Astrophysical Plasma Flows with Stable Stratification. J. Exp. Theor. Phys. 2020, 131, 1032–1055. [Google Scholar] [CrossRef]
- Klimachkov, D.A.; Petrosyan, A.S. Large-scale compressibility in rotating flows of astrophysical plasma in the shallow water approximation. J. Exp. Theor. Phys. 2018, 127, 1136–1152. [Google Scholar] [CrossRef]
- Kupka, F. Thermal Convection in Stars and in Their Atmosphere. Multi-Dimensional Processes. In Stellar Physics; EDP Sciences: Les Ulis, France, 2021; pp. 69–110. [Google Scholar]
- Miesch, M.; Matthaeus, W.; Brandenburg, A.; Petrosyan, A.; Pouquet, A.; Cambon, C.; Jenko, F.; Uzdensky, D.; Stone, J.; Tobias, S.; et al. Large-Eddy Simulations of Magnetohydrodynamic Turbulence in Heliophysics and Astrophysics. Space Sci. Rev. 2015, 194, 97–137. [Google Scholar] [CrossRef]
- Chernyshov, A.A.; Karelsky, K.V.; Petrosyan, A.S. Subgrid-scale modeling for the study of compressible magnetohydrodynamic turbulence in space plasmas. Phys. Uspekhi 2014, 57, 421. [Google Scholar] [CrossRef]
- Schmidt, W. Large Eddy Simulations in Astrophysics. Living Rev. Comput. Astrophys. 2015, 1, 2. [Google Scholar] [CrossRef]
- Kupka, F.; Muthsam, H.J. Modelling of stellar convection. Living Rev. Comput. Astrophys. 2017, 3, 1. [Google Scholar] [CrossRef]
- Balsara, D.S. Higher-order accurate space-time schemes for computational astrophysics—Part I: Finite volume methods. Living Rev. Comput. Astrophys. 2017, 3, 2. [Google Scholar] [CrossRef]
- Almgren, A.S.; Bell, J.B.; Nonaka, A.; Zingale, M. A New Low Mach Number Approach in Astrophysics. Comput. Sci. Eng. 2009, 11, 24–33. [Google Scholar] [CrossRef]
- Karelsky, K.V.; Petrosyan, A.S.; Chernyak, A.V. Nonlinear dynamics of flows of a heavy compressible gas in the shallow water approximation. J. Exp. Theor. Phys. 2012, 114, 1058–1071. [Google Scholar] [CrossRef]
- Karel’skii, K.V.; Petrosyan, A.S.; Chernyak, A.V. Nonlinear theory of the compressible gas flows over a nonuniform boundary in the gravitational field in the shallow-water approximation. J. Exp. Theor. Phys. 2013, 116, 680–697. [Google Scholar] [CrossRef]
- Batchelor, C.K.; Batchelor, G.K. An Introduction to Fluid Dynamics; CUP: Cambridge, UK, 2000. [Google Scholar]
- Hunter, S. Waves in Shallow Water Magnetohydrodynamics. Ph.D. Thesis, The University of Leeds Department of Applied Mathematics, Leeds, UK, August 2015. Available online: http://etheses.whiterose.ac.uk/11475/ (accessed on 2 March 2021).
- Dolzhanskii, F.V. Fundamentals of Geophysical Hydrodynamics; Fizmatli: Moscow, Russia, 2016. (In Russian) [Google Scholar]
- Nezlin, M.V.; Snezhkin, E.N. Rossby Vortices and Spiral Structures-Astrophysics and Plasma Physics in Shallow Water Experiments; Nauka: Moscow, Russia, 1990. (In Russian) [Google Scholar]
- Saio, H. R-mode oscillations in uniformly rotating stars. Astrophys. J. 1982, 256, 717–735. [Google Scholar] [CrossRef]
- Sturrock, P.A.; Bush, R.; Gough, O.O.; Scargle, J.D. Indications of r-mode oscillations in SOHO/MDI solar radius measurements. Astrophys. J. 2015, 804, 47. [Google Scholar] [CrossRef]
- Wolff, C.L. Linear r-mode oscillations in a differentially rotating star. Astrophys. J. 1998, 502, 961–967. [Google Scholar] [CrossRef]
- Karelsky, K.V.; Petrosyan, A.S. Particular solutions and Riemann problem for modified shallow water equations. Fluid Dyn. Res. 2006, 38, 339. [Google Scholar] [CrossRef]
- Ostrovsky, L. Asymptotic Perturbation Theory of Waves; WS: Singapore, 2014. [Google Scholar]
- Newell, A.C. Rossby wave packet interactions. J. Fluid Mech. 1969, 35, 255–271. [Google Scholar] [CrossRef]
- Rieutord, M.; Valdettaro, L. Inertial waves in a rotating spherical shell. J. Fluid Mech. 1997, 341, 77–99. [Google Scholar] [CrossRef]
- Dintrans, B.; Rieutord, M.; Valdettaro, L. Gravito-inertial waves in a rotating stratified sphere or spherical shell. J. Fluid Mech. 1999, 398, 271–297. [Google Scholar] [CrossRef]
- Berkoff, N.A. The Anelastic Approximation: Magnetic Buoyancy and Magnetoconvection. Ph.D. Thesis, University of Leeds, Leeds, UK, July 2011. Available online: https://etheses.whiterose.ac.uk/15942/1/thesis.pdf (accessed on 2 March 2021).
- Spiegel, E.A.; Veronis, G. On the Boussinesq approximation for a compressible fluid. Astrophys. J. 1960, 131, 442. [Google Scholar] [CrossRef]
- Spiegel, E.A.; Weiss, N.O. Magnetic buoyancy and the Boussinesq approximation. Geophys. Astrophys. Fluid Dyn. 1982, 22, 219–234. [Google Scholar] [CrossRef]
- Billant, P.; Chomaz, J.M. Self-similarity of strongly stratified inviscid flows. Phys. Fluids 2001, 13, 1645–1651. [Google Scholar] [CrossRef]
- Yano, J.I. Inertio-gravity waves under the non-traditional f-plane approximation: Singularity in the large-scale limit. J. Fluid Mech. 2017, 810, 475–488. [Google Scholar] [CrossRef]
- Lee, S.; Takada, R. Dispersive estimates for the stably stratified Boussinesq equations. Indiana Univ. Math. J. 2017, 66, 2037–2070. [Google Scholar]
- Takehiro, S.I. Penetration of Alfvén waves into an upper stably-stratified layer excited by magnetoconvection in rotating spherical shells. Phys. Earth Planet. Inter. 2015, 241, 37–43. [Google Scholar] [CrossRef]
- Takehiro, S.I.; Sasaki, Y. Penetration of steady fluid motions into an outer stable layer excited by MHD thermal convection in rotating spherical shells. Phys. Earth Planet. Inter. 2018, 276, 258–264. [Google Scholar] [CrossRef]
- Nakagawa, T. Effect of a stably stratified layer near the outer boundary in numerical simulations of a magnetohydrodynamic dynamo in a rotating spherical shell and its implications for Earth’s core. Phys. Earth Planet. Inter. 2011, 187, 342–352. [Google Scholar] [CrossRef]
- Raymond, D.J. Sound, Inertia-Gravity Waves, and Lamb Waves. 7 September 2011. Available online: http://kestrel.nmt.edu/~raymond/classes/ph589/notes/ssmodes/ssmodes.pdf (accessed on 2 March 2021).
- Klein, R. Scale Analysis of Compressible Flows from an Application Perspective. In Handbook of Mathematical Analysis in Mechanics of Viscous Fluids; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Batchelor, G.K. The conditions for dynamical similarity of motions of a frictionless perfect-gas atmosphere. Q. J. R. Meteorol. Soc. 1953, 79, 224–235. [Google Scholar] [CrossRef]
- Charney, J.G.; Ogura, Y. A numerical model for thermal convection in the atmosphere. J. Meteorol. Soc. Jpn. 1960, 38, 19a. [Google Scholar] [CrossRef]
- Gough, D.O. The anelastic approximation for thermal convection. J. Atmos. Sci. 1969, 26, 448–456. [Google Scholar] [CrossRef]
- Bannon, P.R. On the anelastic approximation for a compressible atmosphere. J. Atmos. Sci. 1996, 53, 3618–3628. [Google Scholar] [CrossRef]
- Calkins, M.A.; Julien, K.; Marti, P. The breakdown of the anelastic approximation in rotating compressible convection: Implications for astrophysical systems. Proc. R. Soc. A 2015, 471, 20140689. [Google Scholar] [CrossRef] [PubMed]
- Paolucci, S. Filtering of Sound from the Navier-Stokes Equations; Sandia National Laboratories: Livermore, CA, USA, 1982; pp. 3–52.
- Botta, N.; Klein, R.; Almgren, A. Dry Atmosphere Asymptotics; Potsdam Institute for Climate Impact Research: Potsdam, Germany, 1999. [Google Scholar]
- Klein, R.; Botta, N.; Schneider, T.; Munz, C.D.; Roller, S.; Meister, A.; Hoffman, L.; Sonar, T. Asymptotic adaptive methods for multi-scale problems in fluid mechanics. J. Eng. Math. 2001, 39, 261–343. [Google Scholar] [CrossRef]
- Braginsky, S.I.; Roberts, P.H. Equations governing convection in Earth’s core and the geodynamo. Geophys. Astrophys. Fluid Dyn. 1995, 79, 1–97. [Google Scholar] [CrossRef]
- Glatzmaier, G.A.; Roberts, P.H. An anelastic evolutionary geodynamo simulation driven by compositional and thermal convection. Phys. D 1996, 97, 81–94. [Google Scholar] [CrossRef]
- Olson, P.; Christensen, U.R. Dipole moment scaling for convection-driven planetary dynamos. Earth Planet. Sci. Lett. 2006, 250, 561–571. [Google Scholar] [CrossRef]
- Jones, C.A.; Kuzanyan, K.M.; Mitchell, R.H. Linear theory of compressible convection in rapidly rotating spherical shells, using the anelastic approximation. J. Fluid Mech. 2009, 634, 291. [Google Scholar] [CrossRef]
- Gilman, P.A.; Glatzmaier, G.A. Compressible convection in a rotating spherical shell. I-Anelastic equations. II-A linear anelastic model. III-Analytic model for compressible vorticity waves. Astrophys. J. Suppl. Ser. 1981, 45, 335–388. [Google Scholar] [CrossRef]
- Yadav, R.K.; Bloxham, J. Deep rotating convection generates the polar hexagon on Saturn. Proc. Natl. Acad. Sci. USA 2020, 117, 13991–13996. [Google Scholar] [CrossRef]
- Glatzmaier, G.A. Numerical simulations of stellar convective dynamos. I. The model and method. J. Comput. Phys. 1984, 55, 461–484. [Google Scholar] [CrossRef]
- Lantz, S.R.; Fan, Y. Anelastic magnetohydrodynamic equations for modeling solar and stellar convection zones. Astrophys. J. Suppl. Ser. 1999, 121, 247. [Google Scholar] [CrossRef]
- Miesch, M.S.; Elliott, J.R.; Toomre, J.; Clune, T.L.; Glatzmaier, G.A.; Gilman, P.A. Three-dimensional spherical simulations of solar convection. I. Differential rotation and pattern evolution achieved with laminar and turbulent states. Astrophys. J. 2000, 532, 593. [Google Scholar] [CrossRef]
- Brun, A.S.; Miesch, M.S.; Toomre, J. Global-scale turbulent convection and magnetic dynamo action in the solar envelope. Astrophys. J. 2004, 614, 1073. [Google Scholar] [CrossRef]
- Brown, B.P.; Browning, M.K.; Brun, A.S.; Miesch, M.S.; Toomre, J. Rapidly rotating suns and active nests of convection. Astrophys. J. 2008, 689, 1354. [Google Scholar] [CrossRef]
- Brown, B.P.; Miesch, M.S.; Browning, M.K.; Brun, A.S.; Toomre, J. Magnetic cycles in a convective dynamo simulation of a young solar-type star. Astrophys. J. 2011, 731, 69. [Google Scholar] [CrossRef]
- Smolarkiewicz, P.K.; Charbonneau, P. EULAG, a computational model for multiscale flows: An MHD extension. J. Comput. Phys. 2013, 236, 608–623. [Google Scholar] [CrossRef]
- Goldstein, J.; Townsend, R.H.D.; Zweibel, E.G. The Tayler Instability in the Anelastic Approximation. Astrophys. J. 2019, 881, 66. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).