Abstract
Fast Radio Bursts (FRBs) represent a novel tool for probing the properties of the universe at cosmological distances. The dispersion measures of FRBs, combined with the redshifts of their host galaxies, has very recently yielded a direct measurement of the baryon content of the universe, and has the potential to directly constrain the location of the “missing baryons”. The first results are consistent with the expectations of ΛCDM for the cosmic density of baryons, and have provided the first constraints on the properties of the very diffuse intergalactic medium (IGM) and circumgalactic medium (CGM) around galaxies. FRBs are the only known extragalactic sources that are compact enough to exhibit diffractive scintillation in addition to showing exponential tails which are typical of scattering in turbulent media. This will allow us to probe the turbulent properties of the circumburst medium, the host galaxy ISM/halo, and intervening halos along the path, as well as the IGM. Measurement of the Hubble constant and the dark energy parameter w can be made with FRBs, but require very large samples of localised FRBs (>) to be effective on their own—they are best combined with other independent surveys to improve the constraints. Ionisation events, such as for He ii, leave a signature in the dispersion measure—redshift relation, and if FRBs exist prior to these times, they can be used to probe the reionisation era, although more than localised FRBs are required.
1. Introduction
Fast radio bursts (FRBs) are millisecond-duration pulses of radio emission that originate at cosmological distances. Around 140 FRBs have been published to date, with the Parkes radio telescope [1,2,3,4], the Arecibo telescope [5], the Green Bank telescope [6,7], the UTMOST telescope [4,8,9], the Australian Square Kilometre Array Pathfinder (ASKAP) [4,10,11,12,13,14], the Canadian Hydrogen Intensity Mapping Experiment (CHIME) [15,16,17,18], the Deep Synoptic Array (DSA-10) [19], the Apertif telescope [20], the FAST telescope [21,22] and the Karl G. Jansky Very Large Array (VLA) [23] all contributing. The bursts are indicative of extremely luminous coherent radiation of brightness temperature K, whose 0.1–10 ms duration confines their emission regions to a radius less than 30–3000 km. Cordes and Chatterjee [24], Petroff et al. [25] and Chatterjee [26] give very good reviews of FRBs and their properties.
The progenitors for FRBs remain a mystery, with a wide range of theories having been advanced to account for their properties, including those involving supernovae in which the FRB is a feature of a young, expanding supernova remnant [27,28] and super-luminous supernovae [29]; the merger/collision of two compact objects such as binary neutron stars (NS-NS) [30,31,32,33], binary white dwarfs (WD-WD) [34] and white dwarf-black hole mergers (WD-BH), the latter via the reconnection of magnetic material [35]; energetic activities from isolated compact objects such as giant pulses from extragalactic pulsars [36]; giant flares from magnetars [37,38]; collision/interaction of neutron stars with AGN [39] and NS “combing” [40]; collapse of supramassive neutron stars [41]; superconducting cosmic strings [42]; possible connection with gamma-ray bursts (GRBs) [43]; and alien beams driving light sails [44]. Platts et al. [45], Zhang [46], Xiao et al. [47] and Lyubarsky [48] summarise FRB progenitor theories and emission mechanisms.
While the majority of the bursts are detected as one-off events, a population of repeating FRBs is emerging. The “repeater”—FRB 121102, is the first of this type, after it was initially discovered with the Arecibo telescope and found to emit many further pulses in an extensive follow-up campaign [49]. Since then, hundreds of bursts have been detected from FRB 121102 and exhibit a wide range of luminosities, width, and temporal and frequency structures [18,50]. Its repeating nature led to the first localisation of an FRB to a host galaxy [51,52,53]. Since the discovery of FRB 121102, sensitive follow-up observations of one-off bursts have revealed many more repeating FRBs: approximately 15% of published sources are known to repeat [17,18,54,55]. Recently, a 16.35-day periodicity was observed for the repeating FRB 180916 source with CHIME [56]. Later, a detection of tentative periodicity of 157 days with a duty cycle of 56% was reported for FRB 121102, in which FRB activity is strongly modulated [57]. The periodicity of these sources suggests a mechanism for periodic modulation either of the burst emission itself, or through external amplification or absorption [56] and also leads to constraints on plausible binary systems in which the progenitor resides [57,58,59]. Furthermore, the bursts from FRB 121102 and FRB 180916 sources have been detected at frequencies in a very wide range from 110 MHz–8 GHz [60,61,62,63]. Recently, CHIME discovered a new repeating FRB 20200120E in the direction of the M81 galaxy. The FRB has a DM of 87.82 pc cm−3, which is the lowest DM recorded from an FRB to date [64]. A detailed review of the radio observation of FRBs is presented in Caleb [65]. Despite all these observations, it remains unclear whether or not all FRB sources repeat and this remains a very active area of research.
A recent advancement in our understanding of possible FRB progenitors is the the discovery of an extremely bright FRB-like signal (FRB 200428) from a known Milky Way magnetar (SGR 1935+2154) [66,67]. The intrinsic energy of FRB 200428 is ≈30 times less than the weakest extragalactic FRB observed to date, so starts to bridge the energy gap between pulsars/magnetars and extragalactic FRBs. Furthermore, an X-ray burst was detected coincident with the radio discovery [68], and this favours emission models that describe synchrotron masers or electromagnetic pulses powered by magnetar bursts and giant flares. No persistent radio emission or an afterglow has yet been reported for the source. The discovery of FRB 200428 implies that active magnetars such as SGR 1935+2154 can produce a population of FRBs visible at extragalactic distances, and also shows that wide-field, relatively inexpensive instruments could find nearby FRBs (out to a few tens of Mpc), offering the tantalising prospects of studying the host galaxies and FRB environments in great detail.
While the physical mechanism and sources of FRBs remain mysteries, the burst itself is all one needs to probe the ionisation, densities and magnetic properties of plasma on cosmological scales. In particular, with just a few bursts, we are already able to detect and characterise the very diffuse intergalactic and circumgalactic media, which are nearly impossible to study using other techniques. This is due to several propagation effects that the wavefront of the FRB undergoes as it traverses these media, experiencing effects such as “dispersion” (a frequency dependent propagation delay in the pulse), as well as pulse scattering, scintillation and Faraday rotation. We describe these effects in the following sub-sections and refer the reader to Petroff et al. [25] for other propagation effects.
1.1. Dispersion Measure
As FRB emission propagates through plasma between the source and Earth, the radio waves are dispersed in time as a function of frequency, quantified by a term called the dispersion measure (DM). Electromagnetic waves propagate through a cold plasma with a group velocity , which is a function of frequency as:
where is the plasma frequency, is the observing frequency and c is the speed of light.
Consequently, higher frequencies arrive before lower frequencies. This frequency dependent delay () between two frequencies and is given by,
where a = 4.1488064239(11) GHz2 cm3 pc−1 ms [69] and the DM for cosmological sources at redshift z is defined as
where d is the distance to the source and is the free electron density along the path traversed by the signal. Thus, DM is a good proxy for the electron column density of free electrons to the source, and in a range of astrophysical cases is also a proxy for the source distance.
The sample of FRBs published to date have DMs in the range 87.8 to 2600 pc cm−3 [4]. For most FRBs the DM is dominated by the contribution from the intergalactic medium (IGM) and offer a novel means of probing this as a function of redshift. This was understood to be the case from the discovery of the very first FRB [1], and was a major driver in searching for more.
1.2. Pulse Scattering and Scintillation
FRBs can be temporally broadened by scattering as they traverse a turbulent medium, through multi-path propagation. Generally, this results in the FRB pulse being convolved with a one-sided exponential tail that can be well modeled as due to a single thin screen [70], in which a plane wave undergoes phase variations as it passes through the screen (note there are also complex FRB temporal profiles for which a simple exponential scattering tail does not apply [71]). The location of the screen between source and observer affects the amplitude of scattering. In such a thin screen model where turbulent plasma follows a Kolmogorov power law, the decay time of the exponential tail or the scattering timescale is expected to scale strongly with frequency, as ([72]):
This dependence has been seen in high signal-to-noise FRBs, and was a strong early argument in their favour as being astrophysical [1,2,73]. Scattering will also cause a detectable angular broadening of the source, which is observable using Very Long Baseline Interferometry (VLBI), for instance, FRB 121102 has angular broadening mas at 1.7 GHz and 0.4–0.5 mas at 5 GHz measured using high-resolution VLBI study of the FRB and its persistent radio counterpart [52].
A relative motion between the source, scattering medium and observer leads to the phenomenon called scintillation, which is manifested as intensity variations on different timescales. The scattered signal is delayed relative to signal that arrives along the direct line-of-sight to a source. The phase difference in the signal because of the different path lengths causes an interference pattern which can be both destructive or constructive. Interference can only occur if , where is the scintillation bandwidth with frequency dependence as:
Thus, scintillation produces pattern of intensity variation in both frequency (dynamic pattern) and time (scintle).
Scintillation can be refractive or diffractive as the signal passes through the clumpy and turbulent plasma, which has electron density variations on a variety of length scales. While DM quantifies the column density of free electrons along the line-of-sight, the scattering measure (SM) is a measure of the electron density fluctuations, given by:
where d is the distance to the source and indicates the strength of the fluctuations along the line-of-sight of a cosmological source.
FRBs are the only known compact extragalactic sources that scintillate coherently. Diffractive scintillation has been detected in bright FRBs such as FRB 150807 [74], where the 100 kHz structure in the spectrum may arise from from weak scattering in the IGM or host galaxy. For UTMOST FRB 170827, spectral modulations on frequency scales of 1.5 MHz and 0.1 MHz are observed, the latter of which may originate in the FRB host galaxy, or its immediate vicinity [71]. Whereas, in the case of FRB 121102, the observed fine-scale frequency structure is consistent with the scintillation from the Milky Way [63]. Finally, we note that the gravitational or plasma lensing can also strongly modulate FRB amplitudes for a wide range of distances. Caustics can produce strong magnifications (≲) on short time scales (∼hrs to day) along with narrow, epoch dependent spectral peaks (0.1 to 1 GHz) [75].
1.3. Faraday Rotation
Faraday rotation is a process where the plane of polarisation of an E-M wave is rotated when it passes through a magnetic field. The rotation of the polarisation position angle (PPA) has a dependence on wavelength
RM is the “rotation measure”, and is given by
where d is the distance to the source, c is the speed of light, e is the electron charge, is the electron mass, is the electron density, is the component of magnetic field parallel to the line-of-sight. RMs have been measured for a sample of FRBs [4]. Most of the them lie in the range from 0 to a few rad m−2 [76,77], except for the repeating FRB 121102 which has an extraordinarily high RM of the order of ≈ rad m−2, suggesting an extreme magneto-ionic circumburst environment [78].
In a scenario where the Faraday rotation originates predominantly in the local environment of the FRB source and/or the interstellar medium (ISM) of the host galaxy [78], a cosmological correction to the RM is given by
The combination of the measurement of RM and DM for a signal can be used to obtain average line-of-sight magnetic field strength , weighted by electron density,
assuming the DM and RM are associated with the same region of magneto-ionic material. Thus, such a combination for FRBs will enable measurements of the mean magnetic field of the IGM, in the same way that RM measurements of pulsars enable measurements of the magnetic field of the Milky Way [79].
1.4. Motivation and Scope of This Review
This review paper describes the cosmological application of FRBs, focusing on their utility to study ionised and magnetised structures on cosmological scales. This is the area in which the most progress has been made recently, via the localisation of FRBs to their host galaxies. FRBs are proving to be an excellent probes to trace the ionised gas in galaxy halos, large-scale structure, and the intergalactic medium. This is described in Section 2, which also presents the problem of missing baryons and how FRBs can be useful in locating them. Section 3 presents FRB application to cosmological parameter estimation. We describe FRBs as probes of reionisation is Section 4. We summarise and discuss the future prospects in Section 5.
2. Probing the Structure of the Universe
As outlined above, DM, scattering and RM measurements for FRBs allow us to probe the circumgalactic, intergalactic, and interstellar medium along the line-of-sight in an entirely novel way. In this section, we review the use of FRBs to this end from on-going surveys and observations.
2.1. The Missing Baryon Problem
In ΛCDM cosmology, measurement of the abundances of light elements in Big Bang Nucleosynthesis (BBN) and of the peaks in the power spectrum of the cosmic microwave background (CMB) indicate that more than ∼95% of the energy density in the universe is in the form of dark matter and dark energy, whereas baryonic matter only comprises ∼5% of the total [80,81]. At high redshift (), most of the expected baryons are found in the Ly absorption forest: the diffuse, photo-ionised IGM with a temperature of – K [82,83]. However, at low-redshifts, the observed baryons in stars, the cold interstellar medium, residual Ly forest gas, O vi, broad H i Ly absorbers (BLA; Doppler parameter km s−1), and hot gas in clusters of galaxies account for only ∼50% of the baryons (cf. Figure 1). The remainder of the cosmic baryons are yet to be identified giving rise to the very well-known problem of the “missing baryons” [84,85,86]. Bregman [87] and McQuinn [88] give excellent reviews of the problem. Finding these missing baryons is important, because the amount and the location of cosmic baryons in the circum-galactic medium (CGM) and IGM is crucial in understanding galaxy evolution via galaxy halo accretion and feedback models.
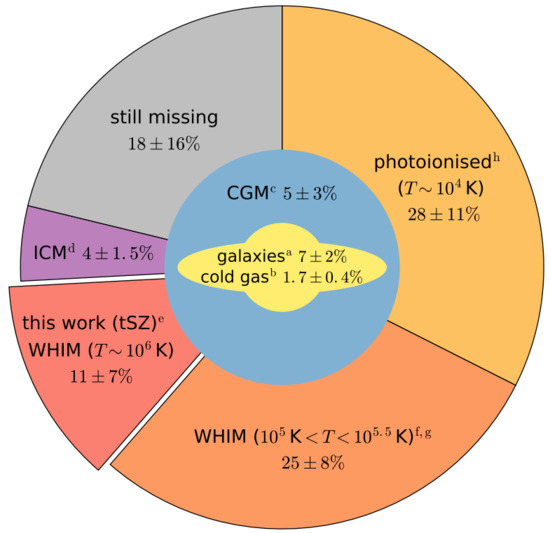
Figure 1.
A budget for baryons in the Cosmos, from de Graaff et al. [100]. Stars, dust and cold gas etc in galaxies account for approximately 10% of the baryons, with the remainder predominantly in an ionised state in the circumgalactic medium (CGM), the Intracluster medium (ICM), and the WHIM (warm-hot intergalactic medium). A fraction of the baryons remains unaccounted for, with estimates ranging up to 50%, although the fraction is smaller in the de Graaff et al. [100] study (as indicated by the “still missing” part of the pie chart). FRBs offer the prospect of locating and characterising the properties of these missing baryons. The figure is reproduced with permission from Astronomy & Astrophysics, ESO.
Cosmological simulations for large-structure formation indicate that the majority of the missing baryons reside in the diffuse Warm-Hot Intergalactic Medium (WHIM), where the IGM has been heated by gravitational shocks and galactic feedback mechanisms to temperatures of – K [89] in a cosmic web between clusters of galaxies [86,90,91]. The WHIM is difficult to detect directly because of its extremely low density, but is predicted to produce absorption lines in UV and X-ray in background sources [92]. Several such detections have been reported, but none are considered definitive [93]. Experiments to detect the WHIM, by targeting the putative filaments connecting galaxy clusters, have also been proposed [94]. An observation of a QSO sightline intersecting 7 independent intercluster axes at impact parameters <3 Mpc (co-moving) at redshifts found a tentative excess of BLAs by a factor of ∼4 with respect to the field [95]. The excess of BLAs could potentially be a signature of the WHIM in intercluster filaments [95,96]. Most recently, Nicastro et al. [97] reported WHIM detection from the measurement of two O vii absorbers, and extrapolate that their measurement may account for all of the missing baryons, but with large uncertainties. A complementary method to search for WHIM present in filaments connecting galaxy and galaxy clusters using the thermal Sunyaev-Zel’dovich (tSZ) effect [98] was also proposed [99,100]. The effect arises from the Compton scattering of CMB photons by ioinzed gas, providing an excellent tool for probing baryonic gas at low and intermediate redshifts.
2.2. The Macquart Relation
The dispersion measure of FRBs, combined with redshifts for the host galaxies, is a unique tool able to directly measure the baryon content of the universe, with the potential to resolve the missing baryon problem [101,102]. We can divide the observed DM of an FRB into four primary components:
where is the contribution from our Galactic ISM, is the contribution from our Galactic halo, is the contribution from the host galaxy including its halo and any gas local to the event, which is a factor of smaller than the source-frame DM, and is the contribution from all other extragalactic gas or IGM. In ΛCDM, can be expressed as
with , where is the proton mass, is the mass fraction of Helium, assumed doubly ionised in this gas, is the fraction of cosmic baryons in diffuse ionised gas (this accounts for dense baryonic phases, e.g., stars, neutral gas), , and and are the current dark matter and dark energy densities in units of . This relationship between DM and redshift is now popularly known as the “Macquart relation” [13].
In the literature, the Macquart relation has been estimated theoretically using analytical models and hydrodynamic cosmological simulations to estimate the density of electrons as a function of redshift z and its variance along different lines-of-sight. Initial work on the DM-z relation assumed the IGM to be fully (or nearly-fully) ionised and homogeneous. These studies yielded approximately linear relations between DM and z for [103,104,105,106].
Studies of the DM-z relation using cosmological hydrodynamical simulations followed, in order to study the scatter due to the cosmic web of filaments, voids and other substructures. McQuinn [102] worked out the DM-z relation with different models for the distribution of cosmic baryons. They showed the distribution of DM is sensitive to the locations of missing baryons, and can determine whether they lie within the virial radius of – M⊙ halos, or whether they lie further out in an intrahalo medium. The basis of this determination is the variation in the DM for a set of FRBs at similar redshifts. The sightline-to-sightline variance in DM observed is predicted to be primarily caused by the scatter in the number of collapsed systems encountered along the line-of-sight of an FRB. More compact halos will have more sightline variance and hence skewed probability distributions whereas diffuse gas around halos will lead to less sightline variance and then more Gaussian-like probability distribution function (pdf) (see Figure 2). Understanding how the variance evolves with redshift can be used to measure feedback (from active galactic nuclei and supernovae) and other processes that regulate the distribution of baryons in the cosmic web [107]. They also showed that a stacking analysis of ∼100 localised FRBs at would place interesting constraints at distances of ≈0.2 to 2 virial radii on the baryonic mass profile surrounding different galaxy types.
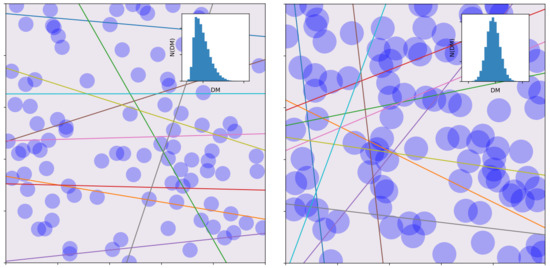
Figure 2.
Right panel: Cartoon representation of compact halos and the resultant skewed probability distribution of the DM distribution as seen along many lines of sight (coloured lines). Left panel: Cartoon representation of diffuse halos and Gaussian-like probability distribution, due to the larger number of lower density sightlines.
Dolag et al. [108] have used the Magneticum simulations to investigate the contributions to FRB DMs from the Milky Way disk and halo, from the Local universe, from cosmological large-scale structure, and from host galaxies. Through this combination of contributors, they have made predictions for the expected DMs of FRBs distributed over different redshift ranges and for differing spatial distributions. They found that the observed DM distribution for a sample of nine extragalactic FRBs is consistent with a cosmological population detectable out to a redshift to 0.9, regardless of the specifics of how FRBs are distributed with respect to large-scale structure or the properties of their host galaxies. Illustris simulations have also been used to estimate the DM-z and the scatter due to inhomogeneous distribution of ionised gas in the IGM [109]. Jaroszynski [110] find ∼13% scatter (1-) in DM to a source at and ∼7% at . Their distribution of DM around the median DM-z relation is close to Gaussian. The IllustrisTNG simulations, which build on Illustris and implement galaxy formation in a full magneto-hydrodynamical context, show that properties beyond the DM-z relation can be probed with FRBs, such as the magnetic field strength of the IGM, the cosmic reionisation history and the optical depth of the CMB [111] (see Section 4). Batten et al. [112] used the EAGLE simulations to investigate the scatter around the mean and shape of the pdfs for redshifts over a billion simulated FRB sightlines. They find that the in EAGLE is consistent with the observations of FRBs [13] and that the probability distribution of extragalactic DMs is strongly non-Gaussian at .
The theoretical predictions and the implications of the DM-z relation have been a major driver of further FRB observations. The most urgent observational priority of FRB science is starting to be fulfilled with the localisation of FRBs and the redshift measurements of their host galaxies [12,13,19,23,51,113,114]. The precise localisation of FRBs with the Australian Square Kilometre Pathfinder Array (ASKAP) has provided the first ensemble of DMFRB and measurements, enabling direct and independent measurement of the missing baryons [13]. Macquart et al. [13] model the scatter in the IGM DM as:
where , is related to the inner density profile of gas in halos, is the slope in the case where density scales as and is a constant. This accounts for sightline-to-sightline scatter in the DM caused by intervening halos. The variance in DMcosmic is also sensitive to the extent by which galactic feedback redistributes the baryons around halos and is also given by for where F quantifies the strength of baryonic feedback. Their “gold sample” of FRBs is over-plotted in the right panel of Figure 3 and is observed to be consistent with the predictions of ΛCDM cosmology which is shown as a black line. The gray zone represent the 2 scatter in the cosmic DM [13].
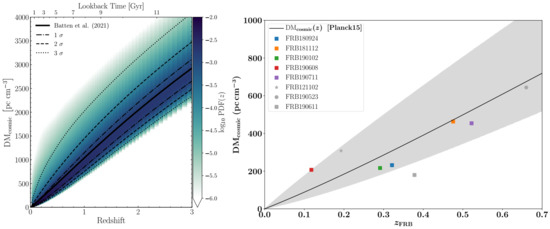
Figure 3.
Left panel: Predictions from cosmological simulations of the Macquart relation and the scatter around it from Batten et al. [112]. These simulations include the effects of under/over-dense regions in the IGM and the circumgalactic medium. The scatter is shown at 1, 2 and 3 around the median DM-z relation. Note that the scatter is quite asymmetric, especially at low redshift (), but becomes more Gaussian at z approaches 3 (the limit of the study). Right panel: Macquart relation (solid line), and the 2- scatter around it (grey area) and DMs and host galaxy redshifts for localised FRBs from ASKAP, DSA and the VLA. The figure is reused with permission from Macquart et al. [13].
We note that James et al. [115] have recently shown that observational biases can affect the DM-z relation such that a monotonic rise no longer pertains in the higher DM regions of a given sample, depending on the luminosity function of the FRBs. A nominal maximum observable DMmax is set by the DM relation and the maximum distance, zmax, at which an FRB can be observed by a given survey. At zmax, large excess DMs above the DM relation will be unobservable due to the extra signal-to-noise penalty from the DM smearing effect. However, FRBs closer than zmax could still be observable even with very large excess DMs, e.g., due to originating from within a galaxy cluster [113], which would push their DM above the supposed DMmax. This causes an inversion in the DM-z relationship, implying that the highest DM FRBs in a large sample are unlikely to have the highest redshifts.
2.3. Turbulence and Magnetisation in the IGM
The existence of bright, short-duration FRBs makes it possible to probe the turbulence in the plasma through which they propagate over cosmological distances [74], constraining the turbulence properties in the IGM scale, the largest scale of turbulence in the universe [116]. Many FRBs show a scattering tail, indicative of multi-path propagation through inhomogenities in the plasma along the line-of-sight. Reported scattering times for FRBs to date are of the order of tens of microseconds to tens of milliseconds at 1 GHz. Many FRBs are found to be “under-scattered” (by more than an order of magnitude) when compared to pulsars [117], indicating that the turbulence effects along the propagation path are very much less than the ISM.
FRB scattering can plausibly arise in the Milky Way ISM and halo, foreground halos, the IGM, the host galaxy ISM and the circum-burst environment.
- Models exist for the scattering effects of the Milky Way ISM through analysis of pulsars [72,118], and good estimates of the scattering due to this source for a given FRB can be made. FRBs are mostly found at high Galactic latitudes such that scattering effects due to the Milky Way ISM are low [119,120]. However, the Milky Way halo may play a role, and this is now starting to be studied with FRBs. The maximum amount of pulse broadening from the Galactic halo has been estimated as μs at 1 GHz, which is comparable to the scattering expected from the Galactic disk for line-of-sight towards the Galactic anti-center or at higher Galactic latitudes [121]. For FRBs which are detected at low Galactic latitudes such as FRB 121102 and FRB 180916, the reported scattering measurements of 40 μs at 1 GHz and 2.7 μs at 1.7 GHz are consistent with the scattering due to the Milky Way [121,122]. For other bursts, high time resolution analysis has shown that the scattering originates well beyond the Milky Way [6,71,73].
- Intervening galaxies [123] are able to contribute to the scattering, but the probability of impact with a disk is low: Macquart and Koay [124] estimate only a 5% chance that a source at will intersect with the inner regions of galaxies (i.e., within 10 kpc). For most FRBs this is not the primary source of scattering.
- Cosmological hydro-dynamical simulations suggest that the FRB host galaxy (ISM and the circumburst medium) and foreground halos may dominate the scattering [125,126]. The host can cause significant broadening and is sufficient to account for some of the observations [117,127,128]. The host contribution depends on the progenitor location within it, and the host’s inclination on the sky. The studies suggest that the pulse broadening is produced by the highly turbulent and dense medium in the immediate vicinity of the FRB, possibly for FRB progenitor models involving young stellar populations [6,49]. Interestingly FRB 180924, FRB 191001 and FRB 190608 which are localised to the outskirts of their host galaxies show large amounts of scattering in the current sample [14,77]. In case of FRB 190608, the studies indicate that the scattering is likely originating within the host galaxy [129,130]. Measurements of scattering for the UTMOST FRB 170827 is consistent with a two-screen model with one screen in the Milky Way and other in the host galaxy of the burst [71]. Furthermore, repeated bursts from some FRBs can be used to monitor the host-galaxy ISM properties on timescales of years, probing AU-scale density inhomogenities in extragalactic ISM.
There is currently considerable debate about whether the observed temporal smearing is mainly caused by the IGM, or whether it can be fully attributed to turbulence in the ISM of the host galaxy of the burst. Yao et al. [131] suggest the importance of the IGM in both dispersion and scattering of FRBs and empirically determined a flat DM-dependence ∝ DM1.3 of the scattering timescale.
A redshift dependence on the temporal smearing can discriminate between scattering that occurs in the host galaxy of the burst and the IGM—specifically, the -DM (or -z) relation is expected to have a weak power-law dependence with opposite effect depending on the dominant source of the scattering. Macquart and Koay [124] describe the redshift dependence on the temporal smearing that occurs in the host galaxy to scale as:
Thus, if the scattering time is dominated by the ISM of the host galaxy, it decreases as a steep function of redshift. This is in stark contrast to the redshift dependence of the temporal smearing time expected of scattering in the IGM, which scales as:
An analysis of -DM conducted for a sample of FRBs found no evidence for any relationship between and DM [73,117], although the time resolution of ≈1 ms may still be too large to probe such effects in all FRBs.
It has been shown recently that the scattering by the IGM in the voids and walls of the cosmic web is weak, but it can be significantly enhanced by the gas in clusters and filaments [125]. Hence, the IGM may dominate the scattering of some FRBs, and the host galaxy dominates others. The redshift dependence of scattering for large samples of localised FRBs with well-measured scattering timescales might distinguish between temporal smearing due to the host galaxy or the IGM.
Finally, the joint analysis of the DM and the RM from distant, linearly polarized FRBs may be used to put constraints on the origin and distribution of extragalactic magnetic fields on cosmological scales [132,133,134,135]. For instance, FRB 110523 has RM rad m−2, implying an electron-weighted average line-of-sight component of the magnetic field, μG [6]. Furthermore, based on a low Faraday rotation ( rad m−2) for FRB 150807, Ravi et al. [74] inferred negligible magnetisation in the circum-burst plasma and constrain the net magnetisation along this sightline to <21 nG, parallel to the line-of-sight. Constraints on the mean magnetic field strength in the IGM have also been reported to be < nG, where is the mean redshift of the magnetised plasma for line-of-sight of localised FRB 180924 [12]. Detection of ≥ FRBs with extragalactic RM uncertainties of a few rad m−2 could eventually distinguish between leading models for seeding the as-yet undetected IGM magnetic field [132,133].
2.4. Probing the CGM
The gas surrounding galaxies outside their ISM and inside the virial radius, typically extending to hundreds of kiloparsecs for Milky Way mass galaxies, is known as the circumgalactic medium (CGM). This medium hosts the large-scale flows of gas and metals that cycle into and out of galaxies over time. Gas accretion fuels star formation and grows the galaxies. Feedback from supernovae or active galactic nuclei (AGN) eject gas and metals from galaxies quenching star formation [136]. Therefore, this “halo gas” influences the process of galaxy formation and its evolution.
Both observations and simulations suggest that the CGM consists of a multi-phase gas with components at very different temperatures over the range – K. Direct evidence for a hot component ( K) comes from diffuse soft X-ray emission [137]. The cooler component is detected through hydrogen Lyman series and absorption lines along quasar sightlines where ions like C iv, N v, O vi, and Ne vii trace the CGM at K and C ii, C iii, Si ii, Si iii, N ii, and N iii trace the CGM at K. Surveys of the CGM of low-redshift L* galaxies demonstrate that this cool gas (∼ K) surrounding the galaxies has mass similar to the Milky Way [138,139]. The cold component ( K) tracers consist of neutral and low ions like H i, Na i, Ca ii, and dust. Tumlinson et al. [140] give an excellent review of the CGM.
There are a number of proposals to explain the production of the multiphase CGM. Gas falling onto galaxies is heated to the virial temperature of the galaxy’s dark matter halo producing the extended, hot corona detected in X-rays [141,142]. In massive galaxies, the hot gas has a long cooling time, so the cooler gas clouds in the halo are formed through radiative cooling, where the high density gas cools faster as the result of thermal instability [143]. The multiphase halo is maintained by (1) feedback from the galaxy in the form of galactic winds which replenishes the halo with hot gas and (2) density peaks that can cool the halo through thermal instability [144]. Thus, this constant cycle of gas heating and cooling can reproduce the observations of hot and cold phases in the CGM. In such models, the cooler clouds are pressure-confined by the hot gas, implying pressure equilibrium between the two phases. These models suggest a hierarchical structure of the CGM where cold clouds are enveloped in warm transition gas which is embedded in the hot halo [145,146].
Furthermore, simulations of galactic feedback, in the form of galactic winds or cosmic rays, interacting with the gaseous halo of a galaxy produce a complex temperature and kinematic structure of the CGM that is consistent with gas properties inferred from quasar absorption line observations [147,148,149]. Such simulations also indicate that a significant fraction of the gas in the CGM was originally located in galaxies and galactic feedback is essential for populating the CGM with metal-enriched gas [150].
Major questions on the properties of the CGM are its total mass, density distribution, ionisation state, metals distribution, inflow/outflow characteristics, turbulence and clumpiness. The properties of FRBs offer the prospect of studying some of these properties in an entirely novel way.
One of the first such opportunities presented itself when an FRB, discovered and localised with ASKAP, was found to pass through the halo of a foreground galaxy [151]. FRB 181112 is localised to a galaxy at a redshift of . The FRB sightline passes at an impact distance of 29 kpc from a Seyfert galaxy (on the basis of nebular emission characteristic of an AGN) with a high stellar mass ( M⊙) at a redshift and thus probes its halo, as presented in the left panel of Figure 4. The DM contribution from the halo of foreground galaxy does not dominate the total DMFRB of 589 pc cm−3 and contributes only 50–120 pc cm−3, depending on assumptions for the density profile and total mass of the halo gas. The RM of the FRB was found to be RM rad m−2 and adopting an upper limit of RM rad m−2, an upper limit on the maximum parallel magnetic field in the halo of foreground galaxy was calculated to be
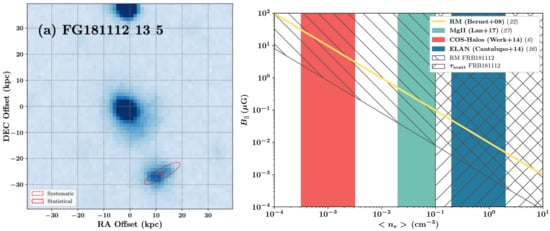
Figure 4.
Left panel: g-band FORS2 image showing the host galaxy of FRB 181112 from Prochaska et al. [151]. The FRB position is presented by the red ellipses with solid/dashed lines indicating the statistical/systematic uncertainty. The FRB sight-line passes through the halo of a foreground galaxy (cataloged as DES J214923.89−525810.43) at an impact factor of 29 kpc. Right panel: Constraints on the coherent magnetic field parallel to the line-of-sight B‖ and electron density in the halo of the foreground galaxy. The hatched regions show the parameter space in B‖, (cool gas) ruled out for the halo of foreground galaxy from the measured RM and scattering for FRB 181112. The results of Prochaska et al. [151] are compared with previous models for the density of cool halo gas (coloured regions) based on ionisation modeling and Ly flourescence. The figures are reused by permission under AAAS’s licence to publish.
This value is lower than previous estimations for halo gas [152] and far lower than measurements from regions above the plane of disks in nearby galaxies [153]. The value implied that either the magnetic field of the halo is low (as compared to the ISM) or that it is largely disordered. The authors also find an upper limit on the scattering to be μs constraining the turbulent properties of the halo gas and its density to be:
assuming a Kolmogorov spectrum of turbulence. Here, approximates the path length through the foreground halo, is the outer scale of turbulence and is the root-mean-square amplitude of the density fluctuations. Their constraints are stronger for the model of cool gas (T K), which is pressure-confined by hot gas, as compared to a hot virialised gas (T K) model for the CGM. Using cm−3 and K, application of Equation (15) with kpc and kpc yields . Since , the filling factor of cool clouds with is required if the clouds are fully turbulent, contradicting prior inferences that cool halo gas has a volume filling fraction of – [154,155,156]. Furthermore, the parameter space ruled out by these observations conflict with several previous inferences for halo gas (see right panel of Figure 4) [152,154,156]. Thus, the observations of Prochaska et al. [151] indicate a lower density of hot gas and a smaller column of cool gas as compared to many models. A similar analysis was performed to study the potential contribution of foreground halos to the observed temporal broadening ( ms at 1.28 GHz) and rotation measure (RM rad m−2) of FRB 190608 [130]. They also found that intervening halos cannot account for large scattering and RM of FRB 190608 and that these are likely to arise from the progenitor environment or the host galaxy.
2.5. Tomographic Reconstruction of the Cosmic Web
The matter distribution of the universe forms an intricate pattern on megaparsec scales known as the Cosmic web [157]. According to simulations, the dark matter halos are embedded in these filamentary structure of matter [158]. The process of accretion in the galaxies within the dark matter halos generate a hot halo of baryons at K and densities cm−3. The measurements of FRBs are sensitive to all the ionised gas along the line-of-sight, tracing this otherwise invisible plasma. Thus, FRBs can be used as quantitative probes of foreground ionised matter. Correlation of the DMs of FRBs with the distribution of foreground galaxy halos offers a unique way to disentangle the cosmic web.
Simha et al. [130] performed an end-to-end study of matter distribution along FRB 190608 sightline using spectroscopic and photometric data. They estimated the contribution of hot, ionised gas in the intervening virialised halos to be DMhalos ≈ 7–28 pc cm−3 using a modified NFW gas density profile. Furthermore, they employed the Monte Carlo Physarum Machine (MCPM) cosmic web reconstruction method to map the large-scale structure intercepted by the FRB sightline as presented in Figure 5. Using this 3D map of the ionised gas in cosmic web filaments, they estimated an IGM contribution to the DM to be DMIGM ≈ 91–126 pc cm−3. Li et al. [159] estimated the cosmic component of the DM (DMcosmic = DMhalos + DMIGM) for sightlines of 5 FRBs, which were localised with large uncertainties, to infer the matter density field along their line-of-sight. Ravi [160] demonstrated that the DMs of 10–100 localised FRBs can be used to measure the distribution of baryons between the CGM and IGM, by comparing measurements of DMcosmic, with predictions given the redshifts and masses of intervening galaxy halos and the FRB redshifts. Thus, localisation of a larger set of FRBs will constrain models of the cosmic web in a region and possibly perform tomographic reconstructions of filamentary structures.
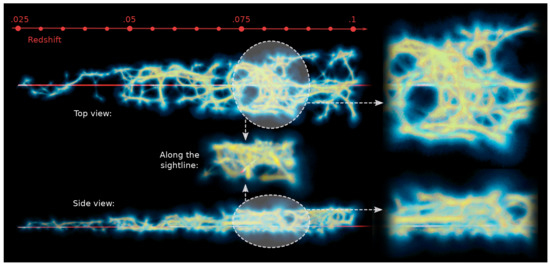
Figure 5.
A 3D model of the cosmic web in physical coordinates reconstructed using the MCPM taken from Simha et al. [130]. The red line passing through the web represents the FRB 190608 sightline where light is assumed to travel from right to left. The cosmic web reconstruction is shown colour-coded by the steady-state Physarum particle trace density (yellow being high and black being low). The figure is reproduced by permission of the AAS.
2.6. FRB Host Galaxy Environments
In the absence of multi-wavelength counterparts to extragalactic FRBs [3,161], analyses of their host galaxy environments is presently the most informative path to identifying their progenitor systems. The localisation of the first repeating FRB 121102 (by the realfast system at the VLA) facilitated the study of the very first host galaxy of an FRB [51]. FRB 121102 was localised to a low-metallicity dwarf galaxy with a high specific star-formation rate (log sSFR = −8.14 yr−1) at redshift [53]. Additionally, the bursts were found to be associated with an unusual radio-continuum nebula, first thought to be a young supernova remnant or pulsar wind nebula, but recent polarimetric observations have revealed that the source has extraordinarily high magnetic field strength suggesting a more extreme magneto-ionic environment [78]. The strength of the magnetic field is decaying with time [162]. The properties of the environment and of the host galaxy for FRB 121102 have led to a concordant model in which bursts are produced by young magnetars, themselves produced in a super-luminous supernova or long gamma-ray burst [163].
Very-long-baseline interferometry (VLBI) localisation of the second repeating source, FRB 180916, showed that it originated from the outer arm of a massive, nearby () spiral galaxy, with an overall low star-formation rate and lack an extreme magneto-ionic environment and radio nebula [114], very different to the dwarf galaxy host of FRB 121102. Recent optical and infrared imaging with integral field spectroscopy observations of FRB 180916 with the Hubble Space Telescope has provided constraints on H luminosity for any star-forming or H ii region at the FRB position. The local star-formation rate is also constrained to be ≤ M⊙ yr−1. Furthermore, this FRB is 250 pc away from the nearest knot of active star formation in the host galaxy and a progenitor source (similar to a magnetar or pulsar) would need 800 kyr to 7 Myr to traverse the observed distance from its presumed birth site. These ages are inconsistent with the progenitor being a young magnetar and are compatible with the ages of high-mass X-ray binaries and gamma-ray binaries [164].
Recently, CHIME reported a detection of the lowest DM repeating FRB 20200120E which was associated with the nearby galaxy M81 with the probability of a chance coincidence of just < [64]. The FRB appears on the outskirts of M81 (projected offset ∼20 kpc) but well inside the extended H i and thick disks. M81 is different from the hosts of other known repeating FRBs in spatial offset, stellar population age, and local environment. Therefore, the repeating FRBs appear not to favour any distinct environments (and/or show a broad range of galaxy environments).
Bhandari et al. [165] analysed the global properties of the first sample of four ASKAP-localised FRB host galaxies. The apparently non-repeating FRBs appear to originate from the outskirts of massive galaxies (log() ∼ 9.4–10.4) with little to moderate star formation, ruling out models that invoke AGN and cosmic superconducting strings as FRB progenitors. They also find that the galaxy colours and star formation rates of the host galaxies show a diversity of properties and are not confined in a well defined locus of a particular class. Furthermore, the global properties of these four host galaxies suggest that FRB progenitors more likely arise from a general stellar population than a very young stellar progenitor.
Later, Heintz et al. [166] presented observations and detailed characterisations of an additional five ASKAP-localised FRB host galaxies and reported that the hosts exhibit a broad, continuous range of colour ( 0.9–2.0), stellar mass (), and star-formation rate () spanning the full parameter space occupied by galaxies (see Figure 6). They also reported an excess of “green valley” galaxies and an excess of emission-line ratios in their sample which indicates a harder radiation field than that generated by star-formation alone. They compared the spatial host-burst offset distribution and other properties with the distributions of long- and short-duration gamma-ray bursts (LGRBs and SGRBs), core-collapse supernovae (CCSNe), and Type Ia SNe. Bhandari et al. [165] and Heintz et al. [166] agreed that compact merger events (WD-WD, NS-NS mergers), accretion-induced WD collapse and CCSNe seem to be plausible mechanisms for the FRBs localised by ASKAP and that the galaxies hosting LGRBs (faint, star-forming galaxies) are less likely to be common hosts for FRBs. This is also consistent with an independent study which compared the host galaxy properties of FRBs with those of stellar transients such as Type Ib/Ic supernovae (SN Ibc), Type II supernovae (SN II), Type Ia supernovae in addition to long and short GRBs [167] and work of Wang et al. [168] which showed that the compact mergers can account for the observed offset distribution of localised FRBs.
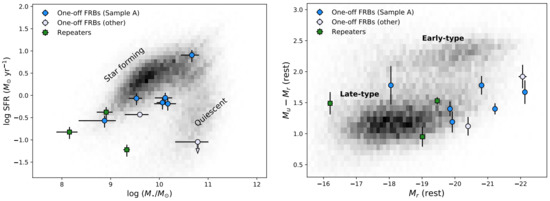
Figure 6.
Left panel: Star-formation rate vs. stellar mass M∗ distribution of FRB hosts taken from Heintz et al. [166]. Right panel: Rest-frame colour-magnitude diagram of the host galaxies of repeating and non-repeating FRBs taken from [166]. The majority of the FRB hosts are part of the brightest galaxy population. The figures are reproduced by permission of the AAS.
Furthermore, Mannings et al. [169] presented a high resolution view of the FRB host environment using ultraviolet and infrared observations from the Hubble Space Telescope (see Figure 7). They place constraints on the spatial distributions of FRBs and find a median host-normalised offset of 1.4, where is the host galaxy half-light radius. They also find that most FRBs are not in regions of elevated local star formation and stellar mass surface densities in comparison to the mean global values of their hosts. Furthermore, five of eight FRB hosts in their sample show clear spiral arm features in IR light, and the positions of well-localised FRBs located in these hosts are consistent with the spiral arms. Their results do not strongly support the progenitor channel of FRBs being connected with the most massive stars, or with events which require kicks and long delay times.
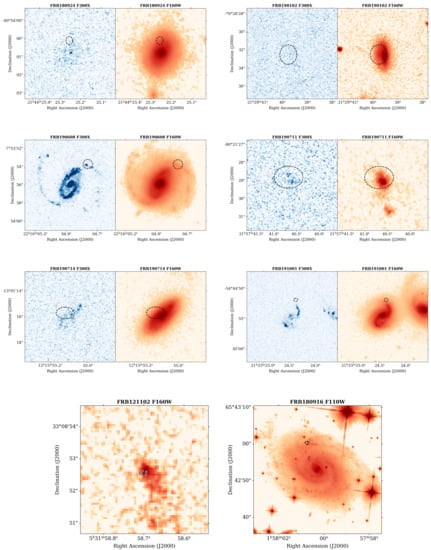
Figure 7.
HST imaging of FRB host galaxies as presented in Mannings et al. [169]. Blue images were obtained with the UV channel F300X filter, while red images were obtained with the IR channel F160W filter. The black ellipse in each image denotes the FRB position.
Additionally, the recent detection of an FRB-like signal in the direction of SGR 1935+2154 in the Milky Way [66,67] motivated the studies comparing the demographics of known FRB hosts with a sample of CCSNe hosts to determine whether FRB progenitors are consistent with a population of magnetars born in CCSNe [170,171]. These studies have led to conflicting results. Recently, Sridhar et al. [172] presented that binaries of stellar-mass compact objects undergoing super-Eddington mass transfer, similar to those which characterise some ultra-luminous X-ray (ULX) sources, can reproduce FRB luminosities and rates. They also show that the host galaxies of FRBs, and their spatial offsets within their hosts, show broad similarities to those of ULX.
In summary, the current data suggests that the majority of FRB sources are not likely to be young stellar progenitors, although they may still contribute to a fraction of the most active magnetars such as FRB 121102. Most FRB sources could be similar to known Galactic magnetars, which did not have an SLSNe or LGRBs progenitor. Thus, exploring the properties of host galaxies to constrain FRB progenitors is an active area of FRB research.
Dispersion Measure Contribution from the Host Galaxy
The DM contribution of a putative host galaxy will depend on galaxy type, the FRB site within it and the viewing angle. Xu and Han [173] have modelled the DM distributions due to the ISM for FRBs arising in elliptical, dwarf and spiral galaxies. They scale the NE2001 model [118] of the Milky Way ISM to the integrated H intensity maps for such hosts, to represent their electron density distributions. They report that contributions to the DM of FRBs from the host galaxy follow a skewed Gaussian distribution. The ensemble average DM distribution for dwarf galaxies is 45 pc cm−3 and for elliptical galaxies is 37 pc cm−3. For spirals, they derive the weighted average of the DM distribution over a range of inclination angles to be 142 pc cm−3.
The redshift measurements of localised FRBs are playing a key role in constraining the DM of the host galaxies. Tendulkar et al. [53] estimated the to be in the range of 55–225 pc cm−3 using for FRB 121102. The mean host contribution for FRB 180924 after correcting for host redshift is estimated to be in the range 30–81 pc cm−3, with the 95% upper limits ranging from 77 to 133 pc cm−3 [12]. The host contribution in this case is much smaller than that anticipated for FRB 121102. Using the relation between optical reddening and hydrogen column density () [174] with DM- correlation [175], Bhandari et al. [14] estimated the DM contribution from the host of FRB 191001 to be 61 pc cm−3. Chittidi et al. [129] performed a high-resolution imaging and spectroscopic analysis of the host galaxy of FRB 190608. Using an estimate of the H emission measure (EM) at the FRB position and the methods of Prochaska and Zheng [113], they derive pc cm−3. Recently, Macquart et al. [13] derived the mean and scatter in the host galaxy DM by performing a joint likelihood of measurements from five ASKAP-localised FRBs again a model probability distribution described by:
where the log-normal distribution has a median value of and variance . Their analysis favour a median host galaxy contribution of ∼100 pc cm−3 with . Li et al. [176] also derived host DM from the data and reached the similar constraints as DMhost pc cm−3.
Yang and Zhang [177] have studied the first derivative of the DM-z relation, and find that the slope (where DME is the extragalactic DM of the FRB), can be used to infer the average host galaxy DM. IllustrisTNG simulations have also been used to derive the DMs due to the host galaxy. Zhang et al. [178] selected a large sample of galaxies with similar properties to observed host galaxies in their simulations and computed the distributions of host galaxy DMs for repeating and non-repeating FRBs. They find a median DMhost to be and pc cm−3 for FRBs like FRB 121102 and FRB 180916, respectively, assuming that the burst sites are tracing the star formation in host galaxies. Furthermore, for apparently non-repeating FRBs, they find the median of DMhost to be 30–70 pc cm−3 in the redshift range 0.1–1.5, assuming that the burst sites are the locations of binary neutron star mergers. Jaroszyński [179] also used IllustrisTNG simulation to estimate the DM which may be attributed to halos of the FRB host galaxies. Their calculations show that in general the contribution of the hosts (with stellar mass greater than M⊙) to the observed DM increases with the redshift, rising to as much as 500 pc cm−3 for high mass galaxies at . This is also true of the scatter in DM around the mean, which may reach 100–200 pc cm−3 at source redshifts ranging between 1–. On the other hand for low mass galaxies, DM and scatter in the DM remain very low, at a few 10 s of DM units only. They conclude that cosmological tests using FRBs will be possible, but that to preserve the level of statistical uncertainty the number of FRBs with known redshift in a sample should be increased by 15–35%.
2.7. Probing the Milky Way ISM and Ionised Halo Using FRBs
The Interstellar Medium in the Milky Way makes up approximately 10% of its baryonic mass [180], with the remainder being primarily in stellar form [181]. The ionised fraction of the ISM is only about 1% by mass [118]. In addition to the ISM, which is chiefly confined to the Milky Way disk, there is a considerable baryonic component in the Milky Way’s CGM. The mass and ionisation state of this (baryonic) halo component has been estimated in a number of ways, but remains poorly constrained. Methods include studies of (1) of the cold and hot components on the Galactic halo using high velocity clouds [113] and column densities of ionised metals (such as Silicon), (2) DM measurements to pulsars in the Magellanic Clouds [182], (3) the diffuse X-ray emission around the Milky Way [183] and (4) the ionised halos formed around galaxies in cosmological simulations [108]. The DMs of pulsars in the Large Magellanic Cloud imply pc cm−3. Prochaska and Zheng [113] obtain pc cm−3 from cold and hot gas surveys. Dolag et al. [108] obtain pc cm−3 for Milky Way type galaxies in cosmological simulations, and Yamasaki and Totani [184] obtain pc cm−3 using X-ray data for the diffuse halo.
Constraining the halo’s mass density and ionisation through DM measurements of nearby FRBs has been proposed by Platts et al. [182], among others. They used pulsars and a small number of nearby FRBs to obtain a conservative upper limit on of 123 pc cm−3 (95% confidence), and estimate that several thousand FRBs are required to significantly improve constraints on . Even with the small number of FRBs in the sample they are already able to rule out a baryonic halo with a density profile like that of the putative dark matter. In the future, precise localisation or identification of a multi-wavelength counterpart for nearby FRBs such as FRB 20200120E [64] will strongly constraint the maximum MW halo contribution to the DM.
3. Constraining Cosmological Parameters Using FRBs
3.1. Dark Energy Equation of State (w) and Baryon Density ()
Cosmological parameter estimation using FRBs was first proposed by searching for a possible association of FRBs and GRBs to measure the intergalactic medium part of the baryon mass fraction of the universe [101]. Gao et al. [185] proposed to conduct cosmography and showed that with several tens of FRB/GRB systems, it is possible to attain reasonable constraints on wCDM models for which the equation of state (EoS) of dark energy (DE) is a constant and parameterized by, . However, to date there is no observational evidence for an FRB/GRB association. FRBs alone can be used to measure w. The distribution of the DM-z relation for FRBs localised at can be used as an independent measure of the DE equation of state using a form of the Macquart relation [101,185] in a flat cosmology model, which is given by:
where and are the ionisation fractions of the intergalactic hydrogen and helium, respectively, and , is mass fraction of H, He [186]. Thousands of localised FRBs are required however.
The combination of FRB data with CMB, baryon acoustic oscillation (BAO), supernovae and the Hubble parameter can be used to improve current estimates of cosmological parameters. Using such a method, Walters et al. [187] found the biggest improvement in constraining . They also report that the inhomogeneity of the IGM poses a serious challenge to the ability of FRBs to improve current constraints. Therefore, the greatest promise of FRB observations for the immediate future seems to be in locating the missing baryons, and not testing concordance or measuring the dark energy equation of state. However, in a recent study, Zhao et al. [188] investigated the capability of future FRB data for improving cosmological parameter estimation in two dynamical dark energy models. They find that the simulated FRB data can break the parameter degeneracies inherent in the current CMB data and the constraints on and w can be improved by about 50% and 80% by combining CMB data with and FRBs, respectively, (see Figure 8). The combination of the FRB and gravitational wave (GW) data provides an independent low-redshift probe to verify the results from the CMB and BAO data. Furthermore, in combining CMB, GW, and FRB data, the main contribution to the constraints comes from the CMB and GW data, but the inclusion of the FRBs could significantly improve the constraints on [188].
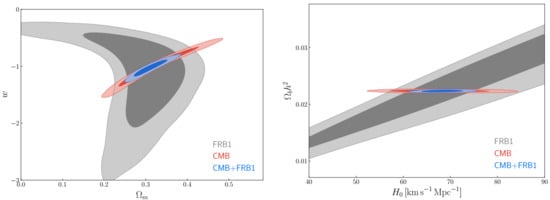
Figure 8.
Figure from Zhao et al. [188] presenting 2D marginalised contours (68.3% and 95.4% confidence level) in the plane (left panel) and the plane (right panel) for the wCDM model, by using () simulated FRBs, CMB, and CMB+FRB data. The figures are reproduced by permission of the AAS.
We note that for some work on cosmological applications of FRBs to date, the contribution to the DM by the host galaxy has been modelled as a constant offset to extragalactic DM typically in the range 50 to 100 pc cm−3. As we improve our understanding of this and other non-cosmological contributions to the DM of FRBs, then large FRB samples could become a useful cosmological distance probe. Removing the host galaxy contribution to the DMs is particularly important for probing dark energy (see, e.g., Kumar and Linder [189]).
The localisation of FRBs and the redshift measurement of their host galaxies is paving a way for testing cosmological experiments. Macquart et al. [13] constrained the baryon density parameter and the feedback parameter F (which quantifies the strength of the baryon feedback—0.1 being strong feedback and 0.4 being weak) by performing a joint likelihood of DMFRB and zFRB measurements of 5 FRBs against a model probability distribution for DMcosmic described by Equation (13). The constraints are presented in Figure 9. They derive a cosmic baryon density of and the ratio of the estimated to that from CMB and BBN measurements is . They also find the most likely (68% confidence) value of F to be (when is constrained to the value set by the CMB+BBN measurements) implying a strong feedback and showed that the current small sample of localised FRB is beginning to constrain viable models for the redistribution of the cosmic baryons by galactic feedback.
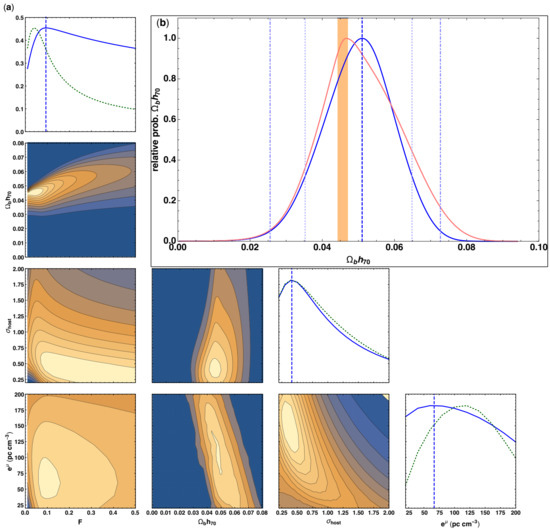
Figure 9.
The density of cosmic baryons derived from the FRB sample taken from Macquart et al. [13]. The constraints on the IGM parameters and F, and the host galaxy parameters and for a log-normal DM distribution are derived using the five gold-standard bursts. The corner plots in panel (a) display the probability that a given value of F, μ or is the consistent with the data against their most likely values, and marginalised over the other parameters: heavy dashed lines represent the most likely values in each case. The green, dotted lines in the corner plots of F, μ or denote the relative likelihood of these parameters when is constrained to the value set by the CMB+BBN measurements. The contours displayed are in increments of 10% of the peak value. Panel (b) displays the corner plot for where the orange shaded region denotes the range to which is confined by CMB+BBN measurements. The dotted and dot-dashed lines represent the 68% and 95% confidence intervals of each parameter, respectively.
3.2. Hubble Parameter
The cosmic expansion rate can be expressed in terms of the Hubble parameter with scale factor , which is also a powerful cosmological probe. In a flat ΛCDM cosmology, can be expressed as
where is the Hubble constant, is the vacuum energy density fraction, and is the matter density fraction. There has been a remarkable progress in improving the accuracy of measurements from 10% uncertainty with the availability of the Hubble Space Telescope [190] to less than 5% by a number of investigations [191,192]. However, there exists a tension between measurements of the Hubble constant made by CMB observations ( km s−1 Mpc−1), and those made from calibrating standard candles such as the expanded sample of the Milky Way Cepheids ( km s−1 Mpc−1) [193].
FRBs have temporal profiles that range from tens of microseconds to several milliseconds, which is shorter than the anticipated delay (∼1 ms) caused by multi-path propagation due to the gravitational lensing of compact objects (e.g., 10–100 M⊙ blackholes) [194]. Extremely high time resolution studies of FRBs and detection of few-microsecond temporal structure such as for FRB 181112 [195] could potentially detect multiple burst copies generated as a consequence of lensing [194]. Methods to distinguish copies of a burst through a lensing event have been developed and applied to FRB data by Farah et al. [71] and Cho et al. [195], based on the expectation of spatial coherence of the emission, which will be manifested as correlation in the voltages between pulses. Thus, FRBs let us probe gravitational lenses in the time domain with more precision and sensitivity than is possible in the spatial domain. A set of lensed FRBs, particularly if they are repeating in nature, would provide a very interesting and complementary measurement of the Hubble constant (constrained with a ∼0.91% uncertainty from 10 such systems) by probing the lens induced time-delays with unprecedented accuracy [196,197,198]. Furthermore, Li et al. [196] show that the cosmic curvature of the universe, k, can also be model independently constrained to a precision of ∼0.076 using a set of lensed FRBs. Finally, it is also shown that a mock FRB sample of 500 FRBs with dispersion measures and redshift information can accurately measure Hubble parameter (with ) using Monte Carlo simulation [199].
4. FRBs as Probes of Reionisation
The Epoch of Reionisation (EoR) is currently an actively researched area in cosmology. It refers to the period in the history of the universe between , when the neutral intergalactic medium was ionised by UV photons emitted by stars and quasars. While studying reionisation can help us understand the process of structure formation in the universe, it affects our ability to measure the CMB radiation propagating through the IGM by scattering the CMB photons and suppressing the amplitude of the primordial anisotropies. Additionally, electron scattering induces large-scale polarisation of the CMB radiation above that produced earlier during recombination. The effect is quantified by a parameter called the optical depth to reionisation, , which provides a measure of the line-of-sight free-electron opacity to CMB radiation. The CMB data currently provides a poor measurement of 6–10% [81,200] and this large uncertainty propagates in the estimation of other cosmological parameters from the CMB data.
The observation of high-redshift FRBs at offers an alternative means to constrain the optical depth. Using the relation between DM- given by,
where cm2 is the Thomson cross-section, can be measured to sub-percent accuracy, assuming FRBs exist during the EoR [201]. Similar studies to a redshift of have also been shown to offer a way to constrain the optical depth [46].
One of the open questions in current cosmology is the redshift of the onset and also the duration of the epoch of reionisation.
The reionisation for H and He i occurred at redshifts . While neutral helium loses its outer electron early, He ii is expected to have its more tightly bound inner electron ionised at . This is referred to as the epoch of He reionisation. The strongest evidence is seen through observational signatures in the far ultraviolet spectra of the He ii Ly forest along the lines-of-sight to several quasars at [202]. However, abundance of high-density systems at low redshifts contaminates the observations of the He ii Ly forest [203] reducing the number of sightlines which places a high statistical uncertainty on the precise timing and nature of the reionisation process (assuming FRBs can be found at such high redshifts). The temperature evolution of the IGM at also provides evidence of the reionisation [204].
The ionisation history of the universe can be expressed using a standard model with the ionisation fraction as
where Y and are mass fractions of He and H, respectively, [205,206]. For redshifts , it is assumed that all of the hydrogen is ionised () and none of the helium is neutral (i.e., it is either singly ionised He ii or fully ionised He iii). For epochs before helium reionisation, and and afterwards, and . In this simple model, ionisation fractions assuming an instantaneous reionisation occurred at redshift are:
where [81]. Thus, the ionisation fraction increases by ∼7.5% due to helium reionisation.
The cosmological DMs of FRBs localised at are sensitive to such changes in ionisation fraction. Figure 10 shows the standard model and its effect on the cosmological DM which changes slope with redshift due to the extra influx of electron density from helium reionisation [101,205]. For these applications, a large population of high-DM FRBs are required. Linder [206] predicted a level detection of He reionisation at for a sample of 500 mock FRBs detected in a survey extending out to . The signal-to-noise of the reionisation amplitude varies between 6.2–2.7 for reionisation occurring in the redshift range 2.5–3.5. Furthermore, Kit Lau et al. [207] finds that 100–1000 FRBs are required for a detection of He ii reionisation with an accuracy of , respectively, assuming an uncertainty of 5–20% in the redshift measurement of FRBs.
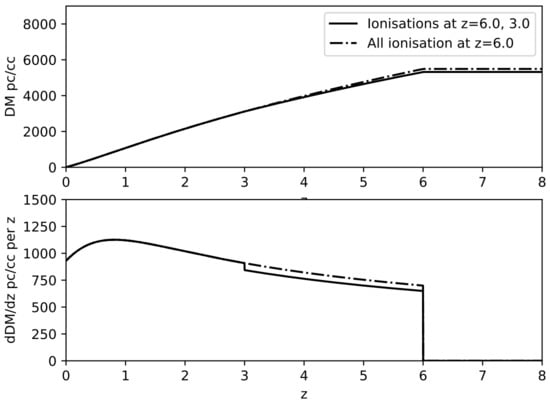
Figure 10.
Illustration of using DM to probe the epoch of reionisation of He ii. Top and bottom panels show DM and its derivative as a function of redshift, respectively. A sharp H i and He i reionisation at and a sharp HeII reionisation at are assumed.
Furthermore, using the DM-z relation in case of a homogeneous model for IGM, it is estimated that more than 1600 localised FRBs are required to distinguish between a model of the universe in which He reionisation occurred at from a model in which it occurred at [208]. Alternatively, the statistical ensemble of the distribution of FRB DMs can also be used to probe He reionisation. A fluence limited survey with FRBs can discriminate different helium reionisation histories at ∼ using the DM-distribution of bursts, without redshift information and ∼ with redshifts [209]. The large-scale clustering observed in the DMs of known FRBs is also very sensitive to the ionisation fraction of the end of reionisation epoch [210]. Thus, the observation of high-redshift FRBs could be a complementary probe to study the reionisation history in the future.
Reionisation does not occur uniformly; rather its duration and onset are likely correlated with the density field. Pagano and Fronenberg [211] show that these correlations could be probed with of order 100 high redshift (z = 8–10) FRBs, and rule out scenarios in which the universe is entirely neutral beyond . Hashimoto et al. [212] analysed scenarios in which reionisation models can be constrained using FRBs for samples with full/partial redshift data, or a luminosity relation exists allowing an independent distance estimate. They show that the reionisation history can be reconstructed with useful fidelity in all three scenarios, for samples of to FRBs found with the SKA.
5. Future Prospects
In the last decade, observations with increasingly sensitive and wide-field instruments have greatly added to our understanding of FRBs. At least events occur over the sky each day to a fluence of a few Jy ms, and a population of repeating sources has emerged [24,25]. ASKAP has played a crucial role in the arcsecond or better localisation of single bursts, which for the first time enabled the studies of their host galaxies. Commensal searches have begun with the VLA and ASKAP while other science programs are being undertaken, and dedicated instruments such as CHIME are already detecting FRBs at around 1 per day. The current small sample of ASKAP localised FRBs have started to provide an observational evidence of the Macquart-relation [13] and unique extragalatic sightlines to study intervening halos [113] and the cosmic web [130]. The high-time resolution analysis of ASKAP FRBs reporting burst substructure down to ∼15 μs timescales in the redshift range 0.3–0.5 has also provided first constraints on compact dark matter [194]. Thus, the potential of FRBs as probes of cosmology has begun to be realised.
The cosmological applications of FRBs described here will only be achievable with large numbers of FRBs (see Table 1). For the missing baryon science, detections of order of events is needed. The use of FRBs as cosmic rulers in which the average DM at a redshift z depends on the geometry of the universe, requires at least events [107]. To detect the He ii reionisation, – FRBs are needed [207] and > FRBs to distinguish between its onset and reionisation histories [208,209]. Furthermore, – FRBs are required for statistical detections of CGM gas densities at different impact parameters to intervening galaxies, characterisation (if present) of a scattering-redshift relation, for testing of CGM-cooling models [213]. Lastly, such large samples are also required for studying the origin and distribution of extragalactic magnetic fields [133] and for better constraints on cosmological parameters [187,188]. However, the optical follow-up observations for host galaxy identification and redshift measurements for such a large sample would be challenging. In such a scenario, photometric surveys such as the Dark Energy Survey [DES] [214] and the Large Synoptic Survey Telescope (LSST) will make host galaxy redshift determinations far less arduous as they aim to identify most galaxies over ∼50% of the sky. Additionally, statistical cross-correlation techniques will also be a key to constraining the redshift distribution, host DM distribution, and the intrinsic luminosity function of FRB populations [215].

Table 1.
Total number of FRBs that are required for cosmological applications.
The detection of multi-wavelength or multi-messenger counterparts to FRBs could well hold the key to revealing the phenomena that produce them. While the bulk of electromagnetic emission traces the movements of electrons and plasma, neutrinos can inform us about energetic atomic decay processes and hadronic accelerations. Meanwhile, gravitational waves directly track the movement of mass in explosive and relativistic phenomena [216]. Wang et al. [217] have shown that if there is any association between compact binary coalescence and (catastrophic) FRBs, it should only apply for a very small fraction of FRBs. There is a possibility that repeating FRBs are produced by continuous magnetosphere interactions between two neutron stars [218]. If so, a connection might be made between repeating FRBs and Laser Interferometer Space Antenna (LISA) GW sources. Furthermore, in a picture where repeating FRBs are produced from magnetars formed after binary neutron star mergers [168,219], GWs are produced at least years before repeating FRBs are emitted. An observationally identified GW-FRB connection can be made only with multi-year multi-messenger observations.
In the near future, commensal searches of FRBs with the coherent ASKAP-CRAFT system will be more sensitive than the current incoherent search system. This will increase the detection rate by a factor of 12 to 25, thereby localising one burst per day of on-sky time, delivering a sample of 1500 FRBs localised with arcsecond accuracy over the next 5 years. Arcsecond to sub-arcsecond localisation will be required for high probability identifications of host galaxies at high redshifts [220]. The ongoing commensal searches of FRBs with the MeerKAT telescope will also deliver a sample of high-DM FRBs [221]. The VLA Low-band Ionosphere and Transient (VLITE)-Fast experiment runs commensally with the VLA science operations at 300–364 MHz and aims to localise FRBs to < accuracy using A- and B-configurations of the VLA. The experiment is now operating close to design capability and is expected to detect and localise roughly 1 FRB per month (though rates are still uncertain) [222]. The real-time searches from The Apertif LOFAR Exploration of the Radio Transient Sky (ALERT) program will provide an arcsecond localisation of an FRB every week [223]. UTMOST-2D project is upgrading the Molonglo Radio telescope to few arcsec localisations for host galaxies [224], and will contribute to the DM-z relation in the near future. Its narrow frequency channels and relatively good sensitivity could localise higher z FRBs than to date. Currently, the most sensitive 500-m FAST telescope with 19-beam receiver has started to deliver a sample of high z and fainter FRBs, but no localisations. The implied all sky event rate with FAST is estimated to be 120,000 FRBs per sky per day above 0.0146 Jy ms [22].
Looking further ahead, the DSA-2000 will also detect and localise FRBs at a rate of ∼– FRBs per year, primarily for the characterisation of the IGM and as a cosmological tool [225]. The Hydrogen Intensity and Real-time Analysis experiment (HIRAX), a radio interferometer being developed in South Africa will consist of 1024 6-m dishes operating in the frequency range 400–800 MHz. HIRAX could find dozens of FRBs per day and be able to measure properties associated with their spectra, pulse arrival times, and spatial distribution [226]. The Canadian Hydrogen Observatory and Radio transient Detector (CHORD) instrument consisting of large core of ulta-wideband 300–1500 MHz dishes proposed to build adjacent to CHIME supplemented by a pair of outrigger stations will deliver a samples of tens of thousands of localised FRBs, and undertake cutting-edge measurements of fundamental physics [227]. The era of the Square Kilometre Array (SKA) promises detection of – FRBs [228]. We note that the radio frequency interference (RFI), continues to worsen at an alarming rate, and should not be ignored, as it will be an anathema to FRB searching that can have serious implications on FRB detection rates. Nevertheless, we are at the verge of a new era of cosmology where FRBs are poised to become a leading means of characterising the structure of the universe.
Author Contributions
Conceptualisation and methodology, S.B., C.F.; writing—original draft preparation, S.B.; writing—review and editing, S.B., C.F. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
We thank the three referees for their useful comments and suggestions which has improved the quality of the manuscript. We are grateful to Adam Batten, Anna de Graff and Xin Zhang for the use of figures. We thank J. Xavier Prochaska and Ron Ekers for feedback on the paper. We also thank Emma Ryan-Weber, Glenn Kacprzak and Clancy James for useful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AGN | Active Galactic Nuclei |
| ASKAP | Australian Square Kilometre Array Pathfinder |
| BAO | Baryon Acoustic Oscillations |
| BBN | Big Bang Nucleosynthesis |
| CCSNe | Core-collapse supernovae |
| CDM | Cold dark matter |
| CGM | Circumgalactic medium |
| CHIME | Canadian Hydrogen Intensity Mapping Experiment |
| CMB | Cosmic Microwave background |
| CRAFT | Commensal Real-time ASKAP Fast Transients |
| DE | Dark Energy |
| DM | Dispersion measure |
| DSA | Deep Synoptic Array |
| EoR | Epoch of reionisation |
| EoS | Equation of State |
| FRB | Fast radio burst |
| GRB | Gamma-Ray Burst |
| GW | Gravitational wave |
| IGM | Intergalactic medium |
| ISM | Interstellar medium |
| LGRBs | Long Gamma-Ray bursts |
| MCPM | Monte Carlo Physarum Machine |
| RFI | Radio Frequency Interference |
| RM | Rotation measure |
| SGRBs | Short Gamma-Ray bursts |
| SKA | Square Kilometre Array |
| VLA | Very Large Array |
| VLBI | Very-long-baseline interferometry |
| WHIM | Warm-Hot Intergalactic Medium |
References
- Lorimer, D.R.; Bailes, M.; McLaughlin, M.A.; Narkevic, D.J.; Crawford, F. A Bright Millisecond Radio Burst of Extragalactic Origin. Science 2007, 318, 777. [Google Scholar] [CrossRef] [PubMed]
- Thornton, D.; Stappers, B.; Bailes, M.; Barsdell, B.; Bates, S.; Bhat, N.D.R.; Burgay, M.; Burke-Spolaor, S.; Champion, D.J.; Coster, P.; et al. A Population of Fast Radio Bursts at Cosmological Distances. Science 2013, 341, 53–56. [Google Scholar] [CrossRef] [PubMed]
- Bhandari, S.; Keane, E.F.; Barr, E.D.; Jameson, A.; Petroff, E.; Johnston, S.; Bailes, M.; Bhat, N.D.R.; Burgay, M.; Burke-Spolaor, S.; et al. The SUrvey for Pulsars and Extragalactic Radio Bursts—II. New FRB discoveries and their follow-up. Mon. Not. R. Astron. Soc. 2018, 475, 1427–1446. [Google Scholar] [CrossRef]
- Petroff, E.; Barr, E.D.; Jameson, A.; Keane, E.F.; Bailes, M.; Kramer, M.; Morello, V.; Tabbara, D.; van Straten, W. FRBCAT: The Fast Radio Burst Catalogue. arXiv 2016, arXiv:1601.03547. [Google Scholar] [CrossRef]
- Spitler, L.G.; Cordes, J.M.; Hessels, J.W.T.; Lorimer, D.R.; McLaughlin, M.A.; Chatterjee, S.; Crawford, F.; Deneva, J.S.; Kaspi, V.M.; Wharton, R.S.; et al. Fast Radio Burst Discovered in the Arecibo Pulsar ALFA Survey. Astrophys. J. 2014, 790, 101. [Google Scholar] [CrossRef]
- Masui, K.; Lin, H.H.; Sievers, J.; Anderson, C.J.; Chang, T.C.; Chen, X.; Ganguly, A.; Jarvis, M.; Kuo, C.Y.; Li, Y.C.; et al. Dense magnetized plasma associated with a fast radio burst. Nature 2015, 528, 523–525. [Google Scholar] [CrossRef]
- Parent, E.; Chawla, P.; Kaspi, V.M.; Agazie, G.Y.; Blumer, H.; DeCesar, M.; Fiore, W.; Fonseca, E.; Hessels, J.W.T.; Kaplan, D.L.; et al. First Discovery of a Fast Radio Burst at 350 MHz by the GBNCC Survey. Astrophys. J. 2020, 904, 92. [Google Scholar] [CrossRef]
- Caleb, M.; Flynn, C.; Bailes, M.; Barr, E.D.; Bateman, T.; Bhandari, S.; Campbell-Wilson, D.; Farah, W.; Green, A.J.; Hunstead, R.W.; et al. The first interferometric detections of fast radio bursts. Mon. Not. R. Astron. Soc. 2017, 468, 3746–3756. [Google Scholar] [CrossRef]
- Farah, W.; Flynn, C.; Bailes, M.; Jameson, A.; Bateman, T.; Campbell-Wilson, D.; Day, C.K.; Deller, A.T.; Green, A.J.; Gupta, V.; et al. Five new real-time detections of fast radio bursts with UTMOST. Mon. Not. R. Astron. Soc. 2019, 488, 2989–3002. [Google Scholar] [CrossRef]
- Bannister, K.W.; Shannon, R.M.; Macquart, J.P.; Flynn, C.; Edwards, P.G.; O’Neill, M.; Osłowski, S.; Bailes, M.; Zackay, B.; Clarke, N.; et al. The Detection of an Extremely Bright Fast Radio Burst in a Phased Array Feed Survey. Astrophys. J. Lett. 2017, 841, L12. [Google Scholar] [CrossRef]
- Shannon, R.M.; Macquart, J.P.; Bannister, K.W.; Ekers, R.D.; James, C.W.; Oslowski, S.; Qiu, H.; Sammons, M.; Hotan, A.W.; Voronkov, M.A.; et al. The dispersion-brightness relation for fast radio bursts from a wide-field survey. Nature 2018, 562, 386–390. [Google Scholar] [CrossRef]
- Bannister, K.W.; Deller, A.T.; Phillips, C.; Macquart, J.P.; Prochaska, J.X.; Tejos, N.; Ryder, S.D.; Sadler, E.M.; Shannon, R.M.; Simha, S.; et al. A single fast radio burst localized to a massive galaxy at cosmological distance. Science 2019, 365, 565–570. [Google Scholar] [CrossRef]
- Macquart, J.P.; Prochaska, J.X.; McQuinn, M.; Bannister, K.W.; Bhandari, S.; Day, C.K.; Deller, A.T.; Ekers, R.D.; James, C.W.; Marnoch, L.; et al. A census of baryons in the universe from localized fast radio bursts. Nature 2020, 581, 391–395. [Google Scholar] [CrossRef] [PubMed]
- Bhandari, S.; Bannister, K.W.; Lenc, E.; Cho, H.; Ekers, R.; Day, C.K.; Deller, A.T.; Flynn, C.; James, C.W.; Macquart, J.P.; et al. Limits on Precursor and Afterglow Radio Emission from a Fast Radio Burst in a Star-forming Galaxy. Astrophys. J. Lett. 2020, 901, L20. [Google Scholar] [CrossRef]
- Amiri, M.; et al. [CHIME/FRB Collaboration] Observations of fast radio bursts at frequencies down to 400 megahertz. Nature 2019, 566, 230–234. [Google Scholar]
- Amiri, M.; et al. [CHIME/FRB Collaboration] A second source of repeating fast radio bursts. Nature 2019, 566, 235–238. [Google Scholar]
- Andersen, B.C.; et al. [CHIME/FRB Collaboration] CHIME/FRB Discovery of Eight New Repeating Fast Radio Burst Sources. Astrophys. J. Lett. 2019, 885, L24. [Google Scholar]
- Fonseca, E.; Andersen, B.C.; Bhardwaj, M.; Chawla, P.; Good, D.C.; Josephy, A.; Kaspi, V.M.; Masui, K.W.; Mckinven, R.; Michilli, D.; et al. Nine New Repeating Fast Radio Burst Sources from CHIME/FRB. Astrophys. J. Lett. 2020, 891, L6. [Google Scholar] [CrossRef]
- Ravi, V.; Catha, M.; D’Addario, L.; Djorgovski, S.G.; Hallinan, G.; Hobbs, R.; Kocz, J.; Kulkarni, S.R.; Shi, J.; Vedantham, H.K.; et al. A fast radio burst localized to a massive galaxy. Nature 2019, 572, 352–354. [Google Scholar] [CrossRef]
- Connor, L.; van Leeuwen, J.; Oostrum, L.C.; Petroff, E.; Maan, Y.; Adams, E.A.K.; Attema, J.J.; Bast, J.E.; Boersma, O.M.; Dénes, H.; et al. A bright, high rotation-measure FRB that skewers the M33 halo. Mon. Not. Roy. Astron. Soc. 2020, 499, 4716–4724. [Google Scholar] [CrossRef]
- Zhu, W.; Li, D.; Luo, R.; Miao, C.; Zhang, B.; Spitler, L.; Lorimer, D.; Kramer, M.; Champion, D.; Yue, Y.; et al. A Fast Radio Burst Discovered in FAST Drift Scan Survey. Astrophys. J. Lett. 2020, 895, L6. [Google Scholar] [CrossRef]
- Niu, C.H.; Li, D.; Luo, R.; Wang, W.Y.; Yao, J.; Zhang, B.; Zhu, W.W.; Wang, P.; Ye, H.; Zhang, Y.K.; et al. CRAFTS for Fast Radio Bursts Extending the dispersion-fluence relation with new FRBs detected by FAST. arXiv 2021, arXiv:2102.10546. [Google Scholar]
- Law, C.J.; Butler, B.J.; Prochaska, J.X.; Zackay, B.; Burke-Spolaor, S.; Mannings, A.; Tejos, N.; Josephy, A.; Andersen, B.; Chawla, P.; et al. A Distant Fast Radio Burst Associated with Its Host Galaxy by the Very Large Array. Astrophys. J. 2020, 899, 161. [Google Scholar] [CrossRef]
- Cordes, J.M.; Chatterjee, S. Fast Radio Bursts: An Extragalactic Enigma. Annu. Rev. Astron. Astrophys. 2019, 57, 417–465. [Google Scholar] [CrossRef]
- Petroff, E.; Hessels, J.W.T.; Lorimer, D.R. Fast radio bursts. Astron. Astrophys. Rev. 2019, 27, 4. [Google Scholar] [CrossRef]
- Chatterjee, S. Progress in Understanding the Enigmatic Fast Radio Bursts. arXiv 2020, arXiv:2012.10377. [Google Scholar]
- Connor, L.; Sievers, J.; Pen, U.L. Non-cosmological FRBs from young supernova remnant pulsars. Mon. Not. R. Astron. Soc. 2016, 458, L19–L23. [Google Scholar]
- Piro, A.L. The Impact of a Supernova Remnant on Fast Radio Bursts. Astrophys. J. 2016, 824, L32. [Google Scholar] [CrossRef]
- Metzger, B.D.; Berger, E.; Margalit, B. Millisecond Magnetar Birth Connects FRB 121102 to Superluminous Supernovae and Long-duration Gamma-Ray Bursts. Astrophys. J. 2017, 841, 14. [Google Scholar] [CrossRef]
- Totani, T. Cosmological Fast Radio Bursts from Binary Neutron Star Mergers. PASJ 2013, 65, L12. [Google Scholar] [CrossRef]
- Wang, J.S.; Yang, Y.P.; Wu, X.F.; Dai, Z.G.; Wang, F.Y. Fast Radio Bursts from the Inspiral of Double Neutron Stars. Astrophys. J. Lett. 2016, 822, L7. [Google Scholar] [CrossRef]
- Dokuchaev, V.I.; Eroshenko, Y.N. Recurrent fast radio bursts from collisions of neutron stars in the evolved stellar clusters. arXiv 2017, arXiv:1701.02492. [Google Scholar]
- Yamasaki, S.; Totani, T.; Kiuchi, K. Repeating and non-repeating fast radio bursts from binary neutron star mergers. Publ. Astron. Soc. Jpn. 2018, 70, 39. [Google Scholar] [CrossRef]
- Kashiyama, K.; Ioka, K.; Mészáros, P. Cosmological Fast Radio Bursts from Binary White Dwarf Mergers. Astrophys. J. Lett. 2013, 776, L39. [Google Scholar] [CrossRef]
- Li, L.B.; Huang, Y.F.; Geng, J.J.; Li, B. A model of fast radio bursts: Collisions between episodic magnetic blobs. Res. Astron. Astrophys. 2018, 18, 061. [Google Scholar] [CrossRef]
- Cordes, J.; Wasserman, I. Supergiant pulses from extragalactic neutron stars. Mon. Not. R. Astron. Soc. 2016, 457, 232–257. [Google Scholar] [CrossRef]
- Popov, S.B.; Postnov, K.A. Hyperflares of SGRs as an engine for millisecond extragalactic radio bursts. arXiv 2017, arXiv:0710.2006. [Google Scholar]
- Pen, U.L.; Connor, L. Local Circumnuclear Magnetar Solution to Extragalactic Fast Radio Bursts. Astrophys. J. 2015, 807, 179. [Google Scholar] [CrossRef]
- Vieyro, F.L.; Romero, G.E.; Bosch-Ramon, V.; Marcote, B.; del Valle, M.V. A model for the repeating FRB 121102 in the AGN scenario. Astron. Astrophys. 2017, 602, A64. [Google Scholar] [CrossRef]
- Zhang, B. A Cosmic Comb Model of Fast Radio Bursts. Astrophys. J. Lett. 2017, 836, L32. [Google Scholar] [CrossRef]
- Falcke, H.; Rezzolla, L. Fast radio bursts: The last sign of supramassive neutron stars. Astron. Astrophys. 2014, 562, A137. [Google Scholar] [CrossRef]
- Zadorozhna, L.V. Fast radio bursts as electromagnetic radiation from cusps on superconducting cosmic strings. Adv. Astron. Space Phys. 2015, 5, 43–50. [Google Scholar] [CrossRef]
- Zhang, B. A Possible Connection between Fast Radio Bursts and Gamma-Ray Bursts. Astrophys. J. Lett. 2014, 780, L21. [Google Scholar] [CrossRef]
- Lingam, M.; Loeb, A. Fast Radio Bursts from Extragalactic Light Sails. Astrophys. J. Lett. 2017, 837, L23. [Google Scholar] [CrossRef]
- Platts, E.; Weltman, A.; Walters, A.; Tendulkar, S.P.; Gordin, J.E.B.; Kandhai, S. A Living Theory Catalogue for Fast Radio Bursts. arXiv 2018, arXiv:1810.05836. [Google Scholar] [CrossRef]
- Zhang, B. The physical mechanisms of fast radio bursts. Nature 2020, 587, 45–53. [Google Scholar] [CrossRef]
- Xiao, D.; Wang, F.; Dai, Z. The Physics of Fast Radio Bursts. arXiv 2021, arXiv:2101.04907. [Google Scholar]
- Lyubarsky, Y. Emission Mechanisms of Fast Radio Bursts. Universe 2021, 7, 56. [Google Scholar] [CrossRef]
- Spitler, L.G.; Scholz, P.; Hessels, J.W.T.; Bogdanov, S.; Brazier, A.; Camilo, F.; Chatterjee, S.; Cordes, J.M.; Crawford, F.; Deneva, J.; et al. A repeating fast radio burst. Nature 2016, 531, 202–205. [Google Scholar] [CrossRef]
- Hessels, J.W.T.; Spitler, L.G.; Seymour, A.D.; Cordes, J.M.; Michilli, D.; Lynch, R.S.; Gourdji, K.; Archibald, A.M.; Bassa, C.G.; Bower, G.C.; et al. FRB 121102 Bursts Show Complex Time-Frequency Structure. Astrophys. J. Lett. 2019, 876, L23. [Google Scholar] [CrossRef]
- Chatterjee, S.; Law, C.J.; Wharton, R.S.; Burke-Spolaor, S.; Hessels, J.W.T.; Bower, G.C.; Cordes, J.M.; Tendulkar, S.P.; Bassa, C.G.; Demorest, P.; et al. A direct localization of a fast radio burst and its host. Nature 2017, 541, 58–61. [Google Scholar] [CrossRef]
- Marcote, B.; Paragi, Z.; Hessels, J.W.T.; Keimpema, A.; van Langevelde, H.J.; Huang, Y.; Bassa, C.G.; Bogdanov, S.; Bower, G.C.; Burke-Spolaor, S.; et al. The Repeating Fast Radio Burst FRB 121102 as Seen on Milliarcsecond Angular Scales. Astrophys. J. Lett. 2017, 834, L8. [Google Scholar] [CrossRef]
- Tendulkar, S.P.; Bassa, C.G.; Cordes, J.M.; Bower, G.C.; Law, C.J.; Chatterjee, S.; Adams, E.A.K.; Bogdanov, S.; Burke-Spolaor, S.; Butler, B.J.; et al. The Host Galaxy and Redshift of the Repeating Fast Radio Burst FRB 121102. Astrophys. J. Lett. 2017, 834, L7. [Google Scholar] [CrossRef]
- Kumar, P.; Shannon, R.M.; Osłowski, S.; Qiu, H.; Bhandari, S.; Farah, W.; Flynn, C.; Kerr, M.; Lorimer, D.R.; Macquart, J.P.; et al. Faint Repetitions from a Bright Fast Radio Burst Source. Astrophys. J. Lett. 2019, 887, L30. [Google Scholar] [CrossRef]
- Kumar, P.; Shannon, R.M.; Flynn, C.; Osłowski, S.; Bhandari, S.; Day, C.K.; Deller, A.T.; Farah, W.; Kaczmarek, J.F.; Kerr, M.; et al. Extremely band-limited repetition from a fast radio burst source. Mon. Not. R. Astron. Soc. 2021, 500, 2525–2531. [Google Scholar] [CrossRef]
- Amiri, M.; et al. [CHIME/FRB Collaboration] Periodic activity from a fast radio burst source. Nature 2020, 582, 351–355. [Google Scholar]
- Rajwade, K.M.; Mickaliger, M.B.; Stappers, B.W.; Morello, V.; Agarwal, D.; Bassa, C.G.; Breton, R.P.; Caleb, M.; Karastergiou, A.; Keane, E.F.; et al. Possible periodic activity in the repeating FRB 121102. Mon. Not. R. Astron. Soc. 2020, 495, 3551–3558. [Google Scholar] [CrossRef]
- Ioka, K.; Zhang, B. A Binary Comb Model for Periodic Fast Radio Bursts. Astrophys. J. Lett. 2020, 893, L26. [Google Scholar] [CrossRef]
- Lyutikov, M.; Barkov, M.V.; Giannios, D. FRB Periodicity: Mild Pulsars in Tight O/B-star Binaries. Astrophys. J. Lett. 2020, 893, L39. [Google Scholar] [CrossRef]
- Pleunis, Z.; Michilli, D.; Bassa, C.G.; Hessels, J.W.T.; Naidu, A.; Andersen, B.C.; Chawla, P.; Fonseca, E.; Gopinath, A.; Kaspi, V.M.; et al. LOFAR Detection of 110–188 MHz Emission and Frequency-Dependent Activity from FRB 20180916B. arXiv 2020, arXiv:2012.08372. [Google Scholar]
- Pilia, M.; Burgay, M.; Possenti, A.; Ridolfi, A.; Gajjar, V.; Corongiu, A.; Perrodin, D.; Bernardi, G.; Naldi, G.; Pupillo, G.; et al. The Lowest-frequency Fast Radio Bursts: Sardinia Radio Telescope Detection of the Periodic FRB 180916 at 328 MHz. Astrophys. J. Lett. 2020, 896, L40. [Google Scholar] [CrossRef]
- Marthi, V.R.; Gautam, T.; Li, D.; Lin, H.H.; Main, R.; Naidu, A.K.; Pen, U.L.; Wharton, R. Detection of 15 bursts from FRB 180916.J0158+65 with the uGMRT. arXiv 2020, arXiv:2007.14404. [Google Scholar]
- Gajjar, V.; Siemion, A.P.V.; Price, D.C.; Law, C.J.; Michilli, D.; Hessels, J.W.T.; Chatterjee, S.; Archibald, A.M.; Bower, G.C.; Brinkman, C.; et al. Highest Frequency Detection of FRB 121102 at 4–8 GHz Using the Breakthrough Listen Digital Backend at the Green Bank Telescope. Astrophys. J. 2018, 863, 2. [Google Scholar] [CrossRef]
- Bhardwaj, M.; Gaensler, B.M.; Kaspi, V.M.; Landecker, T.L.; Mckinven, R.; Michilli, D.; Pleunis, Z.; Tendulkar, S.P.; Andersen, B.C.; Boyle, P.J.; et al. A nearby repeating fast radio burst in the direction of M81. arXiv 2021, arXiv:2103.01295. [Google Scholar]
- Caleb, M. Radio observations of FRBs. Submitted to universe, 2021. [Google Scholar]
- Andersen, B.C.; et al. [CHIME/FRB Collaboration] A bright millisecond-duration radio burst from a Galactic magnetar. Nature 2020, 587, 54–58. [Google Scholar]
- Bochenek, C.D.; Ravi, V.; Belov, K.V.; Hallinan, G.; Kocz, J.; Kulkarni, S.R.; McKenna, D.L. A fast radio burst associated with a Galactic magnetar. Nature 2020, 587, 59–62. [Google Scholar] [CrossRef]
- Mereghetti, S.; Savchenko, V.; Ferrigno, C.; Götz, D.; Rigoselli, M.; Tiengo, A.; Bazzano, A.; Bozzo, E.; Coleiro, A.; Courvoisier, T.J.L.; et al. INTEGRAL Discovery of a Burst with Associated Radio Emission from the Magnetar SGR 1935+2154. Astrophys. J. Lett. 2020, 898, L29. [Google Scholar] [CrossRef]
- Kulkarni, S.R. Dispersion measure: Confusion, Constants & Clarity. arXiv 2020, arXiv:2007.02886. [Google Scholar]
- Williamson, I.P. Pulse broadening due to multiple scattering in the interstellarmedium. Mon. Not. R. Astron. Soc. 1972, 157, 55. [Google Scholar] [CrossRef]
- Farah, W.; Flynn, C.; Bailes, M.; Jameson, A.; Bannister, K.W.; Barr, E.D.; Bateman, T.; Bhand ari, S.; Caleb, M.; Campbell-Wilson, D.; et al. FRB microstructure revealed by the real-time detection of FRB170827. Mon. Not. R. Astron. Soc. 2018, 478, 1209–1217. [Google Scholar] [CrossRef]
- Bhat, N.D.R.; Cordes, J.M.; Camilo, F.; Nice, D.J.; Lorimer, D.R. Multifrequency Observations of Radio Pulse Broadening and Constraints on Interstellar Electron Density Microstructure. Astrophys. J. 2004, 605, 759–783. [Google Scholar] [CrossRef]
- Qiu, H.; Shannon, R.M.; Farah, W.; Macquart, J.P.; Deller, A.T.; Bannister, K.W.; James, C.W.; Flynn, C.; Day, C.K.; Bhandari, S.; et al. A population analysis of pulse broadening in ASKAP fast radio bursts. Mon. Not. R. Astron. Soc. 2020, 497, 1382–1390. [Google Scholar] [CrossRef]
- Ravi, V.; Shannon, R.M.; Bailes, M.; Bannister, K.; Bhandari, S.; Bhat, N.D.R.; Burke-Spolaor, S.; Caleb, M.; Flynn, C.; Jameson, A.; et al. The magnetic field and turbulence of the cosmic web measured using a brilliant fast radio burst. Science 2016, 354, 1249–1252. [Google Scholar] [CrossRef] [PubMed]
- Cordes, J.M.; Wasserman, I.; Hessels, J.W.T.; Lazio, T.J.W.; Chatterjee, S.; Wharton, R.S. Lensing of Fast Radio Bursts by Plasma Structures in Host Galaxies. Astrophys. J. 2017, 842, 35. [Google Scholar] [CrossRef]
- Caleb, M.; Keane, E.F.; van Straten, W.; Kramer, M.; Macquart, J.P.; Bailes, M.; Barr, E.D.; Bhat, N.D.R.; Bhandari, S.; Burgay, M.; et al. The SUrvey for Pulsars and Extragalactic Radio Bursts—III. Polarization properties of FRBs 160102 and 151230. Mon. Not. R. Astron. Soc. 2018, 478, 2046–2055. [Google Scholar] [CrossRef]
- Day, C.K.; Deller, A.T.; Shannon, R.M.; Qiu, H.; Bannister, K.W.; Bhandari, S.; Ekers, R.; Flynn, C.; James, C.W.; Macquart, J.P.; et al. High time resolution and polarization properties of ASKAP-localized fast radio bursts. Mon. Not. R. Astron. Soc. 2020, 497, 3335–3350. [Google Scholar] [CrossRef]
- Michilli, D.; Seymour, A.; Hessels, J.W.T.; Spitler, L.G.; Gajjar, V.; Archibald, A.M.; Bower, G.C.; Chatterjee, S.; Cordes, J.M.; Gourdji, K.; et al. An extreme magneto-ionic environment associated with the fast radio burst source FRB 121102. Nature 2018, 553, 182–185. [Google Scholar] [CrossRef]
- Noutsos, A.; Johnston, S.; Kramer, M.; Karastergiou, A. New pulsar rotation measures and the Galactic magnetic field. Mon. Not. R. Astron. Soc. 2008, 386, 1881–1896. [Google Scholar] [CrossRef]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A.; Yeh, T.H. Big bang nucleosynthesis: Present status. Rev. Mod. Phys. 2016, 88, 015004. [Google Scholar] [CrossRef]
- Ade, P.A.R.; et al. [Planck Collaboration] Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Weinberg, D.H.; Miralda-Escudé, J.; Hernquist, L.; Katz, N. A Lower Bound on the Cosmic Baryon Density. Astrophys. J. 1997, 490, 564–570. [Google Scholar] [CrossRef]
- Rauch, M.; Miralda-Escude, J.; Sargent, W.L.W.; Barlow, T.A.; Weinberg, D.H.; Hernquist, L.; Katz, N.; Cen, R.; Ostriker, J.P. The Opacity of the Lyα Forest and Implications for Ωb and the Ionizing Background. Astrophys. J. 1997, 489, 7–20. [Google Scholar] [CrossRef]
- Fukugita, M.; Peebles, P.J.E. The Cosmic Energy Inventory. Astrophys. J. 2004, 616, 643–668. [Google Scholar] [CrossRef]
- Nicastro, F.; Mathur, S.; Elvis, M. Missing Baryons and the Warm-Hot Intergalactic Medium. Science 2008, 319, 55–57. [Google Scholar] [CrossRef] [PubMed]
- Shull, J.M.; Smith, B.D.; Danforth, C.W. The Baryon Census in a Multiphase Intergalactic Medium: 30% of the Baryons May Still be Missing. Astrophys. J. 2012, 759, 23. [Google Scholar] [CrossRef]
- Bregman, J.N. The Search for the Missing Baryons at Low Redshift. Annu. Rev. Astron. Astrophys. 2007, 45, 221–259. [Google Scholar] [CrossRef]
- McQuinn, M. The Evolution of the Intergalactic Medium. Annu. Rev. Astron. Astrophys. 2016, 54, 313–362. [Google Scholar] [CrossRef]
- Cen, R.; Ostriker, J.P. Where Are the Baryons? II. Feedback Effects. Astrophys. J. 2006, 650, 560–572. [Google Scholar] [CrossRef]
- Cen, R.; Ostriker, J.P. Where Are the Baryons? Astrophys. J. 1999, 514, 1–6. [Google Scholar] [CrossRef]
- Penton, S.V.; Stocke, J.T.; Shull, J.M. The Local Lyα Forest. IV. Space Telescope Imaging Spectrograph G140M Spectra and Results on the Distribution and Baryon Content of H i Absorbers. Astrophys. J. Suppl. Ser. 2004, 152, 29–62. [Google Scholar] [CrossRef]
- Viel, M.; Branchini, E.; Cen, R.; Ostriker, J.P.; Matarrese, S.; Mazzotta, P.; Tully, B. Tracing the warm-hot intergalactic medium in the local universe. Mon. Not. R. Astron. Soc. 2005, 360, 1110–1122. [Google Scholar] [CrossRef][Green Version]
- Yao, Y.; Shull, J.M.; Wang, Q.D.; Cash, W. Detecting the warm-hot intergalactic medium through X-ray absorption lines. Astrophys. J. 2012, 746, 166. [Google Scholar] [CrossRef]
- Vernstrom, T.; Heald, G.; Vazza, F.; Galvin, T.; West, J.; Locatelli, N.; Fornengo, N.; Pinetti, E. Discovery of Magnetic Fields Along Stacked Cosmic Filaments as Revealed by Radio and X-Ray Emission. arXiv 2021, arXiv:2101.09331. [Google Scholar]
- Tejos, N.; Prochaska, J.X.; Crighton, N.H.M.; Morris, S.L.; Werk, J.K.; Theuns, T.; Padilla, N.; Bielby, R.M.; Finn, C.W. Towards the statistical detection of the warm-hot intergalactic medium in intercluster filaments of the cosmic web. Mon. Not. R. Astron. Soc. 2016, 455, 2662–2697. [Google Scholar] [CrossRef]
- Pessa, I.; Tejos, N.; Barrientos, L.F.; Werk, J.; Bielby, R.; Padilla, N.; Morris, S.L.; Prochaska, J.X.; Lopez, S.; Hummels, C. A VLT/MUSE galaxy survey towards QSO Q1410: Looking for a WHIM traced by BLAs in intercluster filaments. Mon. Not. R. Astron. Soc. 2018, 477, 2991–3013. [Google Scholar] [CrossRef]
- Nicastro, F.; Kaastra, J.; Krongold, Y.; Borgani, S.; Branchini, E.; Cen, R.; Dadina, M.; Danforth, C.W.; Elvis, M.; Fiore, F. Observations of the missing baryons in the warm-hot intergalactic medium. Nature 2018, 558, 406–409. [Google Scholar] [CrossRef] [PubMed]
- Zeldovich, Y.B.; Sunyaev, R.A. The Interaction of Matter and Radiation in a Hot-Model universe. Astrophys. Space Sci. 1969, 4, 301–316. [Google Scholar] [CrossRef]
- Tanimura, H.; Hinshaw, G.; McCarthy, I.G.; Van Waerbeke, L.; Aghanim, N.; Ma, Y.Z.; Mead, A.; Hojjati, A.; Tröster, T. A search for warm/hot gas filaments between pairs of SDSS Luminous Red Galaxies. Mon. Not. R. Astron. Soc. 2018, 483, 223–234. [Google Scholar] [CrossRef]
- De Graaff, A.; Cai, Y.C.; Heymans, C.; Peacock, J.A. Probing the missing baryons with the Sunyaev-Zel’dovich effect from filaments. Astron. Astrophys. 2019, 624, A48. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, B. Cosmological Implications of Fast Radio Burst/Gamma-Ray Burst Associations. Astrophys. J. Lett. 2014, 783, L35. [Google Scholar] [CrossRef]
- McQuinn, M. Locating the “Missing” Baryons with Extragalactic Dispersion Measure Estimates. Astrophys. J. Lett. 2014, 780, L33. [Google Scholar] [CrossRef]
- Ioka, K. The Cosmic Dispersion Measure from Gamma-Ray Burst Afterglows: Probing the Reionization History and the Burst Environment. Astrophys. J. Lett. 2003, 598, L79–L82. [Google Scholar] [CrossRef]
- Inoue, S. Probing the cosmic reionization history and local environment of gamma-ray bursts through radio dispersion. Mon. Not. R. Astron. Soc. 2004, 348, 999–1008. [Google Scholar] [CrossRef]
- Shull, J.M.; Danforth, C.W. The Dispersion of Fast Radio Bursts from a Structured Intergalactic Medium at Redshifts z < 1.5. Astrophys. J. Lett. 2018, 852, L11. [Google Scholar]
- Zhang, B. Fast Radio Burst Energetics and Detectability from High Redshifts. Astrophys. J. Lett. 2018, 867, L21. [Google Scholar] [CrossRef]
- Macquart, J.P.; Keane, E.; Grainge, K.; McQuinn, M.; Fender, R.; Hessels, J.; Deller, A.; Bhat, R.; Breton, R.; Chatterjee, S. Fast Transients at Cosmological Distances with the SKA. Advancing Astrophysics with the Square Kilometre Array (AASKA14). arXiv 2017, arXiv:1501.07535. [Google Scholar]
- Dolag, K.; Gaensler, B.M.; Beck, A.M.; Beck, M.C. Constraints on the distribution and energetics of fast radio bursts using cosmological hydrodynamic simulations. Mon. Not. R. Astron. Soc. 2015, 451, 4277–4289. [Google Scholar] [CrossRef]
- Takahashi, R.; Ioka, K.; Mori, A.; Funahashi, K. Statistical modelling of the cosmological dispersion measure. Mon. Not. R. Astron. Soc. 2021, 502, 2615–2629. [Google Scholar] [CrossRef]
- Jaroszynski, M. Fast radio bursts and cosmological tests. Mon. Not. R. Astron. Soc. 2019, 484, 1637–1644. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Yan, K.; Li, C.M.; Zhang, G.Q.; Wang, F.Y. Intergalactic Medium Dispersion Measures of Fast Radio Bursts Estimated from IllustrisTNG Simulation and Their Cosmological Applications. Astrophys. J. 2021, 906, 49. [Google Scholar] [CrossRef]
- Batten, A.J.; Duffy, A.R.; Wijers, N.; Gupta, V.; Flynn, C.; Schaye, J.; Ryan-Weber, E. The Cosmic Dispersion Measure in the EAGLE Simulations. arXiv 2020, arXiv:2011.14547. [Google Scholar]
- Prochaska, J.X.; Zheng, Y. Probing Galactic haloes with fast radio bursts. Mon. Not. R. Astron. Soc. 2019, 485, 648–665. [Google Scholar]
- Marcote, B.; Nimmo, K.; Hessels, J.W.T.; Tendulkar, S.P.; Bassa, C.G.; Paragi, Z.; Keimpema, A.; Bhardwaj, M.; Karuppusamy, R.; Kaspi, V.M.; et al. A repeating fast radio burst source localized to a nearby spiral galaxy. Nature 2020, 577, 190–194. [Google Scholar] [CrossRef]
- James, C.W.; Prochaska, J.X.; Macquart, J.P.; North-Hickey, F.; Bannister, K.W.; Dunning, A. The z–DM distribution of fast radio bursts. arXiv 2021, arXiv:2101.08005. [Google Scholar]
- Xu, S.; Zhang, B. Probing the Intergalactic Turbulence with Fast Radio Bursts. Astrophys. J. Lett. 2020, 898, L48. [Google Scholar] [CrossRef]
- Cordes, J.M.; Wharton, R.S.; Spitler, L.G.; Chatterjee, S.; Wasserman, I. Radio Wave Propagation and the Provenance of Fast Radio Bursts. arXiv 2016, arXiv:1605.05890. [Google Scholar]
- Cordes, J.M.; Lazio, T.J.W. NE2001.I. A New Model for the Galactic Distribution of Free Electrons and its Fluctuations. arXiv 2002, arXiv:astro-ph/0207156. [Google Scholar]
- Petroff, E.; van Straten, W.; Johnston, S.; Bailes, M.; Barr, E.D.; Bates, S.D.; Bhat, N.D.R.; Burgay, M.; Burke-Spolaor, S.; Champion, D.; et al. An Absence of Fast Radio Bursts at Intermediate Galactic Latitudes. Astrophys. J. Lett. 2014, 789, L26. [Google Scholar] [CrossRef]
- Macquart, J.P.; Johnston, S. On the paucity of fast radio bursts at low Galactic latitudes. Mon. Not. R. Astron. Soc. 2015, 451, 3278–3286. [Google Scholar] [CrossRef][Green Version]
- Koch Ocker, S.; Cordes, J.M.; Chatterjee, S. Constraining Galaxy Haloes from the Dispersion and Scattering of Fast Radio Bursts and Pulsars. arXiv 2021, arXiv:2101.04784. [Google Scholar]
- Nimmo, K.; Hessels, J.W.T.; Keimpema, A.; Archibald, A.M.; Cordes, J.M.; Karuppusamy, R.; Kirsten, F.; Li, D.Z.; Marcote, B.; Paragi, Z. Highly polarised microstructure from the repeating FRB 20180916B. arXiv 2020, arXiv:2010.05800. [Google Scholar]
- Prochaska, J.X.; Neeleman, M.; Kanekar, N.; Rafelski, M. ALMA C II 158 μm Imaging of an H I-selected Major Merger at z ∼ 4. Astrophys. J. Lett. 2019, 886, L35. [Google Scholar] [CrossRef]
- Macquart, J.P.; Koay, J.Y. Temporal Smearing of Transient Radio Sources by the Intergalactic Medium. Astrophys. J. 2013, 776, 125. [Google Scholar] [CrossRef]
- Zhu, W.; Feng, L.L.; Zhang, F. The Scattering of FRBs by the Intergalactic Medium: Variations, Strength, and Dependence on Dispersion Measures. Astrophys. J. 2018, 865, 147. [Google Scholar] [CrossRef]
- Zhu, W.; Feng, L.L. The Dispersion Measure and Scattering of Fast Radio Bursts: Contributions from the Intergalactic Medium, Foreground Halos, and Hosts. Astrophys. J. 2021, 906, 95. [Google Scholar] [CrossRef]
- Katz, J.I. Inferences from the Distributions of Fast Radio Burst Pulse Widths, Dispersion Measures, and Fluences. Astrophys. J. 2016, 818, 19. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, B. On the Origin of the Scatter Broadening of Fast Radio Burst Pulses and Astrophysical Implications. Astrophys. J. 2016, 832, 199. [Google Scholar] [CrossRef]
- Chittidi, J.S.; Simha, S.; Mannings, A.; Prochaska, J.X.; Rafelski, M.; Neeleman, M.; Macquart, J.P.; Tejos, N.; Jorgenson, R.A.; Ryder, S.D.; et al. Dissecting the Local Environment of FRB 190608 in the Spiral Arm of its Host Galaxy. arXiv 2020, arXiv:2005.13158. [Google Scholar]
- Simha, S.; Burchett, J.N.; Prochaska, J.X.; Chittidi, J.S.; Elek, O.; Tejos, N.; Jorgenson, R.; Bannister, K.W.; Bhandari, S.; Day, C.K.; et al. Disentangling the Cosmic Web toward FRB 190608. Astrophys. J. 2020, 901, 134. [Google Scholar] [CrossRef]
- Yao, J.M.; Manchester, R.N.; Wang, N. A New Electron-density Model for Estimation of Pulsar and FRB Distances. Astrophys. J. 2017, 835, 29. [Google Scholar] [CrossRef]
- Akahori, T.; Ryu, D.; Gaensler, B.M. Fast Radio Bursts as Probes of Magnetic Fields in the Intergalactic Medium. Astrophys. J. 2016, 824, 105. [Google Scholar] [CrossRef]
- Vazza, F.; Brüggen, M.; Hinz, P.M.; Wittor, D.; Locatelli, N.; Gheller, C. Probing the origin of extragalactic magnetic fields with Fast Radio Bursts. Mon. Not. R. Astron. Soc. 2018, 480, 3907–3915. [Google Scholar] [CrossRef]
- Hackstein, S.; Brüggen, M.; Vazza, F.; Gaensler, B.M.; Heesen, V. Fast radio burst dispersion measures and rotation measures and the origin of intergalactic magnetic fields. Mon. Not. R. Astron. Soc. 2019, 488, 4220–4238. [Google Scholar] [CrossRef]
- Wang, W.Y.; Zhang, B.; Chen, X.; Xu, R. On the magnetoionic environments of fast radio bursts. Mon. Not. R. Astron. Soc. 2020, 499, 355–361. [Google Scholar] [CrossRef]
- Somerville, R.S.; Davé, R. Physical Models of Galaxy Formation in a Cosmological Framework. Annu. Rev. Astron. Astrophys. 2015, 53, 51–113. [Google Scholar] [CrossRef]
- Anderson, M.E.; Bregman, J.N.; Dai, X. Extended Hot Halos around Isolated Galaxies Observed in the ROSAT All-Sky Survey. Astrophys. J. 2013, 762, 106. [Google Scholar] [CrossRef]
- Tumlinson, J.; Thom, C.; Werk, J.K.; Prochaska, J.X.; Tripp, T.M.; Katz, N.; Davé, R.; Oppenheimer, B.D.; Meiring, J.D.; Ford, A.B.; et al. The COS-Halos Survey: Rationale, Design, and a Census of Circumgalactic Neutral Hydrogen. Astrophys. J. 2013, 777, 59. [Google Scholar] [CrossRef]
- Prochaska, J.X.; Weiner, B.; Chen, H.W.; Mulchaey, J.; Cooksey, K. Probing the Intergalactic Medium/Galaxy Connection. V. On the Origin of Lyα and O VI Absorption at z < 0.2. Astrophys. J. 2011, 740, 91. [Google Scholar]
- Tumlinson, J.; Peeples, M.S.; Werk, J.K. The Circumgalactic Medium. Annu. Rev. Astron. Astrophys. 2017, 55, 389–432. [Google Scholar] [CrossRef]
- Fukugita, M.; Peebles, P.J.E. Massive Coronae of Galaxies. Astrophys. J. 2006, 639, 590–599. [Google Scholar] [CrossRef]
- Faerman, Y.; Sternberg, A.; McKee, C.F. Massive Warm/Hot Galaxy Coronae as Probed by UV/X-Ray Oxygen Absorption and Emission. I. Basic Model. Astrophys. J. 2017, 835, 52. [Google Scholar] [CrossRef]
- Maller, A.H.; Bullock, J.S. Multiphase galaxy formation: High-velocity clouds and the missing baryon problem. Mon. Not. R. Astron. Soc. 2004, 355, 694–712. [Google Scholar] [CrossRef]
- Voit, G.M.; Donahue, M.; Bryan, G.L.; McDonald, M. Regulation of star formation in giant galaxies by precipitation, feedback and conduction. Nature 2015, 519, 203–206. [Google Scholar] [CrossRef] [PubMed]
- Stern, J.; Hennawi, J.F.; Prochaska, J.X.; Werk, J.K. A Universal Density Structure for Circumgalactic Gas. Astrophys. J. 2016, 830, 87. [Google Scholar] [CrossRef]
- Liang, C.J.; Remming, I. On the model of the circumgalactic mist: The implications of cloud sizes in galactic winds and haloes. Mon. Not. R. Astron. Soc. 2020, 491, 5056–5072. [Google Scholar] [CrossRef]
- Sarkar, K.C.; Nath, B.B.; Sharma, P. Multiwavelength features of Fermi bubbles as signatures of a Galactic wind. Mon. Not. R. Astron. Soc. 2015, 453, 3827–3838. [Google Scholar] [CrossRef]
- Fielding, D.; Quataert, E.; McCourt, M.; Thompson, T.A. The impact of star formation feedback on the circumgalactic medium. Mon. Not. R. Astron. Soc. 2017, 466, 3810–3826. [Google Scholar] [CrossRef]
- Butsky, I.S.; Quinn, T.R. The Role of Cosmic-ray Transport in Shaping the Simulated Circumgalactic Medium. Astrophys. J. 2018, 868, 108. [Google Scholar] [CrossRef]
- Oppenheimer, B.D.; Davé, R. Cosmological simulations of intergalactic medium enrichment from galactic outflows. Mon. Not. R. Astron. Soc. 2006, 373, 1265–1292. [Google Scholar] [CrossRef]
- Prochaska, J.X.; Macquart, J.P.; McQuinn, M.; Simha, S.; Shannon, R.M.; Day, C.K.; Marnoch, L.; Ryder, S.; Deller, A.; Bannister, K.W.; et al. The low density and magnetization of a massive galaxy halo exposed by a fast radio burst. Science 2019, 366, 231–234. [Google Scholar] [CrossRef] [PubMed]
- Bernet, M.L.; Miniati, F.; Lilly, S.J.; Kronberg, P.P.; Dessauges-Zavadsky, M. Strong magnetic fields in normal galaxies at high redshift. Nature 2008, 454, 302–304. [Google Scholar] [CrossRef]
- Woodfinden, A.; Henriksen, R.N.; Irwin, J.; Mora-Partiarroyo, S.C. Evolving galactic dynamos and fits to the reversing rotation measures in the halo of NGC 4631. Mon. Not. R. Astron. Soc. 2019, 487, 1498–1516. [Google Scholar] [CrossRef]
- Cantalupo, S.; Arrigoni-Battaia, F.; Prochaska, J.X.; Hennawi, J.F.; Madau, P. A cosmic web filament revealed in Lyman-α emission around a luminous high-redshift quasar. Nature 2014, 506, 63–66. [Google Scholar] [CrossRef] [PubMed]
- Werk, J.K.; Prochaska, J.X.; Tumlinson, J.; Peeples, M.S.; Tripp, T.M.; Fox, A.J.; Lehner, N.; Thom, C.; O’Meara, J.M.; Ford, A.B.; et al. The COS-Halos Survey: Physical Conditions and Baryonic Mass in the Low-redshift Circumgalactic Medium. Astrophys. J. 2014, 792, 8. [Google Scholar] [CrossRef]
- Lan, T.W.; Fukugita, M. Mg II Absorbers: Metallicity Evolution and Cloud Morphology. Astrophys. J. 2017, 850, 156. [Google Scholar] [CrossRef]
- Bond, J.R.; Kofman, L.; Pogosyan, D. How filaments of galaxies are woven into the cosmic web. Nature 1996, 380, 603–606. [Google Scholar] [CrossRef]
- Springel, V.; White, S.D.M.; Jenkins, A.; Frenk, C.S.; Yoshida, N.; Gao, L.; Navarro, J.; Thacker, R.; Croton, D.; Helly, J.; et al. Simulations of the formation, evolution and clustering of galaxies and quasars. Nature 2005, 435, 629–636. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhang, B.; Nagamine, K.; Shi, J. The FRB 121102 Host Is Atypical among Nearby Fast Radio Bursts. Astrophys. J. Lett. 2019, 884, L26. [Google Scholar] [CrossRef]
- Ravi, V. Measuring the Circumgalactic and Intergalactic Baryon Contents with Fast Radio Bursts. Astrophys. J. 2019, 872, 88. [Google Scholar] [CrossRef]
- Nicastro, L.; Guidorzi, C.; Palazzi, E.; Zampieri, L.; Turatto, M.; Gardini, A. Multiwavelength Observations of Fast Radio Bursts. Universe 2021, 7, 76. [Google Scholar] [CrossRef]
- Hilmarsson, G.H.; Michilli, D.; Spitler, L.G.; Wharton, R.S.; Demorest, P.; Desvignes, G.; Gourdji, K.; Hackstein, S.; Hessels, J.W.T.; Nimmo, K.; et al. Rotation Measure Evolution of the Repeating Fast Radio Burst Source FRB 121102. arXiv 2020, arXiv:2009.12135. [Google Scholar]
- Margalit, B.; Metzger, B.D. A Concordance Picture of FRB 121102 as a Flaring Magnetar Embedded in a Magnetized Ion-Electron Wind Nebula. Astrophys. J. 2018, 868, L4. [Google Scholar] [CrossRef]
- Tendulkar, S.P.; Gil de Paz, A.; Kirichenko, A.Y.; Hessels, J.W.T.; Bhardwaj, M.; Ávila, F.; Bassa, C.; Chawla, P.; Fonseca, E.; Kaspi, V.M.; et al. The 60-pc Environment of FRB 20180916B. arXiv 2020, arXiv:2011.03257. [Google Scholar]
- Bhandari, S.; Sadler, E.M.; Prochaska, J.X.; Simha, S.; Ryder, S.D.; Marnoch, L.; Bannister, K.W.; Macquart, J.P.; Flynn, C.; Shannon, R.M.; et al. The Host Galaxies and Progenitors of Fast Radio Bursts Localized with the Australian Square Kilometre Array Pathfinder. Astrophys. J. Lett. 2020, 895, L37. [Google Scholar] [CrossRef]
- Heintz, K.E.; Prochaska, J.X.; Simha, S.; Platts, E.; Fong, W.F.; Tejos, N.; Ryder, S.D.; Aggarwal, K.; Bhandari, S.; Day, C.K.; et al. Host Galaxy Properties and Offset Distributions of Fast Radio Bursts: Implications for their Progenitors. arXiv 2020, arXiv:2009.10747. [Google Scholar]
- Li, Y.; Zhang, B. A Comparative Study of Host Galaxy Properties between Fast Radio Bursts and Stellar Transients. Astrophys. J. Lett. 2020, 899, L6. [Google Scholar] [CrossRef]
- Wang, F.Y.; Wang, Y.Y.; Yang, Y.P.; Yu, Y.W.; Zuo, Z.Y.; Dai, Z.G. Fast Radio Bursts from Activity of Neutron Stars Newborn in BNS Mergers: Offset, Birth Rate, and Observational Properties. Astrophys. J. 2020, 891, 72. [Google Scholar] [CrossRef]
- Mannings, A.G.; Fong, W.F.; Simha, S.; Prochaska, J.X.; Rafelski, M.; Kilpatrick, C.D.; Tejos, N.; Heintz, K.E.; Bhandari, S.; Day, C.K.; et al. A High-Resolution View of Fast Radio Burst Host Environments. arXiv 2020, arXiv:2012.11617. [Google Scholar]
- Bochenek, C.D.; Ravi, V.; Dong, D. Localized Fast Radio Bursts Are Consistent with Magnetar Progenitors Formed in Core-collapse Supernovae. Astrophys. J. Lett. 2021, 907, L31. [Google Scholar] [CrossRef]
- Safarzadeh, M.; Prochaska, J.X.; Heintz, K.E.; Fong, W.f. Confronting the Magnetar Interpretation of Fast Radio Bursts through Their Host Galaxy Demographics. Astrophys. J. Lett. 2020, 905, L30. [Google Scholar] [CrossRef]
- Sridhar, N.; Metzger, B.D.; Beniamini, P.; Margalit, B.; Renzo, M.; Sironi, L. Periodic Fast Radio Bursts from ULX-Like Binaries. arXiv 2021, arXiv:2102.06138. [Google Scholar]
- Xu, J.; Han, J.L. Extragalactic dispersion measures of fast radio bursts. Res. Astron. Astrophys. 2015, 15, 1629–1638. [Google Scholar] [CrossRef]
- Güver, T.; Özel, F. The relation between optical extinction and hydrogen column density in the Galaxy. Mon. Not. R. Astron. Soc. 2009, 400, 2050–2053. [Google Scholar] [CrossRef]
- He, C.; Ng, C.Y.; Kaspi, V.M. The Correlation between Dispersion Measure and X-Ray Column Density from Radio Pulsars. Astrophys. J. 2013, 768, 64. [Google Scholar] [CrossRef]
- Li, Z.; Gao, H.; Wei, J.J.; Yang, Y.P.; Zhang, B.; Zhu, Z.H. Cosmology-insensitive estimate of IGM baryon mass fraction from five localized fast radio bursts. Mon. Not. R. Astron. Soc. 2020, 496, L28–L32. [Google Scholar] [CrossRef]
- Yang, Y.P.; Zhang, B. Extracting host galaxy dispersion measure and constraining cosmological parameters using fast radio burst data. Astrophys. J. 2016, 830, L31. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Yu, H.; He, J.H.; Wang, F.Y. Dispersion Measures of Fast Radio Burst Host Galaxies Derived from IllustrisTNG Simulation. Astrophys. J. 2020, 900, 170. [Google Scholar] [CrossRef]
- Jaroszyński, M. FRBs: The Dispersion Measure of Host Galaxies. arXiv 2020, arXiv:2008.04634. [Google Scholar]
- Binney, J.; Tremaine, S. Galactic Dynamics, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Flynn, C.; Holmberg, J.; Portinari, L.; Fuchs, B.; Jahreiß, H. On the mass-to-light ratio of the local Galactic disc and the optical luminosity of the Galaxy. Mon. Not. R. Astron. Soc. 2006, 372, 1149–1160. [Google Scholar] [CrossRef]
- Platts, E.; Prochaska, J.X.; Law, C.J. A Data-driven Technique Using Millisecond Transients to Measure the Milky Way Halo. Astrophys. J. Lett. 2020, 895, L49. [Google Scholar] [CrossRef]
- Nakashima, S.; Inoue, Y.; Yamasaki, N.; Sofue, Y.; Kataoka, J.; Sakai, K. Spatial Distribution of the Milky Way Hot Gaseous Halo Constrained by Suzaku X-Ray Observations. Astrophys. J. 2018, 862, 34. [Google Scholar] [CrossRef]
- Yamasaki, S.; Totani, T. The Galactic Halo Contribution to the Dispersion Measure of Extragalactic Fast Radio Bursts. Astrophys. J. 2020, 888, 105. [Google Scholar] [CrossRef]
- Gao, H.; Li, Z.; Zhang, B. Fast Radio Burst/Gamma-Ray Burst Cosmography. Astrophys. J. 2014, 788, 189. [Google Scholar] [CrossRef]
- Zhou, B.; Li, X.; Wang, T.; Fan, Y.Z.; Wei, D.M. Fast radio bursts as a cosmic probe? Phys. Rev. D 2014, 89, 107303. [Google Scholar] [CrossRef]
- Walters, A.; Weltman, A.; Gaensler, B.M.; Ma, Y.Z.; Witzemann, A. Future Cosmological Constraints From Fast Radio Bursts. Astrophys. J. 2018, 856, 65. [Google Scholar] [CrossRef]
- Zhao, Z.W.; Li, Z.X.; Qi, J.Z.; Gao, H.; Zhang, J.F.; Zhang, X. Cosmological Parameter Estimation for Dynamical Dark Energy Models with Future Fast Radio Burst Observations. Astrophys. J. 2020, 903, 83. [Google Scholar] [CrossRef]
- Kumar, P.; Linder, E.V. Use of fast radio burst dispersion measures as distance measures. Phys. Rev. D 2019, 100, 083533. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Gibson, B.K.; Ferrarese, L.; Kelson, D.D.; Sakai, S.; Mould, J.R.; Kennicutt, R.C., Jr.; Ford, H.C.; Graham, J.A.; et al. Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant. Astrophys. J. 2001, 553, 47–72. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% Determination of the Local Value of the Hubble Constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Suyu, S.H.; Bonvin, V.; Courbin, F.; Fassnacht, C.D.; Rusu, C.E.; Sluse, D.; Treu, T.; Wong, K.C.; Auger, M.W.; Ding, X.; et al. H0LiCOW—I. H0 Lenses in COSMOGRAIL’s Wellspring: Program overview. Mon. Not. R. Astron. Soc. 2017, 468, 2590–2604. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Bowers, J.B.; Macri, L.; Zinn, J.C.; Scolnic, D. Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with ΛCDM. Astrophys. J. 2021, 908, L6. [Google Scholar] [CrossRef]
- Sammons, M.W.; Macquart, J.P.; Ekers, R.D.; Shannon, R.M.; Cho, H.; Prochaska, J.X.; Deller, A.T.; Day, C.K. First Constraints on Compact Dark Matter from Fast Radio Burst Microstructure. Astrophys. J. 2020, 900, 122. [Google Scholar] [CrossRef]
- Cho, H.; Macquart, J.P.; Shannon, R.M.; Deller, A.T.; Morrison, I.S.; Ekers, R.D.; Bannister, K.W.; Farah, W.; Qiu, H.; Sammons, M.W.; et al. Spectropolarimetric Analysis of FRB 181112 at Microsecond Resolution: Implications for Fast Radio Burst Emission Mechanism. Astrophys. J. Lett. 2020, 891, L38. [Google Scholar] [CrossRef]
- Li, Z.X.; Gao, H.; Ding, X.H.; Wang, G.J.; Zhang, B. Strongly lensed repeating fast radio bursts as precision probes of the universe. Nat. Commun. 2018, 9, 3833. [Google Scholar] [CrossRef] [PubMed]
- Zitrin, A.; Eichler, D. Observing Cosmological Processes in Real Time with Repeating Fast Radio Bursts. Astrophys. J. 2018, 866, 101. [Google Scholar] [CrossRef]
- Wagner, J.; Liesenborgs, J.; Eichler, D. Multiply imaged time-varying sources behind galaxy clusters. Comparing fast radio bursts to QSOs, SNe, and GRBs. Astron. Astrophys. 2019, 621, A91. [Google Scholar] [CrossRef]
- Wu, Q.; Yu, H.; Wang, F.Y. A New Method to Measure Hubble Parameter H(z) Using Fast Radio Bursts. Astrophys. J. 2020, 895, 33. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters. Astrophys. J. Suppl. Ser. 2003, 148, 175–194. [Google Scholar] [CrossRef]
- Fialkov, A.; Loeb, A. Constraining the CMB optical depth through the dispersion measure of cosmological radio transients. J. Cosmol. Astropart. Phys. 2016, 2016, 004. [Google Scholar] [CrossRef]
- Syphers, D.; Anderson, S.F.; Zheng, W.; Smith, B.; Pieri, M.; Kriss, G.A.; Meiksin, A.; Schneider, D.P.; Shull, J.M.; York, D.G. He II Lyβ Gunn-Peterson absorption new HST observations and theortical expectations. Astrophys. J. 2011, 742, 99. [Google Scholar] [CrossRef]
- Plante, P.; Trac, H.; Croft, R. Helium Reionization Simulations. III. The Helium Lyman-α Forest. Astrophys. J. 2017, 868. [Google Scholar]
- McQuinn, M.; Lidz, A.; Zaldarriaga, M.; Hernquist, L.; Hopkins, P.F.; Dutta, S.; Faucher-Giguère, C.A. He II Reionization and its Effect on the Intergalactic Medium. Astrophys. J. 2009, 694, 842–866. [Google Scholar] [CrossRef]
- Zheng, Z.; Ofek, E.O.; Kulkarni, S.R.; Neill, J.D.; Juric, M. Probing the Intergalactic Medium with Fast Radio Bursts. Astrophys. J. 2014, 797, 71. [Google Scholar] [CrossRef]
- Linder, E.V. Detecting helium reionization with fast radio bursts. Phys. Rev. D 2020, 101, 103019. [Google Scholar] [CrossRef]
- Kit Lau, A.W.; Mitra, A.; Shafiee, M.; Smoot, G. Constraining HeII Reionization Detection Uncertainties via Fast Radio Bursts. arXiv 2020, arXiv:2006.11072. [Google Scholar]
- Caleb, M.; Flynn, C.; Stappers, B.W. Constraining the era of helium reionization using fast radio bursts. Mon. Not. R. Astron. Soc. 2019, 485, 2281–2286. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Kumar, P.; Linder, E.V. Fast Radio Burst Dispersion Measure Distribution as a Probe of Helium Reionization. arXiv 2020, arXiv:2010.14530. [Google Scholar]
- Dai, J.P.; Xia, J.Q. Reconstruction of Reionization History through Dispersion Measure of Fast Radio Bursts. arXiv 2020, arXiv:2004.11276. [Google Scholar]
- Pagano, M.; Fronenberg, H. Constraining the Epoch of Reionization With Highly Dispersed Fast Radio Bursts. arXiv 2021, arXiv:2103.03252. [Google Scholar]
- Hashimoto, T.; Goto, T.; Lu, T.Y.; On, A.Y.L.; Santos, D.J.D.; Kim, S.J.; Eser, E.K.; Ho, S.C.C.; Hsiao, T.Y.Y.; Lin, L.Y.W. Revealing the cosmic reionization history with fast radio bursts in the era of Square Kilometre Array. Mon. Not. R. Astron. Soc. 2021, 502, 2346–2355. [Google Scholar] [CrossRef]
- Ravi, V.; Battaglia, N.; Burke-Spolaor, S.; Chatterjee, S.; Cordes, J.; Hallinan, G.; Law, C.; Lazio, T.J.W.; Masui, K.; McQuinn, M.; et al. Fast Radio Burst Tomography of the Unseen universe. arXiv 2019, arXiv:1903.06535. [Google Scholar]
- Abbott, T.M.C.; Abdalla, F.B.; Allam, S.; Amara, A.; Annis, J.; Asorey, J.; Avila, S.; Ballester, O.; Banerji, M.; Barkhouse, W.; et al. The Dark Energy Survey: Data Release 1. Astrophys. J. Suppl. Ser. 2018, 239, 18. [Google Scholar] [CrossRef]
- Rafiei-Ravandi, M.; et al. [The Chime/Frb Collaboration] Cross-correlating the First CHIME/FRB Catalog with Photometric Redshift Catalogs of Galaxies. Available online: https://ui.adsabs.harvard.edu/abs/2021AAS...23751001R/abstract (accessed on 29 March 2020).
- Burke-Spolaor, S. Multiple messengers of fast radio bursts. Nat. Astron. 2018, 2, 845–848. [Google Scholar] [CrossRef]
- Wang, M.H.; Ai, S.K.; Li, Z.X.; Xing, N.; Gao, H.; Zhang, B. Testing the Hypothesis of a Compact-binary-coalescence Origin of Fast Radio Bursts Using a Multimessenger Approach. Astrophys. J. Lett. 2020, 891, L39. [Google Scholar] [CrossRef]
- Zhang, B. Fast Radio Bursts from Interacting Binary Neutron Star Systems. Astrophys. J. Lett. 2020, 890, L24. [Google Scholar] [CrossRef]
- Margalit, B.; Berger, E.; Metzger, B.D. Fast Radio Bursts from Magnetars Born in Binary Neutron Star Mergers and Accretion Induced Collapse. Astrophys. J. 2019, 886, 110. [Google Scholar] [CrossRef]
- Aggarwal, K.; Budavári, T.; Deller, A.T.; Eftekhari, T.; James, C.W.; Prochaska, J.X.; Tendulkar, S.P. Probabilistic Association of Transients to their Hosts (PATH). arXiv 2021, arXiv:2102.10627. [Google Scholar]
- Sanidas, S.; Caleb, M.; Driessen, L.; Morello, V.; Rajwade, K.; Stappers, B.W. MeerTRAP: A pulsar and fast transients survey with MeerKAT. Proc. Int. Astron. Union 2017, 13, 406–407. [Google Scholar] [CrossRef]
- Ray, P.S.; Kerr, M.; Bethapudi, S.; Clarke, T.E.; Kassim, N.E.; Taylor, G.B.; Dowell, J.; Deneva, J.S. First Detections from VLITE-FAST: A 350-MHz Commensal System for Detecting and Localizing Fast Radio Transients with the JVLA. Available online: https://ui.adsabs.harvard.edu/abs/2021AAS...23754201R/abstract (accessed on 29 March 2020).
- Maan, Y.; van Leeuwen, J. Real-time searches for fast transients with Apertif and LOFAR. In Proceedings of the 2017 XXXIInd General Assembly and Scientific Symposium of the International Union of Radio Science (URSI GASS), Montreal, QC, USA, 19–26 August 2017; p. 2. [Google Scholar]
- Deller, A.; Flynn, C. Vintage telescope rebooted in the hunt for FRBs. Nat. Astron. 2020, 4, 292. [Google Scholar] [CrossRef]
- Hallinan, G.; Ravi, V.; Weinreb, S.; Kocz, J.; Huang, Y.; Woody, D.P.; Lamb, J.; D’Addario, L.; Catha, M.; Law, C.; et al. The DSA-2000—A Radio Survey Camera. arXiv 2019, arXiv:1907.07648. [Google Scholar]
- Newburgh, L.B.; Bandura, K.; Bucher, M.A.; Chang, T.C.; Chiang, H.C.; Cliche, J.F.; Davé, R.; Dobbs, M.; Clarkson, C.; Ganga, K.M.; et al. HIRAX: A probe of dark energy and radio transients. In Proceedings of the Ground-Based and Airborne Telescopes VI, Edinburgh, UK, 26 June–1 July 2016; Volume 9906, p. 99065X. [Google Scholar]
- Vanderlinde, K.; Liu, A.; Gaensler, B.; Bond, D.; Hinshaw, G.; Ng, C.; Chiang, C.; Stairs, I.; Brown, J.A.; Sievers, J.; et al. The Canadian Hydrogen Observatory and Radio-transient Detector (CHORD). Can. Long Range Plan Astronony Astrophys. White Pap. 2019, 2020, 28. [Google Scholar]
- Fialkov, A.; Loeb, A. A Fast Radio Burst Occurs Every Second throughout the Observable Universe. Astrophys. J. Lett. 2017, 846, L27. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).