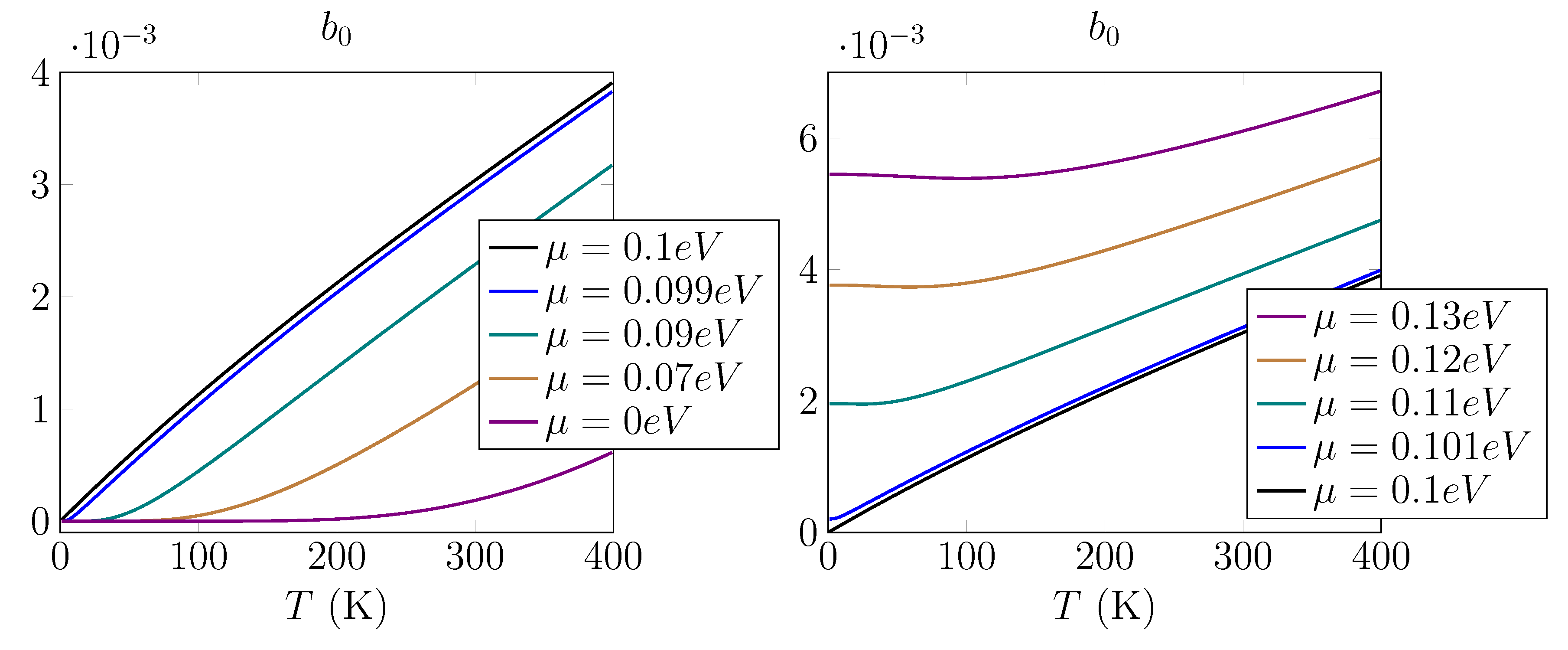1. Introduction
The Casimir [
1] and Casimir-Polder [
2] dispersion forces play an important role in different phenomena [
3,
4]. The Casimir-Polder force is usually referred to as the van der Waals force on large distances between micro-particles and macro-objects when the retardation of interaction is taken into account. The Casimir-Polder force essentially depends on the material of the macro-objects, its dimension, shapes, conductivity, and temperature [
3,
4], and it is important for the interaction of graphene with micro-particles [
5,
6,
7,
8,
9]. The Casimir-Polder force and torque for anisotropic molecules have been the subject of investigations in the recent years from the theoretical point of view [
10,
11,
12,
13,
14], as well as experimentally [
15,
16]. The non-ground state of an atom gives a specific resonant term contribution to the Casimir-Polder force [
17,
18], but, here, we restrict ourself by an atom in the ground state, only.
The thermal corrections to the Casimir-Polder interaction for micro-particle/graphene were considered in Refs. [
19,
20,
21,
22,
23,
24,
25]. In the last few years, much attention has been given to the low-temperature expansion of the Casimir-Polder free energy for the atom/graphene system [
7,
23,
24,
25]. In the case of an atom/ideal plane, the low-temperature correction to the Casimir-Polder free energy is proportional to the fourth degree of temperature
. As opposed to the ideal case, the conductivity of graphene depends on the chemical potential and temperature, and it has temporal and spatial dispersion [
26,
27,
28,
29]. The low-temperature expansion depends on the relations between these macro-parameters.
It was shown in Ref. [
23] that the low-temperature expansion reveals the unusual quadratic
behavior. Next, detailed considerations [
24,
25] showed a more rich picture of low-temperature expansion depending on the relation between chemical potential
and mass gap parameter
m of the Dirac electron. For
, the same quadratic behavior was confirmed, but, in the case
the
, dependence was obtained. In the case of the very specific exact relation
, the linear
dependence was observed. To obtain these results, the authors of Refs. [
24,
25] made the sophisticated treatment of the Matsubara series.
In the present paper, we extend our analysis made in Ref. [
23] in the framework of the Poisson representation of the Matsubara series to all relations between
and
m and confirm results by numerical analysis. The Poisson representation is more suitable for the low-temperature expansions—the zeroth term of the series coincides with a zero-temperature contribution (with possible temperature and chemical potential dependence via conductivity) and the rest of the series gives temperature correction. In Ref. [
23], we considered conductivity of graphene with cutting scattering rate, as in Refs. [
30,
31], where the Kubo approach was used. In this case, the conductivity has a constant value at zero frequencies which depends on the scattering rate parameter
. It leads to the low-temperature dependence
for any relation between chemical potential
and mass gap
m. In the framework of the polarization tensor approach [
27,
29], there is no scattering parameter, and the behavior of the conductivity at zero frequency strongly depends on the relation between
and
m.
In the framework of our approach, we show that, for
, the temperature corrections to the free energy
, and, for
, we obtain correction
, and, in the point
, the linear dependence
appears. Therefore, we confirm expansions obtained in Ref. [
24]. The main contribution for
to the low-temperature expansion of the free energy comes from the expression for energy at zero temperatures (zeroth term of Poisson expansion) via temperature dependence of conductivity. For
, the main contribution comes from the rest part of the series. The point
is a very specific point where the free energy is linear over temperature; therefore, the entropy is constant, and the Nernst theorem is no longer valid. But, for an infinitely small deviation from equality,
shows different regimes where the Nernst theorem holds. The numerical evaluations reveal the singular “beak-shaped” form of the temperature correction of the free energy, which confirms this conclusion. The point
is the point of changing a regime of the temperature dependence of the free energy. The numerical evaluations show that, for any small value of the deviations
, there is a domain of temperatures
T close to the origin where the derivative of the free energy with respect to the temperature, the entropy, is zero for
, and the Nernst theorem is valid. The method developed here may be used to obtain the low-temperature expansion in many other situations.
Throughout the paper, the units are used.
2. The Casimir-Polder Free Energy
Taking into account the Poisson summation formula (see details in Ref. [
23]), the free energy may be represented in the following form
normalized to the
—the Casimir-Polder (CP) energy for an ideal plane/atom at large distance
a. Here, the prime means factor
for
, and we have to use
for imaginary frequency
and wave-vector
k in conductivities
and
. The
is the polarizability of atom or molecule at the imaginary frequency, and the refraction coefficients of TE and TM modes are
The form of the zero terms,
, in (
1) coincides exactly with that obtained for zero temperatures but, in general, with temperature and chemical potential dependence through the conductivities
. We extract the zero,
, term
and we consider the low-temperature expansion for
and
separately. We extract the temperature contribution from
. Then,
where
. Therefore, the total temperature correction,
, consists of two parts,
In general (for the graphene case, for example), the depends on the chemical potential.
The expansion crucially depends on the behavior of the conductivities at zero frequencies. In Ref. [
23], we considered in detail the different models of conductivities with a constant value of conductivity at zero frequencies. In particular, we have taken into account the graphen’s conductivity with finite scattering factor
, which means that the
. As a result, the free energy has the main low-temperature term
for any relation between
and
T. With zero scattering factor, we have to consider this expansion more carefully.
In the framework of the polarization tensor approach [
26], the conductivities of the TM and TE modes read [
27,
29]
where
and
with
being the graphene universal conductivity.
Let us consider, for simplicity, the conductivity in the zero approximation over the Fermi velocity
. In this approximation, we obtain more simple expressions (
)
and we observe that the conductivities have no dependence on
k, which should be the case because the Fermi velocity and wave-vector come in the single combination
.
2.1. Expansion of the
The sum with
, the
, may be represented in the following form [
23]:
where
and
, and
. This representation is suitable for
analysis, which means
.
In the case
, the conductivities do not depend on
k; therefore, we can calculate integral over
s:
where
is the exponential logarithm function. The function
has the following representation as a series
that contains polynomials, as well as logarithmic contributions.
Then, we make expansion over
z,
and use the Lemmas Erdélyi (These lemmas are sometimes called etalon integrals in the asymptotic methods of the stationary phase.) (see Ref. [
32], Equations (1.13) and (1.35)), and Ref. [
23]) to calculate asymptotic
for integral over
z in Equation (
8) for each term of series. The manifest form of the coefficients depends on the specific model of conductivity. We obtain the series (
12) in which we have to make replacements
where
is the digamma function, and then we take the real part (see Equation (
8)) and obtain the following replacements
Then, we make a summation over
and arrive with relation
where
and
is the Riemann zeta function. We observe that the polynomial contributions come from odd
and
. The logarithmic contributions come from odd
. The main contribution reads
where
is the Euler constant. Note that, in general, the coefficients
and
depend on
, and
T.
For the constant conductivity case
and
. Therefore, the main contribution comes from TM mode and reads [
23]
For graphene case, the conductivities are expanded in the following series over
z:
where the coefficients
are functions of
, and
T:
The zero term crucially depends on m and for low temperatures:
Here,
. These asymptotic are illustrated by numerical evaluation in
Figure 1.
In the first case (
19a) with
, the expansion
over
T starts from the constant term (see
Figure 1, right panel), and we obtain the following non-zero coefficients
The main contribution to the
comes from the first term of expansion in Equation (
19a):
In the last case (
19c) with
, the
is exponentially small (see
Figure 1, left panel), and we set it at zero, and the conductivities are expanded as the following:
and the firsts non-zero coefficients read
For the specific case (
19b), when
, we consider the main contribution for
and can set
, as in the case (
19c). Therefore, for all cases, we have the following expansion up to
:
2.2. Expansion of the
The conductivities (6) depend on the temperature, and
have the following low-temperature expansions [
23]
Taking these expansions into account, we obtain the following low-temperature corrections to zero term
where
The functions
are given by Equation (6) and
Therefore, taking into account (
24), we obtain the low-temperature expansion of the free energy
3. Numerical Evaluations
We evaluated numerically the total temperature correction (
5) by using the expression for the free energy in the form of Matsubara sum. We considered the Hydrogen atom at distance
nm from the graphene sheet. The polarizability of the Hydrogen atom in the single oscillator approximation may be found in Ref. [
8], for example. The graphene conductivities are given by Equations (6). We used the Fermi velocity
and the mass gap
eV. To visualize the dynamic of
dependence, we made calculations for the value of
close to
eV. The free energy is normalized to the
—the CPenergy for an ideal plane/atom at large distance
a.
The zero-temperature free energy,
, depends on the chemical potential
, and this dependence is shown in
Figure 2. For
, it has the constant value, and it grows up starting with mass gap
.
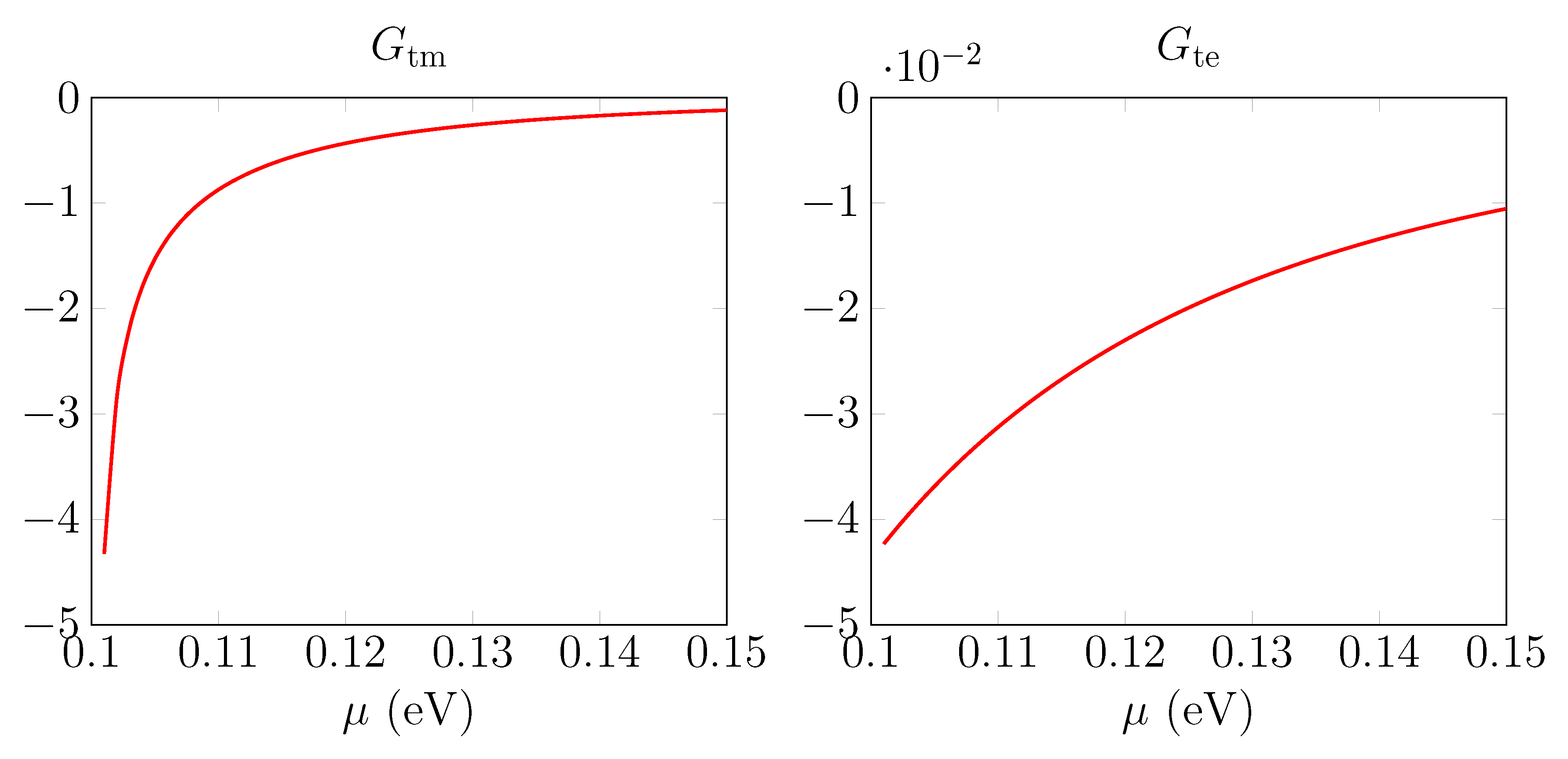
We proceed now to the consideration of the temperature correction,
to the free energy. First of all, let us consider the functions
, which define low temperature expansion for
case (
30a). They are plotted in
Figure 3. We observe that they are negative, and contribution from the TE mode is 100 times smaller.
One comment is in order. Because
, then the temperature correction
close to the
. At the same time, in Refs. [
7,
24], the positive value of correction was observed. The disagreement is connected with that in which we use distance
nm for numerical evaluations, which is out of distances considered in Refs. [
7,
24].
The numerical evaluation of for nm gives the following values and . Again, the main contribution comes from TM mode. The value of strongly depends on the value of the Fermi velocity. For , the .
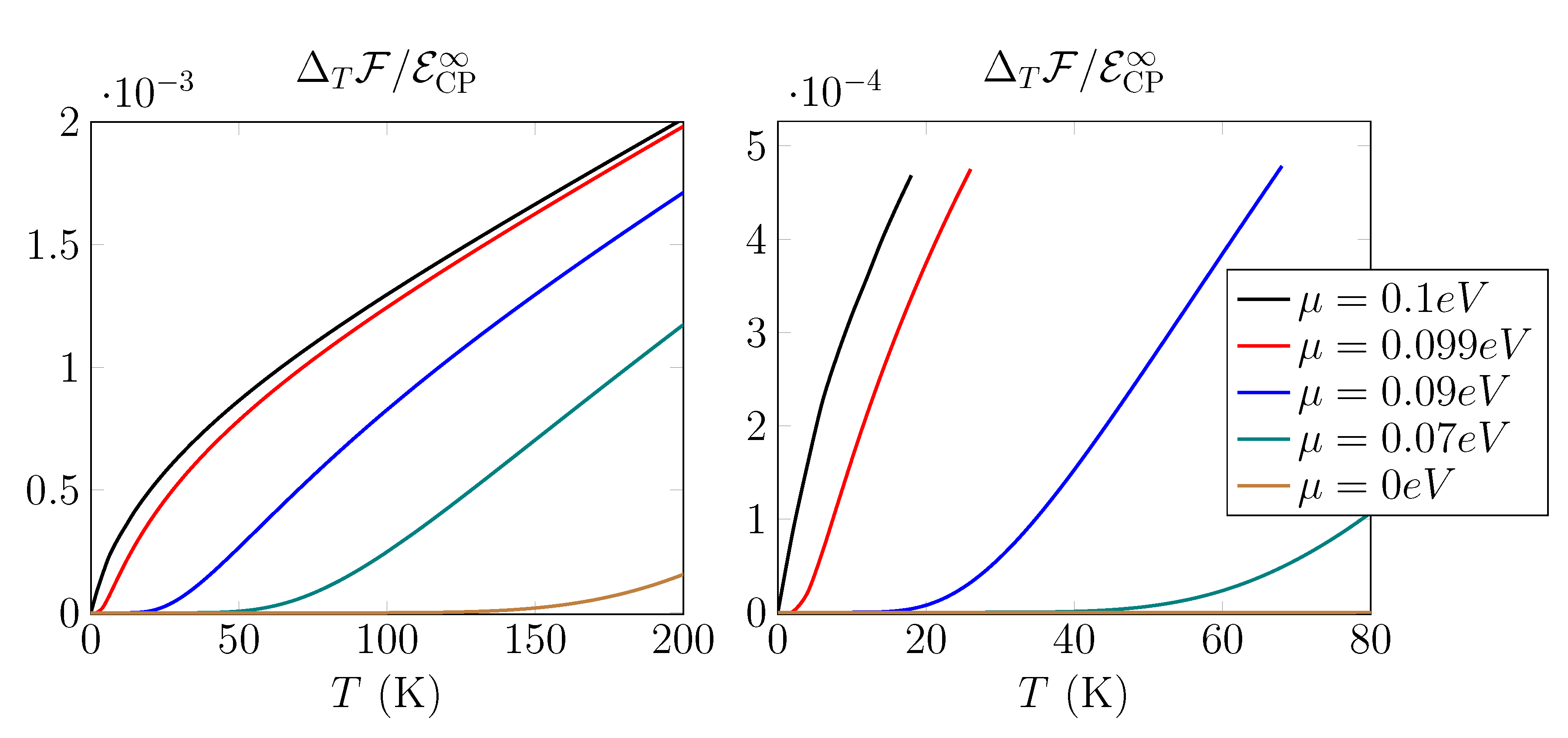
The temperature contribution for
is shown in
Figure 4. We observe that, for low temperatures, the free energy has the form of parabola, ∼
, in agreement with (30) with negative parameter
(see
Figure 3).
The closer
to
m, the smaller domain of temperature
T where this approximation is valid, and the greater value of the parameter of parabola
, in agreement with
Figure 3. If
, this domain becomes zero, and the free energy drastically changes its form. If
, the part of the curve which is out of this domain (the vertical part of the green curve, for example) goes to free energy for this very special position with
(black curve). Therefore, for any infinitely small difference
, the derivative of free energy with respect temperature
T is zero for
, and the Nernst theorem is valid. The experimental realization of the exact equality
cannot be realized, and we conclude that the Nernst theorem is valid for this system.
The temperature contribution for
is shown in
Figure 5. We observe the completely different dependence of the energy on the
.
For zero chemical potential (brown curve), the temperature correction is, in fact, zero for the large domain of temperatures. The closer
to
m, the smaller domain in which temperature correction is zero. According to (30b),
in this domain.
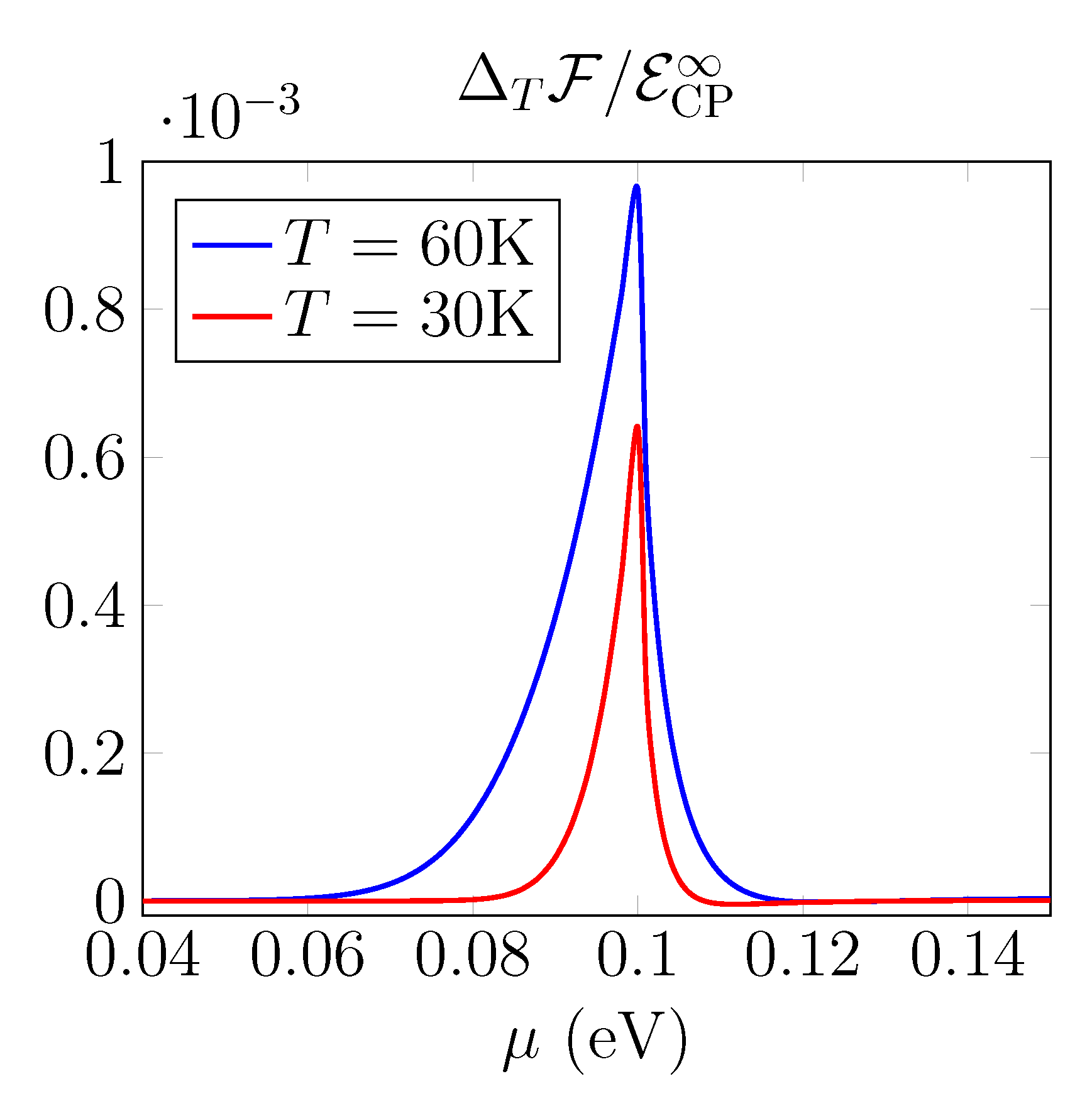
Figure 6 shows the temperature contribution to the free energy as a function of chemical potential. The function has a very sharp form with the maximum for
with a different slope at the left and the right of this point.
The point looks like a phase transition point between different regimes from to . In fact, it is an unstable point—infinitely small deviation from m changes regime.
From
Figure 4 and
Figure 5 and relations (30), we observe the different signs of the entropy,
S, for
and
. The entropy is the negative derivative of the free energy with respect of temperature. Therefore,
(see
Figure 5), and
(see
Figure 4). In both cases, the Nernst theorem is valid,
. The negative entropy of the dispersion forces has already been observed in Refs. [
19,
33] for plain and spherical configurations in the framework of plasma model and was also discussed recently in Ref. [
34].
The domains of temperatures where the low-temperature expansions (30) over dimensionless parameter
are valid depend on the chemical potential
, mass gap
m, and the distance
a between an atom and plain. Let us make some numerical estimations. The mass gap
eV corresponds to the temperature
K. Therefore, the restriction
in Equations (
30a) and (30c) plays the role for
eV, in agreement with
Figure 4 and
Figure 5. The restriction in the second case (30b) plays the role if
eV. The more strong limitation appears due to the huge value of parameter
(for
nm):
K for
nm. It means that, in this case, there is no domain of temperatures where this case is valid, according to above discussion. The restriction
is important starting from
μm. In this case, the effective temperature
K.