Towards Black-Hole Singularity-Resolution in the Lorentzian Gravitational Path Integral

Abstract

Quantum gravity is expected to resolve the singularities of classical general relativity. Based on destructive interference of singular spacetime-configurations in the path integral, we find that higher-order curvature terms may allow to resolve black-hole singularities both in the spherically symmetric and axisymmetric case. In contrast, the Einstein action does not provide a dynamical mechanism for singularity-resolution through destructive interference of these configurations.

1. Introduction

Within general relativity (GR), several solutions of the field equations develop curvature singularities. These signal the geodesic incompleteness of the corresponding spacetimes. The latter include the Schwarzschild, Kerr and Friedmann–Lemaître–Robertson–Walker (FLRW) metrics, all of which are of relevance in astrophysics and cosmology. For instance, detections of gravitational waves from black-hole binaries [1], observations of stars orbiting the galactic center [2] and the very first image of the shadow of a black hole [3] show that astrophysical objects exist for which the spacetime metric is well-approximated by a Kerr metric, at least at a sufficiently large geodesic distance to the object. Yet, that description must ultimately break down, as the curvature singularity of the Kerr metric cannot be physical. This singularity occurs at large values of the local curvature, where quantum-gravitational effects are expected to become important. Therefore, it is a key requirement of quantum gravity to provide a mechanism that reliably resolves such singularities. We assume, that even in the quantum gravitational regime, an effective metric description holds. Thus, the dynamical singularity-resolution mechanism in quantum gravity must result in regular black-hole spacetimes that agree with the Kerr spacetime at low curvature scales and are therefore candidate spacetimes that capture the true nature of the observed compact objects.

We search for such a mechanism within the gravitational path integral. Schematically, it reads

$$Z=\int \mathcal{D}{g}_{\mu \nu }{e}^{iS\left[g_{\mu \nu }\right]},$$

(1)

where all possible metric configurations (modulo diffeomorphisms) are being summed over. Thus, the singular spacetime metrics that constitute solutions of the field equations in GR are included in the path integral. In addition, regular black-hole spacetimes, which agree (approximately) with the Schwarzschild or Kerr solution outside the black-hole horizon but do not harbor a curvature singularity, are also included. We ask whether there can be a dynamics that forces singular black-hole spacetimes to interfere destructively, suppressing the contribution of such spacetimes to the Lorentzian path integral, while regular black-hole solutions provide a finite contribution. The mechanism at work here, see [4], is that any configuration $g_{\mu \nu }$ on which the action $S\left[g_{\mu \nu }\right]$ exhibits a divergence, is excluded from the path integral through destructive interference. The divergence of the action signifies a rapidly oscillating quantum-mechanical phase factor for singular spacetimes. Thus, the singular spacetime and “neighboring” configurations (using an appropriate notion of distance on the configuration space) interfere destructively. Here, it is immaterial, whether or not the considered configurations solve the classical equations of motion. In fact, destructive interference necessarily also involves off-shell configurations.

In this context, it is important to highlight that in the path integral expression (1), S need not be the Einstein–Hilbert action. Indeed, little is known about the form of the microscopic action S in the path integral, as observations actually constrain the effective action $\Gamma$ that is obtained once the microscopic degrees of freedom are integrated over. These observational constraints restrict the leading-order terms in a curvature/derivative expansion of $\Gamma$. For instance, the cosmological constant and the Newton coupling have been determined with good accuracy, while, at the quadratic order in the curvature, the observational constraints on the couplings are not very strong. The couplings are restricted to $\le \mathcal{O}\left({10}^{-61}\right)$ [5], using sub-millimeter tests of Newton’s law [6]. Observational constraints on curvature invariants of cubic or higher-order are not available yet.

Since these observational constraints all apply to the effective action, distinct, theoretical constraints are required to fix the form of the microscopic action S. In fact, demanding a dynamical mechanism for singularity resolution through destructive interference can serve as one such theoretical constraint, as we will show in this paper. Indeed, requiring a divergence of the action on singular spacetimes divides actions into viable candidates and ruled-out dynamics, since a curvature singularity of a given spacetime is not necessarily reflected in a divergence of the action. This happens if the action is built out of only those curvature invariants that remain finite despite a divergence in some other curvature invariants. As a simple example, for the Schwarzschild black hole, the curvature invariant R vanishes everywhere, while the invariant $R_{\mu \nu \kappa \lambda }{R}^{\mu \nu \kappa \lambda }$ diverges. Demanding a dynamics that diverges on singular black-hole spacetimes can therefore serve as a principle to distinguish different candidate dynamics for quantum gravity. Accordingly, we will explore which form of the action is preferred in order to obtain a divergent action integral for different singular black-hole solutions. For cosmology, a similar investigation has been performed previously in [4] and has provided the intriguing result that curvature-squared terms could ensure a homogeneous and isotropic early universe.

A further important theoretical constraint is the predictivity of the theory, linked to its perturbative or non-perturbative renormalizability. Indeed, demanding control over ultraviolet (UV) divergences disfavors the Einstein–Hilbert action

$$S_{\mathrm{EH}}\left[g\right]=\frac{1}{16\pi G_{\mathrm{N}}}\int {\mathrm{d}}^{4}x\sqrt{-g}(R-2\mathrm{\Lambda }),$$

(2)

as it is not asymptotically free and in fact not even perturbatively renormalizable [7,8,9]. Therefore, it cannot be predictive when used beyond the effective field theory regime [10,11], since it features infinitely many free parameters linked to the infinitely many counterterms required for its perturbative renormalization. Additionally, it has been debated whether or not this dynamics can give rise to a well-defined Hartle–Hawking wavefunction, which would provide a well-defined beginning of the universe [12,13,14]. Both points motivate to go beyond the Einstein–Hilbert action. Generalizing to a curvature-squared action of the form

$$S\left[g\right]=\int {\mathrm{d}}^{4}x\sqrt{-g}\left(\frac{1}{16\pi G_{\mathrm{N}}}(R-2\mathrm{\Lambda })+a{R}^2+b{R}_{\mu \nu \kappa \lambda }{R}^{\mu \nu \kappa \lambda }\right),$$

(3)

results in asymptotic freedom [15,16] for an appropriate choice of signs of the couplings, see [17] for a review. Yet, unless $b=0$, this theory appears non-unitarity, as there is a spin-2 ghost entering the perturbative graviton propagator around a flat background, [15], see [18,19] for newer developments on this question.

Finally, the asymptotic-safety scenario [20,21] motivates the presence of higher powers of curvature invariants in the action, see, e.g., [22,23,24,25,26,27,28,29,30,31,32,33,34,35], also in its unimodular form [36]. At present, the form of the fixed-point action is not completely known; the so-called Reuter fixed point and its relevant directions are only determined within truncations of the full space of couplings, see [37,38,39] for reviews. The most important limitation of these results in the present context is their origin in a Euclidean path integral, see [40] for a first step in Lorentzian signature and [41] for a discussion of limitations and open questions. Additionally, those results are obtained within the functional Renormalization Group (RG) framework, see [42] for a review, which does not provide direct access to the microscopic action S [43,44,45]. This motivates us to explore whether a requirement different from the fixed-point requirement can provide useful constraints on the form of the microscopic action.

In summary, we explore whether, in addition to the requirement of predictivity and (non-) perturbative renormalizability, a candidate mechanism for dynamical singularity-resolution of curvature singularities in black-hole spacetimes could also favor the presence of higher curvature terms in the action.

This paper is structured as follows: in Section 2 we first motivate our choice of curvature invariants. We provide the line elements and values of the scalar invariants for various singular and non-singular black-hole spacetimes. In addition, relations between the curvature invariants that are particular for a given spacetime are highlighted. Section 3 establishes our general ansatz for the gravitational action and introduces functions for the spherically symmetric and axisymmetric spacetimes that are used for the subsequent analyses. Following the examination of minimal Einstein–Hilbert and curvature-squared dynamics for both singular and regular spacetimes, we turn to investigate beyond-four-derivative terms in the action. We conclude and provide a short outlook in Section 4.

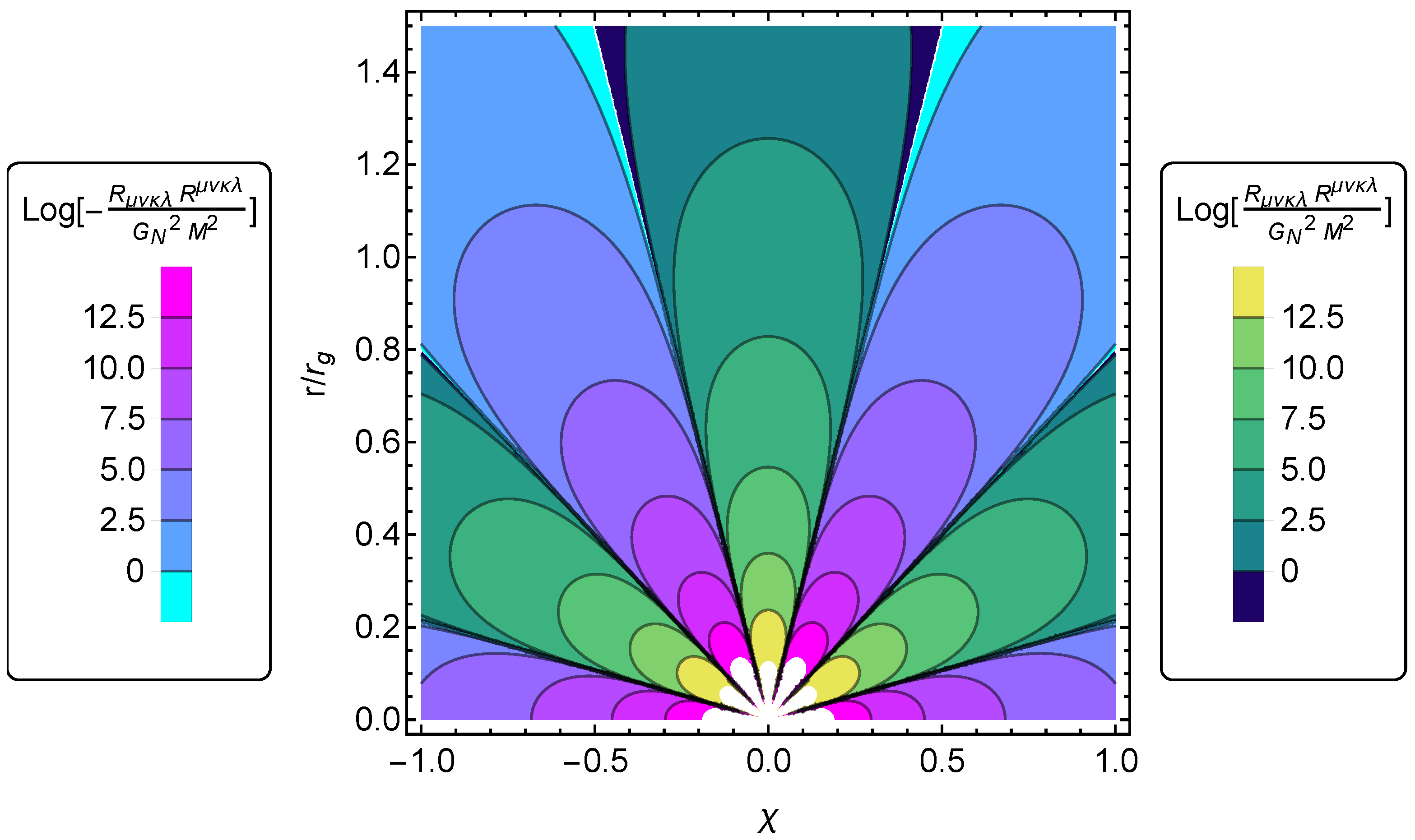
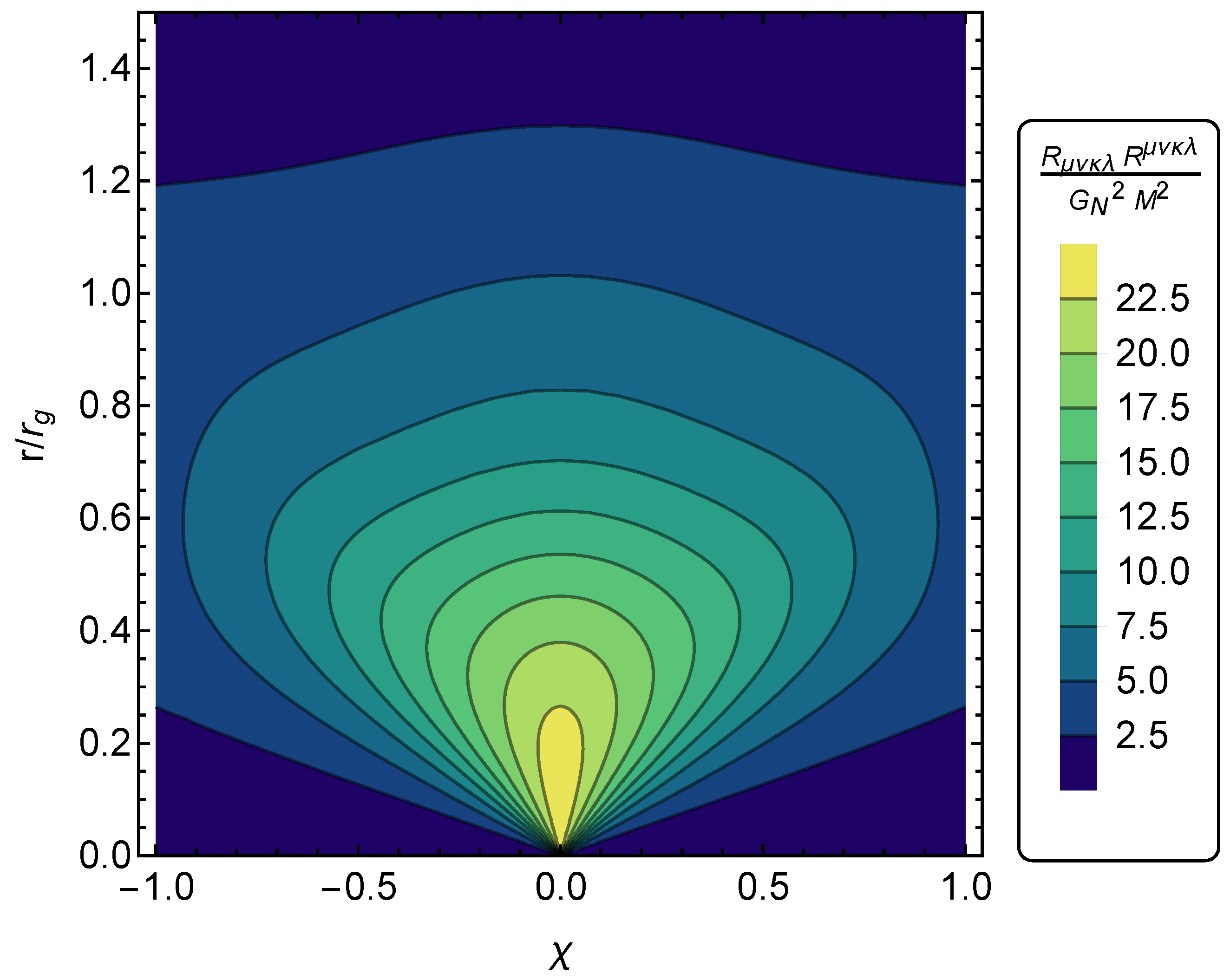
2. Singular and Regular Black-Hole Spacetimes and Their Curvature Invariants

We focus on two classes of black-hole metrics, namely those harboring a spacetime singularity, encoded in a divergent curvature invariant like the Kretschmann scalar, as well as regular ones where the curvature is finite everywhere. For our purposes, it is not relevant whether these black-hole spacetimes constitute solutions to the classical gravitational equations of motion, the Einstein equations, or to modified classical gravitational equations of motion. The gravitational path integral includes all configurations, irrespective of whether or not they solve Einstein’s equations. In particular, we demand a well-defined theory of quantum gravity, that singular black-hole spacetimes interfere destructively. On the other hand, we expect that with the appropriate boundary conditions, a regular black-hole spacetime can emerge from the Lorentzian gravitational path integral as the expectation value for the spacetime geometry—in accordance with the observation of extremely compact objects in astrophysics. Therefore, we demand that (i) singular black-hole spacetimes come with a divergent action, resulting in their destructive interference in the Lorentzian gravitational path integral and (ii) regular black-hole spacetimes come with a finite action, allowing their contribution to the gravitational path integral.

We focus on a set of curvature invariants $K^{\left(i\right)}$ up to mass dimension eight, which is complete in a sense to be detailed below up to mass dimension six:

$$\begin{array}{c}{K}^{\left(1\right)}=R,\hfill \\ K^{\left(2\right)}=R_{\mu \nu }{R}^{\mu \nu },\hfill \\ K^{\left(3\right)}=R_{\mu \nu \kappa \lambda }{R}^{\mu \nu \kappa \lambda },\hfill \\ K^{\left(4\right)}=R{}^{\mu \nu \kappa \lambda }R{}_{\mu }^{\tau }{\kappa }^{\omega }R{}_{\nu \tau \lambda \omega },\hfill \\ K^{\left(5\right)}=R^{\mu \nu \kappa \lambda }{R}_{\kappa \lambda \rho \sigma }{R}_{\mu \nu }^{\rho \sigma },\hfill \\ K^{\left(6\right)}=R{}^{\mu \nu \kappa \lambda ;\tau }R{}_{\mu \nu \kappa \lambda ;\tau },\hfill \\ K^{\left(7\right)}=R_{\mu \nu \kappa \lambda }{R}^{\kappa \lambda \rho \sigma }{R}_{\rho \sigma \alpha \beta }{R}^{\alpha \beta \mu \nu },\hfill \\ K^{\left(8\right)}={\left(K^{\left(3\right)}\right)}^2.\hfill \end{array}$$

(4)

As has been shown in [46], a complete basis of non-derivative invariants can be constructed without including the dual Riemann tensor. Thus, we include invariants built solely out of the Riemann tensor and the metric, for which there are 14 independent ones in the most general case One can see this by considering that the Riemann tensor has 20 independent components in four dimensions, and the metric has 10, but 16 of the 30 independent functions can be removed by a coordinate transformation, see, e.g., [47] for a discussion. Including invariants which contain the covariant derivative, additional invariants are present at each order in an expansion in derivatives and curvature., but only four independent non-vanishing ones for the case of an axisymmetric spacetime which is a vacuum solution to the Einstein equations [47]. We neglect topological invariants like the Gauss-Bonnet term and the Hirzebruch signature. Further, we neglect invariants which contain either R or $R_{\mu \nu }$. It will become clear in our analysis that their inclusion would not alter our main result.

At sixth order in derivatives, a complete set includes both local invariants, which are built purely out of the Riemann tensor and its contractions, as well as derivative invariants which are built out of the Riemann tensor and its derivatives. Following [48], there are two such local invariants at order 6 which do not include either the Ricci scalar nor tensor and one invariant including two covariant derivatives and two Riemann tensors. On the black-hole spacetimes which are solutions to the vacuum Einstein equations, it holds that $K^{\left(4\right)}=2K^{\left(5\right)}$. In the more general case, these two differ and we, therefore, include both. Let us also highlight that $K^{\left(5\right)}$ is the Goroff-Sagnotti counterterm from the two-loop perturbation theory of Einstein gravity [8].

At order four in the curvature, we only include two invariants in order to demonstrate the salient features of this order in the curvature.

2.1. Singular Black-Hole Spacetimes

In the following, we will focus on three paradigmatic examples of singular black-hole spacetimes, namely the Schwarzschild black hole, Kerr black hole, and Vaidya spacetime. We will briefly comment on the case of the additional solutions that appear in classical curvature-squared gravity [49,50] in Section 3.2. In the following, we provide the explicit form of the various curvature invariants for these metrics.

The Schwarzschild spacetime describes a spherically symmetric, static and asymptotically flat black hole in the GR vacuum with line element

$$\mathrm{d}{s}^2=-f\left(r\right)\mathrm{d}{t}^2+f{\left(r\right)}^{-1}\mathrm{d}{r}^2+r^2(\mathrm{d}{\theta }^2+{sin}^2\theta \mathrm{d}{\varphi }^2),$$

(5)

and lapse function

$$f\left(r\right)=1-\frac{2G_{\mathrm{N}}M}{r}.$$

(6)

Here, $G_{\mathrm{N}}$ is the classical Newton coupling and M the black-hole mass measured by a distant observer. The existence of a coordinate singularity at $r=2G_{\mathrm{N}}M$ in these coordinates is irrelevant for our analysis, as we focus on curvature invariants.

As the spacetime is a vacuum solution to the field equations, the Ricci scalar vanishes, $R=K^{\left(1\right)}=0$, as do contractions of the Ricci tensor, e.g., $K^{\left(2\right)}=R_{\mu \nu }{R}^{\mu \nu }=0$. The lowest-order non-vanishing curvature invariant in a curvature expansion is the Kretschmann scalar,

$$K^{\left(3\right)}=\frac{48G_{\mathrm{N}}^2{M}^2}{r^6},$$

(7)

and its divergence at $r=0$ indicates that there is a curvature singularity at the center. The higher-order local curvature invariants can all be expressed in terms of $K^{\left(3\right)}$ following a simple dimensional argument as a direct consequence of the high degree of symmetry of the Schwarzschild spacetime. For instance, except for the numerical prefactor, the relation between $K^{\left(4\right)}$ and $K^{\left(3\right)}$ follows from their mass dimensionality,

$$K^{\left(4\right)}=\frac{1}{\sqrt{48}}{\left(K^{\left(3\right)}\right)}^{3/2}.$$

(8)

Similarly,

$$K^{\left(5\right)}=\frac{1}{\sqrt{12}}{\left(K^{\left(3\right)}\right)}^{3/2},$$

(9)

and finally

$$K^{\left(7\right)}=\frac{1}{4}{\left(K^{\left(3\right)}\right)}^2.$$

(10)

The situation is different for the derivative invariants. While they can still be expressed as a function of $K^{\left(3\right)}$, the black-hole mass M provides an additional mass scale that enters $K^{\left(6\right)}$, such that

$$\begin{array}{cc}{K}^{\left(6\right)}\hfill & =\frac{720G_{\mathrm{N}}^2{M}^2}{r^9}\left(r-2G_{\mathrm{N}}M\right)\hfill \\ \hfill & =\frac{53^{2/3}}{22^{1/3}}{\left(K^{\left(3\right)}\right)}^{4/3}{\left(G_{\mathrm{N}}M\right)}^{-2/3}-\frac{5\sqrt{3}}{8}{\left(K^{\left(3\right)}\right)}^{3/2}.\hfill \end{array}$$

(11)

$K^{\left(6\right)}$ is actually the lowest-order horizon-detecting invariant for the Schwarzschild spacetime, $\left(K^{\left(6\right)}{|}_{r=2G_{\mathrm{N}}M}\right)=0$, see [51].

The Kerr black hole is non-static and only axially symmetric due to its nonzero specific angular momentum $a=J/M$. It will be advantageous for the purpose of efficient evaluation of the curvature invariants [52] to work in rational polynomial coordinates, where $cos\left(\theta \right)=\chi$, such that the line element is given by

$$\begin{array}{cc}\mathrm{d}{s}^2\hfill & =-(1-\frac{2G_{\mathrm{N}}Mr}{{\rho }^2})\mathrm{d}{t}^2-\frac{4G_{\mathrm{N}}Mar(1-{\chi }^2)}{{\rho }^2}\mathrm{d}t\mathrm{d}\varphi +\frac{{\rho }^2}{\Delta }\mathrm{d}{r}^2+\frac{{\rho }^2}{1-{\chi }^2}\mathrm{d}{\chi }^2\hfill \\ \hfill & +\left(1-{\chi }^2\right)(r^2+a^2+2G_{\mathrm{N}}M{a}^{2}r\frac{(1-{\chi }^2)}{{\rho }^2})\mathrm{d}{\varphi }^2,\hfill \end{array}$$

(12)

where

$$\Delta =\Delta \left(r\right)=r^2-2G_{\mathrm{N}}Mr+a^2,$$

(13)

and

$${\rho }^2={\rho }^2(r,\chi )=r^2+a^2{\chi }^2.$$

(14)

Just as in the Schwarzschild case, the first non-vanishing curvature invariant is the Kretschmann scalar, given by

$$K^{\left(3\right)}=\frac{48{G_{\mathrm{N}}}^2{M}^2}{{(r^2+a^2{\chi }^2)}^6}\left(r^6-15r^4{a}^2{\chi }^2+15r^2{a}^4{\chi }^4-a^6{\chi }^6\right).$$

(15)

The ring-singularity is located at $r=0$ in the equatorial plane at $\chi =0$, see Figure 1. In particular, there is a sequence of positive and negative curvature regions around the singularity. Taking the Schwarzschild limit $a\to 0$, the curvature becomes positive everywhere and diverges strongly in the entire $r=0$ surface.

The values of the non-vanishing dimension-six operators are given by

$$K^{\left(4\right)}=\frac{48G_{\mathrm{N}}^3{M}^3}{{(r^2+a^2{\chi }^2)}^9}r\left(r^8-36r^6{a}^2{\chi }^2+126r^4{a}^4{\chi }^4-84r^2{a}^6{\chi }^6+9a^8{\chi }^8\theta \right),$$

(16)

$$K^{\left(5\right)}=2K^{\left(4\right)},$$

(17)

$$K^{\left(6\right)}=\frac{720G_{\mathrm{N}}^2{M}^2}{{(r^2+a^2{\chi }^2)}^9}\left(r^8-28r^6{a}^2{\chi }^2+70r^4{a}^4{\chi }^4-28r^2{a}^6{\chi }^6+a^8{\chi }^8\right)(r(r-2G_{\mathrm{N}}M)+a^2{\chi }^2).$$

(18)

They all exhibit the divergence characteristic for the Kerr spacetime, $K^{\left(i\right)}\to \infty$ for $3\le i\le 6$ and $r\to 0$ at $\chi =0$. In contrast to the Schwarzschild case, $K^{\left(6\right)}$ is no longer horizon-detecting; instead, a particular combination of yet higher-order invariants plays this role [51].

Finally, the dimension-six operator $K^{\left(7\right)}$ is given by

$$K^{\left(7\right)}=\frac{576G_{\mathrm{N}}^4{M}^4}{{(r^2+a^2{\chi }^2)}^{12}}\left(r^{12}-66a^2{r}^{10}{\chi }^2+495a^4{r}^8{\chi }^4-924a^6{r}^6{\chi }^6+495a^8{r}^4{\chi }^8-66a^{10}{r}^2{\chi }^{10}+a^{12}{\chi }^{12}\right).$$

(19)

Further, we consider the imploding Vaidya spacetime [53,54,55,56] as an example for a singular non-vacuum spacetime. In Eddington–Finkelstein coordinates its line element can be expressed as

$$\mathrm{d}{s}^2=-f\left(r\right)\mathrm{d}{v}^2+2\mathrm{d}v\mathrm{d}r+r^2(\mathrm{d}{\theta }^2+{sin}^2\theta \mathrm{d}{\varphi }^2),$$

(20)

where

$$f(r,v)=1-\frac{2G_{\mathrm{N}}M\left(v\right)}{r}.$$

(21)

Here $M\left(v\right)$ is the mass function depending on the advanced time v. In particular, the spacetime is non-static and can be used to describe the formation of a black hole during the gravitational collapse of a radiative source [55,56]. It represents an exact solution to the Einstein equations with energy–momentum tensor $T^{\mu \nu }=\rho k^{\mu }{k}^{\nu }$, where $\rho =\left({\partial }_{v}M\left(v\right)\right)/4\pi r^2$ is the energy density. The fluid’s four-velocity $k_{\mu }$ is a null-vector for radiation, thereby implying that the energy-momentum tensor has a vanishing trace. Therefore, taking the trace of the field equations with vanishing cosmological constant shows that the Ricci scalar is zero,

$$K^{\left(1\right)}=0,$$

(22)

and also

$$K^{\left(2\right)}=0.$$

(23)

On the other hand, the Kretschmann scalar is given by

$$K^{\left(3\right)}=\frac{48{G_{\mathrm{N}}}^2{M}^2\left(v\right)}{r^6}.$$

(24)

Depending on the mass function, the spacetime may contain a singularity at the center. The higher-order, local invariants are related to $K^{\left(3\right)}$ according to dimensional analysis,

$$\begin{array}{ccc}\hfill K^{\left(4\right)}& =& {48}^{-1/2}{\left(K^{\left(3\right)}\right)}^{3/2},\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill K^{\left(5\right)}& =& {12}^{-1/2}{\left(K^{\left(3\right)}\right)}^{3/2},\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill K^{\left(7\right)}& =& \frac{1}{4}{\left(K^{\left(3\right)}\right)}^2.\hfill \end{array}$$

(27)

Finally, the derivative invariant $K^{\left(6\right)}$ is the first invariant that depends on the derivative of the mass function,

$$\begin{array}{ccc}\hfill K^{\left(6\right)}& =& -\frac{144G_{\mathrm{N}}M\left(v\right)}{r^9}\left(10G_{\mathrm{N}}M{\left(v\right)}^2-5G_{\mathrm{N}}M\left(v\right)r+2r^2{M}^{\prime }\left(v\right)\right).\hfill \end{array}$$

(28)

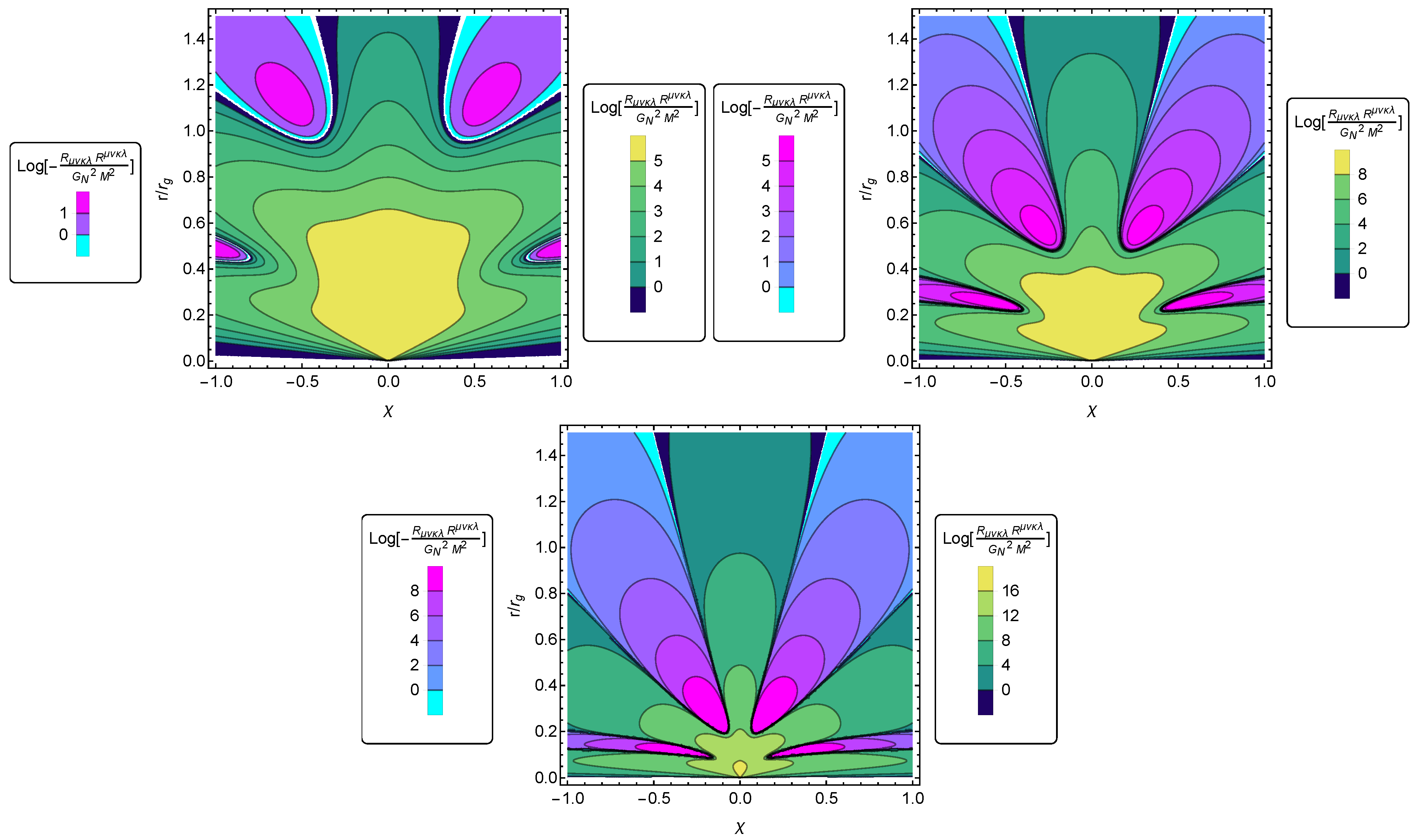
2.2. Regular Black-Hole Spacetimes

Regular black-hole spacetimes are currently being explored in terms of particular quantum-gravity approaches [57,58,59,60,61,62,63,64] as well as from a more agnostic point of view [65,66,67,68,69]. This interest is in part triggered by novel observational opportunities, most importantly, gravitational wave observations from binary black-hole mergers [1], as well as imaging with the Event Horizon Telescope [70]. Given that due to their curvature singularities the observed black holes cannot be the Schwarzschild/Kerr solution from GR (even though observationally, deviations have not been detected yet and are, in fact, expected to be tiny outside the horizon based on a simple dimensional argument (see, however, [71] for alternatives), it becomes key to understand the true nature of the observed objects. Here, we are motivated by the possibility that they could be regular black-hole spacetimes. This requires that these provide a potentially finite contribution to the Lorentzian gravitational path integral and are not suppressed due to a divergent action.

As paradigmatic cases, we will focus on Hayward and Dymnikova spacetimes, as well as the finite-spin counterpart of a Hayward black hole. Within General Relativity, the stability of the inner horizons of such black-hole spacetimes has been discussed in [72,73]; we will ignore such dynamical questions here and only treat these spacetimes as some of many that have to be included in the path integral.

The Hayward black-hole spacetimes [67] are given by the line element (5) with lapse function

$$f\left(r\right)=1-2G_{\mathrm{N}}M\left(\frac{r^2}{r^3+2g^3}\right),$$

(29)

where g is a positive parameter. It plays the role of a transition scale between the Schwarzschild spacetime approximated at large radial distances and de Sitter space for small radii, $r\ll g$. At the center of the spacetime, curvature invariants are regular. The curvature invariants are given by

$$\begin{array}{ccc}\hfill K^{\left(1\right)}& =& \frac{24G_{\mathrm{N}}M}{{(r^3+2g^3)}^3}(-g^3{r}^3+4g^6),\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill K^{\left(2\right)}& =& \frac{288G_{\mathrm{N}}^2{M}^2{g}^6}{{(r^3+2g^3)}^6}\left(5r^6-4r^3{g}^3+8g^6\right),\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill K^{\left(3\right)}& =& \frac{48G_{\mathrm{N}}^2{M}^2}{{(r^3+2g^3)}^6}\left(r^{12}-8r^9{g}^3+72r^6{\gamma }^6-16r^3{g}^9+32g^{12}\right),\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill K^{\left(4\right)}& =& \frac{48G_{\mathrm{N}}^3{M}^3}{{(r^3+2g^3)}^7}\left(r^3-g^3\right)·{\left(r^3-4g^3\right)}^3,\hfill \end{array}$$

(33)

$$K^{\left(5\right)}=\frac{96G_{\mathrm{N}}^3{M}^3}{{(r^3+2g^3)}^9}\left(r^3-4g^3\right)·\left(r^{15}-14g^3{r}^{12}+388r^9{g}^6-424r^6{g}^9+32r^3{g}^{12}-64g^{15}\right),$$

(34)

$$K^{\left(6\right)}=\frac{144G_{\mathrm{N}}^2{M}^2{r}^4}{{(r^3+2g^3)}^9}\left(r^2(r-2G_{\mathrm{N}}M)+2g^3\right)\left(5r^{12}-80r^9{g}^3+1200r^6{g}^6-1856r^3{g}^9+2432g^{12}\right).$$

(35)

Thus, the curvature remains finite at the center and assumes the de Sitter value

$$\underset{r\to 0}{lim}{K}^{\left(3\right)}=\frac{24{G_{\mathrm{N}}}^2{M}^2}{g^6}.$$

(36)

As long as the de Sitter radius remains small enough, $g/r_g\le {(4/3\sqrt{3})}^{2/3}$, an outer event horizon continues to exist. It is worth noting that arguments from quantum gravity have been used to motivate Hayward black holes, see, e.g., [74,75,76]. For instance, the asymptotic-safety-inspired approach to resolve singularities based on a Renormalization Group improvement of classical line elements [57,61,62,77,78] results in an effective Hayward spacetime.

Next, we consider the static and spherically symmetric Dymnikova spacetime with the line element (5) and r-dependent mass function

$$M\left(r\right)=M(1-e^{-\frac{r^3}{2g^3}}).$$

(37)

Here, we only list two selected examples from the set of curvature invariants to highlight the difference to the Schwarzschild spacetime. The Ricci and Kretschmann scalar are non-zero but finite,

$$K^{\left(1\right)}=\frac{3G_{\mathrm{N}}M}{2g^6}{e}^{-\frac{r^2}{2g^3}}(-3r^3+8g^3),$$

(38)

$$K^{\left(3\right)}=\frac{3G_{\mathrm{N}}^2{M}^2}{4r^6{g}^{12}}\left(27r^{12}-48\left(-2+e^{\frac{r^3}{2g^3}}\right)r^6{g}^6-64\left(-1+e^{\frac{r^3}{2g^3}}\right)r^3{g}^9+64{\left(-1+e^{\frac{r^3}{2g^3}}\right)}^2{g}^{12}\right).$$

(39)

At the center, the curvature reduces to that of de Sitter space, just as for the Hayward spacetime (36), whereas it is asymptotically Schwarzschild at large r. The Dymnikova metric has also been motivated as a model for black holes in asymptotically safe gravity [63].

Our final example for regular black holes is the finite-spin counterpart of a Hayward black hole. It is obtained by the application of the Newman–Janis algorithm to the static Hayward spacetime, see [79,80]. It results in a metric given by the Kerr-metric Equation (12) with r-dependent mass function,

$$M\left(r\right)=M\left(\frac{r^3}{r^3+2g^3}\right).$$

(40)

The resulting spacetime is regular everywhere,

$$K^{\left(1\right)}=\frac{24G_{\mathrm{N}}M{g}^3}{(r^2+a^2{\chi }^2){(r^3+2g^3)}^3}{r}^2(-r^3+4g^3),$$

(41)

$$\begin{array}{cc}{K}^{\left(2\right)}\hfill & =\frac{288G_{\mathrm{N}}^2{M}^2{r}^4{g}^6}{{(r^3+2g^3)}^6{(2r^2+a^2{\chi }^2)}^4}·(r^4(8g^6-4g^3{r}^3+5r^6)+4r^2{a}^2{\chi }^2(4g^6-5g^3{r}^3+r^6)\hfill \\ \hfill & +a^4{\chi }^4{(r^3-4g^3)}^2),\hfill \end{array}$$

(42)

and

$$\begin{array}{cc}{K}^{\left(3\right)}\hfill & =\frac{48{G_{\mathrm{N}}}^2{M}^2}{{(r^2+a^2{\chi }^2)}^6{(r^3+2g^3)}^6}(32r^{12}{(r^3+2g^3)}^4-48r^{10}(r^2+a^2{\chi }^2){(r^3+2g^3)}^3(r^3+4g^3)\hfill \\ \hfill & +12g^6{(r^3-4g^3)}^2{r}^4{(r^2+a^2{\chi }^2)}^4+2r^8{\left(r^2+a^2{\chi }^2\right)}^2{(r^3+2g^3)}^2(9r^6+76g^3{r}^3+212g^6)\hfill \\ \hfill & -r^6{(r^2+a^2{\chi }^2)}^3(r^3+2g^3)\left(r^9+6g^3{r}^6+72g^6{r}^3+416g^9\right)).\hfill \end{array}$$

(43)

We do not provide explicit expressions for the higher-order invariants due to their lengthiness.

At the spacetime points where the Kerr metric exhibits a singularity, $(r,\chi )\to (0,0)$, the curvature remains finite. However, the values of some of the curvature invariants at $(r=0,\chi =0)$ depend on how this point is approached, see also [68],

$$\begin{array}{cc}\hfill \underset{r\to 0}{lim}\underset{\chi \to 0}{lim}{K}^{\left(1\right)}=& \frac{12G_{\mathrm{N}}M}{g^3},\hfill \\ \hfill \underset{\chi \to 0}{lim}\underset{r\to 0}{lim}{K}^{\left(1\right)}=& 0.\hfill \end{array}$$

(44)

A similar behavior can be observed for $K^{\left(2\right)},K^{\left(3\right)},K^{\left(4\right)}$ and $K^{\left(5\right)}$. On the other hand, $K^{\left(6\right)}\to 0$ as $r\to 0$, independent of whether one restricts to the equatorial plane first.

Figure 2 shows the Kretschmann curvature for a finite choice of the rotation parameter a and the Hayward parameter g. For smaller values of the spin, the contour areas of constant curvature extend along with larger ranges of the angular coordinate. Thus, spherical symmetry is approximated.

At finite values of the spin parameter, smaller values of the Hayward parameter lead to a strong increase of the absolute value of the Kretschmann scalar along the radial and angular direction towards the critical point $(r,\chi )=(0,0)$. This is consistent with the Kerr singularity occurring for $g\to 0$. At the same time, regions of negative Kretschmann scalar move in towards $(r,\chi )=(0,0)$, cf. Figure 3.

3. Singularity-Resolving Dynamics

In the following, we work with a gravitational action of the form

$$S\left[g\right]=\sum _{i=1}^N{g}_i{\int }_V{\mathrm{d}}^{4}x\sqrt{-g}{K}^{\left(i\right)},$$

(45)

where the $g_i$ denote the corresponding couplings. We will start with the simple choice $S=S_{\mathrm{EH}}$, for which $N=1$, and then include progressively higher invariants, until we find that the spacetime integral results in a divergence. In other words, we will use the main idea from [4] in a slightly different way: demanding that singular spacetimes exhibit a divergence allows us to differentiate between different candidates for gravitational actions.

Here, we are not interested in divergences that arise from the infrared (IR), i.e., large distances, such as one would encounter when integrating the spacetime volume for the entire Minkowski spacetime. Instead, we will introduce an appropriate IR cutoff, indicated by the subscript V in the spacetime integral in Equation (45). In the presence of symmetries, an integration over a non-compact direction associated with a Killing vector trivially results in a (potentially IR-divergent) prefactor, but carries no information on dynamical singularity resolution. Therefore, we will leave out the corresponding integration. For instance, we drop the time integration in the case of a static or stationary metric, since it can be split-off trivially from the integral over curvature invariants, and leads to an IR divergence unless a finite boundary is introduced. Any such constants and/or factors arising from these integrations are omitted in the following. We only carry out the integration over the coordinates the curvature invariant K depends on.

For the spherically symmetric case, all curvature invariants depend on the radial distance to the origin only, i.e., in our choice of coordinates $K^{\left(i\right)}=K^{\left(i\right)}\left(r\right)$. On this basis, we define the functions

$${S_{\mathrm{sph}}}^{\left(i\right)}(r_{\mathrm{UV}},r_{\mathrm{IR}})={\int }_{r_{\mathrm{UV}}}^{r_{\mathrm{IR}}}\mathrm{d}{r}^{\prime }{r}^{\prime 2}{K}^{\left(i\right)}\left(r^{\prime }\right).$$

(46)

The integral runs from a UV cutoff, denoted by $r_{\mathrm{UV}}$, to an IR cutoff, $r_{\mathrm{IR}}$. It will turn out that the limit $r_{\mathrm{IR}}\to \infty$ can be taken trivially, as all spacetimes we consider are asymptotically flat and, therefore, the upper integration boundary does not contribute. We are interested in the limit $r_{\mathrm{UV}}\to 0$, where curvature singularities occur in classical black-hole spacetimes which may lead to divergences in the corresponding actions.

For the axially symmetric case one has to be more careful, since the singularity in the Kerr spacetime lies at $r\to 0$ and $\chi \to 0$, i.e., in the middle of the integration region for the $\chi$-integral. Accordingly, we define the action as

$$S_{\mathrm{ax}}^{\left(i\right)}(r_{\mathrm{UV}},r_{\mathrm{IR}},ϵ)={\int }_{r_{\mathrm{UV}}}^{r_{\mathrm{IR}}}d{r}^{\prime }\left({\int }_{-1}^{-ϵ}d{\chi }^{\prime }(r^{\prime 2}+a^2{\chi }^2)K^{\left(i\right)}(r^{\prime },{\chi }^{\prime })+{\int }_{ϵ}^{1}d{\chi }^{\prime }(r^{\prime 2}+a^2{\chi }^2)K^{\left(i\right)}(r^{\prime },{\chi }^{\prime })\right).$$

(47)

The limits $r_{\mathrm{UV}}\to 0$ and $ϵ\to 0$ have to be taken with some care, while the limit $r_{\mathrm{IR}}\to \infty$ is again trivial due to asymptotic flatness.

The values of the Functions (46) and (47) in general carry non-zero mass dimension, since they only contain the salient part of the action integral and we do not account for the dimensionful coupling constants in front of the curvature invariants in the Lagrangian. The mass dimensions of our action functions depend on the curvature invariant $K^{\left(i\right)}$. In the following, (46) and (47) are nevertheless referred to as the ’action functions’.

3.1. Einstein–Hilbert Dynamics

We first focus on the Einstein–Hilbert action, i.e., we set $N=1$ and consider only $K^{\left(1\right)}=R$ in the action (45).

For a vacuum solution to the Einstein equations with vanishing cosmological constant, the Ricci scalar vanishes, thus, Ricci flatness applies to the Schwarzschild and the Kerr black hole. For the imploding Vaidya spacetime, the four-velocity of the ingoing radiation is a null-vector, such that the Ricci scalar also vanishes. Therefore an Einstein–Hilbert dynamics is ruled out as a viable choice to enable the destructive interference of all singular black-hole metrics in the path integral.

Instead, we are led to conclude that terms beyond the Ricci scalar should be added to the microscopic gravitational action, in order to provide a potential mechanism for destructive interference of singular spacetimes. Thus, there are two independent lines of arguments against the Einstein–Hilbert action as the microscopic action for gravity. First, it does not give rise to an asymptotically free or safe theory, instead, requiring the introduction of a finite new-physics scale, as also indicated by its perturbative non-renormalizability [7,8,9]. Second, it is insufficient to suppress singular cosmological spacetimes [4], and as argued here, singular black-hole spacetimes.

3.2. Curvature-Squared Dynamics

Accordingly, higher-derivative terms should be included in the action. In this subsection, we study the impact of curvature-squared invariants on the behavior of the action around the singularity. Due to the Gauss–Bonnet identity in four dimensions, the combination $\sqrt{-g}(R_{\mu \nu \kappa \lambda }{R}^{\mu \nu \kappa \lambda }-4R_{\mu \nu }{R}^{\mu \nu }+R^2)$ forms a total derivative and can be integrated to provide a topological invariant, which we do not consider in our action. Thus, we limit ourselves to adding $K^{\left(2\right)}$ and $K^{\left(3\right)}$ to the Einstein–Hilbert action. Then the action (45) becomes

$$\begin{array}{c}\hfill S_{\mathrm{quad}}\left[g\right]=\int {\mathrm{d}}^{4}x\sqrt{-g}\left(\frac{K^{\left(1\right)}}{16\pi G_{\mathrm{N}}}+g_2{K}^{\left(2\right)}+g_3{K}^{\left(3\right)}\right).\end{array}$$

(48)

For black-hole metrics which are solutions to the Einstein equations, all but the last term in Equation (48) vanish; thus we focus on the Kretschmann scalar, $K^{\left(3\right)}$. For the Schwarzschild black hole, the action Function (46) diverges in the vicinity of $r=0$, since,

$$\underset{r_{\mathrm{UV}}\to 0}{lim}{S_{\mathrm{sph}}}^{\left(3\right)}(r_{\mathrm{UV}},r_{\mathrm{IR}}\to \infty )=\underset{r_{\mathrm{UV}}\to 0}{lim}\frac{16{G_{\mathrm{N}}}^2{M}^2}{r_{\mathrm{UV}}^3}.$$

(49)

For the Vaidya metric, the integral over the advanced time only contributes by an overall prefactor to the spacetime integral. Therefore the dependence of the action on the radial coordinate is the same as for the Schwarzschild spacetime, resulting in a UV divergence and a corresponding suppression in the path-integral.

To highlight that there is indeed destructive interference based on this divergence, we consider a particular class of deviations from Schwarzschild, which are parameterized by an r-dependent mass function $M\left(r\right)$. We assume that this function can be Taylor-expanded around the origin,

$$M\left(r\right)=\sum _{i=i_{\min }}{r}^i{m}_{\left(i\right)},$$

(50)

with $m^{\left(i\right)}$ the corresponding Taylor coefficients. Herein, none of the coefficients of the Taylor expansion is a priori related to the ADM mass, since the latter is measured at infinity, and depends on $M\left(r\right)$ away from the origin. Thus, various black-hole spacetimes (which are off-shell in GR), could feature the same ADM mass, but be parameterized by varying Taylor coefficients $m_{\left(i\right)}$. For such a parameterization, the corresponding path integral over this restricted configuration space ${\mathcal{C}}_M$ can be written as

$$\int \mathcal{D}{g}_{\mu \nu }{|}_{{\mathcal{C}}_M}=\int {\Pi }_{i}d{m}_{\left(i\right)},$$

(51)

with an appropriate constraint on the $m_{\left(i\right)}$ that we do not work out here since it does not matter for our argument. The leading-order term in $S_{\mathrm{sph}}^{\left(3\right)}$ for $r_{\mathrm{UV}}\to 0$ is of the form

$$S_{\mathrm{sph}}^{\left(3\right)}(r_{\mathrm{UV}},r_{\mathrm{IR}})\sim \frac{G_{\mathrm{N}}^2}{r_{\mathrm{UV}}^3}\left(48m_{\left(0\right)}^2+32m_{\left(0\right)}{m}_{\left(1\right)}{r}_{\mathrm{UV}}+16m_{\left(1\right)}^2{r}_{\mathrm{UV}}^2+32m_{\left(1\right)}{m}_{\left(2\right)}{r}_{\mathrm{UV}}ln(r_{\mathrm{UV}}/r_{\mathrm{IR}})\right)+\mathcal{O}\left(r_{\mathrm{UV}}\right).$$

(52)

Thus, for a large class of black-hole spacetimes, which are off-shell configurations with respect to GR, a UV divergence in the action is present. Only such spacetimes, in which $i_{\min }=2$ in Equation (50), i.e., those for which curvature invariants are not singular enough, display a finite action. The fact that the configuration parameterized by $M\left(r\right)$ are off-shell within GR is immaterial for our considerations. It highlights that the divergence of $S_{\mathrm{sph}}^{\left(3\right)}$ on the Schwarzschild spacetime is not an isolated divergence in configuration space. Instead, a large family of metrics for which deviations from Schwarzschild are encoded in $M\left(r\right)$, feature the same divergence, such that destructive interference between these configurations could happen in the path integral. In particular, within the restricted configuration space given by Equation (51), we find an integral of the form $\int d{m}_{\left(1\right)d{m}_{\left(0\right)}}{e}^{i\left({\alpha }_0{m}_{\left(0\right)}+{\alpha }_1{m}_{\left(1\right)}\right)}$, with ${\alpha }_{0,1}$ diverging factors following from Equation (52). These rapidly varying phase factors lead to destructive interference between the spacetimes in this restricted configuration space.

Alternatively, one may consider off-diagonal elements in the metric, encoding perturbations in the spin-2-mode, i.e., gravitational waves. The result is analogous to the case of $M\left(r\right)$ that we just considered: As long as the perturbations do not lift the central curvature singularity of the spacetime, it will result in a divergence of the higher-derivative action. Therefore, the corresponding perturbed black-hole spacetimes may interfere destructively in the path integral.

Let us also add that for the additional singular black-hole metrics that appear as the solution to the classical equations of motions in curvature-squared gravity, the Kretschmann scalar scales like $r^{-6}$ (for the so-called (1,-1)-family ) and like $r^{-8}$ (for the so-called (2,2) family) near the origin, respectively [49,50], while the volume element scales like $r^2$. Accordingly, an action containing $K^{\left(3\right)}$ will feature a UV divergence on these solutions.

Next, we consider the Kerr metric. Let us first show the result of integrating $\sqrt{g}{K}^{\left(3\right)}$ in the equatorial plane, where

$$\begin{array}{c}\hfill {\int }_{r_{\mathrm{UV}}}^{r_{\mathrm{IR}}\to \infty }dr\sqrt{-g}{K}^{\left(3\right)}{|}_{\chi =0}=\frac{16G_{\mathrm{N}}^2{M}^2}{r_{\mathrm{UV}}^3},\end{array}$$

(53)

which diverges as $r_{\mathrm{UV}}\to 0$. We expect to rediscover this divergence once we also integrate over $\chi$, where all angular directions except $\chi =0$ are expected to provide a non-singular contribution to the action function. Due to the singularity in the equatorial plane, we have to split the integral over the Kretschmann scalar as in Equation (47) and obtain:

$$\begin{array}{cc}\underset{r_{\mathrm{UV}}\to 0}{\lim }\underset{ϵ\to 0}{\lim }{S}_{\mathrm{ax}}^{\left(3\right)}(r_{\mathrm{UV}},\infty ,ϵ)\hfill & =16G_{\mathrm{N}}^2{M}^2\underset{r_{\mathrm{UV}}\to 0}{\lim }\underset{ϵ\to 0}{\lim }(\frac{r_{\mathrm{UV}}^3-r_{\mathrm{UV}}{a}^2}{{(r_{\mathrm{UV}}^2+a^2)}^3}-ϵr_{\mathrm{UV}}\frac{r_{\mathrm{UV}}^2-a^2{ϵ}^2}{{(r_{\mathrm{UV}}^2+a^2{ϵ}^2)}^3}\hfill \\ \hfill & +\frac{r_{\mathrm{UV}}^3-r_{\mathrm{UV}}{a}^2}{{(r_{\mathrm{UV}}^2+a^2)}^3}-ϵr_{\mathrm{UV}}\frac{r_{\mathrm{UV}}^2-a^2{ϵ}^2}{{(r_{\mathrm{UV}}^2+a^2{ϵ}^2)}^3}),\hfill \end{array}$$

(54)

where the contributions vanish in the limit $r_{\mathrm{UV}}\to 0$ except for parts of the contributions from the boundary that approaches the ring-singularity. The vanishing of the remaining contributions is due to the fact that the Kretschmann scalar changes sign between $\chi =-1$ and $\chi =1$ several times, cf. Figure 1. In the above expressions, taking the naive limits $r_{\mathrm{UV}}\to 0$ at finite $ϵ$ or $ϵ\to 0$ at finite $r_{\mathrm{UV}}$ results in a vanishing result. To properly account for the effects of the ring singularity, the limits $ϵ\to 0$ and $r_{\mathrm{UV}}\to 0$ should be taken concertedly, i.e., we define $r_{\mathrm{UV}}=\gamma ϵ$ with some finite $\gamma$, such that taking $ϵ\to 0$ allows us to approach the ring-singularity. As a result, we obtain

$$\begin{array}{ccc}\hfill \underset{ϵ\to 0}{\lim }{S}_{\mathrm{ax}}^{\left(3\right)}(\gamma ϵ,\infty ,ϵ)& =& \underset{ϵ\to 0}{\lim }32\gamma G_{\mathrm{N}}^2{M}^2\frac{{\gamma }^2-a^2}{{({\gamma }^2-a^2)}^3}\frac{1}{{ϵ}^2}.\hfill \end{array}$$

(55)

Therefore, we conclude that the inclusion of the Kretschmann scalar in the Lorentzian action very likely provides a mechanism to dynamically suppress curvature singularities. To confirm that this is indeed the case in the axisymmetric case, deviations from Kerr may be explored, in a similar way to our study of deviations from Schwarzschild. As we do not expect that the change in Killing vectors changes the general mechanism, but simply makes the calculation more lengthy, we do not explicitly show that deviations from Kerr (some of which can be parameterized by considering $M\to M(r,\theta )$) also result in a divergent action.

Conversely, regular black-hole spacetimes should not be ruled out from the path integral. In the following, we therefore verify the finiteness of the integral over the curvature of the regular black-hole spacetimes. This must be independent of the chosen boundary conditions. In particular, the action function for regular black holes must be regular at the point where the Schwarzschild and Kerr spacetimes are singular.

The action Function (46) with the Kretschmann scalar of the static Hayward black hole assumes the form

$${S_{\mathrm{sph}}}^{\left(3\right)}\left(r_{\mathrm{UV}}\right)=\frac{16{G_{\mathrm{N}}}^2{M}^2}{5{(r_{\mathrm{UV}}^3+2g^3)}^5}\left(5r_{\mathrm{UV}}^{12}+120g^6{r}_{\mathrm{UV}}^6+100g^9{r}_{\mathrm{UV}}^3+72g^{12}\right).$$

(56)

It is evident that a non-zero Hayward parameter g ensures a finite and non-zero value of the action function when evaluated over the entire r-range,

$$\underset{r_{\mathrm{UV}}\to 0}{lim}{S_{\mathrm{sph}}}^{\left(3\right)}\left(r_{\mathrm{UV}}\right)=\frac{36{G_{\mathrm{N}}}^2{M}^2}{5g^3}.$$

(57)

For the Dymnikova-spacetime, we obtain a similar result,

$$\underset{r_{\mathrm{UV}}\to 0}{lim}{S_{\mathrm{sph}}}^{\left(3\right)}\left(r_{\mathrm{UV}}\right)=\frac{27{G_{\mathrm{N}}}^2{M}^2}{2g^3}.$$

(58)

Let us now go beyond the highly symmetry-restricted case and consider axisymmetric, regular spacetimes. By considering $S_{\mathrm{ax}}^{\left(3\right)}$ for the rotating Hayward black hole, we can confirm its finiteness and check the Kerr and Schwarzschild results by investigating the appropriate limits of the parameters a and g, cf. Figure 4. There, the expected finiteness of $S_{\mathrm{ax}}^{\left(3\right)}(0,\infty ,0)$ is confirmed numerically for finite g.

These results confirm that including additional terms quadratic in the curvature tensor does not affect the finiteness of the action for regular spacetimes, as expected.

An action that is divergent on a given configuration is expected to result in destructive interference in the path integral, suppressing the contribution of that field configuration. Thus, the results of this subsection show that a curvature-squared action could suppress axi-symmetric and spherically symmetric, singular black-hole spacetimes. At the same time, such an action remains finite for regular black-hole spacetimes, ensuring that they could contribute to the path integral. Here, we do not investigate whether such spacetimes correspond to a saddle-point of the path integral. In particular, such a question can only be meaningfully investigated within a matter-gravity path integral, going beyond the scope of this work.

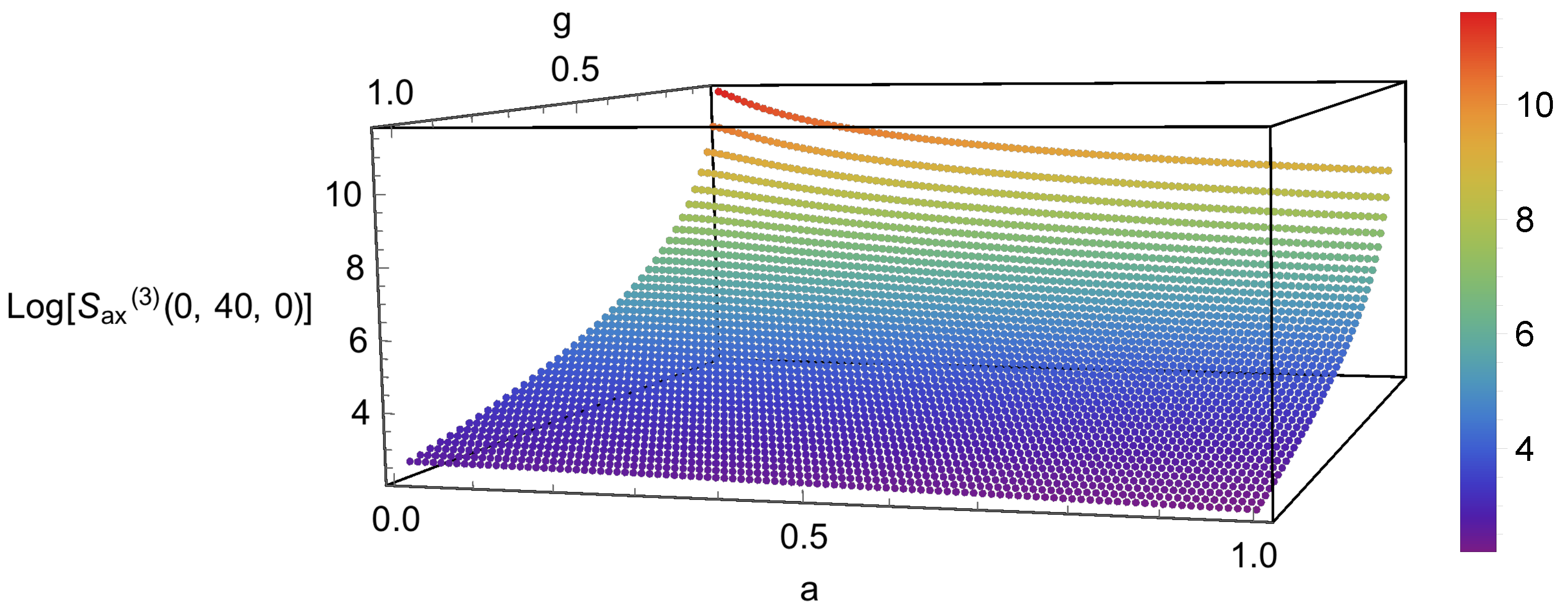
3.3. Beyond Four-Derivative Dynamics

In the previous section, we found that the inclusion of the Kretschmann scalar in the action is sufficient to exclude singular black-hole spacetimes from the path-integral based on the requirement of a finite action for non-zero contributions. Following a principle of canonical power counting, this would be the first term expected to occur in the dynamics when going beyond the Einstein–Hilbert action. Yet, the microscopic gravitational action is not bound to follow canonical power counting, and the coupling of the Kretschmann scalar might vanish in a given quantum gravity setting. This motivates us to go beyond the four-derivative terms in the dynamics.

Interestingly, within the asymptotic-safety program, there are indications that the coupling associated to the invariant $K^{\left(5\right)}$, the Goroff–Sagnotti term, is irrelevant [81], while there might be a gravitational universality class at which other curvature-cubed terms might come with relevant couplings [82].

We expect that an action built from any higher-order curvature invariant that does neither contain R nor $R_{\mu \nu }$ will exhibit an ultraviolet divergence, when evaluated on a singular black-hole spacetime. To provide some evidence for this expectation, we consider a complete basis at order 6 in derivatives and highlight the behavior of two order-8 invariants.

For the Schwarzschild black hole, the integrals over $K^{(4,5,7,8)}$ all exhibit a divergence in the limit $r_{\mathrm{UV}}\to 0$ which follows their dimensionality:

$$\begin{array}{ccc}\hfill S_{\mathrm{sph}}^{(4,5)}(r_{\mathrm{UV}},\infty )& \sim & \frac{G_{\mathrm{N}}^3{M}^3}{r_{\mathrm{UV}}^6},\hfill \end{array}$$

(59)

$$\begin{array}{ccc}\hfill S_{\mathrm{sph}}^{(7,8)}(r_{\mathrm{UV}},\infty )& \sim & \frac{G_{\mathrm{N}}^4{M}^4}{r_{\mathrm{UV}}^9}.\hfill \end{array}$$

(60)

The horizon-detecting invariant $K^{\left(6\right)}$ features a leading divergence $S_{\mathrm{sph}}^{\left(6\right)}(r_{\mathrm{UV}},\infty )\sim r_{\mathrm{UV}}^{-6}$ and a subleading $r_{\mathrm{UV}}^{-5}$ term.

For the Vaidya spacetime, the action function $S_{\mathrm{sph}}^{(4,5,7,8)}$ follows from the Schwarzschild results Equation (59) and Equation () with the substitution $M\to M\left(v\right)$. As the invariant $K^{\left(6\right)}$ is a horizon-detecting one in the Schwarzschild limit, it depends on $M^{\prime }\left(v\right)$ for the Vaidya case, and the corresponding action function reads

$$S_{\mathrm{sph}}^{\left(6\right)}(r_{\mathrm{UV}},\infty )=\frac{24G_{\mathrm{N}}M\left(v\right)}{r_{\mathrm{UV}}^6}\left(6r_{\mathrm{UV}}M\left(v\right)-10M{\left(v\right)}^2-3r_{\mathrm{UV}}^2{M}^{\prime }\left(v\right)\right).$$

(61)

To calculate the action function $S_{\mathrm{ax}}(r_{\mathrm{UV}},r_{\mathrm{IR}},ϵ)$ for the Kerr spacetime, one should again be careful how to take the limits $ϵ\to 0$ and $r_{\mathrm{UV}}\to 0$ in order to account for the presence of the ring singularity. Thus, we set $r_{\mathrm{UV}}=\gamma ϵ$ for some constant $\gamma >0$, and then take $ϵ\to 0$. In this way, we obtain

$$S_{\mathrm{ax}}^{\left(4\right)}(\gamma ϵ,\infty ,ϵ)=\frac{16}{7}{G}_{\mathrm{N}}^3{M}^3\left(\frac{a^6-21a^4{\gamma }^2+35a^2{\gamma }^4-7{\gamma }^6}{{(a^2+{\gamma }^2)}^6{ϵ}^5}-\frac{1}{a^6}\right)+\mathcal{O}\left(ϵ\right),$$

(62)

$$S_{\mathrm{ax}}^{\left(5\right)}(\gamma ϵ,\infty ,ϵ)=2S_{\mathrm{ax}}^{\left(4\right)},$$

(63)

$$\begin{array}{cc}{S}_{\mathrm{ax}}^{\left(6\right)}(\gamma ϵ,\infty ,ϵ)\hfill & =\frac{96}{7}{G}_{\mathrm{N}}^2{M}^2(\frac{G_{\mathrm{N}}M\left(a^6+21a^4{\gamma }^2-105a^2{\gamma }^4+35{\gamma }^6\right)}{{(a^2+{\gamma }^2)}^6{ϵ}^5}\hfill \\ \hfill & -\frac{7\gamma \left(3a^6-7a^4{\gamma }^2-7a^2{\gamma }^4+3{\gamma }^6\right)}{{(a^2+{\gamma }^2)}^6{ϵ}^4}-\frac{G_{\mathrm{N}}M}{a^6})+\mathcal{O}\left(ϵ\right).\hfill \end{array}$$

(64)

Finally, constructing action functions from the two dimension-eight operators we consider, we do not obtain a finite part in the action function:

$$S_{\mathrm{ax}}^{\left(7\right)}(\gamma ϵ,\infty ,ϵ)=-\frac{128}{5}{G}_{\mathrm{N}}^4{M}^4\gamma \frac{\left(5a^4-10a^2{\gamma }^2+{\gamma }^4\right)\left(a^4-10a^2{\gamma }^2+5{\gamma }^4\right)}{{(a^2+{\gamma }^2{ϵ}^2)}^9{ϵ}^8},$$

(65)

$$\begin{array}{cc}{S}_{\mathrm{ax}}^{\left(8\right)}(\gamma ϵ,\infty ,ϵ)\hfill & =\frac{1}{20}{G}_{\mathrm{N}}^4{M}^4\frac{1}{a^9{\gamma }^8{ϵ}^8}(-\frac{1}{{(a^2+{\gamma }^2)}^9}(1575a^{25}\gamma +13,650a^{23}{\gamma }^3+52,290a^{21}{\gamma }^5\hfill \\ \hfill & +116010a^{19}{\gamma }^7+172,505a^{17}{\gamma }^9+116,100a^{15}{\gamma }^{11}+300,924a^{13}{\gamma }^{13}+166,100a^{11}{\gamma }^{15}\hfill \\ \hfill & +172,505a^9{\gamma }^{17}+116,010a^7{\gamma }^{19}+52,290a^5{\gamma }^{21}+13,650a^3{\gamma }^{23}+1575a{\gamma }^{25})\hfill \\ \hfill & +1575(a^8-{\gamma }^8{ϵ}^8)\mathrm{arccot}\left(\frac{\gamma ϵ}{a}\right)-1575(a^8-{\gamma }^8)\arctan \left(\frac{a}{\gamma }\right)).\hfill \end{array}$$

(66)

As we expected, the inclusion of any of these curvature invariants suffices to render the action divergent and thus provides a dynamical mechanism to resolve black-hole singularities.

4. Conclusions and Outlook

In this paper, we have used a mechanism of dynamical singularity-resolution in black-hole spacetimes to motivate the inclusion of higher-order curvature invariants in the microscopic gravitational action in the Lorentzian path integral. Specifically, we have shown that the inclusion of a complete basis of invariants constructed from the Riemann tensor of mass dimension four leads to a divergent action for the Schwarzschild, Kerr and Vaidya spacetimes. These divergences are associated with large values of the curvature, i.e., to the central curvature singularity. In turn, a divergent action in the Lorentzian path integral corresponds to an infinitely fast oscillation of the quantum-mechanical phase factor and is hence expected to result in a dynamical suppression of the corresponding field configurations through destructive interference. Thus, the presence of higher-order curvature invariants constructed from the Riemann tensor, which reflect the curvature singularities of various black-hole spacetimes, providing a dynamical mechanism to resolve those singularities. Thereby, they fulfill a key requirement for a viable quantum theory of gravity. This is in contrast to the Einstein–Hilbert action, which vanishes when evaluated on these spacetimes, as these are vacuum solutions of GR. In addition to its perturbative renormalizability, its failure to provide a mechanism for dynamical singularity-resolution is a second reason to discard the Einstein–Hilbert action as a candidate for a fundamental action for gravity. Beyond GR, either Stelle’s higher-derivative gravity [15] or asymptotically safe gravity, both of which contain appropriate higher-curvature terms, could fulfill our criterion.

Let us make several comments regarding our results:

(i)

To dynamically suppress singular black-hole spacetimes that are vacuum solutions of Einstein equations, a local action constructed from higher powers of R or $R_{\mu \nu }$ alone is insufficient and invariants built out of the Riemann tensor are required. In turn, a local action containing these further invariants may feature ghosts These could be avoided by including appropriate functions of the curvature invariants [83,84] or might be present, but not result in a physical inconsistency of the theory [18,19]. which would be absent if one would restrict to higher powers in R, only. The latter could be taken as a motivation to focus on $f\left(R\right)$-type of actions for gravity. Here, we provide evidence that $f\left(R\right)$ actions, while potentially providing physically interesting effective descriptions of gravity, fail at a key requirement of quantum gravity, namely dynamical singularity-resolution. In some sense, therefore, the challenge of potential ghosts and the dynamical resolution of singularities appear to be two sides of the same coin.

(ii)

The contribution of black-hole spacetimes to the gravitational path integral has been used to argue that quantum gravity should result in the violation of global symmetries [85,86,87]. The argument hinges on the presence of black-hole spacetimes in the gravitational path integral. As we have argued, this depends on the choice of dynamics. The latter is also key to understand the final state of black-hole evaporation. Our study motivates that under certain circumstances, at least the contribution of certain singular black-hole spacetimes to the gravitational path integral could vanish. This could in turn imply that quantum-gravity approaches which feature such higher-order terms in the action might not generically violate global symmetries. This might for instance include asymptotically safe gravity, where indeed results in Euclidean studies of truncated dynamics for gravity-matter systems do not provide any indications for the violation of global symmetries [88,89].

Our work motivates several potential extensions:

First, our study can be extended to include additional singular black-hole spacetimes, in particular additional models of spherical and non-spherical collapse, in order to investigate whether our proposed mechanism for dynamical singularity-resolution also removes those spacetimes from the path integral. Since perturbations of black-hole spacetimes, i.e., quasinormal modes, do not affect the presence of the singularity, our present study already extends directly to perturbed Kerr and Schwarzschild spacetimes

Second, there is an interesting question to explore in a semi-classical framework: By requiring that regular black-hole spacetimes correspond to a saddle-point of the action, one might find a principle that further distinguishes between the various possible curvature terms.

Third, given a candidate for the microscopic action S in the Lorentzian path integral, motivated by singularity-resolution, one may next ask whether this action provides a different conclusion to the viability of the Hartle-Hawking wavefunction, using the methods in [13,90].

Fourth, changing the underlying symmetries in the path integral, e.g., to foliation-preserving diffeomorphisms, as, e.g., in Horava-Lifshitz gravity [91] (see [92] for a recent review), could require different invariants to be included for singularity-resolution. In this spirit, a comparison of diverse quantum-field-theoretic proposals for gravity which differ in (a) the underlying (gauge) symmetries and/or (b) the choice of fields, see, e.g., [93,94,95,96] for proposals which are classically equivalent to GR, could be illuminating. In particular, demanding destructive interference between singular field configurations could provide a principle to distinguish between different candidate theories.