1. Introduction
Modulation of the electron temperature using periodic HF heating to cause oscillation of ionospheric conductivity and forming the ELF/VLF virtual antenna in the ionosphere was proposed and tested by Willis and Davis [
1] and Getmantsev et al. [
2].
In the last 40 years, with the continuous upgrading of heaters (i.e., ionospheric heating facilities), some methods of improving the efficiency of modulated heating have been proposed and applied such as Beam Painting [
3], Geometric Modulation [
4], Preheating-AM [
5], Dual-Beam HF Modulation [
6], and so on. However, these methods are essentially improved methods based on amplitude modulation (AM), and as such are still electrojet-dependent modulation methods. To excite ELF/VLF waves by modulated heating over a wide range of time and space, some electrojet-independent modulation methods have been proposed, such as Thermal Cubic Nonlinearity Modulation [
7], Ionospheric Current Drive [
8], and Lower Hybrid (LH)-to-whistler Mode Conversion [
9]. There is also a method called beat-wave (BW) modulation [
10,
11], but due to the controversy of its mechanism and the source region of the stimulated ELF/VLF waves, it is not clear whether it is an electrojet-independent method or not. Some scientists [
12,
13,
14,
15,
16,
17,
18] believe that the source region of BW modulation is in the D region and the mechanism of beat-wave modulation is in essence consistent with AM (i.e., thermal nonlinearity) which is an electrojet-dependent modulation method. Others [
19,
20,
21,
22,
23] hold the idea that the source region of BW modulation is in the F region, which means BW modulation is an electrojet-independent modulation method whose mechanism is ponderomotive nonlinearity.
By comparing the excitation efficiency of ELF/VLF waves by AM and BW in each frequency band using HIPAS heating facility, the experimental results showed that the ELF/VLF signal excited by AM is strongest at almost all frequencies, although BW can produce more stable signals under certain circumstances [
24]. Barr and Stubbe [
10] confirmed this conclusion by experiments carried out by EISCAT heating facility. Ma et al. [
18] carried out a series of experiments and found a strong correlation between amplitude and current. These results support the theory that the mechanism of BW is thermal nonlinearity in the D region. On these bases, Fedorenko et al. [
25] analyzed the polarization characteristics of ELF/VLF waves generated by BW at EISCAT and demonstrated that the domination of left-hand mode at a distance of 660 km could be interpreted by the “trapping” effect of the Earth-ionosphere waveguide.
Kuo et al. [
11] proposed that the mechanism of BW is ponderomotive nonlinearity in the F region, which means BW is an electrojet-independent modulation method. Based on this theory, Kuo et al. [
19] conducted experiments and found that BW is more effective than AM in the VLF range. Cohen et al. [
14] also pointed out that BW produces stronger amplitudes than AM when modulated frequency is higher than 5 kHz.
According to the theory of BW by electrojet modulation in the D region, the modulation efficiency decreases with an increase of the modulated frequency [
14], while according to the theory of BW by ponderomotive force in the F region, the modulation efficiency increases with an increase of the modulated frequency [
11].
In summary, mechanism and the source region of BW is still controversial. This paper is to explore this controversy. In this context, physical models are constructed so that AM and BW by electrojet modulation in the D region as well as BW by ponderomotive force in the F region can be simulated respectively; and a new method to identify the mechanism and source region of BW is proposed.
2. Physical Model
2.1. Amplitude Modulation
The essence of AM is to repeat “heating-cooling” process in the ionosphere at a certain ELF/VLF frequency by switching on and off high-power high-frequency radio wave transmitters at this ELF/VLF frequency. Since the ionospheric conductivity is a function of electron temperature, it changes at the same frequency during the “heating-cooling” process, in the presence of ionospheric electric field, the ionospheric electrojet will be modulated and generates ELF/VLF waves. In addition, it is worth noting that the model in this section applies to the D and lower E region below 120 km.
The change of electron temperature can be calculated by electronic energy equation [
26]:
where
is Boltzmann constant;
and
are absorption and loss terms of electronic energy, respectively. The absorption rate is given by [
26]:
where
is the energy flux [
26]:
where
l is the altitude, ERP is the effective radiated power. The absorption coefficient
is given by [
26]:
where
is the angular frequency of the HF wave,
is the velocity of light,
is the imaginary part of the complex refraction index.
The loss of electron energy in the ionosphere is mainly realized by collisions, its mechanism is very complex, mainly including (1) elastic collisions with positive ions and neutral particles; (2) rotational excitation of O
2 and N
2; (3) vibrational excitation of O
2, and N
2; (4) electronic excitation of O; (5) fine structure excitation of O. Detailed expressions are given by [
27].
The change of electron density can be calculated by continuity equation [
28]:
where
is production rate,
is recombination coefficient. In the lower ionosphere, the molecular ions (NO
+ and O
2+) are the most important in recombination process, so
can be expressed as [
28]:
where [X] represents the density of particle X. The diffusion effect of the electron is ignored during the heating process.
The heating and cooling time constants of the electron temperature are ~ms [
5,
26], while the heating and cooling time constants of the electron temperature are several minutes [
5]. In this paper, we mainly focus on stimulating ELF/VLF waves whose frequencies are greater than 1 kHz, which means the heating and cooling periods are less than 1 ms, so the change of electron density is negligible during the modulated heating process. On the other hand, the perturbation of electron density will remain for a long time after preheating, while the electron temperature will return to the initial state in a short time (~ms), therefore, the change of electron density is important while the change of electron temperature is negligible for preheating process as described later in this paper.
The electric current in the ionosphere is [
29]:
where
is the natural electric field,
is the ionospheric conductivity. Two components of the ionospheric conductivity need to be considered in the modulation of electrojet, they are Pedersen conductivity
and Hall conductivity
[
16]:
The first term on the right-hand side represents the electron conductivity, and the second term represents the ion conductivity. In the heating process, the electron temperature rises rapidly and significantly compared to changes in ion temperature so the influence of ion conductivity can be ignored in the modulation process. Changes of electron temperature during “heating-cooling” process act on electron density
, collision frequency between electrons and neutral particles
, and causes periodical variation of conductivity so that oscillating current is generated [
28]:
and are the height-integrated Pedersen and Hall conductivity, respectively. , where and are disturbances of and .
The magnetic field intensity of ELF/VLF waves received from the ground is [
28]:
where
is the horizontal cross-sectional area of the disturbed region.
is the distance from the disturbed region to the receiver on the ground,
is the permeability of free space.
2.2. Beat-Wave Modulation
BW modulation is a modulation technique which transmits two high-frequency continuous waves with frequencies
and
respectively to stimulate ELF/VLF waves with frequency
. There are still controversies about the source region and mechanism of ELF/VLF waves generated by BW. Therefore, two theories about the mechanism of BW are considered: (1) based on the theory of electrojet modulation (BW in the D region) and (2) based on the theory of ponderomotive force (BW in the F region). The first theory is essentially the same as AM (
Section 2.1) and only the change of the power of HF waves during the BW process needs to be taken into consideration [
10]. Therefore, model of BW modulation based on the ponderomotive force [
11] is presented in this section.
The nonlinear beating current density at the beat frequency of the two HF waves is given by [
11]:
where
is the electron gyrofrequency,
is the electron velocity induced by the HF heater,
is the electron density,
represents a VLF bandpass filter.
During the BW modulation process, the heater is split into two sub-arrays, transmitting continuous waves with a frequency difference in the ELF/VLF range, the frequency difference is the BW frequency. The electric field of the total HF heater is given by [
11]:
where “
” represent O-waves and X-waves, respectively.
is the amplitude of each sub-array.
,
is the phase difference between the radiations of the sub-arrays.
and
are the heater radian frequency and wave number, respectively. Electron velocity induced by the heater is given by [
11]:
Substituting Equation (14) into Equation (12), (12) becomes [
11]:
where
, “
” represent O-waves and X-waves respectively, the beating currents generated by X-waves and O-waves have a ratio proportional to
, which means X-waves are more effective to generate the BW current than O-waves. Modeling (15) as a localized time harmonic current source with a gain factor G accounting for the finite size of the current distribution as well as the guiding effect of the geomagnetic field on the VLF wave propagation, then the phasor function
of the vector potential of the ELF/VLF radiation is given by [
11]:
where
is the wave number of the ELF/VLF wave.
Finally, the magnetic field of the ELF/VLF radiation is given by [
11]:
2.3. Model Verification
In this part, we simulate the ELF/VLF wave intensity generated by AM and BW modulation based on the two theories, and compare the results with those in some references to verify the validity of our model. In this paper, all the simulations based on the theory of electrojet modulation are underdense modulated heating, the time step is , the height range is 65–120 km with a spatial resolution of 1 km. All the simulations based on the theory of ponderomotive force are overdense modulated heating, the time step is 0.1 ms, the height range is 120–400 km with a spatial resolution of 10 km × 10 km.
2.3.1. Based on the Theory of Electrojet Modulation
The validity of our physical model was verified by comparing our simulation results with [
16]. The result (as shown in
Figure 1) for comparison with our simulation is that of 20 November 2014, 1200 LT, the location of heating site is 69.6°N, 19.2°E (Tromsø, EISCAT), the parameters of the HF wave are 1.16 GW, X-wave [
16]. It is worth noting that the parameters of the heater above are not the real parameters of EISCAT, actually, they are the parameters of HAARP (High-frequency Active Auroral Research Program) [
14]. This is because Li et al. [
16] want to show the possible results of BW at EISCAT if the heater of EISCAT has the same performance as HAARP. The frequencies of these two continuous waves are
and
where
with modulation frequencies
from 1 to 10 kHz. The parameters of background ionosphere and atmosphere are from IRI-2016 and NRLMSISE-00 model, respectively. The foE and foF2 are 1.48 MHz and 7.57 MHz respectively, which means both the AM and BW here are underdense modulated heating processes.
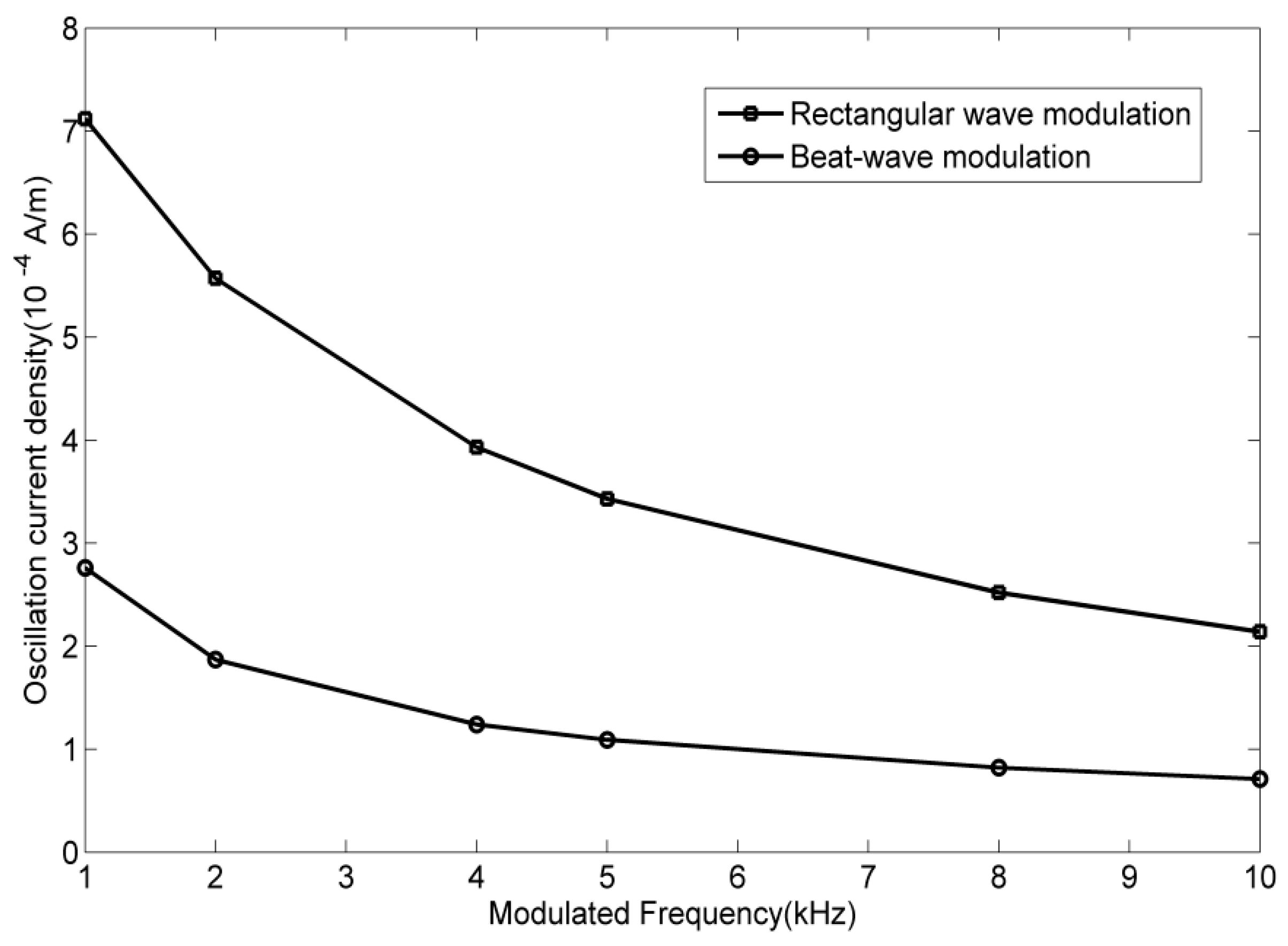
Our simulation results of both AM and BW shown in
Figure 2 were obtained by the physical model established in
Section 2.1. Comparison of our simulation results (
Figure 2) with [
16] (
Figure 1), illustrates that just as with AM, BW based on electrojet modulation has the property that the modulation efficiency decreases with the increase of modulation frequency. In addition, AM is more effective than BW under the same conditions which is also consistent with the conclusions reached by Villaseñor [
24] and Barr and Stubbe [
10] through experiments.
2.3.2. Based on the Theory of Ponderomotive Force
Simulation results based on the theory of ponderomotive force proposed by Kuo et al. [
11] is presented in this section to verify the validity of our physical model. The experiment [
11] chosen was conducted on 4 April 2010, 0800 UT, at the location of 62.4°N, 145.2°W (HAARP). The parameters of background ionosphere and atmosphere are from IRI-2016 and NRLMSISE-00 model, respectively. HF waves were transmitted by the HAARP transmitter facility with an ERP of 570 MW, where
with modulation frequencies
.
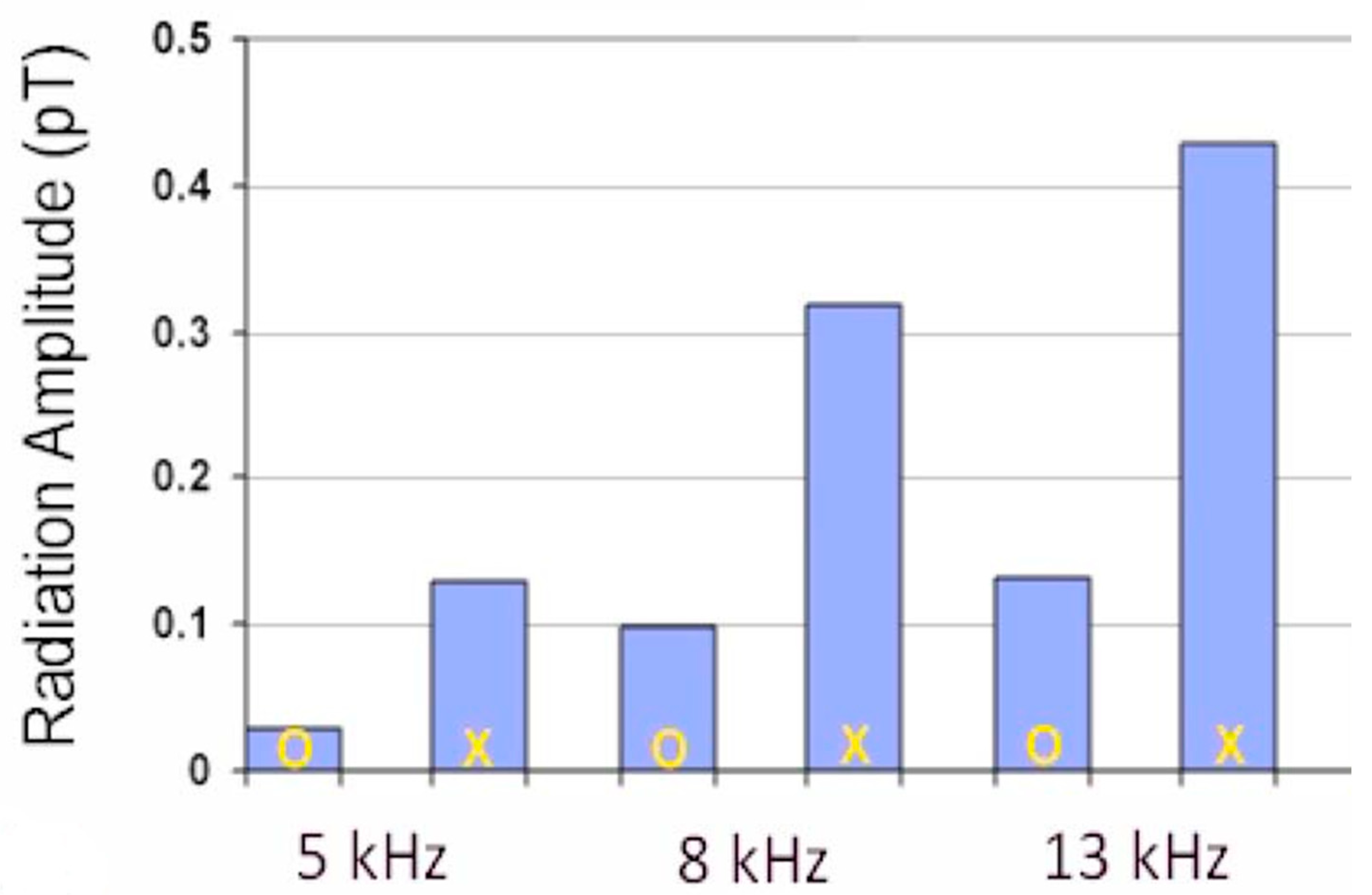
Figure 3 is the radiation amplitude received on the ground [
11]. It can be seen from this figure that in contrast to the theory of BW based on electrojet modulation, the efficiency of BW based on ponderomotive force increases with the increase of the modulation frequency. Moreover, as indicated in Equation (15), X-wave are much more efficient than O-wave for BW modulation.
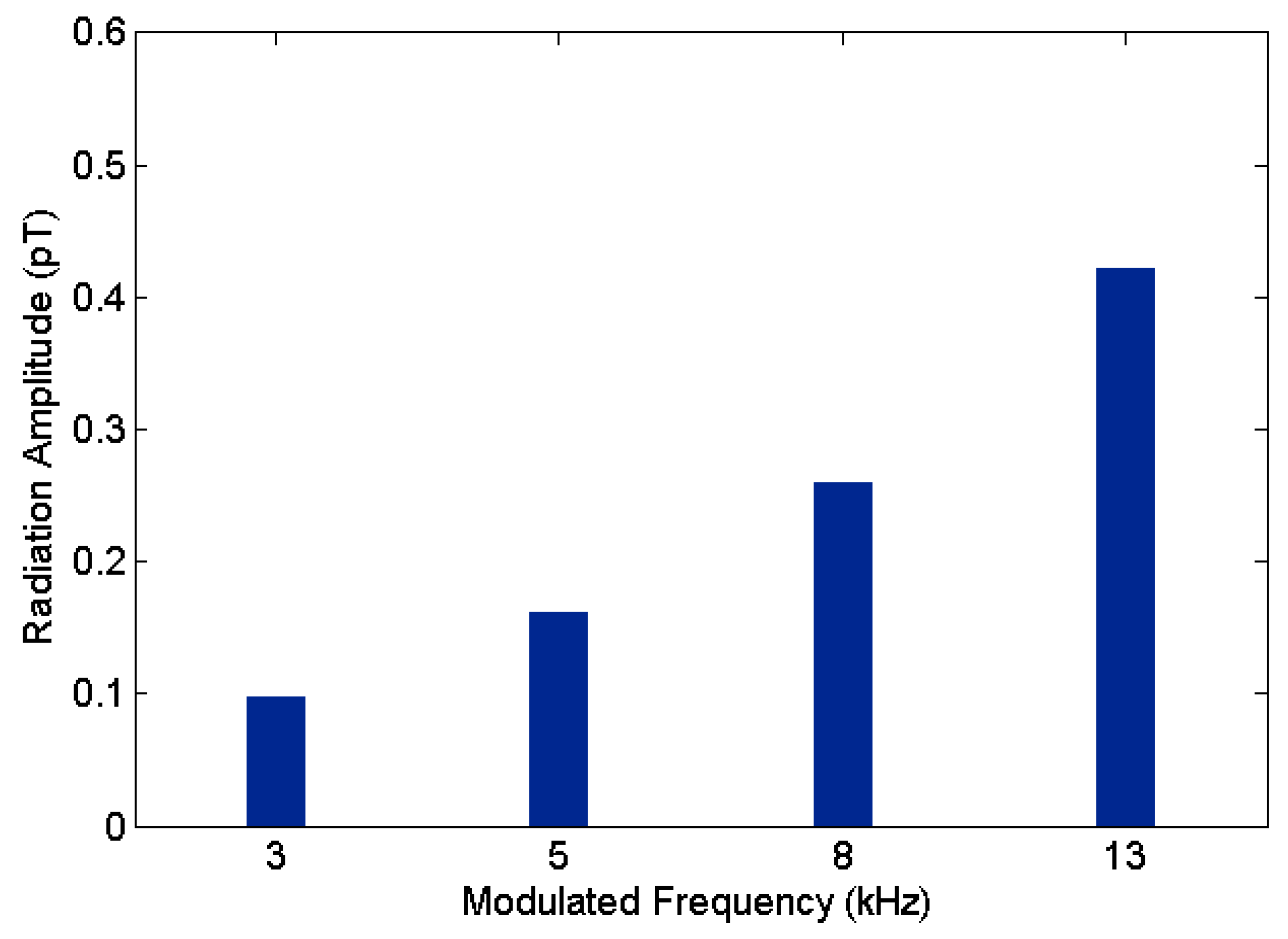
The simulation results shown in
Figure 4 indicates a good agreement with [
11], among which results of BW were obtained by the physical model established in
Section 2.2. The foE is 1.48 MHz, while the fxF2 is 3.7 MHz, which means the BW is an overdense modulated heating process.
In summary, it can be seen that the two different theories of BW modulations have different or even completely opposite effect on the variation trend of the modulation efficiency with the modulation frequency. Therefore, mechanism of BW cannot be inferred from the existing experimental observations reported in the literature. In fact, some scholars who support the theory of BW based on electrojet modulation [
14] and others who support the theory of BW based on ponderomotive force [
11] have also indicated that the possible effect of another theory cannot be completely ruled out. So, in some cases the experimental results may be the effect of the combination of both mechanisms.
3. Identification of Mechanism and Source of BW
In the previous section, two different theories of BW with different or even completely opposite conclusions regarding the variation trend of the modulation efficiency with the modulation frequency were reported. According to the theory of BW based on electrojet modulation, the modulation efficiency decreases with increase in the modulation frequency, whereas, the theory of BW based on ponderomotive force, results in an increase in the modulation efficiency when the modulation frequency is increased. In addition, these two theories correspond to different source region of generating ELF/VLF waves. The main purpose of this paper is to propose a new method based on preheating technique to determine the dominant or more important mechanism when one or both mechanisms may be acting simultaneously.
3.1. Introduction of Preheating
Preheating is a modulated heating technique proposed by Milikh and Papadopoulos [
5], which is essentially a method to change the background ionospheric parameters and thus affect the modulation efficiency by carrying out ionospheric heating before modulated heating. As shown on their simulations, a preheating of the lower ionosphere by a long HF-pulse (more than 500 s) can increase the peak intensity of the ELF/VLF signal by up to 7 dB. The physical mechanism of preheating is shown on Equations (1)–(6), the key of its effect on modulated heating is that the electron density in the lower ionosphere increases after a period of preheating, which will affect the modulated heating in two aspects. In case of electrojet modulation in D region, the increase of background electron density will increase the conductivity during the modulated heating process so that the modulation efficiency can be improved. For the BW based on the ponderomotive nonlinearity in F region, there is no study at this point. However, it can be noted that the “enhanced” D region after preheating will improve the D region absorption effect, which means the energy of HF waves actually reaching the F region will be further reduced, and therefore the modulation efficiency is expected to be reduced as well. Therefore, since different theories of BW modulations based on different physical mechanisms and source region positions have different responses to preheating process, preheating may be a useful method to distinguish the physical mechanism and source region of BW modulation.
3.2. The Effect of D Region Absorption
D region absorption can severely limit HF heating of the upper ionosphere. This effect is hard to be offset by simply increasing the effective radiated power of the transmitted HF waves because the D region absorption also increases with increasing heating power [
30]. Tomko et al. [
30] found that in the case with an obvious D region, at 100 km the attenuation of wave energy by self-absorption is about 3 dB for 100 MW of ionospheric heating and if one doubles the heating power to 200 MW, the self-absorption attenuation rises to more than 5 dB, which means that the remaining energy is less than 30%.
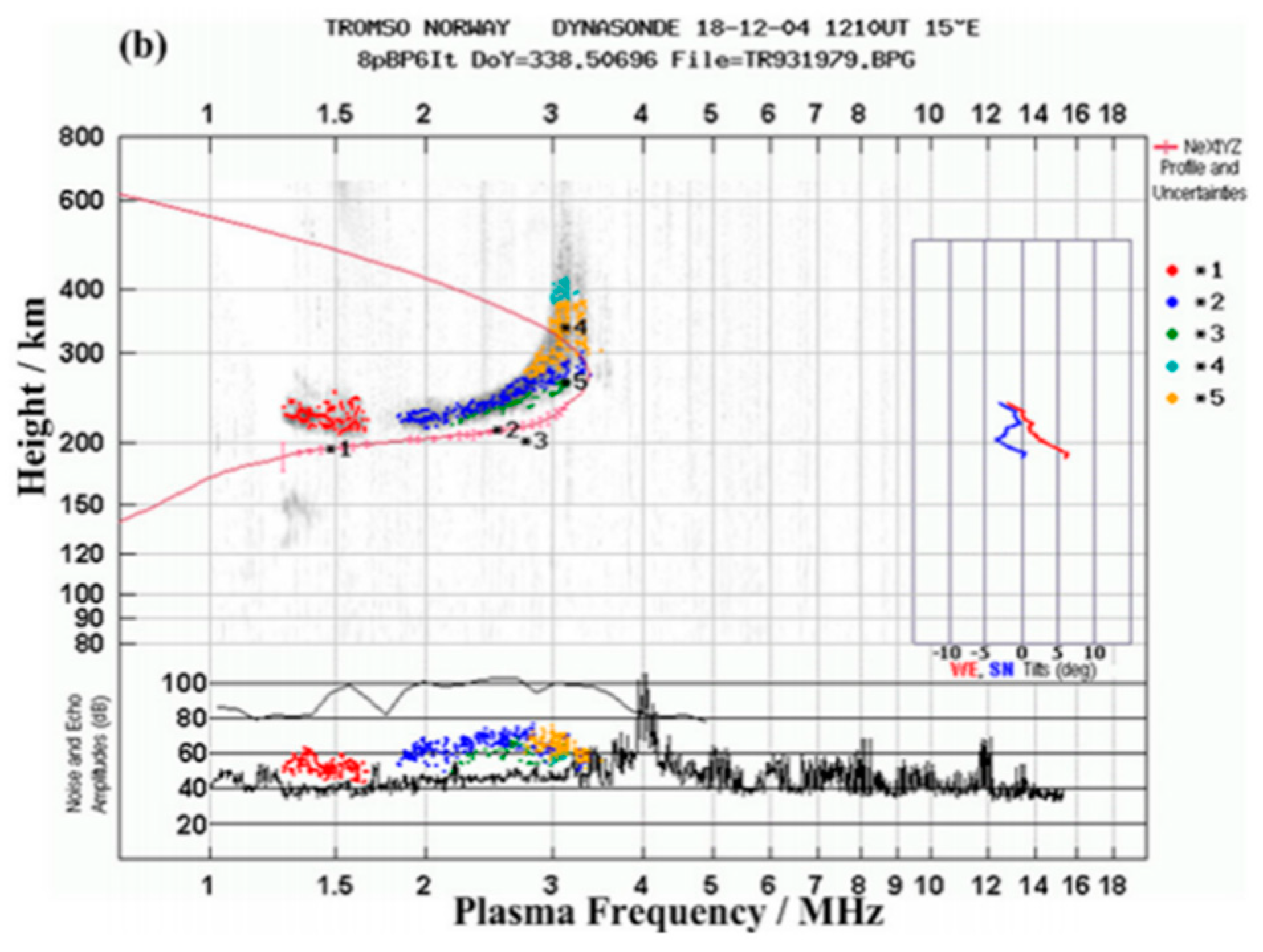
Experiment [
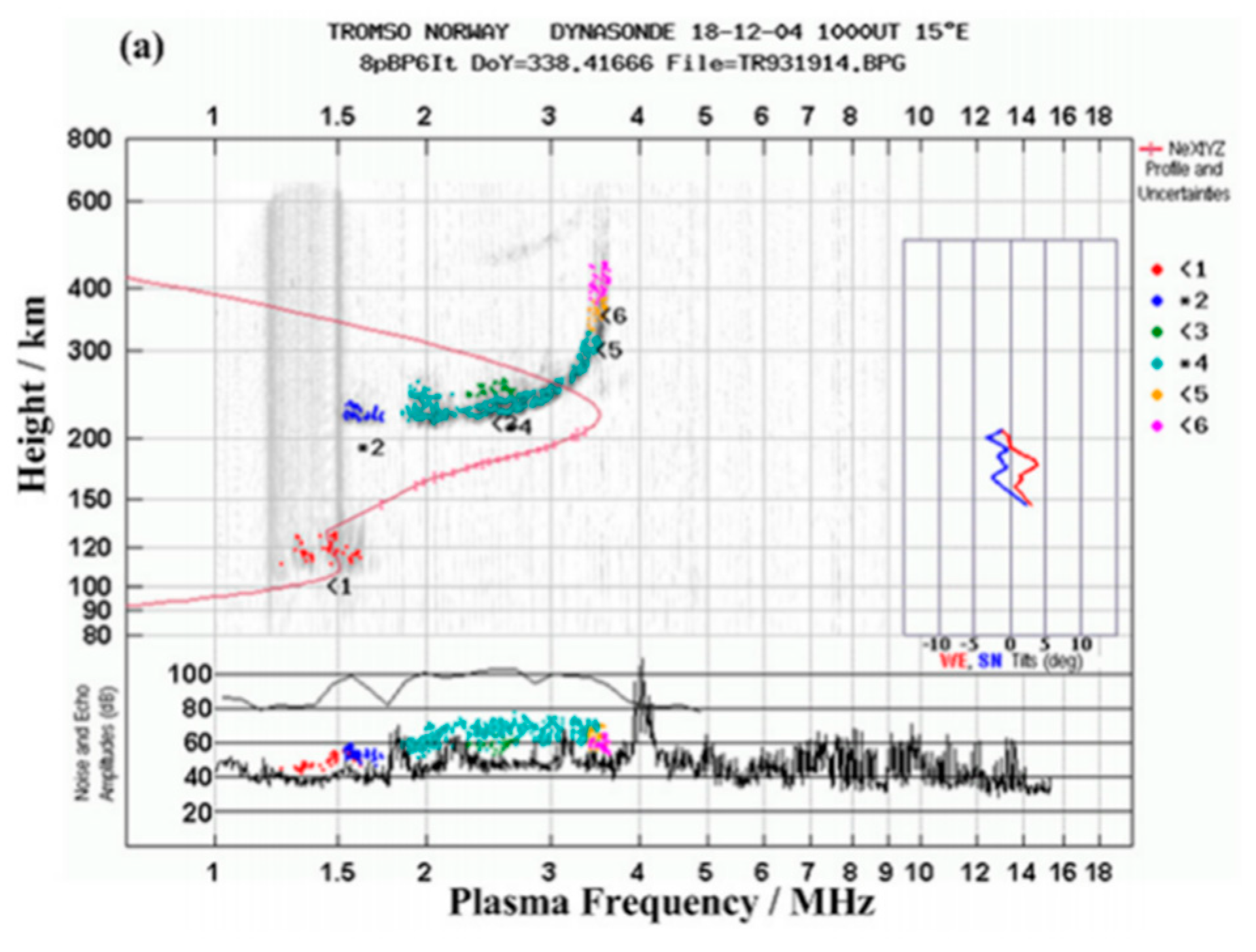
23] carried out on 4 December 2018 at Tromsø, EISCAT is chosen as an example to illustrate the importance of D region absorption to BW in F region.
Figure 5a,b are ionograms on 1000 UT and 1210 UT respectively. The main difference of these two figures is that there is a strong D-E region in 1000 UT but the ionization of lower ionosphere weakens and the D layer disappears in 1210 UT, which reduces the absorption attenuation of HF waves in the lower ionosphere. Therefore, the background field in these two periods represent if D region absorption exists or not.
Table 1 shows the comparison of simulation results with experimental observations when carrying out BW modulation in the presence and absence of D region absorption. The frequency and ERP of transmitted HF waves are 4.04 MHz and 170 MW respectively, the modulation frequency is 2017 Hz. The receiver located at 69.737°N, 18.896°E, about 15 km east of EISCAT heating facility. It can be seen that there is a strong D region absorption at 1000 UT, so the ELF signal amplitude observed in the experiment is much smaller than the simulation results when we ignore the D region absorption effect. However, the simulation results are very close to the experimental observation results when the attenuation of wave energy caused by D layer absorption is taken into consideration. In addition, the attenuation of wave energy in the lower ionosphere do not need to be considered on 1210 UT because the ionization of lower ionosphere weakens and the D region disappears, the simulation results are in good agreement with the experimental results.
3.3. Impact of Preheating on BW
3.3.1. BW in the D Region
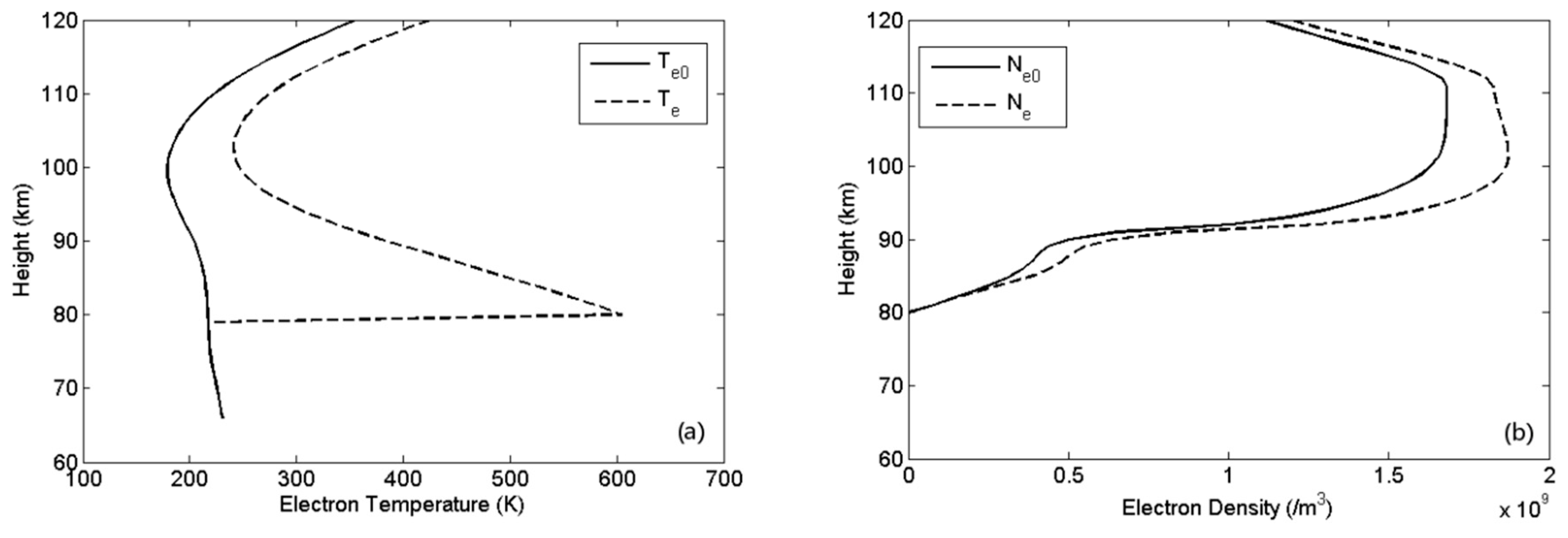
Simulation of the impact of preheating on BW based on electrojet modulation is illustrated in this section. In this case, the source region of generating ELF/VLF waves was in the D region. Parameters of background ionosphere and atmosphere are on 16 March 2008, 1300 UT, HAARP which were obtained by IRI-2016 and NRLMSISE-00. The frequency, ERP, and mode of HF waves were 2.75 MHz, 420 MW, and X-mode, respectively. The preheating wave was 4 MHz, 100 MW, X-wave, and the duration of preheating was 5 s. The foE is only 0.36 MHz, which means both the preheating and BW process are for underdense heating.
The solid and dashed lines in
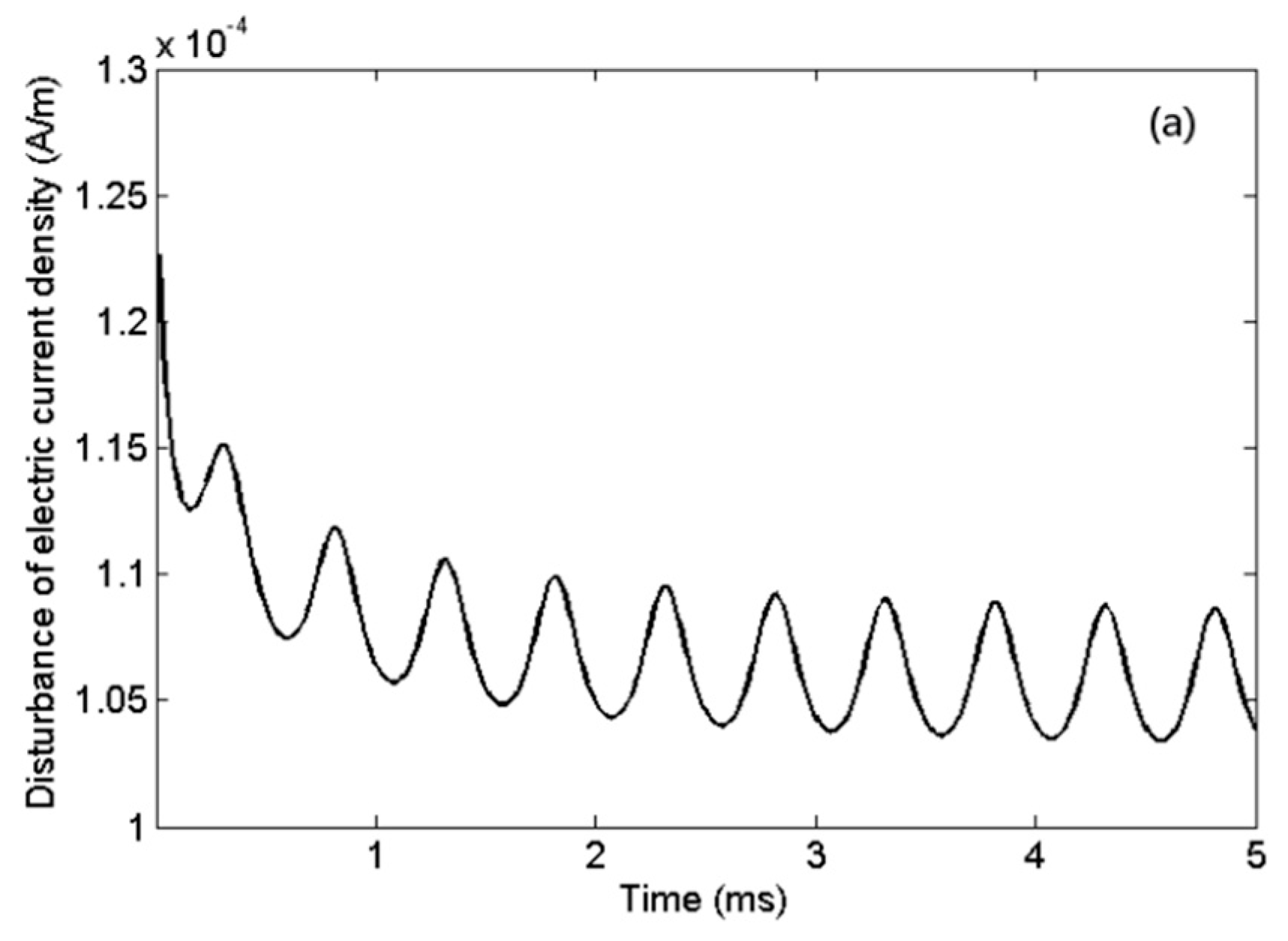
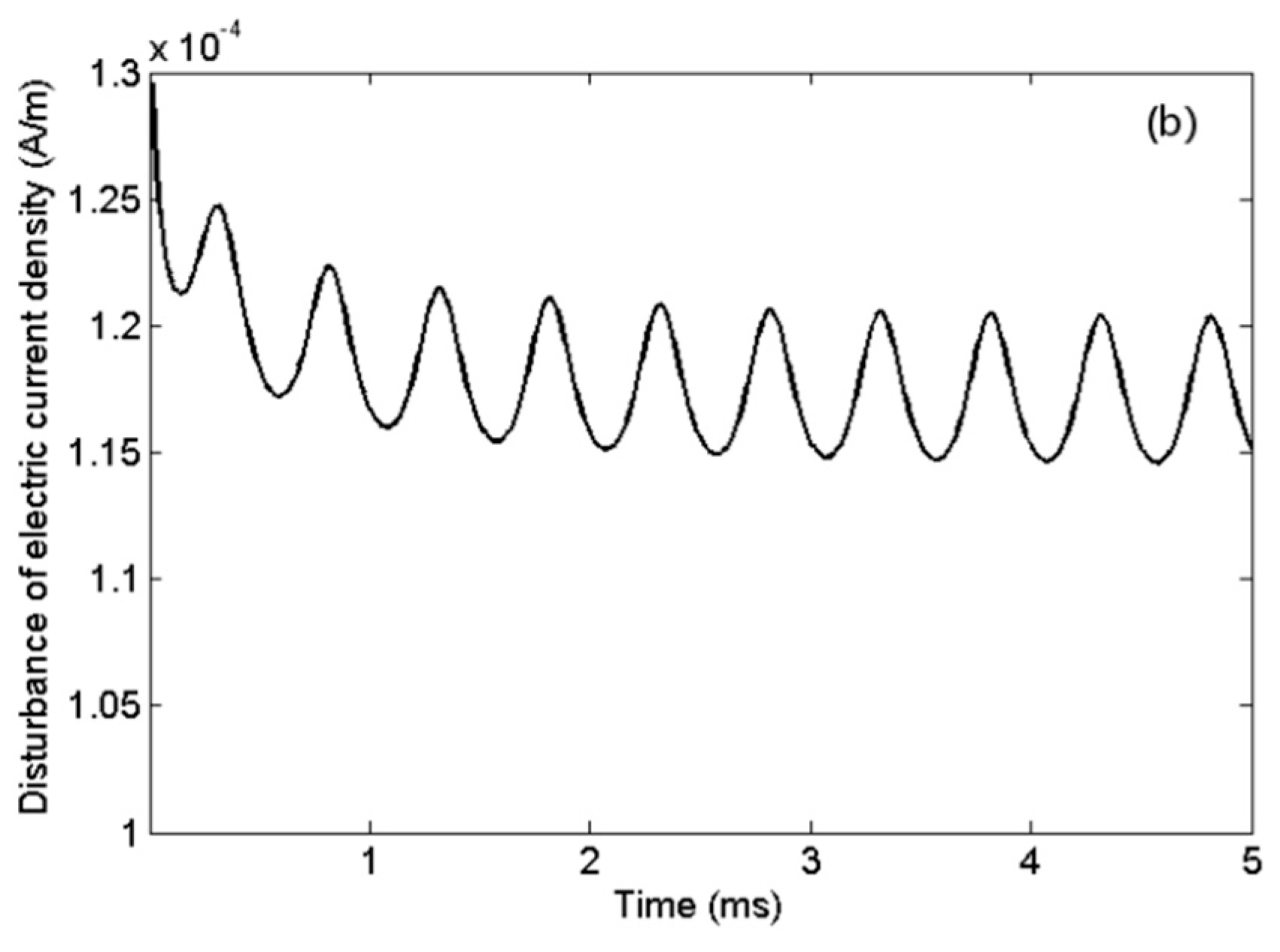
Figure 6 represent the profile of electron temperature and electron density (calculated by Equations (1) and (5) respectively) before and after preheating, respectively. It can be seen from the figure that both electron temperature and electron density in the D and E region above 80 km increases significantly after preheating for 5 s. According to Equations (8)–(10), an increase in background electron density can cause an increase in the conductivity and disturbance of current density. For the modulation frequency of 2000 Hz, the variation of current density disturbance for BW modulation before and after preheating were simulated as shown in
Figure 7. When disturbances were basically stable, the disturbance of electric current density modulated by BW after preheating floated around 1.18 × 10
−4 A/m, while the disturbance of electric current density modulated by BW without preheating floated around 1.06 × 10
−4 A/m, which means that the preheating process indeed increase the disturbance of current density modulated by BW. Finally, the signal amplitude of ELF waves obtained by receivers on the ground can be calculated using Equation (11). In this case, the receiver located at Chistochina (62.62°N, −144.62°W, 37 km from HAARP). The same method was used to calculate the effect of preheating on the signal amplitude of ELF/VLF waves when the modulated frequencies were 3 kHz and 4 kHz, and the results are shown in
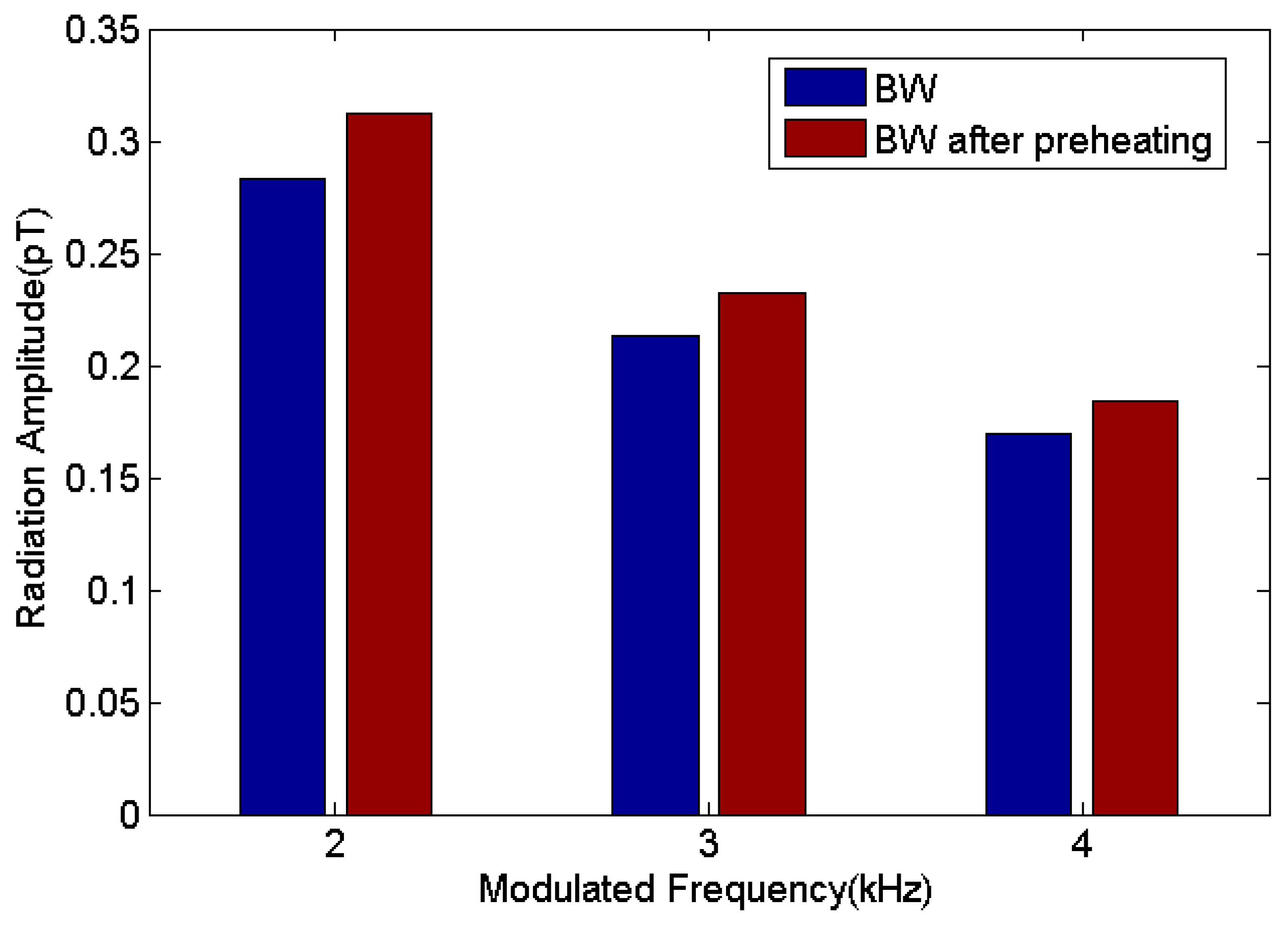
Figure 8. It can be seen from
Figure 8 that although the modulation efficiency of BW after preheating still decreases with the increase of the modulated frequency which is a characteristic of electrojet modulation, preheating can increase the modulation efficiency at all modulated frequencies.
3.3.2. BW in the F Region
The impact of preheating on BW based on ponderomotive nonlinearity is explored. In this case, it is assumed that the source region of generating ELF/VLF waves was in the F region. Background parameters of ionosphere and atmosphere are the same as in
Section 3.2 (4 December 2018 1000 UT, Tromsø, EISCAT). Parameters of HF waves for modulated heating are 4.04 MHz, 170 MW, X-wave. Parameters of HF waves for preheating are 4 MHz, 100 MW, X-wave, the duration of preheating is 5 s. The foE is 1.5 MHz, while the fxF2 is 4.3 MHz, which means the preheating process is for underdense heating, but the BW process is for overdense heating.
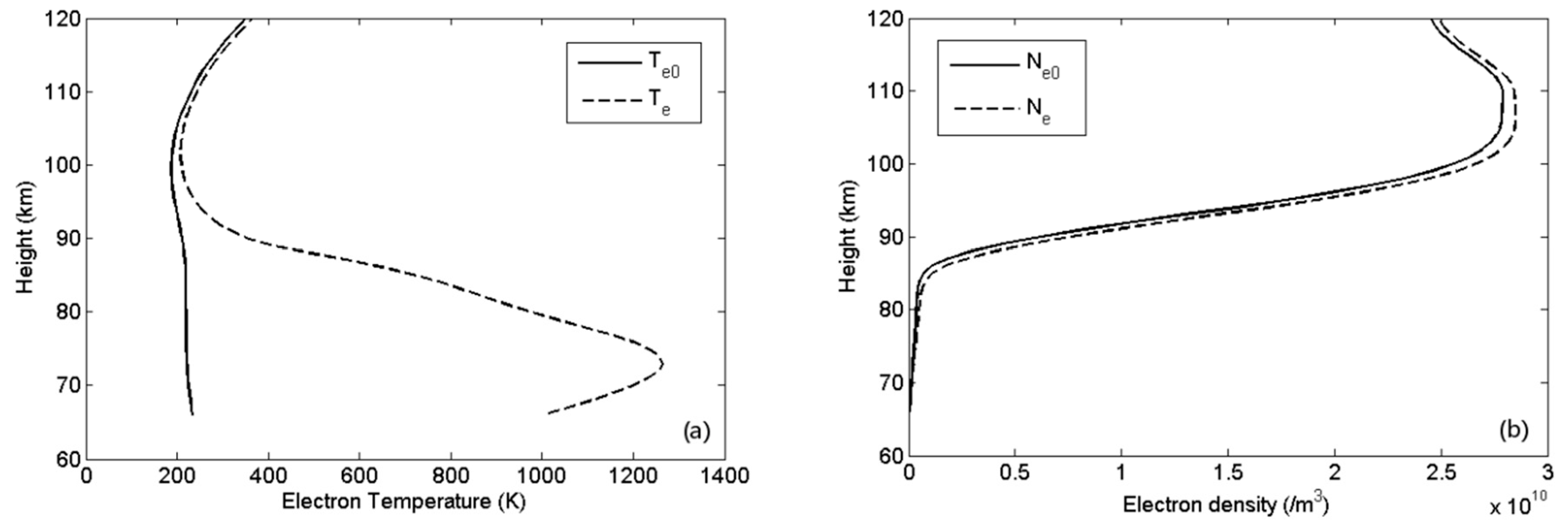
The solid and dashed lines in
Figure 9 represent the profile of electron temperature and electron density (calculated by Equations (1) and (5) respectively) before and after preheating, respectively. It can be seen from the figure that both electron temperature and electron density in the D and E region increases after preheating for 5 s.
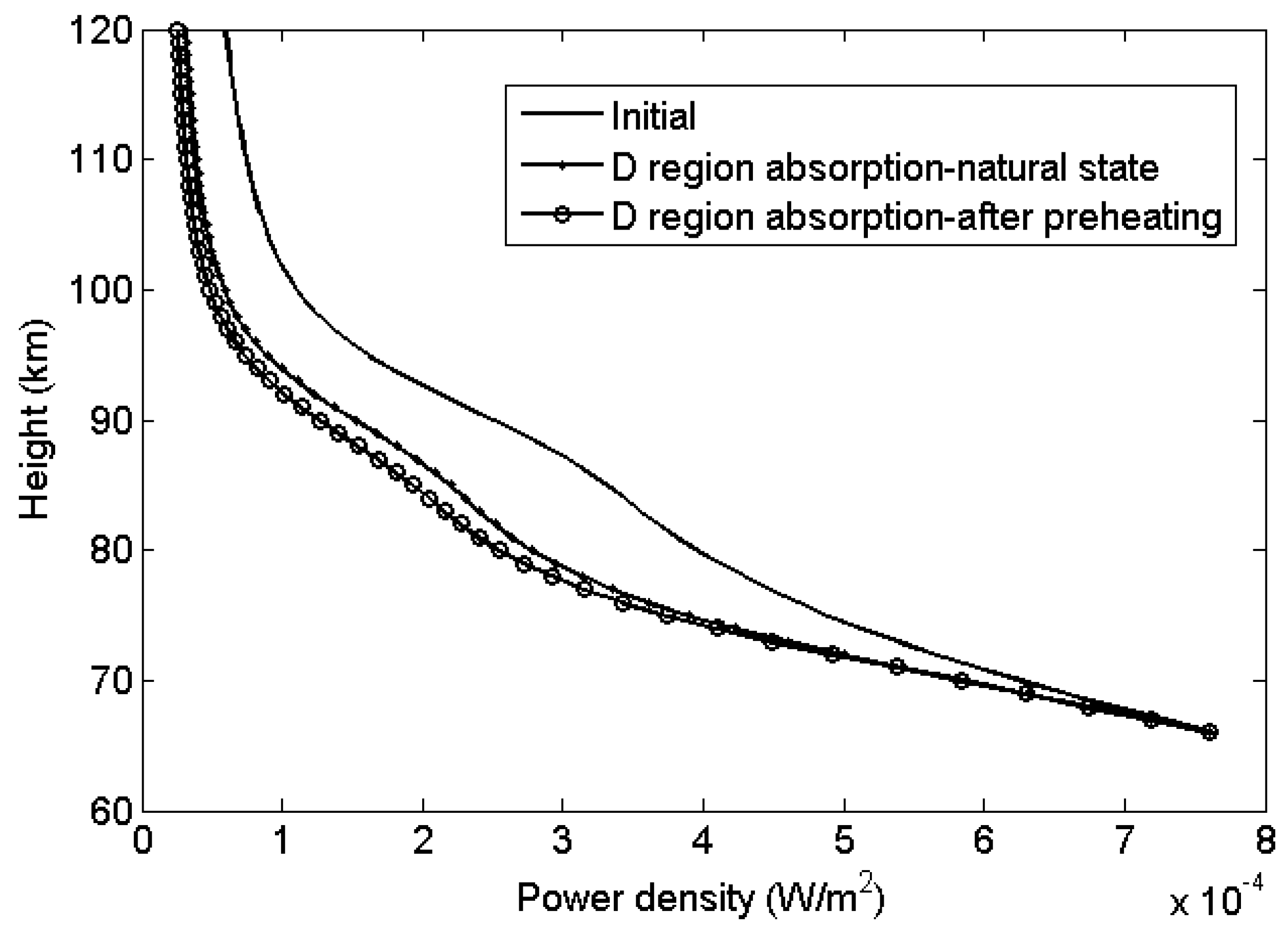
It can be seen from
Figure 10 that the power density of HF waves is reduced by D region absorption significantly. The “Initial” represents the background field without any heating process. According to calculation, when carrying out BW modulation without preheating, the power density drops to 52.4% of its initial value at the height of 120 km. In addition, the D region absorption effect becomes stronger after preheating, the power density for BW modulation after preheating for 5 s at the height of 120km is only 42.9% of its initial value.
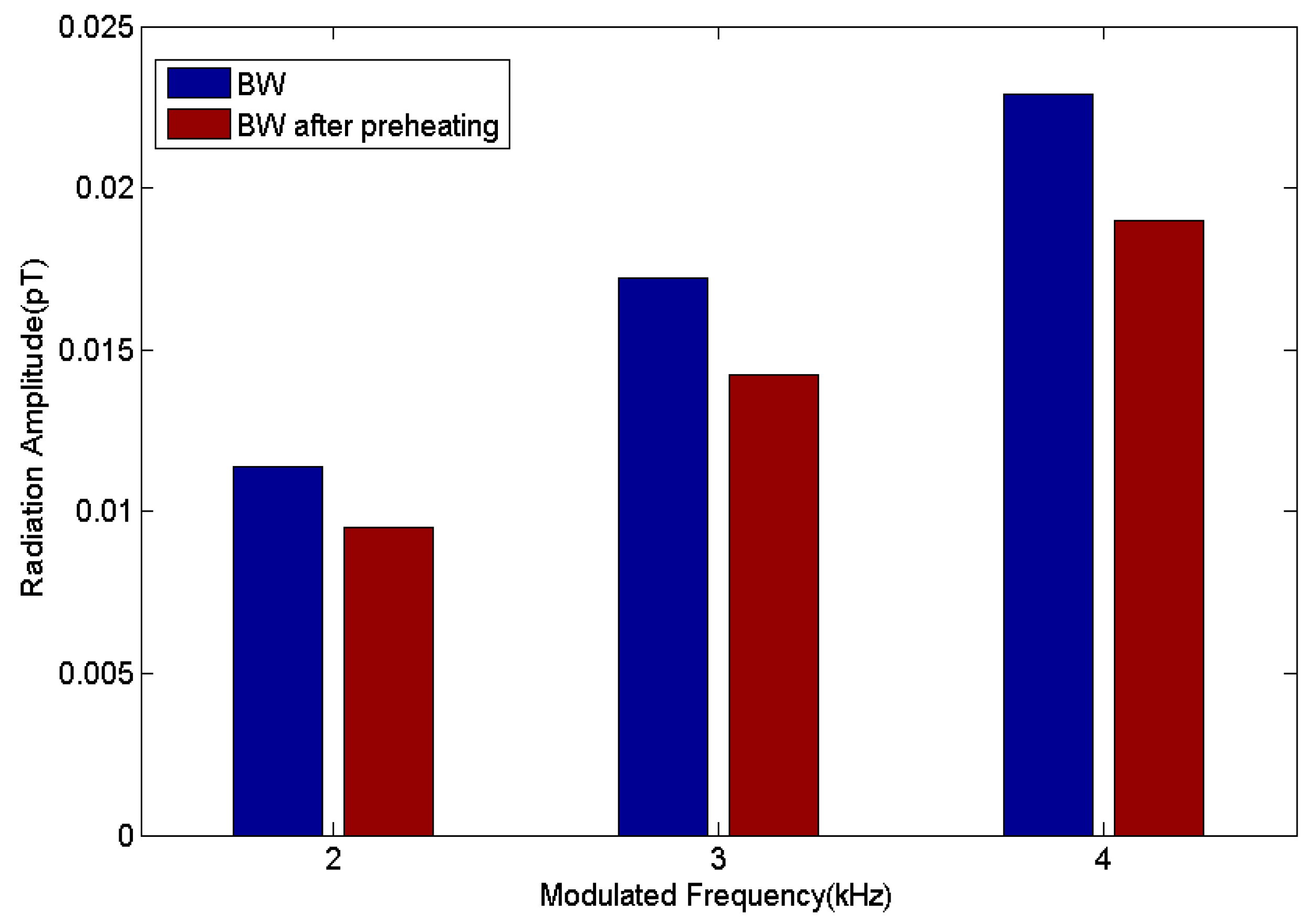
According to calculation, signal amplitudes of ELF/VLF waves (received at 69.737°N, 18.896°E, about 15 km east of EISCAT) generated by BW in F region and BW in F region after preheating with modulated frequencies at 2 kHz, 3 kHz, 4 kHz are shown in
Figure 11. Preheating does not change the characteristic of the modulation efficiency of BW in F region. The efficiency increases with the increase of the modulated frequency, but the modulation efficiency is reduced for all modulated frequencies compared with the case of no preheating.
4. Summary and Conclusions
The main findings are summarized below:
(1) The modulation efficiency of AM and BW based on electrojet modulation has the same variation trend with the modulation frequency, i.e., they both decrease with increasing the modulation frequency, and that AM is more effective than BW for ELF/VLF waves modulation at each modulation frequency.
(2) The modulation efficiency of BW based on ponderomotive force and AM is quite opposite regarding modulation frequency, i.e., the efficiency of BW based on ponderomotive force increases with the increase in modulation frequency. Therefore, AM is more suitable for ELF/VLF waves modulation at lower frequencies, while BW is more suitable for VLF waves modulation at higher frequencies.
(3) When there are strong D and E regions in the ionosphere, the BW modulation in the F region will be affected by the strong D region absorption effect, the efficiency of BW modulation in the F region will be far lower than expected because of the attenuation of wave energy in the lower ionosphere.
(4) The background electron density is increased in the lower ionosphere when preheated for a period of time, which leads to increased conductivity and modulated current density, as a result, the modulation efficiency of BW modulation in the D region is improved. The modulation efficiency of BW modulation in the D region after preheating keep the characteristic of decreasing with the increase of the modulated frequency, but in general, the modulation efficiency at all frequencies can be improved by preheating when compared with that without preheating.
(5) In the presence of D and E regions in the ionosphere, the lower ionosphere can be further strengthened by preheating, which means greater impact of D region absorption on BW in the F region, as a result, less wave energy is transmitted to F region and therefore the modulation efficiency is reduced. Preheating does not change the characteristic that the modulation efficiency of BW in F region increases with the increase of the modulated frequency, but the modulation efficiency at all frequencies is weakened by preheating when compared with the case of without preheating.
To sum up, since the preheating process has opposite influence and effect on the efficiency of BW in D region and F region, it can be used as a new method to determine the physical mechanism and source region of BW. However, it still needs to be tested and verified by experiments, for example, the following experiment is suggested: a sub-process of “BW-cooling-preheating-BW” is cycled for several times with an interval of several minutes between two sub-processes, during which the strength of ELF/VLF signals generated by BW before and after preheating in each sub-process is observed and compared, finally, by combining with our conclusions, the enhancement or weakening effect of preheating observed during the experiment can be used as an identification of the source region of BW.
Furthermore, Larchenko et al. [
31] found that there is a strong correlation between the strength of ELF/VLF waves generated by AM and the equivalent current which is an infinitely thin sheet of current located at an altitude of 100 km. This may become another possible way to determine the source region of BW.