The Role of Longitudinal Polarizations in Horndeski and Macroscopic Gravity: Introducing Gravitational Plasmas
Abstract
1. Introduction
2. Longitudinal Degrees of Freedom and Gauge-Invariant Technique
3. Gravitational Waves in Matter
3.1. Macroscopic Gravity
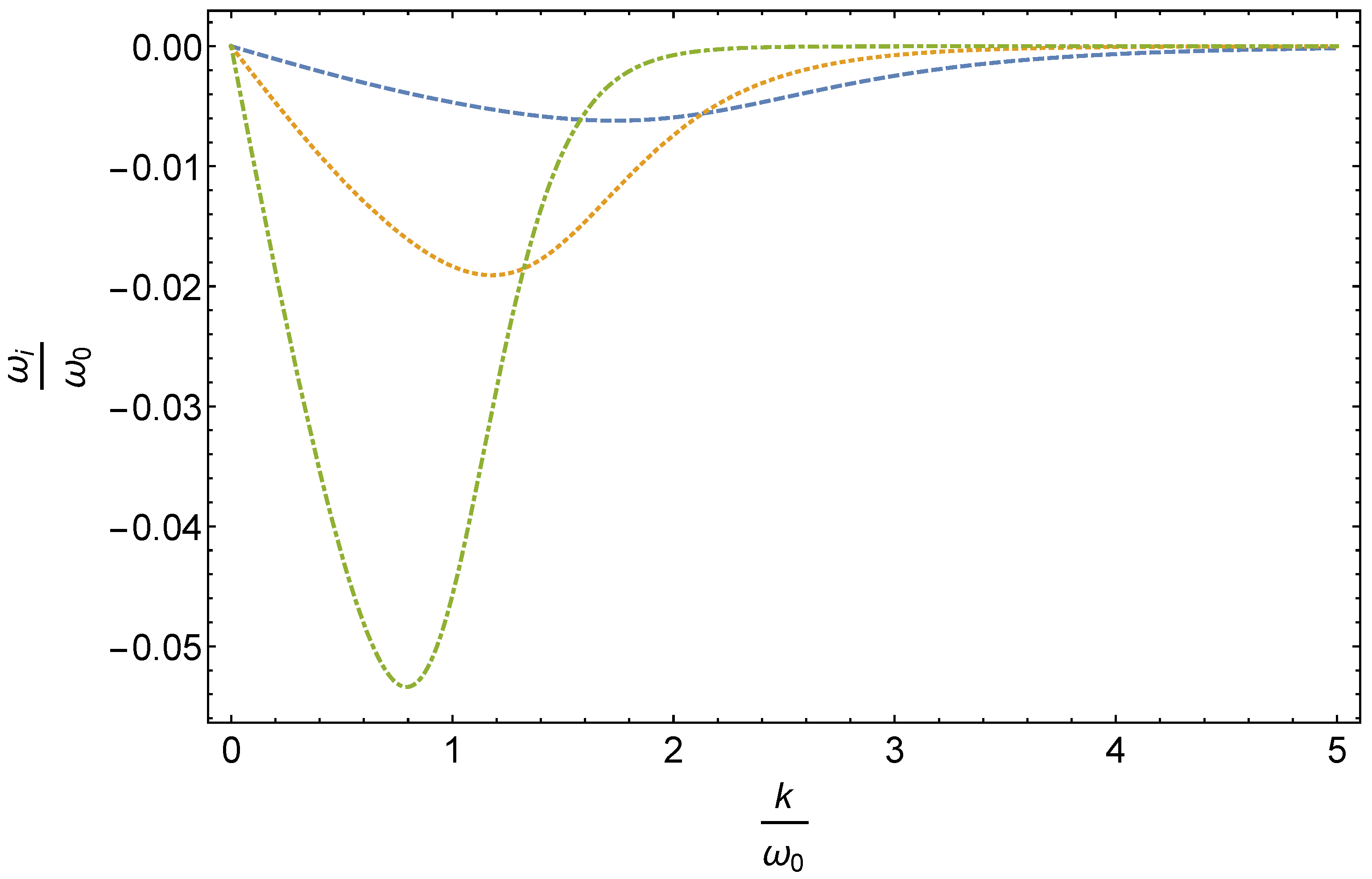
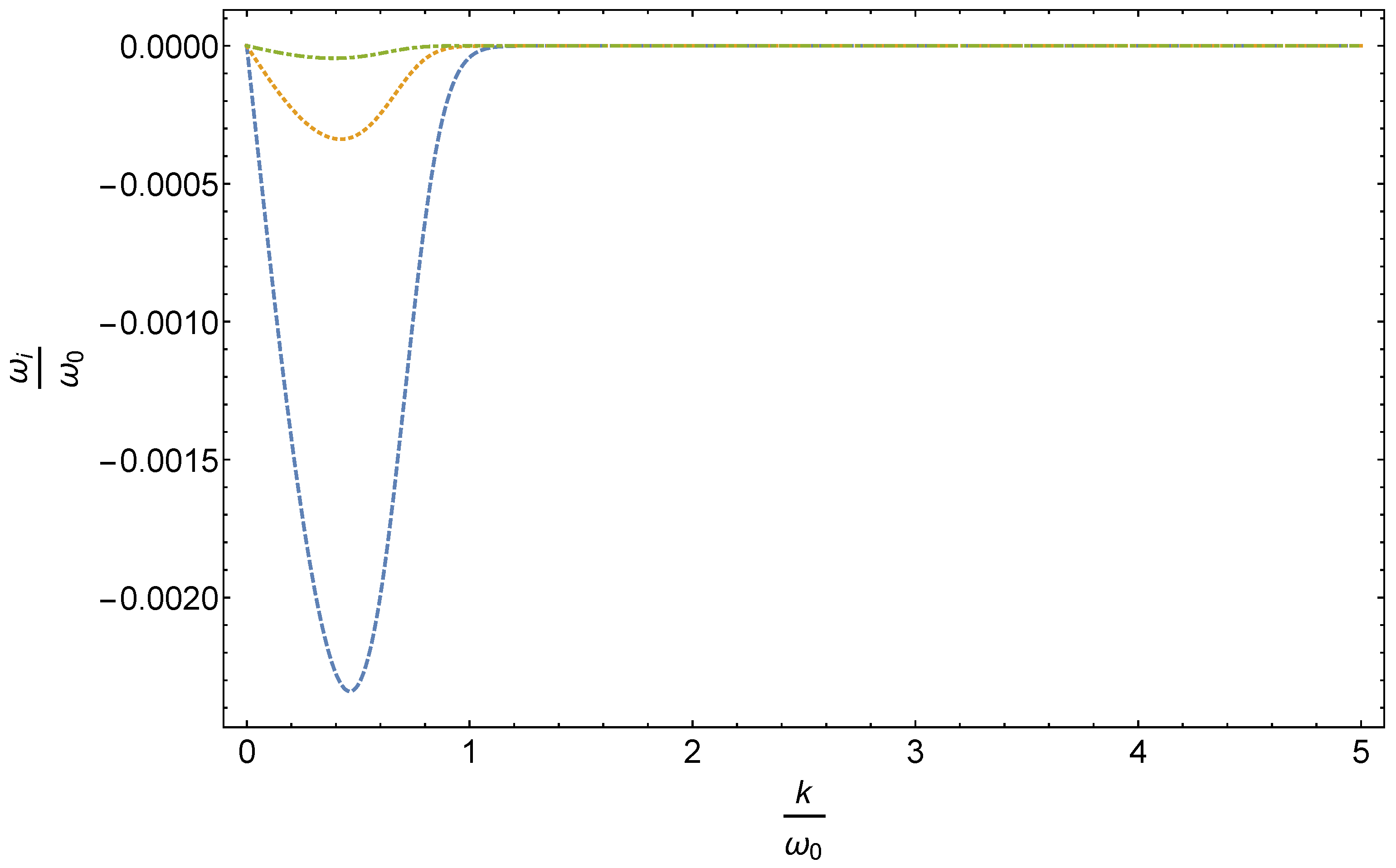
3.2. Landau Damping for Gravitational Scalar Waves
4. Concluding Remarks
Funding
Conflicts of Interest
| 1 | When we work within the linearized theory, we can consider in all respects the perturbation as a dynamical tensor field living on a Minkowski spacetime—see, for instance, the discussion in Ch. 2 of [10]. |
| 2 | For all details concerning the properties and the asymptotic behavior of , , and their decomposition, we remind the reader to [131]. |
| 3 | We indicate with and the real and imaginary part of the angular frequency, respectively. The same notation is also used to denote the real and imaginary part of the dielectric functions. |
| 4 | We denote with a bar quantities that are normalized with the proper frequency , e.g., and equivalently for the others. |
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170608: Observation of a 19-solar-mass Binary Black Hole Coalescence. Astrophys. J. Lett. 2017, 851, L35. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. Phys. Rev. X 2019, 9, 031040. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GWTC-2: Compact Binary Coalescences Observed by LIGO and Virgo During the First Half of the Third Observing Run. Phys. Rev. X 2021, 11, 021053. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run. arXiv 2021, arXiv:2111.03606. [Google Scholar]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agarwal, D.; et al. GWTC-2.1: Deep Extended Catalog of Compact Binary Coalescences Observed by LIGO and Virgo During the First Half of the Third Observing Run. arXiv 2021, arXiv:2108.01045. [Google Scholar]
- Maggiore, M. Gravitational Waves. Vol. 1: Theory and Experiments; Oxford Master Series in Physics; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Maggiore, M. Gravitational Waves. Vol. 2: Astrophysics and Cosmology; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Chatziioannou, K.; Yunes, N.; Cornish, N. Model-Independent Test of General Relativity: An Extended post-Einsteinian Framework with Complete Polarization Content. Phys. Rev. D 2012, 86, 022004. [Google Scholar] [CrossRef]
- Healy, J.; Bode, T.; Haas, R.; Pazos, E.; Laguna, P.; Shoemaker, D.; Yunes, N. Late Inspiral and Merger of Binary Black Holes in Scalar-Tensor Theories of Gravity. Class. Quant. Grav. 2012, 29, 232002. [Google Scholar] [CrossRef]
- Berti, E.; Cardoso, V.; Gualtieri, L.; Horbatsch, M.; Sperhake, U. Numerical simulations of single and binary black holes in scalar-tensor theories: Circumventing the no-hair theorem. Phys. Rev. D 2013, 87, 124020. [Google Scholar] [CrossRef]
- Shibata, M.; Taniguchi, K.; Okawa, H.; Buonanno, A. Coalescence of binary neutron stars in a scalar-tensor theory of gravity. Phys. Rev. D 2014, 89, 084005. [Google Scholar] [CrossRef]
- Bambi, C. Testing black hole candidates with electromagnetic radiation. Rev. Mod. Phys. 2017, 89, 025001. [Google Scholar] [CrossRef]
- Isi, M.; Weinstein, A.J.; Mead, C.; Pitkin, M. Detecting Beyond-Einstein Polarizations of Continuous Gravitational Waves. Phys. Rev. D 2015, 91, 082002. [Google Scholar] [CrossRef]
- Cardoso, V.; Hopper, S.; Macedo, C.F.B.; Palenzuela, C.; Pani, P. Gravitational-wave signatures of exotic compact objects and of quantum corrections at the horizon scale. Phys. Rev. D 2016, 94, 084031. [Google Scholar] [CrossRef]
- Yunes, N.; Yagi, K.; Pretorius, F. Theoretical Physics Implications of the Binary Black-Hole Mergers GW150914 and GW151226. Phys. Rev. D 2016, 94, 084002. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Tests of general relativity with GW150914. Phys. Rev. Lett. 2016, 116, 221101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Astrophysical Implications of the Binary Black-Hole Merger GW150914. Astrophys. J. Lett. 2016, 818, L22. [Google Scholar] [CrossRef]
- Ezquiaga, J.M.; Zumalacárregui, M. Dark Energy After GW170817: Dead Ends and the Road Ahead. Phys. Rev. Lett. 2017, 119, 251304. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Tests of General Relativity with GW170817. Phys. Rev. Lett. 2019, 123, 011102. [Google Scholar] [CrossRef]
- Crisostomi, M.; Koyama, K. Vainshtein mechanism after GW170817. Phys. Rev. D 2018, 97, 021301. [Google Scholar] [CrossRef]
- Calcagni, G.; Kuroyanagi, S.; Marsat, S.; Sakellariadou, M.; Tamanini, N.; Tasinato, G. Quantum gravity and gravitational-wave astronomy. JCAP 2019, 10, 012. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Tests of General Relativity with the Binary Black Hole Signals from the LIGO-Virgo Catalog GWTC-1. Phys. Rev. D 2019, 100, 104036. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Tests of general relativity with binary black holes from the second LIGO-Virgo gravitational-wave transient catalog. Phys. Rev. D 2021, 103, 122002. [Google Scholar] [CrossRef]
- Lovelock, D. The Einstein tensor and its generalizations. J. Math. Phys. 1971, 12, 498–501. [Google Scholar] [CrossRef]
- Lovelock, D. The four-dimensionality of space and the einstein tensor. J. Math. Phys. 1972, 13, 874–876. [Google Scholar] [CrossRef]
- Jackiw, R.; Pi, S.Y. Chern-Simons modification of general relativity. Phys. Rev. D 2003, 68, 104012. [Google Scholar] [CrossRef]
- Flanagan, E.E. Higher order gravity theories and scalar tensor theories. Class. Quant. Grav. 2003, 21, 417–426. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified Gauss-Bonnet theory as gravitational alternative for dark energy. Phys. Lett. B 2005, 631, 1–6. [Google Scholar] [CrossRef]
- Beltran Jimenez, J.; Heisenberg, L.; Olmo, G.J.; Rubiera-Garcia, D. Born–Infeld inspired modifications of gravity. Phys. Rept. 2018, 727, 1–129. [Google Scholar] [CrossRef]
- Afonso, V.I.; Olmo, G.J.; Orazi, E.; Rubiera-Garcia, D. Mapping nonlinear gravity into General Relativity with nonlinear electrodynamics. Eur. Phys. J. C 2018, 78, 866. [Google Scholar] [CrossRef] [PubMed]
- Afonso, V.I.; Olmo, G.J.; Rubiera-Garcia, D. Mapping Ricci-based theories of gravity into general relativity. Phys. Rev. D 2018, 97, 021503. [Google Scholar] [CrossRef]
- Delhom, A.; Nascimento, J.R.; Olmo, G.J.; Petrov, A.Y.; Porfírio, P.J. Metric-affine bumblebee gravity: Classical aspects. Eur. Phys. J. C 2021, 81, 287. [Google Scholar] [CrossRef]
- Delhom, A.; Olmo, G.J.; Orazi, E. Ricci-Based Gravity theories and their impact on Maxwell and nonlinear electromagnetic models. JHEP 2019, 11, 149. [Google Scholar] [CrossRef]
- Iosifidis, D.; Ravera, L. Parity Violating Metric-Affine Gravity Theories. arXiv 2020, arXiv:2009.03328. [Google Scholar] [CrossRef]
- Bombacigno, F.; Boudet, S.; Olmo, G.J.; Montani, G. Big bounce and future time singularity resolution in Bianchi I cosmologies: The projective invariant Nieh-Yan case. Phys. Rev. D 2021, 103, 124031. [Google Scholar] [CrossRef]
- Stelle, K.S. Renormalization of Higher Derivative Quantum Gravity. Phys. Rev. D 1977, 16, 953–969. [Google Scholar] [CrossRef]
- Benedetti, D.; Machado, P.F.; Saueressig, F. Asymptotic safety in higher-derivative gravity. Mod. Phys. Lett. A 2009, 24, 2233–2241. [Google Scholar] [CrossRef]
- Modesto, L. Super-renormalizable Quantum Gravity. Phys. Rev. D 2012, 86, 044005. [Google Scholar] [CrossRef]
- Lauscher, O.; Reuter, M. Is quantum Einstein gravity nonperturbatively renormalizable? Class. Quant. Grav. 2002, 19, 483–492. [Google Scholar] [CrossRef]
- Salvio, A. Quadratic Gravity. Front. Phys. 2018, 6, 77. [Google Scholar] [CrossRef]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. A Class of viable modified f(R) gravities describing inflation and the onset of accelerated expansion. Phys. Rev. D 2008, 77, 046009. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rept. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. The virial theorem and the dark matter problem in hybrid metric-Palatini gravity. JCAP 2013, 2013, 024. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Cosmology of hybrid metric-Palatini f(X)-gravity. JCAP 2013, 2013, 011. [Google Scholar] [CrossRef]
- Tamanini, N.; Boehmer, C.G. Generalized hybrid metric-Palatini gravity. Phys. Rev. D 2013, 87, 084031. [Google Scholar] [CrossRef]
- Bahamonde, S.; Böhmer, C.G.; Carloni, S.; Copeland, E.J.; Fang, W.; Tamanini, N. Dynamical systems applied to cosmology: Dark energy and modified gravity. Phys. Rept. 2018, 775–777, 1–122. [Google Scholar] [CrossRef]
- Rosa, J.A.L.; Carloni, S.; Lemos, J.P.d.S.e.; Lobo, F.S.N. Cosmological solutions in generalized hybrid metric-Palatini gravity. Phys. Rev. D 2017, 95, 124035. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Afonso, V.I.; Bejarano, C.; Beltran Jimenez, J.; Olmo, G.J.; Orazi, E. The trivial role of torsion in projective invariant theories of gravity with non-minimally coupled matter fields. Class. Quant. Grav. 2017, 34, 235003. [Google Scholar] [CrossRef]
- Iosifidis, D. Exactly Solvable Connections in Metric-Affine Gravity. Class. Quant. Grav. 2019, 36, 085001. [Google Scholar] [CrossRef]
- Beltrán Jiménez, J.; Delhom, A. Ghosts in metric-affine higher order curvature gravity. Eur. Phys. J. C 2019, 79, 656. [Google Scholar] [CrossRef]
- Iosifidis, D. Linear Transformations on Affine-Connections. Class. Quant. Grav. 2020, 37, 085010. [Google Scholar] [CrossRef]
- Latorre, A.D.I.; Olmo, G.J.; Ronco, M. Observable traces of non-metricity: New constraints on metric-affine gravity. Phys. Lett. B 2018, 780, 294–299. [Google Scholar] [CrossRef]
- Capozziello, S.; Cianci, R.; Stornaiolo, C.; Vignolo, S. f(R) gravity with torsion: The Metric-affine approach. Class. Quant. Grav. 2007, 24, 6417–6430. [Google Scholar] [CrossRef]
- Olmo, G.J. Palatini approach to modified gravity: f(R) theories and beyond. Int. J. Mod. Phys. D 2011, 20, 413–462. [Google Scholar] [CrossRef]
- Iosifidis, D.; Petkou, A.C.; Tsagas, C.G. Torsion/non-metricity duality in f(R) gravity. Gen. Rel. Grav. 2019, 51, 66. [Google Scholar] [CrossRef]
- Delhom, A.; Lobo, I.P.; Olmo, G.J.; Romero, C. A generalized Weyl structure with arbitrary non-metricity. Eur. Phys. J. C 2019, 79, 878. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D. Nonsingular Black Holes in f(R) Theories. Universe 2015, 1, 173–185. [Google Scholar] [CrossRef]
- Bambi, C.; Cardenas-Avendano, A.; Olmo, G.J.; Rubiera-Garcia, D. Wormholes and nonsingular spacetimes in Palatini f(R) gravity. Phys. Rev. D 2016, 93, 064016. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D.; Sanchez-Puente, A. Impact of curvature divergences on physical observers in a wormhole space–time with horizons. Class. Quant. Grav. 2016, 33, 115007. [Google Scholar] [CrossRef]
- Menchon, C.; Olmo, G.J.; Rubiera-Garcia, D. Nonsingular black holes, wormholes, and de Sitter cores from anisotropic fluids. Phys. Rev. D 2017, 96, 104028. [Google Scholar] [CrossRef]
- Nascimento, J.R.; Olmo, G.J.; Porfirio, P.J.; Petrov, A.Y.; Soares, A.R. Global Monopole in Palatini f(R) gravity. Phys. Rev. D 2019, 99, 064053. [Google Scholar] [CrossRef]
- Bejarano, C.; Delhom, A.; Jiménez-Cano, A.; Olmo, G.J.; Rubiera-Garcia, D. Geometric inequivalence of metric and Palatini formulations of General Relativity. Phys. Lett. B 2020, 802, 135275. [Google Scholar] [CrossRef]
- Guerrero, M.; Olmo, G.J.; Rubiera-Garcia, D.; Gómez, D.S.C. Shadows and optical appearance of black bounces illuminated by a thin accretion disk. JCAP 2021, 2021, 036. [Google Scholar] [CrossRef]
- Guerrero, M.; Mora-Pérez, G.; Olmo, G.J.; Orazi, E.; Rubiera-Garcia, D. Charged BTZ-type solutions in Eddington-inspired Born-Infeld gravity. arXiv 2021, arXiv:2108.09594. [Google Scholar] [CrossRef]
- Olmo, G.J.; Orazi, E.; Rubiera-Garcia, D. Multicenter solutions in Eddington-inspired Born–Infeld gravity. Eur. Phys. J. C 2020, 80, 1018. [Google Scholar] [CrossRef]
- Bombacigno, F.; Cianfrani, F.; Montani, G. Big-bounce cosmology in the presence of Immirzi field. Phys. Rev. D 2016, 94, 64021. [Google Scholar] [CrossRef]
- Bombacigno, F.; Montani, G. Big bounce cosmology for Palatini R2 gravity with a Nieh–Yan term. Eur. Phys. J. C 2019, 79, 405. [Google Scholar] [CrossRef]
- Benisty, D.; Olmo, G.J.; Rubiera-Garcia, D. Singularity-free and cosmologically viable Born-Infeld gravity with scalar matter. arXiv 2021, arXiv:2103.15437. [Google Scholar] [CrossRef]
- Beltran Jimenez, J.; Heisenberg, L.; Olmo, G.J.; Rubiera-Garcia, D. On gravitational waves in Born-Infeld inspired non-singular cosmologies. JCAP 2017, 10, 029. [Google Scholar] [CrossRef]
- Berry, C.P.; Gair, J.R. Linearized f(R) Gravity: Gravitational Radiation and Solar System Tests. Phys. Rev. D 2011, 83, 104022. [Google Scholar] [CrossRef]
- Iorio, L.; Ruggiero, M.L. Solar system tests of some models of modified gravity proposed to explain galactic rotation curves without dark matter. Schol. Res. Exch. 2008, 2008, 968393. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. First search for nontensorial gravitational waves from known pulsars. Phys. Rev. Lett. 2018, 120, 031104. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Search for Tensor, Vector, and Scalar Polarizations in the Stochastic Gravitational-Wave Background. Phys. Rev. Lett. 2018, 120, 201102. [Google Scholar] [CrossRef]
- Callister, T.; Biscoveanu, A.S.; Christensen, N.; Isi, M.; Matas, A.; Minazzoli, O.; Regimbau, T.; Sakellariadou, M.; Tasson, J.; Thrane, E. Polarization-based Tests of Gravity with the Stochastic Gravitational-Wave Background. Phys. Rev. X 2017, 7, 041058. [Google Scholar] [CrossRef]
- Andriot, D.; Lucena Gómez, G. Signatures of extra dimensions in gravitational waves. JCAP 2017, 06, 048. [Google Scholar] [CrossRef]
- Sagunski, L.; Zhang, J.; Johnson, M.C.; Lehner, L.; Sakellariadou, M.; Liebling, S.L.; Palenzuela, C.; Neilsen, D. Neutron star mergers as a probe of modifications of general relativity with finite-range scalar forces. Phys. Rev. D 2018, 97, 064016. [Google Scholar] [CrossRef]
- Liang, D.; Gong, Y.; Hou, S.; Liu, Y. Polarizations of gravitational waves in f(R) gravity. Phys. Rev. D 2017, 95, 104034. [Google Scholar] [CrossRef]
- Hou, S.; Gong, Y.; Liu, Y. Polarizations of Gravitational Waves in Horndeski Theory. Eur. Phys. J. C 2018, 78, 378. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K.; Fronimos, F.P. Quantitative Predictions for f(R) Gravity Primordial Gravitational Waves. arXiv 2021, arXiv:2108.11231. [Google Scholar]
- Horndeski, G.W. Conservation of Charge and the Einstein-Maxwell Field Equations. J. Math. Phys. 1976, 17, 1980–1987. [Google Scholar] [CrossRef]
- Tasinato, G. Cosmic Acceleration from Abelian Symmetry Breaking. JHEP 2014, 04, 067. [Google Scholar] [CrossRef]
- Allys, E.; Peter, P.; Rodriguez, Y. Generalized Proca action for an Abelian vector field. JCAP 2016, 2016, 004. [Google Scholar] [CrossRef]
- Allys, E.; Beltran Almeida, J.P.; Peter, P.; Rodríguez, Y. On the 4D generalized Proca action for an Abelian vector field. JCAP 2016, 09, 026. [Google Scholar] [CrossRef]
- Rodriguez, Y.; Navarro, A.A. Scalar and vector Galileons. J. Phys. Conf. Ser. 2017, 831, 012004. [Google Scholar] [CrossRef]
- Gallego Cadavid, A.; Rodriguez, Y. A systematic procedure to build the beyond generalized Proca field theory. Phys. Lett. B 2019, 798, 134958. [Google Scholar] [CrossRef]
- Allys, E.; Peter, P.; Rodriguez, Y. Generalized SU(2) Proca Theory. Phys. Rev. D 2016, 94, 084041. [Google Scholar] [CrossRef]
- Gallego Cadavid, A.; Rodriguez, Y.; Gómez, L.G. Generalized SU(2) Proca theory reconstructed and beyond. Phys. Rev. D 2020, 102, 104066. [Google Scholar] [CrossRef]
- Gallego Cadavid, A.; Nieto, C.M.; Rodriguez, Y. Towards the extended SU(2) Proca theory. arXiv 2021, arXiv:hep-th/2110.14623. [Google Scholar]
- Rodríguez, Y.; Navarro, A.A. Non-Abelian S-term dark energy and inflation. Phys. Dark Univ. 2018, 19, 129–136. [Google Scholar] [CrossRef]
- Gómez, L.G.; Rodríguez, Y. Stability Conditions in the Generalized SU(2) Proca Theory. Phys. Rev. D 2019, 100, 084048. [Google Scholar] [CrossRef]
- Garnica, J.C.; Gomez, L.G.; Navarro, A.A.; Rodriguez, Y. Constant-roll inflation in the generalized SU(2) Proca theory. arXiv 2021, arXiv:2109.10154. [Google Scholar]
- Heisenberg, L. Generalization of the Proca Action. JCAP 2014, 5, 015. [Google Scholar] [CrossRef]
- Heisenberg, L.; Kase, R.; Tsujikawa, S. Beyond generalized Proca theories. Phys. Lett. B 2016, 760, 617–626. [Google Scholar] [CrossRef]
- Heisenberg, L. Scalar-Vector-Tensor Gravity Theories. JCAP 2018, 10, 054. [Google Scholar] [CrossRef]
- Beltran Jimenez, J.; Durrer, R.; Heisenberg, L.; Thorsrud, M. Stability of Horndeski vector-tensor interactions. JCAP 2013, 10, 064. [Google Scholar] [CrossRef]
- Montani, G.; Moretti, F. Modified Gravitational Waves Across Galaxies from Macroscopic Gravity. Phys. Rev. D 2019, 100, 024045. [Google Scholar] [CrossRef]
- Moretti, F.; Bombacigno, F.; Montani, G. Gravitational Landau Damping for massive scalar modes. Eur. Phys. J. C 2020, 80, 1203. [Google Scholar] [CrossRef]
- Moretti, F.; Bombacigno, F.; Montani, G. Gauge invariant formulation of metric f (R) gravity for gravitational waves. Phys. Rev. D 2019, 100, 084014. [Google Scholar] [CrossRef]
- Hawking, S.W. Perturbations of an expanding universe. Astrophys. J. 1966, 145, 544–554. [Google Scholar] [CrossRef]
- Madore, J. The absorption of gravitational radiation by a dissipative fluid. Commun. Math. Phys. 1973, 30, 335–340. [Google Scholar] [CrossRef]
- Zakharov, A.V. A kinetic theory for the growth of perturbations in an isotropic cosmological model, and the ultrarelativistic limit. Sov. Astron. 1978, 22, 528–535. [Google Scholar]
- Weinberg, S. Damping of tensor modes in cosmology. Phys. Rev. D 2004, 69, 023503. [Google Scholar] [CrossRef]
- Flauger, R.; Weinberg, S. Gravitational Waves in Cold Dark Matter. Phys. Rev. D 2018, 97, 123506. [Google Scholar] [CrossRef]
- Lattanzi, M.; Montani, G. On the interaction between thermalized neutrinos and cosmological gravitational waves above the electroweak unification scale. Mod. Phys. Lett. A 2005, 20, 2607–2618. [Google Scholar] [CrossRef]
- Lattanzi, M.; Benini, R.; Montani, G. A possible signature of cosmic neutrino decoupling in the nHz region of the spectrum of primordial gravitational waves. Class. Quant. Grav. 2010, 27, 194008. [Google Scholar] [CrossRef]
- Benini, R.; Lattanzi, M.; Montani, G. Signatures of the neutrino thermal history in the spectrum of primordial gravitational waves. Gen. Rel. Grav. 2011, 43, 945–958. [Google Scholar] [CrossRef][Green Version]
- Mendonça, J.T.; Martins, A.M.; Guerreiro, A. Field quantization in a plasma: Photon mass and charge. Phys. Rev. E 2000, 62, 2989–2991. [Google Scholar] [CrossRef]
- Mendonça, J.T.; Oliveira e Silva, L. Regular and stochastic acceleration of photons. Phys. Rev. E 1994, 49, 3520–3523. [Google Scholar] [CrossRef]
- Pitaevskii, L.; Lifshitz, E. Physical Kinetics; Elsevier Science: Amsterdam, The Netherlands, 2012; Volume 10. [Google Scholar]
- Fiorucci, D.; Harms, J.; Barsuglia, M.; Fiori, I.; Paoletti, F. Impact of infrasound atmospheric noise on gravity detectors used for astrophysical and geophysical applications. Phys. Rev. D 2018, 97, 062003. [Google Scholar] [CrossRef]
- Naf, J.; Jetzer, P.; Sereno, M. On Gravitational Waves in Spacetimes with a Nonvanishing Cosmological Constant. Phys. Rev. D 2009, 79, 024014. [Google Scholar] [CrossRef]
- Bernabeu, J.; Espriu, D.; Puigdomenech, D. Gravitational waves in the presence of a cosmological constant. Phys. Rev. D 2011, 84, 063523. [Google Scholar] [CrossRef]
- Özer, H.; Delice, O. Gravitational waves in Brans–Dicke theory with a cosmological constant. Eur. Phys. J. C 2021, 81, 326. [Google Scholar] [CrossRef]
- Hobbs, G.; Archibald, A.; Arzoumanian, Z.; Backer, D.; Bailes, M.; Bhat, N.D.R.; Burgay, M.; Burke-Spolaor, S.; Champion, D.; Cognard, I.; et al. The International Pulsar Timing Array project: Using pulsars as a gravitational wave detector. Class. Quantum Gravity 2010, 27, 084013. [Google Scholar] [CrossRef]
- Hobbs, G. Pulsars as gravitational wave detectors. Astrophys. Space Sci. Proc. 2011, 21, 229. [Google Scholar] [CrossRef]
- Lentati, L.; Taylor, S.R.; Mingarelli, C.M.F.; Sesana, A.; Sanidas, S.A.; Vecchio, A.; Caballero, R.N.; Lee, K.J.; van Haasteren, R.; Babak, S.; et al. European Pulsar Timing Array Limits On An Isotropic Stochastic Gravitational-Wave Background. Mon. Not. R. Astron. Soc. 2015, 453, 2576–2598. [Google Scholar] [CrossRef]
- Ananda, K.N.; Clarkson, C.; Wands, D. The Cosmological gravitational wave background from primordial density perturbations. Phys. Rev. D 2007, 75, 123518. [Google Scholar] [CrossRef]
- Caprini, C.; Hindmarsh, M.; Huber, S.; Konstandin, T.; Kozaczuk, J.; Nardini, G.; No, J.M.; Petiteau, A.; Schwaller, P.; Servant, G.; et al. Science with the space-based interferometer eLISA. II: Gravitational waves from cosmological phase transitions. JCAP 2016, 04, 001. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85–88. [Google Scholar] [CrossRef]
- Caprini, C.; Figueroa, D.G. Cosmological Backgrounds of Gravitational Waves. Class. Quant. Grav. 2018, 35, 163001. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Ahmed, Z.; Aikin, R.W.; Alexander, K.D.; Barkats, D.; Benton, S.J.; Bischoff, C.A.; Bock, J.J.; Bowens-Rubin, R.; Brevik, J.A. et al. BICEP2 / Keck Array x: Constraints on Primordial Gravitational Waves using Planck, WMAP, and New BICEP2/Keck Observations through the 2015 Season. Phys. Rev. Lett. 2018, 121, 221301. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, S. Cosmology; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Flanagan, E.E.; Hughes, S.A. The Basics of gravitational wave theory. New J. Phys. 2005, 7, 204. [Google Scholar] [CrossRef]
- Blas, D.; Pujolas, O.; Sibiryakov, S. On the Extra Mode and Inconsistency of Horava Gravity. JHEP 2009, 10, 029. [Google Scholar] [CrossRef]
- Ruegg, H.; Ruiz-Altaba, M. The Stueckelberg field. Int. J. Mod. Phys. A 2004, 19, 3265–3348. [Google Scholar] [CrossRef]
- Beltran Jimenez, J.; Heisenberg, L. Derivative self-interactions for a massive vector field. Phys. Lett. B 2016, 757, 405–411. [Google Scholar] [CrossRef]
- Hinterbichler, K.; Saravani, M. Stückelberg approach to quadratic curvature gravity and its decoupling limits. Phys. Rev. D 2016, 93, 065006. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Langlois, D.; Saito, R.; Yamauchi, D.; Noui, K. Scalar-tensor theories and modified gravity in the wake of GW170817. Phys. Rev. D 2018, 97, 061501. [Google Scholar] [CrossRef]
- Creminelli, P.; Vernizzi, F. Dark Energy after GW170817 and GRB170817A. Phys. Rev. Lett. 2017, 119, 251302. [Google Scholar] [CrossRef] [PubMed]
- Sakstein, J.; Jain, B. Implications of the Neutron Star Merger GW170817 for Cosmological Scalar-Tensor Theories. Phys. Rev. Lett. 2017, 119, 251303. [Google Scholar] [CrossRef]
- Bombacigno, F.; Moretti, F.; Montani, G. Scalar modes in extended hybrid metric-Palatini gravity: Weak field phenomenology. Phys. Rev. D 2019, 100, 124036. [Google Scholar] [CrossRef]
- Rosa, J.A.L.; Lobo, F.S.N.; Olmo, G.J. Weak-field regime of the generalized hybrid metric-Palatini gravity. arXiv 2021, arXiv:2104.10890. [Google Scholar] [CrossRef]
- Madore, J. The dispersion of gravitational waves. Commun. Math. Phys. 1972, 27, 291–302. [Google Scholar] [CrossRef]
- Prasanna, A.R. Propagation of gravitational waves through a dispersive medium. Phys. Lett. A 1999, 257, 120–122. [Google Scholar] [CrossRef]
- Anile, A.M.; Pirronello, V. High-frequency gravitational waves in a dissipative fluid. Nuovo Cimento B Ser. 1978, 48, 90–101. [Google Scholar] [CrossRef]
- Goswami, G.; Chakravarty, G.K.; Mohanty, S.; Prasanna, A.R. Constraints on cosmological viscosity and self interacting dark matter from gravitational wave observations. Phys. Rev. D 2017, 95, 103509. [Google Scholar] [CrossRef]
- Barta, D.; Vasúth, M. Dispersion of gravitational waves in cold spherical interstellar medium. Int. J. Mod. Phys. D 2017, 27, 1850040. [Google Scholar] [CrossRef]
- Ehlers, J.; Prasanna, A.; Breuer, R. Propagation of Gravitational Waves Through Pressureless Matter. Class. Quant. Grav. 1987, 4, 253–264. [Google Scholar] [CrossRef]
- Polnarev, A.G. Interaction between weak gravitational waves and a gas. Zh. Eksp. Teor. Fiz. 1972, 62, 834–837. [Google Scholar]
- Chesters, D. Dispersion of Gravitational Waves by a Collisionless Gas. Phys. Rev. D 1973, 7, 2863. [Google Scholar] [CrossRef]
- Landau, L.D. On the vibrations of the electronic plasma. J. Phys. 1946, 10, 25–34. [Google Scholar]
- Asseo, E.; Gerbal, D.; Heyvaerts, J.; Signore, M. General-relativistic kinetic theory of waves in a massive particle medium. Phys. Rev. D 1976, 13, 2724–2735. [Google Scholar] [CrossRef]
- Gayer, S.; Kennel, C. Possibility of Landau damping of gravitational waves. Phys. Rev. D 1979, 19, 1070–1083. [Google Scholar] [CrossRef]
- Jüttner, F. Das Maxwellsche Gesetz der Geschwindigkeitsverteilung in der Relativtheorie. Ann. Phys. 1911, 339, 856–882. [Google Scholar] [CrossRef]
- Ignatyev, Y.G.; Shulikovsky, V.Y. Relativistic kinetics of collisional damping of gravitational waves in a hot universe. Grav. Cosmol. 2006, 12, 321–327. [Google Scholar]
- Baym, G.; Patil, S.P.; Pethick, C. Damping of gravitational waves by matter. Phys. Rev. D 2017, 96, 084033. [Google Scholar] [CrossRef]
- Stefanek, B.A.; Repko, W.W. Analytic description of the damping of gravitational waves by free streaming neutrinos. Phys. Rev. D 2013, 88, 083536. [Google Scholar] [CrossRef]
- Milillo, I.; Lattanzi, M.; Montani, G. On the coupling between spinning particles and cosmological gravitational waves. Int. J. Mod. Phys. A 2008, 23, 1278–1281. [Google Scholar] [CrossRef]
- Szekeres, P. Linearized gravitation theory in macroscopic media. Ann. Phys. 1971, 64, 599–630. [Google Scholar] [CrossRef]
- Montani, G.; Ruffini, R.; Zalaletdinov, R.M. The Gravitational polarization in general relativity: Solution to Szekeres’ model of quadrupole polarization. Class. Quant. Grav. 2003, 20, 4195–4212. [Google Scholar] [CrossRef]
- Svitek, O. The damping of gravitational waves in dust. Phys. Scr. 2009, 79, 025003. [Google Scholar] [CrossRef]
- Fierz, M.; Pauli, W. On relativistic wave equations for particles of arbitrary spin in an electromagnetic field. Proc. R. Soc. Lond. A 1939, 173, 211–232. [Google Scholar] [CrossRef]
- De Rham, C.; Gabadadze, G.; Tolley, A.J. Resummation of Massive Gravity. Phys. Rev. Lett. 2011, 106, 231101. [Google Scholar] [CrossRef] [PubMed]
- Lu, B.Q.; Huang, D.; Wu, Y.L.; Zhou, Y.F. Damping of gravitational waves in a viscous Universe and its implication for dark matter self-interactions. arXiv 2018, arXiv:1803.11397. [Google Scholar]
- Bahamonde, S.; Dialektopoulos, K.F.; Gakis, V.; Levi Said, J. Reviving Horndeski theory using teleparallel gravity after GW170817. Phys. Rev. D 2020, 101, 084060. [Google Scholar] [CrossRef]
- Bahamonde, S.; Caruana, M.; Dialektopoulos, K.F.; Gakis, V.; Hohmann, M.; Levi Said, J.; Saridakis, E.N.; Sultana, J. Gravitational-wave propagation and polarizations in the teleparallel analog of Horndeski gravity. Phys. Rev. D 2021, 104, 084082. [Google Scholar] [CrossRef]
- Dong, Y.Q.; Liu, Y.X. Polarization Modes of Gravitational Waves in Palatini Horndeski theory. arXiv 2021, arXiv:2111.07352. [Google Scholar]
- Lynden-Bell, D. The stability and vibrations of a gas of stars. Mont. Not. R. Astron. Soc. 1962, 124, 279. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moretti, F.; Bombacigno, F.; Montani, G. The Role of Longitudinal Polarizations in Horndeski and Macroscopic Gravity: Introducing Gravitational Plasmas. Universe 2021, 7, 496. https://doi.org/10.3390/universe7120496
Moretti F, Bombacigno F, Montani G. The Role of Longitudinal Polarizations in Horndeski and Macroscopic Gravity: Introducing Gravitational Plasmas. Universe. 2021; 7(12):496. https://doi.org/10.3390/universe7120496
Chicago/Turabian StyleMoretti, Fabio, Flavio Bombacigno, and Giovanni Montani. 2021. "The Role of Longitudinal Polarizations in Horndeski and Macroscopic Gravity: Introducing Gravitational Plasmas" Universe 7, no. 12: 496. https://doi.org/10.3390/universe7120496
APA StyleMoretti, F., Bombacigno, F., & Montani, G. (2021). The Role of Longitudinal Polarizations in Horndeski and Macroscopic Gravity: Introducing Gravitational Plasmas. Universe, 7(12), 496. https://doi.org/10.3390/universe7120496






