A Fit to the Available e+e− →
Abstract
1. Introduction
2. The Coulomb Factor
The Strong Coulomb-Like Correction
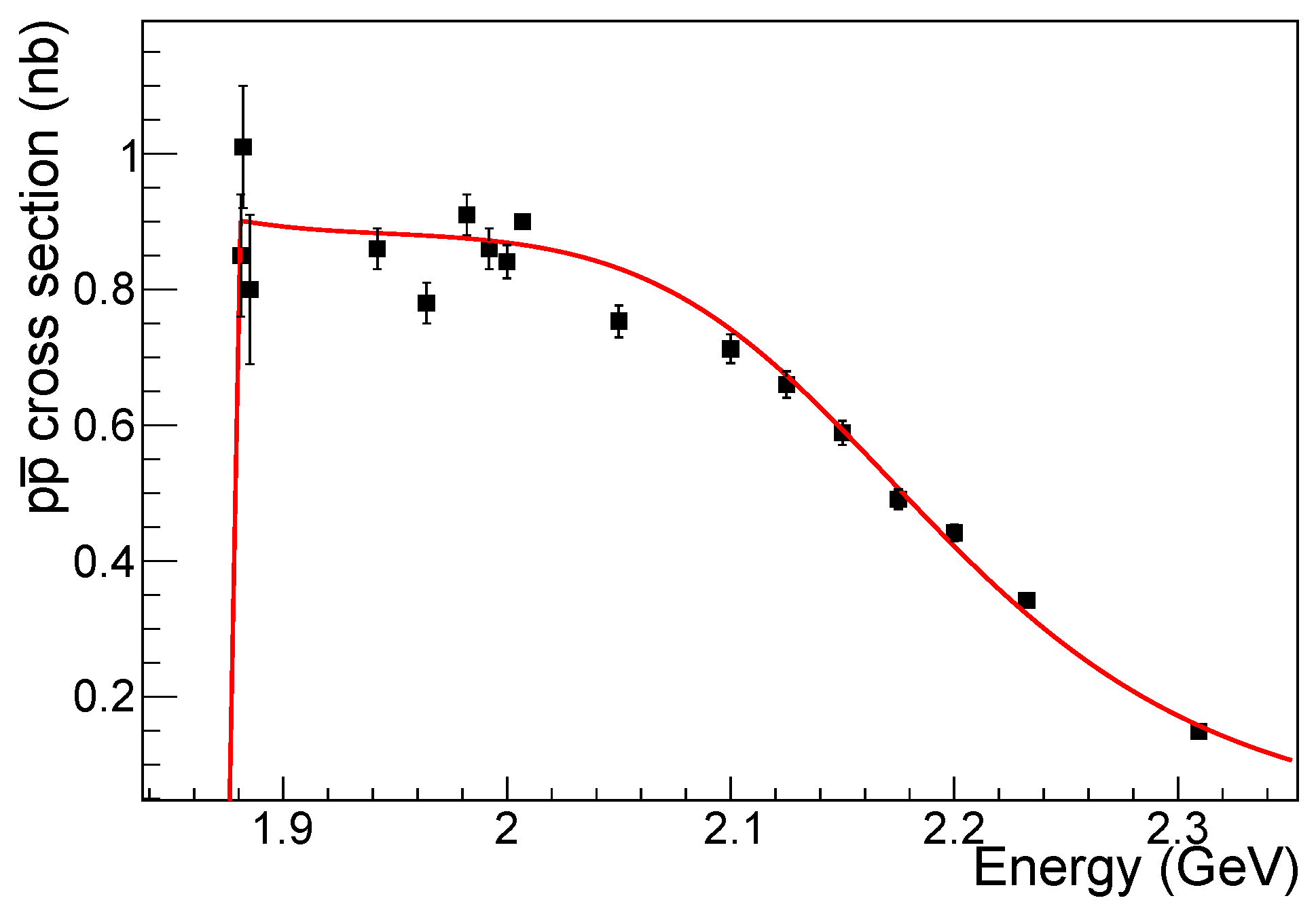
3. The Fit to Cross Section
3.1. The Non-Resonant Component
3.2. Adding the Resonant Component
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ablikim, M. et al. [BESIII Collaboration] Measurement of proton electromagnetic form factors in the time-link region using initial stare radiation at BESIII. Phys. Lett. B 2021, 817, 136328. [Google Scholar] [CrossRef]
- Ablikim, M. et al. [BESIII Collaboration] New Features the Electromagnetic Structure of the Neutron. arXiv 2021, arXiv:2103.12486. [Google Scholar]
- Ablikim, M. et al. [BESIII Collaboration] Observation of a cross-section enhancement near mass threshold in e+e− → . Phys. Rev. D 2018, 97, 032013. [Google Scholar] [CrossRef]
- Ablikim, M. et al. [BESIII Collaboration] Measurement of Σ+ and Σ− time-like electromagnetic form factors for center-of-mass energies from 2.3864 to 3.0200 GeV. Phys. Lett. B 2021, 814, 136110. [Google Scholar] [CrossRef]
- Ablikim, M. et al. [BESIII Collaboration] Measurement of cross section for e+e− → Ξ−Ξ¯+ near threshold at BESIII. Phys. Rev. D 2021, 103, 012005. [Google Scholar] [CrossRef]
- Pakhlova, G. et al. [Belle Collaboration] Observation of a near-threshold enhancement in the e+e− → cross section using initial-state radiation. Phys. Rev. Lett. 2008, 101, 172001. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.L. et al. [BELLE Collaboration] Measurement of e+e− → π+π−ψ (2S) via Initial State Radiation at Belle. Phys. Rev. D 2015, 91, 112007. [Google Scholar] [CrossRef]
- Lees, J.P. et al. [BaBar Collaboration] Study of the reaction e+e− → ψ (2S)π+π− via initial-state radiation at BaBar. Phys. Rev. D 2014, 89, 111103. [Google Scholar] [CrossRef]
- Godfrey, S.; Isgur, N. Mesons in a Relativized Quark Model with Chromodynamics. Phys. Rev. D 1985, 32, 189–231. [Google Scholar] [CrossRef]
- Brambilla, N.; Eidelman, S.; Hanhart, C.; Nefediev, A.; Shen, C.-P.; Thomas, C.E.; Vairo, A.; Yuan, C.-Z. The XYZ states: Experimental and theoretical status and perspective. Phys. Rep. 2020, 873, 1–154. [Google Scholar] [CrossRef]
- Ablikim, M. et al. [BESIII Collaboration] Precision measurement of e+e− → cross section near threshold. Phys. Rev. Lett. 2018, 120, 132001. [Google Scholar]
- Dai, L.-Y.; Haidenbauer, J.; Meissner, U.-G. Re-examining the X(4360) resonance in the reaction e+e−→ . Phys. Rev. D 2017, 96, 116001. [Google Scholar] [CrossRef]
- Epelbaum, E.; Hammer, H.-W.; Meissner, U.-G. Modern Theory of Nuclear Forces. Rev. Mod. Phys. 2009, 81, 1773–1825. [Google Scholar] [CrossRef]
- Epelbaum, E.; Krebs, H.; Meissner, U.-G. Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order. Eur. Phys. J. A 2015, 51, 53. [Google Scholar] [CrossRef]
- Landau, L.; Lifschitz, E. Course of Theoretical Physics, 2nd ed.; Pergamon Press: London, UK, 1982; Volume 4. [Google Scholar]
- Sakharov, A.D. Interaction of Electron and Positron in Pair Production. Zh. Eksp. Teor. Fiz 1948, 18, 631–635. [Google Scholar]
- Ablikim, M. et al. [BESIII Collaboration] Measurement of proton electromagnetic form factors in e+e− → in the energy region 2.00–3.08 GeV. Phys. Rev. Lett. 2020, 124, 042001. [Google Scholar] [CrossRef]
- Ablikim, M. et al. [BESIII Collaboration] Study of the process e+e− → via initial state radiation at BESIII. Phys. Rev. D 2019, 99, 092002. [Google Scholar] [CrossRef]
- Solodov, E.P. et al. [CMD-3 Collaboration] The and multihadron production at the threshold at VEPP2000. EPJ Web Conf. 2019, 212, 07002. [Google Scholar] [CrossRef][Green Version]
- Aubert, B. et al. [BaBar Collaboration] A Study of e+e− → using initial state radiation with BABAR. Phys. Rev. D 2006, 73, 012005. [Google Scholar] [CrossRef]
- Lees, J.P. et al. [BaBar Collaboration] Study of e+e− → via initial-state radiation at BABAR. Phys. Rev. D 2013, 87, 092005. [Google Scholar]
- Baldini, R.; Pacetti, S.; Zallo, A.; Zichichi, A. Unexpected features of e+e− → and e+e− → cross section near threshold. Eur. Phys. J. A 2009, 39, 315–321. [Google Scholar] [CrossRef]
- Baldini, R.; Pacetti, S.; Zallo, A. No Sommerfeld resummation factor in e+e− → ? Eur. Phys. J A 2012, 48, 33. [Google Scholar] [CrossRef]
- Kerbikov, B.; Stavinsky, A.; Fedotov, V. Model independent view on the low mass proton anti-proton enhancement. Phys. Rev. C 2004, 69, 055205. [Google Scholar] [CrossRef]
- Bugg, D.V. Reintepreting several narrow resonances as threshold cusps. Phys. Lett. B 2004, 598, 8. [Google Scholar] [CrossRef][Green Version]
- Zou, B.S.; Chiang, H.C. One pion exchange final state interaction and the p anti-p near threshold enhancement in J/ψ → γ decays. Phys. Rev. D 2004, 69, 034004. [Google Scholar] [CrossRef]
- Loiseau, B.; Wycech, S. Antiproton-proton channels in J/psi decays. Phys. Rev. C 2005, 72, 011001. [Google Scholar] [CrossRef]
- Haidenbauer, J.; Meissner, U.-G.; Sibirtsev, A. Near Threshold p anti-p enhancement in B and J/psi decay. Phys. Rev. D 2006, 74, 017501. [Google Scholar] [CrossRef]
- Sibirtsev, A.; Haidenbauer, J.; Krewald, S.; Meissner, U.-G.; Thomas, A.W. Near threshold enhancement of the p anti-p mass spectrum in J/psi decay. Phys. Rev. D 2005, 71, 054010. [Google Scholar] [CrossRef]
- Dmitriev, V.F.; Milstein, A.I. Final state interaction effects in the e+e− → process near threshold. Phys. Lett. B 2007, 658, 13. [Google Scholar] [CrossRef]
- Zyla, P.A. et al. [Particle Data Group] The Review of Particle Physics (2021). Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Ablikim, M. et al. [BESIII Collaboration] Future Physics Programme of BESIII. Chin. Phys. C 2020, 44, 040001. [Google Scholar]
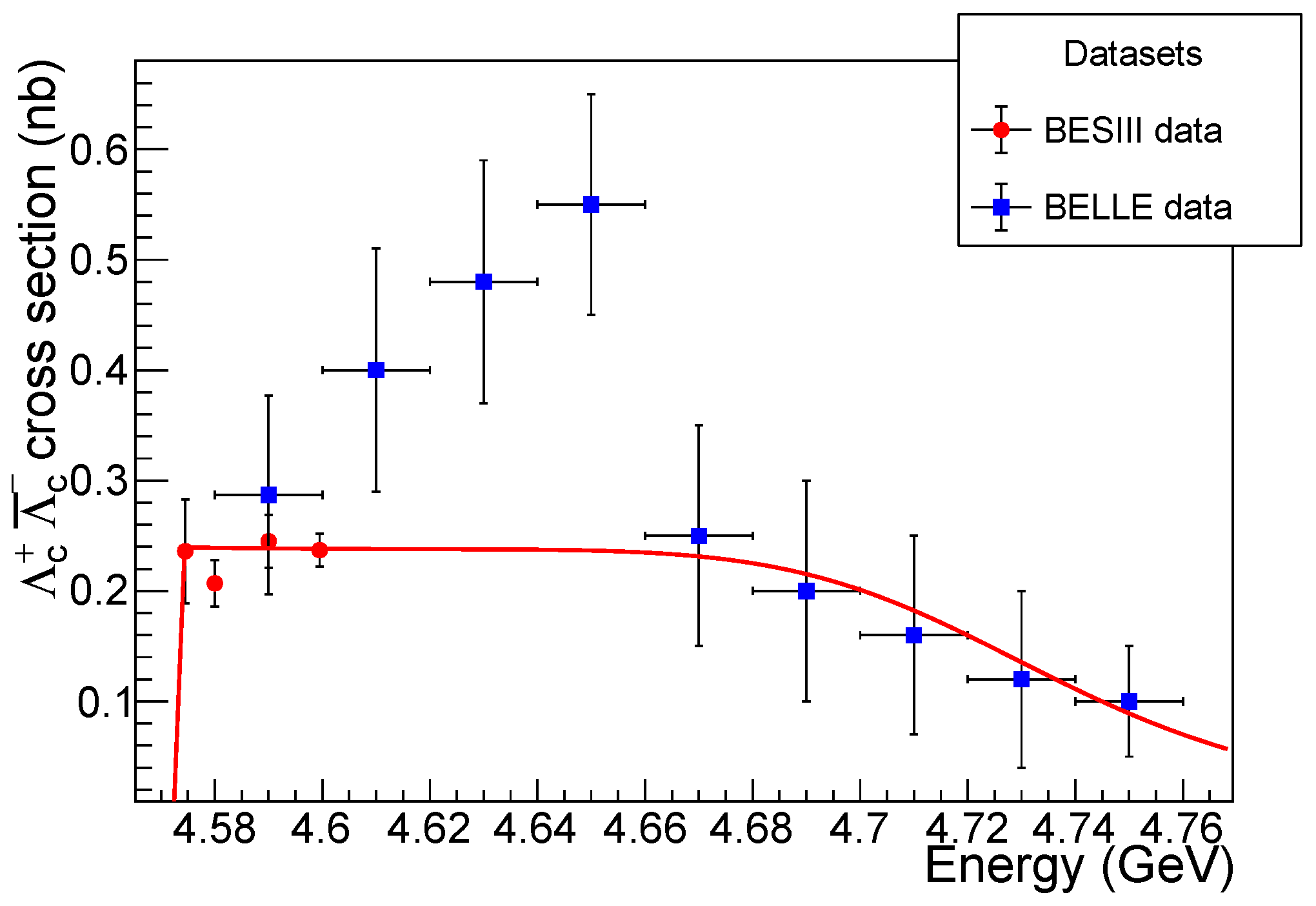
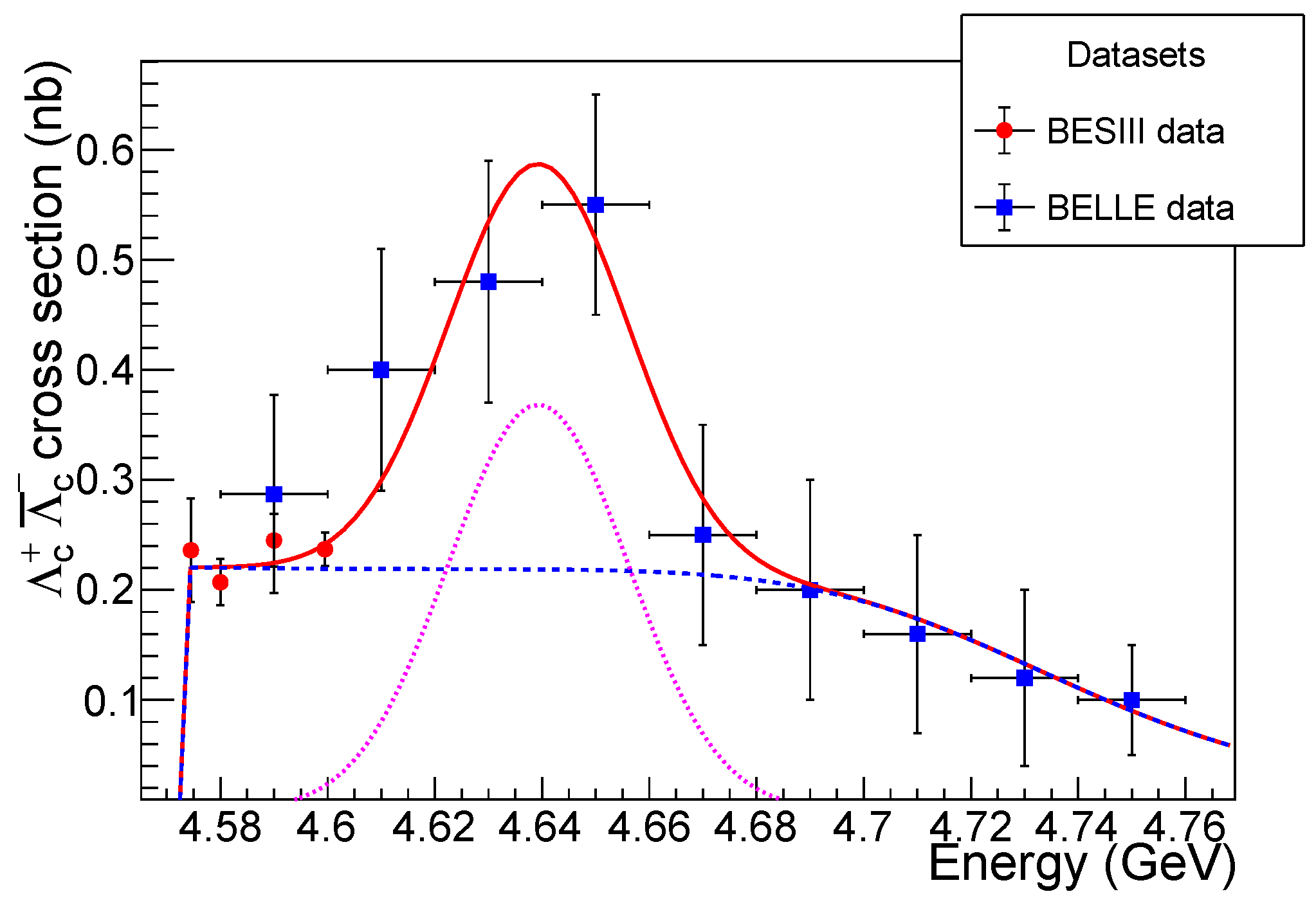
| Mass/GeV/ | /nb | /nb |
|---|---|---|
| 4.58 | 0.239 | 0.221 |
| 4.61 | 0.238 | 0.299 |
| 4.64 | 0.237 | 0.587 |
| 4.67 | 0.231 | 0.282 |
| 4.7 | 0.201 | 0.190 |
| 4.73 | 0.135 | 0.133 |
| 4.76 | 0.07 | 0.071 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amoroso, A.; Bagnasco, S.; Baldini Ferroli, R.; Balossino, I.; Bertani, M.; Bettoni, D.; Bianchi, F.; Bortone, A.; Calcaterra, A.; Cibinetto, G.;
et al. A Fit to the Available e+e− →
Amoroso A, Bagnasco S, Baldini Ferroli R, Balossino I, Bertani M, Bettoni D, Bianchi F, Bortone A, Calcaterra A, Cibinetto G,
et al. A Fit to the Available e+e− →
Amoroso, Antonio, Stefano Bagnasco, Rinaldo Baldini Ferroli, Ilaria Balossino, Monica Bertani, Diego Bettoni, Fabrizio Bianchi, Alberto Bortone, Alessandro Calcaterra, Gianluigi Cibinetto,
and et al. 2021. "A Fit to the Available e+e− →
Amoroso, A., Bagnasco, S., Baldini Ferroli, R., Balossino, I., Bertani, M., Bettoni, D., Bianchi, F., Bortone, A., Calcaterra, A., Cibinetto, G., Cossio, F., De Mori, F., Da Rocha Rolo, M. D., Destefanis, M., Farinelli, R., Fava, L., Felici, G., Gaido, L., Garzia, I.,
... Spataro, S.
(2021). A Fit to the Available e+e− →







