Asymptotic Safety: Swampland or Wonderland?
Abstract
1. Introduction
2. An Overview of Swampland Conjectures
- The weak gravity conjecture (WGC) [64] relates the mass and charge of light states and black holes;
- The trans-Planckian censorship conjecture (TCC) [160,161] constrains sub-Planckian cosmological perturbations to remain sub-Planckian across inflation, and leads to bounds on the lifetime of metastable de Sitter configurations as well as on the parameter that appears in the dSC, at least in asymptotic regions of field space.
2.1. Weak Gravity Conjecture and Black Holes
2.2. de Sitter and Trans-Planckian Censorship
3. One-Loop RG Flow in Quadratic Gravity
4. Results
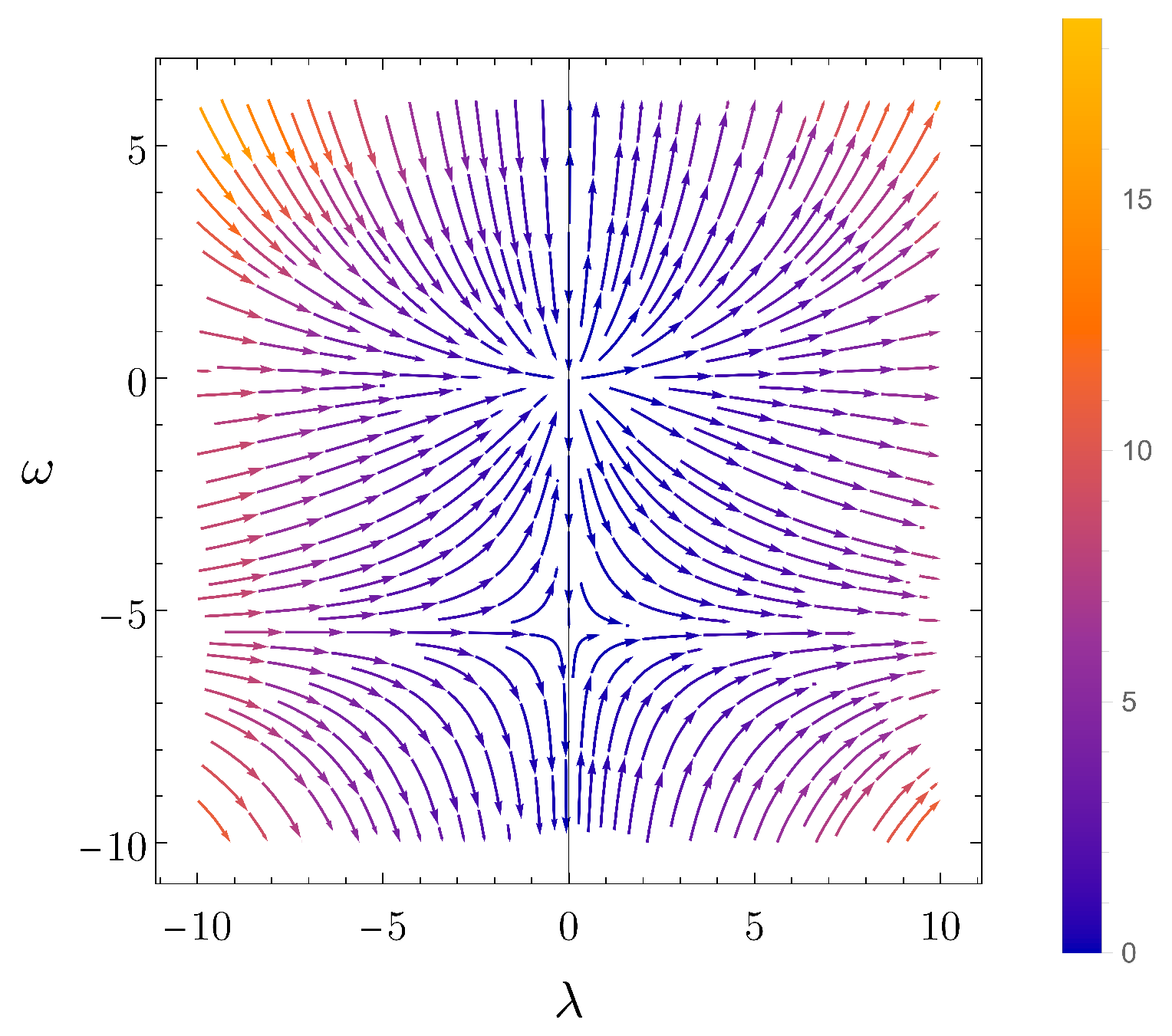
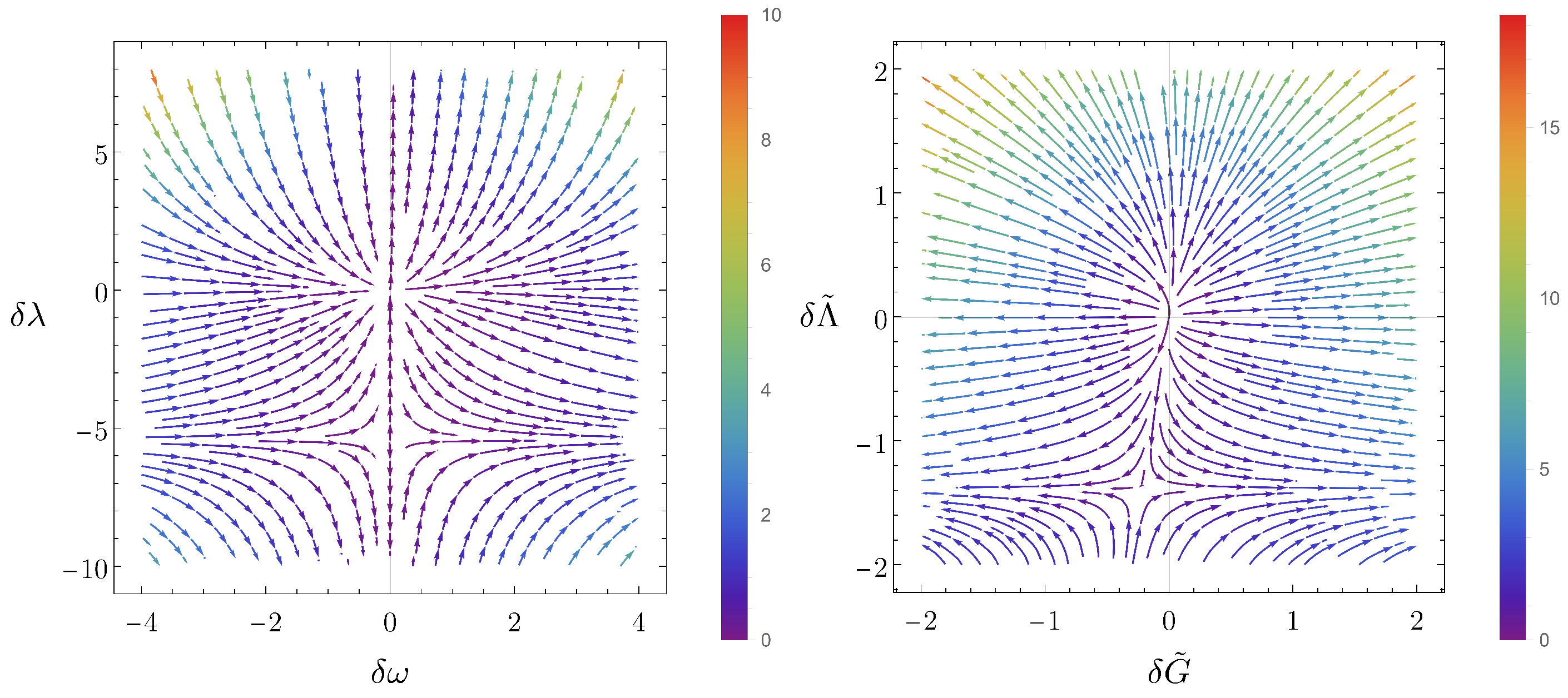
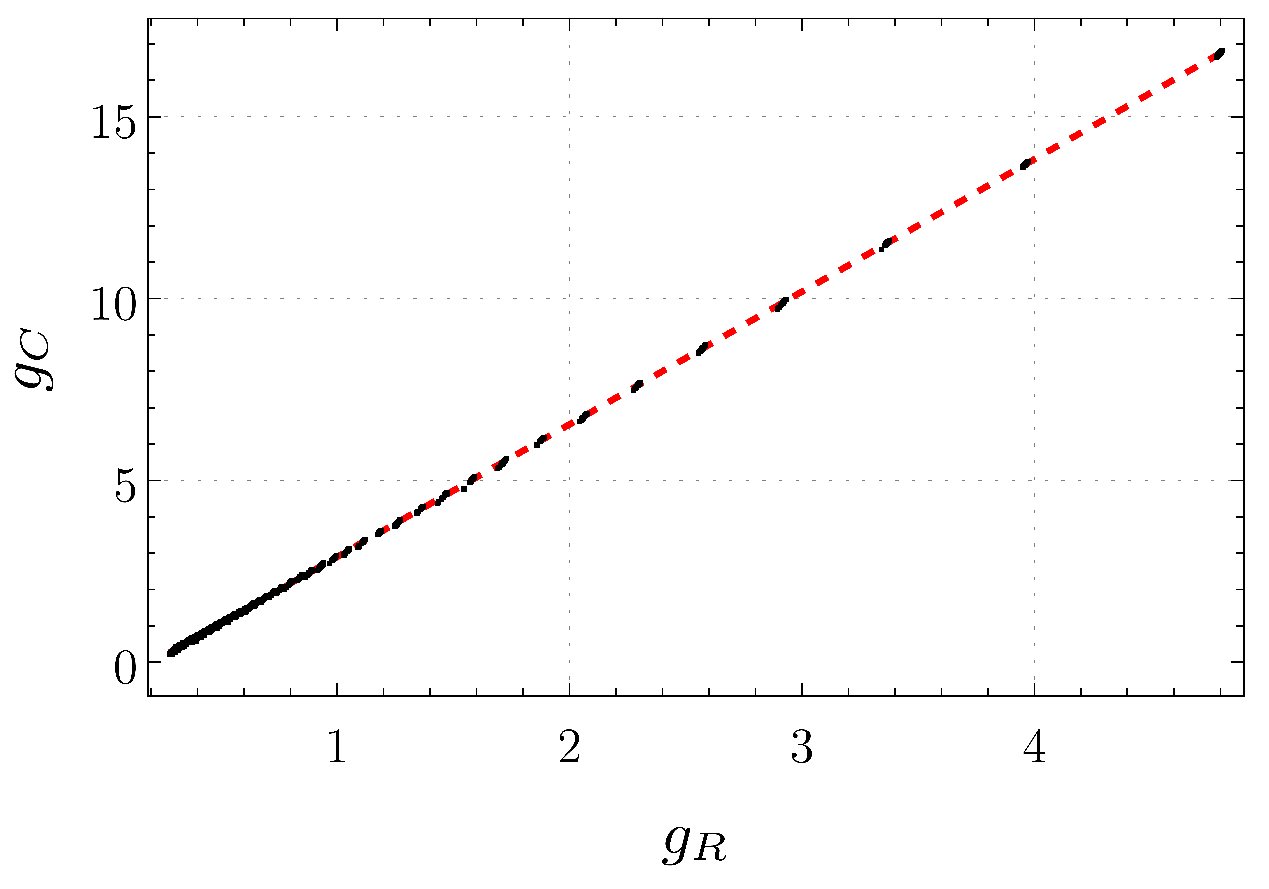
4.1. Infrared Limit of Asymptotically Safe RG Trajectories in One-Loop Quadratic Gravity
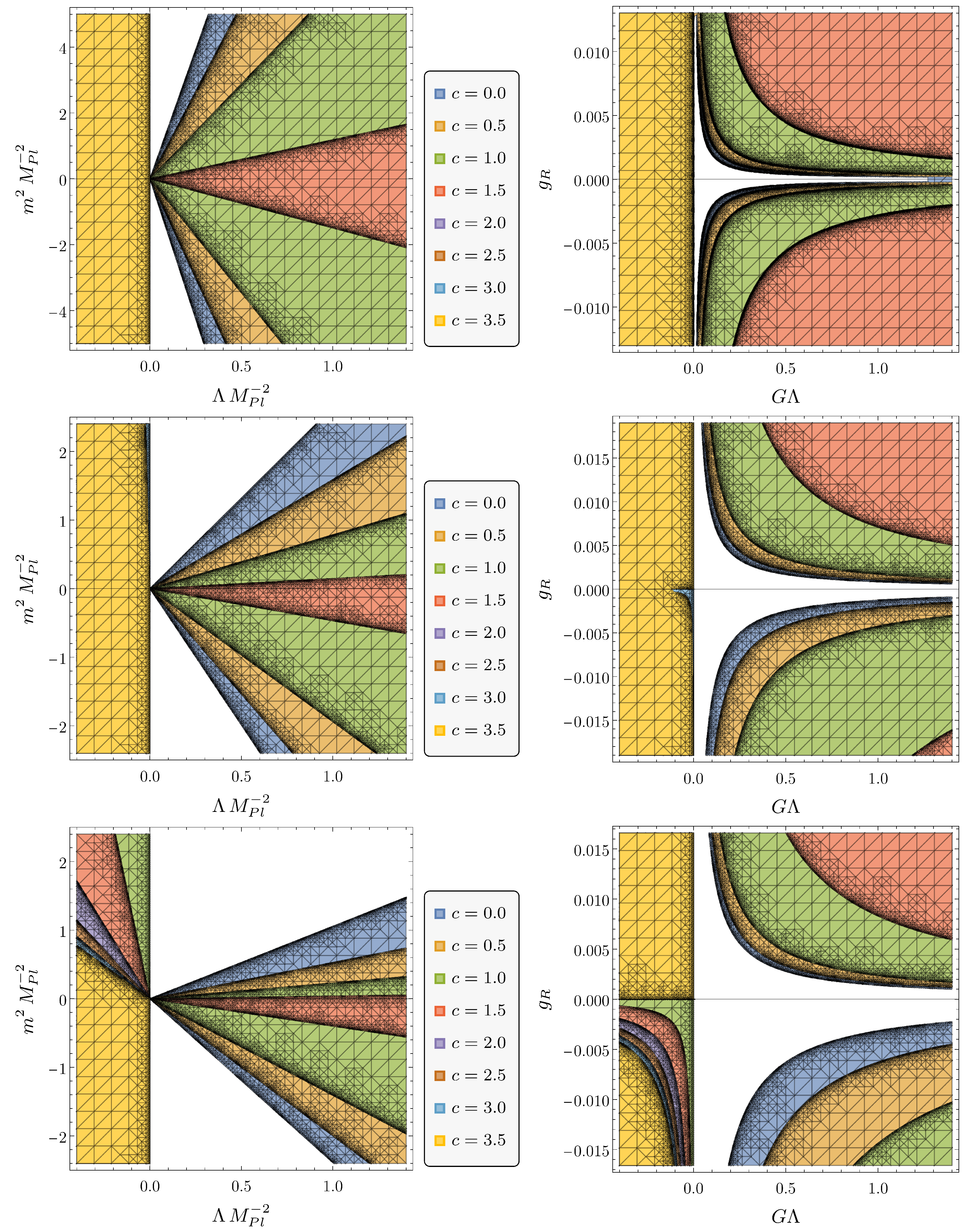
4.2. Constraints on Quadratic Gravity from WGC
4.3. Constraints on Quadratic Gravity from dS and TC Conjectures
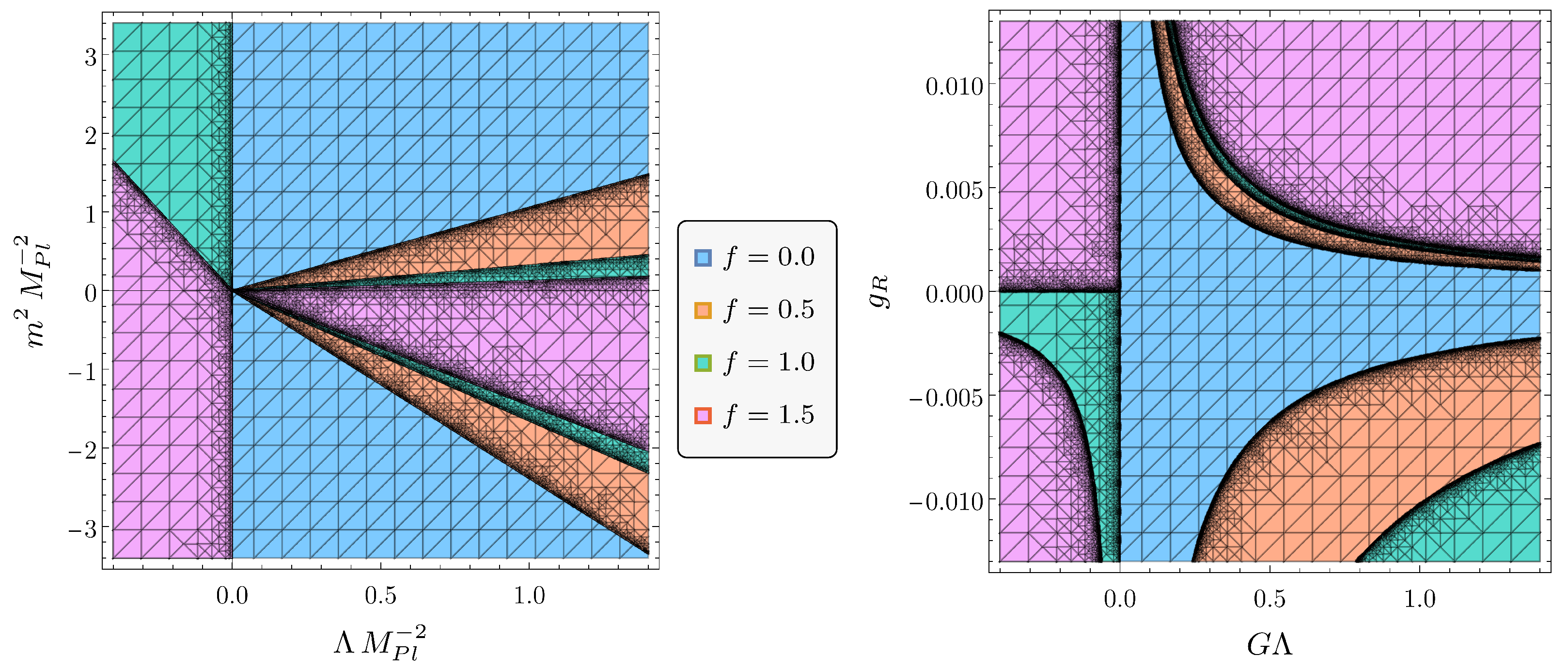
4.4. Intersections of Allowed Regions: Compatibility of Asymptotic Safety with dS, TC and WG Conjectures
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | See also [81] for related discussions on the weak gravity conjecture in the context of asymptotically safe gravity. |
| 2 | |
| 3 | |
| 4 | For Einstein-Maxwell theory, the extremality bound reads . |
| 5 | Another instance of the interplay between duality and the WGC has been studied in [170]. |
| 6 | |
| 7 | Let us remark that here “quadratic” refers to the order in the curvatures. In terms of derivatives, the action in Equation (11) is quartic. |
| 8 | Note that, since we are interested in the IR regime, our convention for the RG time is such that in the IR. |
| 9 | Although 2 and 4 are not the canonical mass dimensions of G and , they are the canonical dimension of the couplings and that multiply the operators and . This occurs because the transformation between these couplings is non-singular, as explained in [180]. On the other hand, at the Gaussian fixed point the transformation between the couplings is singular, and the dimensions change accordingly. |
| 10 | Notice that our convention for the Planck mass differs from the more widespread “reduced” Planck mass . |
| 11 | |
| 12 |
References
- ’t Hooft, G.; Veltman, M.J.G. One loop divergencies in the theory of gravitation. Ann. Inst. Henri Poincare Phys. Theor. A 1974, 20, 69–94. [Google Scholar]
- Goroff, M.H.; Sagnotti, A. The ultraviolet behavior of Einstein gravity. Nucl. Phys. B 1986, 266, 709–736. [Google Scholar] [CrossRef]
- Goroff, M.H.; Sagnotti, A. Quantum gravity at two loops. Phys. Lett. B 1985, 160, 81–86. [Google Scholar] [CrossRef]
- Vafa, C. The String landscape and the swampland. arXiv 2005, arXiv:hep-th/0509212. [Google Scholar]
- Berglund, P.; Mayr, P. Non-perturbative superpotentials in F-theory and string duality. J. High Energy Phys. 2013, 1, 114. [Google Scholar] [CrossRef][Green Version]
- Gonzalo, E.; Ibáñez, L.E.; Uranga, A.M. Modular symmetries and the swampland conjectures. J. High Energy Phys. 2019, 5, 105. [Google Scholar] [CrossRef]
- Marchesano, F.; Wiesner, M. Instantons and infinite distances. J. High Energy Phys. 2019, 8, 088. [Google Scholar] [CrossRef]
- Blumenhagen, R.; Brinkmann, M.; Makridou, A. Quantum Log-Corrections to Swampland Conjectures. J. High Energy Phys. 2020, 2, 064. [Google Scholar] [CrossRef]
- Baume, F.; Marchesano, F.; Wiesner, M. Instanton Corrections and Emergent Strings. J. High Energy Phys. 2020, 4, 174. [Google Scholar] [CrossRef]
- Palti, E.; Vafa, C.; Weigand, T. Supersymmetric Protection and the Swampland. J. High Energy Phys. 2020, 6, 168. [Google Scholar] [CrossRef]
- Marchesano, F.; Prieto, D.; Wiesner, M. F-theory flux vacua at large complex structure. arXiv 2021, arXiv:2105.09326. [Google Scholar]
- Lee, S.J.; Lerche, W.; Weigand, T. Tensionless Strings and the Weak Gravity Conjecture. J. High Energy Phys. 2018, 10, 164. [Google Scholar] [CrossRef]
- Lee, S.J.; Lerche, W.; Weigand, T. A Stringy Test of the Scalar Weak Gravity Conjecture. Nucl. Phys. B 2019, 938, 321–350. [Google Scholar] [CrossRef]
- Lee, S.J.; Lerche, W.; Weigand, T. Modular Fluxes, Elliptic Genera, and Weak Gravity Conjectures in Four Dimensions. J. High Energy Phys. 2019, 8, 104. [Google Scholar] [CrossRef]
- Lee, S.J.; Lerche, W.; Weigand, T. Emergent Strings, Duality and Weak Coupling Limits for Two-Form Fields. arXiv 2019, arXiv:1904.06344. [Google Scholar]
- Klaewer, D.; Lee, S.J.; Weigand, T.; Wiesner, M. Quantum corrections in 4d N = 1 infinite distance limits and the weak gravity conjecture. J. High Energy Phys. 2021, 3, 252. [Google Scholar] [CrossRef]
- Klaewer, D. Modular Curves and the Refined Distance Conjecture. arXiv 2021, arXiv:2108.00021. [Google Scholar]
- Grimm, T.W.; Palti, E.; Valenzuela, I. Infinite Distances in Field Space and Massless Towers of States. J. High Energy Phys. 2018, 8, 143. [Google Scholar] [CrossRef]
- Grimm, T.W.; Van De Heisteeg, D. Infinite Distances and the Axion Weak Gravity Conjecture. J. High Energy Phys. 2020, 3, 020. [Google Scholar] [CrossRef]
- Grimm, T.W.; Li, C.; Valenzuela, I. Asymptotic Flux Compactifications and the Swampland. J. High Energy Phys. 2020, 6, 009, Erratum in 2021, 1, 007. [Google Scholar] [CrossRef]
- Gendler, N.; Valenzuela, I. Merging the weak gravity and distance conjectures using BPS extremal black holes. J. High Energy Phys. 2021, 1, 176. [Google Scholar] [CrossRef]
- Grimm, T.W.; Li, C. Universal axion backreaction in flux compactifications. J. High Energy Phys. 2021, 6, 067. [Google Scholar] [CrossRef]
- Bastian, B.; Grimm, T.W.; van de Heisteeg, D. Modelling General Asymptotic Calabi-Yau Periods. arXiv 2021, arXiv:2105.02232. [Google Scholar]
- Basile, I.; Lanza, S. de Sitter in non-supersymmetric string theories: No-go theorems and brane-worlds. J. High Energy Phys. 2020, 10, 108. [Google Scholar] [CrossRef]
- Basile, I. Supersymmetry breaking, brane dynamics and Swampland conjectures. arXiv 2021, arXiv:2106.04574. [Google Scholar]
- Kachru, S.; Kallosh, R.; Linde, A.D.; Trivedi, S.P. De Sitter vacua in string theory. Phys. Rev. D 2003, 68, 046005. [Google Scholar] [CrossRef]
- Balasubramanian, V.; Berglund, P.; Conlon, J.P.; Quevedo, F. Systematics of moduli stabilisation in Calabi-Yau flux compactifications. J. High Energy Phys. 2005, 3, 007. [Google Scholar] [CrossRef]
- Koerber, P.; Martucci, L. From ten to four and back again: How to generalize the geometry. J. High Energy Phys. 2007, 8, 059. [Google Scholar] [CrossRef]
- Danielsson, U.H.; Haque, S.S.; Shiu, G.; Van Riet, T. Towards Classical de Sitter Solutions in String Theory. J. High Energy Phys. 2009, 9, 114. [Google Scholar] [CrossRef]
- Moritz, J.; Retolaza, A.; Westphal, A. Toward de Sitter space from ten dimensions. Phys. Rev. D 2018, 97, 046010. [Google Scholar] [CrossRef]
- Kallosh, R.; Wrase, T. dS Supergravity from 10d. Fortsch. Phys. 2019, 67, 1800071. [Google Scholar] [CrossRef]
- Bena, I.; Dudas, E.; Graña, M.; Lüst, S. Uplifting Runaways. Fortsch. Phys. 2019, 67, 1800100. [Google Scholar] [CrossRef]
- Gautason, F.; Van Hemelryck, V.; Van Riet, T. The Tension between 10D Supergravity and dS Uplifts. Fortsch. Phys. 2019, 67, 1800091. [Google Scholar] [CrossRef]
- Córdova, C.; De Luca, G.B.; Tomasiello, A. Classical de Sitter Solutions of 10-Dimensional Supergravity. Phys. Rev. Lett. 2019, 122, 091601. [Google Scholar] [CrossRef] [PubMed]
- Blåbäck, J.; Danielsson, U.; Dibitetto, G.; Giri, S. Constructing stable de Sitter in M-theory from higher curvature corrections. J. High Energy Phys. 2019, 9, 042. [Google Scholar] [CrossRef]
- Hamada, Y.; Hebecker, A.; Shiu, G.; Soler, P. Understanding KKLT from a 10d perspective. J. High Energy Phys. 2019, 6, 019. [Google Scholar] [CrossRef]
- Gautason, F.; Van Hemelryck, V.; Van Riet, T.; Venken, G. A 10d view on the KKLT AdS vacuum and uplifting. J. High Energy Phys. 2020, 6, 074. [Google Scholar] [CrossRef]
- Cribiori, N.; Junghans, D. No classical (anti-)de Sitter solutions with O8-planes. Phys. Lett. B 2019, 793, 54–58. [Google Scholar] [CrossRef]
- Andriot, D. Open problems on classical de Sitter solutions. Fortsch. Phys. 2019, 67, 1900026. [Google Scholar] [CrossRef]
- Shukla, P. T-dualizing de Sitter no-go scenarios. Phys. Rev. D 2020, 102, 026014. [Google Scholar] [CrossRef]
- Shukla, P. Rigid nongeometric orientifolds and the swampland. Phys. Rev. D 2021, 103, 086010. [Google Scholar] [CrossRef]
- Córdova, C.; De Luca, G.B.; Tomasiello, A. New de Sitter Solutions in Ten Dimensions and Orientifold Singularities. arXiv 2019, arXiv:1911.04498. [Google Scholar] [CrossRef]
- Andriot, D.; Marconnet, P.; Wrase, T. New de Sitter solutions of 10d type IIB supergravity. J. High Energy Phys. 2020, 8, 076. [Google Scholar] [CrossRef]
- Andriot, D.; Marconnet, P.; Wrase, T. Intricacies of classical de Sitter string backgrounds. arXiv 2020, arXiv:2006.01848. [Google Scholar]
- Farakos, F.; Kehagias, A.; Liatsos, N. de Sitter decay through goldstino evaporation. J. High Energy Phys. 2021, 2, 186. [Google Scholar] [CrossRef]
- Gao, X.; Hebecker, A.; Junghans, D. Control issues of KKLT. Fortsch. Phys. 2020, 68, 2000089. [Google Scholar] [CrossRef]
- Bena, I.; De Luca, G.B.; Graña, M.; Lo Monaco, G. Oh, wait, O8 de Sitter may be unstable! J. High Energy Phys. 2021, 3, 168. [Google Scholar] [CrossRef]
- Bena, I.; Blåbäck, J.; Graña, M.; Lüst, S. The Tadpole Problem. arXiv 2020, arXiv:2010.10519. [Google Scholar]
- Crinò, C.; Quevedo, F.; Valandro, R. On de Sitter String Vacua from Anti-D3-Branes in the Large Volume Scenario. J. High Energy Phys. 2021, 3, 258. [Google Scholar] [CrossRef]
- Dine, M.; Law-Smith, J.A.P.; Sun, S.; Wood, D.; Yu, Y. Obstacles to Constructing de Sitter Space in String Theory. J. High Energy Phys. 2021, 2, 050. [Google Scholar] [CrossRef]
- Basiouris, V.; Leontaris, G.K. Note on de Sitter vacua from perturbative and non-perturbative dynamics in type IIB/F-theory compactifications. Phys. Lett. B 2020, 810, 135809. [Google Scholar] [CrossRef]
- Cribiori, N.; Dall’agata, G.; Farakos, F. Weak gravity versus de Sitter. J. High Energy Phys. 2021, 4, 046. [Google Scholar] [CrossRef]
- Hebecker, A.; Leonhardt, S. Winding Uplifts and the Challenges of Weak and Strong SUSY Breaking in AdS. J. High Energy Phys. 2021, 3, 284. [Google Scholar] [CrossRef]
- Andriot, D. Tachyonic de Sitter solutions of 10d type II supergravities. arXiv 2021, arXiv:2101.06251. [Google Scholar]
- De Luca, G.B.; Silverstein, E.; Torroba, G. Hyperbolic compactification of M-theory and de Sitter quantum gravity. arXiv 2021, arXiv:2104.13380. [Google Scholar]
- Cicoli, M.; Etxebarria, I.n.G.; Quevedo, F.; Schachner, A.; Shukla, P.; Valandro, R. The Standard Model Quiver in de Sitter String Compactifications. arXiv 2021, arXiv:2106.11964. [Google Scholar]
- Cribiori, N.; Junghans, D.; Van Hemelryck, V.; Van Riet, T.; Wrase, T. Scale-separated AdS4 vacua of IIA orientifolds and M-theory. arXiv 2021, arXiv:2107.00019. [Google Scholar]
- Dine, M.; Seiberg, N. Is the Superstring Weakly Coupled? Phys. Lett. B 1985, 162, 299–302. [Google Scholar] [CrossRef]
- Montero, M.; Vafa, C. Cobordism Conjecture, Anomalies, and the String Lamppost Principle. J. High Energy Phys. 2021, 1, 063. [Google Scholar] [CrossRef]
- Misner, C.W.; Wheeler, J.A. Classical physics as geometry: Gravitation, electromagnetism, unquantized charge, and mass as properties of curved empty space. Ann. Phys. 1957, 2, 525–603. [Google Scholar] [CrossRef]
- Polchinski, J. Monopoles, duality, and string theory. Int. J. Mod. Phys. A 2004, 19S1, 145–156. [Google Scholar] [CrossRef]
- Banks, T.; Seiberg, N. Symmetries and Strings in Field Theory and Gravity. Phys. Rev. D 2011, 83, 084019. [Google Scholar] [CrossRef]
- Harlow, D.; Ooguri, H. Symmetries in quantum field theory and quantum gravity. Commun. Math. Phys. 2021, 383, 1669–1804. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Motl, L.; Nicolis, A.; Vafa, C. The String landscape, black holes and gravity as the weakest force. J. High Energy Phys. 2007, 6, 060. [Google Scholar] [CrossRef]
- Benedetti, D.; Groh, K.; Machado, P.F.; Saueressig, F. The universal RG machine. J. High Energy Phys. 2011, 6, 79. [Google Scholar] [CrossRef]
- Knorr, B. The derivative expansion in asymptotically safe quantum gravity: General setup and quartic order. arXiv 2021, arXiv:2104.11336. [Google Scholar]
- Belgacem, E.; Dirian, Y.; Foffa, S.; Maggiore, M. Nonlocal gravity. Conceptual aspects and cosmological predictions. J. Cosmol. Astropart. Phys. 2018, 3, 002. [Google Scholar] [CrossRef]
- Knorr, B.; Saueressig, F. Towards reconstructing the quantum effective action of gravity. Phys. Rev. Lett. 2018, 121, 161304. [Google Scholar] [CrossRef]
- Guerrieri, A.; Penedones, J.; Vieira, P. Where is String Theory? arXiv 2021, arXiv:2102.02847. [Google Scholar]
- Caron-Huot, S.; Mazac, D.; Rastelli, L.; Simmons-Duffin, D. Sharp Boundaries for the Swampland. arXiv 2021, arXiv:2102.08951. [Google Scholar]
- De Rham, C.; Melville, S.; Tolley, A.J.; Zhou, S.Y. UV complete me: Positivity Bounds for Particles with Spin. J. High Energy Phys. 2018, 3, 011. [Google Scholar] [CrossRef]
- De Rham, C.; Melville, S.; Tolley, A.J. Improved Positivity Bounds and Massive Gravity. J. High Energy Phys. 2018, 4, 083. [Google Scholar] [CrossRef]
- De Rham, C.; Melville, S.; Tolley, A.J.; Zhou, S.Y. Positivity Bounds for Massive Spin-1 and Spin-2 Fields. J. High Energy Phys. 2019, 3, 182. [Google Scholar] [CrossRef]
- De Rham, C.; Heisenberg, L.; Tolley, A.J. Spin-2 fields and the weak gravity conjecture. Phys. Rev. D 2019, 100, 104033. [Google Scholar] [CrossRef]
- Alberte, L.; de Rham, C.; Momeni, A.; Rumbutis, J.; Tolley, A.J. EFT of Interacting Spin-2 Fields. J. High Energy Phys. 2020, 1, 131. [Google Scholar] [CrossRef]
- Alberte, L.; de Rham, C.; Momeni, A.; Rumbutis, J.; Tolley, A.J. Positivity Constraints on Interacting Spin-2 Fields. J. High Energy Phys. 2020, 3, 097. [Google Scholar] [CrossRef]
- Alberte, L.; de Rham, C.; Momeni, A.; Rumbutis, J.; Tolley, A.J. Positivity Constraints on Interacting Pseudo-Linear Spin-2 Fields. J. High Energy Phys. 2020, 7, 121. [Google Scholar] [CrossRef]
- Alberte, L.; de Rham, C.; Jaitly, S.; Tolley, A.J. QED positivity bounds. Phys. Rev. D 2021, 103, 125020. [Google Scholar] [CrossRef]
- Alberte, L.; de Rham, C.; Jaitly, S.; Tolley, A.J. Positivity Bounds and the Massless Spin-2 Pole. Phys. Rev. D 2020, 102, 125023. [Google Scholar] [CrossRef]
- De Rham, C.; Melville, S.; Noller, J. Positivity Bounds on Dark Energy: When Matter Matters. arXiv 2021, arXiv:2103.06855. [Google Scholar]
- De Alwis, S.; Eichhorn, A.; Held, A.; Pawlowski, J.M.; Schiffer, M.; Versteegen, F. Asymptotic safety, string theory and the weak gravity conjecture. Phys. Lett. B 2019, 798, 134991. [Google Scholar] [CrossRef]
- Weinberg, S. Critical Phenomena for Field Theorists. In Erice Subnuclear Physics; Springer: Boston, MA, USA, 1976. [Google Scholar]
- Dupuis, N.; Canet, L.; Eichhorn, A.; Metzner, W.; Pawlowski, J.; Tissier, M.; Wschebor, N. The nonperturbative functional renormalization group and its applications. arXiv 2020, arXiv:2006.04853. [Google Scholar]
- Souma, W. Non-Trivial Ultraviolet Fixed Point in Quantum Gravity. Prog. Theor. Phys. 1999, 102, 181–195. [Google Scholar] [CrossRef]
- Lauscher, O.; Reuter, M. Flow equation of quantum Einstein gravity in a higher-derivative truncation. Phys. Rev. D 2002, 66, 025026. [Google Scholar] [CrossRef]
- Litim, D.F. Fixed Points of Quantum Gravity. Phys. Rev. Lett. 2004, 92, 201301. [Google Scholar] [CrossRef] [PubMed]
- Codello, A.; Percacci, R. Fixed Points of Higher-Derivative Gravity. Phys. Rev. Lett. 2006, 97, 221301. [Google Scholar] [CrossRef] [PubMed]
- Machado, P.F.; Saueressig, F. On the renormalization group flow of f(R)-gravity. Phys. Rev. D 2008, 77, 124045. [Google Scholar] [CrossRef]
- Benedetti, D.; Machado, P.F.; Saueressig, F. Asymptotic Safety in Higher-Derivative Gravity. Mod. Phys. Lett. A 2009, 24, 2233–2241. [Google Scholar] [CrossRef]
- Dietz, J.A.; Morris, T.R. Asymptotic safety in the f(R) approximation. J. High Energy Phys. 2013, 1, 108. [Google Scholar] [CrossRef]
- Donà, P.; Eichhorn, A.; Percacci, R. Matter matters in asymptotically safe quantum gravity. Phys. Rev. D 2014, 89, 084035. [Google Scholar] [CrossRef]
- Eichhorn, A. On unimodular quantum gravity. Class. Quantum Gravity 2013, 30, 115016. [Google Scholar] [CrossRef]
- Donà, P.; Eichhorn, A.; Percacci, R. Consistency of matter models with asymptotically safe quantum gravity. Can. J. Phys. 2015, 93, 988–994. [Google Scholar] [CrossRef]
- Christiansen, N.; Knorr, B.; Pawlowski, J.M.; Rodigast, A. Global Flows in Quantum Gravity. Phys. Rev. 2016, D93, 044036. [Google Scholar] [CrossRef]
- Falls, K.; Litim, D.; Nikolakopoulos, K.; Rahmede, C. Further evidence for asymptotic safety of quantum gravity. Phys. Rev. D 2016, 93, 104022. [Google Scholar] [CrossRef]
- Christiansen, N.; Knorr, B.; Meibohm, J.; Pawlowski, J.M.; Reichert, M. Local Quantum Gravity. Phys. Rev. 2015, D92, 121501. [Google Scholar] [CrossRef]
- Meibohm, J.; Pawlowski, J.M.; Reichert, M. Asymptotic safety of gravity-matter systems. Phys. Rev. D 2016, 93, 084035. [Google Scholar] [CrossRef]
- Oda, K.Y.; Yamada, M. Non-minimal coupling in Higgs-Yukawa model with asymptotically safe gravity. Class. Quantum Gravity 2016, 33, 125011. [Google Scholar] [CrossRef]
- Donà, P.; Eichhorn, A.; Labus, P.; Percacci, R. Asymptotic safety in an interacting system of gravity and scalar matter. Phys. Rev. D 2016, 93, 044049. [Google Scholar] [CrossRef]
- Biemans, J.; Platania, A.; Saueressig, F. Quantum gravity on foliated spacetimes: Asymptotically safe and sound. Phys. Rev. 2017, D95, 086013. [Google Scholar] [CrossRef]
- Eichhorn, A.; Held, A.; Pawlowski, J.M. Quantum-gravity effects on a Higgs-Yukawa model. Phys. Rev. D 2016, 94, 104027. [Google Scholar] [CrossRef]
- Dietz, J.A.; Morris, T.R.; Slade, Z.H. Fixed point structure of the conformal factor field in quantum gravity. Phys. Rev. D 2016, 94, 124014. [Google Scholar] [CrossRef]
- Falls, K.; Ohta, N. Renormalization group equation for f(R) gravity on hyperbolic spaces. Phys. Rev. D 2016, 94, 084005. [Google Scholar] [CrossRef]
- Gies, H.; Knorr, B.; Lippoldt, S.; Saueressig, F. Gravitational Two-Loop Counterterm Is Asymptotically Safe. Phys. Rev. Lett. 2016, 116, 211302. [Google Scholar] [CrossRef]
- Biemans, J.; Platania, A.; Saueressig, F. Renormalization group fixed points of foliated gravity-matter systems. J. High Energy Phys. 2017, 5, 093. [Google Scholar] [CrossRef]
- Christiansen, N.; Litim, D.F.; Pawlowski, J.M.; Reichert, M. Asymptotic safety of gravity with matter. Phys. Rev. 2018, D97, 106012. [Google Scholar] [CrossRef]
- Hamada, Y.; Yamada, M. Asymptotic safety of higher derivative quantum gravity non-minimally coupled with a matter system. J. High Energy Phys. 2017, 8, 070. [Google Scholar] [CrossRef]
- Platania, A.; Saueressig, F. Functional Renormalization Group Flows on Friedman–Lemaître–Robertson–Walker backgrounds. Found. Phys. 2018, 48, 1291–1304. [Google Scholar] [CrossRef]
- Falls, K.; King, C.R.; Litim, D.F.; Nikolakopoulos, K.; Rahmede, C. Asymptotic safety of quantum gravity beyond Ricci scalars. Phys. Rev. 2018, D97, 086006. [Google Scholar] [CrossRef]
- De Brito, G.P.; Ohta, N.; Pereira, A.D.; Tomaz, A.A.; Yamada, M. Asymptotic safety and field parametrization dependence in the f(R) truncation. arXiv 2018, arXiv:1805.09656. [Google Scholar] [CrossRef]
- Eichhorn, A.; Lippoldt, S.; Schiffer, M. Zooming in on fermions and quantum gravity. Phys. Rev. 2019, D99, 086002. [Google Scholar] [CrossRef]
- Eichhorn, A.; Schiffer, M. d = 4 as the critical dimensionality of asymptotically safe interactions. Phys. Lett. 2019, B793, 383–389. [Google Scholar] [CrossRef]
- De Brito, G.P.; Eichhorn, A.; Pereira, A.D. A link that matters: Towards phenomenological tests of unimodular asymptotic safety. J. High Energy Phys. 2019, 9, 100. [Google Scholar] [CrossRef]
- Donoghue, J.F. A Critique of the Asymptotic Safety Program. Front. Phys. 2020, 8, 56. [Google Scholar] [CrossRef]
- Bonanno, A.; Eichhorn, A.; Gies, H.; Pawlowski, J.M.; Percacci, R.; Reuter, M.; Saueressig, F.; Vacca, G.P. Critical reflections on asymptotically safe gravity. Front. Phys. 2020, 8, 269. [Google Scholar] [CrossRef]
- Bonanno, A.; Saueressig, F. Asymptotically safe cosmology—A status report. C. R. Phys. 2017, 18, 254–264. [Google Scholar] [CrossRef]
- Platania, A. From renormalization group flows to cosmology. Front. Phys. 2020, 8, 188. [Google Scholar] [CrossRef]
- Bonanno, A.; Reuter, M. Spacetime structure of an evaporating black hole in quantum gravity. Phys. Rev. 2006, D73, 083005. [Google Scholar] [CrossRef]
- Falls, K.; Litim, D.F. Black hole thermodynamics under the microscope. Phys. Rev. 2014, D89, 084002. [Google Scholar] [CrossRef]
- Torres, R.; Fayos, F. On the quantum corrected gravitational collapse. Phys. Lett. B 2015, 747, 245–250. [Google Scholar] [CrossRef]
- Koch, B.; Rioseco, P. Black Hole Solutions for Scale Dependent Couplings: The de Sitter and the Reissner-Nordström Case. Class. Quantum Gravity 2016, 33, 035002. [Google Scholar] [CrossRef]
- Bonanno, A.; Platania, A. Asymptotically safe inflation from quadratic gravity. Phys. Lett. 2015, B750, 638–642. [Google Scholar] [CrossRef]
- Bonanno, A.; Platania, A. Asymptotically Safe R+R2 gravity. PoS 2016, corfu2015, 159. [Google Scholar] [CrossRef][Green Version]
- Kofinas, G.; Zarikas, V. Asymptotically Safe gravity and non-singular inflationary Big Bang with vacuum birth. Phys. Rev. 2016, D94, 103514. [Google Scholar] [CrossRef]
- Falls, K.; Litim, D.F.; Nikolakopoulos, K.; Rahmede, C. On de Sitter solutions in asymptotically safe f(R) theories. Class. Quantum Gravity 2018, 35, 135006. [Google Scholar] [CrossRef]
- Bonanno, A.; Koch, B.; Platania, A. Cosmic Censorship in Quantum Einstein Gravity. Class. Quantum Gravity 2017, 34, 095012. [Google Scholar] [CrossRef]
- Bonanno, A.; Gabriele Gionti, S.J.; Platania, A. Bouncing and emergent cosmologies from Arnowitt-Deser-Misner RG flows. Class. Quantum Gravity 2018, 35, 065004. [Google Scholar] [CrossRef]
- Bonanno, A.; Koch, B.; Platania, A. Asymptotically Safe gravitational collapse: Kuroda-Papapetrou RG-improved model. PoS 2017, corfu2016, 058. [Google Scholar] [CrossRef][Green Version]
- Bonanno, A.; Koch, B.; Platania, A. Gravitational collapse in Quantum Einstein Gravity. arXiv 2017, arXiv:1710.10845. [Google Scholar] [CrossRef]
- Bonanno, A.; Platania, A.; Saueressig, F. Cosmological bounds on the field content of asymptotically safe gravity-matter models. arXiv 2018, arXiv:1803.02355. [Google Scholar] [CrossRef]
- Liu, L.H.; Prokopec, T.; Starobinsky, A.A. Inflation in an effective gravitational model and asymptotic safety. Phys. Rev. 2018, D98, 043505. [Google Scholar] [CrossRef]
- Majhi, A. Singularity from star collapse, torsion and asymptotic safety of gravity. arXiv 2018, arXiv:1804.00960. [Google Scholar]
- Anagnostopoulos, F.K.; Basilakos, S.; Kofinas, G.; Zarikas, V. Constraining the Asymptotically Safe Cosmology: Cosmic acceleration without dark energy. J. Cosmol. Astropart. Phys. 2019, 1902, 053. [Google Scholar] [CrossRef]
- Adeifeoba, A.; Eichhorn, A.; Platania, A. Towards conditions for black-hole singularity-resolution in asymptotically safe quantum gravity. Class. Quantum Gravity 2018, 35, 225007. [Google Scholar] [CrossRef]
- Pawlowski, J.M.; Stock, D. Quantum-improved Schwarzschild-(A)dS and Kerr-(A)dS spacetimes. Phys. Rev. 2018, D98, 106008. [Google Scholar] [CrossRef]
- Gubitosi, G.; Ooijer, R.; Ripken, C.; Saueressig, F. Consistent early and late time cosmology from the RG flow of gravity. J. Cosmol. Astropart. Phys. 2018, 1812, 004. [Google Scholar] [CrossRef]
- Platania, A. The inflationary mechanism in Asymptotically Safe Gravity. Universe 2019, 5, 189. [Google Scholar] [CrossRef]
- Platania, A. Dynamical renormalization of black-hole spacetimes. Eur. Phys. J. 2019, C79, 470. [Google Scholar] [CrossRef]
- Bonanno, A.; Casadio, R.; Platania, A. Gravitational antiscreening in stellar interiors. J. Cosmol. Astropart. Phys. 2020, 2001, 022. [Google Scholar] [CrossRef]
- Held, A.; Gold, R.; Eichhorn, A. Asymptotic safety casts its shadow. J. Cosmol. Astropart. Phys. 2019, 1906, 029. [Google Scholar] [CrossRef]
- Bosma, L.; Knorr, B.; Saueressig, F. Resolving Spacetime Singularities within Asymptotic Safety. Phys. Rev. Lett. 2019, 123, 101301. [Google Scholar] [CrossRef]
- Niedermaier, M.R. Gravitational Fixed Points from Perturbation Theory. Phys. Rev. Lett. 2009, 103, 101303. [Google Scholar] [CrossRef]
- Niedermaier, M. Gravitational fixed points and asymptotic safety from perturbation theory. Nucl. Phys. B 2010, 833, 226–270. [Google Scholar] [CrossRef]
- Cribiori, N.; Lust, D.; Scalisi, M. The gravitino and the swampland. J. High Energy Phys. 2021, 6, 071. [Google Scholar] [CrossRef]
- Castellano, A.; Font, A.; Herraez, A.; Ibáñez, L.E. A Gravitino Distance Conjecture. arXiv 2021, arXiv:2104.10181. [Google Scholar]
- Bonnefoy, Q.; Dudas, E.; Lüst, S. On the weak gravity conjecture in string theory with broken supersymmetry. Nucl. Phys. B 2019, 947, 114738. [Google Scholar] [CrossRef]
- Mourad, J.; Sagnotti, A. An Update on Brane Supersymmetry Breaking. arXiv 2017, arXiv:1711.11494. [Google Scholar]
- Basile, I. Supersymmetry Breaking and Stability in String Vacua: Brane dynamics, bubbles and the swampland. La Rivista del Nuovo Cimento 2021, 1, 98. [Google Scholar] [CrossRef]
- Mourad, J.; Sagnotti, A. String (In)Stability Issues with Broken Supersymmetry. arXiv 2021, arXiv:2107.04064. [Google Scholar]
- Palti, E. The Swampland: Introduction and Review. Fortsch. Phys. 2019, 67, 1900037. [Google Scholar] [CrossRef]
- Van Beest, M.; Calderón-Infante, J.; Mirfendereski, D.; Valenzuela, I. Lectures on the Swampland Program in String Compactifications. arXiv 2021, arXiv:2102.01111. [Google Scholar]
- Andriot, D.; Cribiori, N.; Erkinger, D. The web of swampland conjectures and the TCC bound. J. High Energy Phys. 2020, 7, 162. [Google Scholar] [CrossRef]
- Lanza, S.; Marchesano, F.; Martucci, L.; Valenzuela, I. Swampland Conjectures for Strings and Membranes. J. High Energy Phys. 2021, 2, 006. [Google Scholar] [CrossRef]
- Ooguri, H.; Vafa, C. On the Geometry of the String Landscape and the Swampland. Nucl. Phys. B 2007, 766, 21–33. [Google Scholar] [CrossRef]
- Ooguri, H.; Palti, E.; Shiu, G.; Vafa, C. Distance and de Sitter Conjectures on the Swampland. Phys. Lett. B 2019, 788, 180–184. [Google Scholar] [CrossRef]
- Graña, M.; Herráez, A. The Swampland Conjectures: A bridge from Quantum Gravity to Particle Physics. arXiv 2021, arXiv:2107.00087. [Google Scholar]
- Obied, G.; Ooguri, H.; Spodyneiko, L.; Vafa, C. De Sitter Space and the Swampland. arXiv 2018, arXiv:1806.08362. [Google Scholar]
- Garg, S.K.; Krishnan, C. Bounds on Slow Roll and the de Sitter Swampland. J. High Energy Phys. 2019, 11, 075. [Google Scholar] [CrossRef]
- Andriot, D.; Roupec, C. Further refining the de Sitter swampland conjecture. Fortsch. Phys. 2019, 67, 1800105. [Google Scholar] [CrossRef]
- Bedroya, A.; Vafa, C. Trans-Planckian Censorship and the Swampland. J. High Energy Phys. 2020, 9, 123. [Google Scholar] [CrossRef]
- Brandenberger, R. Trans-Planckian Censorship Conjecture and Early Universe Cosmology. arXiv 2021, arXiv:2102.09641. [Google Scholar]
- Giddings, S.B. Black holes and massive remnants. Phys. Rev. 1992, D46, 1347–1352. [Google Scholar] [CrossRef]
- Susskind, L. Trouble for remnants. arXiv 1995, arXiv:hep-th/9501106. [Google Scholar]
- Kats, Y.; Motl, L.; Padi, M. Higher-order corrections to mass-charge relation of extremal black holes. J. High Energy Phys. 2007, 12, 068. [Google Scholar] [CrossRef]
- Cheung, C.; Liu, J.; Remmen, G.N. Proof of the Weak Gravity Conjecture from Black Hole Entropy. J. High Energy Phys. 2018, 10, 004. [Google Scholar] [CrossRef]
- Charles, A.M.; Larsen, F.; Mayerson, D.R. Non-Renormalization For Non-Supersymmetric Black Holes. J. High Energy Phys. 2017, 8, 048. [Google Scholar] [CrossRef]
- Hamada, Y.; Noumi, T.; Shiu, G. Weak Gravity Conjecture from Unitarity and Causality. Phys. Rev. Lett. 2019, 123, 051601. [Google Scholar] [CrossRef]
- Charles, A.M. The Weak Gravity Conjecture, RG Flows, and Supersymmetry. arXiv 2019, arXiv:1906.07734. [Google Scholar]
- Cano, P.A.; Murcia, A. Duality-invariant extensions of Einstein-Maxwell theory. arXiv 2021, arXiv:2104.07674. [Google Scholar]
- Loges, G.J.; Noumi, T.; Shiu, G. Duality and Supersymmetry Constraints on the Weak Gravity Conjecture. J. High Energy Phys. 2020, 11, 008. [Google Scholar] [CrossRef]
- Kinney, W.H.; Vagnozzi, S.; Visinelli, L. The zoo plot meets the swampland: Mutual (in)consistency of single-field inflation, string conjectures, and cosmological data. Class. Quantum Gravity 2019, 36, 117001. [Google Scholar] [CrossRef]
- Rudelius, T. Dimensional Reduction and (Anti) de Sitter Bounds. arXiv 2021, arXiv:2101.11617. [Google Scholar]
- Rudelius, T. Conditions for (No) Eternal Inflation. J. Cosmol. Astropart. Phys. 2019, 8, 009. [Google Scholar] [CrossRef]
- Chojnacki, J.; Krajecka, J.; Kwapisz, J.H.; Slowik, O.; Strag, A. Is asymptotically safe inflation eternal? J. Cosmol. Astropart. Phys. 2021, 4, 076. [Google Scholar] [CrossRef]
- Jonas, C.; Lehners, J.L.; Quintin, J. Cosmological consequences of a principle of finite amplitudes. Phys. Rev. D 2021, 103, 103525. [Google Scholar] [CrossRef]
- Lüst, D.; Palti, E.; Vafa, C. AdS and the Swampland. Phys. Lett. B 2019, 797, 134867. [Google Scholar] [CrossRef]
- Bedroya, A.; Brandenberger, R.; Loverde, M.; Vafa, C. Trans-Planckian Censorship and Inflationary Cosmology. Phys. Rev. D 2020, 101, 103502. [Google Scholar] [CrossRef]
- Codello, A.; Percacci, R.; Rahmede, C. Investigating the ultraviolet properties of gravity with a Wilsonian renormalization group equation. Ann. Phys. 2009, 324, 414–469. [Google Scholar] [CrossRef]
- Saueressig, F.; Groh, K.; Rechenberger, S.; Zanusso, O. Higher Derivative Gravity from the Universal Renormalization Group Machine. arXiv 2011, arXiv:1111.1743. [Google Scholar]
- Percacci, R. Asymptotic Safety. arXiv 2007, arXiv:0709.3851. [Google Scholar]
- Litim, D.; Satz, A. Limit cycles and quantum gravity. arXiv 2012, arXiv:1205.4218. [Google Scholar]
- Knorr, B.; Ripken, C.; Saueressig, F. Form Factors in Asymptotic Safety: Conceptual ideas and computational toolbox. Class. Quantum Gravity 2019, 36, 234001. [Google Scholar] [CrossRef]
- Draper, T.; Knorr, B.; Ripken, C.; Saueressig, F. Finite Quantum Gravity Amplitudes: No Strings Attached. Phys. Rev. Lett. 2020, 125, 181301. [Google Scholar] [CrossRef]
- Draper, T.; Knorr, B.; Ripken, C.; Saueressig, F. Graviton-Mediated Scattering Amplitudes from the Quantum Effective Action. J. High Energy Phys. 2020, 11, 136. [Google Scholar] [CrossRef]
- Riegert, R.J. A Nonlocal Action for the Trace Anomaly. Phys. Lett. B 1984, 134, 56–60. [Google Scholar] [CrossRef]
- Deser, S. Conformal anomalies: Recent progress. Helv. Phys. Acta 1996, 69, 570–581. [Google Scholar]
- Erdmenger, J.; Osborn, H. Conserved currents and the energy momentum tensor in conformally invariant theories for general dimensions. Nucl. Phys. B 1997, 483, 431–474. [Google Scholar] [CrossRef]
- Erdmenger, J. Conformally covariant differential operators: Properties and applications. Class. Quantum Gravity 1997, 14, 2061–2084. [Google Scholar] [CrossRef]
- Deser, S. Closed form effective conformal anomaly actions in D >= 4. Phys. Lett. B 2000, 479, 315–320. [Google Scholar] [CrossRef][Green Version]
- Bautista, T.; Benevides, A.; Dabholkar, A. Nonlocal Quantum Effective Actions in Weyl-Flat Spacetimes. J. High Energy Phys. 2018, 6, 055. [Google Scholar] [CrossRef]
- Donoghue, J.F.; El-Menoufi, B.K. Covariant non-local action for massless QED and the curvature expansion. J. High Energy Phys. 2015, 10, 044. [Google Scholar] [CrossRef]
- Benedetti, D.; Machado, P.F.; Saueressig, F. Taming perturbative divergences in asymptotically safe gravity. Nucl. Phys. B 2010, 824, 168–191. [Google Scholar] [CrossRef][Green Version]
- Stelle, K.S. Classical Gravity with Higher Derivatives. Class. Quantum Gravity 1978, 9, 353–371. [Google Scholar] [CrossRef]
- Platania, A.; Wetterich, C. Non-perturbative unitarity and fictitious ghosts in quantum gravity. Phys. Lett. B 2020, 811, 135911. [Google Scholar] [CrossRef]
- Bonanno, A.; Denz, T.; Pawlowski, J.M.; Reichert, M. Reconstructing the graviton. arXiv 2021, arXiv:2102.02217. [Google Scholar]
- Myers, R.C.; Simon, J.Z. Black Hole Thermodynamics in Lovelock Gravity. Phys. Rev. D 1988, 38, 2434–2444. [Google Scholar] [CrossRef]
- Myers, R.C. Black holes in higher curvature gravity. In Black Holes, Gravitational Radiation and the Universe: Essays in Honor of C.V. Vishveshwara; Iyer, B.R., Bhawal, B., Eds.; Springer: Dordrecht, The Netherlands, 1998. [Google Scholar] [CrossRef]
- Clunan, T.; Ross, S.F.; Smith, D.J. On Gauss-Bonnet black hole entropy. Class. Quantum Gravity 2004, 21, 3447–3458. [Google Scholar] [CrossRef]
- Martin, J.; Ringeval, C.; Vennin, V. Encyclopædia Inflationaris. Phys. Dark Univ. 2014, 5, 75–235. [Google Scholar] [CrossRef]
- Basile, I.; Platania, A. Cosmological α′-corrections from the functional renormalization group. J. High Energy Phys. 2020, 21, 045. [Google Scholar] [CrossRef]
- Basile, I.; Platania, A. String Tension between de Sitter vacua and Curvature Corrections. arXiv 2021, arXiv:2103.06276. [Google Scholar]
- Percacci, R. An Introduction to Covariant Quantum Gravity and Asymptotic Safety. In 100 Years of General Relativity; World Scientific: Singapore, 2017; Volume 3. [Google Scholar] [CrossRef]
- Reuter, M.; Saueressig, F. Quantum Gravity and the Functional Renormalization Group; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Pawlowski, J.M.; Reichert, M. Quantum gravity: A fluctuating point of view. arXiv 2020, arXiv:2007.10353. [Google Scholar]
- Falls, K.; Ohta, N.; Percacci, R. Towards the determination of the dimension of the critical surface in asymptotically safe gravity. Phys. Lett. B 2020, 810, 135773. [Google Scholar] [CrossRef]
- Barvinsky, A.O.; Vilkovisky, G.A. Beyond the Schwinger-Dewitt Technique: Converting Loops Into Trees and In-In Currents. Nucl. Phys. B 1987, 282, 163–188. [Google Scholar] [CrossRef]
- Barvinsky, A.O.; Vilkovisky, G.A. Covariant perturbation theory. 2: Second order in the curvature. General algorithms. Nucl. Phys. B 1990, 333, 471–511. [Google Scholar] [CrossRef]
- Barvinsky, A.O.; Vilkovisky, G.A. Covariant perturbation theory. 3: Spectral representations of the third order form-factors. Nucl. Phys. B 1990, 333, 512–524. [Google Scholar] [CrossRef]
- Barvinsky, A.O.; Gusev, Y.V.; Zhytnikov, V.V.; Vilkovisky, G.A. Covariant perturbation theory. 4. Third order in the curvature. arXiv 1993, arXiv:0911.1168. [Google Scholar]
- Avramidi, I.G. The Nonlocal Structure of the One Loop Effective Action via Partial Summation of the Asymptotic Expansion. Phys. Lett. B 1990, 236, 443–449. [Google Scholar] [CrossRef]
- Codello, A.; Zanusso, O. On the non-local heat kernel expansion. J. Math. Phys. 2013, 54, 013513. [Google Scholar] [CrossRef]
- Ohta, N.; Rachwal, L. Effective action from the functional renormalization group. Eur. Phys. J. C 2020, 80, 877. [Google Scholar] [CrossRef]
- Donnelly, W.; Giddings, S.B. Diffeomorphism-invariant observables and their nonlocal algebra. Phys. Rev. D 2016, 93, 024030, Erratum in 2016, 94, 029903. [Google Scholar] [CrossRef]
- Rejzner, K. Effective quantum gravity observables and locally covariant QFT. Int. J. Mod. Phys. 2017, 1, 13–28. [Google Scholar] [CrossRef]
- Donnelly, W.; Giddings, S.B. Observables, gravitational dressing, and obstructions to locality and subsystems. Phys. Rev. D 2016, 94, 104038. [Google Scholar] [CrossRef]
- Klitgaard, N.; Loll, R. Introducing Quantum Ricci Curvature. Phys. Rev. D 2018, 97, 046008. [Google Scholar] [CrossRef]
- Rudelius, T. Asymptotic Observables and the Swampland. arXiv 2021, arXiv:2106.09026. [Google Scholar]
- Susskind, L.; Thorlacius, L.; Uglum, J. The Stretched horizon and black hole complementarity. Phys. Rev. D 1993, 48, 3743–3761. [Google Scholar] [CrossRef] [PubMed]
- Almheiri, A.; Marolf, D.; Polchinski, J.; Sully, J. Black Holes: Complementarity or Firewalls? J. High Energy Phys. 2013, 2, 062. [Google Scholar] [CrossRef]
- Giddings, S.B. Nonviolent nonlocality. Phys. Rev. D 2013, 88, 064023. [Google Scholar] [CrossRef]
- Dvali, G.; Gomez, C.; Isermann, R.S.; Lüst, D.; Stieberger, S. Black hole formation and classicalization in ultra-Planckian 2 − N scattering. Nucl. Phys. B 2015, 893, 187–235. [Google Scholar] [CrossRef]
- Keltner, L.; Tolley, A.J. UV properties of Galileons: Spectral Densities. arXiv 2015, arXiv:1502.05706. [Google Scholar]
- Mann, R.B. Black Holes: Thermodynamics, Information, and Firewalls; Springer Briefs in Physics; Springer: Berlin, Germany, 2015. [Google Scholar] [CrossRef]
- Modesto, L. Super-renormalizable Quantum Gravity. Phys. Rev. D 2012, 86, 044005. [Google Scholar] [CrossRef]
- Modesto, L.; Rachwał, L.A. Nonlocal quantum gravity: A review. Int. J. Mod. Phys. D 2017, 26, 1730020. [Google Scholar] [CrossRef]
- Buoninfante, L.; Lambiase, G.; Mazumdar, A. Ghost-free infinite derivative quantum field theory. Nucl. Phys. B 2019, 944, 114646. [Google Scholar] [CrossRef]
- Buoninfante, L.; Koshelev, A.S.; Lambiase, G.; Mazumdar, A. Classical properties of non-local, ghost- and singularity-free gravity. J. Cosmol. Astropart. Phys. 2018, 9, 034. [Google Scholar] [CrossRef]
- Giddings, S.B. Locality in quantum gravity and string theory. Phys. Rev. D 2006, 74, 106006. [Google Scholar] [CrossRef]
- Buoninfante, L.; Di Filippo, F.; Mukohyama, S. On the assumptions leading to the information loss paradox. arXiv 2021, arXiv:2107.05662. [Google Scholar]
- Veneziano, G. Scale factor duality for classical and quantum strings. Phys. Lett. B 1991, 265, 287–294. [Google Scholar] [CrossRef]
- Meissner, K.; Veneziano, G. Symmetries of cosmological superstring vacua. Phys. Lett. B 1991, 267, 33–36. [Google Scholar] [CrossRef]
- Meissner, K.A. Symmetries of higher order string gravity actions. Phys. Lett. B 1997, 392, 298–304. [Google Scholar] [CrossRef]
- Hohm, O.; Zwiebach, B. T-duality Constraints on Higher Derivatives Revisited. J. High Energy Phys. 2016, 4, 101. [Google Scholar] [CrossRef]
- Hohm, O.; Zwiebach, B. Non-perturbative de Sitter vacua via α′ corrections. Int. J. Mod. Phys. D 2019, 28, 1943002. [Google Scholar] [CrossRef]
- Hohm, O.; Zwiebach, B. Duality invariant cosmology to all orders in α′. Phys. Rev. D 2019, 100, 126011. [Google Scholar] [CrossRef]
- Held, A. Effective asymptotic safety and its predictive power: Gauge-Yukawa theories. Front. Phys. 2020, 8, 341. [Google Scholar] [CrossRef]
- Eichhorn, A.; Pauly, M. Constraining power of asymptotic safety for scalar fields. Phys. Rev. D 2021, 103, 026006. [Google Scholar] [CrossRef]
- Ali, P.; Eichhorn, A.; Pauly, M.; Scherer, M.M. Constraints on discrete global symmetries in quantum gravity. J. High Energy Phys. 2021, 5, 036. [Google Scholar] [CrossRef]
- Banks, T.; Dixon, L.J. Constraints on String Vacua with Space-Time Supersymmetry. Nucl. Phys. B 1988, 307, 93–108. [Google Scholar] [CrossRef]
- Kallosh, R.; Linde, A.D.; Linde, D.A.; Susskind, L. Gravity and global symmetries. Phys. Rev. D 1995, 52, 912–935. [Google Scholar] [CrossRef]
- McNamara, J.; Vafa, C. Cobordism Classes and the Swampland. arXiv 2019, arXiv:1909.10355. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basile, I.; Platania, A. Asymptotic Safety: Swampland or Wonderland? Universe 2021, 7, 389. https://doi.org/10.3390/universe7100389
Basile I, Platania A. Asymptotic Safety: Swampland or Wonderland? Universe. 2021; 7(10):389. https://doi.org/10.3390/universe7100389
Chicago/Turabian StyleBasile, Ivano, and Alessia Platania. 2021. "Asymptotic Safety: Swampland or Wonderland?" Universe 7, no. 10: 389. https://doi.org/10.3390/universe7100389
APA StyleBasile, I., & Platania, A. (2021). Asymptotic Safety: Swampland or Wonderland? Universe, 7(10), 389. https://doi.org/10.3390/universe7100389






