Multi-Modal Clustering Events Observed by Horizon-10T and Axion Quark Nuggets

Abstract

The Horizon-10T collaboration have reported observation of Multi-Modal Events (MME) containing multiple peaks suggesting their clustering origin. These events are proven to be hard to explain in terms of conventional cosmic rays (CR). We propose that these MMEs might be result of the dark matter annihilation events within the so-called axion quark nugget (AQN) dark matter model, which was originally invented for completely different purpose to explain the observed similarity between the dark and the visible components in the Universe, i.e., ${\mathrm{\Omega }}_{\mathrm{DM}}\sim {\mathrm{\Omega }}_{\mathrm{visible}}$ without any fitting parameters. We support this proposal by demonstrating that the observations, including the frequency of appearance, intensity, the spatial distribution, the time duration, the clustering features, and many other properties nicely match the emission characteristics of the AQN annihilation events in atmosphere. We list a number of features of the AQN events which are very distinct from conventional CR air showers. The observation (non-observation) of these features may substantiate (refute) our proposal.

1. Introduction

In this work we discuss two naively unrelated stories. The first one deals with the recent puzzling observations [1,2,3,4,5] by the Horizon-10T (H10T) collaboration of the Multi-Modal Events (MME).

The second one is the study of a specific dark matter (DM) model, the so-called axion quark nugget (AQN) model [6], see a brief overview of this model below. We overview the corresponding events below in details. We also highlight some difficulties in interpretation of these events in terms of the standard CR air showers. The unusual features of MME include:

1. 

“clustering puzzle”: Two or more peaks separated by ∼${10}^2$ ns are present in several detection points, while entire event may last ∼${10}^3$ ns. It can be viewed as many fronts separated by ∼(${10}^2$–${10}^3$) ns, instead of a single front;

2. 

“particle density puzzle”: The number density of particles recorded at different detection points apparently weakly dependent on distance from Extensive Air Showers (EAS) axis;

3. 

“pulse width puzzle”: The width of each individual pulse is around (20–35) ns and apparently does not depend on distance from EAS axis;

4. 

“intensity puzzle”: The observed intensity of the events (measured in units of a number of particles per unit area) is of order $\rho \sim$ (100–300) ${\mathrm{m}}^{-2}$

When measured at distances (300–800) m from EAS axis. Such intensity would correspond to the CR energy of the primary particle on the level $E_p\gtrsim {10}^{19}$ eV which would have dramatically different event rate in comparison with observed rate recorded by H10T.

Before we proceed with our explanation of the proposal to view the MMEs as the AQN events one should mention that similar unusual features of the CR air showers have been noticed long ago for the first time by Jelley and Whitehouse [7] in 1953. Later, EAS exhibiting the unusual time structures were studied by several independent experiments, see e.g., [8]. We refer to ref. [2] for overview and references of the older observations and studies of such unusual events.

The considerable recent advances in rising the resolution (on the level of a few ns) has allowed the H10T collaboration dramatically improve the collection and analysis of the MMEs. In particular, during ∼3500 h of operation the H10T collaboration collected more than ${10}^3$ MMEs.

In what follows we overview the observation [1,2,3,4,5] by emphasizing the puzzling nature of these events if interpreted as conventional EAS events. At the same time the same observations can be explained in very natural way if interpreted in terms of the AQN annihilation events as we shall argue in this work. One should mention here that a similar conclusion has been also reached for a different type of unusual CR-like events. First, it has been argued in [9,10] that the Telescope Array (TA) “mysterious bursts” [11,12] can be naturally interpreted as the AQN events. Secondly, it has been also argued in [13] that the Antarctic Impulse Transient Antenna (ANITA) observation [14,15,16] of two anomalous events with noninverted polarity might be also a consequence of the AQN annihilation events. Important comment here that in all those cases the basic parameters of the AQN model remain the same as they have been fixed long ago from dramatically different observations in a very different context.

Our presentation is organized as follows. In next Section 2 we explain why the observation [1,2,3,4,5] listed as 1–4 puzzles are very mysterious events if interpreted as conventional EAS events. In Section 3 we give a brief overview of the AQN framework with emphasize on the key elements relevant for the present studies. In Section 4 we formulate our proposal on identification of the unusual Multi-Modal Events with the upward moving AQN events. In Section 5 we estimate the event rate. Our main section is Section 6 where we estimate a variety of relevant time scales and the intensity of the events. In the same section we also confront our proposal with observations and argue that puzzles 1–4 can be naturally understood within the AQN framework. Section 7 is our conclusion where we suggest several tests which may substantiate or refute our proposal on identification of the Multi-Modal Cluster Events with the upward moving AQNs.

2. Conventional CR Picture Confronts the MME Observations

This section is devoted to the first part of our story where we describe the MME observations [1,2,3,4,5] and argue why the observed events are inconsistent with conventional CR interpretation, while the next Section 3 is devoted to the second part of our story, the AQN dark matter model.

We start by reviewing the conventional picture of the EAS. It is normally assumed that EAS can be thought as a disk -pancake with well defined EAS axis. It is also assumed that EAS represents an uniform, without any breaks structure. The standard picture also assumes that the particle density drops smoothly with distance when moving away from the core, while the thickness of the EAS pancake increases with the distance from the core. Now we want to see why this conventional picture is in dramatic contradiction with observations of the MME events.

1. 

Indeed, a typical MME is shown on Figure 1 where a complicated temporal features are explicitly seen. Several peaks separated by ∼${10}^2$ ns in a single detector represent the “clustering puzzle”, listed above. In conventional EAS picture one should see a single pulse in each given detector with the amplitude which depends on the distance from the EAS axis. It is not what actually observed by H10T.

2. 

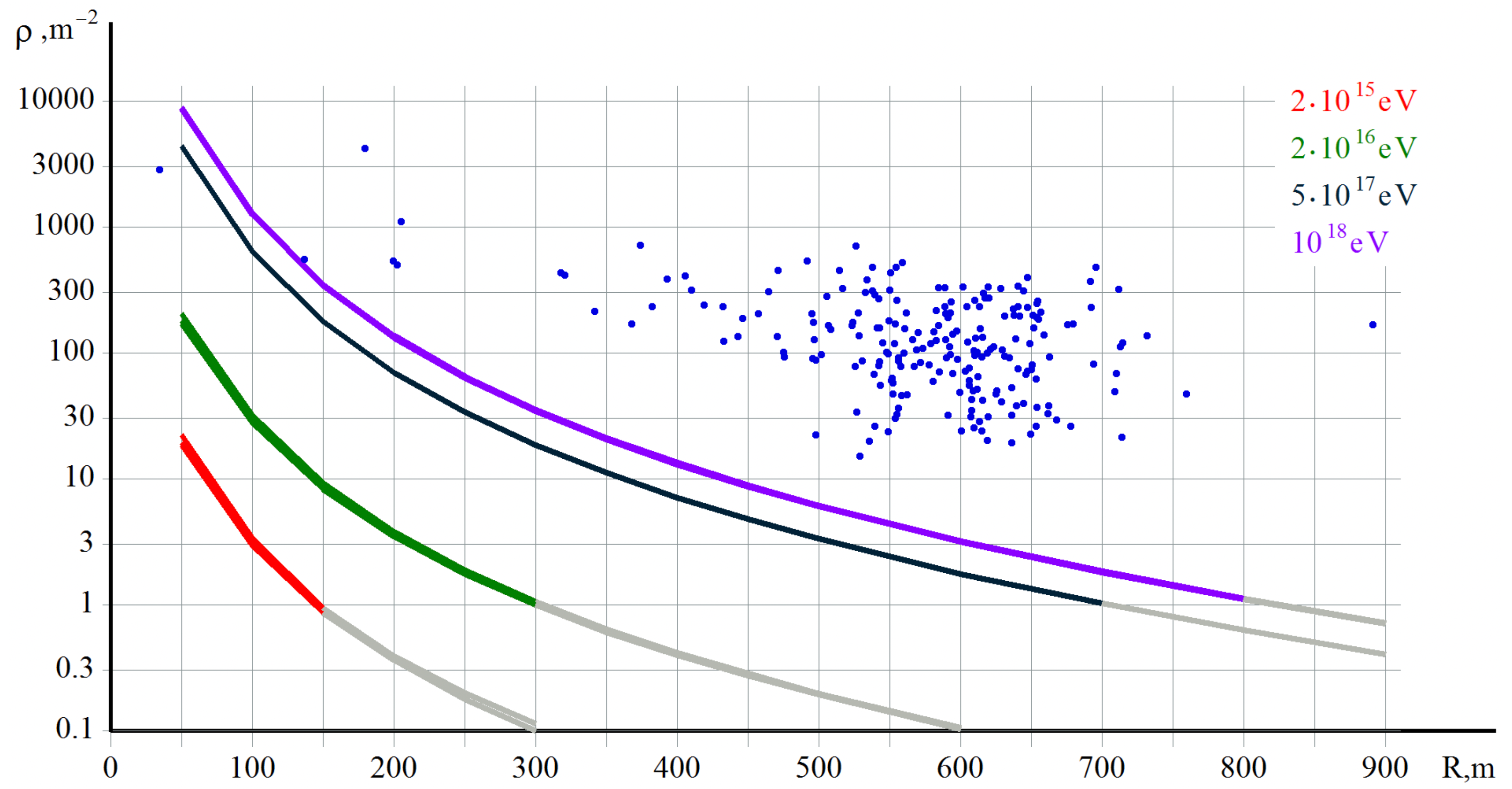
The manifestation of the “particle density puzzle” is as follows. On Figure 2 we show the particle density distribution $\rho \left(R\right)$ in simulated EAS disk versus distance from axis for different energies shown by solid lines with different colours, depending on energy of the CR. In particular, for energy of the primary particle on the level of ${10}^{17}$ eV one should expect a strong suppression ∼${10}^3$ when distance R to the EAS axis changes from $R\simeq 100$ m to $R\simeq 700$ m. It is not what actually observed by H10T: the density of the particles $\rho \left(R\right)$ is not very sensitive to the distance to the EAS axis, and remains essentially flat for the entire region of observations. Furthermore, the magnitude of the density $\rho \left(R\right)$ is much higher than it is normally expected for CR energies ∼(${10}^{17}$–${10}^{18}$) eV.

3. 

The manifestation of the “pulse width puzzle” is as follows. On Figure 3 we show the simulated EAS disk width versus distance from axis for different energies shown by solid lines in different colours. As explained above the thickness of the EAS pancake increases with the distance from the core. Therefore, the pulse width must also increase correspondingly as shown by sold lines on Figure 3 for different energies. It is not what actually observed by H10T: all MME events show similar duration of the pulse width on the level of (20–35) ns irrespective to the distance to the AES axis. This observation is in dramatic conflict with conventional picture as outlined above.

4. 

The manifestation of the “intensity puzzle” is as follows. The Figure 2 suggests that the charged particle density $\rho \left(R\right)$ varies between (30–300) particles per m${}^2$ at the distances (500–700) m from the EAS axis. This is at least factor ${10}^2$ above the expected $\rho \left(R\right)$ for the primary particle with energy in the interval (${10}^{17}$–${10}^{18}$) eV. Only the particles with energies well above ${10}^{19}$ eV could generate such enormous particle density as shown on Figure 2. However the frequency of appearance for such highly energetic particles is only once every few years. This represents the “intensity puzzle” when the intensity of the events estimated from $\rho \left(R\right)$ for MME is several orders of magnitude higher than the energy estimated by the event rate. This shows a dramatic inconsistency between the measured intensity and observed event rate carried out by one and the same detector.

We conclude this section with the following comment. From the puzzles listed above it must be obvious that the events detected by H10T are not the conventional CR air showers as they demonstrate enormous inconsistency with standard CR interpretation. What it could be? Before we put forward our proposal we would like to briefly overview in next Section 3 the second part of our story- the AQN dark matter model.

3. The AQN Dark Matter Model

We start with few historical remarks and motivation of the AQN model in Section 3.1, while in Section 3.2 we overview recent observations of CR-like events (such as puzzling bursts observed by the TA experiment and ANITA’s two anomalous events with non-inverted polarity) of some mysterious events which could be explained by the AQN events hitting the Earth. Finally, in Section 3.3 we briefly overview some specific features of the AQNs traversing the Earth (such as internal temperature, level of ionization, etc.). These characteristics will be important for the present study interpreting the MMEs as the AQN events.

3.1. The Basics

The AQN dark matter model [6] was invented long ago with a single motivation to explain in natural way the observed similarity between the dark matter and the visible densities in the Universe, i.e., ${\mathrm{\Omega }}_{\mathrm{DM}}\sim {\mathrm{\Omega }}_{\mathrm{visible}}$ without any fitting parameters. We refer to recent brief review [17] on the AQN model. Here we want to mention few key elements which are important for this work.

The AQN construction in many respects is similar to the Witten’s quark nuggets, see [18,19,20], and review [21]. This type of DM is “cosmologically dark” not because of the weakness of the AQN interactions, but due to their small cross-section-to-mass ratio, which scales down many observable consequences of an otherwise strongly-interacting DM candidate.

There are two additional elements in the AQN model compared to the original models [18,19,20,21]:

(a). First new element is the presence of the axion domain walls which are copiously produced during the QCD transition. The axion field $\theta \left(x\right)$ plays a dual role in this framework: it serves as an additional stabilization factor for the nuggets, which helps to alleviate a number of problems with the original nugget construction [18,19,20,21]. Furthermore, the same axion field $\theta \left(x\right)$ generates the strong and coherent $\mathcal{CP}$ violation in the entire visible Universe. This is because the $\theta \left(x\right)$ axion field before the QCD epoch could be thought as classical $\mathcal{CP}$ violating field correlated on the scale of the entire Universe.

One should comment here that the axion field had been introduced into the theory to resolve the so-called the strong $\mathcal{CP}$ problem which is related to the fundamental initial parameter ${\theta }_0\ne 0$. The axion remains the most compelling resolution of the strong $\mathcal{CP}$ problem and it also represents a DM candidate, see original papers on the axion [22,23,24,25,26,27,28], and recent reviews [29,30,31,32,33,34,35,36,37]. The most recent constraints on the axion mass for entire broad classical window $m_a\in$ (${10}^{-6}$–${10}^{-3}$) $\mathrm{eV}$ is set by the CAST collaboration [38], while the world best constraints in specific narrow bands around $m_a\sim {10}^{-5}$ eV are imposed by different cavity type detectors, see review articles mentioned above for references and details.

One should also comment here that in recent years many researchers consider the so-called axion-like models when the axion coupling constant $f_a$ and its mass $m_a$ are completely decoupled, in contrast with the original models [22,23,24,25,26,27,28] when these parameters are linked: $m_a{f}_a\sim {\mathrm{\Lambda }}_{\mathrm{QCD}}^2$. In axion-like models the strong $\mathcal{CP}$ problem is not resolved. However, the axion itself remains a feasible DM candidate. It may produce a number of interesting observable effects. In particular, ultra light axion DM may significantly affect structure formation at small scales [39].

We should emphasize that in this work we assume a classical window for the axion mass $m_a\in$ (${10}^{-6}$–${10}^{-3}$) $\mathrm{eV}$. Furthermore, the axions which are produced from the AQNs have dramatically different spectral features, and therefore, the corresponding axion searches should have very different strategies, see recent brief review [17] covering this topic. In the present work we do not study the axions and their possible detections. Instead, this work is devoted to very different observables, other than the axions, which emerge as a result of the AQN annihilation events as discussed in Section 3.2.

(b). Another feature of the AQN model which plays absolutely crucial role for the present work is that nuggets can be made of matter as well as antimatter during the QCD transition. Precisely the coherence of the $\mathcal{CP}$ violating field on large scale mentioned above provides a preferential production of one species of nuggets made of antimatter over another species made of matter. The preference is determined by the initial sign of the $\theta$ field when the formation of the AQN nuggets starts. The direct consequence of this feature along with coherent $\mathcal{CP}$ violation in entire Universe is that the DM density, ${\mathrm{\Omega }}_{\mathrm{DM}}$, and the visible density, ${\mathrm{\Omega }}_{\mathrm{visible}}$, will automatically assume the same order of magnitude densities ${\mathrm{\Omega }}_{\mathrm{DM}}\sim {\mathrm{\Omega }}_{\mathrm{visible}}$ without any fine tuning as they both proportional to one and the same dimensional parameter ${\mathrm{\Lambda }}_{\mathrm{QCD}}$. We refer to the brief review [17] devoted to the specific questions related to the nugget’s formation, generation of the baryon asymmetry, and survival pattern of the nuggets during the evolution in early Universe with its unfriendly environment.

One should emphasize that AQNs are absolutely stable configurations on cosmological scales. Furthermore, the antimatter which is hidden in form of the very dense nuggets is unavailable for annihilation unless the AQNs hit the stars or the planets.

However, when the AQNs hit the stars or the planets it may lead to observable phenomena. The strongest direct detection limit1 is set by the IceCube Observatory’s, see brief review [17] for the details:

$$\begin{array}{c}\hfill \langle B\rangle >3·{10}^{24}[\mathrm{direct}\left(\mathrm{non}\right)\mathrm{detection}\mathrm{constraint}],\end{array}$$

(1)

where we formulated the constraints in term of the AQN’s baryon charge B rather than in terms of its mass $M\approx m_{p}B$. Similar limits are also obtainable from the ANITA and from geothermal constraints which are also consistent with (1) as estimated in [41].

While ground based direct searches offer the most unambiguous channel for the detection of quark nuggets the flux of nuggets is inversely proportional to the nugget’s mass and consequently even the largest available conventional dark matter detectors are incapable to exclude the entire potential mass range of the nuggets. Instead, the large area detectors which are normally designed for analyzing the high energy CR are much better suited for our studies of the AQNs as we discuss in next Section 3.2.

3.2. When the AQNs Hit the Earth…

For our present work, however, the most relevant studies are related to the effects which may occur when the AQNs made of antimatter hit the Earth and continue to propagate in deep underground in very dense environment. In this case the most of the energy deposition will occur in the Earth’s interior. The corresponding signals are very hard to detect as the photons, electrons and positrons will be quickly absorbed by surrounding dense material deep underground, while the emissions of the very weakly interacting neutrinos and axions are hard to recover. In this short subsection we want to mention several observed phenomena which could be related to the AQN annihilation events when the nuggets propagate in the Earth’s atmosphere.

We start with the Telescope Array (TA) experiment which has recorded [11,12] several short time bursts of air shower like events. These events are very unusual and cannot be interpreted in terms of conventional CR single showers. In particular, if one tries to fit the observed bursts (cluster events) with conventional code, the energy for CR events should be in ${10}^{13}$ eV energy range to match the frequency of appearance, while the observed bursts correspond to (${10}^{18}$–${10}^{19}$) eV energy range as estimated by signal amplitude and distribution. Therefore, the estimated energy from individual events within the bursts is five to six orders of magnitude higher than the energy estimated by event rate [11,12]. It has been argued in [9,10] that these bursts represent the direct manifestation of the AQN annihilation events.

This feature, in many aspects, is very similar to the intensity puzzle listed in previous Section 2, where analogous dramatic inconsistency (between the observed intensity and measured event rate) is recorded by H10T instrument.

Our next example is the observed seasonal variations of the X ray background in the near-Earth environment. To be more precise, the XMM-Newton at $11\sigma$ confidence level [42] had recorded the seasonal variations in the 2–6 keV energy range at distances $r\gtrsim 8R_{\oplus }$ where the measurements are effectively had been performed. The authors [42] argue that conventional astrophysical sources have been ruled out. Furthermore, the XMM-Newton’s operations exclude pointing at the Sun and at the Earth directly, diminishing a possible direct X ray background from the Earth and the Sun. It has been argued in [43] that this seasonal variation may be naturally explained by the AQNs exiting the Earth. The AQNs continue the emission of the X rays at $r\gtrsim 8R_{\oplus }$, long after the nuggets exit the Earth’s atmosphere. It has been also shown that the spectrum and the intensity computed in [43] almost identically match the observed spectrum [42].

The final example we want to mention here is the observation by ANITA [14,15,16] of two anomalous events with noninverted polarity. These two events had been identified as the Earth emergent upward going CR-like events with exit angles of $-{27}^0$ and $-{35}^0$ relative to the horizon. These anomalous events are in dramatic tension with the standard model because neutrinos are exceedingly unlikely to traverse through Earth at a distance of ≳$5\times {10}^3$km with such ultrahigh energy, even accounting for the ${\nu }_{\tau }$ regeneration [14]. The analysis [44] reviewed the high-energy neutrino events from the IceCube Neutrino Observatory and inferred that the ${\nu }_{\tau }$ interpretation is excluded by at least $5\sigma$ confidence level. We advocated in [13] that these two anomalous events with noninverted polarity observed by ANITA could be interpreted as the upward going AQNs.

The applications [43] to the X ray emission in the near-Earth environment and the ANITA anomalous events [13] are especially relevant for the present work because both these phenomena are originated from the AQN upward going (Earth emergent) events when the AQNs traversed through the Earth interior and exit the Earth surface. As we shall argue in this work the MME events could be also the consequence of the same upward moving AQNs.

However, there is an additional technical challenging problem to be addressed for the application to MME analysis. The point is that the ANITA anomalous events are generated by AQNs which just crossed the surface and entered the Earth’s atmosphere (upward-going events). Exactly at this instant large number of electrons instantaneously released into atmosphere and generated the radio pulse measured by ANITA. In contrast, the X rays are observed by XMM-Newton at very large distances $r\gtrsim 8R_{\oplus }$ from Earth. In this case the impact of the atmospheric material at $r\lesssim 60$ km can be ignored, and the cooling of the AQN is dominated by nugget’s propagation in an empty space. The application to MME, which is the topic of the present work, deals with an intermediate stage between these two cases: it is not the first instant when the AQN enters the atmosphere emerging from the interior, and it is not the asymptotically far away when the AQN propagates in empty space. In other words, we need to know the emission pattern and the energy deposition rate for the AQNs when they propagate in the atmosphere, and the impact of the atmospheric surrounding material cannot be ignored. We formulate our proposal in Section 4 where we argue that emission of the electrons by the AQN in form of the well-separated “bunches” may explain the unusual features of the MME observations.

However, before we present our arguments supporting this interpretation of the MME unusual events (as highlighted in Section 2) we should overview the basic characteristics of the AQNs traversing the Earth, which represents the topic of the next Section 3.3.

3.3. Internal Structure of the AQN

The goal here is to explain the basic features of the AQNs when they enter the dense regions of the surrounding material and annihilation processes start. The related computations originally have been carried out in [45] in application to the galactic environment with a typical density of surrounding visible baryons of order $n_{\mathrm{galaxy}}\sim 300{\mathrm{cm}}^{-3}$ in the galactic center, in dramatic contrast with dense region in the Earth’s interior when $n_{\mathrm{rock}}\sim {10}^{24}{\mathrm{cm}}^{-3}$ and atmosphere with $n_{\mathrm{air}}\sim {10}^{21}{\mathrm{cm}}^{-3}$. We review these computations with few additional elements which must be implemented in case of propagation in the Earth’s atmosphere and interior when the density of the environment is much greater than in the galactic environment.

The total surface emissivity from electrosphere has been computed in [45] and it is given by

$$F_{\mathrm{tot}}\approx \frac{16}{3}\frac{T^4{\alpha }^{5/2}}{\pi }\sqrt[4]{\frac{T}{m}},$$

(2)

where $\alpha \approx 1/137$ is the fine structure constant, $m=511\mathrm{keV}$ is the mass of electron, and T is the internal temperature of the AQN. One should emphasize that the emission from the electrosphere is not thermal, and the spectrum is dramatically different from black body radiation, see [45], see also Appendix A with more details.

A typical internal temperature of the AQNs for very dilute galactic environment can be estimated from the condition that the radiative output of Equation (2) must balance the flux of energy onto the nugget

$$\begin{array}{c}\hfill F_{\mathrm{tot}}\left(4\pi R^2\right)\approx \kappa ·\left(\pi R^2\right)·\left(2\mathrm{GeV}\right)·n·v_{\mathrm{AQN}},\end{array}$$

(3)

where n represents the number density of the environment. The left hand side accounts for the total energy radiation from the AQN’s surface per unit time as given by (2) while the right hand side accounts for the rate of annihilation events when each successful annihilation event of a single baryon charge produces ∼$2m_p{c}^2\approx 2\mathrm{GeV}$ energy. In Equation (3) we assume that the nugget is characterized by the geometrical cross section $\pi R^2$ when it propagates in environment with local density n with velocity $v_{\mathrm{AQN}}\sim {10}^{-3}c$.

The factor $\kappa$ is introduced to account for the fact that not all matter striking the AQN will annihilate and not all of the energy released by an annihilation will be thermalized in the AQNs by changing the internal temperature T. In particular, some portion of the energy will be released in form of the axions, neutrinos2. The high probability of reflection at the sharp quark matter surface lowers the value of $\kappa$. The propagation of an ionized (negatively charged) nugget in a highly ionized plasma (such as solar corona) will increase the effective cross section. As a consequence, the value of $\kappa$ could be very large as reviewed in [17] in application to the solar corona heating problem.

The internal AQN temperature had been estimated previously for a number of cases. It may assume dramatically different values, mostly due to the huge difference in number density n entering (3). In particular, for the galactic environment $T_{\mathrm{galaxy}}\approx 1$ eV, while in deep Earth’s interior it could be as high as $T_{\mathrm{rock}}\approx$ (100–200) keV. Precisely this value of T had been used as initial temperature of the nuggets in the proposal [43] explaining the seasonal variations of the X rays observed the XMM-Newton at $11\sigma$ confidence level [42] at distances $r\sim$ (6–10) $R_{\oplus }$ from the Earth surface.

The crucial element for the study [43] was the emission rate by AQNs at very high temperatures $T\approx$ (100–200) keV. In this case the emission is not determined by simple Bremsstrahlung radiation given by (2) which is only valid for relatively low temperatures. In the high temperature regime a number of many-body effects in the electrosphere, that were previously ignored, become important. In particular, it includes: the generation of the plasma frequency in electrosphere, which suppresses the low frequency emission. Also, the the AQNs get ionized which dramatically decreases the density of positrons in electrosphere, and consequently suppresses the emission, among many others effects. All these complications have been carefully considered in [43] in applications to the seasonal variations of the X rays as observed the XMM-Newton, and we refer to that paper for the details. Here we quote the result of these studies. The rate of emission can be effectively represented as follows:

$$\begin{array}{c}\hfill \frac{d{E}_{\mathrm{emiss}}}{dt}\sim \left(4\pi R^2\right)\eta (T,R)F_{\mathrm{tot}}\left(T\right)\end{array}$$

(4)

where factor $\eta (T,R)$ is a result of strong ionization of the electrosphere, which leads to the corresponding suppression of the emission. The details of this suppression are explained in Appendix A and given by (A12). This suppression is a direct consequence of high internal temperature T when a large number of weakly bound positrons are expanded over much larger distances order of R rather than distributed over much shorter distances of order $m^{-1}$ around the nugget’s core. This basically determines the suppression factor $\eta \sim {\left(mR\right)}^{-1}\sim {10}^{-6}$.

In both previously considered applications (to ANITA [13] and to XMM-Newton [43] experiments) when the upward moving AQNs with high $T\approx$ (100–200) keV play the key role in the explanations of the observations, we ignored an additional3 annihilation events with atmospheric material as we already mentioned at the end of the previous Section 3.2. Now we want to include the corresponding physics in our analysis.

First of all we want to estimate the number of direct head-on collisions of the atmospheric molecules with AQN per unit time. It can be estimated as follows:

$$\begin{array}{c}\hfill \frac{dN}{dt}\simeq \left(\pi R^2\right)N_{\mathrm{m}}{v}_{\mathrm{AQN}}\simeq 0.8·{10}^{18}\left(\frac{n_{\mathrm{air}}}{{10}^{21}{\mathrm{cm}}^{-3}}\right){\mathrm{s}}^{-1},\end{array}$$

(5)

where $N_m\simeq 2.7·{10}^{19}{\mathrm{cm}}^{-3}$ is the molecular density in atmosphere when each molecule contains approximately 30 baryons such that the typical density of surrounding baryons in air is $n_{\mathrm{air}}\simeq 30·N_m\simeq {10}^{21}{\mathrm{cm}}^{-3}$. The dominant portion of these collisions are the elastic scattering processes rather than successful annihilation events suppressed by parameters $\kappa$ as discussed above. The energy being deposited to the AQN per unit time as a result of annihilating processes can be estimated as follows

$$\begin{array}{ccc}\hfill & & \frac{d{E}_{\mathrm{deposit}}}{dt}\approx \left(2\mathrm{GeV}\right)·\kappa ·\frac{dN}{dt}\hfill \\ & \approx & 1.6·{10}^{18}·\kappa ·\left(\frac{n_{\mathrm{air}}}{{10}^{21}{\mathrm{cm}}^{-3}}\right)\frac{\mathrm{GeV}}{\mathrm{s}},\hfill \end{array}$$

(6)

One should emphasize that this energy is being deposited into the AQN which is already at full capacity with very high temperature $T\simeq$ (100–200) keV accumulated during a long journey in much denser Earth’s interior.

What is the mechanism to release this extra energy? In other words: In what form the energy (6) could be emitted into the surrounding atmosphere as it cannot be easily transferred to the AQN’s quark core (as it is already saturated, see footnote 3)?

There are two qualitatively different regimes which can be normally realized in such circumstances. If a typical time scale ${\tau }_{deposit}$ to deposit a specific amount of energy (let us say, 1 GeV) determined by (6) is longer than the time scale ${\tau }_{\mathrm{cool}}$ to release the same amount of energy, i.e., ${\tau }_{deposit}\gtrsim {\tau }_{\mathrm{cool}}$ than a continuous cooling process takes place and the temperature slowly decreases. This is a thermodynamically equilibrium behaviour which can be analyzed using conventional technical tools4.

The second option is realized when the time scale to deposit the energy ${\tau }_{deposit}$ is much shorter than the time scale of cooling processes, i.e., ${\tau }_{deposit}\ll {\tau }_{\mathrm{cool}}$, in which case the burst-like (explosion like, eruption-like blasts) non- equilibrium processes must occur. These eruption-like events will release the extra accumulated energy in form of very short pulses, which cannot be described as conventional cooling equilibrium processes. These short pulses must alternate with much longer periods of accumulation energy which inevitably end with subsequent eruption-like events. In other words, in this case, the non-equilibrium fast equilibration process can be thought as the eruption-like event5.

Now we give a numerical estimation for the cooling rate determined by (4) to find out what regime is realized in given circumstances. The order of magnitude estimate can be expressed as follows:

$$\begin{array}{c}\hfill \frac{d{E}_{\mathrm{emiss}}}{dt}\sim {10}^{16}{\left(\frac{T}{100\mathrm{keV}}\right)}^{\frac{17}{4}}\frac{\mathrm{GeV}}{\mathrm{s}}.\end{array}$$

(7)

Comparing this estimate for cooling rate with estimate for the deposition rate (6) one concludes that the rate of energy deposition is much shorter than the rate at which the system is capable to release the same amount of energy in form of the photon’s emission. As a result, we arrive to the conclusion that second option when ${\tau }_{deposit}\ll {\tau }_{\mathrm{cool}}$ is realized. This conclusion inevitably implies the eruption like events must occur, and these very short explosions must be alternated with much longer periods of time when the energy is being accumulated by the AQNs. These longer periods of the energy accumulations also must end with consequent eruption-like blasts. This alternating pattern continues as long as following condition holds:

$$\begin{array}{c}\hfill {\tau }_{deposit}\ll {\tau }_{\mathrm{cool}}\Rightarrow \left(\mathrm{short}\mathrm{eruptions}\mathrm{occur}\right).\end{array}$$

(8)

With these preliminary comments with estimates from the previous studies on the AQN features we are now in position to formulate the proposal interpreting the MME events observed by X10T collaboration in terms of the upward moving AQNs, which is the topic of the next Section 4.

4. MME as the AQN Event

In this Section we formulate the basic idea of our proposal on identification of the unusual Multi-Modal Events with the upward moving AQN events, while supporting estimates on the event rate, the intensity, and the variety of time scales will be presented in following Section 5 and Section 6.

The AQNs which propagate in the Earth’s interior are very hot. Their temperature could be as hot as $T\approx$ (100–200) keV at the moment of exit on the Earth’s surface as we discussed in [43] in the application to studies of the seasonal variations of the X rays observed by XMM-Newton at very large distances $r\sim$ (6–10) $R_{\oplus }$ from the Earth. At such large distances the AQN’s cooling can be described by conventional thermodynamically equilibrium processes with well defined spectrum, see footnote 4. It should be contrasted with our application to ANITA anomalous events [13] when the same upward moving AQNs just crossed the surface and entered the Earth’s atmosphere. In this case the dominant cooling mechanism is realized in form of short burst-like events according to (8). The outcome of these short burst-like events is emission of numerous bunches (clumps) of relativistic electrons. These eruption like events are analogous to lightning flashes from footnote 5.

In our studies [13] we focused on an estimation of the number of emitted electrons N and their energy $\langle E\rangle \sim 10\mathrm{MeV}$ which, according to the proposal [13], essentially determine the intensity and the spectral features of the ANITA anomalous events. These electrons will be always accompanied by the emission of much more numerous number of photons with typical energy of order $\omega \sim T\approx$ (100–200) keV, which in fact represent the dominant fast non- equilibrium mechanism of cooling of the system in these circumstances (8).

Precisely these multiple explosion-like emissions of photons and electrons will be identified with Multi-Modal Events with their unusual features reviewed in Section 2. The mean free path of the photons with $\omega \sim T$ is relatively short, measured in meters. Therefore, they cannot be directly observed. In contrast, the mean free path of the energetic electrons at sea level with $\langle E\rangle \sim 10\mathrm{MeV}$ is around several kilometres in atmosphere (and even longer at the elevation of 3346 m where H10T is located). The propagation of these ultra-relativistic electrons takes place in the background of the geomagnetic field $\mathcal{B}\sim 0.5\mathrm{G}$ which determines the instantaneous curvature $\rho \sim 3$ km of the electron’s trajectories with such energies, see Section 5 with relevant estimates. Due to the large component of magnetic field parallel to the Earth’s surface the electrons may move in downward direction even if they are initially emitted in upward direction. Our proposal is that precisely these downward moving energetic electrons could mimic the CR and could be responsible for the Multi-Modal pulses as detected by H10T instrument.

Any precise computation during a short period of time of emission is very hard problem of non-equilibrium dynamics, which is beyond the scope of the present work. Fortunately, the observable intensity, the event rate, the time delays between the pulses are determined in the AQN framework by the basic characteristics of the model and are not very sensitive to the details of this non-equilibrium mechanism of production and its corresponding time scales. This is because all these observables depend on several parameters such as typical energy $\langle E\rangle \sim 10\mathrm{MeV}$ of the emitted electrons, typical number of emitted electrons N, the deposition rate (6) and the cooling rate (7) which had been previously estimated for very different purposes in different circumstances. We shall use the same parameters in the present work.

In particular, the number of electrons $N\sim$ (${10}^8$–${10}^9$) emitted by AQNs is very hard to compute from the first principles. However it can be fixed by the observed intensity and spectral features of the anomalous ANITA radio pulses assuming, of course, that these observed radio pulses with inverted polarities are due to the upward moving AQNs [13]. The typical energy $\langle E\rangle \sim 10\mathrm{MeV}$ of these electrons is also consistent with duration of the observed pulses [13]. The next Section 5 is devoted to the estimation of the event rate of MME, while Section 6 is devoted to explanations of the puzzles which demonstrate a dramatic deviation from conventional CR picture as formulated in Section 2. We shall argue that the observed MME features are consistent with our AQN-based interpretation.

5. Event Rate of MME

This section is devoted to estimate of the event rate of MMEs within the AQN framework. We anticipate that this evaluation is expected to be very qualitative estimation due to large uncertainties in parameters and rare occurrence of the observed MMEs. In particular, it is known that key parameter, the DM density locally may dramatically deviate from the well established average global value ${\rho }_{\mathrm{DM}}\approx 0.3\mathrm{GeV}{\mathrm{cm}}^{-3}$. Nevertheless we would like to present such estimate to demonstrate that our interpretation of MMEs as an outcome of upward-going AQNs is at least a self-consistent proposal. In what follows we use the same formulae we used for the estimates of the frequency of appearance of the ANITA Anomalous Events [13] such that the numerous uncertainties related to the local DM density or/and the AQN size distribution would not dramatically affect our estimates below if they are normalized to the ANITA event rate.

We start with the same formula from [13] for the expected number $\mathcal{N}$ of the MMEs assuming that they are induced by the AQNs:

$$\mathcal{N}\approx {\mathcal{A}}_{\mathrm{eff}}\mathcal{T}\Delta \mathrm{\Omega }\frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}A\mathrm{d}\mathrm{\Omega }},$$

(9)

where $\Delta \mathrm{\Omega }\approx 2\pi$ for the isotropic AQN flux, and the expression for the local rate of upward-going AQNs per unit area is given by:

$$\begin{array}{ccc}\hfill & & \frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}A\mathrm{d}\mathrm{\Omega }}\approx \frac{\mathrm{\Phi }}{4\pi R_{\oplus }^2}\approx 4·{10}^{-2}\left(\frac{{10}^{25}}{\langle B\rangle }\right)\frac{\mathrm{events}}{\mathrm{yr}·{\mathrm{km}}^2},\hfill \\ & & \mathrm{\Phi }\approx \frac{2·{10}^7}{\mathrm{yr}}\left(\frac{{\rho }_{\mathrm{DM}}}{0.3\mathrm{GeV}{\mathrm{cm}}^{-3}}\right)\left(\frac{v_{\mathrm{AQN}}}{220\mathrm{km}{\mathrm{s}}^{-1}}\right)\left(\frac{{10}^{25}}{\langle B\rangle }\right),\hfill \end{array}$$

(10)

where ${\rho }_{\mathrm{DM}}$ is the local density of DM and $R_{\oplus }=6371$km is the radius of the Earth and $\mathrm{\Phi }$ is the total hit rate of AQNs on Earth [48]. In Formula (9) the $\mathcal{T}$ is the time of operation while ${\mathcal{A}}_{\mathrm{eff}}$ is the effective area to be estimated below.

The estimation of the effective area ${\mathcal{A}}_{\mathrm{eff}}$ is a complicated task as it is not simply determined by the area of the detectors similar to standard CR analysis. Instead, it is determined by the area along the AQN’s path where it can emit the bunches of electrons in form of short pulses which can mimic the CR as outlined in previous Section 4. The area ${\mathcal{A}}_{\mathrm{eff}}\sim L_{\mathrm{AQN}}·D_{\mathrm{AQN}}$ can be thought as a strip of length $L_{\mathrm{AQN}}$ and width $D_{\mathrm{AQN}}$.

To estimate these parameters let us consider an AQN moving in upward direction with angle ${\theta }_{\mathrm{AQN}}$ with respect to the Earth’s surface such that upward velocity component is $(v_{\mathrm{AQN}}·sin{\theta }_{\mathrm{AQN}})$. This vertical velocity component determines the maximal height h of the atmosphere where the atmospheric density is still sufficiently high such that condition (8) holds. We estimate $h\approx$ (30–50) km where the atmospheric density falls by two order of magnitude such that conventional X-ray emission (which had been used in computations [43] to explain the seasonal variations observed by XMM Newton) becomes the dominant cooling process at higher altitudes. This condition determines the maximal length $L_{\mathrm{AQN}}$ and time scale ${\tau }_{\mathrm{AQN}}$ when the AQNs can emit the bunches of electrons in form of pulses which we identify with MMEs and which can mimic the CR air showers as outlined in previous Section 4. Numerically these parameters are estimated as follows:

$$\begin{array}{ccc}\hfill {\tau }_{\mathrm{AQN}}& \sim & \frac{h}{(v_{\mathrm{AQN}}·sin{\theta }_{\mathrm{AQN}})}\sim 0.2\mathrm{s},\hfill \\ \hfill L_{\mathrm{AQN}}& \sim & hcot{\theta }_{\mathrm{AQN}}\sim \left(50–90\right)\mathrm{km},\hfill \end{array}$$

(11)

where we used ${\theta }_{\mathrm{AQN}}\simeq 30°$ for an order of magnitude numerical estimates.

To estimate the width of the strip $D_{\mathrm{AQN}}$ we recall that the geomagnetic field $\mathcal{B}$ in location of the H10T instrument can be characterized by two numbers: it has strong component in up to down direction ${\mathcal{B}}_{\mathrm{down}}\simeq 0.49$ G, and strong component from south to north direction ${\mathcal{B}}_{\mathrm{north}}\simeq 0.24$ G, see e.g., [49].

Assuming that the energetic electrons with $\langle E\rangle \sim 10\mathrm{MeV}$ will be emitted along the ${\mathbf{v}}_{\mathrm{AQN}}$-direction one can estimate instantaneous radius of curvature $\rho$, see e.g., Jackson [50]:

$$\rho \approx \frac{\gamma mc}{e\mathcal{B}sin{\theta }_{\mathcal{B}}}\approx 2.8\mathrm{km}\left(\frac{\gamma }{20}\right),\gamma \equiv \frac{\langle E\rangle }{m}$$

(12)

where $\mathcal{B}\approx {\mathcal{B}}_{\mathrm{north}}\approx 0.24$ G is the local magnetic field strength, which changes the direction of the electrons from upward to downward moving such that they can mimic the CR air showers. The angle ${\theta }_{\mathcal{B}}$ is the angle between the particle electron velocity $\mathbf{v}$ and magnetic direction. We choose ${\theta }_{\mathcal{B}}\approx 30°$ in (12) for the numerical estimates.

Now we estimate the relevant scale $\lambda$ which determines the survival pattern of the electron’s bunches. It is mostly determined by the Coulomb elastic scattering with cross section ${\sigma }_{\mathrm{Coul}}$

$$\begin{array}{c}\hfill {\sigma }_{\mathrm{Coul}}\approx \frac{{\alpha }^2}{E^2{\theta }^4}\approx 3·{10}^{-27}{\left(\frac{1/2}{\theta }\right)}^4{\left(\frac{20}{\gamma }\right)}^2{\mathrm{cm}}^2.\end{array}$$

(13)

The electrons with $\theta \gtrsim 1/2$ may strongly deviate from their main paths and cease to stay with majority of particles forming the bunch (which eventually becomes the pulse being interpreted as MME). The corresponding length scale $\lambda \left(h\right)$ at altitude h (accounting for the air-density $n_{\mathrm{air}}\left(h\right)$ variation) is estimated as follows

$$\begin{array}{c}\hfill \lambda \left(h\right)\sim \frac{1}{{\sigma }_{\mathrm{Coul}}{n}_{\mathrm{air}}\left(h\right)}\sim 3·exp\left(\frac{h}{8\mathrm{km}}\right)\mathrm{km}.\end{array}$$

(14)

The physical meaning of $\lambda$ is the length distance particles propagate at which the majority of the particles in the bunch remain within the bunch before the dispersing to much larger distances when they cease to be a part of the pulse (burst). Important comment here is that $\lambda \gtrsim \rho$ such that the majority of electrons within the bunch do not strongly re-scatter, and therefore survive the change in orientation due to the geomagnetic field $\mathcal{B}$ (from upward to downward direction).

The width of the strip $D_{\mathrm{AQN}}$ now can be roughly estimated as follows:

$$\begin{array}{c}\hfill D_{\mathrm{AQN}}\sim \lambda \sim 3·exp\left(\frac{h}{8\mathrm{km}}\right)·\left(\frac{\gamma }{20}\right)\mathrm{km}.\end{array}$$

(15)

Combining all the estimates above one arrives to the following order of magnitude estimation for the expected number of MME events:

$$\mathcal{N}\approx 0.5·{10}^2 \mathrm{events}\left(\frac{{\mathcal{A}}_{\mathrm{eff}}}{500{\mathrm{km}}^2}\right)\left(\frac{\mathcal{T}}{0.4\mathrm{yr}}\right).$$

(16)

This estimate carries enormous internal uncertainty due to a number of reasons. First, as we already mentioned the parameters entering (10) for the basic normalization, the flux $\mathrm{\Phi }$, are in fact not precisely known. Indeed, the fundamental parameter such as ${\rho }_{\mathrm{DM}}$ may dramatically deviate locally (by factor 2 or even 3) from the well established average global value ${\rho }_{\mathrm{DM}}\approx 0.3\mathrm{GeV}{\mathrm{cm}}^{-3}$. Furthermore, the size distribution factor entering (10) in form ${\langle B\rangle }^{-1}$ had been fixed from dramatically different physics (including solar corona heating puzzle) and can easily deviate by similar factor 2 or 3. Furthermore, the effective area ${\mathcal{A}}_{\mathrm{eff}}$ could also deviate by factor 2 or 3 in comparison with expression (16) because the important parameter h which essentially determines the effective area ${\mathcal{A}}_{\mathrm{eff}}$ cannot be precisely evaluated as it depends on condition (8) which itself is determined by complex internal dynamics of the nuggets. As a result we consider the Formula (16) as an order of magnitude estimate at the very best. However, our main arguments of the identification of the MMEs with the AQN events are not based on the estimate (16). We present this estimate here exclusively for illustrative purposes. Our main arguments are based on specific qualitative features (formulated as puzzles) which have been listed in Section 1, and which cannot be explained in terms of the conventional CR air showers as highlighted in Section 2.

This order of magnitude estimate should be compared with observed frequency of appearance of the MMEs. According to [2] the observations from start until August 2016 during $\mathcal{T}\approx 3500\mathrm{h}\approx 0.4\mathrm{yr}$ of operation the H10T instrument had detected ${\mathcal{N}}_{\mathrm{obs}}\simeq {10}^3$ MMEs. According to [4] the observations from 15 February 2018 to 12 May 2018 (which corresponds to $\mathcal{T}\approx 0.25\mathrm{yr}$) the H10T instrument had detected ${\mathcal{N}}_{\mathrm{obs}}=217$ MMEs.

The AQN based estimations (16), if literally taken, suggest that number of events $\mathcal{N}$ is almost one order of magnitude lower than ${\mathcal{N}}_{\mathrm{obs}}$ events observed by H10T. Nevertheless, we consider this order of magnitude estimation (16) being consistent with our proposal due to many uncertainties mentioned above.

It is interesting to note that the numerical suppression factor ∼$0.1$ (between computed $\mathcal{N}$ and observed ${\mathcal{N}}_{\mathrm{obs}}$ values) which appears in our order of magnitude estimates (16) is very similar to suppression factor ∼$0.1$ which occurred in analogous estimates for the mysterious TA bursts [9] and the ANITA anomalous events [13]. This similarity hints on a common origin for all these phenomena. Therefore, if one normalize $\mathcal{N}$ to the observed ANITA anomalous events (assuming that all three phenomena originated from the same AQN based physics) one arrives to correct order of magnitude estimate as the suppression factor ∼$0.1$ is approximately the same for all three phenomena estimated for the mysterious TA bursts in [9], the ANITA anomalous events in [13], and Multi-Modal Events estimated in (16). The main uncertainty related to the basic normalization of the flux $\mathrm{\Phi }$ cancels out if such relative ratios are considered.

As we mentioned above, our main arguments leading to the identification of the MMEs with the AQN events are not based on an order of magnitude estimate of the frequency of appearance (16). Rather, our main arguments are based on specific qualitative features (formulated as puzzles) and which cannot be explained in terms of the conventional CR air showers. We consider a qualitative agreement between the observations and our theoretical estimates (to be discussed in next Section 6) as the strong arguments supporting our identification.

6. AQN Proposal Confronts the MME Observations

We start this section by estimating the particle number density $\rho \left(R\right)$ which appears in formulation of the puzzles in Section 2 describing the observations [1,2,3,4,5]. The particle number density in the AQN framework is determined by the number of particles which could be observed at the detector site. Assuming that the total number of electrons being emitted in form of a pulse (as a result of erupted burst) is similar to the number of particles which was used in our analysis [13] of the ANITA anomalous events $N\simeq$ (${10}^8$–${10}^9$) we arrive to the following estimate for $\rho \left(R\right)$:

$$\begin{array}{c}\hfill \rho \left(R\right)\sim \frac{N}{{(\lambda \Delta \theta )}^2}\sim \frac{({10}^8-{10}^9)}{{\left(2.5\mathrm{km}\right)}^2}\sim \frac{(20-200)}{{\mathrm{m}}^2}\end{array}$$

(17)

where the area which is hit by the bunch of particles from a single burst is estimated as ${(\lambda \Delta \theta )}^2$ with $\lambda \left(h\right)$ given by (14) at the detector site with $h\simeq 4$ km. It is assumed that the particles are propagating within the cone with angle $\Delta \theta \lesssim 1/2$.

Our next task is the estimation of the time delay between the pulses within the same cluster. The corresponding time delay can be estimated from the condition that the energy deposited into the AQN during time ${\tau }_{\mathrm{delay}}$ must be released in form of the eruption when $N\simeq$ (${10}^8$–${10}^9$) electrons being emitted in form of a single pulse. As we mentioned previously, the dominant portion of the energy in such eruption is released in form of the photons with energy $\omega \sim T$ which always accompany the electron’s emission as a result of these bursts. The relative ratio r between these two components is estimated in Appendix B, see Equation (A14). Numerically, the estimate can be presented as follows:

$$\begin{array}{c}\hfill r\equiv \frac{\langle E_{e^{+}{e}^{-}}\rangle }{\langle E_{\gamma }\rangle }\sim \frac{\alpha }{2\pi }exp\left(-\frac{2m}{T}\right)\sim 0.7·{10}^{-5},\end{array}$$

(18)

where for numerical estimates we use $T\simeq 200$ keV. We must emphasize that (18) is really an order of magnitude estimate as mechanism of emission is determined by a very complex physics as highlighted in Appendix B. Furthermore, the corresponding eruption event is not a thermodynamically equilibrium process as we already mentioned previously. The dominant contribution in form of the photon’s emission during a single pulse can be estimated in terms of these parameters as follows

$$\begin{array}{c}\hfill \langle E_{\gamma }\rangle \sim N·\left(2m\right)·r^{-1}\sim 1.4·\left({10}^{10}–{10}^{11}\right)\mathrm{GeV},\end{array}$$

(19)

where we use the numerical value for $N\in \left({10}^8–{10}^9\right)$ extracted from analysis of the ANITA anomalous events [13] and parameter r is given by (18). In this estimate we assumed that the energy of the pair $\langle E_{e^{+}{e}^{-}}\rangle \sim 2mN$ computed at the moment of the pair creation. The released energy during a single pulse (19) determines the time delay ${\tau }_{\mathrm{delay}}$ between the pulses within the same cluster:

$$\begin{array}{c}\hfill {\tau }_{\mathrm{delay}}^{-1}\sim \frac{d{E}_{\mathrm{deposit}}/dt}{\langle E_{\gamma }\rangle }\sim \kappa \frac{{10}^{18}·\mathrm{GeV}{\mathrm{s}}^{-1}}{({10}^{10}-{10}^{11})\mathrm{GeV}},\end{array}$$

(20)

where we used numerical value for $(d{E}_{\mathrm{deposit}}/dt)$ from (6) with density of atmosphere at $h\simeq 4$ km where the detector H10T is located. Our final, the order of magnitude estimate for the time delay ${\tau }_{\mathrm{delay}}$ between the pulses can be represented as follows

$$\begin{array}{c}\hfill {\tau }_{\mathrm{delay}}\sim \left(\frac{0.1}{\kappa }\right)·\left({10}^2–{10}^3\right)\mathrm{ns},\end{array}$$

(21)

where we use $\kappa \simeq 0.1$ in (21) for numerical estimates which was previously extracted from studies of the emission in the dilute galactic environment, see footnote 2.

We would like to make few comments on uncertainties related to the estimate (21). The main uncertainties are related to the parameters r and N entering (19). The parameter r as defined by (18) is very hard to estimate as discussed in Appendix B where we mentioned that the related question for much simpler problem on emission from the bare quark stars remains to be a matter of debates. Our system is much more complex than the bare quark star because of the small size of the nuggets when the thermal equilibrium cannot be established, in contrast with quark stars. This is precisely the reason why we use parameter N from analysis of the ANITA anomalous events [13], rather than from theoretical estimates. Another source of uncertainty is parameter $\kappa$ entering (21). This parameter was defined in Equation (3) with explanation of many uncertainties related to its numerical value6. Therefore, the time delay ${\tau }_{\mathrm{delay}}$ as given by (21) should be considered as an order of magnitude estimate at the very best. It obviously cannot be computed from the first principles similar to any other parameters when one deals with any complex systems, see also footnote 6.

However, the important point here is that the time scale ${\tau }_{\mathrm{delay}}$ may dramatically vary from event to event as it strongly depends on many parameters entering the problem as mentioned above. In particular, it obviously strongly depends on intensity (number of emitted particles N) of a previous pulse. Essentially the parameter (21) should be interpreted as a preparation time the system requires for the next eruption.

The strong variation of the ${\tau }_{\mathrm{delay}}$ should be contrasted with another parameter which is the time duration of a single pulse ${\tau }_{\mathrm{pulse}}$. In the AQN framework this parameter must not vary much from one event to another as it is entirely determined by internal dynamics of the AQN during the eruption irrespective to the intensity of the previous events, and irrespective to the prehistory of the AQN propagation as long as condition (8) is met7. In different words, our proposal suggests that

$$\begin{array}{c}\hfill {\tau }_{\mathrm{pulse}}\approx \mathrm{constant},\end{array}$$

(22)

where the constant cannot be computed from first principles as it is entirely determined by the non-equilibrium dynamics of the AQN at the instant of eruption8.

Now we are prepared to confront the basic consequences of our proposal (identifying the MMEs with the AQN annihilation events) with observations.

1. “clustering puzzle”: The multiple number of events is a very generic feature of the system as explained at the very end of Section 3.3 as long as condition (8) is met. The time delays between the pulses ${\tau }_{\mathrm{delay}}$ dramatically fluctuate between different events. The window for these variations is huge according to (21). In fact, it could be even well outside of this window. The time delays ${\tau }_{\mathrm{delay}}$ may considerably vary even for different events within the same cluster at the same detection point, which is consistent with observed cluster shown on Figure 1. Furthermore, the AQN itself remains almost at the same location as the displacement $\Delta l_{\mathrm{AQN}}$ during entire cluster of events is very tiny

$$\begin{array}{c}\hfill \Delta l_{\mathrm{AQN}}\sim v_{\mathrm{AQN}}·{\tau }_{\mathrm{delay}}\sim 20\mathrm{cm},\end{array}$$

(23)

which implies that all individual bunches making the cluster are likely to be emitted by the AQN along the same direction, and can be recorded and classified as MME by H10T. Each event can be viewed as an approximately uniform front as mere notion of the “EAS axis” does not exist in this framework, see also next item. However, each individual event may appear to arrive from slightly different direction due to the inherent spread of the emitted electrons at the moment of eruption.

2. “particle density puzzle”: Particle density distribution $\rho \left(R\right)$ in the AQN framework is estimated by (17) and it shows strong fluctuation from one event to another event. These variations are mostly related to the intensity of the individual bursts being expressed by the number of electrons in the bunch N. However, the distinct feature of the distribution in the AQN framework is that it does not depend on R, as the notion of the “EAS axis” does not exist in this framework as we already mentioned. All these generic features of the AQN framework are perfectly consistent with H10T observations as presented on Figure 2. However, these observed features are in dramatic contradiction with conventional EAS prediction shown by solid lines on Figure 2 with different colours, depending on energy of the CR.

Furthermore, the magnitude of the density $\rho \left(R\right)$ in the AQN framework (which is mostly determined by parameter N) is much higher than one normally expects for CR energies ∼$\left({10}^{17}–{10}^{18}\right)$ eV. The corresponding parameter N representing the number of electrons in the bunch was not fitted for the present studies to match the observations. Instead, it was extracted from different experiment in dramatically different circumstances (in proposal [13] to explain the ANITA anomalous events as the AQN events).

3. “pulse width puzzle”: In the AQN framework the width of the pulse (22) cannot vary much from one event to another. It is a fundamental feature of the framework because the duration of the pulse is entirely determined by internal dynamics of the AQN during the blast as long as condition (8) is met, see footnote 7 with a comment. This feature is in perfect agreement with observations [4]

$$\begin{array}{c}\hfill {\tau }_{\mathrm{pulse}}\approx \left(20–35\right)\mathrm{ns}\Leftarrow \left[\mathrm{observations}\right]\end{array}$$

(24)

for all recorded MMEs. At the same time, this feature is in dramatic conflict with conventional picture when the duration of the pulse must depend on the distance to the EAS axis as shown by sold lines on Figure 3. This basic prediction of the conventional CR analysis is due to increase of the thickness of the EAS pancake with the distance from the EAS axis. As we already mentioned the mere notions such as the “EAS axis” and the “thickness of the EAS pancake” do not exist in the AQN framework.

4. “intensity puzzle”: Particle density distribution $\rho \left(R\right)$ in the AQN framework is estimated by (17). The corresponding event to event fluctuations do not depend on the distance to the EAS axis as we already mentioned. Such intensity of the events as given by (17) in the AQN framework is consistent with observations shown on Figure 2. However, the observations are in dramatic conflict with conventional CR analysis when such huge intensity could be generated by a primary particle with energy well above ${10}^{19}$ eV with dramatically lower event rate on the level of once every few years. The frequency of appearance in the AQN framework is estimated in Section 5, and it is consistent with observed event rate.

We conclude this section with the following comment. All our formulae presented in this section are the order of magnitude estimations at the very best, as they include many inherent uncertainties which are inevitable features of any composite system (such as AQN) propagating in a complex environment (such as Earth atmosphere) with very large Mach number M, see footnote 6.

Nevertheless, the emergent picture suggests that all the puzzles formulated in Section 1 and Section 2 can be naturally understood within the AQN framework as explained above in items 1–4. Needless to say that the crucial phenomenological parameters used in the estimates had been fixed long ago for dramatically different observations in different circumstances for different environments as overviewed in Section 3.

7. Conclusions and Future Development

Our basic results can be summarized as follows. We have argued that all the puzzles formulated in Section 1 and Section 2 can be naturally understood within the AQN framework as explained in items 1–4 in previous Section, and we do not need to repeat these arguments again in this Conclusion. Instead, we want to discuss the drastic differences between the events induced by conventional CR showers and the AQNs. These dramatic distinct features can be tested by the future experiments, such that our proposal can be discriminated from any other proposals and suggestions. We list below the following typical features of the AQN events and contrast them with any other possible mechanisms which could be responsible for MMEs.

• The events which are generated by the bunches of electrons as a result of eruption of the propagating AQN in the Earth atmosphere suggests an enormous number of possibilities to generate different clusters when each event within a given cluster may have very different intensity from a previous and consequent events with very different time delays between the events. In other words, the AQN proposal suggests that there should be large variety of shapes and delays between the events with very different patterns due to the complexity of the AQN system. It should be contrasted, for example, with hypothesis of “delayed particles” (which was originally suggested to explain the MMEs) in which case all clusters must be the same as they should be determined by a specific pattern of decaying fundamental particle of unknown nature.
• A “rule of thumb” suggests that a typical number of charged particles (mostly electrons and positrons) in CR air shower is $E_{\mathrm{CR}}/\mathrm{GeV}$, which implies that $N\approx \left({10}^8–{10}^9\right)$ for the energy of the primary particle $E_{\mathrm{CR}}\approx \left({10}^{17}–{10}^{18}\right)$ eV. This estimate suggests that any detector which is designed to study the EAS with energies $E_{\mathrm{CR}}\approx \left({10}^{17}–{10}^{18}\right)$ eV are, in principle, capable to study MMEs if the resolution of the detectors is in ∼10-ns level, similar to H10T, see also item 4 below as an alternative option to properly select and discriminate the MMEs.
• In particular, we expect that the extension of the H10T detector would produce more multiple pulses (at each given detector) instead of simple bimodal pulses. We also expect that more detectors in the area will be recording MMEs because the area covered by each individual pulse is relatively large (few kilometres) according to (17), which is well above the present size of H10T instrument.
• A large number of charged particles $N\approx \left({10}^8–{10}^9\right)$ in the background of the geomagnetic field $\mathcal{B}\sim 0.5$ gauss will produce the radio pulse in both cases: the CR-induced radio pulse [51,52] as well as AQN-induced radio pulse [13]. However, these pulses can be easily discriminated from each other as argued in [13].

The main reason for the dramatic differences between these two radio pulses is that the AQN event could be viewed as an (approximately) uniform front of size $\lambda \Delta \theta \sim$ km with a constant width, while EAS is characterized by central axis. In different words, the number of particles per unit area $\rho \left(R\right)$ in the AQN case does not depend on the distance from the central axis, in huge contrast with conventional CR air showers when $\rho \left(R\right)$ strongly depends the distance from the central axis. The width of the “pancake” in CR air shower also strongly depends on R. As a result, the effective number of coherent particles contributing to the radio pulse is highly sensitive to the width of the “pancake” when it becomes close to the wavelength of the radio pulse. These distinct features lead to very different spectral properties of the radio pulses in these two cases, which can be viewed as an independent characteristic of MMEs. In fact, this unique feature can be used in future studies for purpose of discrimination and proper selection of the Multi-Modal Clustering Events.

If future studies and tests (including the detecting of the synchronized radio pulses with MMEs as suggested above) indeed substantiate our proposal it would be a strong argument supporting the AQN nature of the MMEs.

We conclude this work with the following comment. We estimated the event rates for three dramatically different puzzling CR-like events: for mysterious TA bursts [9], for the ANITA anomalous events [13], and finally for the Multi-Modal Events in this work as estimated in (16). All three puzzling phenomena are proportional to one and the same AQN flux (10). The self-consistency between all three estimates hints on a common nature for these puzzling CR-like events. We interpret this self-consistency in the event rates as an additional indirect argument supporting the AQN nature for all three mysterious phenomena, while our direct arguments are presented in Section 6 and listed as item 1–4. We finish on this optimistic note.