Correlations between Earthquake Properties and Characteristics of Possible ULF Geomagnetic Precursor over Multiple Earthquakes
Abstract
1. Introduction
2. Instrumentation and Data Acquisition
3. Methodology
3.1. Precusor Detection
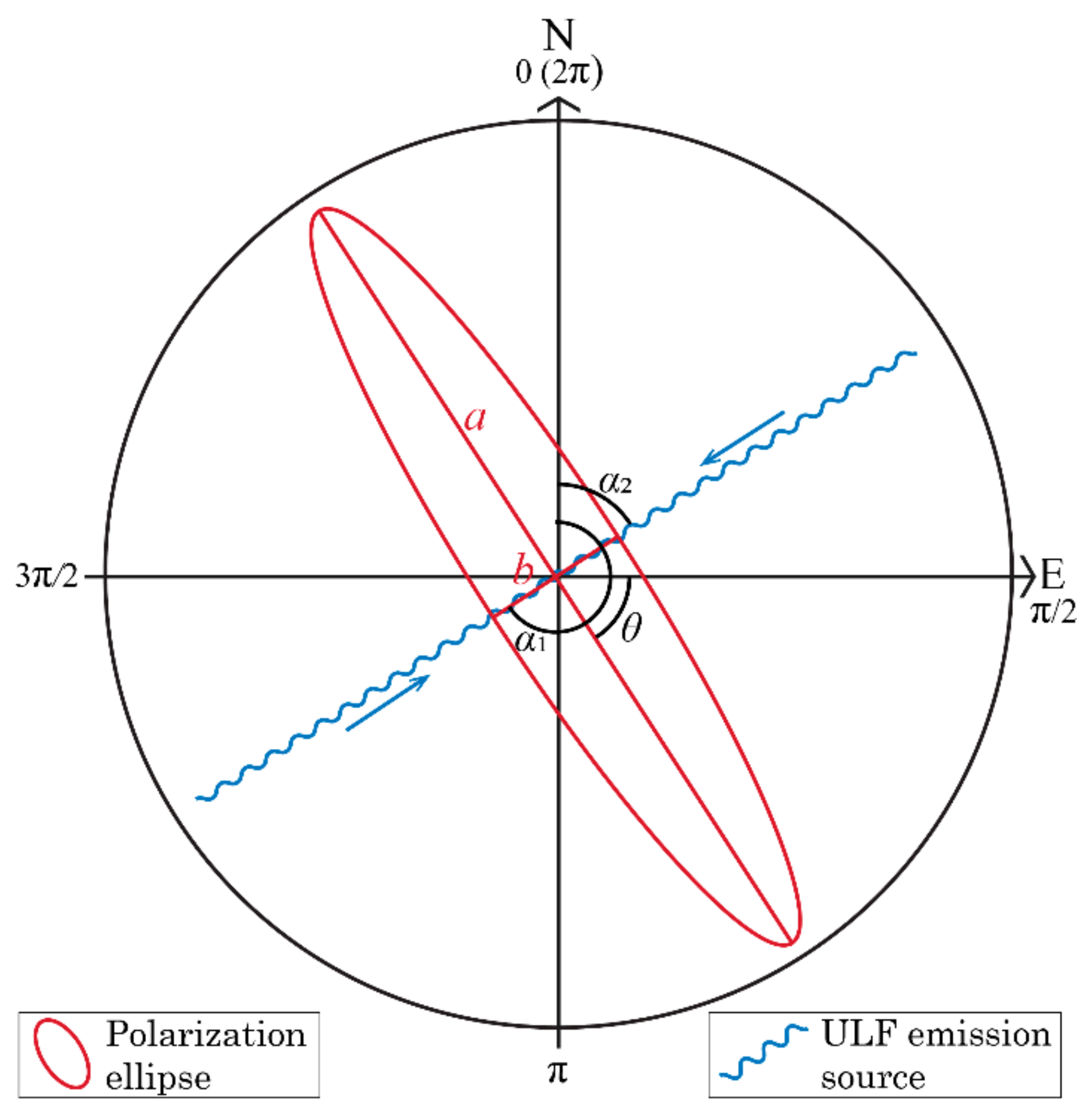
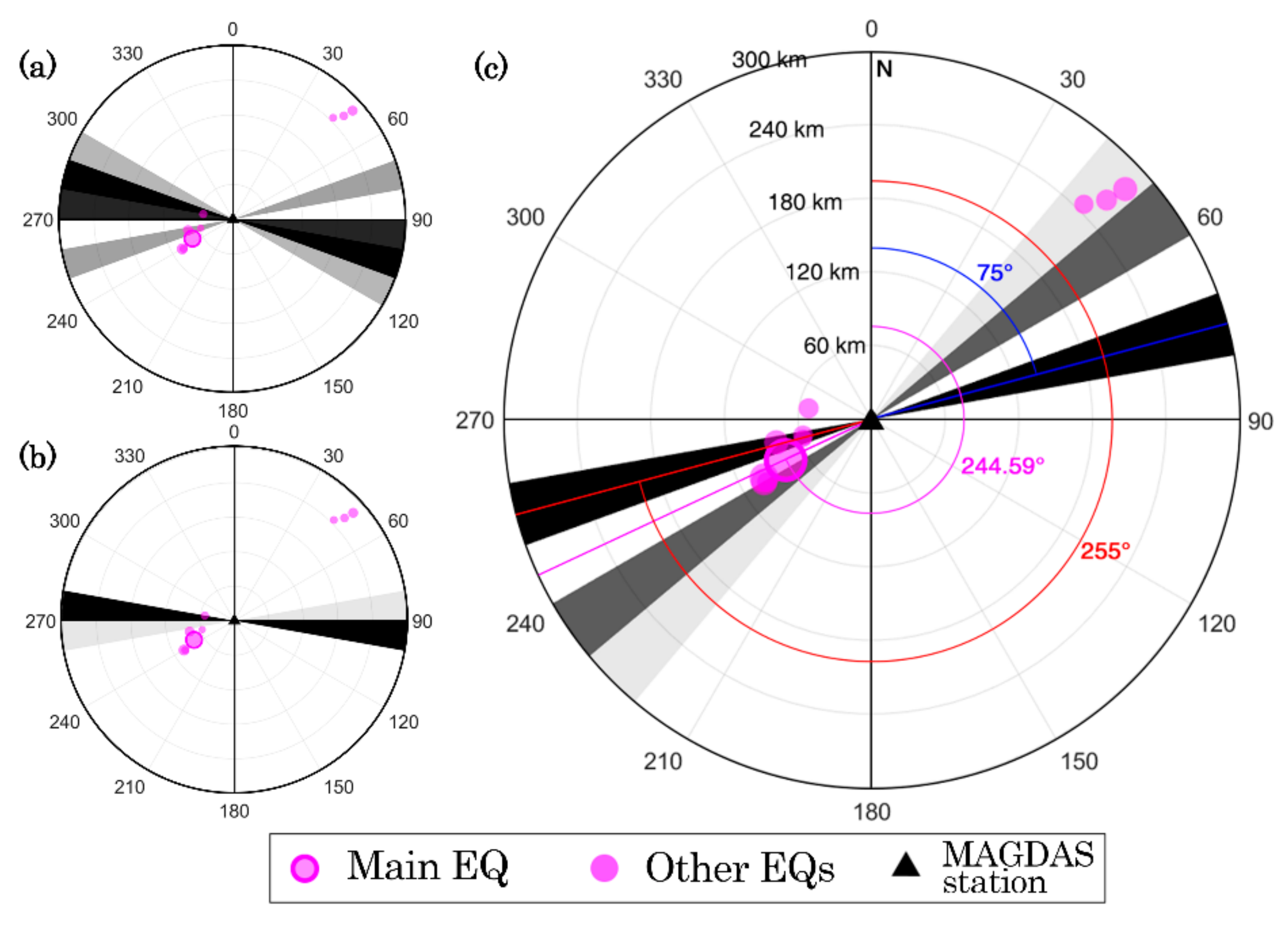
3.2. Direction Estimation
4. Results and Discussion
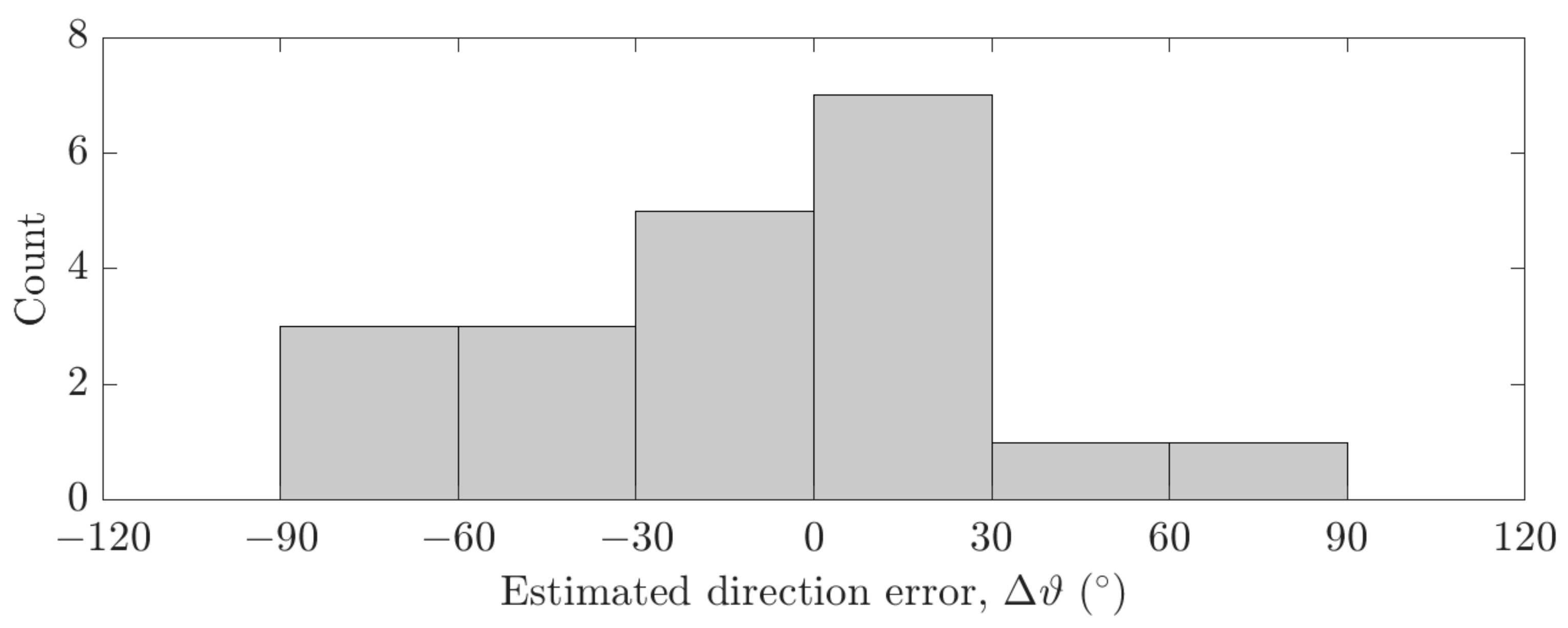
4.1. Precursor Detection and Direction Estimation
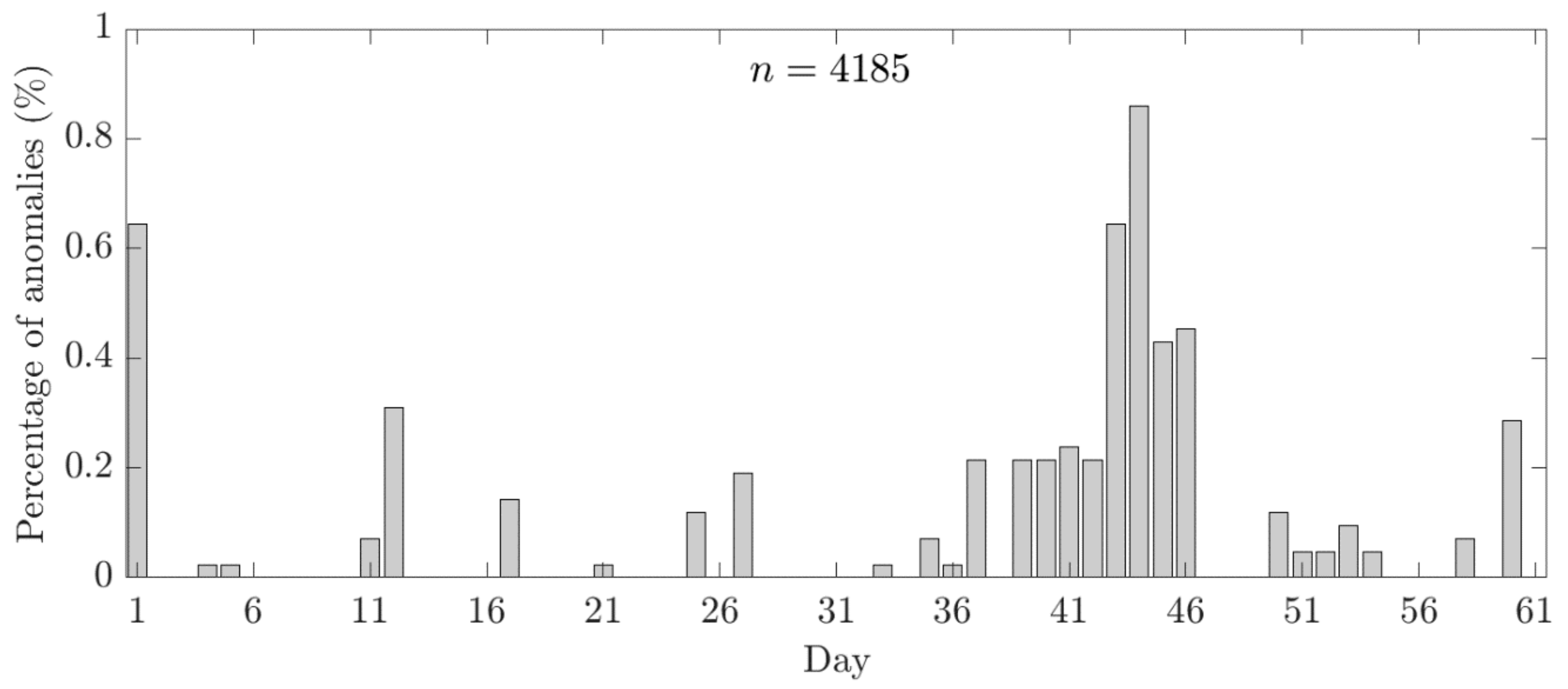
4.2. Statistics of Precursor Presences
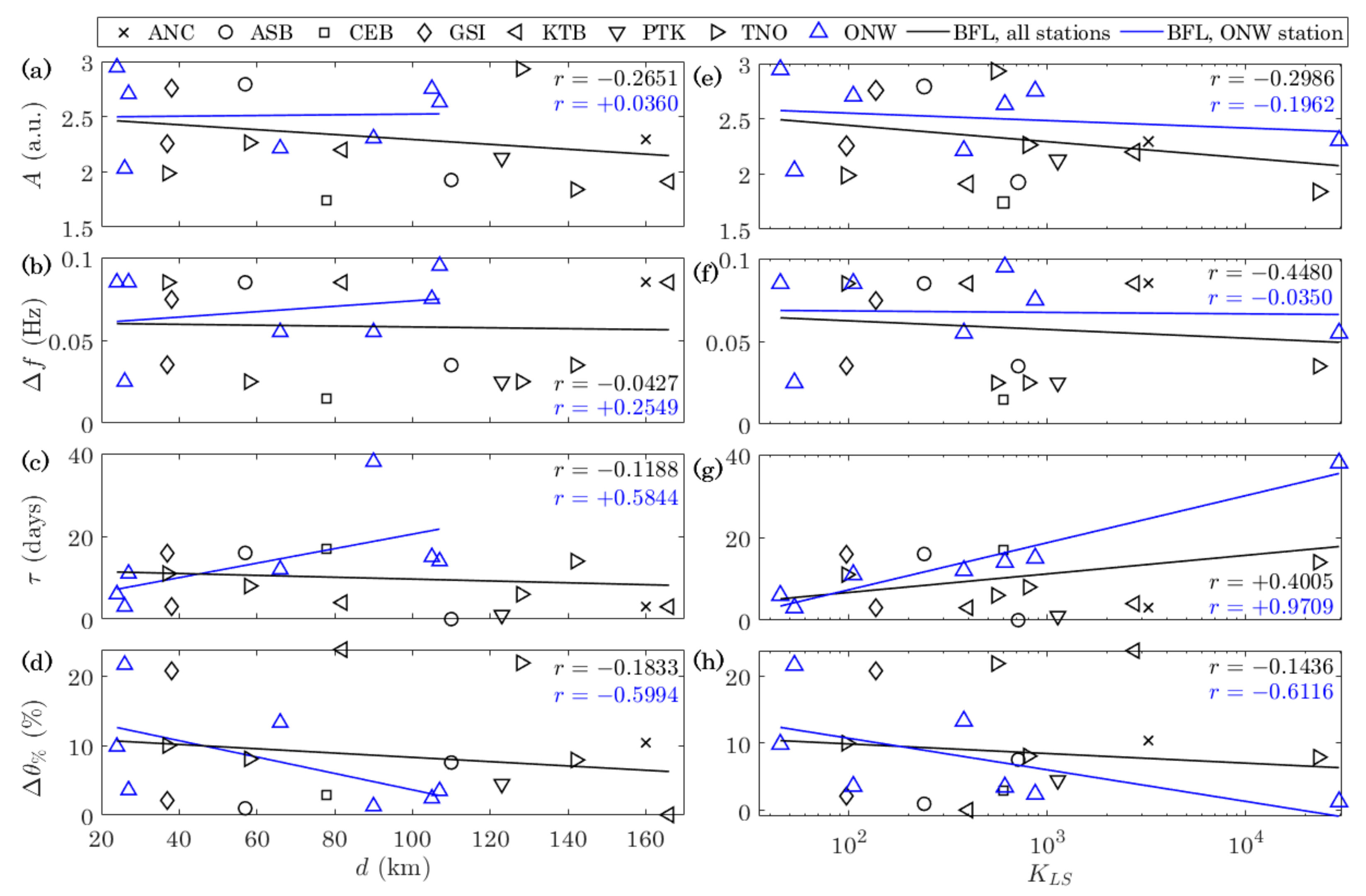
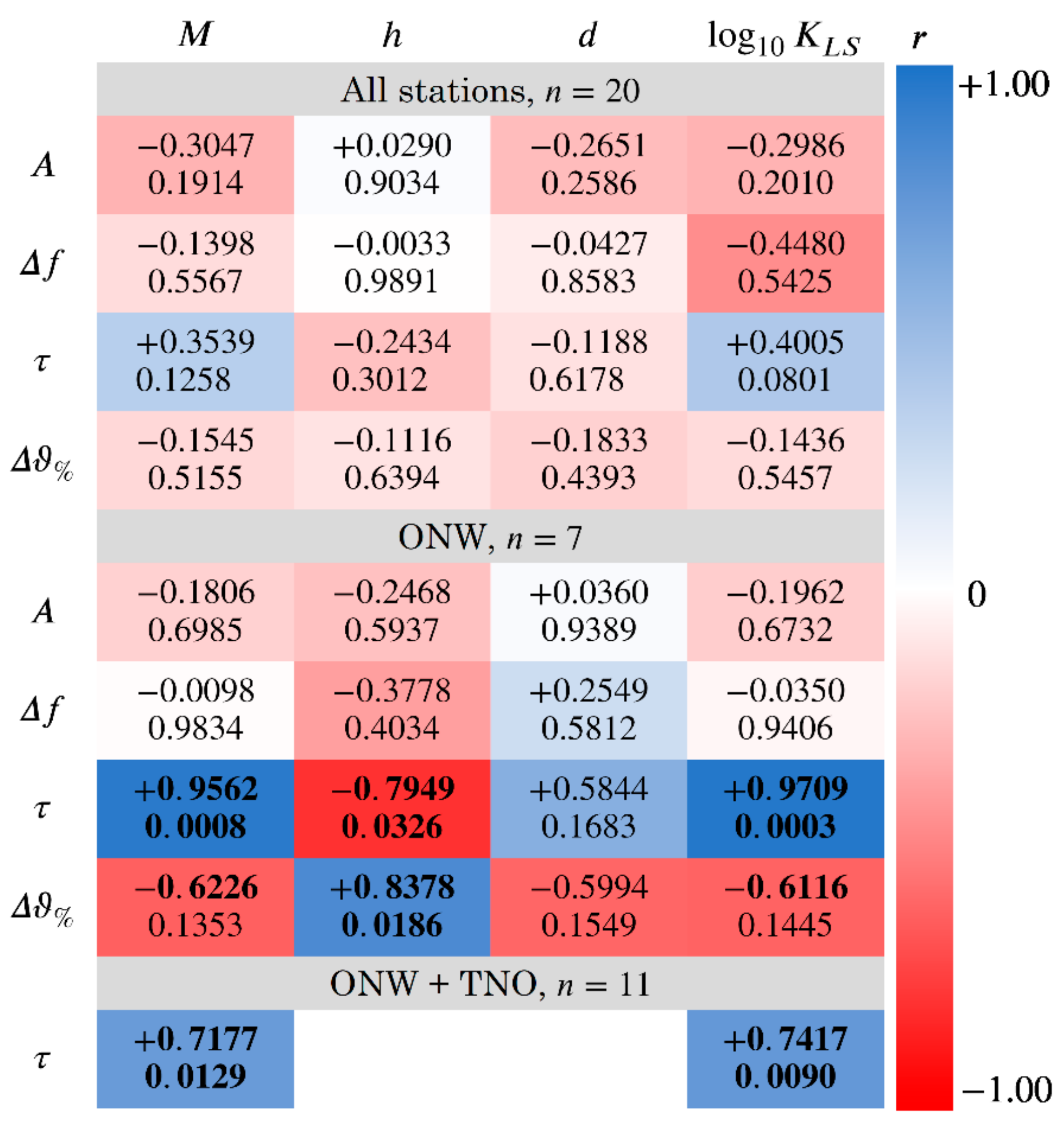
4.3. Correlation Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Potirakis, S.; Schekotov, A.; Contoyiannis, Y.; Balasis, G.; Koulouras, G.; Melis, N.; Boutsi, A.; Hayakawa, M.; Eftaxias, K.; Nomicos, C. On possible electromagnetic precursors to a significant earthquake (Mw = 6.3) occurred in Lesvos (Greece) on 12 June 2017. Entropy 2019, 21, 241. [Google Scholar] [CrossRef] [PubMed]
- Yusof, K.A.; Abdullah, M.; Hamid, N.S.A.; Ahadi, S.; Yoshikawa, A. Normalized polarization ratio analysis for ULF precursor detection of the 2009 M7.6 Sumatra and 2015 M6.8 Honshu earthquakes. J. Kejuruteraan 2020, 3, 35–41. [Google Scholar] [CrossRef]
- Schekotov, A.; Chebrov, D.; Hayakawa, M.; Belyaev, G.G.; Berseneva, N. Short-term earthquake prediction in Kamchatka using low-frequency magnetic fields. Nat. Hazards 2020, 100, 735–755. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Hayakawa, M. On the generation mechanism of ULF seismogenic electromagnetic emissions. Phys. Earth Planet. Inter. 1998, 105, 201–210. [Google Scholar] [CrossRef]
- Fedorov, E.N.; Pilipenko, V.; Uyeda, S. Electric and magnetic fields generated by electrokinetic processes in a conductive crust. Phys. Chem. Earth Part C 2001, 26, 793–799. [Google Scholar] [CrossRef]
- Sorokin, V.M.; Pokhotelov, O.A. Generation of ULF geomagnetic pulsations during early stage of earthquake preparation. J. Atmos. Sol. Terr. Phy. 2010, 72, 763–766. [Google Scholar] [CrossRef]
- Yamazaki, K. Temporal variations in magnetic signals generated by the piezomagnetic effect for dislocation sources in a uniform medium. Geophys. J. Int. 2016, 206, 130–141. [Google Scholar] [CrossRef]
- Dudkin, F.; Korepanov, V.; Yang, D.; Li, Q.; Leontyeva, O. Analysis of the local lithospheric magnetic activity before and after Panzhihua Mw = 6.0 earthquake (30 August 2008, China). Nat. Hazards Earth Syst. Sci. 2011, 11, 3171–3180. [Google Scholar] [CrossRef]
- Prattes, G.; Schwingenschuh, K.; Eichelberger, H.U.; Magnes, W.; Boudjada, M.; Stachel, M.; Vellante, M.; Villante, U.; Wesztergom, V.; Nenovski, P. Ultra Low Frequency (ULF) European multi station magnetic field analysis before and during the 2009 earthquake at L’Aquila regarding regional geotechnical information. Nat. Hazards Earth Syst. Sci. 2011, 11, 1959–1968. [Google Scholar] [CrossRef]
- Siingh, D.; Singh, A.K.; Patel, R.P.; Singh, R.; Singh, R.P.; Veenadhari, B.; Mukherjee, M. Thunderstorms, lightning, sprites and magnetospheric whistler-mode radio waves. Surv. Geophys. 2008, 29, 499–551. [Google Scholar] [CrossRef]
- Berthelier, J.-J.; Malingre, M.; Pfaff, R.; Seran, E.; Pottelette, R.; Jasperse, J.; Lebreton, J.-P.; Parrot, M. Lightning-induced plasma turbulence and ion heating in equatorial ionospheric depletions. Nat. Geosci. 2008, 1, 101–105. [Google Scholar] [CrossRef]
- Rietveld, M.T.; Stubbe, P.; Kopka, H. On the frequency dependence of ELF/VLF waves produced by modulated ionospheric heating. Radio Sci. 1989, 24, 270–278. [Google Scholar] [CrossRef]
- Papadopoulos, K. The magnetic response of the ionosphere to pulsed HF heating. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Stanica, D.A.; Stanica, D. ULF pre-seismic geomagnetic anomalous signal related to Mw8.1 offshore Chiapas earthquake, Mexico on 8 September 2017. Entropy 2019, 21, 29. [Google Scholar] [CrossRef] [PubMed]
- Yusof, K.A.; Hamid, N.S.A.; Abdullah, M.; Ahadi, S.; Yoshikawa, A. Assessment of signal processing methods for geomagnetic precursor of the 2012 M6.9 Visayas, Philippines earthquake. Acta Geophys. 2019, 142, 1297–1306. [Google Scholar] [CrossRef]
- Hirano, T.; Hattori, K. ULF geomagnetic changes possibly associated with the 2008 Iwate–Miyagi Nairiku earthquake. J. Asian Earth Sci. 2011, 41, 442–449. [Google Scholar] [CrossRef]
- Masci, F. Comment on “Ultra Low Frequency (ULF) European multi station magnetic field analysis before and during the 2009 earthquake at L’Aquila regarding regional geotechnical information” by Prattes et al. (2011). Nat. Hazards Earth Syst. Sci. 2012, 12, 1717–1719. [Google Scholar] [CrossRef]
- Masci, F.; Thomas, J.N. Are there new findings in the search for ULF magnetic precursors to earthquakes? J. Geophys. Res. 2015, 120, 10289–10304. [Google Scholar] [CrossRef]
- Potirakis, S.; Hayakawa, M.; Schekotov, A. Fractal analysis of the ground-recorded ULF magnetic fields prior to the 11 March 2011 Tohoku earthquake (Mw=9): Discriminating possible earthquake precursors from space-sourced disturbances. Nat. Hazards 2017, 85, 59–86. [Google Scholar] [CrossRef]
- Ohta, K.; Izutsu, J.; Schekotov, A.; Hayakawa, M. The ULF/ELF electromagnetic radiation before the 11 March 2011 Japanese earthquake. Radio Sci. 2013, 48, 589–596. [Google Scholar] [CrossRef]
- Chauhan, V.; Singh, O.P.; Pandey, U.; Singh, B.; Arora, B.R.; Rawat, G.; Pathan, B.M.; Sinha, A.K.; Sharma, A.K.; Patil, A.V. A search for precursor of earthquakes from multi-station ULF observation and TEC measurements in India. Indian J. Radio Space 2012, 41, 543–556. [Google Scholar]
- Ahadi, S.; Puspito, T.; Ibrahim, G.; Saroso, S.; Yumoto, K.; Yoshikawa, A.; Muzli, M. Anomalous ULF emissions and their possible association with the strong earthquakes in Sumatra, Indonesia, during 2007–2012. J. Math. Fund. Sci. 2015, 47, 84–103. [Google Scholar] [CrossRef]
- Yumoto, K.; MAGDAS Group. Space weather activities at SERC for IHY: MAGDAS. Bull. Seismol. Soc. Am. 2007, 35, 511–522. [Google Scholar]
- Bello, S.A.; Abdullah, M.; Hamid, N.S.A.; Yoshikawa, A.; Olawepo, A.O. Variations of B0 and B1 with the solar quiet Sq-current system and comparison with IRI-2012 model at Ilorin. Adv. Space Res. 2017, 60, 307–316. [Google Scholar] [CrossRef]
- Hayakawa, M. Earthquake Prediction with Radio Techniques; John Wiley & Sons Pte Ltd.: Singapore, 2015; ISBN 1118770161. [Google Scholar]
- Molchanov, O.A.; Hayakawa, M. Seismo Electromagnetics and Related Phenomena: History and Latest Results; Terrapub: Tokyo, Japan, 2008; ISBN 978-4-88704-143-1. [Google Scholar]
- Rostoker, G. Geomagnetic indices. Rev. Geophys. 1972, 10, 935–950. [Google Scholar] [CrossRef]
- Namgaladze, A.; Karpov, M.; Knyazeva, M. Seismogenic disturbances of the ionosphere during high geomagnetic activity. Atmosphere 2019, 10, 359. [Google Scholar] [CrossRef]
- Gonzalez, W.D.; Joselyn, J.A.; Kamide, Y.; Kroehl, H.W.; Rostoker, G.; Tsurutani, B.T.; Vasyliunas, V.M. What is a geomagnetic storm? J. Geophys. Res. 1994, 99, 5771. [Google Scholar] [CrossRef]
- Yaso, N.; Hasbi, A.M.; Abdullah, M. Investigation of ionospheric and magnetic response during the 2011 Tohoku earthquake using ground based measurement. Indian J. Radio Space 2016, 45, 115–125. [Google Scholar]
- Hasbi, A.M.; Mohd Ali, M.A.; Misran, N. Ionospheric variations before some large earthquakes over Sumatra. Nat. Hazards Earth Syst. Sci. 2011, 11, 597–611. [Google Scholar] [CrossRef]
- Hayakawa, M.; Kawate, R.; Molchanov, O.A.; Yumoto, K. Results of ultra-low-frequency magnetic field measurements during the Guam Earthquake of 8 August 1993. Geophys. Res. Lett. 1996, 23, 241–244. [Google Scholar] [CrossRef]
- Yusof, K.A.; Abdullah, M.; Hamid, N.S.A.; Ahadi, S. On effective ULF frequency ranges for geomagnetic earthquake precursor. In Proceedings of the International Conference on Space Weather and Satellite Application (ICeSSAT 2018), UiTM Shah Alam, Selangor, Malaysia, 7–9 August 2019; Jusoh, M.H., Yaacob, N., Radzi, Z.M., Manut, A., Eds.; IOP Science: Bristol, UK, 2019; pp. 1–8. [Google Scholar]
- Ida, Y.; Yang, D.; Li, Q.; Sun, H.; Hayakawa, M. Detection of ULF electromagnetic emissions as a precursor to an earthquake in China with an improved polarization analysis. Nat. Hazards Earth Syst. Sci. 2008, 8, 775–777. [Google Scholar] [CrossRef]
- Rawat, G.; Chauhan, V.; Dhamodharan, S. Fractal dimension variability in ULF magnetic field with reference to local earthquakes at MPGO, Ghuttu. Geomat. Nat. Hazards Risk 2016, 7, 1937–1947. [Google Scholar] [CrossRef]
- Takla, E.M.; Yumoto, K.; Okano, S.; Uozumi, T.; Abe, S. The signature of the 2011 Tohoku mega earthquake on the geomagnetic field measurements in Japan. NRIAG J. Astron. Geophys. 2013, 2, 185–195. [Google Scholar] [CrossRef]
- Singh, Y.P.; Badruddin. Statistical considerations in superposed epoch analysis and its applications in space research. J. Atmos. Sol. Terr. Phy. 2006, 68, 803–813. [Google Scholar] [CrossRef]
- Hattori, K.; Han, P.; Yoshino, C.; Febriani, F.; Yamaguchi, H.; Chen, C.-H. Investigation of ULF seismo-magnetic phenomena in Kanto, Japan during 2000–2010: Case studies and statistical studies. Surv. Geophys. 2013, 34, 293–316. [Google Scholar] [CrossRef]
- Evans, J.D. Straightforward Statistics for the Behavioral Sciences; Brooks/Cole: Pacific Grove, CA, USA, 1996; ISBN 9780534231002. [Google Scholar]
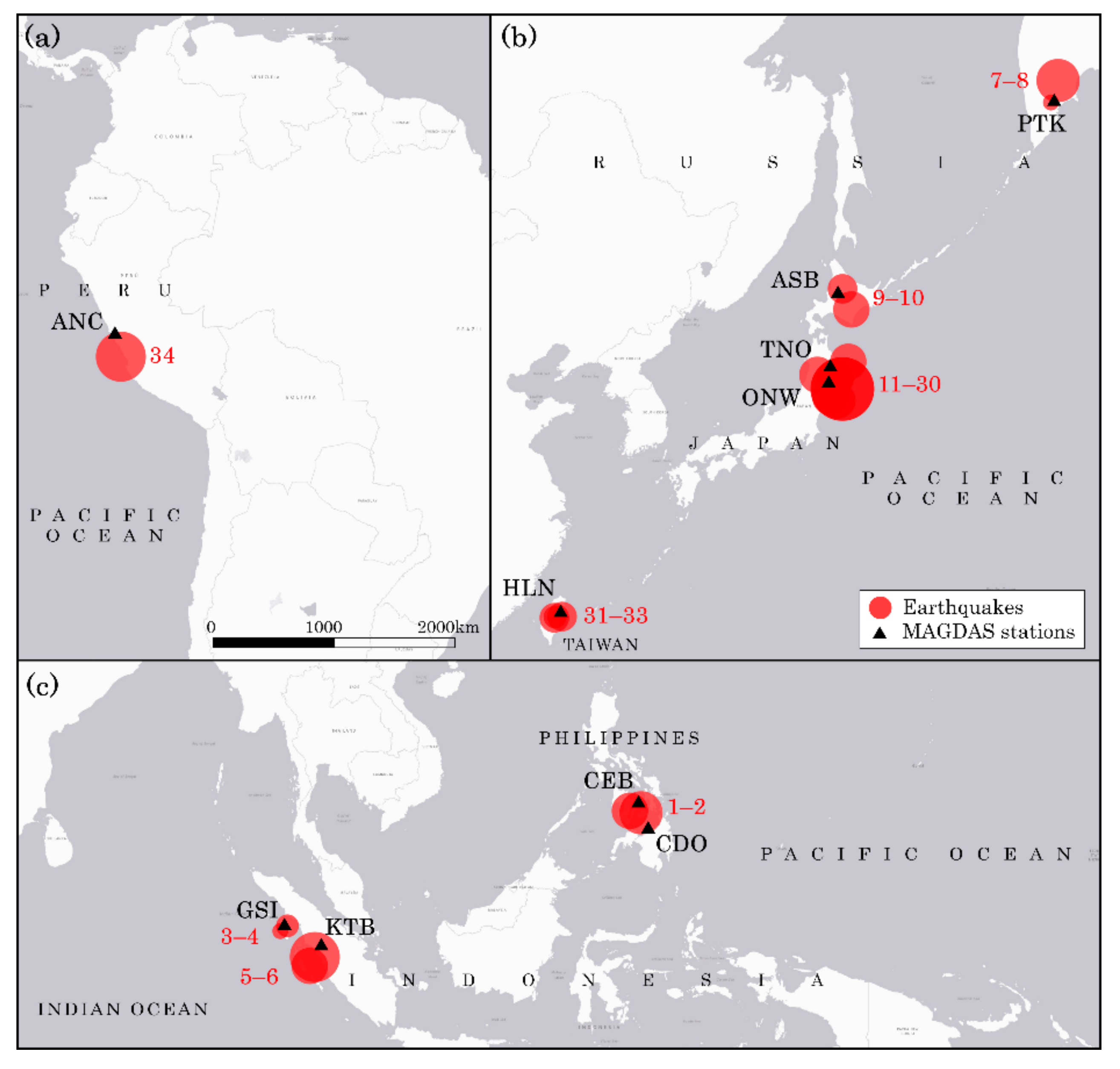


| Region | Code | Location | Lat. (°N) 1 | Lon. (°E) 1 | Year (s) 2 |
|---|---|---|---|---|---|
| Southeast Asia | CEB | Cebu, Philippines | 10.36 | 123.91 | 2011–2012 |
| CDO | Cagayan De Oro, Philippines | 8.46 | 124.63 | 2013 | |
| GSI | Gunung Sitoli, Indonesia | 1.18 | 97.34 | 2014–2015 | |
| KTB | Kotatabang, Indonesia | −0.20 | 100.32 | 2009 | |
| East Asia | PTK | Paratunka, Russia | 52.94 | 158.25 | 2013, 2015–2016 |
| ASB | Ashibetsu, Japan | 43.46 | 142.17 | 2011–2013 | |
| TNO | Tohno, Japan | 39.30 | 141.60 | 2011, 2013–2015 | |
| ONW | Onagawa, Japan | 38.40 | 141.47 | 2008, 2010–2013, 2015–2016 | |
| HLN | Hualien, Taiwan | 23.90 | 121.55 | 2009–2013 | |
| South America | ANC | Ancon, Peru | −11.77 | −77.15 | 2007 |
| ID 1 | Date (UT) | Lat. (°N) | Lon. (°E) | M2 | h (km) 3 | Station 4 | d (km) 5 | (°) 7 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 February 2012 | 10.06 | 123.27 | 6.7 | 40 | CEB | 78 | 597 | 244.59 |
| 2 | 15 October 2013 | 09.92 | 124.10 | 7.1 | 15 | CDO | 172 | 776 | 340.33 |
| 3 | 14 September 2014 | 01.17 | 097.27 | 5.5 | 30 | GSI | 37 | 97 | 247.25 |
| 4 | 8 May 2015 | 01.56 | 097.80 | 5.7 | 40 | GSI | 38 | 137 | 40.22 |
| 5 | 16 August 2009 | −01.42 | 099.46 | 6.7 | 30 | KTB | 166 | 398 | 215.17 |
| 6 | 30 September 2009 | −00.76 | 099.84 | 7.6 | 80 | KTB | 82 | 2754 | 220.60 |
| 7 | 26 February 2013 | 53.06 | 158.01 | 5.3 | 132 | PTK | 21 | 78 | 309.82 |
| 8 | 30 January 2016 | 54.03 | 158.54 | 7.2 | 159 | PTK | 123 | 1128 | 8.88 |
| 9 | 21 October 2011 | 43.91 | 142.51 | 6.1 | 182 | ASB | 57 | 239 | 28.53 |
| 10 | 2 February 2013 | 42.79 | 143.17 | 6.9 | 100 | ASB | 110 | 712 | 132.21 |
| 11 | 11 March 2011 | 38.30 | 142.50 | 9.0 | 22 | TNO | 142 | 23,214 | 146.48 |
| 12 | 31 March 2013 | 39.12 | 141.88 | 5.5 | 35 | TNO | 37 | 97 | 138.97 |
| 13 | 16 February 2015 | 39.87 | 142.94 | 6.8 | 15 | TNO | 128 | 553 | 63.73 |
| 14 | 12 May 2015 | 38.95 | 141.99 | 6.8 | 40 | TNO | 58 | 799 | 144.12 |
| 15 | 1 June 2008 | 38.51 | 141.77 | 5.1 | 60 | ONW | 26 | 53 | 72.77 |
| 16 | 13 June 2008 | 39.12 | 140.64 | 7.0 | 33 | ONW | 105 | 868 | 316.34 |
| 17 | 19 July 2008 | 37.63 | 142.13 | 6.8 | 30 | ONW | 107 | 610 | 147.50 |
| 18 | 11 March 2011 | 38.30 | 142.50 | 9.0 | 22 | ONW | 90 | 29,554 | 99.61 |
| 19 | 14 March 2010 | 37.82 | 141.61 | 6.6 | 40 | ONW | 70 | 525 | 170.59 |
| 20 | 25 January 2012 | 38.21 | 141.69 | 5.3 | 49 | ONW | 31 | 72 | 144.32 |
| 21 | 8 March 2012 | 38.63 | 141.66 | 5.0 | 52 | ONW | 26 | 45 | 36.48 |
| 22 | 5 May 2012 | 38.25 | 141.54 | 5.2 | 50 | ONW | 22 | 65 | 166.07 |
| 23 | 17 June 2012 | 38.97 | 141.83 | 6.4 | 60 | ONW | 66 | 379 | 27.15 |
| 24 | 29 August 2012 | 38.49 | 141.78 | 5.5 | 48 | ONW | 27 | 105 | 77.89 |
| 25 | 25 October 2012 | 38.33 | 141.84 | 5.6 | 50 | ONW | 34 | 119 | 111.18 |
| 26 | 21 November 2012 | 38.55 | 141.72 | 5.0 | 53 | ONW | 24 | 45 | 59.57 |
| 27 | 17 April 2013 | 38.53 | 141.56 | 5.9 | 45 | ONW | 12 | 237 | 34.81 |
| 28 | 4 August 2013 | 38.26 | 141.81 | 5.8 | 60 | ONW | 35 | 166 | 124.72 |
| 29 | 12 May 2015 | 38.95 | 141.99 | 6.8 | 40 | ONW | 72 | 732 | 37.81 |
| 30 | 26 April 2016 | 38.22 | 141.63 | 5.0 | 52 | ONW | 28 | 44 | 151.81 |
| 31 | 19 December 2009 | 23.87 | 121.66 | 6.4 | 48 | HLN | 12 | 565 | 106.59 |
| 32 | 27 March 2013 | 23.84 | 121.13 | 6.0 | 21 | HLN | 43 | 221 | 261.21 |
| 33 | 2 June 2013 | 23.79 | 121.08 | 6.2 | 20 | HLN | 49 | 299 | 255.74 |
| 34 | 15 August 2007 | −13.14 | −076.71 | 7.9 | 40 | ANC | 160 | 3240 | 162.64 |
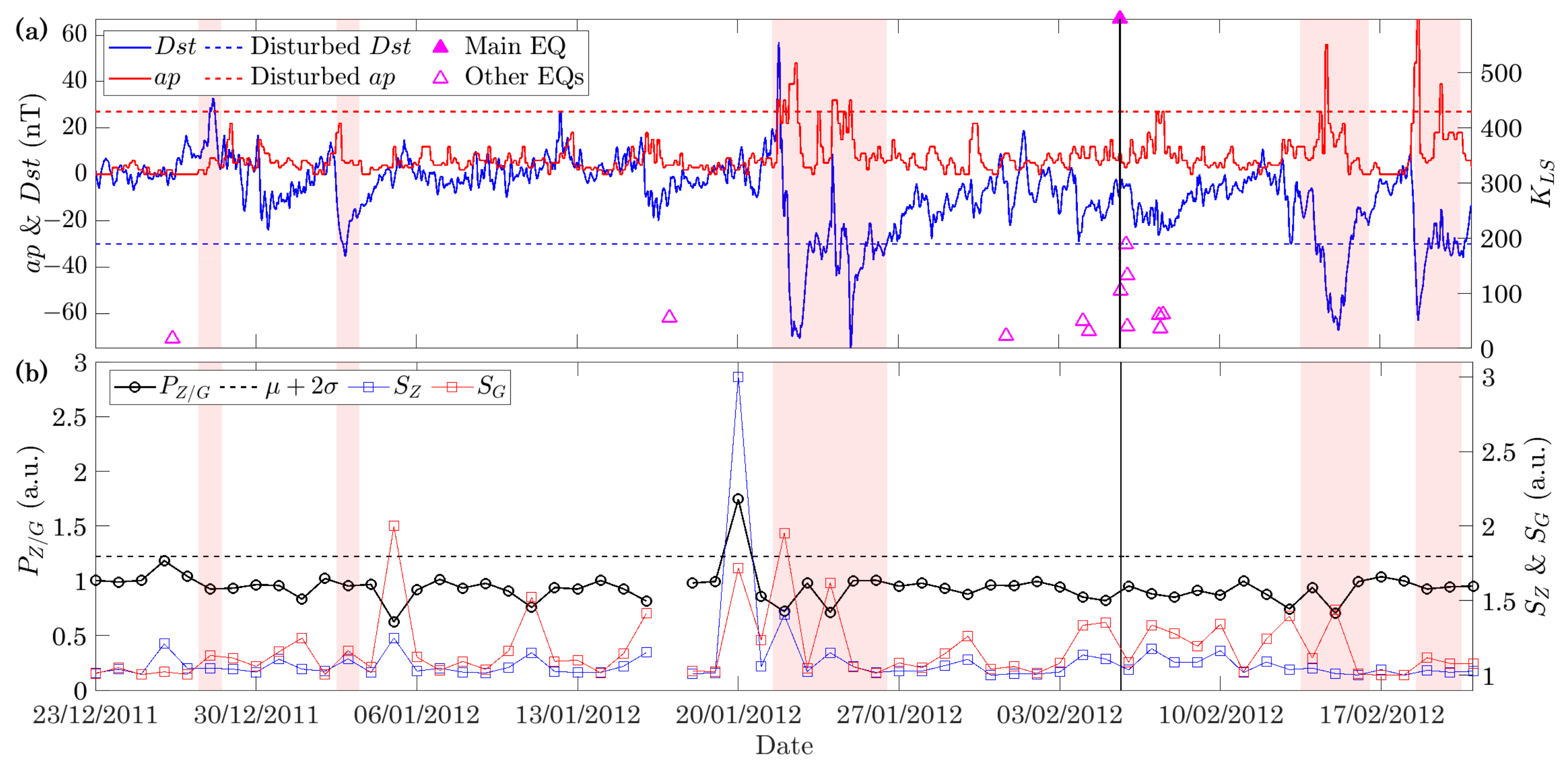
| ID 1 | A (a.u.) 2 | Δf (Hz) 3 | (Days) 4 | (°) 6 | ap, Dst (nT) 9 | |||
|---|---|---|---|---|---|---|---|---|
| 1 | 1.746 | 0.01–0.02 | 17 | 01–05 | 255 | −10.41 | 2.892 | 5, −5 |
| 3 | 2.254 | 0.03–0.04 | 16 | 01–05 | 255 | −7.75 | 2.153 | 22, −26 |
| 4 | 2.763 | 0.07–0.08 | 3 | 22–02 | 115 | −74.78 | 20.772 | 4, −9 |
| 5 | 1.911 | 0.08–0.09 | 3 | 00–04 | 215 | 0.17 | 0.047 | 3, −7 |
| 6 | 2.199 | 0.08–0.09 | 4 | 22–02 | 135 | 85.60 | 23.778 | 4, 11 |
| 8 | 2.126 | 0.02–0.03 | 1 | 02–06 | 25 | −16.12 | 4.478 | 3, −2 |
| 9 | 2.793 | 0.08–0.09 | 16 | 00–04 | 25 | 3.53 | 0.981 | 22, −23 |
| 10 | 1.926 | 0.03–0.04 | 0 10 | 22–02 | 105 | 27.21 | 7.558 | 7, −18 |
| 11 | 1.840 | 0.03–0.04 | 14 | 00–04 | 175 | −28.52 | 7.922 | 4, 0 |
| 12 | 1.987 | 0.08–0.09 | 11 | 22–02 | 175 | −36.03 | 10.008 | 9, −28 |
| 13 | 2.932 | 0.02–0.03 | 6 | 00–04 | 345 | −78.73 | 21.869 | 6, −8 |
| 14 | 2.264 | 0.02–0.03 | 8 | 22–02 | 115 | 29.12 | 8.089 | 12, −6 |
| 15 | 2.029 | 0.02–0.03 | 3 | 02–06 | 355 | −77.77 | 21.603 | 12, −4 |
| 16 | 2.752 | 0.07–0.08 | 15 | 22–02 | 325 | −8.66 | 2.406 | 12, −11 |
| 17 | 2.630 | 0.09–0.10 | 14 | 23–03 | 135 | 12.50 | 3.472 | 12, −10 |
| 18 | 2.304 | 0.05–0.06 | 38 | 00–04 | 95 | 4.61 | 1.281 | 18, −19 |
| 23 | 2.213 | 0.05–0.06 | 12 | 22–02 | 75 | −47.85 | 13.292 | 27, −26 |
| 24 | 2.706 | 0.08–0.09 | 11 | 01–05 | 65 | 12.89 | 3.581 | 22, −6 |
| 26 | 2.946 | 0.08–0.09 | 6 | 00–04 | 95 | −35.43 | 9.842 | 3, −23 |
| 34 | 2.298 | 0.08–0.09 | 3 | 02–06 | 125 | 37.64 | 10.456 | 7, −18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yusof, K.A.; Abdullah, M.; Hamid, N.S.A.; Ahadi, S.; Yoshikawa, A. Correlations between Earthquake Properties and Characteristics of Possible ULF Geomagnetic Precursor over Multiple Earthquakes. Universe 2021, 7, 20. https://doi.org/10.3390/universe7010020
Yusof KA, Abdullah M, Hamid NSA, Ahadi S, Yoshikawa A. Correlations between Earthquake Properties and Characteristics of Possible ULF Geomagnetic Precursor over Multiple Earthquakes. Universe. 2021; 7(1):20. https://doi.org/10.3390/universe7010020
Chicago/Turabian StyleYusof, Khairul Adib, Mardina Abdullah, Nurul Shazana Abdul Hamid, Suaidi Ahadi, and Akimasa Yoshikawa. 2021. "Correlations between Earthquake Properties and Characteristics of Possible ULF Geomagnetic Precursor over Multiple Earthquakes" Universe 7, no. 1: 20. https://doi.org/10.3390/universe7010020
APA StyleYusof, K. A., Abdullah, M., Hamid, N. S. A., Ahadi, S., & Yoshikawa, A. (2021). Correlations between Earthquake Properties and Characteristics of Possible ULF Geomagnetic Precursor over Multiple Earthquakes. Universe, 7(1), 20. https://doi.org/10.3390/universe7010020







