Abstract
The solar system is populated with, other than planets, a wide variety of minor bodies, the majority of which are represented by asteroids. Most of their orbits are comprised of those between Mars and Jupiter, thus forming a population named Main Belt. However, some asteroids can run on trajectories that come close to, or even intersect, the orbit of the Earth. These objects are known as Near Earth Asteroids (NEAs) or Near Earth Objects (NEOs) and may entail a risk of collision with our planet. Predicting the occurrence of such collisions as early as possible is the task of Impact Monitoring (IM). Dedicated algorithms are in charge of orbit determination and risk assessment for any detected NEO, but their efficiency is limited in cases in which the object has been observed for a short period of time, as is the case with newly discovered asteroids and, more worryingly, imminent impactors: objects due to hit the Earth, detected only a few days or hours in advance of impacts. This timespan might be too short to take any effective safety countermeasure. For this reason, a necessary improvement of current observation capabilities is underway through the construction of dedicated telescopes, e.g., the NEO Survey Telescope (NEOSTEL), also known as “Fly-Eye”. Thanks to these developments, the number of discovered NEOs and, consequently, imminent impactors detected per year, is expected to increase, thus requiring an improvement of the methods and algorithms used to handle such cases. In this paper we present two new tools, based on the Admissible Region (AR) concept, dedicated to the observers, aiming to facilitate the planning of follow-up observations of NEOs by rapidly assessing the possibility of them being imminent impactors and the remaining visibility time from any given station.
1. Introduction
Every night astronomers (professionals and amateurs) scan the sky looking for new or already discovered natural objects (asteroids, comets). Collected observations are sent to the Minor Planet Center (MPC), responsible, under the auspices of the International Astronomical Union (IAU), for orbit computation and classification of small solar system bodies. Newly observed objects are temporarily recorded on the NEO Confirmation Page (NEOCP), until enough information is available to confirm them or until they are removed after a week of being unconfirmed.
When just discovered, asteroids have strongly undetermined orbits, being weakly constrained by the few available astrometric observations. However it is crucial to clarify whether a given object represents a risk for the Earth in a near or remote future: this is the goal of Impact Monitoring (IM), a relatively young field of research ([1,2]). Two IM dedicated automatic systems, CLOMON2 (at University of Pisa/SpaceDyS/ESA-NEO Coordination Centre (NEOCC)) and Sentry (at Jet Propulsion Laboratory (JPL)/NASA), have been developed approximately 20 years ago ([3]). Both systems scan the Confidence Region (CR), i.e., the 6-dimensional uncertainty region associated to the orbit, and sample the Line Of Variations (LOV, a differentiable curve representing a kind of spine of the CR, [4]), with a finite number of Virtual Asteroids (VAs), each of which represents an orbit statistically compatible with the observations. VAs that, after propagation to the time of a close approach with the Earth, reveal a nonzero probability of collision are marked as Virtual Impactors (VIs).
The LOV method is very useful when the CR is elongated and thin, but this is not the case when the observed arc is very short: in this eventuality the uncertainty results to be wide in at least two directions and the LOV is not a reliable representative of the entire region ([5]). Unfortunately, this is precisely the case of very small asteroids observed only shortly before a close approach or an impact with the Earth (the so-called imminent impactors). With the aim to address the issue, three dedicated systems have recently been developed: SCOUT (at JPL/NASA, [6]), NEORANGER (at University of Helsinki, [7]) and NEOScan (at University of Pisa/SpaceDyS, [8]). Taking the latter as an example, NEOScan consults the NEOCP of the Minor Planet Center (MPC) every two minutes, extracting and analysing data through the use of algorithms based on the Admissible Region (AR), a tool widely used also in the field of space debris orbit determination ([9,10]).
However, in order to adequately face the problem, it is quite clear that an improvement of current observation capabilities is necessary and, in this frame, new dedicated telescopes, such as the NEOSTEL Fly-Eye telescope ([11]), are being realized and are expected to increase the number of Near-Earth Objects (NEOs) and, consequently, imminent impactors detected per year, thus requiring an improvement of the methods and algorithms used to handle such cases. Moreover, when few observations are available and the uncertainty associated to the orbit is large, rapid follow-up is necessary to confirm or dismiss the possibility of an impact. In this scenario, this paper focuses on the development and testing of new IM tools dedicated to the observers, aiming to facilitate the planning of follow-up observations of imminent impactors. The methods and algorithms we propose are completely general and applicable to any telescope, provided that the limiting magnitude and observatory code are known. The software we used and into which we implement the new features is OrbFit1: a multipurpose code, developed at University of Pisa, able to perform orbit determination, propagations and IM computations. Further information about OrbFit and its functionalities is provided in Appendix A.
The paper is structured as follows. Section 2.1 briefly introduces the concept of AR, upon which our new tools are built. Section 3 discusses the priority list, highlighting the difference between its original role and the new meaning it acquired in the context of the recently developed IM systems. Section 4 and Section 5 represent the core of this work, proposing two new tools ideated to facilitate the planning of follow-up observations of newly discovered NEOs. The first tool computes the Minimum Orbit Intersection Distance (MOID, [12,13,14]) of a given object and gives its graphical representation on the AR plane, allowing to identify at first glance the groups of VAs that might lead to a close encounter with the Earth. A fit of the points with near-zero MOID allows to draw a MOID = 0 line that, if close enough to the nominal solution, shows if an impact is possible. The second tool computes the remaining visibility time for a given object from an observatory of choice. Combining the outputs of the two tools, we can select the objects for which to solicit immediate follow-up, before they collide with our planet or become unobservable and, possibly, lost with a nonzero probability of impacting at a later close approach. We illustrate our results with some examples of how the tools perform on real-life cases. In Section 7, we draw some conclusions.
2. Background and Definitions
We will now introduce some concepts and key definitions that we believe necessary for a full comprehension of the work described in this paper. For a more complete mathematical background, we refer the interested reader to the papers cited in this Section.
2.1. Attributables and Admissible Region
Optical observations produce information about the position and velocity of the observed object on the celestial sphere, expressed in terms of right ascension , declination and their derivatives, while leaving undetermined the range and range rate with respect to the observer’s position. A collection of astrometric measurements assumed to correspond to the same moving object constitutes a tracklet.
It is useful in practice to define, following [15], a set of orbital elements that summarises all the information obtained from observations: the attributable orbital elements
The vector that synthesises all of the information obtainable from a single observed arc is called attributable and is defined as
Given an attributable, to obtain an orbit we need to choose a couple among an infinite range of possibilities. By restricting the choice, following some exclusion criteria, to a subset of the - plane, Milani et al. in [9] introduced the concept of AR. Provided that it is compact, the AR can be sampled with different techniques to generate a swarm of VAs, similarly to what is done with the Confidence Region. The AR can thus be used in those cases in which few observations are available and the CR, being wide in two dimensions, is not well approximated by the LOV. The boundaries of the AR can be defined as follows:
- The outer boundary corresponds to the limit for which an object belongs to the Solar System, i.e., the two-body energy relative to the Sun is negative:where k is the Gauss constant and represents the heliocentric position of the object;
- The inner boundary is the limit for which an object is not a satellite of the Earth, i.e., the two-body energy relative to the Earth is positive (assuming that the observations are geocentric):
where is the ratio between the masses of the Earth and the Sun.
The AR can be sampled in different ways to generate a set of Virtual Asteroids (VAs) with the suitable characteristics for each case. At the time when the first IM systems became operational, computation time was a major limiting factor to the density of the sampling, and the triangulation sampling method was proposed. Following the improvement of the capabilities of modern calculators, new, computationally heavier sampling techniques have been introduced. A simple but useful choice is to sample the AR with the nodes of a rectangular grid. Then, an evaluation of the two-body energy for each node allows to exclude the points that fall outside of the AR. The preliminary grid thus obtained can be densified at a later step by increasing the number of nodes, in order to achieve a higher resolution.
If a preliminary orbit is available, it is possible to sample the AR with a faster method than the above described one. The “cobweb” sampling was introduced in [16] and allows to scan the AR with a set of VAs that is centred on the nominal solution and denser in its neighbourhood. The sampling points are selected along the level curves of the target function used to minimize the RMS of the observational residuals. These curves are the restriction to the () plane of the five-dimensional concentric ellipsoids defined in the orbital elements space by the quadratic form associated to the normal matrix ( being the covariance matrix).
We then define the Manifold Of Variations (MOV) as in [17]:
Definition 1.
Given a subset K of the AR, we define the Manifold Of Variations to be the set of points such that and is the local minimum of , when it exists.
In the above, Q is the target function used to minimise observational residuals:
where indicates the m-dimensional vector of the residuals and W is the weight matrix.
2.2. Minimum Orbital Intersection Distance
Being the minimum Euclidean distance d between any two points on two different orbits, the MOID can be used as a warning for possible collisions between NEOs and the Earth. A large MOID indicates that the asteroid is not going to impact the Earth in the near future, while a small one does not necessarily imply a collision, since this quantity does not consider the actual position occupied by the bodies on their respective orbits: even if the orbits cross, the encounter might not happen if the timing is not right. Still, objects with a small MOID should be carefully followed to confirm or exclude the possibility of a collision in subsequent returns, especially when the orbit is known with large uncertainties.
Definition 2.
Let be a set of 10 orbital elements, composed by two subsets of five elements each, describing the geometric configuration of the orbits of a NEO and the Earth respectively. In addition, we define the vector , consisting of two parameters along the orbits (e.g., the true anomalies).
The Keplerian distance function is then defined as:
where and are two sets of Cartesian coordinates describing the positions of the two bodies in a reference frame centred in the common focus.
The MOID is usually calculated by finding the absolute minimum among the stationary points of , squared to be smooth even when . The most accredited analytical method, currently the standard tool for MOID computation, is the one proposed by Gronchi in [18].
3. Priority List
At the time when classical algorithms came to be, their computational efficiency was strongly limited by hardware constraints: in particular, it was not possible to perform calculations fast enough to analyse all of the objects for which new observations became available in a single day. This led to the establishment of a priority list to signal to the observers which objects to follow-up first.
3.1. Classical IM Algorithms
CLOMON, the first IM algorithm to be developed, was able to list the objects with a minimal encounter distance less than 0.1 au and such that the uncertainty region was large enough that linear approximation was not applicable. Entries were then ordered on the basis of a score given by the combined evaluation of the nominal MOID and of a parameter called RUNOFF, representing the along-track uncertainty resulting from a 100 years propagation. The search for VIs was then conducted starting from the objects with the highest score, while entries at the bottom of the list might have never been analysed.
The score attribution method used by CLOMON suffered from a selection effect: the uncertainty associated to the MOID is large for objects that are discovered far away from the Earth, which is often the case for large asteroids that, even when their collision probability is low, should be analysed, since an impact would release a great amount of energy and potentially cause great damage. Some of these objects might have not been rated as hazardous if their MOID exceeded 0.05 au, even if initial conditions with vanishing MOID could have been present within the large CR [3].
Second generation algorithms (i.e., Sentry and CLOMON2) use an improved score attribution rule: multiple solutions are computed for each NEO that shows a high RUNOFF (greater than 0.7 au for CLOMON2, while for Sentry the threshold is 1 au), from which the uncertainty of the MOID is calculated. The score is assigned on the basis of the minimum MOID resulting from the multiple solutions, instead of the nominal MOID. This method gives a high priority to some objects that CLOMON would not analyse, allowing to find numerous VIs.
However, as already mentioned, classical IM algorithms use the LOV method, wich is not suitable for the case of imminent impactors, thus dedicated systems that directly analyse NEOCP entries and apply the AR formalism, such as NEOScan, have recently been introduced.
3.2. Algorithms for Imminent Impactors
Nowadays, the improvement in observational capabilities to be achieved thanks to the introduction of new dedicated detectors is expected to entail an increase in the number of entries in the NEOCP. Such an eventuality fosters the need, no longer due to computational power constraints, as was the case when classical IM algorithms had just been introduced, for a new version of the priority list to determine the order in which follow-up observations need to be performed, if at all. The necessity to make a choice of what objects to observe is now dictated by the limited number and time availability of the observatories able to perform the follow-up. As an example, NEOScan assigns priority on the basis of two quantities, obtained as follows.
For each VI resulting from the AR analysis, the associated Impact Probability (IP) (obtained by integration of the probability density function propagation to the sampling space) and geodetic curvature are computed and used to assign an impact flag: an integer between 0 and 4 that serves the purpose of easily communicating to the observers the necessity to prioritise the observation of a given object [8]. The criteria for the assignment of the flag are listed in Table 1.

Table 1.
Conditions on impact probability and curvature to assign the impact flag to an object, from [8].
Furthermore, the system is able to compute the probability (known as object-category score) of the object to belong to one of the following dynamical categories:
- Near Earth Object (NEO),
- Main Belt Object (MBO): either belonging to the Main Belt or a Jupiter Trojan,
- Distant Object (DO): object with q > 28 au,
- Scattered Object (SO), not comprised in any of the previous classes.
The score gives a first insight into the nature of a newly discovered object, allowing to make a priori assumptions about the urgency for follow-up observations. To minimize the number of unjustified alarms, objects for which available observations are less than 3 or cover a shorter time span than 30 min are denoted as nonsignificant cases, unless a reliable nominal solution exists.
The ideation of a fast and reliable way to assign follow-up priority is still an open challenge, that we contribute to face by introducing new software tools dedicated to the task.
In our opinion, an ideal priority list should be based upon three criteria:
- After the evaluation of the object-category score (indicative of the probability of an object to belong to a specific dynamical group), objects with NEO score equal or close to 1 should be prioritised with respect to those with a high probability of belonging to a different category;
- A high priority should be assigned to objects with near zero MOID, likely to have VIs;
- Among the objects that are assigned a high priority by criteria 1 and 2, those that will remain visible for a shorter time should be observed first.
This work focuses on providing the observers with two software tools that could facilitate the combined evaluation of conditions 2 and 3.
Both tools are designed to be embedded into the fitobs (the main program of the OrbFit distribution part) code and make use of some of its functionalities. In particular, fitobs computes the MOV for a given set of observations of an object and passes it on to the tools.
4. Analysis of the MOID = 0 Curve (Tool 1)
After the computation of the MOV, obtained by fitobs by sampling the AR with a grid or a cobweb, as described in Section 2.1, Tool 1 loops over the resulting MOV points, computing and assigning to each couple the respective value of the MOID and its covariance. The MOID computation is done by searching for the minimum points of the Keplerian distance function according to Gronchi’s method ([18]).
The MOV points are then represented on the Admissible Region, according to the following colour-code:
- Green dots have MOID > 0.05 au, thus representing non-hazardous orbits;
- Yellow dots have au < MOID ≤ 0.05 au, thus representing the orbits for which the object, if big enough, is to be considered a Potentially Hazardous Asteroid (PHA);
- Red dots correspond to au < MOID au, where the upper threshold is of the order of the Earth radius;
- Black dots correspond to MOID au. We consider this points compatible with MOID=0 and observe that, when present, their disposition on the range-range rate plane follows a curved line;
- A black cross highlights the least squares orbit.
All representations of the AR that appear in this work also show the following lines:
- Red line: outer boundary of the AR, outside of which the object would not belong to the solar system;
- Green line: inner boundary of the AR, left of which the object would be a satellite of the Earth;
- Magenta solid lines: lines corresponding to thresholds in absolute magnitude H;
- Magenta dashed line: shooting star limit, i.e., the line left of which the absolute magnitude is H > 34.5, corresponding to a small object that would completely disintegrate into the atmosphere [9].
When performed, a fit of the MOID=0 curve with a degree 2 polynomial was represented as a black solid line.
4.1. Test Cases
We ran tests of Tool 1 over data collected for various objects. Here we present the most meaningful results obtained divided in three classes of objects: past impactors, lost asteroids and NEOCP objects.
4.1.1. Past Impactors
With the term past impactors we indicate objects that have been discovered before their impact with the Earth. We tested Tool 1 over this category of objects, that, at present, comprises only four entries, listed below.
- 2008TC3: discovered 19 h before impact by the Catalina Sky Survey (CSS) on 7 October 2008, it measured 4.1 metres in diameter. It exploded at an estimated 37 kilometres altitude above the Nubian Desert in Sudan. A tracklet of seven observations was enough to determine an Impact Probability (IP) of 99.7% [19]. Soon after discovery, hundreds of astrometric observations submitted to the Minor Planet Center allowed for the computation of the impact corridor and the later retrieval of residuals of the meteorite.In Figure 1 we show the output of Tool 1 for tracklets of 4 and seven observations. We observe that using the first batch of observations, Tool 1 finds a large number of MOV points below the MOID < 10−5 threshold, corresponding to a high follow-up priority.
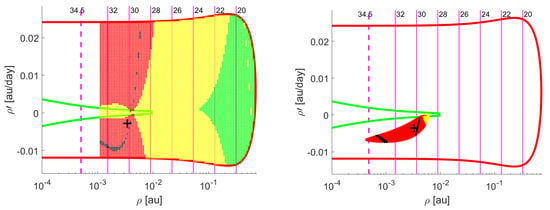 Figure 1. Tool 1 tested on tracklets of four observations (left) and seven observations (right) for asteroid 2008TC3.
Figure 1. Tool 1 tested on tracklets of four observations (left) and seven observations (right) for asteroid 2008TC3. - 2014AA: discovered on New Year’s Eve, 21 h before impact, this object had very little follow-up. This was mainly due to the peculiar night of its first detection, since the MPC staffing does not support routine manual intervention on weekends and holidays. The resulting delay in recognition of the imminent impact made the necessity of an automated warning system very clear. Still, as demonstrated in [20], the few observations available were sufficient to compute a 100% IP.In Figure 2 we show the output of Tool 1 for tracklets of 3 and seven observations. From the three observations tracklet, we obtained a grid sampling of the AR, showing a large portion of the MOV having MOID < 10−5, while the least squares orbit was found on the MOID=0 line. Both these circumstances would have awarded 2014AA a very high priority score. The seven observations tracklet made it possible to compute a reliable nominal solution and, consequently, to sample the MOV with a cobweb. Since the nominal solution still lay on the MOID=0 line, the impact was virtually certain.
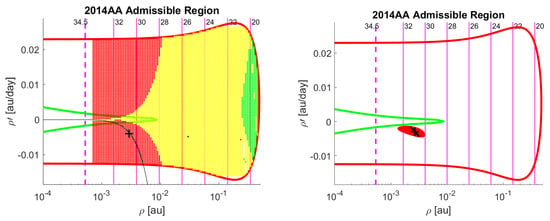 Figure 2. Tool 1 tested on tracklets of three observations (left) and seven observations (right) for asteroid 2014AA.
Figure 2. Tool 1 tested on tracklets of three observations (left) and seven observations (right) for asteroid 2014AA. - 2019MO: discovered by the Asteroid Terrestrial-impact Last Alert System (ATLAS) Mauna Loa observatory on 22 June 2019 at 9:49 (less than 12 h before impact) this object was a small (4-6 metres in diameter) Apollo-type Near-Earth Asteroid. It was at first registered in the NEOCP with four observations and pointed out as an imminent impactor by NEOScan, but the low score assigned prevented prompt follow-up, so that three additional observations from the Pan-STARRS2 images were recovered only after the impact [21], a procedure known as “precovery”. In Figure 3 we show the output of Tool 1 for the first tracklet of four observations and for the seven observations “precovered” tracklet. Post-impact computations revealed that earlier availability of the seven observations tracklet would have yielded IP = 99.8%, thus resulting in a high priority score: a clear proof of the fact that the current priority assignment criteria are in need of improvement.
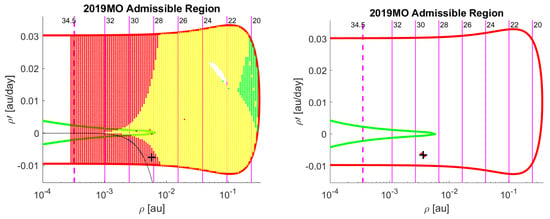 Figure 3. Tool 1 tested on tracklets of four observations (left) and seven observations (right) for asteroid 2019MO.
Figure 3. Tool 1 tested on tracklets of four observations (left) and seven observations (right) for asteroid 2019MO. - 2018LA: a small Apollo-type NEA discovered by the Mt. Lemmon Survey on 2 June 2018. Only 8 h later, it impacted the Earth’s atmosphere over Botswana, becoming the third imminent impactor ever detected and the first opportunity to test NEOScan on a real case. The object could not be detected before it came very close to the Earth due to its high entry velocity and small size (the estimated diameter was of a few metres). In the following hours after the first observational data were published on the NEOCP, follow-up observations were performed and four tracklets were obtained. Results of the four runs of Tool 1 over the tracklets of 3, 11, 12 and 14 observations are shown in Figure 4.
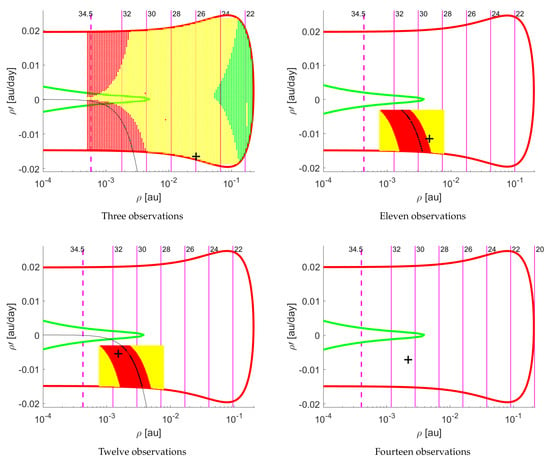 Figure 4. Tool 1 tested on the four tracklets of observations belonging to asteroid 2018LA. From top left to bottom right, runs for 3, 11, 12 and 14 observations.
Figure 4. Tool 1 tested on the four tracklets of observations belonging to asteroid 2018LA. From top left to bottom right, runs for 3, 11, 12 and 14 observations.
Seeing how the four past impactors behaved, we state that to determine if an object poses an imminent threat, the MOID = 0 line has a relevant predictive value. To back up this statement we take two objects for which the nominal solution did not lie exactly on the line, (i.e., 2018LA and 2019MO) and show that even in these cases it provides useful information. For 2018LA, we performed a second degree polynomial fit to the MOID = 0 points obtained from the 12 observations tracklet, finding the following fit parameters:
Even if the reliable nominal solution found from the 14 observations tracklet does not belong to the MOID=0 line, we can see that it falls inside the uncertainty range of the fit, as shown in Figure 5, where the blue solid lines have been drawn by assigning to the fit polynomial the maximal and minimal values of the parameters allowed by their uncertainty.
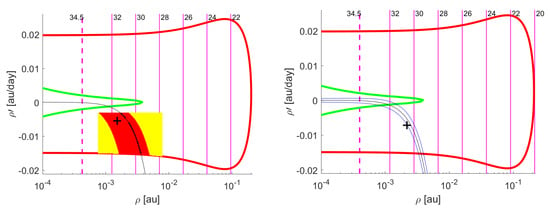
Figure 5.
Fit (black curve) and uncertainty (blue curves) of the MOID = 0 line for 2018LA.
The same procedure has been repeated for 2019MO, obtaining the following fit parameters from the four observations tracklet:
and drawing the corresponding curves on the AR obtained from the seven observations tracklet. The reliable nominal solution and cobweb fall inside the fit uncertainty region, as shown in Figure 6.
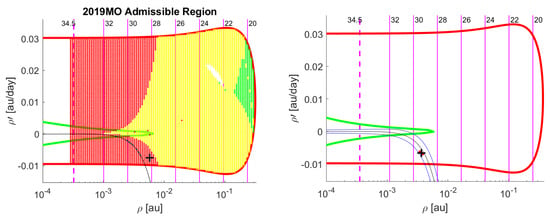
Figure 6.
Fit (black curve) and uncertainty (blue curves) of the MOID = 0 line for 2019MO.
For three out of the four past impactors, the line has substantially the same shape. This suggest the possibility of finding a common expression that would enable us to draw the line a priori on the AR of a generic NEO and search for its intersections with the MOV. This would require an analytical treatment, which is beyond the aim of our work, or a statistical study on past impactors, not possible with such a small amount of test cases. For this reason, further development of the matter is left to future works.
The peculiar shape of the MOID = 0 line found for 2008TC3 also requires further investigation, that we suggest to carry on as a comparative study of the prior-to-impact trajectories of the four past impactors.
4.1.2. Lost Asteroids
An object is marked as lost when, due to the large uncertainty of its orbit, its is more likely to be rediscovered by chance than by looking at the predicted position. An especially alarming situation is that of NEOs that become lost while still having VIs. Prompt follow-up could prevent this occurrence, thus this is another context in which our tools would prove useful. We provide two examples of lost NEOs over which Tool 1 has been tested, 2001CA21 and 2012PB20.
- 2001CA21: this large object (estimated about 600 m in diameter), was observed for the first time on 2 September 2001 by the Lincoln Near-Earth Asteroid Research (LINEAR) Sky Survey, that also performed follow-up on the following night. A third batch of observations was delivered by the Table Mountain Observatory on September 4 and some VIs were found. With a total of 13 observations, the object has been declared lost, while the possibility of an impact with the Earth has not been dismissed.We selected this object as a test case for Tool 1: results are shown in Figure 7. After the first night of observations, the graph shows that the object was very likely to be a PHA, but chances of an impact were low, given the small number of points with MOID . Observations from the second night allow to compute a reliable nominal solution and to restrict the MOV to a cobweb. Probability of collision is confirmed by our test to be low, although nonzero, even after the third night of observations, in accord with the IP computed by CLOMON2, that for no VI results greater than .
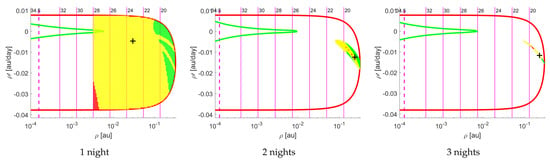 Figure 7. Test of Tool 1 for asteroid 2001CA21: evolution of the MOV over three nights of observations.
Figure 7. Test of Tool 1 for asteroid 2001CA21: evolution of the MOV over three nights of observations. - 2012PB20: this 40m object was discovered by the Panoramic Survey Telescope and rapid response System (Pan-STARRS) and was declared lost after two months of observation. A total of 46 observations from different sites is available for this object, thus the orbit is determined well enough to suppose that it could be “recovered” at a later close approach with our planet. The object presents some VIs, the first one as soon as February 2087. Based on the results of the test of Tool 1 for 2012PB20, shown in Figure 8, we would have assigned the object a low follow-up priority, since the MOV appears to comprise no points with low MOID.
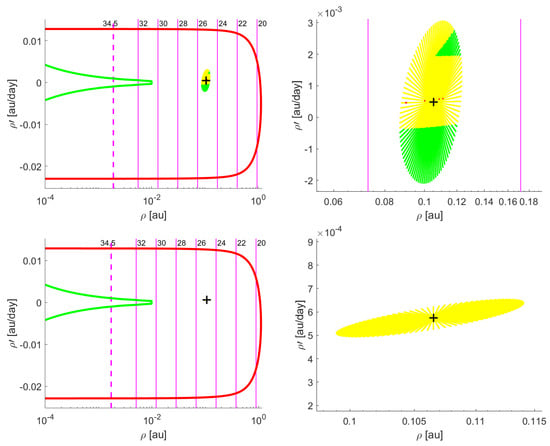 Figure 8. Tool 1 tested on asteroid 2012PB20. Top panels show the output of a run with four observations as it appears on the AR (left) and zooming in on the MOV points (right). Analogously, bottom panels show the output for a test over eight observations, yielding low IP since no point shows MOID ≤ 5 × 10−5 au.
Figure 8. Tool 1 tested on asteroid 2012PB20. Top panels show the output of a run with four observations as it appears on the AR (left) and zooming in on the MOV points (right). Analogously, bottom panels show the output for a test over eight observations, yielding low IP since no point shows MOID ≤ 5 × 10−5 au.
4.1.3. NEOCP Objects
Finally, we ran tests of Tool 1 over NEOCP data. Due to the transitory nature of the NEOCP risk list, the objects we picked for our tests were later removed from the Confirmation Page and can now be found in the Near Earth Objects Dynamic Site (NEODyS) risk list under their permanent designations. Here we present our results for two exemplary cases, C33TRV2 and C3D1M72.
- C33TRV2: discovered by the Catalina Sky Survey on 28 August 2020, this object was observed for two nights, the first of which provided a set of eight observations, while during the second night five more detections were added. It was removed from the NEOCP on September 10, as it was conferred the official designation 2020QE7. Results of the test of Tool 1 for this object are shown in Figure 9. The test yields a high chance of the MOID being greater than au.
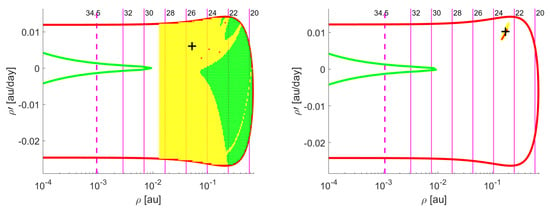 Figure 9. Results of the test of Tool 1 for asteroid C33TRV2 after the first night of observation (left) and after the second night (right).
Figure 9. Results of the test of Tool 1 for asteroid C33TRV2 after the first night of observation (left) and after the second night (right). - C3D1M72: This object was discovered by the Catalina Sky Survey on 24 September 2020. After five batches of observations on different nights were provided, the asteroid was removed from the NEOCP on September 29 and was conferred the official designation 2020SV6. Results of the test of Tool 1 for this object are shown in Figure 10. The test shows that after five observations a nominal solution was already available and presented large MOID, thus the object did not need immediate follow-up.
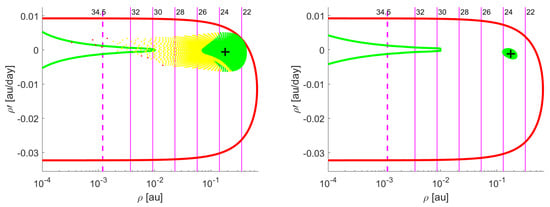 Figure 10. Tool 1 tested on tracklets of five observations (left) and 11 observations (right) for asteroid C3D1M72.
Figure 10. Tool 1 tested on tracklets of five observations (left) and 11 observations (right) for asteroid C3D1M72.
5. Evaluation of the End of Visibility Time (Tool 2)
The third priority criterion calls for the introduction of a new parameter: the End of Visibility (EoV), defined as the difference between the time at which the object has been observed last and the time at which it becomes unobservable from a given station.
This happens when at least one of the following conditions is verified:
- The visual magnitude of the object reaches a value that exceeds the limiting magnitude of the considered telescope;
- Solar elongation (i.e., the angular separation between the object and the Sun as seen by the observer) is less than 50°;
- The relative air mass is greater than 2, which corresponds to the object having an elevation of less than 30° above the horizon;
- The Sun is above the observer’s horizon. To exclude the effect of twilight, we consider this condition to be verified when solar elevation is greater than −18°.
Those listed are the conditions that were set in this work. More binding constraints could easily be set by taking other parameters into account, e.g., the angular distance from the galactic plane or the Moon.
The tool requires the user to input the observatory code and the limiting magnitude of the telescope for which to predict the EoV. The observatories that appear in our study, with estimates for their limiting magnitudes are listed in Table 2. In addition to the telescopes appearing in the table, we also simulated observations from the future location of the Fly-Eye telescope by entering the code of an instrument situated in the same facility (Galhassin Robotic Telescope, L34) and the Fly-Eye’s expected limiting magnitude .

Table 2.
List of the observatory codes and respective limiting magnitudes used in this work.
Tool 2 is an iterative algorithm that propagates the MOV points to a time
where is the time of the last recorded observation and is a time step that we set equal to one hour. A shorter step would be desirable, but unfortunately our tool does not allow for higher time resolution, since tests conducted with smaller values of revealed computational instability issues. This indeed is a fault to be addressed in future work.
At each step, the visibility conditions are checked and, if the object results to be observable from the given observatory, k is incremented and the propagation is prolonged of an hour. At the n-th step, when the object results no longer visible, the tool gives as an output the quantity EoV = tk − t0. The availability of this information allows to schedule follow-up observations for the night, in order to privilege objects that are visible for a short time.
The EoV is then represented on the AR by attributing a colour to each of the MOV points, according to the following colour code:
- • EoV < 1 h;
- • 1 h < EoV < 2 h;
- • 2 h < EoV < 3 h;
- • 3 h < EoV < 4 h;
- • 4 h < EoV < 5 h;
- • EoV > 5 h.
A magenta cross higlights the least squares solution.
5.1. Test Cases
We tested Tool 2 over data collected for objects listed in the NEOCP, in the NEODyS risk page and for the four past impactors. Here we present some examples of results obtained.
5.1.1. Eov from Different Observatories
To verify the consistency of our EoV results, we ran Tool 2 multiple times for the same object, changing the observatory code. We chose three different stations in Arizona: 699 Lowell Observatory (), G96 Mount Lemmon Observatory (), V06 Steward Observatory (). 699 is located approximately 340 km north of V06, while G96 and V06 are about 32 km apart. Figure 11 shows the coordinates of the observatory sites on a geographic map. The stations spread over less than one degree in longitude, thus the chosen object crosses the corresponding meridian approximately at the same time at each location. The spread in latitude is less than 3°, so the only relevant parameter to determine the EoV is the limiting magnitude.
Figure 11.
Coordinates of observatories 699, G96 and V06 marked on a geographic map.
The test subject in the example we present is C35FJJ2. The object was listed in the NEOCP at the time when the test was conducted (10 September 2020), but was later removed from the Confirmation Page on September 22, as it was not confirmed.
The test yields EoV < 1 h for and 1 h < EoV < 2 h for , while gives an intermediate result, with some MOV points below each threshold. Graphical representation of the results is given in Figure 12. To confirm that the different outputs are due to the variation in limiting magnitude, we repeated the test imposing the same value for each station, obtaining three identical graphs.
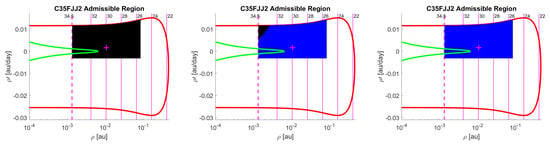
Figure 12.
EoV for asteroid C35FJJ2 from three different observatories located in Arizona. From left to right: 699 Lowell Observatory, G96 Mount Lemmon Observatory, V06 Steward Observatory.
5.1.2. Comparison between Eov and Actual Observed Time
We tested Tool 2 over batches of observations for various objects, aiming to confirm the reliability of our results. By selecting all observations performed until a certain , we compare the EoV for the night and the observatory of the last detection considered, with the actual timespan covered by the subsequent observations. As an example, we show the results obtained for 2012PB20 in Table 3.

Table 3.
Comparison between EoV, computed from the time of the last chosen observation, and actual observation time ta for asteroid 2012PB20.
We notice that for each selected batch of detections, subsequent observation lasted for a shorter time than the EoV. After the first batch of observations, the difference is particularly substantial, since three hours were available but observations cover an arc shorter than one hour. This might be ascribable to various causes, such as technical difficulties, bad weather conditions, limited availability of the telescope, and so on.
The test was repeated for several objects and in most cases the EoV resulted compatible with an upper limit to the observation time. The tool did not produce satisfactory results in the case of past impactors, since it systematically underestimated the EoV for these objects. The reason is likely to lie in the fact that the trajectory of imminent impactors, if discovered when very close to collision, might need a different set of visibility conditions. The test not always succeeding shows that there is room for improvement, but nonetheless an indicative value for the EoV is sufficient to decide if follow-up for a given object is urgent.
6. Combining The Results
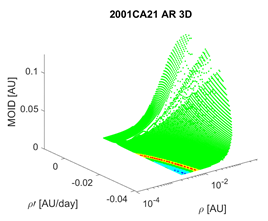
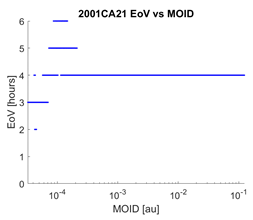
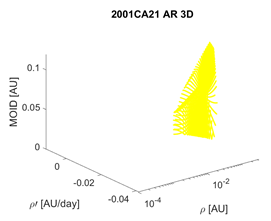
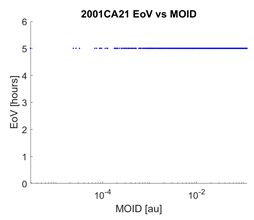
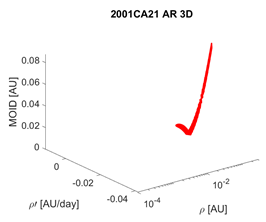
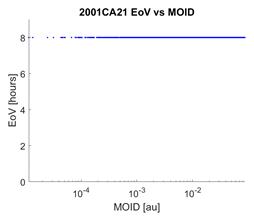
Tools 1 and 2 acquire maximum significance when their outputs are combined, i.e., when the coincidence of a small value of the MOID with a short EoV is evaluated. We chose to represent this information by means of a 3D graph, where we find , and the MOID on the axes, while the colour of the points is indicative of the EoV (with the same legend defined in Section 5). Table 4 contains the results of this treatment applied to 2001CA21 as observed from LINEAR, showing the variability of the EoV from night to night. Combination of the EoV and MOID values results in a low follow-up priority for this object with respect to the others previously mentioned. Still, it would have been prioritized over objects for which no impacting orbits were found, while knowing the EoV would have allowed to schedule follow-up observations, even if not urgent, for a time before the object was lost.

Table 4.
Combination of the results of Tools 1 and 2 for each night of observation of asteroid 2001CA21. The second column contains the 3D representation of the AR, while in the third column each MOV point is represented on a MOID-EoV graph.
Overall, we believe that our tools represent a valuable asset, especially when facing cases of imminent impactors or of objects that would become lost, if not promptly provided with adequate follow-up.
7. Conclusions
Addressing the need for an accurate follow-up priority attribution for NEOCP objects, in order to promptly identify imminent impactors in a large list of new detections, we proposed two tools that would prove useful in this frame.
Tool 1 performed well in the tests we conducted, being able to determine which objects had a high IP from the relative position on the MOV of the least squares orbit with respect to the MOID = 0 line, proving especially useful when dealing with imminent impactors. However, due to the lack of past impactors to employ in further trial, statistical confirmation of its proficiency will have to be demanded to a later time, when more test subjects will be available. In a future work, we plan to address the issue by testing our tools over a synthetic population of NEOs, similarly to what was done in simulations by Torralba et al. [22].
As for Tool 2, its accuracy could be improved by adding more visibility conditions, but the corrections would be of little impact if the computational instability issue is not solved first and the EoV resolution is not reduced below the 1 h threshold. Moreover, further study of the cases in which the tool failed the undergone tests is required.
Once perfected and thoroughly tested, our tools will be released into the OrbFit distribution part, thus they will be available under General Public License as soon as possible.
Author Contributions
Conceptualization, M.M. and G.T.; methodology, M.M.; software, M.M. and G.T.; validation, G.T.; writing–original draft preparation, M.M.; writing–review and editing, G.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. The APC was funded by University of Pisa, through the project PRA 2020-82 Dynamical systems in logic, geometry, mathematical physics and building science.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The observational data are available in on-line systems like NEODyS or MPC-NEOCP. The computed data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AR | Admissible Region |
| ATLAS | Asteroid Terrestrial-impact Last Alert System |
| CR | Confidence Region |
| CSS | Catalina Sky Survey |
| EoV | End of Visibility |
| ESA | European Space Agency |
| IAU | International Astronomical Union |
| IM | Impact Monitoring |
| IP | Impact Probability |
| JPL | Jet Propulsion Laboratory |
| LINEAR | Lincoln Near-Earth Asteroid Research |
| LONEOS | Lowell Observatory Near-Earth-Object Search |
| LOV | Line Of Variations |
| MOID | Minimum Orbital Intersection Distance |
| MOV | Manifold Of Variations |
| MPC | Minor Planet Center |
| NASA | National Aeronautics and Space Administration |
| NEA | Near Earth Asteroid |
| NEO | Near Earth Object |
| NEOCC | NEO Coordination Centre |
| NEOCP | NEO Confirmation Page |
| NEODyS | Near Earth Objects Dynamic Site |
| NEOSTEL | NEO Survey TELescope |
| Pan-STARRS | Panoramic Survey Telescope and Rapid Response System |
| PHA | Potentially Hazardous Asteroid |
| TP | Target Plane |
| VA | Virtual Asteroid |
| VI | Virtual Impactor |
Appendix A. Software Resources: Orbfit
The software used to conduct this work is the 5.0 version of OrbFit (coded in Fortran 90/95), which automatically computes the orbits of all NEAs, registers close encounters along multiple solutions and searches for possible impacts. Results are published on the NEODyS website2.
OrbFit is split in a non-distribution part, comprehensive of the programs dedicated to Impact Monitoring, and a distribution part, available under General Public License, consisting of four programs: Orbfit, Bineph, Catpro and the main one: Fitobs.
- Orbfit is a batch only, no questions asked by program. It can even run with no input options file, just by giving the asteroid name in the standard input;
- Catpro is a propagator to move the reference epoch of an orbit catalog to another epoch;
- Bineph is used to add perturbations from minor bodies to the dynamic model. By default, perturbations due to Ceres, Pallas and Vesta are included. Since version 4.3, OrbFit is also able to include the Yarkovsky effect as a seventh parameter in the orbit equation;
- Fitobs is a menu driven, interactive program, which allows for various data processing procedures. It implements some Impact Monitoring features for both classical IM and imminent impactors.
The non-distribution programs dedicated to classical Impact Monitoring are neomult, cateph2 and resret3tp.
The program neomult takes as inputs the asteroid designation name and the available files containing the record of the observations and the elements sets. It then performs a round of differential corrections and the LOV sampling, allowing to choose between equally spaced points along the curve or a uniform-in-probability sampling. Thus multiple solutions (VAs) are obtained and listed in output files, to be read as inputs by cateph2, that propagates them in time, detecting and, if the close approach distance is found to be au, recording close approaches with the Earth. Propagation is carried out by the propagator RADAU 15, based upon a Runge-Kutta-Gauss method with a variable step (smaller in the proximity of close approaches, to increase precision).
The kernel of the software is the program resret3tp, that takes as input the output files of cateph2 and performs a complete Target Plane (TP) analysis (see Farnocchia et al. [2] for details) for each orbit, computing stretching and width w (i.e., the semimajor and semiminor axes in the ellipsoid approximation, as defined in Dimare et al. [21]) of the Confidence Region. Close approaches are then divided into showers (i.e., sorted by date), and for each VA, lists of consecutive indexes (known as “returns”) are produced. For each return, the program computes the MOID and, if au, searches for local minima of d.
If the return consists of a single TP point, the Newton’s method with bounded step is applied. If the procedure converges and during the iteration two consecutive TP points are found with values of the derivative function having opposite sign, then a minimum might be found by means of the regula falsi.
In case the return consists of at least two points, the suitable iterative method (regula falsi or Newton’s method) is applied, depending on the geometry of the return.
If a minimum is found, a risk control is performed by comparing the impact parameter with the quantity , where is the minimum distance related to the minimum point. If the VA is rated as a VI and Impact Probability is computed. If and a filtering procedure for spurious VIs is passed, then a real impactor has been found and its data are written into a risk file, together with the IP and the Palermo scale3 value, to be published on the NEODyS risk page.
In this work, we mainly used Fitobs, that is able to run most of the neomult, cateph2 and resret3tp routines, but also to process imminent impactor cases through the formalism of the AR. It is in fact able to compute attributables and the arc type, and to sample the AR with a grid or, in case a nominal solution is available, a cobweb, as described in Section 2.1.
References
- Tommei, G. A new way of thinking about Impact Monitoring of Near-Earth Objects. In Proceedings of the 1st NEO and Debris Detection Conference, Darmstadt, Germany, 22–24 January 2019. [Google Scholar]
- Farnocchia, D. Impact hazard monitoring: Theory and implementation. Proc. Int. Astron. Union 2015, 10, 221–230. [Google Scholar] [CrossRef]
- Milani, A.; Chesley, S.R.; Sansaturio, M.E.; Tommei, G.; Valsecchi, G.B. Nonlinear impact monitoring: Line of variation searches for impactors. Icarus 2005, 173, 362–384. [Google Scholar] [CrossRef]
- Milani, A.; Sansaturio, M.E.; Tommei, G.; Arratia, O.; Chesley, S.R. Multiple solutions for asteroid orbits: Computational procedure and applications. Astron. Astrophys. 2005, 431, 729–746. [Google Scholar] [CrossRef]
- Tommei, G. Nonlinear impact monitoring: 2-dimensional sampling. Proc. Int. Astron. Union 2004, 2004, 259–264. [Google Scholar] [CrossRef][Green Version]
- Farnocchia, D.; Chesley, S.R.; Micheli, M. Systematic ranging and late warning asteroid impacts. Icarus 2015, 258, 18–27. [Google Scholar] [CrossRef]
- Solin, O.; Granvik, M. Monitoring near-Earth-object discoveries for imminent impactors. Astron. Astrophys. 2018, 616, A176. [Google Scholar] [CrossRef]
- Spoto, F.; Del Vigna, A.; Milani, A.; Tommei, G.; Tanga, P.; Mignard, F.; Carry, B.; Thuillot, W.; David, P. Short arc orbit determination and imminent impactors in the Gaia era. Astron. Astrophys. 2018, 614, A27. [Google Scholar]
- Milani, A.; Gronchi, G.F.; Vitturi, M.D.; Knežević, Z. Orbit determination with very short arcs. I admissible regions. Celest. Mech. Dyn. Astron. 2004, 90, 57–85. [Google Scholar] [CrossRef]
- Tommei, G.; Milani, A.; Rossi, A. Orbit determination of space debris: Admissible regions. Celest. Mech. Dyn. Astron. 2007, 97, 289–304. [Google Scholar] [CrossRef]
- Cibin, L.; Chiarini, M.; Gregori, P.; Bernardi, F.; Ragazzoni, R.; Sessler, G.; Kugel, U. The Fly-Eye telescope, development and first factory tests results. In Proceedings of the 1st NEO and Debris Detection Conference, Darmstadt, Germany, 22–24 January 2019. [Google Scholar]
- Gronchi, G.F. An Algebraic Method to Compute the Critical Points of the Distance Function Between Two Keplerian Orbits. Celest. Mech. Dyn. Astron. 2005, 93, 295–329. [Google Scholar] [CrossRef]
- Gronchi, G.F.; Tommei, G.; Milani, A. Mutual geometry of confocal Keplerian orbits: Uncertainty of the MOID and search for virtual PHAs. Proc. Int. Astron. Union 2006, 2, 3–14. [Google Scholar] [CrossRef]
- Gronchi, G.F.; Tommei, G. On the uncertainty of the minimal distance between two confocal Keplerian orbits. Discret. Contin. Dyn. Syst. B 2007, 7, 755. [Google Scholar] [CrossRef]
- Milani, A.; Gronchi, G.F.; Knežević, Z.; Sansaturio, M.E.; Arratia, O. Orbit determination with very short arcs: II. Identifications. Icarus 2005, 179, 350–374. [Google Scholar] [CrossRef]
- Tommei, G. Impact Monitoring of Near-Earth Objects: Theoretical and Computational Results. Ph.D. Thesis, University of Pisa, Pisa, Italy, 2006. [Google Scholar]
- Del Vigna, A. The Manifold Of Variations: Hazard assessment of short-term impactors. Celest. Mech. Dyn. Astron. 2020, 132, 1–15. [Google Scholar] [CrossRef]
- Gronchi, G.F. On the stationary points of the squared distance between two ellipses with a common focus. SIAM J. Sci. Comput. 2002, 24, 61–80. [Google Scholar] [CrossRef]
- Farnocchia, D.; Jenniskens, P.; Robertson, D.K.; Chesley, S.R.; Dimare, L.; Chodas, P.W. The impact trajectory of asteroid 2008TC3. Icarus 2017, 294, 218–226. [Google Scholar] [CrossRef][Green Version]
- Chesley, S.R.; Farnocchia, D.; Brown, P.G.; Chodas, P.W. Orbit estimation for late warning asteroid impacts: The case of 2014 AA. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; pp. 1–8. [Google Scholar]
- Dimare, L.; Del Vigna, A.; Bracali Cioci, D.; Bernardi, F. Use of the semilinear method to predict the impact corridor on ground. Celest. Mech. Dyn. Astron. 2020, 132, 1–30. [Google Scholar] [CrossRef]
- Ramirez Torralba, O.; Jehn, R.; Koschny, D.; Frühauf, M.; Jehn, L.; Praus, A. Simulation of Sky Surveys with the Flyeye Telescope. In Proceedings of the 1st NEO and Debris Detection Conference, Darmstadt, Germany, 22–24 January 2019. [Google Scholar]
- Chesley, S.R.; Chodas, P.W.; Milani, A.; Valsecchi, G.B.; Yeomans, D.K. Quantifying the risk posed by potential Earth impacts. Icarus 2002, 159, 423–432. [Google Scholar] [CrossRef]
| 1 | |
| 2 | |
| 3 | A scale proposed in [23], developed to classify the potential hazard of an impact, by combining and expected impact energy in a single value. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).