Abstract
The scalar field of space-time film is considered as unified fundamental field. The field model under consideration is the space-time generalization of the model for a two-dimensional thin film. The force and metrical interactions between solitons are considered. These interactions correspond to the electromagnetic and gravitational interactions respectively. The metrical interaction and its correspondence to the gravitational one are considered in detail. The practical applications of this approach are briefly discussed.
1. Introduction
1.1. Unified Fundamental Field
The concept of unified fundamental field has existed for a sufficiently long time. According to this concept, matter in all its multiformity can be considered as a solution of some nonlinear field model.
In particular, all elementary particles must be represented by soliton solutions of the model. In this case their interactions are the consequence of the field model nonlinearity.
The nonlinearity violates the superposition property for solutions of the appropriate linearized model. According to this property the sum of solutions is also solution. The violation of the superposition property is interpreted as the interaction of particles.
It is reasonable that the interaction of big material objects containing many particles is explained by the same way.
Attempts to propose models of the unified field theory have been made by many well-known researchers. It is known that the creator of general relativity theory A. Einstein was adherent of this concept. He tried to create a unified field theory for the rest of his life.
1.2. Attempts to Create a Unified Field Theory
Electromagnetic field satisfied nonlinear equations was considered as unified field. First of all we must notice two known nonlinear electrodynamics model, namely, Mie [1] and Born—Infeld models [2].
Einstein considered, in particular, the field of metrical tensor for curved space-time as unified field [3]. In this connection nonsymmetrical metric was also considered [4].
Heisenberg tried to build a unified theory of spinor field [5].
All these attempts were not completely successful. In particular, within the framework of these theories, no solution has been obtained that corresponds with a sufficient degree of realism to any elementary particle. It should be noted that this problem is extremely difficult mathematically.
1.3. The Question as to the Tensor Rank of the Field
It is evident that the question as to the tensor rank of a unified field is highly important.
In the above-mentioned attempts to construct a unified field theory, the choice of the tensor rank of the field was based on certain correspondence considerations.
For example, the nonlinear electrodynamics models generalized the linear electrodynamics which was successful in certain limits.
The variants of Einstein’s unified theories generalized his own gravitational theory which was successful in certain limits.
Heisenberg’s theory of a unified spinor field was based on Dirac’s linear theory which was successful in certain limits.
1.4. The Force and Metrical Interactions of Particles-Solitons
As a natural criterion for the acceptability of the unified field model, we should consider the possibility in its framework for description of the two long-range interactions of material objects, namely electromagnetism and gravitation.
A number of the author’s works were devoted to the unification of electromagnetism and gravitation in the framework of Born—Infeld nonlinear electrodynamics (see, for example, [6,7,8,9]).
In this case, the electromagnetic interaction of particles-solitons is a consequence of the integral conservation law for energy-momentum. This type of interaction is called the force one.
The description of gravity in the framework of nonlinear electrodynamics is based on the effect of induced space-time curvature by a weak field of distant particles-solitons at the location of the test particle. This type of interaction is called the metrical one.
1.5. Scalar Field
Force and metric interactions of particles-solitons are inherent in all nonlinear field models that are invariant under shifts and rotations in four-dimensional space-time.
Thus we can consider a simpler model of a scalar unified field, since it also allows us to describe electromagnetism and gravity [10].
In particular, the tensor character of the electromagnetic field is due to the determination of the integral force through the integral over a closed surface surrounding the test particle under the force interaction [11].
It should be emphasized that the electromagnetic field of antisymmetric tensor of the second rank appears at a certain point when a test particle is placed there. In the absence of such a particle, only a configuration of the scalar field is present near this point, but it generates the electromagnetic interaction with any charged particle.
2. The Unified Field
2.1. Space-Time Film
We consider the following generally covariant world volume action and the appropriate variational principle [12]:
where , , is space-time volume, is four-dimensional volume element, ,
are components of metric tensor for flat four-dimensional space-time, is scalar real field function, is dimensional constant. The Greek indices take values . The tensor can be called the world tensor.
The model (1) can be considered as a relativistic generalization of the appropriate expression for the mathematical model of two-dimensional minimal thin film in the tree-dimensional space of our everyday experience.
2.2. Energy-Momentum Density Tensor
Customary method gives the following canonical energy-momentum density tensor of the model in Cartesian coordinates
 where is the constant diagonal metrical tensor for flat space-time with signature or . As we see, the canonical tensor is symmetrical.
where is the constant diagonal metrical tensor for flat space-time with signature or . As we see, the canonical tensor is symmetrical.
To obtain finite integral characteristics of solutions in infinite space-time we introduce the regularized energy-momentum density tensor with the following formula:
 where
where  is a regularizing symmetrical energy-momentum density tensor. Here we will use the constant regularizing tensor
is a regularizing symmetrical energy-momentum density tensor. Here we will use the constant regularizing tensor
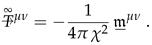
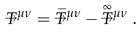
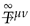 is a regularizing symmetrical energy-momentum density tensor. Here we will use the constant regularizing tensor
is a regularizing symmetrical energy-momentum density tensor. Here we will use the constant regularizing tensor
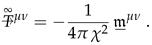
In general case we can take a symmetrical tensor satisfying the differential conservation law as the regularizing tensor. A special choice of this tensor can provide the convergence of energy integral for a certain class of solutions.
2.3. Equation of Space-Time Film
The variational principle (1) gives the following model field equation in Cartesian coordinates [12]:
This field equation can be written in the following remarkable form [10]:
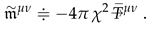 where
where 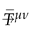 is the canonical energy-momentum density tensor (2). Here we introduce the effective metric which will be considered below.
is the canonical energy-momentum density tensor (2). Here we introduce the effective metric which will be considered below.
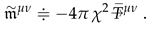
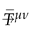 is the canonical energy-momentum density tensor (2). Here we introduce the effective metric which will be considered below.
is the canonical energy-momentum density tensor (2). Here we introduce the effective metric which will be considered below.Equation (6) transforms to ordinary linear wave equation with :
2.4. Effective Metric and Curved Space-Time
The characteristic equation of the model has the following form which is obtained directly from (6a):
Equation gives a three-dimensional characteristic hypersurface of the field model in four-dimensional space-time.
As is known, the problem of propagation of a weak high-frequency quasi-plane wave with a given background field in a nonlinear model gives the dispersion relation for the components of the wave four-vector that coincides with the characteristic equation [8]. The dispersion relation or a dependence between the frequency of the wave and its three-dimensional wave vector defines the wave front propagation.
Thus the components in Equation (8) can also be considered as the components of the wave four-vector of a high-frequency quasi-plane wave propagating in an effective curved space-time with the metric .
Equation (8) sets the motion of such wave packets that, in the absence of a background field, would move at the speed of light. Thus this equation determines the trajectories of massless particles. For the trajectory of a massive particle, the considered approach gives the equation of a geodesic line in an effective curved space-time with the metric . This theme is considered below in Section 4.
3. Solitons-Particles
3.1. Solitons Are Material Particles
Solitons are spatially localized solutions of nonlinear field models. Solitons-particles are soliton solutions of the unified field model corresponding to elementary particles.
Another name for soliton is solitary wave. But linear field models can also have the solutions in the form of solitary waves. Because of linearity of the models these solutions can have an arbitrarily small amplitude. Thus we shall call these solitary waves the weak solitons.
Not long ago, a class of exact soliton solutions propagating with the speed of light was obtained for the model of space-time film [12]. A subclass of these solutions has properties which allow to correlate it with photons. Other subclasses of these solutions may relate to various types of neutrino.
At the present time, among exact soliton solutions for massive particles we know the simplest spherically symmetrical soliton in intrinsic coordinate system or spheron [11]. It has a rest energy and electrical charge but does not have angular momentum or spin.
There is a defined progress in the finding of approximate soliton solutions of the toroidal configuration containing an oscillating part [13]. These solutions can also have a spin in addition to the rest mass and charge.
3.2. Oscillating Parts of Solitons-Particles
First of all the existence of oscillating parts in solitons-particles is necessary for the description of observable wave properties for elementary particles.
But in the framework of the unified field theory under consideration the oscillating parts are necessary for the description of real gravitation. We shall discuss this question below.
When we move away from the localization region of a soliton-particle, the field of space-time film satisfies approximately the linear wave Equation (7).
Elementary oscillating solutions of the linear wave equation in the spherical coordinate system decrease in amplitude as . Let us take the following simple solution as example:
where the point under symbols denotes the belonging to the intrinsic coordinate system.
According to the definition given in the previous subsection, this solution is a weak soliton.
The asymptotic form such as we have in (9a) leads to the divergence of energy integral at infinity.
However, the investigation of toroidal configurations [13] shows that there can be solitons with oscillating part without the asymptotic form of type (9a) whose energy is finite. But we can suppose in this case that the wave mode of type (9a) will appear for interacting solitons.
Thus we assume that a soliton-particle in the intrinsic coordinate system has both static and oscillating parts. This representation is appropriate to usual decomposition of time-periodic solution in temporal Fourier series. Of course, the static and oscillating parts of a soliton-particle are not separate soliton solutions.
The oscillating part is a standing wave having perhaps sufficiently complicated configuration. Using a space-time rotation we can obtain a moving soliton from the rest one. In this case the standing wave transforms to moving one. The moving soliton is obtained with the help of the following substitution for the intrinsic coordinates of the soliton:
where , is a matrix of space-time rotation, in particular, Lorentz transformations, is the coordinate system in which the soliton is moving.
We have the following dispersion relation for the wave four-vector components of this moving wave:
where is the angular frequency of the standing wave in intrinsic coordinate system of the soliton, are the frequency and wave vector components of the traveling wave.
4. Gravitation
4.1. Gravitation as the Metrical Interaction of Solitons
The effect of induced gravitation in nonlinear electrodynamics is the subject of a sufficient number of works by the author [6,7,8,9,10,14,15,16,17,18], including an article in the encyclopedia [6] and a monograph [8].
Now this analysis is applied to the space-time film model with insignificant modification.
Let us consider the problem of propagation of a small amplitude wave with a rest frequency against a background given field of distant solitons-particles.
For distinctness we take the simple solution of the linear wave Equation (9a). This solution has the form of a standing wave in the intrinsic coordinate system. It has a finite amplitude at the coordinate origin which can be taken sufficiently small.
Let us consider the sum of the background field generated by distant solitons and a moving fast-oscillating weak soliton of type (9) but with a slow time-dependent velocity parameter  and a small constant amplitude :
and a small constant amplitude :
 and a small constant amplitude :
and a small constant amplitude :
Here we consider the weak soliton with a constant amplitude as some approximation for a soliton-particle whose amplitude is defined by an exact solution. If there is an additional field of remote solitons , the soliton solution is modified, and its amplitude could also be changed. However, it is natural to assume that the soliton-particle has a maximum amplitude which is significantly greater than the field of distant solitons-particles. Then the weak field of distant particles will not significantly affect the amplitude of the considered soliton-particle. Thus if we consider the weak soliton instead of the soliton-particle, we actually investigate the influence of the distant solitons field to the part of soliton-particle which is sufficiently far from its center and has a small amplitude. The movement of this weak part should direct the entire soliton-particle, since it is a modified exact solution.
We substitute this sum (11a) in the equation of space-time film (6). According to the made assumptions (11b), we keep only the terms with the second derivatives of the weak soliton field in the obtained equation.
Here we suppose an averaging of the effective metric (6b) with the background field over a defined space-time localization region for the weak soliton . The averaged components of the effective metric are the constant components of the decomposition for the effective metric components in four-dimensional Fourier series in this soliton localization region.
Then we obtain the following equation:
where the averaged effective metric depends on the derivatives of the background field: . Here below we use the designation for the averaged effective metric in an effort to simplify the designations.
We consider that the averaged background effective metric is almost constant in the space-time localization region of the weak soliton . In this region, let us find a coordinate transformation which reduces the Equation (12) to ordinary wave one (7).
Let we have the following relations for the coordinate differentials:
where the matrix and are mutually inverse and satisfy the relations
Then the solutions of Equation (12) in the limited region under consideration has the form
where is a solution of the linear wave Equation (7), in particular, the weak soliton (9a). Here the functions are defined by the transformation (13).
The averaged background effective metric calculated in an the expanded four-dimensional space defines a Riemann space which is not generally flat. Also, in general, it is not possible to find the coordinate transformation satisfying (13) and (14) everywhere.
But we can write this transformation approximately in the following form:
where is a position of energy center for the weak soliton at the time , is called a normalized wave vector such that
Taking into account the transformation (16) we obtain that is a phase of the wave . Then we have the following its wave vector components:
It should be emphasized that the substitution of type (16b) for to the solution (9a) is the known approach to solving the problem of wave propagation in an inhomogeneous medium [19]. In this approach, the wave phase is considered as an unknown coordinate function, and the substitution of the modified wave solution into the equation gives a dispersion relation for this wave.
Now let us obtain a trajectory of energy center for the weak soliton . We use the intrinsic time (16b) at the point as a parameter of movement . Taking also we have
where is the four velocity. We have the last relation in (19b) in accordance to (13) and (19a).
Let us introduce the inverse tensor to the tensor :
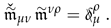
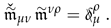
We have from (20) and (21) the following relation at the point :
This leads to the well-known expression in general relativity theory:
We have also from (20) the following relation at the point
One must note that although and are defined as components of second-order matrix, they are actually four-vectors.
Indeed, if we consider the problem in another coordinate system then we have
This means that the intrinsic time is not changed for such transformations or it behaves as scalar. Thus is a four-vector according to the definition (16b).
As noted above, is the phase of the wave which is, of course, relativistic invariant. Then the function can be called the normalized phase. Thus we can write the following definition for the normalized wave vector which is in agreement with (16b) and (16c):
Then, according to (16a), the three-dimensional coordinate system is moving coupled with the localization region of the weak soliton. Thus we have and at the point and
Therefore are a four-vector according to definition (19b).
Now let us obtain the trajectory equation for . Differentiation of dispersion relation (18) with respect to certain coordinate with consideration of relations (16c) and (20) gives the following equation at the point :
Substituting (24) into (28) and using (21) we obtain the trajectory equation in the following form:
where
As can be seen, this equation is the geodesic line one for the introduced effective Riemann space with the metric .
Thus a weak soliton with rest frequency and small constant amplitude under the influence of distant solitons behaves as massive particle in gravitational field.
We can assume that the obtained Equation (29) describes also the movement of a soliton-particle under the influence of distant solitons-particles.
4.2. Newtonian Potential
The geodesic line Equation (29) in zero speed approximation contains the component only. Let us write it in the following form:
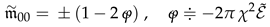 where
where 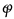 is the scalar potential of the gravitational field, is an averaged energy density for the field of distant solitons. Here the averaging is performed over a space-time volume including a localization region of the soliton and a relevant time interval.
is the scalar potential of the gravitational field, is an averaged energy density for the field of distant solitons. Here the averaging is performed over a space-time volume including a localization region of the soliton and a relevant time interval.
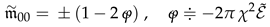
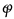 is the scalar potential of the gravitational field, is an averaged energy density for the field of distant solitons. Here the averaging is performed over a space-time volume including a localization region of the soliton and a relevant time interval.
is the scalar potential of the gravitational field, is an averaged energy density for the field of distant solitons. Here the averaging is performed over a space-time volume including a localization region of the soliton and a relevant time interval.In order to have the real gravitation in our consideration we must obtain the following expression for the gravitational potential:
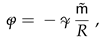 where
where 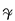 is the gravitational constant, is a mass for agglomeration of distant solitons-particles, R is a distance from the energy center of this agglomeration.
is the gravitational constant, is a mass for agglomeration of distant solitons-particles, R is a distance from the energy center of this agglomeration.
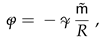
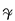 is the gravitational constant, is a mass for agglomeration of distant solitons-particles, R is a distance from the energy center of this agglomeration.
is the gravitational constant, is a mass for agglomeration of distant solitons-particles, R is a distance from the energy center of this agglomeration.Thus we must obtain the following asymptotic form for the averaged energy density as :
4.3. The Role of Wave Background
Let us elucidate how we can obtain the necessary asymptotic form for the averaged energy density (32).
If we consider only static parts of charged solitons-particles () then the appropriate energy density will decrease apparently as .
Taking into consideration the oscillating parts of interacting solitons-particles with decreasing amplitude as (as, for example, for the weak soliton (9a)) gives the decrease of the averaged energy density as .
To obtain the asymptotic for the potential 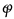 we must also take into account a wave background with almost constant amplitude in space. This wave background must undoubtedly exist in the space where there is a bulk of oscillating solitons-particles.
we must also take into account a wave background with almost constant amplitude in space. This wave background must undoubtedly exist in the space where there is a bulk of oscillating solitons-particles.
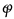 we must also take into account a wave background with almost constant amplitude in space. This wave background must undoubtedly exist in the space where there is a bulk of oscillating solitons-particles.
we must also take into account a wave background with almost constant amplitude in space. This wave background must undoubtedly exist in the space where there is a bulk of oscillating solitons-particles.Then we must represent the field generating the effective metric in the form of the following sum:
where is the field of distant solitons containing the fast oscillating part with amplitude decreasing as (just as in the weak soliton (9a)), is the wave background field with almost constant amplitude.
The substitution of the field (33) to the energy density gives the terms which are proportional to . The following averaging of energy density can give the appropriate term in expression for the potential 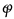 which is proportional to . This expectation seems reasonable because the interaction between the fields and , due to the nonlinearity of the model, can lead to a certain synchronization of the phases for these fast oscillating fields. In this case, the necessary asymptotic term will be kept in the averaged energy density as a result of the averaging of the products and .
which is proportional to . This expectation seems reasonable because the interaction between the fields and , due to the nonlinearity of the model, can lead to a certain synchronization of the phases for these fast oscillating fields. In this case, the necessary asymptotic term will be kept in the averaged energy density as a result of the averaging of the products and .
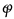 which is proportional to . This expectation seems reasonable because the interaction between the fields and , due to the nonlinearity of the model, can lead to a certain synchronization of the phases for these fast oscillating fields. In this case, the necessary asymptotic term will be kept in the averaged energy density as a result of the averaging of the products and .
which is proportional to . This expectation seems reasonable because the interaction between the fields and , due to the nonlinearity of the model, can lead to a certain synchronization of the phases for these fast oscillating fields. In this case, the necessary asymptotic term will be kept in the averaged energy density as a result of the averaging of the products and .Thus the gravitational constant is defined by two factors
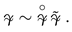 where
where 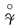 is a constant of proportionality between an amplitude of the fast oscillating field of distant agglomeration of solitons-particles and its total mass ,
is a constant of proportionality between an amplitude of the fast oscillating field of distant agglomeration of solitons-particles and its total mass , 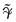 defines the amplitude of the wave background in the considered space-time region.
defines the amplitude of the wave background in the considered space-time region.
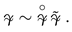
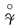 is a constant of proportionality between an amplitude of the fast oscillating field of distant agglomeration of solitons-particles and its total mass ,
is a constant of proportionality between an amplitude of the fast oscillating field of distant agglomeration of solitons-particles and its total mass , 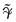 defines the amplitude of the wave background in the considered space-time region.
defines the amplitude of the wave background in the considered space-time region.5. Practical Applications
5.1. Possible Explanation for the Dark Matter Effect
We assume that the amplitude of the wave background (the factor 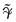 in (34)) may vary slightly in space. In this case we must assume that the gravitational constant is not really constant but it can also change slightly. Perhaps the observable effects of so-called dark matter [20] can be explained by a weak spatial dependence of the gravitational constant
in (34)) may vary slightly in space. In this case we must assume that the gravitational constant is not really constant but it can also change slightly. Perhaps the observable effects of so-called dark matter [20] can be explained by a weak spatial dependence of the gravitational constant 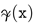 .
.
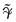 in (34)) may vary slightly in space. In this case we must assume that the gravitational constant is not really constant but it can also change slightly. Perhaps the observable effects of so-called dark matter [20] can be explained by a weak spatial dependence of the gravitational constant
in (34)) may vary slightly in space. In this case we must assume that the gravitational constant is not really constant but it can also change slightly. Perhaps the observable effects of so-called dark matter [20] can be explained by a weak spatial dependence of the gravitational constant 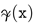 .
.It should also be noted that the concept of gravitational constant is connected with the concept of point mass. But the effective metric in the induced gravitation theory is defined by the wave background and the field of distant solitons-particles. The latter can have various spatial forms that satisfy the model equation asymptotically.
In other words, for defined space-time configurations of big clusters of massive bodies, the law of inverse proportional dependence on distance for the averaged energy density (32) can be violated. Thus the approach under consideration shows a similarity with the approach of so called modified Newtonian dynamics (MOND) [21].
On the other hand, in the approach under consideration, the gravitational field is induced by the fundamental field of space-time film, which we consider to be material. However, the oscillating parts of solitons-particles extending far beyond the visible matter do not directly generate the observable radiation. In this sense, we can talk about dark matter.
The appropriate ideas for explanation of the dark matter effect require further study and separate publication.
5.2. About the Possibility of Gravitational Screening
We have seen that in this approach, the existence of the long-range gravitational potential is associated with the presence of the wave background.
Then if the wave background is cut off or weakened with the help of some method, then the gravitational interaction will also be weakened. In this case we can talk about gravitational screening.
Estimations of possible frequency of the wave background show [8] that the gravitational screening requires a metamaterial from which a gamma-ray mirror can be made.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mie, G. Grundlagen einer theorie der materie. Ann. der Phys. 1912, 37, 511–534. [Google Scholar] [CrossRef]
- Born, M.; Infeld, L. Foundation of the new field theory. Proc. Roy. Soc. A 1934, 144, 425–451. [Google Scholar] [CrossRef]
- Einstein, A. Théorie unitaire de champ physique. Ann. Inst. Henri Poincare 1930, 1, 1–24. [Google Scholar]
- Einstein, A.; Kaufmann, B. Algebraic properties of the field in the relativistic theory of the asymmetric field. Ann. Math. 1954, 59, 230–244. [Google Scholar] [CrossRef]
- Heisenberg, W. Introduction to the Unified Field Theory of Elementary Particles; Interscience Publishers: London, UK; New York, NY, USA; Sydney, Australia, 1966. [Google Scholar]
- Chernitskii, A.A. Born-Infeld equations. In Encyclopedia of Nonlinear Science; Scott, A., Ed.; Routledge: New York, NY, USA; London, UK, 2005; pp. 67–69. [Google Scholar]
- Chernitskii, A.A. Gravitation and electromagnetism in theory of a unified four-vector field. Gravit. Cosmol. 2006, 12, 130–132. [Google Scholar]
- Chernitskii, A.A. Nonlinear Electrodynamics: Singular Solitons and Their Interactions (in Russian); ENGECON: Saint-Petersburg, Russia, 2012. [Google Scholar]
- Chernitskii, A.A. Dyons and interactions in nonlinear (Born-Infeld) electrodynamics. J. High Energy Phys. 1999, 10, 1–34. [Google Scholar] [CrossRef][Green Version]
- Chernitskii, A.A. Induced gravitation in nonlinear field models. Int. J. Mod. Phys. Conf. Ser. 2016, 41, 1660119. [Google Scholar] [CrossRef]
- Chernitskii, A.A. About long-range interaction of spheroidal solitons in scalar feld nonlinear model. J. Phys. Conf. Ser. 2017, 938, 012029. [Google Scholar] [CrossRef]
- Chernitskii, A.A. Lightlike shell solitons of extremal space-time film. J. Phys. Commun. 2018, 2, 105013. [Google Scholar] [CrossRef]
- Chernitskii, A.A. About toroidal soliton-particle of extremal space-time film. J. Phys. Conf. Ser. 2020, 1435, 012054. [Google Scholar] [CrossRef]
- Chernitskii, A.A. Gravitation as an effect of nonlinear electrodynamics. Gravit. Cosmol. 2011, 17, 198–200. [Google Scholar] [CrossRef]
- Chernitskii, A.A. Induced gravitation as nonlinear electrodynamics effect. Gravit. Cosmol. 2002, 8, 157–160. [Google Scholar]
- Chernitskii, A.A. Long-range interaction of four-vector field solitons of the Minkowskian space. Theoret. Math. Phys. 1992, 90, 260. [Google Scholar] [CrossRef]
- Chernitskii, A.A. Light beams distortion in nonlinear electrodynamics. J. High Energy Phys. 1998, 15, 1–5. [Google Scholar] [CrossRef]
- Chernitskii, A.A. On unification of gravitation and electromagnetism in the framework of a general-relativistic approach. Gravit. Cosmol. 2009, 15, 151–153. [Google Scholar] [CrossRef]
- Whitham, G.B. Linear and Nonlinear Waves; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Bertone, G.; Hooper, D. History of dark matter. Rev. Mod. Phys. 2018, 90, 045002. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).