Evidence for Solar Modulation on the Millennial-Scale Climate Change of Earth
Abstract
1. Introduction
2. Data and Methods
3. Results
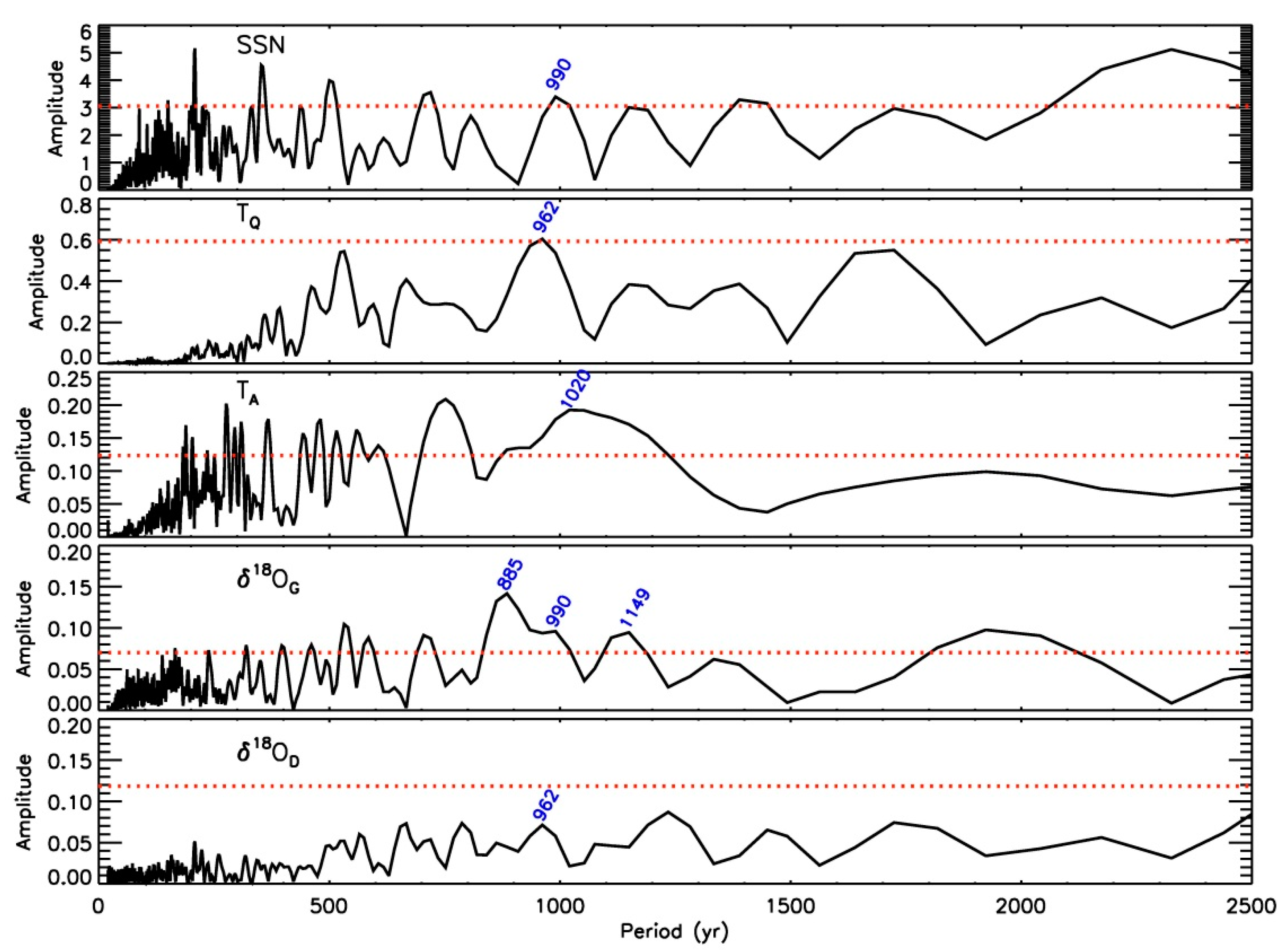
3.1. Eddy Cycle in SSN and Climate Indices
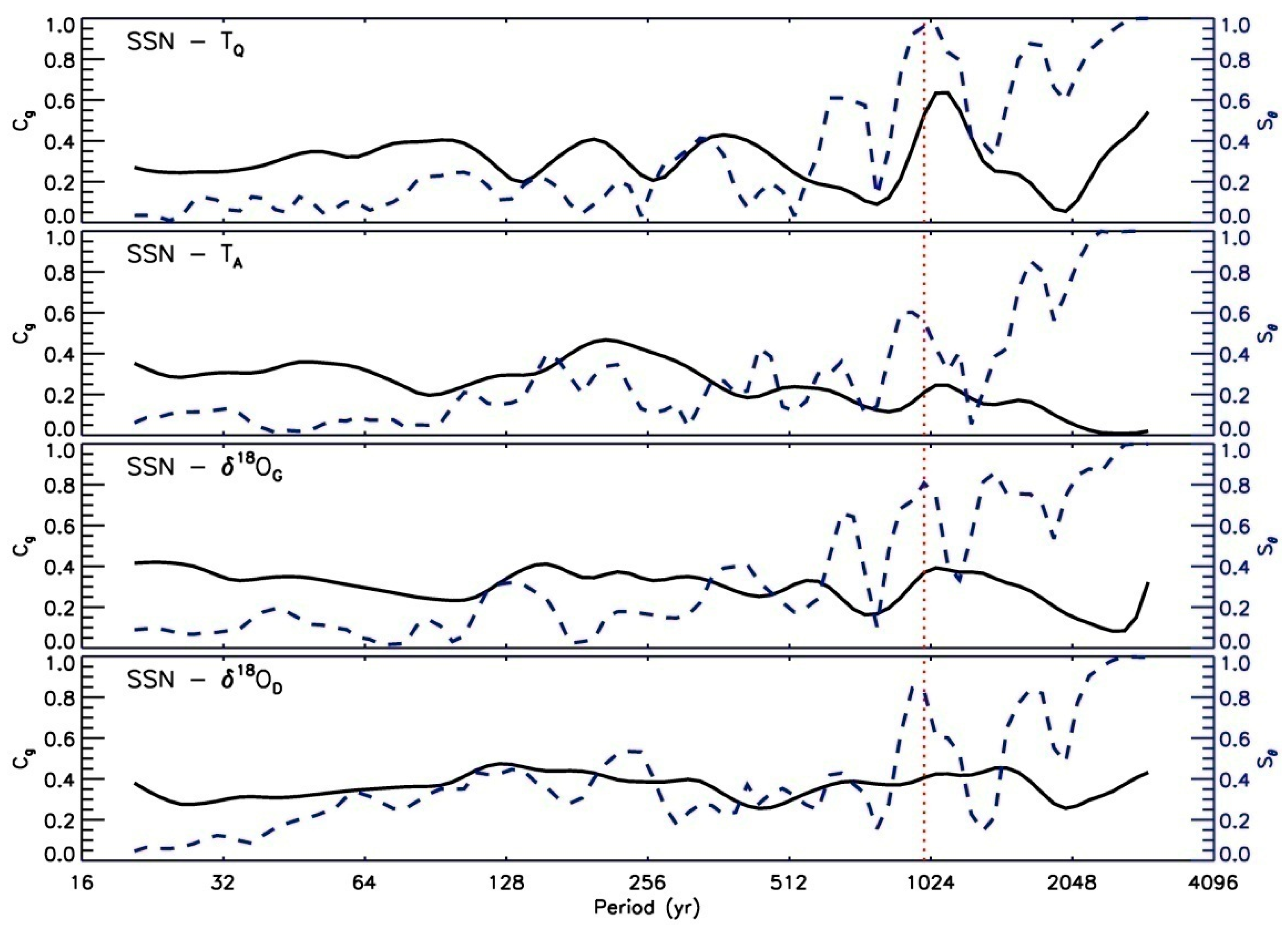
3.2. Cross-Wavelet Analysis
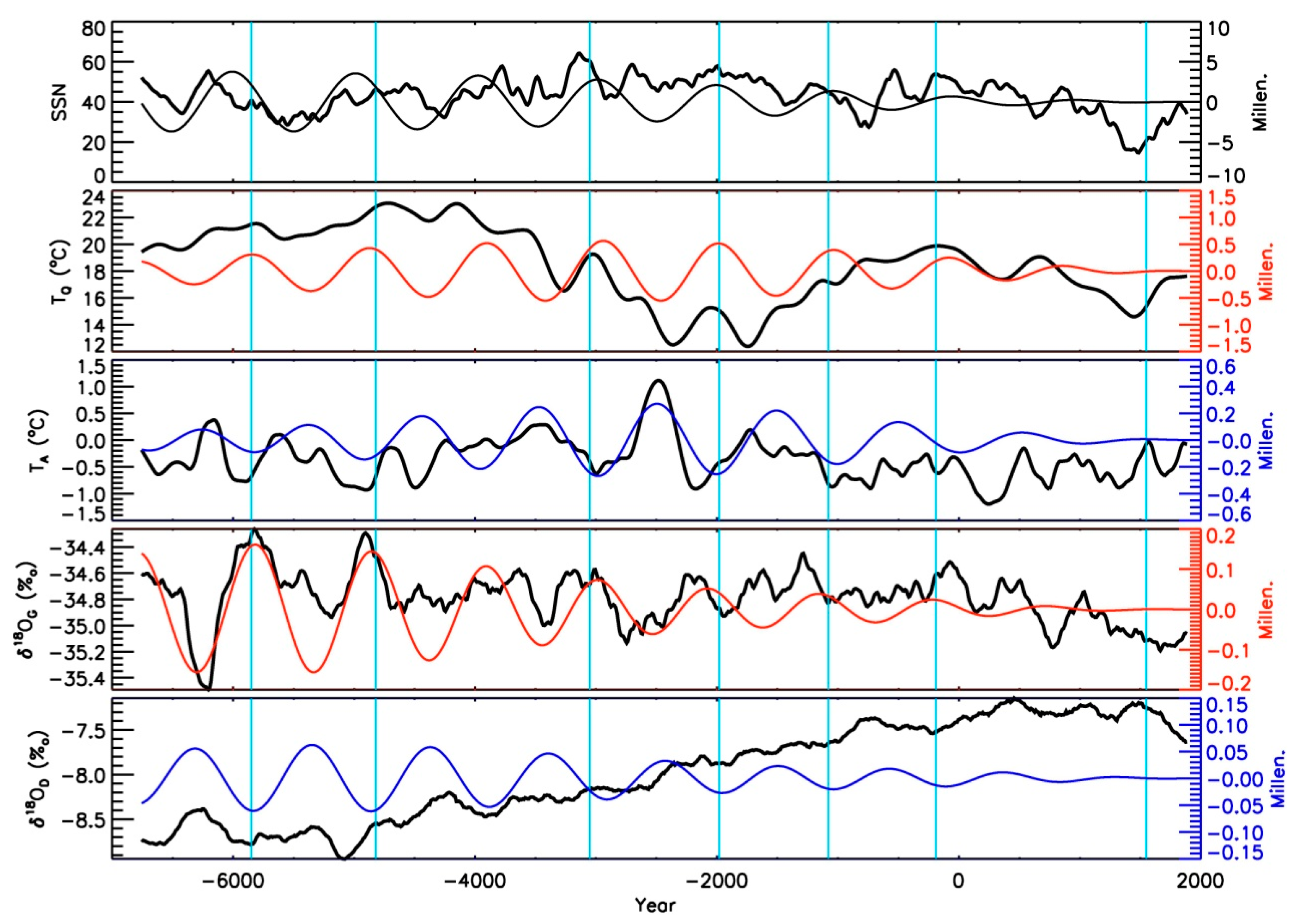
3.3. Millennial Oscillations and Solar Modulation
4. Summary and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Haigh, J.D. The impact of solar variability on climate. Science 1996, 272, 981–985. [Google Scholar] [CrossRef] [PubMed]
- Gray, L.J.; Beer, J.; Geller, M.; Geller, M.; Haigh, J.D.; Lockwood, M.; Matthes, K.; Cubasch, U.; Fleitmann, D.; Harrison, G.; et al. Solar influences on climate. Rev. Geophys. 2010, 48, RG4001. [Google Scholar] [CrossRef]
- Soon, W.; Connolly, R.; Connolly, M. Re-evaluating the role of solar variability on Northern Hemisphere temperature trends since the 19th Century. Earth Sci. Rev. 2015, 150, 409–452. [Google Scholar] [CrossRef]
- Eddy, J.A. The Maunder minimum. Science 1976, 192, 1189–1202. [Google Scholar] [CrossRef] [PubMed]
- Reid, G.C. Influence of solar variability on global sea surface temperatures. Nature 1987, 329, 142–143. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lassen, K. Length of the solar cycle: An indicator of solar activity closely associated with climate. Science 1991, 254, 698–700. [Google Scholar] [CrossRef]
- Ziskin, S.; Shaviv, N.J. Quantifying the role of solar radiative forcing over the 20th century. Adv. Space Res. 2012, 50, 762–776. [Google Scholar] [CrossRef]
- Wu, C.J.; Usoskin, I.G.; Krivova, N.; Kovaltsov, G.A.; Baroni, M.; Bard, E.; Solanki, S.K. Solar activity over nine millennia: A consistent multi-proxy reconstruction. Astron. Astrophys. 2018, 615, A93. [Google Scholar] [CrossRef]
- Petit, J.R.; Jouzel, J.; Raynaud, D.; Barkov, N.I.; Barnola, J.M.; Basile, I.; Bender, M.; Chappellaz, J.; Davis, J.; Delaygue, G.; et al. Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica. Nature 1999, 399, 429–436. [Google Scholar] [CrossRef]
- Hou, J.; Huang, Y.; Zhao, J.; Liu, Z.; Colman, S.; An, Z. Large Holocene summer temperature oscillations and impact on the peopling of the northeastern Tibetan Plateau. Geophys. Res. Lett. 2016, 43, 1323–1330. [Google Scholar] [CrossRef]
- Stuiver, M.; Grootes, P.M. GISP2 oxygen isotope ratios. Quat. Res. 2000, 53, 277–284. [Google Scholar] [CrossRef]
- Wang, Y.J.; Cheng, H.; Edwards, R.L.; He, Y.Q.; Kong, X.G.; An, Z.S.; Wu, J.Y.; Kelly, M.J.; Dykoski, C.A.; Li, X.D. The Holocene Asian monsoon: Links to solar changes and north Atlantic climate. Science 2005, 308, 854–857. [Google Scholar] [CrossRef] [PubMed]
- Lomb, N.R. Least-squares frequency analysis of unequally spaced data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in astronomical time series analysis. II. Statistical aspects of spectral analysis of unevenly spaced data. Astrophys. J. 1982, 263, 835–853. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlin. Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Suess, H.E. The radio carbon recordin tree rings of the last 8000 years. Radiocarbon 1980, 22, 200–209. [Google Scholar] [CrossRef]
- Abreu, J.A.; Beer, J.; Ferriz-Mas, A.; McCracken, K.G.; Steinhilber, F. Is there a planetary influence on solar activity? Astron. Astrophys. 2012, 584, A88. [Google Scholar] [CrossRef]
- McCracken, K.G.; Beer, J.; Steinhilber, F.; Abreu, J. A phenomenological study of the cosmic ray variations over the past 9400 years, and their implications regarding solar activity and the solar dynamo. Sol. Phys. 2013, 286, 609–627. [Google Scholar] [CrossRef]
- McCracken, K.G.; Beer, J.; Steinhilber, F. Evidence for planetary forcing of the cosmic ray intensity and solar activity throughout the past 9400 years. Sol. Phys. 2014, 289, 3207–3229. [Google Scholar] [CrossRef]
- Zhao, X.H.; Feng, X.S. Correlation between solar activity and the local temperature of Antarctica during the past 11,000 years. J. Atmos. Sol. Terr. Phys. 2015, 122, 26–33. [Google Scholar] [CrossRef]
- Ebisuzaki, W. A method to estimate the statistical significance of a correlation when the data are serially correlated. J. Clim. 1995, 10, 2147–2153. [Google Scholar] [CrossRef]
- Macias-Fauria, M.; Grinsted, A.; Helama, S.; Holopainen, J. Persistence matters: Estimation of the statistical significance of paleoclimatic reconstruction statistics from autocorrelated time series. Dendrochronologia 2012, 30, 179–187. [Google Scholar] [CrossRef]
- Eroglu, D.; McRobie, F.H.; Ozken, I.; Stemler, T.; Wyrwoll, K.H.; Breitenbach, S.F.M.; Marwan, N.; Kurths, J. See-saw relationship of the Holocene East Asian-Australian summer monsoon. Nat. Commun. 2016, 7, 12929. [Google Scholar] [CrossRef] [PubMed]
- Broecker, W.S. Paleocean circulation during the last deglaciation: A bipolar seesaw? Paleoceanography 1998, 13, 119–121. [Google Scholar] [CrossRef]
- Stocker, T.F. Past and future reorganizations in the climate system. Quat. Sci. Rev. 2000, 19, 301–319. [Google Scholar] [CrossRef]
- Blunier, T.; Brook, E.J. Timing of millennial-scale climate change in Antarctica and Greenland during the last glacial period. Science 2001, 291, 109–112. [Google Scholar] [CrossRef]
- Denton, G.H.; Broecker, W.S. Wobbly ocean conveyor circulation during the Holocene? Quat. Sci. Rev. 2008, 27, 1939–1950. [Google Scholar] [CrossRef]
- Swingedouw, D.; Terray, L.; Cassou, C.; Voldoire, A.; Salas-Mélia, D.; Servonnat, J. Natural forcing of climate during the last millennium: Fingerprint of solar activity. Clim. Dyn. 2011, 36, 1349–1364. [Google Scholar] [CrossRef]
- Rella, S.F.; Uchida, M. A southern ocean trigger for northwest Pacific ventilation during the Holocene? Sci. Rep. 2014, 4, 4046. [Google Scholar] [CrossRef]
- WAIS Divide Project Members. Precise interpolar phasing of abrupt climate change during the last ice age. Nature 2015, 520, 661–665. [Google Scholar] [CrossRef] [PubMed]
- Stocker, T.F.; Johnsen, S.J. A minimum thermodynamic model for the bipolar seesaw. Paleoceanography 2003, 18, 1087. [Google Scholar] [CrossRef]
- Li, Z.; Knipp, D.; Wang, W.; Sheng, C.; Qian, L.; Flynn, S. A comparison study of NO cooling between TIMED/SABER measurements and TIEGCM simulations. J. Geophys. Res. Space Phys. 2018, 123, 8714–8729. [Google Scholar] [CrossRef]
- Li, Z.; Knipp, D.; Wang, W. Understanding the behaviors of thermospheric Nitric Oxide cooling during the 15 May 2005 geomagnetic storm. J. Geophys. Res. Space Phys. 2019, 124, 2113–2126. [Google Scholar] [CrossRef]
- Li, Z.; Knipp, D.; Wang, W.; Shi, Y.; Wang, M.; Su, Y.; Li, J. An EOFs study of thermospheric nitric Oxide flux based on TIEGCM simulations. J. Geophys. Res. Space Phys. 2019, 124, 9695–9708. [Google Scholar] [CrossRef]
- White, W.B.; Liu, Z. Resonant excitation of the quasi-decadal oscillation by the 11-year signal in the Sun’s irradiance. J. Geophys. Res. Ocean. 2008, 113, C01002. [Google Scholar] [CrossRef]
- Meehl, G.A.; Arblaster, J.M.; Matthes, K.; Sassi, F.; van Loon, H. Amplifying the Pacific climate system response to a small 11-yr solar cycle forcing. Science 2009, 325, 1114–1118. [Google Scholar] [CrossRef] [PubMed]
- Wunsch, C. Greenland-Antarctic phase relations and millennial time-scale climate fluctuations in the Greenland ice-cores. Quat. Sci. Rev. 2003, 22, 1631–1646. [Google Scholar] [CrossRef]
| Climate Indices | TQ | TA | δ18OG | δ18OD |
|---|---|---|---|---|
| CC | 0.76 | −0.74 | 0.58 | −0.67 |
| Significance | 0.08 | 0.11 | 0.18 | 0.15 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Soon, W.; Velasco Herrera, V.M. Evidence for Solar Modulation on the Millennial-Scale Climate Change of Earth. Universe 2020, 6, 153. https://doi.org/10.3390/universe6090153
Zhao X, Soon W, Velasco Herrera VM. Evidence for Solar Modulation on the Millennial-Scale Climate Change of Earth. Universe. 2020; 6(9):153. https://doi.org/10.3390/universe6090153
Chicago/Turabian StyleZhao, Xinhua, Willie Soon, and Victor M. Velasco Herrera. 2020. "Evidence for Solar Modulation on the Millennial-Scale Climate Change of Earth" Universe 6, no. 9: 153. https://doi.org/10.3390/universe6090153
APA StyleZhao, X., Soon, W., & Velasco Herrera, V. M. (2020). Evidence for Solar Modulation on the Millennial-Scale Climate Change of Earth. Universe, 6(9), 153. https://doi.org/10.3390/universe6090153





