Possible Wormhole Candidates in Active Galactic Nuclei
Abstract
1. Introduction
2. Radiative Efficiency of AGNs with WHs
3. Estimations of Radiative Efficiency
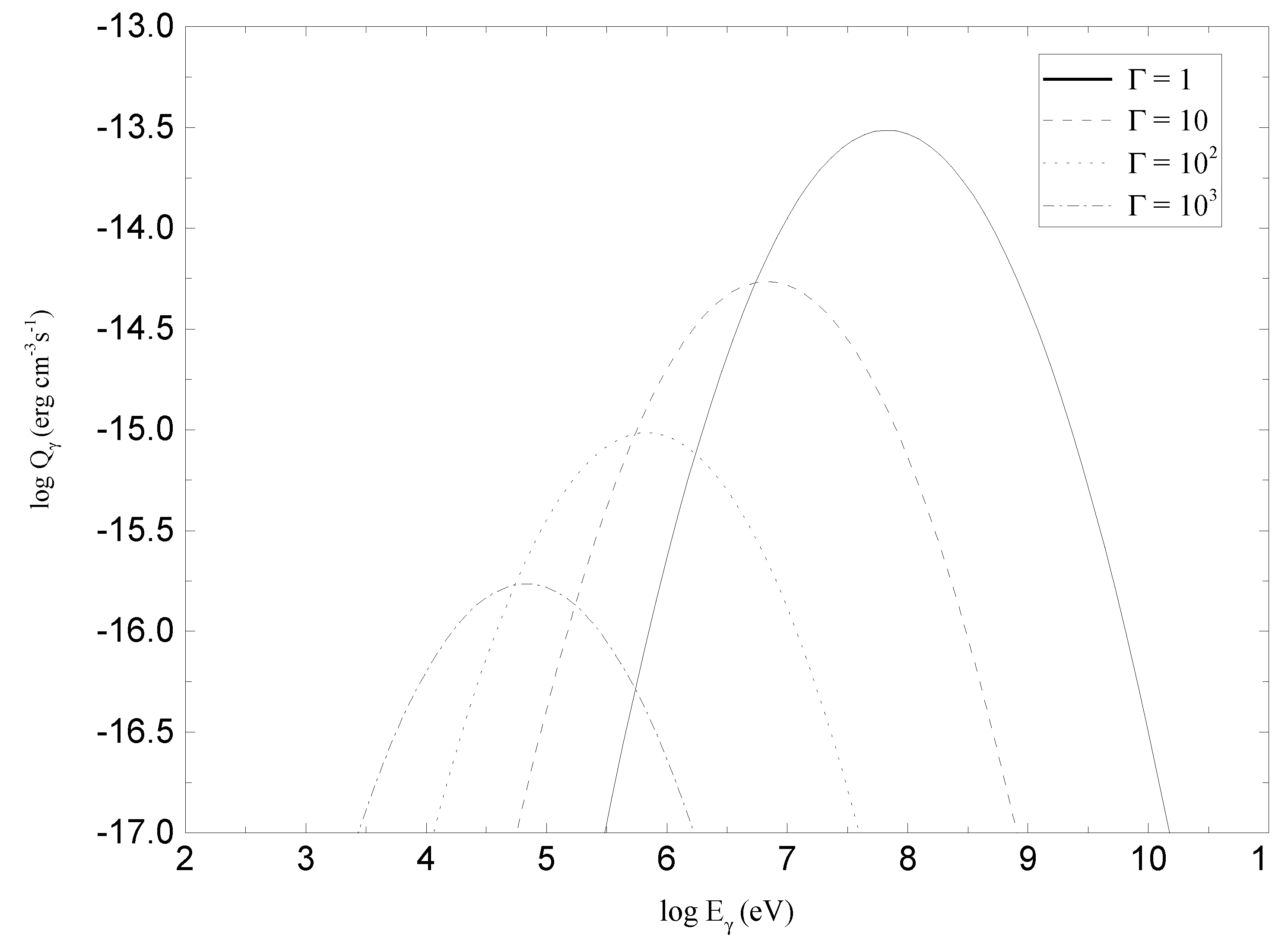
4. High Energy Photons from Accretion on a Schwarzschild-like Wormholes
- the plasma layer is heated (only) by the collision of the fluxes; and,
- the magnetic field, the interaction of the infalling matter with the outcoming radiation, and the backreaction of the spheres on the metric of the wormhole are negligible.
5. Conclusions
- Eight AGNs may contain WH instead of SMBH judging from their radiative efficiency.
- A peak at about (0.1–10) MeV range may appear in the spectrum of an AGN with WH. This peak can be quite high, comparable to the observed radiation of NLS1.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kardashev, N.S.; Novikov, I.D.; Shatskiy, A.A. Astrophysics of Wormholes. Int. J. Mod. Phys. 2007, 16, 909–926. [Google Scholar] [CrossRef]
- Bambi, C. Can the supermassive objects at the centers of galaxies be traversable wormholes? The first test of strong gravity for mm/sub-mm very long baseline interferometry facilities. Phys. Rev. D 2013, 87, 107501. [Google Scholar] [CrossRef]
- Li, Z.; Bambi, C. Distinguishing black holes and wormholes with orbiting hot spots. Phys. Rev. D 2014, 90, 024071. [Google Scholar] [CrossRef]
- Zhou, M.; Cardenas-Avendano, A.; Bambi, C.; Kleihaus, B.; Kunz, J. Search for astrophysical rotating Ellis wormholes with x-ray reflection spectroscopy. Phys. Rev. D 2016, 94, 024036. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation. Astrophys. J. 1972, 178, 347–370. [Google Scholar] [CrossRef]
- Thorne, K.S. Disk-Accretion onto a Black Hole. II. Evolution of the Hole. Astrophys. J. 1974, 191, 507–520. [Google Scholar] [CrossRef]
- Harko, T.; Kovács, Z.; Lobo, F.S.N. Thin accretion disks in stationary axisymmetric wormhole spacetimes. Phys. Rev. D 2009, 79, 064001. [Google Scholar] [CrossRef]
- Lobo, F.S.N. Wormholes, Warp Drives and Energy Conditions. Fundam. Theor. Phys. 2017, 189. [Google Scholar] [CrossRef]
- Teo, E. Rotating traversable wormholes. Phys. Rev. D 1998, 58, 024014. [Google Scholar] [CrossRef]
- Marin, F. Are there reliable methods to estimate the nuclear orientation of Seyfert galaxies? Mon. Not. R. Astron. Soc. 2016, 460, 3679–3705. [Google Scholar] [CrossRef]
- Du, P.; Hu, C.; Lu, K.X.; Wang, F.; Qiu, J.; Li, Y.R.; Bai, J.M.; Kaspi, S.; Netzer, H.; Wang, J.M.; et al. Supermassive Black Holes with High Accretion Rates in Active Galactic Nuclei. I. First Results from a New Reverberation Mapping Campaign. Astrophys. J. 2014, 782, 45. [Google Scholar] [CrossRef]
- Trakhtenbrot, B. The Most Massive Active Black Holes at z ~ 1.5–3.5 have High Spins and Radiative Efficiencies. Astrophys. J. Lett. 2014, 789, L9. [Google Scholar] [CrossRef]
- Davis, S.W.; Laor, A. The Radiative Efficiency of Accretion Flows in Individual Active Galactic Nuclei. Astrophys. J. 2011, 728, 98. [Google Scholar] [CrossRef]
- Raimundo, S.I.; Fabian, A.C.; Vasudevan, R.V.; Gandhi, P.; Wu, J. Can we measure the accretion efficiency of active galactic nuclei? Mon. Not. R. Astron. Soc. 2012, 419, 2529–2544. [Google Scholar] [CrossRef][Green Version]
- Lawther, D.; Vestergaard, M.; Raimundo, S.; Grupe, D. A catalogue of optical to X-ray spectral energy distributions of z ≈ 2 quasars observed with Swift—I. First results. Mon. Not. R. Astron. Soc. 2017, 467, 4674–4710. [Google Scholar] [CrossRef]
- Hopkins, P.F.; Richards, G.T.; Hernquist, L. An Observational Determination of the Bolometric Quasar Luminosity Function. Astrophys. J. 2007, 654, 731–753. [Google Scholar] [CrossRef]
- Krasnikov, S. Schwarzschild-like wormholes as accelerators. Phys. Rev. D 2018, 98, 104048. [Google Scholar] [CrossRef]
- Paliya, V.S.; Parker, M.L.; Jiang, J.; Fabian, A.C.; Brenneman, L.; Ajello, M.; Hartmann, D. General Physical Properties of Gamma-Ray-emitting Narrow-line Seyfert 1 Galaxies. Astrophys. J. 2019, 872, 169. [Google Scholar] [CrossRef]
- Kynoch, D.; Landt, H.; Ward, M.J.; Done, C.; Boisson, C.; Baloković, M.; Angelakis, E.; Myserlis, I. The relativistic jet of the γ-ray emitting narrow-line Seyfert 1 galaxy PKS J1222+0413. Mon. Not. R. Astron. Soc. 2019, 487, 181–197. [Google Scholar] [CrossRef]
- Madejski, G.G.; Sikora, M. Gamma-Ray Observations of Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 2016, 54, 725–760. [Google Scholar] [CrossRef]
- Baghmanyan, V.; Sahakyan, N. X-ray and γ-ray emissions from NLSy1 galaxies. Int. J. Mod. Phys. 2018, 27, 1844001. [Google Scholar] [CrossRef]
- Hu, C.; Wang, J.M.; Ho, L.C.; Chen, Y.M.; Zhang, H.T.; Bian, W.H.; Xue, S.J. A Systematic Analysis of Fe II Emission in Quasars: Evidence for Inflow to the Central Black Hole. Astrophys. J. 2008, 687, 78–96. [Google Scholar] [CrossRef]
- Bian, W.H.; Zhao, Y.H. Accretion Rates and the Accretion Efficiency in AGNs. Publ. Astron. Soc. Jpn. 2003, 55, 599–603. [Google Scholar] [CrossRef]
- Collin, S.; Kawaguchi, T. Super-Eddington accretion rates in Narrow Line Seyfert 1 galaxies. Astron. Astrophys. 2004, 426, 797–808. [Google Scholar] [CrossRef]
- Shankar, F.; Weinberg, D.H.; Miralda-Escudé, J. Accretion-driven evolution of black holes: Eddington ratios, duty cycles and active galaxy fractions. Mon. Not. R. Astron. Soc. 2013, 428, 421–446. [Google Scholar] [CrossRef]
- Aversa, R.; Lapi, A.; de Zotti, G.; Shankar, F.; Danese, L. Black Hole and Galaxy Coevolution from Continuity Equation and Abundance Matching. Astrophys. J. 2015, 810, 74. [Google Scholar] [CrossRef]
- Tucci, M.; Volonteri, M. Constraining supermassive black hole evolution through the continuity equation. Astron. Astrophys. 2017, 600, A64. [Google Scholar] [CrossRef]
- Marscher, A.P.; Vestrand, W.T.; Scott, J.S. Neutrino, gamma-ray, electron, and positron production in an ultrarelativistic plasma. Astrophys. J. 1980, 241, 1166–1174. [Google Scholar] [CrossRef]
- Kolykhalov, P.I.; Syunyaev, R.A. Gamma emission during spherically symmetric accretion onto black holes in binary stellar systems. Sov. Astron. 1979, 23, 189–192. [Google Scholar]
- Dermer, C.D. Binary Collision Rates of Relativistic Thermal Plasmas. II. Spectra. Astrophys. J. 1986, 307, 47–59. [Google Scholar] [CrossRef]
| Object | i | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NGC 7213 | 21 | 44.3 | ||||||||
| PG 1302-102 | 32 | 46.33 | ||||||||
| Mrk 877 | 20 | 45.33 | ||||||||
| Mrk 6 | 26 | 44.56 | ||||||||
| UGC 3973 | 19 | 44.31 | ||||||||
| Mrk 1018 | 8.60 | 45 | 44.90 | 0.013 | 0.785 | 0.913 | 0.629 | 0.633 | 0.517 | 1.070 |
| Mrk 1383 | 30 | 45.78 | ||||||||
| Mrk 876 | 27 | 45.81 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piotrovich, M.; Krasnikov, S.; Buliga, S.; Natsvlishvili, T. Possible Wormhole Candidates in Active Galactic Nuclei. Universe 2020, 6, 120. https://doi.org/10.3390/universe6080120
Piotrovich M, Krasnikov S, Buliga S, Natsvlishvili T. Possible Wormhole Candidates in Active Galactic Nuclei. Universe. 2020; 6(8):120. https://doi.org/10.3390/universe6080120
Chicago/Turabian StylePiotrovich, Mikhail, Serguei Krasnikov, Stanislava Buliga, and Tinatin Natsvlishvili. 2020. "Possible Wormhole Candidates in Active Galactic Nuclei" Universe 6, no. 8: 120. https://doi.org/10.3390/universe6080120
APA StylePiotrovich, M., Krasnikov, S., Buliga, S., & Natsvlishvili, T. (2020). Possible Wormhole Candidates in Active Galactic Nuclei. Universe, 6(8), 120. https://doi.org/10.3390/universe6080120





